Introduction

Removal of contaminants such as arsenic (As) from wastewater by adsorption mechanisms remains the most effective method (Elizalde-González et al. 2001). Most studies in the field of adsorption for the removal of heavy metals from water have mainly focused on the use of AC, activated alumina, sand impregnated with iron, polymer resins, hydrous ferric oxide and natural ores (Addo Ntim and Mitra 2011). Although AC has been found to be more effective relative to the other adsorbents mentioned above, especially for the removal of heavy metals from aqueous solutions, with percentage removal ranging from 82 to 96% (Ribeiro et al. 2006), this technique may not be adequate when it comes to a heavy metal like As(III) which is known to be highly soluble in water. Arsenic exists in two different oxidation states (1) arsenite, As(III) and (2) arsenate, As(V). As(III) is different from As(V) in a number of ways. Firstly, difficulties arise when it comes to the removal of As(III) from wastewater compared to arsenate As(V) due to its high solubility in the aqueous environment, hence As(III) which is the most toxic is also the most difficult to remove from water (Pattanayak et al. 2000). Secondly, whereas As(V) is mostly removed by outer-sphere complexation, i.e., by electrostatic attraction (Cheng et al. 2016), As(III) can be removed by inner-sphere complexation, which is a covalent bonding as demonstrated in this study.

On the other hand, the long-term effects of drinking water contaminated with arsenic include cancer of the skin, lung, bladder, and kidney, skin thickening, neurological disorders, muscular weakness and nausea (Jain and Ali 2000; WHO 1981). This has led to numerous studies regarding the improvement of AC by magnetic modification to increase its capacity to remove heavy metal contaminants. The MAC adsorbents exhibited magnetic properties with greater efficiency for the adsorption of contaminants from aqueous solution (Xu et al. 2010). Whereas palm kernel shells were used in the production of AC due to its high carbon content and low organic content (Daud and Ali 2004), while at the same time high quality of AC can be synthesized from PKS waste (Adhoum and Monser 2002; Budinova et al. 2006; Hussein et al. 1996).

One major advantage of the MAC is that it exhibits magnetic characteristics, in addition to having demonstrated to be effective for adsorption in dilute solutions, while its high specific surface area due to the presence of microporous structure results in greater capacity for the adsorption of heavy metals (Nakahira et al. 2006). So far, magnetization has been identified as being potentially important in improving the sorption characteristics of organic adsorbents with well-developed structures, i.e., of woody feedstock such as PKS (Trakal et al. 2016). However, previous studies on the removal of As(III) from wastewater employed the use of biochar made from empty fruit bunch and rice husks (Samsuri et al. 2013), which are fibrous in nature, unlike the PKS feedstock used in this study, which is a woody feedstock. Moreover, they used biochar which is a different material. Another problem with their study was that they did not carry out a desorption test to ascertain the stability of the Fe-coated organic adsorbents. Further, their study was on competitive adsorption between As(III) and As(V). Similarly, in the paper by Payne and Abdel-Fattah (2005) using Fe-coated AC for the removal of As(III) and As(V) from water, they relied on commercially procured AC, which had a poorly developed structure and hence was only able to remove 60% As(III) from waste water unlike in this study where 95% removal was achieved by using MPKS which has a well-developed structure. In addition, they did not look at the magnetic properties of the Fe-coated AC.

Therefore, the influence of the MAC on the removal of As(III) from waste water has not been completely elucidated. The objectives of this study are: (1) to prepare magnetic activated carbon for the removal of arsenic from water; (2) to optimize the parameters for As(III) sorption using Box–Behnken design; (3) to study the sorption–desorption of As(III) onto the prepared magnetic activated carbon.

Experimental

Chemicals and reagents

Phosphoric acid (H3PO4, 85 wt%, Merck, Germany) was used to pretreat and impregnate the raw materials. The chemical reagents for the preparation of magnetic activated carbon were of three kinds: (1) iron (III) chloride (>96%): Sigma-Aldrich; (2) iron (II) sulfate (99.5%), Qrec; (3) sodium hydroxide, Merck Germany. A 1000 ppm stock solution of arsenite, As(III), was prepared in double distilled water from 0.05 M sodium arsenite (NaAsO2) prepared by Fluka. Hydrochloric acid (HCl) and sodium hydroxide (NaOH) were used to adjust the solution pH of As(III).

Experimental methods

Material development and characterization

The raw PKSs (100 g) used in this study were obtained from a palm oil estate located at Jalan Sawah, Pekan Nenas, Johor Bahru, Malaysia. Sample pretreatment was carried out by weighing out a 50-g portion of the raw PKS, which was ground and sieved to particle sizes in the range of 75–250 μm, then soaked and impregnated with 10 mL of 30 wt% of phosphoric acid, H3PO4, at room temperature with PKS-to-acid ratio of 1:1. The sample was left impregnated for 24 h, and afterwards it was washed with distilled water and dried at room temperature.

A 10-g portion of the pre-treated PKSs was transferred into five conical flasks containing different concentrations of H3PO4, i.e., 10, 20, 30, 40 and 50% wt/wt, respectively. Similarly, the pre-treated PKS was treated again using dilute acid (10, 20 and 30% wt/wt H3PO4). This was done to determine the appropriate surface area at which if the surface area obtained by using dilute acid was high, then the use of concentrated acid can be reduced and the experimental costs will be less. This ratio (1:1) implied that 10 g of the raw PKSs was soaked in 10 g of H3PO4 for 24 h. The excess acid was then filtered and the soaked PKSs were placed in a muffle furnace and heated at 200 °C for 30 min to initiate the carbonization process.

Subsequently, the temperature of the furnace was increased to the range of 400–550 °C and held for 2 h followed by cooling to room temperature. Afterwards, the samples were thoroughly washed and rinsed using vacuum filtration with hot distilled water to remove all the excess acid until the pH of the filtrate was approximately 7. The samples were then dried in the oven at a temperature of 110 °C for 24 h. The AC samples were then stored in desiccators for further characterization and adsorption studies. The preparation of the MPKSF was achieved by utilizing a suspension of ferric chloride/ferrous sulfate. The characterization experiments were conducted on the MPKSF by Fourier transform infrared spectroscopy (FTIR), X-ray diffraction (XRD), particle size analysis, nitrogen adsorption analysis, scanning electron microscopy (SEM), field emission scanning electron microscopy (FESEM), energy dispersive X-ray spectrometry (EDX) and the point of zero charge (pHpzc) was also determined as part of the characterization. The magnetic saturation of the MAC sample was characterized using vibrating sample magnetometer (VSM).

Batch experimental procedure and testing methods

Batch experiments were carried out by grinding the MPKSF into fine powder of 75 μm particle sizes. The stock solution was prepared by diluting 0.05 M of sodium arsenite (NaAsO2) with distilled water up to a concentration of 1000 ppm to give a 1000 ppm arsenite (As(III)) stock solution. The pH of the solution was then adjusted using hydrochloric acid (HCl) until it reached a pH of 7. A 0.05–0.30 g portion of the powdered MPKSF was placed into a conical flask together with 200 mL arsenite solution. The solution was then shaken for 24 h at different temperatures ranging from 10 to 40 °C. The contact time in the shaker was also varied ranging from 5 to 720 min. The initial concentration of the arsenite solution was varied ranging from 5 to 100 μg L−1. This was done to mimic the drinking water standard. The preliminary experiment was conducted at an equilibrium time of 180 min. After that, the suspension was filtered through 0.45-μm pore size membrane filter.

The preliminary study on the adsorption of As(III) on MPKSF, was divided into 6 factors and are described briefly namely (1) effect of contact time, which was found to be 180 min and established to be the time taken to reach adsorption–desorption equilibrium; (2) effect of initial As(III) concentration, which was found to be 5–70 μg L−1 with percentage removal of 87.58–89.42%; (3) effect of adsorbent dosage, was found to be 0.3 g, which resulted in an increase in percentage removal of As(III) from 42.17 to 96.58%. This was due to a higher dose of adsorbent utilized which provides greater proportion of adsorption sites for As(III) to bind on the MPKSF surface (Yao et al. 2014); (4) effect of pH, in this case, the effect of the initial solution pH in the range of 6–8 on the adsorption of As(III) onto the MPKSF, indicated that the removal of As(III) was better under pH 6 and 7, (5) effect of temperature, in this case, a temperature of 30 °C was considered preferable for the adsorption of the As(III) onto the MPKSF.

The residual arsenic solution was analyzed using graphite furnace atomic absorption spectrometry (GFAAS). And the same procedures were repeated using a real water waste sample from Skudai River, Johor Bahru Malaysia, spiked with arsenite to analyze the percentage of arsenite removal using MPKSF.

Determination of pHpzc (point of zero charge) of the samples

The pHpzc of both PKSAC and MPKSF was determined. A 50-mL solution of 0.01 M NaCl was placed in a closed Erlenmeyer flask. The pH of the solution was adjusted to achieve a suspension pH of between 2 and 12 by adding 0.1 M HCl or 0.1 M NaOH solutions in ten conical flasks. Approximately 0.15 g each of the PKSAC and MPKSF were added and the final pH was measured after 48 h. The pH of each solution recorded was plotted. The intersection of pHinitial and pHfinal of the solution was then taken as the pHpzc.

Desorption procedure of magnetic activated carbon (MPKSF)

The optimum amount of MPKSF loaded with arsenite (48.08 μg g−1) obtained after the adsorption process was then added into a 50 mL of distilled water in a centrifuge tube. The solution was shaken at 150 rpm and then agitated at specific time intervals for up to 48 h. The solution was then centrifuged and the supernatant was collected for further analysis to examine the concentration of As(III) desorbed from the MPKSF. The desorption procedure was repeated three times and the MPKSF adsorbent was reserved for further analysis.

Graphite furnace atomic absorption spectrometry (GFAAS)

The detection and the concentration of arsenite were conducted by a graphite furnace atomic absorption spectrometry (GFAAS). The samples were analyzed in triplicates, to obtain the optimum result of 10–40 μg L−1. A small amount of the sample which was in the range of 20–100 μL was placed into the graphite tube manually. Further, the arsenite samples were acidified with nitric acid to a pH of less than 2. Upon injection of the samples into the graphite tube, they are vaporized. Subsequently, the amount of light energy absorbed in the vapor was considered to be proportional to the atomic concentration.

Box–Behnken design

In this study, the Box–Behnken design was used to optimize the number of experiments to be conducted with the aim of determining the probable interactions between the parameters under study and their influence on the adsorption of As(III) onto the MPKSF. Further characteristics of the Box–Behnken design has been described elsewhere (Kumar et al. 2008).

In Table 1, the experimental parameters and a 3-level 5-factorial Box–Behnken experimental design are presented. This was applied to examine and validate the adsorption system parameters influencing the adsorption of As(III) onto the MPKSF. Contact time (5–720 min), pH (6–8), adsorbent dose (0.05–0.30 g), initial As(III) concentration (5–100 µg L−1), temperature (20–40 °C) represent the variable input parameters. The factor levels (3) were coded as (−1 = low, 0 = medium level or central point, and +1 = high level). Response surface methodology (RSM) was applied to the experimental data using the Design Expert statistical software version 7.1.6 by Stat-Ease, Inc., Minneapolis, USA.

Table 1 Independent parameters and their levels used for Box–Behnken design
Full size table

The regression equation of the designed experiment was obtained by applying four models namely linear, interactive, quadratic and cubic models which were fitted to the experimental data obtained from the design system.

To select the best model, i.e., after the responses have been recorded, the data were analyzed using three different tests in order to decide the adequacy of the models stated above to represent the adsorption process of MPKSF–As. These validation tests are the sequential model sum of squares (F test), lack-of-fit test and the model summary statistics. Further, a quadratic polynomial was used to explain the relationship between the parameters and As(III) residual concentration (%).

The second-order polynomial is represented by Eq. (1):

$$\varUpsilon \, = \beta_{0} + \sum\limits_{i - 1}^{k} {\beta_{i} x_{i} } + \sum\limits_{i - 1}^{k} {\beta_{ii} x_{i}^{2} } + \sum\limits_{{1s_{i} s_{j} }}^{k} {\beta_{ij} x_{i} x_{j} } + \varepsilon ,$$
(1)

where the terms have their established meanings (Kunamneni and Singh 2005; Shehzad et al. 2016). A design of 46 tests was formulated.

Results and discussion

Characterization of adsorbents

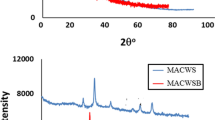
The characterization results (detailed characterization of the adsorbent (s) has been described elsewhere, Anyika et al. 2017) revealed that the MPKSF presented better characteristics and was therefore selected as the sole adsorbent for the adsorption studies. It presented a higher BET surface area of 257 m2 g−1, higher pore volume of 0.1124 cc g−1 and higher magnetic properties with a magnetic saturation of 49.55 emu g−1. The FTIR spectrum of the MPKSF exhibited intense OH bending at 1629 cm−1 which can be attributed to the presence of oxygen in the samples, while the absorption bands at 1093 and 579 cm−1 indicated the presence of C–O stretching and metal–oxygen (M–O) bands due to the interaction of iron and oxygen. To illustrate that the MPKSF acquired magnetic properties, the XRD data were analyzed. The MPKSF exhibited the presence of Fe3O4 at 2θ 30.75°, 35.95°, 57.35°, 63.20° from the XRD diffractogram. Similarly, three peaks at 2θ 19.30°, 43.45°, 54.10° and a peak at 2θ 24.40° which can be assigned to γ-Fe2O3 and α-Fe2O3, respectively, were detected.

The point of zero charge of the MPKSF was determined to explain the surface charge phenomena as well as the magnetic properties of the MPKSF. With respect to the surface charge, the point of zero charge of MPKSF occurred at pH 5.94. Since As(III) is positively charged, it is critical for the surface of the MPKSF to be negatively charged in order for the adsorption process to occur. As the solution pH is higher than 5.94, the surface of the MPKSF exhibits greater formation of hydroxide ions. However, at pH 6 and 7, the MPKSF demonstrated greater adsorption compared to pH 8. This was presumed to have resulted from the formation of As(III) precipitate at a higher pH hence reducing the adsorption efficiency. Additionally, at higher pH, As(III) has the potential to be oxidized to As(V), which may significantly reduce the adsorption of As(III) onto the MPKSF (Vance 2002). In Table 2, the initial pH and final pH of the reaction solutions for both adsorbent samples, PKSAC and MPKSF are presented.

Table 2 Initial and final pH value of PKSAC and MPKSF reaction solutions
Full size table

In Fig. 1a, b, a plot of pHfinal versus pHinitial for adsorbent PKSAC and MPKSF is presented. From the graph, the point of zero charge (pHpzc) of the sample represents the point where the plot of final pH versus initial pH intersects with the line at which the final pH equals to the initial pH. The blue line in both graphs indicates the line of pHfinal = pHinitial, while the red and green curves indicate the plots of pHfinal against pHinitial for PKSAC and MPKSF, respectively. Figure 1a shows that the pHpzc of PKSAC adsorbent was 3.94, which indicated that the sample was acidic, due to the impregnation of PKSAC using phosphoric acid (H3PO4). A suitable acid activation results in the production of high quality and high surface area AC (Yakout and Sharaf El-Deen 2016). In the adsorption process of As(III) onto MPKSF, at a pH above the point of zero charge of the MPKSF, i.e., pHpzc = 5.94, its surface becomes negatively charged, hence the protonated As(III) will have a greater affinity towards the MPKSF surface. Based on the Box–Behnken optimization, the optimum adsorption occurred at pH 6.55, which conformed to the aquatic environmental range of pH of 5–9 (Zou et al. 2016).

Fig. 1
figure 1

a Graph of pHfinal versus pHinitial for the adsorbent PKSAC suspension. b Graph of pHfinal versus pHinitial graph for the adsorbent MPKSF suspension

Full size image

As seen in Fig. 1b, the pHpzc value of MPKSF decreased its acidity to attain a pH of 5.94. This may be due to the iron oxide extracted from the ferric chloride/ferrous sulfate solution (FeOF) which was used in the production of MPKSF. To further illustrate that the MPKSF acquired magnetic properties, the hydration of Fe3O4 in aqueous solution resulted in the formation of α-Fe2O3 in an acidic condition as depicted by the reaction in Eq. (2). To illustrate that α-Fe2O3 was formed, previous studies have reported that the pHpzc for the untreated Fe3O4 was 6.5 while for γ-Fe2O3, it was at pH 5.9 (Milonjić et al. 1983) which indicate that the value of pH for both was nearly acidic even in the untreated condition. Further, Schwertmann and Murad (1983) had reported that α-Fe2O3 is predominantly formed at pH 7–8. In this study, it was demonstrated that upon impregnation of the PKSAC with FeOF, the acidity of the modified PKSAC (MPKSF) was reduced from 3.94 to 5.94 due to the formation of α-Fe2O3 from the reaction of Fe3O4 with water as represented by the Eq. (2) below:

$$2{\text{Fe}}_{3} {\text{O}}_{4} + {\text{H}}_{2} {\text{O}} \rightleftharpoons 3{\text{Fe}}_{2} {\text{O}}_{3} + 2{\text{H}}^{ + } + 2e^{ - } .$$
(2)

Box–Behnken statistical analysis

In Table 3, the most important parameters influencing the efficiency of adsorption of As(III) onto the MPKSF are represented by the letters: A, B, C, D and E, which represents the coded symbols for the respective factors: contact time, pH, adsorbent dosage, initial As(III) concentration and the temperature parameters. The combined effects of these factors were evaluated by performing experiments on the different combinations of these parameters.

Table 3 Experimental, actual and predicted values of Y for As(III) onto MPKSF
Full size table

The applied Box–Behnken model can be expressed as Eq. (3):

$$\begin{aligned} Y & = X_{0} + X_{1} A + X_{2} B + X_{3} C + X_{4} D + X_{5} E + X_{6} AB + X_{7} AC + X_{8} AD \\ & \quad + X_{9} AE + X_{10} BC + X_{11} BD + X_{12} BE + X_{13} CD + X_{14} CE + X_{15} DE + X_{16} A^{2} \\ & \quad + X_{17} B^{2} + X_{18} C^{2} + X_{19} D^{2} + X_{20} E^{2} , \\ \end{aligned}$$
(3)

where Y is the response, X 0 and X i depicted the global mean and other regression coefficients, respectively, while A, B, C, D and E are the coded symbols for the respective factors: contact time, pH, adsorbent dosage, initial As(III) concentration and the temperature parameters.

In Table 4, the statistical significance of the ratio of mean square variation due to regression and mean square residual error was tested using ANOVA. The results of the ANOVA indicated that the F values obtained for all the regressions were higher, which indicated that that majority of the variation in the response can be explained by the regression equation (Kumar et al. 2008). To determine whether the F is large enough to result in a statistical significance, the p value is examined. In this case, the model is considered to be statistically significant if the values under the column p > F value is <0.05 (Table 4) (Segurola et al. 1999). The ANOVA result for the MPKSF–As design system shows that the F value of 99.63 and its p value of <0.05 imply that the model was significant towards the response. Hence in this analysis, A, B, C, D, AC, AD, BC, CD, CE, C 2 and D 2 were the significant terms (Table 4). Besides, the ANOVA results for the MPKSF–As adsorption system showed that the F value is 99.63 (Table 4), indicating that the terms on the model are having a significant effect on the response.

Table 4 ANOVA for response surface quadratic model (Y)
Full size table

In Table 5, the adequacy of the model for the adsorption of As(III) onto the MPKSF was determined by three tests: (1) sequential model sum of squares; (2) lack-of-fit tests; (3) model summary statistics. The results showed that the p value for majority of the regression were <0.05. This implied that one of the terms in the regression equation was significantly correlated to the response variable. Further, the quadratic model was found to yield the best fit of R 2, Adjusted R 2 and predicted R 2 values of 0.9876, 0.9777 and 0.9505, respectively (Table 5). This also implied that the model does not explain 1% of the experimental results. Again, the high R 2 values in Table 5 and the p value of <0.0001 in Table 4, indicate that the quadratic polynomial was highly significant in explaining the relationship between the parameters and As(III) residual concentration (%).

Table 5 Adequacy of the model tested for MPKSF–As design system
Full size table

In Table 5, since the cubic model was established to be aliased, the quadratic model was therefore, chosen to be used for further analysis. Further, under the lack of fit (Table 5) the F value is not significant, with an F value of 4.79 and the p value of 0.0687. This shows that the lack of fit was not significant relative to the pure error. However, the lack-of-fit value indicates that there is 6.87% possibility that the error resulted from noise. Thus, the non-significant value for the lack of fit showed that the model was valid for further analysis. The final mathematical equation given by the Box–Behnken design in terms of actual values determined by Design Expert software is presented in Eq. (4).

Removal of As(III) (%) is given by:

$$\begin{aligned} Y & = 85.53 + 6.29 \times A - 2.78 \times B + 17.07 \times C + 0.43 \times D + 1.38 \times E \\ & \quad - 0.15 \times A \times B - 15.09 \times A \times C + 2.99 \times A \times D + 1.09 \times A \times E \\ & \quad + 14.20 \times B \times C + 0.27 \times B \times D - 1.21 \times B \times E + 20.04 \times C \times D \\ & \quad - 13.22 \times C \times E - 1.14 \times D \times E + 4.05 \times A^{2} + 1.01 \times B^{2} - 23.07 \times C^{2} \\ & \quad - 7.56 \times D^{2} + 4.89 \times E^{2} . \\ \end{aligned}$$
(4)

The equation implied that the constant with a value of 85.53 (see Eq. (4)) which is independent of any factor or interaction between factors suggests that the average removal of As(III) by MPKSF was 85.53%. Although this average removal is independent of the factors in the experimental setup (Kumar et al. 2008). In addition, Eq. (4) shows that pH and initial As(III) concentration had a positive effect while contact time, temperature and adsorbent dosage had a negative effect on the adsorption percentage of As(III) by MPKSF. In general, the positive sign represents the synergistic effect and the negative sign shows the antagonistic effect on the adsorption process (Tan et al. 2008). Further, the positive value of the model term indicates the effect that favors the optimization process while the negative model term value represents the inverse interaction between the parameters with the response.

Adsorption studies

In this study, the Box–Behnken design was used for the optimization of the selected parameters. Thus, the effects of these parameters on the MPKSF–As adsorption was shown by the response surface plots using two parameters simultaneously while the remaining parameters were set at their center points. However, it should be noted that since two parameters were used simultaneously, hence, only one set of the figures were presented per variable, while the rest were referred to accordingly under the affected variables, i.e., from “Effect of temperature” to “Effect of contact time”.

Effect of selected variables and response surface plots

Effect of pH

As seen in Fig. 2a–d, the combined effects of pH with contact time, initial As(III) concentration, adsorbent dosage and temperature, respectively, were presented. From the responses, the lower value of As(III) residual indicates a higher percentage of removal as given by Eq. (5):

Fig. 2
figure 2

3D response surface plots for As(III) removal vs a contact time (5–720 min) and the pH of the adsorbent MPKSF suspension (6–8); b initial As concentration (5–100 µg L−1) and pH (6–8); c adsorbent dose (0.05–0.3 g) and the pH of the adsorbent MPKSF suspension (6–8); d temperature (20–40 °C) and the pH of the adsorbent MPKSF suspension (6–8)

Full size image
$$\% {\text{ Removal}} = \left( {\frac{{C_{\text{initial}} - C_{\text{final}} }}{{C_{\text{initial}} }}} \right) \times 100\% .$$
(5)

Figure 2a shows the interaction between the effect of pH and the contact time of As(III) solution with the MPKSF adsorbent. The optimum removal of As occurred at pH 6.55 and at a contact time of 44.73 min with a removal percentage of 94.76% as the other parameters were set to their center points. Figure 2b illustrates the interaction of initial As(III) concentration with pH with the optimum removal of As(III) achieved at pH 6.55 at an initial As(III) concentration of 5 μg L−1 with a removal percentage of 99.10%.

Further, Fig. 2c, d shows the relationships between pH with adsorbent dosage and temperature, respectively. The excluded parameters for the respective response surface plots remain at their center points. Figure 2c shows that the removal of As(III) attained a maximum of 100% at pH 8 with an adsorbent dose of 0.3 g, while the other parameters were at their center points. In Fig. 2d, the relationship between pH and temperature gives an optimum removal of 91.89% at pH 6 and a temperature of 40 °C.

As reported previously, the pHpzc value for MPKSF was 5.94. At a pH above the pHpzc value, the As(III) cations are attracted to the negatively charged surface of MPKSF, which resulted from the deprotonation of MPKSF hydroxyl groups. Meanwhile, at pH lower than pHpzc, the adsorption of As(III) cations occurs only slightly because the surface of MPKSF is positively charged due to the protonation of MPKSF hydroxyl group. Thus, a solution pH of 6.55 provides the optimum condition for adsorption of MPKSF–As.

Effect of temperature

The experiment was conducted within a temperature range of 20–40 °C. As seen in Fig. 2d (refer to Fig. 2d in “Effect of pH” above for the effect of temperature and pH) and 3a–c, the relationships between temperature and pH, contact time, adsorbent dose and initial concentration, respectively, are presented. All the four response surface plots show that the removal of As(III) increases with temperature. Thus, the adsorption process could be described as an endothermic process, as the removal of As(III) is optimum at higher temperatures with efficiency of 91–100% removal.

Fig. 3
figure 3

3D response surface plots for As(III) removal vs a temperature (20–40 °C) and contact time (5–720 min); b temperature (20–40 °C) and adsorbent dosage (0.05–0.3 g); c temperature (20–40 °C) and initial As(III) concentration (5–100 µg L−1)

Full size image

Effect of adsorbent dosage

Refer to Fig. 2c under “Effect of pH” and Fig. 3b under “Effect of temperature” above and Fig. 4a, b under “Effect of contact time” below, for the combined effect of adsorbent (MPKSF) dose with pH, temperature, contact time and initial As(III) concentration, respectively. The results showed that the percentage removal increases as the adsorbent dose increases. The increase in the amount of adsorbent used can be attributed to the formation of a greater surface area and provides more available vacant sites for the adsorption of As(III) on MPKSF surface.

Fig. 4
figure 4

3D response surface plots for As(III) removal vs a contact time (5–720 min) and adsorbent dose (0.05–0.3 g); b initial As(III) concentration (5–100 µg L−1) and adsorbent dose (0.05–0.3 g); c initial As(III) concentration (5–100 µg L−1) and contact time (5–720 min)

Full size image

Effect of initial As(III) concentration

Adsorption of MPKSF–As was carried out with different initial concentrations ranging from 5 to 100 μg L−1. Refer to Fig. 2b under “Effect of pH” and 3c under “Effect of temperature” above, and Fig. 4b, c, under “Effect of contact time” below. The results illustrates the combined effect of initial As(III) concentration with pH of the adsorbent MPKSF suspension, temperature, adsorbent dose and contact time, respectively, while two parameters are kept constant. As shown by the response surface plots, it revealed that as the initial concentration increases, some of the percentage removal data showed increasing pattern while other percentages removal data became slightly decreased. In this case, other parameters need to be considered especially the adsorbent dosage which provides the information on the available vacant adsorption sites for adsorption of As(III) at higher concentrations.

Effect of contact time

Refer to Fig. 2a (under “Effect of pH”, and Fig. 3a under “Effect of temperature”) above, and Fig. 4a, c below. The results illustrate the combined response surface plots of contact time with pH of the adsorbent MPKSF suspension, temperature, adsorbent dosage and initial As concentration, respectively. It shows that the increase in contact time duration causes the removal percentages of As(III) to increase. As the contact time increased, the adsorbate had enough time to disperse and be adsorbed onto the surface and into the pores of MPKSF until the adsorption reached equilibrium at an optimum contact time.

Optimization using desirability function

A desirable value for each input parameter and the response can be selected. The multiple response methods was applied to obtain the optimum condition for the five parameters used including contact time, pH, adsorbent dose, initial As(III) concentration and temperature. The numerical optimization reveals the points that maximize the desirability function. In this study, the maximum level for As(III) removal was set for desirability at a minimum level of contact time (5 min), minimum adsorbent dosage (0.05 g), the maximum level of initial As(III) concentration (100 µg L−1), the level of solution pH in the range of 6–8 and the level of temperature within a range of 20–40 °C (data not shown for the desirability ramp).

Using Eq. (5) reported previously to determine the removal percentage, 96% removal of As(III) was achieved using the optimal conditions at contact time of 45 min, initial As(III) concentration maximized to 100 μg L−1, adsorbent dosage of 0.29 g, initial solution pH of 6.55 and the temperature at 26 °C as shown in Table 6. Experimentally, these optimum values are applied in a verification experiment and resulted in 95% removal of As(III) by MPKSF adsorbent with a percentage error of 1% as compared to the predicted removal of As(III). Thus, this indicated that the Box–Behnken design model is reliable for the optimization of various parameters used in an adsorption process.

Table 6 Optimal condition and model validation for As(III) removal by MPKSF
Full size table

Adsorption equilibrium studies of As(III) onto MPKSF adsorbent

Adsorption isotherm models

In this study, several isotherm models were applied to determine the type of adsorption that occurred on the magnetic activated carbon surface, by fitting the data to the Langmuir, Freundlich, and Temkin isotherm models. The correlation coefficient, R2 obtained from the isothermal plots was used to identify the isotherm model that best described the adsorption of As(III) onto MPKSF.

The Langmuir adsorption isotherm model

The Langmuir is represented by the following equations; (1) Eq. (6) which was formulated based on the kinetic theory; (2) Eq. (7) depicts the equation for the value of adsorbate adsorbed on the adsorbent; (3) the linear form of the Langmuir equation is given by Eq. (8):

$$\frac{x}{m} = q_{\text{e}} = \frac{{q_{\hbox{max} } K_{\text{L}} C_{\text{e}} }}{{1 + K_{\text{L}} C_{\text{e}} }},$$
(6)
$$q_{\text{e}} = \frac{{\left( {C_{\text{o}} - C_{\text{e}} } \right)V}}{m},$$
(7)
$$\frac{{C_{\text{e}} }}{{q_{\text{e}} }} = \frac{{C_{\text{e}} }}{{q_{ \hbox{max} } }} + \frac{1}{{q_{ \hbox{max} } K_{\text{L}} }},$$
(8)

where x = mass of adsorbate adsorbed (μg), m = mass of adsorbent (g), V = volume of solution used for adsorption process (L), C e = equilibrium concentration (μg L−1), C o = initial concentration (μg L−1), q e = amount of adsorbate adsorbed at equilibrium (μg g−1), q max = maximum adsorption at monolayer coverage, K L = Langmuir isotherm constant (L μg−1).

To assess the Langmuir isotherm model, a graph of C e/q e against C e is plotted, a straight line is obtained and the values of K L and q max are computed from the values of the slope and intercept of the graph. The fitted isotherm in this study was illustrated by a plot of equilibrium concentration of adsorbate C e on the adsorbent, q e, i.e., C e/q e against the equilibrium concentration of adsorbate, C e. Figure 5 depicts the fitted As(III) adsorption isotherm which indicated the presence of a linear part of plotted curve at low C e followed by a slight curvature around C e = 2.56 μg L−1 towards the completion of coverage of the monolayer with the R 2 value of 0.9599. Hence, this indicated that adsorption of arsenite onto MPKSF is L-type (having no strict plateau). A similar observation was reported by El-Said et al. (2009) whose study demonstrated the adsorption of As(III) and As(V) using Nigella sativa L.

Fig. 5
figure 5

Langmuir equilibrium isotherm for the adsorption of As(III) onto MPKSF

Full size image

Further, the inherent feature of this isotherm namely a dimensionless constant separation factor, R L can be expressed as an equilibrium parameter. The parameter is calculated using Eq. (9). The effect of the separation factor on the adsorption nature of the Langmuir isotherm is summarized in Table 7.

Table 7 Effect of separation factor on Langmuir isotherm
Full size table
$$R_{\text{L}} = \frac{1}{{1 + K_{\text{L}} C_{\text{o}} }},$$
(9)

where C o = initial concentration of surfactant (mg dm−3), K L = Langmuir isotherm constant.

To illustrate, that the homogeneous adsorption process predicted by the Langmuir isotherm assumes a monolayer adsorption of molecules onto the surface of the adsorbent. The Langmuir linear plot of the specific adsorption (C e/q e) against the equilibrium concentration (C e) for adsorption of As(III) onto MPKSF is depicted in Fig. 6. The C e was obtained after 180 min. The correlation coefficient (R 2) obtained from the Langmuir isotherm is 0.9973, which indicates that the adsorption data of the As(III) onto the MPKSF surface was well fitted to the Langmuir isotherm model. The monolayer adsorption capacity (q max) of As(III) onto MPKSF was found to be 48.08 μg g−1.

Fig. 6
figure 6

Langmuir isotherm representing the variation of specific adsorption (C e/q e) against the equilibrium concentration (C e) for adsorption of As(III) onto MPKSF

Full size image

A dimensionless equilibrium parameter, R L was used to express the nature of adsorption of the Langmuir isotherm. The R L value calculated from the adsorption data is 0.0765 indicating that the adsorption of As(III) on MPKSF was a favorable process as the R L value lies between 0 to 1 (0 < R L < 1) at an equilibrium temperature of 30 °C (Table 7).

The Freundlich isotherm model

This isotherm was applied as an empirical model which considers the data often fit to the empirical equation stated in Eq. (10):

$$\frac{x}{m} = q_{\text{e}} = K_{\text{F}} C_{\text{e}}^{{\frac{1}{n}}} ,$$
(10)

where x = weight of solute adsorbed, m = weight of adsorbent, C e = equilibrium concentration of adsorbate (mg L−1), q e = amount of solute adsorbed at equilibrium (mg g−1), K F and n = Freundlich isotherm constant (mg g−1)

From the isotherm, the n value reveals the nature of the adsorption, i.e., how favorable the adsorption process was. The value of n was used as the linearity parameter implying that if the n value lies between one and ten, this indicates a favorable sorption process of the adsorbent (Freundlich 1906). The effect of the n value on the nature of adsorption as represented by the Freundlich isotherm is shown in Table 4. The linear form of the equation is given by Eq. (11). A graph of log (x/m) against log C e results in a straight line at which the value slope and intercept are the value of 1/n and log K F, respectively.

$$\log \frac{x}{m} = \log q_{\text{e}} = \log K_{\text{F}} + \frac{1}{n}\log C_{\text{e}} .$$
(11)

A multilayer adsorption for the heterogeneous surface is indicated by the Freundlich isotherm model. The heterogeneous system of adsorption assumes that there is no formation of monolayer adsorption of As(III) on MPKSF. Figure 7 illustrates the plot of log q e against log C e. The correlation coefficient, R 2 obtained from the graph illustrates that the Freundlich isotherm model is not well fitted to the adsorption data with an R 2 value of 0.9744. The Freundlich constants, K F and the n value are shown in Table 8.

Fig. 7
figure 7

Freundlich isotherm indicating the variation of log q e with respect to log C e for adsorption of As(III) onto MPKSF

Full size image
Table 8 Effect of n values on Freundlich isotherm
Full size table

The slope of the Freundlich isotherm (Fig. 7) shows that the 1/n value is less than 1 and this has shown that the process is a favorable physical adsorption process. The smaller 1/n value indicates that a strong bond is present between the adsorbent and adsorbate molecules (Okeola and Odebunmi 2010).

In the paper by Mayo et al. (2007), it was demonstrated that the adsorption of As(III) and As(V) onto Fe3O4 nanoparticles exhibits the surface complexation reaction by forming either inner-sphere monodentate or bidentate-binuclear complex with iron oxide (Fe3O4). A similar reaction of magnesium with iron oxide, i.e., Fe3O4 and γ-Fe2O3 was reported by Jolsterå et al. (2012). The proposed adsorption of As(III) and Fe3O4 in MPKSF is depicted in Fig. 8 and supported by the FTIR analysis of the MPKSF–As.

Fig. 8
figure 8

(adapted from Ciuró Juncosa 2008; O’Reilly et al. 2001)

Proposed adsorption of As(III) onto MPKSF.

Full size image

It is well known that sodium arsenite can be represented as sodium ortho-arsenite (Na3AsO3) and sodium meta-arsenite (NaAsO2), the latter was used in this study for adsorption. Based on Fig. 9, MPKSF reacted with arsenous acid (H3AsO3) which is produced according to the chemical reaction (Eq. 11). Firstly, sodium meta-arsenite reacts with water producing arsenic trioxide with sodium ions and hydroxide ions followed by the slow hydrolysis of arsenic trioxide. The reaction proceeds in a basic condition, finally producing arsenous acid:

Fig. 9
figure 9

Temkin isotherm showing the variation of q e against ln C e for adsorption of As(III) onto MPKSF

Full size image
$$2{\text{NaAsO}}_{2} + {\text{H}}_{2} {\text{O}} \to {\text{As}}_{2} {\text{O}}_{3} + 2{\text{Na}}^{ + } + 2{\text{OH}}^{ - } {\mathop{\longrightarrow}\limits^{{{\text{slow}}\;{\text{hydrolysis}}}}}2{\text{H}}_{3} {\text{AsO}}_{3} .$$
(12)

Liu et al. (2015) reported that magnetite (Fe3O4) is known as a mixture of two iron oxides which are composed of 67% of Fe(III) and 33% of Fe(II). In the adsorption study, the major Fe(III) species was reported to interact with As(III) to form either inner-sphere monodentate or bidentate-binuclear complex. This can be attributed to the oxidation reaction which takes place in the presence of oxygen under atmospheric experimental conditions hence suggesting the oxidation of Fe(II) to Fe(III).

Temkin isotherm

The Temkin isotherm model was applied to consider the effect of the interactions between the adsorbent and the adsorbate on an adsorption isotherm. The model assumes that the heat of adsorption of the molecules present in the adsorbed layer is reducing linearly with the coverage of the molecules instead of in logarithmic pattern due to this interaction (Temkin 1941). This means that as the coverage of adsorbed layer increased, the heat of adsorption decreased.

Temkin isotherm is given by Eq. (13):

$$q_{e} = \left( {\frac{RT}{{b_{T} }}} \right)\ln (AC_{e} ).$$
(13)

The linear form of Eq. 13 is given by:

$$q_{e} = \frac{RT}{b}\ln A + \frac{RT}{b}\ln C_{e} .$$
(14)

Substituting RT/b with B and hence,

$$q_{\text{e}} = B\ln A + B\ln C_{\text{e}} ,$$
(15)

where b = Temkin isotherm constant, A = equilibrium binding constant correspond to maximum binding energy, R = gas constant (8.314 J mol−1 K−1), T = absolute temperature, K.

The values of constant A and B are obtained from a plot of q e against ln C e.

Figure 9 shows the plot of q e against ln C e whereby the slope and intercept values obtained from the graph plot are used to calculate Temkin constant A, and the heat of sorption constant B. The R 2 value obtained from the linear plot of Temkin isotherm model is 0.9816 indicating that the adsorption data are applicable to this model. Similar observations have been reported by Itodo and Itodo (2010) on the adsorption of atrazine onto sheanut shell. Similarly by Hamdaoui and Naffrechoux (2007) whose study demonstrated the adsorption of phenol and chlorophenol onto granular activated carbon. Maurya and Mittal (2006) had also established the linear Temkin plot for the adsorption of methylene blue and Rhodamine B onto activated carbon.

Comparing the three correlation coefficients; R 2 for the three isotherms, the Langmuir isotherm gave the best fit of adsorption isotherm with highest correlation coefficient, R 2 value of 0.9973 followed by Temkin (0.9816) and Freundlich (0.9744) isotherm models (Table 9). Langmuir isotherm implies that adsorption of As(III) onto MPKSF adsorbent occurs in a monolayer adsorption at which when the available sorption sites of MPKSF are fully occupied, no further adsorption process can take place at those sites. It is corroborated by the formation of inner-sphere complexes between iron oxide and As(III) molecules on MPKSF surface.

Table 9 Langmuir, Freundlich and Temkin isotherm model parameters and correlation coefficient for adsorption of As(III) on MPKSF
Full size table

The R 2 value for Langmuir and Freundlich are 0.9973 and 0.9744, respectively (Table 9). The Temkin isotherm shows that the heat of adsorption is low (9.72 J mol−1) indicating physical adsorption. Furthermore, the calculated Freundlich (q max) (54.48 μg g−1) was higher than the adsorption capacity (q max = 48.08 μg g−1) determined from the Langmuir isotherm. Based on the q max value obtained, the adsorption of As(III) is more of a physical adsorption as described by the Freundlich isotherm. Studies by Liu et al. (2015) reported that the presence of chemical interaction between As(III) and iron oxide forming inner-sphere surface complex can be best explained by Langmuir isotherm, suggesting a monolayer As(III) adsorption onto the Fe3O4 surface. However, they also reported that the adsorption of As(III) onto AC showed the best fit with Freundlich isotherm. Based on the experimental data, it is suggested that both chemisorption, involving the formation of inner-sphere complex and physisorption on activated carbon occurred in the adsorption of As(III) onto MPKSF.

Desorption of As(III) from MPKSF

Desorption experiment was conducted to examine the reusability of the MPKSF adsorbent and the reversibility of the adsorption process. Figure 10 illustrates the percentage desorption of As(III) from MPKSF. During the first stage of desorption using distilled water, the percentage of As(III) desorbed in the solution was 0.72% followed by 0.78 and 0.97% at second and third stages of desorption, respectively. The small amount of As(III) detected after the first desorption (Des1) was presumably due to the complexation reaction between As(III) ions with the iron in MPKSF adsorbent (CiuróJuncosa 2008) which prevents the dissociation of As(III) from iron oxide on the surface of MPKSF. This is also consistent with the results of the Langmuir adsorption isotherm, thus explaining the formation of chemical bonds between As(III) and the surface of MPKSF which prevent the As(III) from desorbing easily from MPKSF.

Fig. 10
figure 10

Desorption of As(III) from MPKSF. Data obtained: n = 3 for each desorption experiment

Full size image

Identification of the proposed mechanism of the adsorption of As(III) onto the MPKSF

Fourier transform infrared spectroscopy (FTIR) analysis

As stated previously a mechanism was proposed for the adsorption of As(III) onto the MPKSF, in this section, this mechanism was identified using the results of the spectroscopy studies and supported by the results of the characterization of the MPKSF after the adsorption. Figure 11 shows the FTIR spectrum of MPKSF after adsorption of As(III) (MPKSF–As). Five peaks could be observed in the spectrum identified at wavenumber of 3430, 1625, 1387, 1078 and 573 cm−1. These are assigned to the functional groups OH, C=O, C–C, C–O, and M–O, respectively.

Fig. 11
figure 11

FTIR spectrum of MPKSF and MPKSF–As

Full size image

Both spectra of MPKSF before and after adsorption show the presence of peaks at a wavenumber of 3430, 1625 and 573 cm−1. Additionally, in MPKSF–As, two new peaks were detected at 1387 cm−1 and around 800 cm−1 which are assigned to C–C bending (Mayo et al. 2007) and As–O interaction (Ito et al. 1995), respectively, on MPKSF surface after adsorption. However, the spectrum showed a less significant band at 800 cm−1. Thus the EDX analysis data are used to validate the presence of As(III). According to Sayle (2000), at a pH lower than the pKa value, the molecules will be mostly protonated. Thus, the negatively charged MPKSF provides greater affinity towards the protonated As(III) ions at pH lower than 9.2 which result in the formation of inner-sphere complexes between As(III) and Fe3O4 in MPKSF. Additionally, Bundschuh et al. (2005) reported that as the pH increases, the dominant negative charges are present on adsorbent surface hence interference with the adsorption of As(III) and As(V) are significantly governed by the surface charge of adsorbent.

X-ray diffraction (XRD) analysis

Figure 12 illustrates the diffractogram pattern of MPKSF after adsorption (MPKSF–As). The pattern obtained is quite similar to the diffractogram of MPKSF before the adsorption process. There are four intense peaks assigned to Fe3O4 at 2θ 30.45°, 35.75°, 57.85° and 63.00°, meanwhile one peak at 2θ 43.35° is assigned to γ-Fe2O3, respectively. The increment in crystallite size of MPKSF–As is probably due to crystal defect after the adsorption of As(III) onto the MPKSF. This is consistent with the work of Mandal et al. (2013) on the adsorption of As(III) by zirconium polyacrylamide hybrid material. However, no crystalline As(III) was detected using this analysis, probably due to the small amount of As(III) adsorbed on MPKSF.

Fig. 12
figure 12

XRD diffractogram of MPKSF–As

Full size image

Scanning electron microscopy (SEM) analysis

The morphology of MPKSF–As under magnification of 1550× is depicted in Fig. 13a illustrating that MPKSF–As surface experienced a distinct change as compared to MPKSF. In addition, the presence of a layer of coating on the surface is presumably assigned to the adsorbed layer of As(III) complexes on the MPKSF. The entire coverage of As(III) in the pores as depicted in Fig. 13b under higher magnification (6200×) shows that the adsorption of As(III) occurs evenly over the surface and in the pores of MPKSF. Further, it can be seen that As(III) particles do not block the external pores as it is still observed clearly even after adsorbing As(III). With respect to both figures, it shows that the pore size of MPKSF was affected after the adsorption process. The size of the pores reduced compared to the pore size of MPKSF before adsorption. This is possibly due to the formation of the inner-sphere complexes of As(III) ion with Fe3O4 in MPKSF on the walls of the external pores.

Fig. 13
figure 13

Micrograph of MPKSF–As under magnification a ×1550 and b ×6200

Full size image

Energy dispersive X-ray analysis (EDX) analysis

The energy dispersive X-ray analysis is used to detect the presence of arsenic after adsorption by MPKSF. Figure 14 illustrates EDX spectrum of MPKSF–As. The spectrum showed the peaks similar to the untreated MPKSF for carbon, oxygen, iron and phosphorus. However, after the adsorption process, the presence of As(III) was detected with a composition of 0.52% as illustrated in Table 10 below. The amount of arsenic detected is small due to the low concentration of As used in the adsorption process which is in the range of 5–100 μg L−1. The composition of other elements present in the sample was unaffected by the adsorption process as the composition of these elements are quite similar to the composition of the untreated MPKSF.

Fig. 14
figure 14

EDX spectrum for MPKSF–As sample

Full size image
Table 10 Elemental analysis for sample MPKSF and MPKSF–As
Full size table

Conclusions

This study demonstrated that the MPKSF effectively removed As(III) from waste water by the formation of inner-sphere complexes between the Fe and the As(III). Further, desorption of the sorbed As(III) was found to be in very minute concentrations, thereby suggesting that the sorbed As(III) was rigidly bound by inner-sphere complexation mechanism. An efficient adsorption process was revealed to take place at pH 6 and 7 and at a longer contact time. The initial As(III) concentration and adsorbent dose were concluded to be dependent on each other due to the availability of adsorption binding sites for As(III) presented by greater dose of the MPKSF. Further, the higher reaction temperature was shown to generate more residual As(III) in the solution hence reducing the removal efficiency of As(III) by MPKSF.

The predicted results from the designed experiment on the adsorption of As(III) onto MPKSF using Box–Behnken statistical data revealed that 96% of As(III) removal was achieved utilizing the optimal conditions at contact time of 44.73 min, initial As(III) concentration maximized to 100 μg L−1, adsorbent dosage of 0.29 g, initial solution pH of 6.55 and the temperature at 26.38 °C. A verification experiment conducted using a real waste water sample resulted in a 95% As(III) removal, which indicated that 0.96% error had occurred.

The adsorption studies suggest that the adsorption of As(III) onto the MPKSF was highly dependent on pH and contact time relative to the initial As(III) concentration, adsorbent dose and temperature. The adsorption data of the As(III) onto the MPKSF was well described by the Langmuir isotherm followed by Temkin and Freundlich isotherms.