Introduction

Urbanization has caused massive increases in impervious coverages and as a result the amount of stormwater runoff, which in turn can have harmful effects on urban and suburban streams. Streams erode their beds and banks as they meander across the surface of the earth in a dynamic natural way (Saraswat et al. 2016). Numerous research studies have demonstrated the significant contribution of streambank erosion to total sediment loading (Simon and Darby 1999; Sekely et al. 2002; Evans et al. 2006). Konrad et al. (2005) studied the impact of urban development on stream flow and streambed stability. They examined 16 streams in the Puget Lowland, WA, USA, using three streamflow metrics that integrate storm-scale effects of urban development over annual to decadal timescales. They concluded that the increase in the magnitude of frequent high flows is due to urban development but flows’ cumulative duration has no important consequences on channel form and bed stability in gravel bed streams. Cheveney and Buchberger 2013 conducted a study to evaluate the impact of GI in mimicking pre-development scenario in the Mill Creek Watershed, which is located in southwestern Ohio. They applied a water balance analysis using the modeling software, Aquacycle. They noticed that two values were significantly changed, the total volume of water entering and leaving the watershed increased by 28% and the annual evapotranspiration declined by 22% compared to pre-development conditions. They conclude that with proper planning and implementation of appropriate GI, there could be a reduction in the negative impact of urban runoff and mimic pre-development scenario.

To restore or maintain channel stability, the incision of the channel bed and erosion of the stream banks must be prevented. Stability of a streambed can be attained by acquiring the balance between sediment supply and sediment transport capacity, while stream bank stability can be attained by maintaining the applied shear stress to be below erosive thresholds (Lawler 1995). These thresholds can be estimated by defining the critical shear stress at which soil detachment begins. The erosion rate will remain zero as long as the critical shear stresses are higher than the applied shear stress (Hanson and Temple 2002). Sediments resulting from stream bank erosion can account for 85% of watershed sediment yields and bank retreat rates of 1.5–1100 m/year have been documented in several studies (Prosser et al. 2000; Simon et al. 2000; Wallbrink et al. 1998).The total damage to natural resources and human health due to water pollution by sediment costs an estimated $16 billion annually in North America (Osterkamp et al. 1998).

Streambank erosion occurs as a result of changes in streamflow, water flooding or the discharge of concentrated runoff from other sources. The consequences of streambank erosion are not limited to the streambanks only but also it might impair the water quality and cause significant economic damage to the surrounding ecosystem. Low Impact Development (LID) or Green Infrastructure (GI) was developed to mimic the natural water cycle of the land by reducing the negative impact of stormwater runoff on water bodies and eventually human health. It is important to note that the two terms LID and GI have been used in this study interchangeably. LID practices are structural or non-structural management practices that aim to decrease the impacts of urbanization and sediments on water quality. GI includes the installation of any of the following structural measures to retrofit existing infrastructure and reduce runoff volumes and peak flows: bioretention, green roofs, rainwater harvesting, and permeable pavements (Damodaram et al. 2010). Regulatory enforcement of GI implementation results in an urgent need for quantitative information on GI practice effectiveness for sediment and stream erosion (Lee and Jones-Lee 2002). While GIs have been mentioned in the literature for stormwater management (Dietz and Clausen 2008; Elliott and Trowsdale 2007; Hood et al. 2007; Bedan and Clausen 2009) there is little research that studied GI impact on the downstream reduction of stream bank erosion in urban areas (Burns et al. 2015; Jia et al. 2015). Some studies (Bledsoe 2002; Krishnappan and Marsalek 2002; Gassman et al. 2007) addressed GI effectiveness through field experiments, very few studies addressed GI effect on stream erosion using computer modeling. Modeling allows large-scale evaluations as well as varying variables to assess several scenarios. One example is what McCuen and Moglen (1988) suggested as a multi-criterion approach to mitigate channel instability. This approach requires the cumulative, post-development bed load transport volume not to exceed the pre-development amount for the 2-year recurrence interval. Although this approach provided some insights into reducing total runoff on a watershed scale it did not evaluate the impact of GI and shear stresses. Additional models were developed that include a stream bank erosion component including: The Système Hydrologique Européen (SHE) (Abbott et al. 1986), Soil and water assessment tool (SWAT) (Neitsch et al. 2002), Watershed Erosion Prediction Project (WEPP) (Flanagan et al. 2001), and Conservation Channel Evolution and Pollutant Transport System (CONCEPTS) (Langendoen 2000). Mostly, these models use the excess shear stress equation for determining rates of erosion but the GI component is slight to not be integrated.

Jeong et al. (2011) developed a sub-daily algorithm which was integrated into the Soil and Water Assessment Tool (SWAT) to simulate urban best management practices such as detention basins, wet ponds, sedimentation filtration ponds, and retention irrigation systems. The algorithm was tested for predicting sediment yield and total runoff but not for potential stream bank erosion. Other studies have utilized SWAT to test for GI performance based on several factors including urban pattern/land use, design parameters, and water quality volumes (Brander et al. 2004, Gilroy and McCuen 2009, Williams and Wise 2006). However, most of these studies have been focusing on agricultural areas and seeking to optimize the use of good agricultural practices. Urban settings increase the complexity of such types of modeling as inputs and variables are more difficult to model and do change over space and time dramatically.

The overall goal of this study was to model the impact of GI on urban stream flows and bank shear stress using SWAT. The specific objectives of this study were to: (1) develop a simple way to represent bioretention and permeable pavement in the SWAT model, and (2) investigate the influence of GI in reducing total volumes of stormwater runoff, peak flows, and excess shear stress.

Materials and methods

Case study area

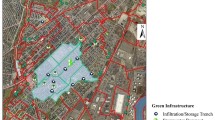
The study site is the Blunn Creek watershed located in Austin, Texas (Fig. 1). The watershed was estimated to have 34.8% impervious cover in 2003 and the total catchment area is 2.56 square kilometer. The creek has a length of 4.83 km. The total population estimated to be living in the watershed area in 2013 was 6000 and projected to be 6810 by 2030 (City of Austin 2013).

Fig. 1
figure 1

Blunn Creek watershed in Austin, Texas

Full size image

SWAT model development, calibration, validation, and sensitivity analysis

Model development

ArcSWAT modeling package, which runs the 2012 version of the SWAT model (SWAT 2012.10.4) within the ESRI ArcGIS 10.1 environment (DiLuzio et al. 2004), was used in this study. The preprocessing of the GIS data was facilitated through the interface. These included elevation, soil, land use, and weather as basic model inputs. SWAT was applied and the output format was modified to 15-min time steps (from the typical daily time step output) (Jeong et al. 2011). The watershed was divided into 14 subbasins and each subbasin was parameterized using a series of HRUs (hydrologic response units) which were a particular combination of land cover, soil, and management. At each HRU, soil water content, nutrient cycles, crop growth, and management practices were simulated and then aggregated for the subbasin by a weighted average method. Each subbasin had physical and climatic data such as reach geometry, slope, and climatic data. Estimated flow was calculated for each subbasin and routed through the stream system. SWAT considers evapotranspiration, surface runoff, percolation, groundwater return flow, lateral subsurface flow, and channel transmission losses. Runoff is simulated and estimated with the Green-Ampt Infiltration method (Mein and Larson 1973). Stream flows and volumes of runoff were evaluated at the watershed outlet and at the end of each subbasin. Data used in the modeling were the following: 15-min rainfall data downloaded from the Flood Early Warning System and Water Quality Monitoring sections at the City of Austin (COA) station (rainfall distribution for type III region), daily temperature data from the Austin and Austin–Bergstrom National Oceanic and Atmospheric Administration weather stations were used, weather zone from (WGEN_US_COOP_1960_2010), 3 m integer Digital Elevation Model (DEM) developed by City of Austin based on 2003 LIDAR data and SSURGO soil data Natural Resources Conservation Services (NRCS).

Calibration and validation

The model was calibrated and validated at the watershed outlet for a period of 2 years before installing any GI. Sub-daily flow measurements were available at The United States Geological Survey (USGS) station 08157700 (Fig. 1) and were retrieved from USGS website for the period between 1998 and 1999 for the calibration. Validation procedures for the period between 2001 and 2002 were conducted to ensure the validity of the selected uncertainty parameters through the calibration process. The performance of each simulation was assessed by the coefficient of determination (R 2) and Nash–Sutcliffe coefficient of efficiency (Nash and Sutcliffe 1970), NS was computed as follows:

$${\text{NS}} = 1 - \frac{{\mathop \sum \nolimits (Qo - Qm)^{2} }}{{\mathop \sum \nolimits (Qo - \overline{Qo} )^{2} }}$$
(1)

where Q o is the observed discharge (m3/s), Q m is the modeled discharge (m3/s), and \(\overline{Qo}\) is the average observed discharge (m3/s).

A “warm-up period” consisting of the first year of simulation was not considered when computing the NS value to avoid the influence of initial conditions such as soil water content and eventually runoff estimates.

Sensitivity analysis

Sensitivity analysis is the study and investigation of how uncertainty in the output of a model can be influenced by different sources of uncertainties in the model input (Saltelli et al. 2009). In this study, a sensitivity analysis was conducted to investigate the impact of input parameters in estimating flow at a 15-min time interval. The sensitivity of 13 parameters related to stream flow and SWAT was indexed and those highly ranked parameters were selected for calibrating the model. The evaluation was based on the Latin hypercube one factor at a time (LH‐OAT) sampling method that is incorporated with the one‐factor‐at‐a‐time analysis technique (Wang et al. 2005) (Eq. 2). LH-OAT is a screening method which is incorporated in SWAT. The method works best when the number of intervals used for the Latin hypercube sampling is high enough to obtain converged parameter (Van Griensven and Meixner 2006).

$$S_{ij} = \frac{{\frac{{\left| {M\left( {x_{1} , \ldots ,x_{i} + \Delta x_{i} , \ldots ,x_{K} } \right) - M\left( {x_{1} , \ldots ,x_{i} , \ldots x_{K} } \right)} \right|}}{{M\left( {x_{1} , \ldots ,x_{i} + \Delta x_{i} , \ldots ,x_{K} } \right) + M\left( {x_{1} , \ldots ,x_{i} , \ldots x_{K} } \right)}}}}{{\left| {\Delta x_{i} } \right|/x_{i} }}$$
(2)

where S ij is the relative partial effect of parameter x i around LH point j, K is the number of parameters, M is the model output (time series result of stream flow at every time step at the watershed outlet).

SWAT Calibration and Uncertainty Procedures (SWAT-CUP), which is a program that interfaces with SWAT (Abbaspour et al. 2007) was used for this sensitivity analysis (Fig. 2). This program includes three calibration procedures that are capable of calibrating and evaluating SWAT outputs. These procedures include generalized likelihood uncertainty estimation (GLUE) (Beven and Binley 1992), Parameter Solution (ParaSol) (Van Griensven and Meixner 2006), and Sequential Uncertainty FItting (SUFI-2) (Abbaspour et al. 2007). In this study, the multisite semi-automated inverse modeling routine SUFI-2 was used.

Fig. 2
figure 2

The interaction between calibration program and SWAT in SWAT-CUP (Abbaspour et al. 2007)

Full size image

Green infrastructure representation in SWAT

Several types and the combination of GI were applied and represented in the Blunn Creek watershed including detention pond alone (DP), bioretention/rain garden alone (RG), permeable pavement alone (PP), and a combination of RG and PP (RG + PP). These configuration options were selected based on their ease of adoption by developers, their potential effectiveness, and their applicability in the Blunn Creek watershed. The DP was placed in the middle of the watershed on the stream network (Fig. 2) as it is aimed at representing a typical regional detention facility constructed by the City of Austin. RGs were installed in each subbasin and sized to treat a runoff from 1.5-in. rainfall while PP was represented in only 27% of the total watershed area which represents the total potential parking space in the watershed. This representation for the PP was based on a typical average parking lot area in Dallas, TX downtown that has the same watershed area as Blunn Creek watershed (City of Dallas 2011). PP was also sized to retain runoff from 1.5 in. of rainfall. The various scenarios were run over the calibrated and validated base model.

Detention pond development in SWAT

There are two types of DP employed in the Austin area: on-site detention (offline) and regional detention (online). The current version of SWAT considers only the regional detention which is placed online or in other words, onstream. According to the City of Austin code of development, small storms (2 and 5-year) are allowed to pass through virtually uncontrolled and there is only volume backup during the larger runoff events that drain out in less than 24 h. A hypothetical detention pond was designed according to the City of Austin standards. Pond sizes were calculated as follows: a raster surface was converted to contour lines with 0.30-m contour intervals. A 12-m-high line segment representing a dam was placed at the end of subbasin 10 as shown in Fig. 3 to represent the width of the detention pond across the creek. This width was based on the current geometry of the channel and could not be wider than the channel due to current development and residential areas adjacent to the channel. Following the contour line, an area of 3608 m2 was delineated which is the extended lines from the two ends of the 12-m contour line. The average depth of the pond is 3 m which was calculated directly from the geometry of the channel. A stepped weir was used for the outflow and its height was based on the required storage volumes for the following design storms: 2 years, 25 years, and 100 years.

Fig. 3
figure 3

Location of a detention pond in the watershed

Full size image

The pond was designed and sized based on the US Soil Conservation Service rainfall distribution for type III region (Travis County). The total surface area of the resulted detention pond located in subbasin 10 was 2624 m2.

Bioretention/rain garden and permeable pavement representation in SWAT

RG and PP were represented by modifying existing Best Management Practices (BMPs) within the SWAT program. The current version of SWAT does not incorporate RG or PP within the BMP package. For the purpose of this study, the Sedimentation Filtration (Sedfil) module was modified to act as RG and PP. There are three designs of Sedfil offered by SWAT; full-scale, partial scale and sedimentation pond only. The full-scale design allows the entire water quality volume to be held in the sedimentation basin and later discharge slowly to the filtration basin via a perforated riser pipe. The second design “partial Sedfil” distributes the water quality volume between the filtration and sedimentation chambers after foregoing the perforated riser pipe (City Of Austin 2011, Fig. 4). The water quality volume estimated by SWAT can be expressed as follows (City Of Austin 2011):

Fig. 4
figure 4

Schematic of Austin sedimentation/filtration basins [Courtesy of City of Austin (2011)]: a configuration of full/partial sedimentation filtration basins; b riser pipe outlet system and flow spreader in full type systems

Full size image
$$V_{{wq}} = 0.07 \times \left\langle {0.5 + \left| {\frac{{{\text{Impervious area }}}}{{{\text{Total drainage area}}}} - 0.2} \right| \times 1} \right\rangle \times A_{d}$$
(3)

where V wq is the water quality volume (m3) (the runoff volume that includes 90% of all rainfall events in a given year, HydroCAD 2017) and A d is drainage area of the GI (m2).

The partial scale design was used in this study to simulate both bioretention and permeable pavement. Two parameters were considered in adjusting the Sedfil design; water ponding and depth of filtration media. A typical standard of a bioretention and a permeable pavement surface area that is 3–10% of the total catchment area was followed to meet the 1.5 in storm target (City Of Austin 2011). The initial run was executed with an automatic sizing function to size the pipes required to release runoff inside (from sedimentation to filtration) and outside (discharge) the system. To minimize the function of the sedimentation basin and concentrate on a filtration basin only, which represent the bioretention/permeable pavement, the surface area of the sedimentation area was selected to represent a forebay area that might be installed before a bioretention area. In the case of the permeable pavement, the forebay was totally ignored by selecting the lowest number that the model would allow to minimize this effect. The outlet orifice pipe of the sedimentation basin was selected to be bigger than the one for the filtration to divert most of the runoff to the filtration basin where it will be treated. The depth of the filtration media for the bioretention was selected to be 1200 mm and maximum ponding depth of the water to be 420 mm. The depth of the filtration media for the permeable pavement was 356 mm and maximum ponding depth of the water was 10 mm. One RG and one PP were placed at each subbasin in the watershed and that resulted in total surface areas equivalent to 61217 m2 and 35526 m2 for RG and PP, respectively. It is important to note that the ponding and filtration depths for both bioretention and permeable pavement were selected based on City of Austin Stormwater Manual (City of Austin 2011).

Channel geometry and hydraulic properties

Federal Emergency Management Agency floodplain maps for the watershed were downloaded and imported into the Hydrologic Engineering Center’s-River Analysis System (HEC-RAS) 4.1.0 software (United States Army Corps of Engineers 2010).

Each subbasin in SWAT was divided into multi-river stations and each station had a unique cross section. Cross-sectional analysis was developed for each subbasin, exported to Microsoft Excel format, and utilized as an input for an interactive software package (WinXSPRO) that is designed to analyze stream channel cross-sectional data (US Forest Service 2005). The WinXSPRO 3.0 program was utilized to estimate the channel hydraulic properties for each subbasin (Hardy et al. 2005). The program developed a stage–discharge relationship based on the cross section from HEC-RAS and slope from SWAT then calculated the velocity and shear stress for various stages.

Potential erosion estimates

The potential impact of urban development on stream bank erosion potentials was evaluated using annual excess stream flow (Glick and Gosselink 2011). This study investigated the potential bank erosion in the main channel and did not account for flows that exceed bankfull and spills into the floodplain. The rate of energy dissipation against the bed and banks of a stream was estimated. Using the developed stage–discharge relationships, shear (\(\tau )\) and critical shear (\(\tau_{c} )\) stresses in Pa were computed using the following equations (Knighton 1998):

$$\tau = \gamma_{w} \times D_{H} \times S_{{\begin{array}{*{20}c} {W } \\ \\ \end{array} }}$$
(4)
$$\tau_{c} = \theta_{c} \times \left( {S_{g} - 1} \right) \times \gamma_{w} \times d_{50}$$
(5)

where γ w is the density of water (kg/m3); D H is the depth of water (m); S w is the channel slope; S g is the specific gravity of soil, 2.65 g/cm3; d 50 is the median particle diameter (50 and 0.5 mm); θ c is the critical Shield’s parameter.

The critical Shield’s parameter is a non-dimensional number used to calculate the initiation of motion of sediment in a fluid flow. The critical Shield’s parameter was determined using shield parameter curves for different soil types (Julien 1995). After determining average soil particle diameter size, the corresponded Shield’s parameter value was selected. The median particle sizes considered in this study are listed in Table 1.

Table 1 Median soil particle sizes and classification used in potential erosion estimates
Full size table

After calculating critical stresses for the various particle sizes in Table 1, shear stress was calculated for a selected 24-h period during which a storm event occurred on July 1, 2002 (Fig. 5). 51 mm of rain fell in 24 h. The shear stress was calculated for every 15-min increment for the current conditions (no green infrastructure), the detention pond scenario (DP), the rain garden scenario (RG), the permeable pavement scenario (PP), and the rain garden plus permeable pavement scenario (RG + PP). The results of all scenarios were compared to each other and to the critical shear stress of the various particle sizes.

Fig. 5
figure 5

Hydrograph of the storm during the 24-h period of July 1, 2002

Full size image

In addition, the exceedance of critical shear stress and average cumulative exceedance of critical shear stress were calculated for 25 years of annual runoff data. All the scenarios were run from 1987 to 2012, the first 2 years were used as a warm-up period and the rest for the analyses. Cumulative excess shear (CE) was calculated using the following relationship (Glick and Gosselink 2011):

$${\text{CE}} = \, \varSigma \, \left( {\tau \, - \, \tau c} \right),\quad {\text{for all}}\;\tau \, > \, \tau c \, \left( {\text{Pa}} \right)$$
(6)

In addition to the shear stress calculations, reduction in total storm volume as well as peak flow from 2-year, 10-year, 25-year, and 100-year type III design storms and July 1, 2002, storm was calculated for the current conditions (no green infrastructure) and the DP, RG, PP, and RG + PP scenarios.

A comparison between mean differences in runoff volume using a t test was conducted for the actual storm in 15-min increments comparing the effect of the various GI and the current condition. A significant level of α < 0.05 was selected.

Results and discussion

Calibration, validation, and sensitivity analysis

Based on the initial run, knowledge of the problem and software, and a relative sensitivity analysis (varying all parameters simultaneously), a decision was made to include eight parameters in the calibration (Table 2). The parameters were given ranks for their sensitivity to the model calibration.

Table 2 Parameter sensitivities for SUFI-2
Full size table

Calibrated stream flows for a 2-year period with a 15-min time step simulation had an R 2 = 0.78 and NS = 0.78. The goodness-of-fit and efficiency of the model were tested using the main objective functions mentioned in Table 3. These five objective functions were analyzed using SUFI-2 uncertainty technique for the best-fit model.

Table 3 Stream flow calibration results for sub-hourly 15-min time step SWAT model
Full size table

Results also showed that the p factor [(the percentage of observations bracketed by the 95% prediction uncertainty (95PPU)] brackets 56% of the observation and r factor (average number of measured variables divided by the standard deviation of these measured variables) equals 0.54.

Validation procedures using data from 2001 to 2002 were conducted to evaluate the calibration process. NS value for validation was 0.67 and R 2 value equals to 0.70 for the sub-hourly 15-min time step model. All in all, the comparison between observed and simulated streamflow showed that there is a good agreement between the observed and simulated discharge which was verified by high values of R 2 and NS. Accordingly, the calibrated model was used to evaluate the GI scenarios.

Potential erosion estimates

Critical shear stress for the following median soil particle sizes was calculated using Eq. 5 for d50 values of 0.5, 10, 20, and 32 mm, and was found to 0.33, 7.18, 15.32, and 25.86 Pa, respectively. The results, illustrated in Fig. 6, show the potential shear stress for July 1, 2002, storm event by integrating different levels of GI and a current scenario without GI.

Fig. 6
figure 6

Shear stresses (Pa) for current scenario and different scenarios of GIs (current; RG rain garden alone, PP permeable pavement alone, DP detention pond alone, RG + PP rain garden and permeable pavement) for the 24-h period during the July 1, 2002 storm event. Horizontal lines indicate the critical shear stress for various particle sizes

Full size image

The scenario that accounts for a combination of RG and PP based on SedFil modifications resulted in the greatest reductions in shear stress. RG came in the second order with respect to greatest reductions in shear stresses. The DP contributed to lowering shear stresses and peak flow especially at the beginning of the storm. In general, the SedFil accounts for a ponding area where runoff will be captured and seeps out or overflows within 24 h. This functionality of the SedFil contributed to reducing peak flows, volumes and slightly delaying the peak flows.

As expected, the 0.5-mm soil particle diameter had the highest excess shear and potential erosion while the 32 mm had the lowest excess shear stress for the current scenario without any GI. This is similar to the findings of Konrad et al. (2005), which showed that the largest the soil particle the less excess shear stress and the less potential for erosion. The impact of GI on reducing cumulative excess shear stress for all the soil particle sizes during the 1987–2002 period is shown in Fig. 7.

Fig. 7
figure 7

Reduction percentages in excess shear stress for different soil particle diameters (mm) and by utilizing different types of green infrastructure for 25 years of storm data at Blunn Creek

Full size image

The same trend continued to hold and combining PP and RG modifications resulted in the greatest reduction in excess shear stress for all soil particle diameters. Adding RG alone resulted in the second greatest reduction in excess shear stress. The DP had fewer reduction percentages than RG due to the fact that the design of the pond accounted for flows above the flow associated with critical shear stress for a longer period of time such as a 100-year storm.

Volume and peak flow reduction

The volume of runoff detained by GI is affected by design parameter, spatial location, and storage depth of the GI. In this section and based on City of Austin design standards for GI, we analyzed the effect of the GI on peak flow and total annual volume for the following recurrence intervals: 2 years, 10 years, 25 years and 100 years using a type III storm. Percentage of annual reductions for volumes and peak flows are shown in Table 4.

Table 4 Reduction percentages in runoff volumes and peak flow for different recurrence intervals and for the current and GI scenarios
Full size table

Combining PP and RG continued to result with the greatest reduction percentages for both runoff volumes and peak flows for all recurrence intervals. RG had the second greatest reduction in runoff volumes and peak flows followed by PP and the DP scenario had the least reduction percentages. Excess shear analysis for both design storms and real storm in the Blunn Creek showed agreement with findings. All in all, this reduction in total runoff could prevent not only stream bank from getting eroded only but also contributes to restoring pre-development hydrology which has an important role in maintaining the aquatic life and restoring the ecological system. In addition, maintaining pre-development hydrology throughout the peak flow reduction encourages water storage and infiltration, which in turn reduces urban flooding and at the same time increases recharging local groundwater aquifers and streams. It is important to note that the average reduction in both total volumes of runoff and peak flow is consistent with the finding of Cheveney and Buchberger (2013) for the studied scenarios.

A t test comparison for each 15-min increment (96 in a 24-h period) for each GI as compared to the current situation was performed for runoff volume of the July 1, 2002 storm. All results showed that the reduction in volumes was highly significant for all GIs with 95 percent confidence (Table 5).

Table 5 Summary t test: paired two sample for means current and GI
Full size table

To summarize, these results present simple and accurate methods of quantifying and analyzing the effect of urbanization as well as the hydraulic benefits of GI in reducing stream bank erosion throughout the reduction in total volumes of runoff, exceedance of shear stress and peak flow. These configuration options of GI could provide design guidance for developers in urban areas with respect to quantifying hydrological impact and designing parameters to meet cities’ concerns pertaining to stream bank erosion.

Summary and conclusions

The sub-hourly 15-min time step SWAT model was developed and integrated with different levels of GI to study their impact on the exceedance of critical shear stress and potential stream bank erosion. GIs studied were detention pond, bioretention/rain garden, and permeable pavement. Calibrated stream flows for a 2-year period using the 15- min time step had an R 2 of 0.78 and an NS of 0.78. The 2-year validation period had an R 2 of 0.70 and an NS of 0.67.

The bioretention and permeable pavement were represented into SWAT model based on SedFil modifications. While the detention pond used SWAT Detention pond module. The scenario that combines permeable pavement with rain garden resulted in the greatest potential of reduction in runoff volumes, peak flows, and excess shear stress under both actual and design storms. Bioretention as a stand-alone resulted in the second potential greatest reduction and detention pond alone had the least reduction percentages. All study scenarios showed a significant difference in mean runoff volume at 95% confidence rate.

This study shows that a careful planning at the watershed scale using GI can significantly reduce streambank erosion in urban areas, thus reducing the need for costly stream restoration projects. This study offers developers and city planners an option to establish a proper configuration system of GIs to tackle urban stormwater runoff challenges. Additionally, the study provides stormwater modelers with simple and practical methods to represent GIs into publically available programs such as SWAT to evaluate deployment options of GI on a watershed scale.