Introduction

Watershed management strategies are vital to efficiently utilize the natural resource as to maintain environmental regime. Watershed models that are capable of capturing hydrological processes in a dynamic manner can be used to provide an enhanced understanding of the relationship between land and water management options. In recent years, hydrologic models are more and more widely applied by hydrologists and resource managers as a tool to understand and manage ecological and human activities that affect watershed systems (Zhang 2009). Several models have been developed [Système Hydrologique Européen (SHE) (Abbott et al. 1986; Bathurst and O’Connell 1992; Refsgaard and Storm 1995), Institute of Hydrology Distributed Model (IHDM) (Beven and Morris 1987) and the THALES (Grayson et al. 1992), Basin Scale Hydrological Model (BSHM) (Yu and Schwartz 1998), Soil and Water Assessment tool (SWAT) (Arnold et al. 1998, etc.] in the past that can continuously simulate stream flow, erosion or nutrient loss from a watershed (Table 1). One such model is the Soil and Water Assessment Tools (SWAT) model, which is a continuous time model that operates on a daily time step. The objective in model development is to predict the impact of management on runoff, sediment and agricultural chemical yields in large and small watershed (Shrivastava et al. 2004). Application of SWAT model in runoff and sediment yield modeling (Srinivasan et al. 1993, 1998, 2010; Srinivasan and Arnold 1994; Cho et al. 1995; Rosenthal et al. 1995; Bingner et al. 1997; Peterson and Hamlett 1998; Arnold et al. 1999; Shrivastava et al. 2004; Chaplot 2005; Setegn et al. 2008; Betrie et al. 2011; Murty et al. 2013; Suryavanshi 2013) has drawn significant attention over the past two decades due to its simplicity to address wide range of watershed problems at desired spatial and temporal scales. Many researchers have tested the capability of SWAT model under data scare conditions. Ndomba et al. (2008) intended to validate the Soil and Water Assessment Tool (SWAT) model in data scarce environment. Their results indicated the satisfactory performance of swat model with or without the use of observed flows data. The major advantage of the model is that, unlike other conventional conceptual simulation models, it does not require much calibration (Gosain et al. 2005). The SWAT model was originally developed to operate in large‐scale ungauged basins with little or no calibration efforts (Arnold et al. 1998). It attempts to incorporate spatially distributed and physically distributed watershed inputs to simulate a set of comprehensive processes, such as hydrology (both surface and subsurface up to the shallow aquifer), sedimentation, crop/vegetative growth, pesticides, bacteria, and comprehensive nutrient cycling in soils, streams, and crop uptake. Most SWAT parameters can be estimated automatically using the GIS interface and meteorological information combined with internal model databases (Srinivasan et al. 1998; Zhang et al. 2008).

Table 1 List of some available models with their processes
Full size table

Semrakalwana, a small rural village in Allahabad, India has experienced insufficient water supply at the end of the dry seasons. Current village activities that require water included domestic farming system based on surface and ground water. These farming system include Crops, Dairy, Boundary Plantations, goatry, Poultry, Horticulture, Vermicompost, Agro forestry, Piggery activities (Denis 2013).

In India, topographical conditions, soil conditions, rainfall pattern and cultivation practices are different from those in the other parts of the world (Pandey et al. 2008). Therefore, it is required to evaluate the physical based models such as SWAT for a small agricultural dominant watershed. Hence, the present study was carried out with the explicit objective of evaluating SWAT model (in an unguaged catchment) and analysing the water balance components of Semra watershed as well as Semrakalwana village.

Materials and methods

Description of the study area

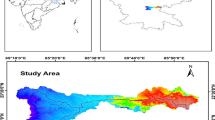
The Semrakalwana village (=4.31 km2), located in Tons river basin is considered as a study area (latitude 25o16′31N and longitude 82o4′55E) for this present study (Fig. 1). The study area is dominated by loamy soil. The major crops grown in the study area are wheat followed by pulses and potato. Orchards consisting of citrus plants are also grown in the study area. The study area is a part of humid subtropical climate and has an annual mean temperature of 26 °C with a minimum temperature of 2 °C in winters and a maximum of 48 °C in summers. The hot and dry summers begins from the month of March and carries on till June with May being the hottest months while winters falls between the months of November till end of February.

Fig. 1
figure 1

Location map of study area

Full size image

Data acquisition

Meteorological data

Historical daily rainfall and minimum and maximum data of eight years (2006–2013) were collected from IMD, Pune. Other meteorological data such as minimum and maximum temperature, solar radiation, relative humidity and PET were collected from Department of Forestry and Environment, Sam Higginbottom Institute of Agriculture, Technology and Sciences, Allahabad.

Rainfall

The study area has an average annual rainfall of 1066.8 mm from the last 8 years data (2006–2013, recorded by meteorological department Pune). Rainfall is fairly distributed over the area (Fig. 2a).

Fig. 2
figure 2

Daily values of rainfall (a); max and min temperature (b); solar radiation (c) and relative humidity (d) of Allahabad for 2006–2013

Full size image
Temperature

The basin experiences a moderate climate with a maximum temperature of 45 °C and minimum temperature of 29 °C. The maximum temperature was observed during summer season starting from March and ends in the last week of May. Minimum temperature was recorded in January. Monthly variation of minimum and maximum temperature from 2006 to 2013 is shown in Fig. 2b.

Solar radiation

The daily (2006–2013) variation of solar radiation of the study area is shown in Fig. 2c.

Relative humidity

The daily (2006–2013) relative humidity of the study area remains high with values ranging from 15 to 95%. The pictorial representation of yearly relative humidity is shown in Fig. 2d.

Satellite data

The cloud free digital data of the LANDSAT imaginary with 30 m spatial resolution was used to generate the land use/cover map of the study area (Fig. 3). Most common land use classification method, the supervised classification, was used in this study. The classification was carried out by the Ground Control Points (GCPs). These GCPs were collected with the help of hand held GPS during field visit of the study area during August–December 2014. Each pixel in the image dataset was then categorised into the land use class it most closely resembles. The classified land use/cover classes were found to be agricultural land, rural residential area, waste/barren land and water body.

Fig. 3
figure 3

Land use map of study area

Full size image

Advanced Space-borne Thermal Emission and Reflection Radiometer (ASTER) data was used for generation of the digital elevation model (DEM) of the study area (Fig. 4). ASTER elevation data which is available on public domain (http://gdem.ersdac.jspacesystems.or.jp) under joint operation of NASA and Japan’s Ministry of Economy, Trade and Industry (METI), provides high-resolution images in 15 different bands of the electromagnetic spectrum, ranging from visible to thermal infrared light with resolution of 30 m. The study area comprises loamy and clayey soil association (Fig. 5). Area occupied by each land use, soil and slope classes is presented in Table 2.

Fig. 4
figure 4

Digital elevation model of the study area

Full size image
Fig. 5
figure 5

Soil map of study area

Full size image
Table 2 Area occupied by each land use, soil and slope classes
Full size table

Brief description of SWAT model

The SWAT is a continuous time model that operates on a daily/sub-daily time step. It is a physically based model and can operate on large basins for long period of time (Arnold et al. 1998). The SWAT as described by Bian et al. (1996) is a semi-empirical and semi-physically based model. It adopts existing mathematical equations approximating the physical behaviour of the hydrologic system. It is also an advanced lumped or semi-distributed model dividing the catchment into discrete area units for analysis which makes it suitable for integration with a GIS. The Basin is subdivided into sub-basins that are spatially related to one another. This configuration preserves the natural channels and flow paths of the basin. Further, the sub basins are divided into hydrological response units (HRU’s). HRUs are discrete areas of similar slope, soil and land use through which water is expected to flow in a more or less homogenous fashion. It lumps the results at the outflow of each unique area. Final results are then summarized for the whole basin at the final outlet. Each of these is analyzed separately to improve the accuracy of the model, but results are lumped per sub basin and averaged for the entire catchment in the final report.

No matter what physical problem is studied using SWAT, water balance is the driving force behind everything that happens in the watershed (Neitsch et al. 2005). Water Balancing simply means; finding out how much water comes into the system and then finding out where that water goes. In terms of water balance storages for each HRU in the watershed, four layered storage possibilities exist. Snow is the first, then a soil profile of up to 2 m, followed by a shallow aquifer underneath it comprising the next 18 m up to 20 m, and a deep aquifer sitting below 20 m underground is the final storage space from which water is ultimately completely lost to the SWAT system. Water balance equation used by the SWAT model is given below:

$${\text{SW}}_{t} = {\text{SW}} + \sum_{t - 1}^{t} (R-Q-{\text{ET}}-P-{\text{QR}})$$
(1)

where SW t is the final soil water content (mm), SW is the initial soil water content (mm), t is the time (days), R is the amount of precipitation (mm), Q is the amount of surface runoff (mm), ET is the amount of evapotranspiration (mm), P is percolation (mm) and QR is the amount of return flow (mm).

SWAT model setup for the study area

The SWAT model setup was carried out with Arc GIS interface (Arc SWAT 2009.93.7a). The interface helped in watershed parameterization and model input. The input parameters of the model were extracted from the satellite imageries, DEM analysis, soil maps and field observations. The stream network was generated by the use of a threshold area that defines the origin of a stream. The delineation scheme with moderate subdivision level gives the best modeling efficiency (Gong et al. 2010). In this study, threshold value is considered as 0.5 ha. Hydrological response units (HRUs) were created using unique land use/cover, soil and slope layers. A total number of two sub basins and 50 HRUs were created in the study area.

Criteria for model evaluation

For scientifically sound model evaluation, a combination of different efficiency criteria is recommended (Krause et al. 2005). In this study, well-known statistical criterion such as Coefficient of determination (R 2), Nash–Sutcliffe coefficient (E NS), Index of agreement (d), Modified forms of Nash–Sutcliffe coefficient (E) and Index of agreement (d1), Percent bias (PBIAS) and RMSE-observations Standard deviation Ratio (RSR) were used to evaluate model performance where, \(Y_{i}^{\text{obs}}\) is the ith observed data, \(Y_{\text{mean}}^{\text{obs}}\) is mean of observed data, \(Y_{i}^{\text{sim}}\) is the ith simulated value, \(Y_{\text{mean}}^{\text{sim}}\) is the mean of model simulated value, and N is the total number of events.

The coefficient of determination (R 2 ) Willmot (1981) and Legates and McCabe (1999)

$$R^{2} = \left( {\frac{{\sum\nolimits_{i = 0}^{n} {\left( {Y_{i}^{\text{obs}} - Y_{\text{mean}}^{\text{obs}} } \right)\left( {Y_{i}^{\text{sim}} - Y_{\text{mean}}^{\text{sim}} } \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {\left( {Y_{i}^{\text{obs}} - Y_{\text{mean}}^{\text{obs}} } \right)^{2} \sqrt {\sum\nolimits_{i = 1}^{n} {\left( {Y_{i}^{\text{sim}} - Y_{\text{mean}}^{\text{sim}} } \right)^{2} } } } } }}} \right)^{2}$$
(2)

Nash–Sutcliffe coefficient (E NS ) Nash and Sutcliffe (1970)

$$E_{\text{NS}} = 1 - \left[ {\frac{{\sum\nolimits_{i = 1}^{n} {\left( {Y_{i}^{\text{obs}} - Y_{i}^{\text{sim}} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{n} {\left( {Y_{i}^{\text{obs}} - Y_{\text{mean}}^{\text{obs}} } \right)^{2} } }}} \right]$$
(3)

Index of agreement (d) Willmot (1981)

$$d = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {\left| {Y_{i}^{\text{obs}} - Y_{i}^{\text{sim}} } \right|^{2} } }}{{\sum\nolimits_{i = 1}^{n} {\left( {\left| {Y_{i}^{\text{sim}} - Y_{\text{mean}}^{\text{obs}} } \right| + \left| {Y_{i}^{\text{obs}} - Y_{\text{mean}}^{\text{obs}} } \right|} \right)}^{2} }}$$
(4)

Modified forms of Nash–Sutcliffe coefficient (E) and Index of agreement (d1) Krause et al. (2005)

$$E = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {\left| {Y_{i}^{\text{obs}} - Y_{i}^{\text{sim}} } \right|^{j} } }}{{\sum\nolimits_{i = 1}^{n} {\left| {Y_{i}^{\text{obs}} - Y_{\text{mean}}^{\text{obs}} } \right|}^{j} }}\quad {\text{with}}\;j \in N$$
(5)
$$d1 = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {\left| {Y_{i}^{\text{obs}} - Y_{i}^{\text{sim}} } \right|^{j} } }}{{\sum\nolimits_{i = 1}^{n} {\left( {\left| {Y_{i}^{\text{sim}} - Y_{\text{mean}}^{\text{obs}} } \right| + \left| {Y_{i}^{\text{obs}} - Y_{\text{mean}}^{\text{obs}} } \right|} \right)}^{j} }}\quad {\text{with}}\;j \in N$$
(6)

Percent bias (PBIAS) Gupta et al. (1999)

$${\text{PBIAS}} = \left[ {\frac{{\sum\nolimits_{i = 1}^{n} {(Y_{i}^{\text{obs}} - Y_{i}^{\text{sim}} ) \times (100)} }}{{\sum\nolimits_{i = 1}^{n} {(Y_{i}^{\text{obs}} )} }}} \right]$$
(7)

RMSE-observations Standard deviation Ratio (RSR) Chu and Shirmohammadi (2004), Singh et al. (2004), Vazquez-Amábile and Engel (2005) and Legates and McCabe (1999)

$${\text{RSR}} = \frac{\text{RMSE}}{{{\text{STDEV}}_{\text{obs}} }} = \frac{{\left[ {\sqrt {\sum\nolimits_{i = 1}^{n} {(Y_{i}^{\text{obs}} - Y_{i}^{\text{sim}} )^{2} } } } \right]}}{{\left[ {\sqrt {\sum\nolimits_{i = 1}^{n} {(Y_{i}^{\text{obs}} - Y_{i}^{\text{sim}} )^{2} } } } \right]}}$$
(8)

Sensitivity analysis of SWAT model parameters

Sensitivity analysis was carried out to examine the relative changes in the flow with respect to change in selected model input variables. In this study, a LH-OAT sensitivity analysis, which is incorporated in SWAT, is used to perform sensitivity analysis. The analysis was carried out based on the objective function of the SSQ for 20 model parameters and 10 intervals of LH sampling. After set-up of the SWAT model and incorporating all the input parameters simulations were carried out and sensitivity analysis was run for the period of 8 years (2006–2013). The parameters selected for the sensitivity analysis and their rank with the mean values after analyzing their sensitivity to flow are exhibited in Table 3. The parameter producing the highest average percentage change in the objective function value is ranked as most sensitive. The result of the sensitivity analysis indicates that, CN is the most sensitive parameter to the output followed by soil evaporation compensation factor (ESCO), available water capacity of the soil layer (SOL_AWC), soil depth (SOL_Z) maximum potential leaf area index (BLAI), threshold depth of water in the shallow aquifer for return flow to occur (GWQMN) groundwater revap coefficient (GW_REVAP), maximum canopy storage (CANMX), hydraulic conductivity in main channel (CH_K2) and threshold depth of water in shallow aquifer for revap to occur (REVAPMN), respectively. The least sensitive parameters observed were average slope length (SLSUBBSN), average slope steepness (SLOPE) and biological mixing efficiency (BIOMIX), respectively. Sensitivity analysis indicated the overall importance of all parameters in determining the runoff of the study area. All the parameters generally govern the surface and subsurface hydrological processes and stream routing. These results illustrates how parameter sensitivity is site specific and depends on land use, topography and soil types compared to other studies.

Table 3 SWAT parameters with rank according to sensitivity to the simulated output
Full size table

Evaluation of SWAT model

The study area (Semra watershed) is a small ungauged watershed. For the study area, stream flow data was not available. Due to this limitation proper model calibration was not performed in this study. The study has to rely on the next foremost component of hydrological cycle, i.e. Evapotranspiration. An attempt was made to evaluate the performance of the SWAT model with the help of observed ETP data obtained from SHIATS weather station for a period 2008–2013. The main focus of this manuscript is evaluating SWAT model in an unguaged catchment and analysing the water balance components. The major advantage of the SWAT model is that unlike the other conventional conceptual simulation models, it does not require much calibration, and therefore, can be used on ungauged watersheds (in fact, the usual situation) (Gosain et al. 2005, 2006, 2011; Margaret et al. 2015).

The observed and simulated daily ETP for the validation period along with 1:1 line is shown in Fig. 6. It is observed from the figure that the simulated ETP values are distributed uniformly about the 1:1 line. A high value of coefficient of determination (R 2 = 0.78) indicates a close relationship between the observed and simulated ETP. Further, the efficiency of the model for simulating ETP was tested by statistical analysis and the results are presented in Table 4. A high value of Nash–Sutcliffe model efficiency of 0.77 indicates that there is a good agreement between the observed and simulated ETP during evaluation period. The range of index of agreement, modified forms of Nash–Sutcliffe coefficient (E) and modified forms of index of agreement (d1) are similar to that of R 2 and lies between 0 (no correlation) and 1 (perfect fit) and found to be 0.83, 0.71 and 0.73, respectively. The optimal value of PBIAS is 0.0, with low-magnitude values indicating accurate model simulation. Positive values indicate model underestimation bias, and negative values indicate model overestimation bias (Gupta et al. 1999). The value of PBIAS was found to be 3.19. RSR varies from the optimal value of 0 to a large positive value. The lower is the RSR, the lower RMSE, and the better the model simulation performance (Krause et al. 2005). The RSR value was found to be 3.97 which can be termed as “good rating”. Thus, the results indicate that the overall prediction of ETP by the SWAT model during the evaluation period was satisfactory, and therefore, can be employed in a small agricultural dominated unguaged watershed.

Fig. 6
figure 6

Comparison between the daily observed and predicted PET from 2008 to 2013 for model validation

Full size image
Table 4 Statistical analysis of observed and simulated ETP for the years 2008–2013
Full size table

Water balancing of Semrakalwana village

A water balancing analysis was performed in the Semrakalwana village which is a part of Semra watershed. Water balancing analysis was performed on hydrologic response unit (HRU) basis. This is the smallest spatial unit of the model, and this approach lumps all similar land uses, soils, and slopes within a sub-basin based upon user-defined thresholds. Figure 7 depicts the spatial distribution of various water balance component on HRU basis. For the Semrakalwana village, average annual rainfall was found to be 1064–1066 mm. The average annual surface runoff varied from 379 to 386 mm while the evapotranspiration of the village was in the range of 359–364 mm. The average annual percolation and return flow was found to be 265–272 mm and 147–255 mm, respectively. The initial soil water content of the village was found in the range of 328–335 mm while the final soil water content was 356–362 mm.

Fig. 7
figure 7

Spatial distribution of various water balance component of Semrakalawan village

Full size image

Water balance analysis of Semra watershed

An analysis was also performed out to evaluate the seasonal and yearly water balance of the Semra watershed for the period of 2008–2013 (6 years). The water balancing analysis was classified into three seasons, i.e. Kharif season (August–October), Rabi season (November–April) and Zaid season (May–July). The water balance of Semra watershed consisting rainfall, evapotranspiration, surface runoff and water yield components are exhibited in Table 5.

Table 5 Average seasonal and annual water balance of Semra watershed
Full size table

Kharif season

It is observed from Table 5, that about 50% (530.14 mm) of annual rainfall (1066.8 mm) occurs during Kharif season. Out of total yearly runoff of 421.88 mm about 45% of runoff occurs in Kharif season. The water yield (water that leaves the sub basin and contributes to stream flow that is Runoff + groundwater flow in shallow aquifer-transmission losses) in Kharif season was almost 46% of the annual water yield (705.65 mm). The study area falls under the Tons river basin. Tons basin is a rain-fed river so the hydrology of the study area is greatly influenced by rainfall. The Tons river swells up and floods occur during rainy season and dries up in the summer. Therefore, if the water is not stored in Kharif season, famine like conditions is created during the remaining part of the year. ET contribution in the Kharif season was found to be 46.51% (151.69) of yearly ET. ET has a large impact on water and other natural resources and distribution and abundance of these resources are governed by the volume and seasonality of available moisture (Neilson et al. 1992).

Rabi season

This is lean season with average rainfall of only 197.1 mm (Table 5). The runoff contribution in Rabi season is about 18% of the yearly runoff. Being a rain-fed watershed, the Rabi season (winter crop season) is adversely affected due to less availability of water for crops. It has to be noted that the economic conditions of the people restricts the cultivators to put up tube wells, shallow wells or tanks with their own resources. ET contribution in the Rabi season was found to be 24% of the yearly ET. The water yield from this season is 148.72 mm which is 21% of the annual water yield contribution. Water yield was found to be lowest in this season (compare to Kharif and Zaid) may be because the unsaturated condition of the soil in the study area and the reduction in the quantity of the rainfall followed by the reduction in the surface runoff contribution to the stream flow during this season.

Zaid season

About 32% (341.63 mm) of the yearly rainfall occurred in Zaid season (Table 5). The percentage of runoff occurred in the study area in Zaid season is about 37% (154.47 mm) of the yearly runoff (421.88 mm). On the other hand the ET contribution in this season was found to be about 29% (95.99 mm) of yearly ET. Water yield was found to be 231.1 mm which is 33% of the annual water yield.

Yearly water balance

It was observed that, out of 1066.8 mm annual average rainfall, 421.88 mm flows out as surface runoff from the study area (Table 5). The annual average water yield was found to be 705.65 mm. While the average annual ET of the study area was 326.1 mm. The study area is agricultural dominated watershed; however, the economic condition of a large population depends on agriculture, remains under-privileged due to agro-climatic condition and poor management of water resources. Conservation structures such as check dams, farm ponds, tanks, stop dams, rock fill dams, percolation tank, vegetative barrier can be constructed in study area to reduce monsoon runoff and conserve it for basin requirements in lean period. Appropriate best management practices like strip cropping, grassed waterways and vegetative filter strips can also be implemented for better water management.

Summary and conclusions

SWAT model was appraised to be a fair model for water-balance study in the agricultural dominated sub basins. Due to unavailability of the observed runoff data, the performance of the model was evaluated using observed PET. The results of SWAT model revealed that the SWAT model does not require much calibration and can be used in predicting the water balancing components of the study area. The SWAT model was applied to analyze seasonal and annual water budget for Semrakalwana village and Semra watershed. Water balancing analysis of Semrakalwana village was performed on HRU basis. The average annual rainfall and runoff was found to be nearly 1065 and 383 mm, respectively. The evapotranspiration of the village was found to be approximately 362 mm. The average annual percolation and return flow was found to be approximately 270 and 147–255 mm, respectively. The initial soil water content of the village was found in the range of 328–335 mm while the final soil water content was 356–362 mm. The water balancing analysis was also performed on seasonal (Kharif, Rabi and Zaid seasons) as well as on yearly basis. The seasonal hydrological assessment exhibited that about 50% of annual rainfall (1066.8 mm) occurs during Kharif season. In the Rabi season which is lean season, rainfall was found to be 197.1 mm and during the season of Zaid the rainfall was about 341 mm. The water yield (water that leaves the sub basin and contributes to stream flow) in Kharif season was almost 46% of the annual water yield. In the Rabi season it was found to be lowest with 148.72 mm while in the season of Zaid it was found to be 231.1 mm. ET contribution in the Kharif season was found to be 46.51% (151.69) of yearly ET. In the Rabi and Zaid seasons ET was found to be 78.96 and 95.99 mm, respectively. The yearly water balance revealed that out of 1066.8 mm annual average rainfall, 421.88 mm flows out as surface runoff. The annual average water yield was 705.65 mm and the average annual ET of the study area was found to be 326.1 mm.

The geological features of the study area and economic condition of the people, circumscribes the use of tube wells, shallow wells or tanks with their own resources. Moreover, the economic condition of a large population depends on agriculture and allied activities, remains under-privileged due to uncertain agro-climatic condition and poor management of water resources. As the study area fall under a rain-fed river basin (Tons river basin) with no contribution from snowmelt, the winter and summer season are highly affected by less water availability for crops and municipal use. Appropriate best management practices like strip cropping, grassed waterways and vegetative filter strips can also be employed for better water management in the basin.