Introduction

Improper maintenance of WWTP can trigger serious ecological and public health problems and also it may be a reason for various water borne diseases affecting human health and aquatic life. Nitrogen and phosphorous are the key nutrients supporting the growth of algae and organic matter which instigate eutrophication in water bodies. Various control actions have to be implemented for efficient monitoring of process performance during the operation of wastewater treatment plant (WWTP) (Boelee et al. 2011). Models are necessary for the reason that, the effects of tuning the operating variables can be studied more transiently on a computer than by doing experiments. Hence, many alternative schemes and operational strategies can be evaluated without the need for physical trials of each scenario (Thalla et al. 2010; Pai et al. 2011). By simulating the performance assessment models using suitable influential variables, one can rapidly respond to any changes in the processes and devise operational strategies to shift the plant to new operating conditions which improves its stability, the quality of the effluent and at the same time achieve reduction in the running costs (Miller et al. 1997; Nair et al. 2016; Kumar and Saravanan 2009). Several deterministic, stochastic and time series-based models have been developed for predicting the performance of WWTPs, (Guo et al. 2014; Ráduly et al. 2007; Denai et al. 2004; Erdirencelebi and Yalpir 2011; González et al. 2009). In the recent past, soft computing tools such as artificial neural network (ANN), adaptive neuro-fuzzy inference system (ANFIS) have also been widely used for wastewater treatment prediction studies (Belanche et al. 1998; Elmolla et al. 2010; Cakmakci 2007).

Nitrogen is a major wastewater nutrient and exists in various forms, including free ammonia, organic nitrogen, nitrate and nitrite each of which may be assessed for in a variety of ways. Fresh wastewater nitrogen is generally present in the ammonia and organic nitrogen forms, with the minute corpus of nitrite and nitrate forms (Sharma and Chopra 2015). The effluent may consist of either ammonia or nitrate nitrogen depending on the extent of nitrification, which exists within the treatment plant. Under routine conditions, the nitrite form of nitrogen does not exist in fat quantities due to its instantaneous oxidation or transformation to nitrate (Zhang and Gao 2000). Total Kjeldahl Nitrogen (TKN) is a chemical analysis to ascertain both the organic and the ammonia nitrogen. The TKN value corresponds to a total nitrogen concentration, which is the summation of organic nitrogen compounds and ammonia nitrogen [TKN = org-N + NH4–N (mg/L)]. Nitrogen mainly occurs in wastewater in the TKN form. After biological wastewater treatment, TKN mostly appears as oxidized nitrite (Liu et al. 2013).

The objective of the current study is to investigate the applicability of support vector machine (SVM) and adaptive neuro-fuzzy inference system (ANFIS) modeling approach for predicting the Kjeldahl Nitrogen removal from a domestic WWTP. Support vector machine is a unique state-of-the-art classification and regression technique based on the framework of Vapnik’s statistical learning theory (Cortes and Vapnik 1995) designed to solve complex regression problems. The hybrid neuro-fuzzy approach developed from the combination of neural network and fuzzy system paves way for implementing an effective tool/algorithm for solving non-linear and complex real-world problems. Due to its abilities, such as handling imprecisions, uncertainties and large data sets, adaptive neuro-fuzzy inference system (ANFIS) is evolved to be one of the commonly used techniques. ANFIS trains the influencing parameters of the fuzzy inference system through a learning algorithm deduced from neural network (Jang 1993). Considering the difficulties associated with the conventional or analytical approaches and the experimentation/computational cost, SVM and ANFIS techniques are suitable choices to predict the Kjeldahl Nitrogen removal in the system.

Description of WWTP and data analysis

The data sets were obtained from the Kavoor Wastewater Treatment Plant (WWTP) situated at Mangalore which serves a population of 440,000. The design capacity of the WWTP is 43.5 MLD, respectively. The normal operating DO in the aerobic reactor was about 1.7–2.5 mg/L. The sludge retention time was about 8–10 days with a hydraulic retention time of 7–8 h. The mixed liquor suspended solids (MLSS) maintained in the aerobic reactor was about 4200–4500 mg/L. The data set contains daily time series data analyzed and recorded at the WWTP plant during the period June–Sept 2014 with a total of 88 data points (period of 4 months) of seven variables, namely pH, total solids (TS), chemical oxygen demand (COD), temperature (T), free ammonia (FA), ammonia nitrogen (AN) and total Kjeldahl Nitrogen (TKN). The Kavoor WWTP adopts a biological treatment process, which possess the capability to remove phosphorus and nitrogen simultaneously under anaerobic and aerobic environments. The Kavoor WWTP consists of screening, grit chamber, anaerobic, aerobic reactors and a secondary clarifier as shown in Fig. 1. Complete removal of total Kjeldahl Nitrogen (TKN) is practically unachievable in the WWTP’s having a pre-anaerobic system, wherein the anaerobic reactor is positioned behind the aerobic reactor and the mixed liquor involving nitrate is recirculated to the aerobic reactor from the secondary clarifier. The nitrate recirculation rate needs to be intensified, so as to improve the TKN removal efficiency, which steers to higher power consumption and dissolved oxygen (DO) return from the aerobic reactor (Liu et al. 2013).

Fig. 1
figure 1

Schematic flow diagram of Kavoor WWTP

Full size image

The raw influent is fed into the bar screen, followed by grit chamber, anaerobic, and aerobic reactors, subsequently the sludge from the secondary clarifier is restored to the aerobic reactor. The treatment plant incorporates a simultaneous nitrification and denitrification (SND) process which initiates with partial nitrification of NH4+ to nitrite and successively continues with an immediate reduction of nitrite to N2 gas. In SND process, nitrification and denitrification exist simultaneously in the same reactor basin under identical operating conditions (Breisha 2010). The main factors affecting nitrogen removal efficiency are temperature, nitrate concentration, dissolved oxygen, alkalinity, pH, BOD, COD and free ammonia concentration. At high temperatures (between 28 and 38 °C) the specific growth rate of ammonia oxidizing bacteria (AOB) will be higher than that of nitrite oxidizing bacteria NOB effecting in enhanced nitrogen removal rate via nitrite. Nitrifiers are vulnerable to temperature than heterotrophic bacteria. Optimal pH for effective nitrification is somewhere between 7 and 8.5. pH lower than 6 can cause inhibition. Alkalinity acts as a source of carbon for nitrifier growth. Nitrifiers are very sensitive to diverse kinds of compounds present in wastewater and get inhibited at very low DO levels. If the operating solids retention time (SRT) is lesser than the minimum SRT, nitrification process will be hampered. COD plays a role during denitrification process. Even though high DO concentrations are required to augment the activity of nitrifiers in the reactor, denitrification gets inhibited by excess oxygen. Free ammonia also inhibits the ammonium and nitrite oxidation during nitrification and denitrification processes. Hence, in the present context, the factors such as influent pH, COD, total solids (TS), temperature (T), free ammonia (FA), ammonia nitrogen (AN) and total Kjeldahl Nitrogen (TKN) are used as predictors to predict the effluent total Kjeldahl Nitrogen (TKN) concentrations using artificial intelligence (AI) models. The influent and effluent wastewater characteristics are analyzed on a daily basis by adopting the grab sampling technique. The details of sampling source and the laboratory methods of wastewater analysis are provided in Table 1. Sampling is carried out between 8 am and 10 am every day as the plant receives its peak flow. The descriptive statistics of the observed variables of WWTP are presented in Table 2. The Xmax, Xmin, Xmean, SD, & Cv denotes the maximum, minimum, mean, standard deviation and variance of the data respectively.

Table 1 Sampling source and the laboratory methods of wastewater analysis
Full size table
Table 2 Statistical indices of various parameters of WWTP
Full size table

Methodology

Support vector machine

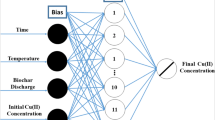
Support vector machine is a unique state-of-the-art classification and regression technique based on the framework of Vapnik’s statistical learning theory (Cortes and Vapnik 1995) designed to solve complex regression problems. The SVM technique has been effectively used to perform multivariate function estimation, nonlinear regression problems, etc. due to its competence to escape from local minima, improved generalization capability and sparse representation of the solution (Vapnik 1999). SVM is based on structural risk minimization principle wherein it addresses the problem of overfitting by balancing the model’s complexity. Non-linear problems are tackled by transforming them into linear ones in multi-dimensional feature space using Kernel functions. The structure of SVM is as represented in Fig. 2. With the innovation of Vapnik’s ε-insensitivity loss function, the SVM is still more capable to solve nonlinear regression problems (Smola and Schölkopf 2004). In order to achieve a good generalization performance, it is essential to find certain optimal hyper-parameters of SVM model. The hyper-parameters that need to be tuned are the regularization parameter (C) that controls the generalization performance of SVM, secondly the kernel parameter specific to the type of kernel adopted and finally the radius of ε—insensitive zone which determines the number of support vectors (Cristianini and Shawe-Taylor 2000; Kecman 2001). A brief description and derivation of support vector regression can be referred from various literatures (Smola and Scholkopf 2004; Cristianini and Shawe-Taylor 2000; Raghavendra and Deka 2015a).

Fig. 2
figure 2

(Source: Raghavendra and Deka 2014)

Schematic diagram of SVM and ANFIS Structure

Full size image

ANFIS architecture

ANFIS, a hybrid fuzzy logic-based technique integrated with the learning power of artificial neural network improves the performance of any kind of intelligent system by utilizing knowledge acquired after learning. For a real-time input–output dataset, a hybrid learning algorithm such as ANFIS constructs a backpropagation gradient descent and least squares methods associatively to frame a fuzzy inference system whose membership function parameters are iteratively tuned or adjusted. Adaptive neuro-fuzzy inference systems comprise of a mainly five layers—rule base, database, fuzzification interface, defuzzification interface and decision making unit (Jovanovic et al. 2004; Raghavendra and Deka 2015b). The generalized ANFIS architecture proposed is summarized below.

The ANFIS is a fuzzy Sugeno model that allocates the structure of adaptive systems to assist learning and adaptation. ANFIS architecture comprises of five layers. Every single node in layer 1 is an adaptive node with a node function which may be anyone among the membership functions. Every node of layer 2 is a fixed node labeled ‘π’ which signposts the firing strength of each rule. All nodes of layer 3 are fixed nodes labeled as ‘N’ which demonstrates the normalized firing strength of each rule. The layer 4 is as similar to layer 1 wherein every node is an adaptive node governed by a node function. The layer 5 being a single fixed node labeled ‘Σ’, representing the final output (f), defined as the summation of all arriving signals.

Figure 2, shows the implementation of two fuzzy rules using ANFIS architecture. The appropriate choice of the type and the parameters of the fuzzy membership functions and rules play a vital role in achieving the desired performance but in most circumstances, it is problematic (Raghavendra et al. 2015). Sometimes these parameters are chosen on the basis of trial and error method which enlightens the importance of tuning the fuzzy system. The main objective of training the ANFIS system is to govern the optimal premise and resultant parameters. ANFIS can be used to train the FIS model by modifying the membership function parameters based on error chosen criterion to cope with the training data. The FIS model having parameters related to the least checking data model error is selected, when ANFIS contains the checking data and training data.

Performance evaluation

The level of confidence over the predictions of any developed model is assessed by using suitable statistical indices. Correlation coefficient (CC), root mean square error (RMSE) and Nash–Sutcliffe error (NSE) were used to evaluate the model accuracies. Although RMSE values are used to distinguish model performance in training and testing period, it can also be used to compare the performance of individual model to other predictive models. To assess the performance of ANFIS models the following statistical indices were adopted.

  1. 1.

    Correlation coefficient (CC)

    $${\text{CC}} = \frac{{\sum\limits_{i = 1}^{n} {\left( {X_{i} - \bar{X}} \right) \times \left( {Y_{i} - \bar{Y}} \right)} }}{{\sqrt {\sum\limits_{i = 1}^{n} {\left( {X_{i} - \bar{X}} \right)^{2} \times \sum\limits_{i = 1}^{n} {\left( {Y_{i} - \bar{Y}} \right)^{2} } } } }}.$$
    (1)
  2. 2.

    Root mean square error (RMSE)

    $${\text{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^{n} {\left( {X_{i} - Y_{i} } \right)^{2} } }}{n}} .$$
    (2)
  3. 3.

    Nash–Sutcliffe coefficient (NSE)

    $${\text{NSE}} = 1 - \frac{{\sum\limits_{i = 1}^{n} {\left( {X_{i} - Y_{i} } \right)^{2} } }}{{\sum\limits_{i = 1}^{n} {\left( {X_{i} - \bar{X}} \right)^{2} } }},$$
    (3)

    where X = observed/actual values; Y = predicted values; \(\overline{X}\) = mean of actual data values; n = total number of values.

Results and discussion

The dataset is split into ‘train dataset’ which includes 74% (65 data points) of data in the period of 2nd June 2014 to 30th August 2014 and ‘test dataset’ composed of the remaining 26% data (23 data points) in the period of 1st September 2014 to 30th September 2014. The train dataset was used to build/simulate the model and the test dataset was employed to evaluate the performance of the built model. In order to investigate the dependency between variables that influence total Kjeldahl Nitrogen (TKN), cross-correlation coefficients between effluent TKN and each input parameter were analyzed and are presented in Table 3. This data were exercised to assist in selecting input variables for ANFIS and SVM models. From Table 3, it can be noticed that the effluent TKN at the time (t) is strongly correlated with the influent total Kjeldahl Nitrogen concentration [with a correlation value of 0.952(in train dataset) and 0.92(test)]; Influent ammonia nitrogen concentration [with a correlation value of 0.916(train) and 0.85(test)]; and the influent free ammonia concentration [with a correlation value of 0.87(train) and 0.76(test)]. The cross-correlation coefficients between the effluent TKN and other variables (influent total solids, COD concentrations, temperature) were also found to be fairly influential. The cross-correlation coefficients between the effluent TKN and the influent pH ranged from −0.597(train) and −0.532(test). The negative correlation indicates that a high occurrence or amount of TKN is rendered in the effluent during decreased pH of the influent.

Table 3 Cross-correlation between effluent total Kjeldahl Nitrogen (TKN) and other parameters
Full size table

The analysis is carried out to predict the concentration of effluent Kjeldahl Nitrogen using influent pH, TS, COD, Free ammonia, ammonia nitrogen, Kjeldahl Nitrogen as input variables. The cross-validation search is used to determine the optimal SVM hyper-parameters (C, γ and ε). SVM with RBF kernel function is implemented in the present case. The optimal parameters obtained after tuning the SVM model are as tabulated in Table 4. The modeling of ANFIS is carried out in MATLAB platform. The results obtained from SVM and ANFIS models with Gbell and trapezoidal MFs are depicted in the form of various statistical indices like RMSE, CC and NSE through tables and various plots. The optimal ANFIS architecture as presented in Table 4 is obtained after tuning fuzzy MF and rules of certain number and type.

Table 4 Details of SVM and ANFIS architecture
Full size table

The prediction errors of the models in the training and testing phases are as presented in Table 5. In the SVM model, the RMSE and NSE are significantly less in both training and testing stages when compared to that of ANFIS models. The magnitude of RMSE and NSE computation infers that the ANFIS model with Gbell membership function closely predicts the effluent Kjeldahl Nitrogen concentration than that of trapezoidal membership function. Here, the RMSE = 0.795 mg/L, NSE = 0.79 and CC = 0.85 of ANFIS model with Gbell membership function during test phase verifies the close agreement of concentration of effluent Kjeldahl Nitrogen with the observed concentration. The comparative evaluation of results obtained from Gbell and trapezoidal ANFIS models along with the SVM model during the prediction of effluent Kjeldahl Nitrogen is as presented in the form of graph (Fig. 3).

Table 5 Statistical results of SVM and ANFIS models
Full size table
Fig. 3
figure 3

Comparative performance evaluation of SVM and ANFIS models

Full size image

The SVM algorithm outperformed the ANFIS models, particularly in the testing stage. The prediction errors and correlation statistic of the SVM algorithm is relatively better than the ANFIS models as presented in Figs. 3 and 4, respectively. It is common to see that each and every model gets better solutions in the training stage as compared to that of testing stage. The possible reason for this is, the models will be trained over the range of dataset with specific maximum and minimum values. The mean of the dataset will also influence during training of a model. However, during testing of the model with another dataset of different minima and maxima, the model is usually unsuccessful to catch up the limits of the testing dataset. From the time series graph as presented in Fig. 4 during the effluent Kjeldahl Nitrogen prediction, it is observed that the SVM model closely follows the observed time series. The ANFIS model with Gbell MF appears to have the accepted accuracy during both training and testing phase.

Fig. 4
figure 4

Predicted effluent Kjeldahl Nitrogen concentration of SVM and ANFIS models during testing

Full size image

Figure 5 shows closely spaced scatters of the predicted and observed effluent Kjeldahl Nitrogen concentrations of SVM and ANFIS models during the testing phase. The reasonable dependence of a variable can be verified through the coefficient of determination (R 2) which ranges between 0 and 1 signposting the predictable extent of the dependent variable. The data points in the upper and lower extremes of the scatter plot of SVM model do not deviate to a great extent from the line of best fit indicating the goodness of the fit/model. In SVM model 82.48% of the variations in total Kjeldahl Nitrogen prediction is explained by taking into account of pH, TS, COD, T, FA and AN as predictors. It can be observed that ANFIS model with trapezoidal MF has more number of outliers than that of the SVM and Gbell ANFIS models during the test phase. From this, it can be ascertained that SVM model has higher consistency and robust performance during prediction.

Fig. 5
figure 5

Scatter plot of observed v/s Predicted of SVM and ANFIS models during testing

Full size image

Summary and conclusions

Much research has endorsed that biological wastewater treatment is an extremely viable treatment technology regarding nitrification–denitrification and phosphorus removal. In conjunction with optimized plant design and operating parameters, the biological wastewater treatment guarantees high effluent quality in terms of nitrates, ammonia, and phosphates existing in wastewater. According to contemporary European regulation, the total phosphorus and nitrogen in treated effluent should be in the range of 1–2 and 10–15 mg/L, respectively. In many situations, where the risk of public exposure to the reclaimed water exists, effective monitoring of effluent quality is necessary. The data related to influent pollutants, including the total suspended solids (TSS) and COD are utilized for immediate or short-term effluent quality prediction to provide information for efficient operation of the treatment process. In this study, the artificial intelligence models—SVM and ANFIS are being applied for the prediction of effluent Kjeldahl Nitrogen concentration yielded from a biological wastewater treatment plant. SVM and ANFIS models with Gbell and trapezoidal membership functions are tested in the study with input variables such as influent pH, TS, COD, Free ammonia, ammonia nitrogen and Kjeldahl Nitrogen. From the results presented above, cross-validation search was able to set the SVM parameters efficiently and thereby improve the forecasting efficiency of SVM. SVM models provided reliable prediction results than the ANFIS models. Among ANFIS models, Gbell MF MODEL was found to be slightly efficient in modeling the nonlinear time series. However, due to the computational complexity of various membership functions, trapezoidal membership function was found to be incompatible to model the effluent Kjeldahl Nitrogen concentration in the present study.