Introduction

Flood is a natural phenomenon, which threatens the life and properties of a large number of people all over the world, on a yearly basis. Flood discharge is of high importance in studies regarding water resource exploitation, flood control, construction of dams, basin management, and hydrologic studies. Therefore, the accuracy of these studies and the safety of waterworks and water structures depend on the methods of studies to a large extent. It is impossible to manage water resources in basins without accurate determination of the peak flood discharge (Bhadra et al. 2008; USBR 1998). The advances in flood estimation techniques have made it possible to use rainfall–runoff models to assess the hydrographic properties of flood in watersheds and decrease the risks of flood (Yonatan et al. 2009).

Non-accurate determination of rainfall and the costly process of collecting hydrologic data and statistics are among the difficulties of estimating flood properties in basins (Lopez et al. 2005; Vahabi and Ghafouri 2009). Today, it is a routine approach to use models to simulate rainfall–runoff, to access flood properties, including time-to-peak discharge. Therefore, the calibration and assessment of models are an inevitable and necessary task. WMS is a conceptual model which consists of different methods, including TR-55 (Technical Release 55), TR-20, SCS, HEC-1, and NFF (National Flood Frequency Regression Equation) (EMRL 1998). A number of studies have been conducted to employ this model for determining the peak flood discharge of different basins. Akbarpour and Sharifi (2005) used GIS (Geographical Information system) to obtain the physiographical characteristics of slope map, soil texture, and runoff curves of Bayeg and Rashtkhar basins, but determined the peak flood discharge of both basins using the WMS model. Based on their studies and sensitivity analysis, soil texture is an influential factor of peak flood discharge.

Benavides et al. (2001) evaluated flood control solutions through combined approaches available in GIS and other hydrologic software and obtained flood plain mapping in Cleakbasin. The obtained results suggested that a combined use of flood estimation techniques can increase the accuracy of estimation in the studied basin.

Dastorani et al. (2010) estimated flood discharge in UK basins with no registered statistics using artificial neural networks and reported satisfactory results. In their study, they expressed that to obtain satisfactory results, it is necessary to adopt a proper approach to identify and classify uniform basins.

Patrick et al. (2002) adopted six different approaches to estimate the mean flood discharge in Ontario, Canada, and compared their results.

Considering the fact that WMS has different methods for determining peak flood discharge, the accurate use of this model requires the investigation of each method, to select the model which best fits the flood data of the studied region. Therefore, this study tends to assess and calibrate the TR-20, TR-55, and HEC-1 methods of the WMS model in a given geographical region in Southwest Iran.

Materials and methods

Studied region

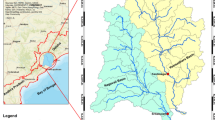
Simili Alluvial plain is located in Southwest Iran along the asphalted Ahvaz-Baghmalek road between Baghmalek and Haftgel cities, 70 km away from the northeast of Haftgel. The plain is surrounded by its mountains and is considered as a flat plain of Khuzestan Province. It lies within 49o21″–49o30″ longitude and 31o39″–31o44″ latitude. Simili is a plain that stretches from the northwest to the southwest and is surrounded by hilly heights. Its height is almost 563 m with a general slope from the east-southwest to northwest. Its area is approximately 49 km2. Figure 1 shows the location of the studied plain in Iran and Khuzestan Province.

Fig. 1
figure 1

Location of the studied region in Iran

Full size image

Physiographic studies

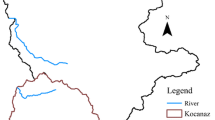
Basin physiography or in a simpler word, morphology, is a base subject of the hydrology field, and important parameters, such as the area, slope, and time of concentration along with the length gradient of the main stream, will be the main outcomes of this field. The studied basin map (scale: 1:25,000) and WMS model were used to conduct physiographic studies. This study used Arc GIS 9.2 and Arc Hydro Extension to obtain the properties of the studied basin. DEM (Digital Elevation Map) of the National Cartographic Center, NCC, was used for this purpose. The studied region of Simili basin was determined by putting the map sheets (58531se, 58532nw, 58532ne, 5852sw, 58532se, 59532sw, 59532nw, and 5953sw) together and merging them in River Tools. Figure 2 shows the DEM of the studied region, as well as the stream lines of the studied basin. Figure 3 shows the sub-basins of the studied basin, and Table 1 summarizes its features.

Fig. 2
figure 2

DEM map of the studied region

Full size image
Fig. 3
figure 3

Sub-basins of the Simili basin

Full size image
Table 1 Physiographic data of the Simili basin
Full size table

Results and discussion

Estimation of peak flood discharge using SCS method

Since there was no stream gauge (hydrometric station) in the studied area, the US, Soil Conservation Service method, SCS was used to extract the unit hydrography (UH) of sub-basins. The concentration time of the basin was derived from the following relation (Hydrologic Engineering Center 1998):

$${\text{Tc}} = \left( {\frac{{0.871L^{3} }}{\Delta h}} \right)^{0.385}$$
(1)

where Tc is time of concentration (h), L is the flow length (m), \(\Delta h\) is the difference between the minimum and maximum heights of the region.

However, the difference between the minimum and maximum heights of the region is derived from the following relation:

$$\Delta h = H_{\hbox{max} } - H_{\hbox{min} } .$$
(2)

To estimate the basin flood using the SCS approach, the following steps were utilized.

Selection of storm duration

Since the time of concentration of the studied basin is 4.5 h (less than 6 h), the continuity of storm was considered as 6 h.

Storm height

Given P (24, T) in the studied station, the maximum 6-h precipitation with different return periods, P (6, t), is derived from the following equation:

$$P_{(6,T)} = \frac{{P_{(24,T)} }}{1.48}.$$
(3)

Since the concentration time of the studied sub-basins is less than 6 h, the storm continuity was considered as 6 h. As mentioned previously, in the SCS method, the minimum storm duration is 6 h unless the time of concentration of a basin becomes more than 6 h, where the minimum storm duration is considered equal to the time of concentration. Table 2 summarizes the results of 6-h precipitation analysis.

Table 2 Design precipitation calculation results in summary
Full size table

Determination of curve number (CN)

To determine the mean CN coefficient on the surface of the design basin, the surface geological status of the basin, vegetation, and land applications were studied accurately and the CN coefficient was estimated. In general, soil hydrologic groups were divided into four subgroups: A, B, C, and D, which represent high permeability, moderate permeability, low permeability, and very low permeability, respectively (Poorhemmat and Sedghi 1999). Geological studies have reported weak vegetation for all four hydrologic groups in accordance with the investigations of the vegetation status of the basin, field visits, and SCS definition. Based on geological studies, permeability, vegetation, mean slope, and hydrologic conditions of basin soil, the CN value of the Simili basin was estimated to be 85. Therefore, it can be said that the basin soil lies inside group A from the hydrologic properties point of view. However, all estimations were practiced under average humidity condition.

Estimation of excess rainfall hyetograph

The basin rainfall–runoff is divided into two sections. Parts of it flows on the surface of the basin (surface runoff), while the remainder is lost as infiltration into the soil or vaporization (Akbarpour and Sharifi 2005; Remizas and Sedghi 1984). Rainfall which flows on the surface of basin and generates flood is called excess rainfall. The amount of excess rainfall for each rainfall is derived from the following relation based on the SCS method. Table 3 shows the results obtained from the calculation:

Table 3 Precipitation hyetograph with a return period of 100 years in the studied region
Full size table
$$S = \frac{25{,}400}{\text{CN}} - 254$$
(4)
$$Q = \frac{(P - 0.2S)}{(P + 0.8S)}$$
(5)

where S is the potential maximum retention (mm), CN is the runoff curve number, Q is runoff in mm, and P is the rainfall in mm

Calculation of basin unit hydrograph

Hydrograph and unit hydrograph are typical approaches for determining the peak flood discharge of a basin for different return periods. In this method, flood hydrograph was done based on the physiographic and rainfall properties of the studied basin. The synthetic unit hydrograph is derived from different methods, and the most important of which is the SCS. Figure 4 shows the unit hydrograph of the studied basin.

Fig. 4
figure 4

Unit hydrograph of the studied basin

Full size image

When the basin unit hydrograph was derived, the design flood hydrograph was calculated based on excess rainfall duration and design rainfall hyetograph. Based on the calculated results, the calculated peak flood rate for a return period of 100 years equals 179 m3. Figure 5 illustrates the design flood hydrograph with a 100-year return period.

Fig. 5
figure 5

Flood hydrograph with a 100-year return period provided by SCS

Full size image

Estimation of peak flood discharge using WMS

To calculate peak flood discharge using the WMS model, first, digital maps were entered into the software. Following the drawing of stream lines and determination of basin drainage outlet, the basin was closed and its features were extracted. Figure 6 shows the studied basin shape using this model. Here, after extracting the basin parameters, the peak flood discharge was estimated using HEC-1, TR20, and TR55 methods. In this study, the peak flood discharge was calculated by considering a 100-year return period. Figures 7, 8, and 9 show the results obtained using the aforementioned methods.

Fig. 6
figure 6

Simili basin

Full size image
Fig. 7
figure 7

100-year flood discharge hydrograph estimation using TR20

Full size image
Fig. 8
figure 8

100-year flood discharge hydrograph estimation using TR55

Full size image
Fig. 9
figure 9

100-year flood discharge hydrograph estimation using HEC-1

Full size image

Estimation of peak flood discharge using empirical methods (Dicken’s method)

Different studies on Khuzestan watersheds have adopted different empirical equations to calculate the peak flood discharge in basins with no statistics. A series of studies were conducted using 11 stream gauges of the province, where after reconstruction and completion of the station’s statistics, a new equation was generated in terms of area and return period, using the correlation between area and a 500-year return period flood of Dicken’s equation. This new equation can be applied in Khuzestan Province with a confidence level of 99 % for basins with areas up to 10,000 km2. This new equation was derived as follows (Shahidi and Shahmohammadi 2006):

$$Q\,{\text{m}}^{3} /{\text{s}} = (2/59{\text{Tr}}^{0/5235} )A_{{{\text{km}}^{2} }}^{{(0/692{\text{Tr}}^{0/0388} )}} .$$
(6)

By replacing the area of the Simili basin and a return period of 100 year, the peak flood discharge of the basin was calculated as 691.5 m3/s.

Discussion and conclusion

As shown in Table  1, Dicken’s empirical method calculated a peak flood discharge of 691.5 m3/s, while that of SCS was 179 m3/s, implying a significant difference between the former and the latter. This may be attributed to the CN calculation errors of SCS. However, the peak flood discharge calculated using TR55 was 407 m3/s and its difference with empirical values is less than that of the SCS method.

The peak flood discharge derived from TR20 was 107 m3/s, which is significantly different from the values derived from other approaches. In addition, the peak flood discharge derived from the HEC-1 method was 381 m3/s, which is lower than that calculated using Dicken’s empirical method. It seems that among the different methods used for determining the peak flood discharge of Khuzestan basins, the TR55 method of the WMS model offered values that are closer to the real values. Among the different methods of the WMS model, TR55-HEC-1 and TR20 methods had the highest accuracy in Southwest Iran, respectively.

There are various factors involved in the flowing of runoff and flooding, including intensity of rainfall, watershed slope, soil infiltrability, topographic conditions, topographic features, vegetation, and soil saturation (Thomas, 1968; Eard 1975). Riggs (1973), showed that watershed area could be the most important factor in runoff discharge, whereas the current study indicated that the adoption of the method for calculating the peak discharge of the hydrograph, even in the same watershed, could yield very different results. In addition to the peak discharge, the time of peak discharge and volume of instantaneous peak discharge will vary by selecting different methods. There are areas in the northern part of the Simili watershed suitable for farming. Moreover, Hansson et al. (2008) found that natural disasters, such as floodwater runoff, initially affect the local agriculture. Hence, simulation and modeling of floodwater runoff and modeling the floodwater are among the key parameters in floodwater management of the region. The TR-55 method is employed for watersheds smaller than 25 square miles, concentration time of shorter than 10 h, rainfall of less than 50 inches, and rainfall duration of shorter than 24 h. All these factors apply to the Simili watershed. Therefore, the greater accuracy of the results from this method than those from Dickens’ empirical model may be because the TR-55 model meets all the required conditions. With respect to floodwater volume also, considering the maximum flood discharge estimated in the empirical method, the floodwater volume estimated in the TR-55 method is closer to the actual values, because it estimates the maximum floodwater volume. Following the TR-55 method, the HEC-1, TR-20, and SCS methods rank second to fourth, as they estimate floodwater volumes of 5.06, 4.58, and 3.97 million cubic meters, respectively. Since the rainfall duration considered for the Simili watershed is 6 h, and the concentration time calculated based on morphological features of the watershed was 4.5 h, the time for the hydrograph peak discharge should be longer than the concentration time. According to Table 4, the time for hydrograph peak discharge calculated using HEC-1 is 3 h, which is less than the time of concentration for the watershed. Hence, it cannot be an accurate value. This becomes clearer by considering the estimated floodwater volume that indicates that a large volume of runoff is generated within a short time; since the Simili watershed is rectangular and the main channel in the watershed has a low slope, we expect the base time of the flood hydrograph to be longer that that derived from the HEC-1 method. This could be due to the rainfall distribution pattern considered in HEC-1, which is the same distribution pattern in SCS for rainfall duration of 6 h. In their studies, Modarres and Sarhadi (2010) found that the adoption of a single pattern of rainfall distribution could not provide acceptable results from simulations of maximum instantaneous discharge and hydrograph. Features related to rainfall are among the most important factors in hydrograph simulation. Due to the insufficient statistics at the hydrometric stations in the region, however, the distribution of rainfall in the region cannot be incorporated into the model. The peak discharge obtained from SCS was 25 % less than that obtained from Dicken’s empirical method. Moreover, the flood volume calculated by this method is lower as compared to those in other methods. Studies in Iran have demonstrated that the SCS method delivers accurate results for concentration time of down to 6 h, but not for concentration time of less than that. This could be due to the insensitivity of SCS to low rainfall depths. Hence, concentration time of less than 6 h should be modified (Alizadeh 2006). There are two procedures for using SCS in calculating peak discharge in small watersheds: (1) coefficients or graphs that modify peak discharge for small watersheds and (2) runoff is obtained for concentration time of 6 h, and then, the unit hydrograph is used (Mc Cuen 1989). The same logic is used in TR-55. The TR-20 calculated the minimum discharge (15 % of the value obtained from Dickens’ empirical method) with the maximum time to reach the peak discharge (about 13 h). This method involves using the unit hydrograph of the US Army Corps Engineers (2000). This model is based on the average unit hydrograph obtained from rainfall–runoff data for small agricultural watersheds in the United States, and the unit hydrograph of the watershed is calculated through using the dimensionless hydrograph in TR-20 (Chow et al. 1988; Nourani et al. 2009). Since the watershed lag time in this method is entered into the model as the main parameter, the results may drift apart from actual values in the case, the watershed concentration time is not calculated well. Moreover, the reference unit hydrograph in this method is that for small agricultural watershed in the United States. Therefore, differences in climatic conditions in generating the reference hydrographs in this method caused results obtained from using it in southwest of Iran to be far from the actual values. In a study across northeast of Iran, Lalozaee et al. (2013) found that HEC-1 provided more accurate results than TR-20.

Table 4 Flood discharge properties using different methods
Full size table

Conclusions

According to the results, it can be argued that, among the different methods used for estimating flood discharge in the southwest of Iran, the results obtained from the WMS model are lower than the empirical method. In fact, all the methods in the WMS model require calibration in the study region. In the small watersheds in the southwest of Iran, the TR-55 model yields better results than other methods, because the conditions required from using this model are satisfied. Moreover, the results obtained from this method can be pushed closer to the actual values if the watershed concentration time is calculated more accurately. Results of the present research showed that the HEC-1 model did not provide an accurate estimate of floodwater volume. Given the high sensitivity of this method to rainfall distribution across the region, an analysis of rainfall across the region is required to obtain desirable results and the rainfall distribution and its time distribution should be pushed close to the corresponding values in the region. Furthermore, the results of the present study indicated that the poor accuracy of SCS resulted from the fact that it is used for large watersheds with concentration times of longer than 6 h. It was revealed that the adoption of this method requires that the coefficients for conversion of peak discharge to peak discharge of small watersheds should be determined. Results indicated that the inaccuracy of TR-20 was due to different climatic conditions in the extraction of unit hydrographs compared to the climatic conditions across southwest of Iran.