Abstract
The research aimed to investigate a new approach for spatiotemporal groundwater monitoring network optimization using hydrogeological modeling to improve monitoring strategies. Unmonitored concentrations were incorporated at different potential monitoring locations into the groundwater monitoring optimization method. The proposed method was applied in the contaminated megasite, Bitterfeld/Wolfen, Germany. Based on an existing 3-D geological model, 3-D groundwater flow was obtained from flow velocity simulation using initial and boundary conditions. The 3-D groundwater transport model was used to simulate transport of α-HCH with an initial ideal concentration of 100 mg/L injected at various hydrogeological layers in the model. Particle tracking for contaminant and groundwater flow velocity realizations were made. The spatial optimization result suggested that 30 out of 462 wells in the Quaternary aquifer (6.49 %) and 14 out of 357 wells in the Tertiary aquifer (3.92 %) were redundant. With a gradual increase in the width of the particle track path line, from 0 to 100 m, the number of redundant wells remarkably increased, in both aquifers. The results of temporal optimization showed different sampling frequencies for monitoring wells. The groundwater and contaminant flow direction resulting from particle tracks obtained from hydrogeological modeling was verified by the variogram modeling through α-HCH data from 2003 to 2009. Groundwater monitoring strategies can be substantially improved by removing the existing spatio-temporal redundancy as well as incorporating unmonitored network along with sampling at recommended interval of time. However, the use of this model-based method is only recommended in the areas along with site-specific experts’ knowledge.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Groundwater is an integral part of the hydrologic system. The quantity and quality of groundwater are major concerns, which depend on the underlying rock formations and their structural fabric, the thickness of weathered material, the topography and climatic conditions (Singh et al. 2011, 2013). In groundwater studies, models are developed and applied to predict the fate and movement of groundwater physiochemical aspects in natural as well as hypothetical scenarios. A regional groundwater flow model calibrated under unsteady-state conditions is important aspect for investigation of the hydrodynamic characteristics for various groundwater management options (Ebraheem et al. 2004). Transferring data to information helps to build knowledge to decision support and ultimately to assess impacts (Avtar et al. 2012; Srivastava et al. 2012).
Groundwater monitoring is an imperative requirement for all water resource management programs (Ebraheem et al. 2003; van Geer et al. 2006; Neupane et al. 2014). To prevent adverse effects on the environment, affordable and energy-efficient treatment methods for these sites are required (Borsdorf et al. 2001) for which regular monitoring is the key. A typical groundwater monitoring program, among others, documents ground water pollution status and evaluates the effectiveness of water protection measures (Diwakar and Thakur 2011). Large-scale contaminated sites with multiple contaminants in the groundwater present a challenge to risk assessment (Heidrich et al. 2004; Heidrich 2004) and an economic burden at many industrial as well as urban groundwater monitoring sites (UIZ 2015). It is evident that though several optimization methods exist, a majority of them fail to take into consideration the hydrology and hydrogeological characteristics of the aquifer.
Groundwater models are designed to portray simplified version of real groundwater scenarios. They are used to simulate and predict aquifer conditions (Prickett 1975). Sand tank models, analog models and mathematical models are the broad categories of groundwater models. Practically, mathematical models are the set of differential equations which have been known and used to control various functions including simulation of subsurface flow and solute transport (Meyer and Brill 1988; Gossel 2009) at various scales (Singh and Woolhiser 2002; Ashraf and Ahmad 2008). The history of development of modeling tools can be traced back to the late 1960’s. Nevertheless, the models describing multidimensional and multiple species solute transport is a relatively new arena (Elango et al. 2004).
The aim of this research is to investigate new approach for spatiotemporal groundwater monitoring network optimization using hydrogeological modeling to improve groundwater monitoring strategies. Unmonitored concentrations were incorporated at different potential monitoring locations into the groundwater monitoring optimization method. The outcomes of this approach were tested against the results obtained from geostatistical method of variogram modeling through estimation of groundwater flow direction.
Study area and data used
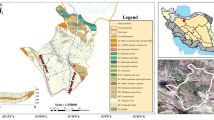
Bitterfeld/Wolfen, located in the Federal State of Saxony-Anhalt, Germany was chosen as a study area (Fig. 1). An area of 320 km2 (latitude 51°30′12.6″–51°41′44″ and longitude 12°5′26″–12°26′0.5″), was used for the three-dimensional (3-D) hydrogeological flow and transport modeling (Gossel et al. 2009).
A location map of the study area in Bitterfeld, Federal State of Saxony-Anhalt, Germany (a Saxony-Anhalt in eastern Germany, b Federal State of Saxony-Anhalt, c model area. d Study area of 100 km2 used for monitoring network optimization in Bitterfeld/Wolfen showing location of reference monitoring wells)
In an urbanized zone of Bitterfeld/Wolfen (latitude 51°35′30″–51°41′30″ and longitude 12°14′10″–12°20′0.5″), with a long-term monitoring network (LTM) of 357 wells in the Tertiary and 462 wells in the Quaternary aquifers, an area of about 100 km2 was selected for spatio-temporal optimization purpose.
Outwash sediments from glacial deposits occupy the western part of the study location whereas the eastern part of the study area is covered by flood plains of the Mulde river (Stollberg 2013). The geology of the research area shows the presence of Pre-tertiary rocks (overlaid by Cenozoic sediments), separated hydro-geologically from one another by clay layer at a depth of 50–70 m (Heidrich et al. 2004). An upper Quarternary aquifer system, lower tertiary aquifer system and pre-tertiary basement have been discovered in the research area (Stollberg et al. 2009).
An existing 3-D geological model of 64 km2 and a 3-D hydrogeological model of 320 km2, developed at the Department of Hydrogeology and Environmental Geology, Martin Luther University, Halle (Saale), Germany, were used to understand the spatial and temporal hydrogeological heterogeneity of the area (Wollmann 2008; Gossel et al. 2009). The groundwater contaminants are heterogeneously distributed and vary temporally in the flow direction.
Contaminant concentration data of α-Hexachlorocyclohexane (α-HCH), taken from the year 2003 to 2009 has been used for variogram modeling. A total of 4032 samples for α-HCH of the period 2003–2009 were used as shown in Table 1.
Statistical attributes of the contaminant used for the variogram modeling are given in Table 2 (Thakur 2015).
Methods
Design and improvement of monitoring strategies requires the description of its components. The components of groundwater monitoring strategy which has been analyzed as a case study of monitoring scenario in the study area are represented in the logic diagram (Fig. 2).
Hydrogeological modeling
In this study, a 3-D groundwater hydrogeological modeling approach was used to simulate near realistic conditions in the study area when limited by data availability.
3-D groundwater hydrogeological modeling
With the existing spatial variation of material properties, flux boundaries and the pre-conceived possibility of fine discretization in the study area, Finite element method (Diersch 2014) was chosen over Finite difference method (Mitchell and Griffiths 1980) for hydrogeological modeling.
3-D groundwater flow model
An assumption of effectively constant properties of the medium is made for deriving 3-D groundwater flow equation for small representative elemental volume (REV). Water flowing in and out to this volume (i.e., the water flux) is used to balance mass along with Darcy’s law. Darcy’s Law combined with continuity equation for inhomogeneous anisotropic confined aquifer is given by the Eq. 1. The continuity equation explains the change in storage to be the difference between mass flowing in and out across the boundaries for a given increment of time (Δt).
For a homogeneous anisotropic confined aquifer, Eq. 3 takes the form as shown in Eq. 2.
For the range of scenario analysis, the groundwater flow model was given the initial and boundary conditions for simulation. For the research site, these conditions were set in terms of global groundwater table elevation, water levels along river courses, model inflows and outflows (fluxes), groundwater recharge, and injection/extraction due to pumping wells. Initial and boundary conditions as well as material characteristics determine the flow in groundwater flow modeling.
Initial conditions
The distribution of head within the modeled area at the beginning (t = 0) represent the initial condition given by the following equation (Diersch 1998).
Historical scenario of the aquifer was considered in the assignment of initial conditions to the model.
Boundary conditions
Boundary conditions incorporate historical groundwater dynamics in the Bitterfeld/Wolfen site including spatio-temporal variations resulting from lignite mining, shift in Mulde river course and seasonal groundwater level fluctuation. Four kinds of boundary conditions must be applied, first of which is a hydraulic head boundary condition [units is (L)], applied to define hydraulic head to node. This boundary defines inflow and outflow in the model; inflow occurring in the area when neighbouring nodes are at lower potential, while an effective gradient from neighbouring nodes defines the outflow from the model.
Another boundary condition called the Neumann Boundary Condition [unit is (L/T)] is used to define inflow and outflow in the numerical model at a model element in which inflows are regarded as negative and outflows are considered positive in defining the boundary conditions. Third kind of boundary condition, the Cauchy condition pertains to transfer or leakage of a surface water body (Chen 1987). It defines a reference head combined with a conductance parameter, for example, the rivers or lakes with restricted connection to groundwater.
The equation defining the inflow/outflow in an area perpendicular to flow (A) with the transfer rate Φ is given as follows
where Q is inflow or outflow to/from the model [units is (L)], h ref is the reference water level, and h is the current hydraulic head in the groundwater. Also, the transfer rate is given by:
where K is the hydraulic conductivity of the clogging layer, and d is the thickness of the clogging layer.
The fourth kind of boundary condition relates to the specific extraction rate to a node or a group of nodes along the well screen at well location.
3-D groundwater transport model (forward-in-time)
The study, modeled in a 3-D environment simulated the transport of a single species, α-HCH, incorporating initial and boundary conditions as well as nature of transport material in the study area.
Initial conditions
As in the case of flow initial condition, the transport initial condition refers to the amount of mass distributed in the modeled area at the beginning (t = 0). For this purpose, an initial idealistic α-HCH concentration (100 mg/L) was induced at various hydrogeological layers of the model at a multi-source location. The resultant idealistic plume distribution was the underlying vision for such idealistic concentration consideration. The source locations of α-HCH, based on site investigation data and literature review, include permanent and temporal mass production sites as well as disposals sites for α-HCH (Heidrich et al. 2004; Paschke et al. 2006; Petelet-Giraud et al. 2007).
Boundary conditions
The first kind of boundary condition (BC), i.e., the Dirichlet boundary condition (Cheng and Cheng 2005) defines the solute concentration (M/L3) at the selected model nodes. It results in the inflow into and outflow from the neighboring nodes depending upon concentration gradient in the model. Another set of boundary condition is the mass flux boundary condition, which defines the fluxes in mass at the nodes enclosing faces of elements. This BC (Diersch 2009) is given by:
where q mass is the mass transport BC flux, q flow is the flow BC flux and c is the concentration of the inflowing water.
In addition, a third kind of BC, mass transfer boundary condition, defines a reference concentration linked to the concentration of groundwater with a separating medium. The transfer rate (M/L3) (Diersch 2009) is given by:
where Q mass is the inflow or outflow to/from the model, A is relevant area, Φ is transfer rate, c ref is reference concentration, and c is current concentration in groundwater.
Again, a nodal sink or source boundary condition (M/T) for mass transport has been used which defines extraction/injection of solute to a node. Again, among the existing boundary conditions (Gossel et al. 2009), another BC, i.e., the Dirichlet boundary condition was incorporated which defines solute concentration in the model area at the selected nodes. Within the modeled area, the assignment of this BC was with reference to α-HCH production as well as disposals sites in Bitterfeld/Wolfen.
Transport material
Mass transport of material has a significant bearing on transport of contaminants along with the initial and boundary conditions. Transport related processes including advective, diffusive, dispersive transport, porosity sorption, decay and reaction kinetics are incorporated into the model so as to represent mass transport of material. To improve the existing model (Gossel et al. 2009), sorption and diffusion coefficients were incorporated considering α-HCH as a transport material. In the view of improving the existing model (Gossel et al. 2009), sorption and diffusion coefficients for α-HCH (transport material) were incorporated in the model.
Temporal control
As per the aim of this research, the developed model was applied in LTM network optimization. The prognostic groundwater flow and contaminant plume were required for the LTM network optimization. Long-term groundwater monitoring has been planned for 20–25 years in the study area (Reed et al. 2001; Kollat and Reed 2007). In line with this planning period, the model was simulated for 21 years (7665 days) with an initial time step length of 0.001 day.
Exporting head, mass and velocity
For the optimization of the existing LTM network in the urbanized area of 100 km2 in Bitterfeld/Wolfen, 462 reference wells in the Quaternary aquifer and 357 reference wells in the Tertiary aquifer, were incorporated into the transport model for outlining the spatio-temporal virtual contaminant situation. The reference monitoring wells with their latitude, longitude and screen level elevations were assigned at 3-D nodes of the finite element mesh. The hydraulic head (m a.s.l.), the solute concentration (mg/L) and flow velocity (m/day) were recorded in the form of time series data at the reference monitoring wells. With these recorded hydraulic heads, the solute concentration and flow velocity were exported and used for the optimization of the existing LTM network. With these available data from the model, they were exported to be used in the optimization of the existing LTM network.
Particle tracking
Particle tracking was carried out through previously simulated groundwater model which was performed in both forward (downstream) and backward (upstream) directions to the normal oriented flow velocity field. This was meant to assess the past and future positions of the imaginary solute particles. Also, reverse particle tracking (backward particle tracking) estimated the possible source location and travel time in the modeled area.
LTM network optimization based on hydrogeological model
By presenting the transient nature or pollution plume, dynamic monitoring network optimization, can potentially eliminate temporal redundancy, proving to be more efficient economically. The optimization methodology was developed including both steady state and transient state of plumes as depicted in Fig. 3. Incorporating the track of solute concentration and its dynamics, the monitoring network accounted for a transient state of plumes which signifies time varying network optimization. Therefore, the resulting optimization would be more accurate and economically efficient.
Steps involved in the spatial optimization of the monitoring network using 3-D groundwater hydrogeological modeling showing three conditional models for the monitoring network optimization [Modified from Thakur (2013)]
Spatial optimization of the LTM network
Transient transport model was used for the simulation of pollutant concentration for reference wells in both the Quaternary aquifer and the Tertiary aquifer (462 and 357 wells, respectively) which were used as an input to the spatial optimization model (Fig. 3). Head and flow velocity has been used for comparative analysis of random fluctuation of mass.
Three optimization models proposed to select the best subset of monitoring well locations from a large groundwater monitoring network are presented below:
Model 1: wells on the same path line from the same aquifer are designated to be redundant. This means that if there are more than two wells on the same particle track, the middle one is selected as essential while others are regarded redundant.
Model 2: for prognostic optimization, more than two monitoring wells on the same particle track suggest that the well located at the beginning of the track need not be monitored. On the same particle track, essential wells should be selected from other remaining wells.
Model 3: it considers optimization towards the contaminant source location. The well located at the beginning of path line from the contaminant source location should have high priority for monitoring. If multiple wells are located near the contaminant source location on the same particle track, the ones near the contaminant sources will have less priority for consideration.
In addition to these criteria, in all of these models, wells in areas showing high temporal fluctuation of contaminant concentration with high groundwater flow velocity are not consigned as redundant wells.
Temporal optimization of the LTM network
Groundwater flow velocity and contaminant transport guides the temporal concentration variation in the research area. Flow velocity acts as a major element in temporal optimization of the LTM network; therefore, it is important to understand properly the way it acts. The steady state flow model was used to estimate flow velocity realizations at 462 and 357 reference wells locations in the Quaternary and Tertiary aquifers, respectively. These flow velocity realizations are used as inputs for temporal optimization of the monitoring network (Fig. 4).
The simulated flow velocity in the model ranges from 2.1 × 10−6 to 1.1 m/day. The obtained flow velocities were divided into five classes and accordingly were attributed the necessary sampling frequencies ranging from 3 months to 3 years (Table 3).
Validation of groundwater flow direction
Groundwater flow direction obtained through hydrogeological modeling was validated using a variogram modeling tool which gives the prominent groundwater and contaminant flow direction on the basis of range and sill.
The dependency of groundwater monitoring has been studied using directional variograms which can be written as:
The experimental variogram estimation was carried out using Golden Surfer software (2011). Valid variogram models that incorporate directional dependence were constructed. Standard models such as spherical, exponential, Gaussian, and power were used to model the data set. The best fitting model, considering range, sill, nugget effect and shape of the model, was selected. A variogram was constructed from α-HCH concentration data set for each year from 2003 to 2009, according to the seasons (summer: May–October; winter: November–April), and to hydrologic seasons (March–May: high groundwater level, September–November: low groundwater level). The range and sill were estimated for various directional variogram models on the basis of which prominent flow direction was visualised.
Improving groundwater monitoring strategies
Strategic planning of monitoring network optimization is crucial to groundwater monitoring since it is an important component of monitoring strategies (Thakur et al. 2011a; Thakur 2013). With an overall objective to improve monitoring strategies, the developed and existing methods were applied to the observed and model-based data sets for the mega-contaminated site, Bitterfeld/Wolfen. On the basis of outcomes from hydrogeological modeling and the spatio-temporal optimization of existing monitoring network, the improved strategies were set forth.
Results
Hydrogeological modeling
Groundwater contamination scenario in the study area was simulated with the help of groundwater steady state flow and transient transport models used in this study. With an aim to portray historical scenario of multi-source groundwater contamination, initial transport and boundary conditions were employed. The simulated contaminant scenario was observed at 462 reference wells in the Quaternary aquifer and 357 reference wells in the Tertiary aquifer.
3-D groundwater hydrogeological modeling
The hydrogeological model was simulated for a period from 2005 to 2025 (21 years). It was used to estimate head, mass and flow velocity at different potential unmonitored and monitored locations. Transport of solute was used to locate the solute mass, a medium for advective and dispersive transport, for the monitoring network optimization.
Model geometry
At an initial step, the problem was defined using an existing numerical groundwater flow model established by Gossel, Stollberg et al. (2009) in the study area.
The existing model was modified for use with transport BC and the outcomes were used as a basis for monitoring network optimization. The model domain comprising an area of 320 km2 was subdivided into number of triangular shaped elements in both horizontal and vertical scale (Fig. 5). The modeled area had a finite element mesh consisting 1475,708 triangle elements connected with 770,450 nodes (in 37 hydrogeological layers) (Stollberg 2013). The mining and dump-sites areas seem to have higher mesh density than outer areas.
The model domain comprising an area of 320 km2 was subdivided into a number of triangular shaped elements in both horizontal and vertical scale (Fig. 5). The modeled area had a finite element mesh consisting 1475,708 triangle elements connected with 770,450 nodes (in 37 hydrogeological layers) (Stollberg 2013).
Overview of hydrogeological units and layers for the model with their respective hydraulic conductivities shows that the vertical structure of the model has 13 individual hydrogeological units which are represented by 37 hydrogeological layers in the model, whose respective hydraulic conductivity correspond to hydrogeological units as per Wollmann (2004), Hubert (2005) and Gossel, Stollberg et al. (2009). Depending on the hydrogeological units in the study area, specific value of hydraulic conductivity was given to each hydrogeological layer in the model (Gossel, Stollberg et al. 2009).
To fit the model parameters, initial and boundary conditions for each different hydrogeological unit, each unit was categorized into 3 numerical layers except the first and last units which were represented by only 2 numerical layers.
3-D groundwater flow model
To optimize LTM network from the flow model, the simulated groundwater flow scenario of the study area, Bitterfeld/Wolfen for 25th December, 2025 was visualized. The groundwater flow velocity was visualized using contour lines and particle tracks from the FEFLOW result file (*.dac). The 3-D groundwater flow scenario illustrates a dominant flow with a high gradient in the industrial area (Fig. 6).
Relatively high groundwater flow velocity was observed in the historical mining area lying in the Quaternary aquifer. In the modeled area (320 km2), in the later part of the model period, the groundwater flow velocity ranges from 2.49 m/day to 3.95 × 10−20 m/day. But, the monitoring network, which should be optimized using the model result, only covers the mining area, dump site, industrial and urban area of about 100 km2, where the groundwater flow velocity ranges from 2.12 × 10−6 to 5.1 × 10−2 m/day. Furthermore, the extracted set of groundwater velocity results data and accessory information (i.e., name, coordinates, and elevation of the monitoring well, screen depth, stratigraphical geological layer, stratigraphical horizon [Quaternary (Q), Tertiary (T) and Quaternary–Tertiary (Q-T)]) have been used for the LTM network optimization.
3-D groundwater transport model (forward-in-time)
Transport of α-HCH was simulated through the use of 3-D groundwater transient transport model by incorporation of initial and boundary conditions along with the nature of the transport material in the study area. The simulated mass scenario in the timeframe for 25th December 2025 was visualized while using the transport model for LTM network optimization (Fig. 7).
The groundwater contaminant mass scenario visualization was made using contour lines from the FEFLOW result file (*.dac). The solute concentration [mg/L] was recorded in the form of time series data at the reference monitoring wells. The obtained solute concentration (mg/L) was used for the analysis of spatiotemporal change of the ideal contaminant species (α-HCH) in the existing LTM network. Comparatively, the groundwater mass transport system is very complex at the Bitterfeld/Wolfen megasite. In this transport simulation of the α-HCH concentration, 100 mg/L α-HCH concentration was induced at various hydrogeological layers of the model at the multi-source locations as the initial condition. After 21 years of simulation too, the concentration of α-HCH seemed to be higher at Antonie, Titanteich, Übergabebahnhof, and Fasanen Dump sites. The resultant high concentration of the contaminant should be taken into account during the optimization of the monitoring network. To gain the idea on the location of contaminant mass, advective particle tracking methods were used to track the path lines of the course of transportation of solute transport in the groundwater (Fig. 8).
LTM network optimization using hydrogeological model
The model, thus, simulated gives an account of head, mass and velocity at 462 and 357 reference wells, respectively, in the Quaternary and Tertiary aquifers to aid in visualizing such parameters at unmonitored locations (Figs. 6 and 7 for flow velocity and mass, respectively). To optimize LTM network for future scenarios, the head, mass and flow velocity for the date 25th December 2025 was used.
Spatial optimization of the LTM network
LTM network was optimized using hydrogeological modeling method individually for the Quaternary aquifer and the Tertiary aquifer. In both aquifers, overlying the particle tracks with the locations of existing monitoring wells shows that more than one well was located on some of the contaminant flow path lines (Fig. 8). The results from modeled particle tracks depicted that some of the contaminant flow path lines consisted of more than one well, and thence, following the first LTM network optimization model statement relating the redundancy of more than one well on the same path line for specific aquifer type, the redundancy in the existing monitoring network was identified.
The optimization result based on the first model described in “Exporting head, mass and velocity” suggests that 30 out of 462 wells in the Quaternary aquifer (6.49 %) and 14 out of 357 wells in the Tertiary aquifer (3.92 %) were redundant. These relatively low numbers of redundant wells are due to the narrow width of the particle track. When subjected to greater width of the particle track path line, i.e., gradually increasing it from 0 to 100 m, the number of redundant wells increased remarkably in number in both aquifers, as shown in Table 4.
Since it is evident that drastic change in groundwater situation is not generally observed, the width of the track was gradually increased by maintaining buffer zone of 0–100 m around the particle track, all performed using ArcGIS. Table 4 provides the list of redundant monitoring wells in each aquifer using first spatial optimization model (Model 1) with the buffer zone from 0 to 100 m around the particle track in the optimized LTM network.
Table 4 clearly shows that with a buffer zone of 100 m around the particle track, the LTM network optimization using the first model states 145 of the 462 wells in the Quaternary aquifer (31.38 %) and 105 of the 357 wells in the Tertiary aquifer (29.41 %) to be redundant. The spatial distribution of such essential and redundant wells is shown in Fig. 9.
Particle tracking and contaminant concentration was used for monitoring network optimization in this research. Head and flow velocity were used to provide additional information for comparative analysis of random fluctuations of mass at various reference monitoring wells in the study area. Compared to the first proposed optimization model, the second and third models categorize the wells as essential and redundant with a subjective priority of redundancy.
Temporal optimization of the LTM network
The LTM network was also optimized temporally using the method as detailed in “Temporal optimization of the LTM Network”. Figure 10 shows the locations of monitoring wells with differently recommended sampling interval.
The results of temporal optimization show that the total of the groundwater monitoring in each type of aquifers should be sampled at the intervals as presented in the Table 5.
Alongside the results, it is recommended that the monitoring wells located in the mining and urban areas should be sampled more frequently than the wells located in south-eastern part of the study area.
Groundwater flow direction
Groundwater flow direction was analyzed through variogram modeling as a part of its dependency on LTM network optimization and to compare with the results obtained from hydrogeological modeling methods.
The experimental variogram, with each 30° lag direction, shows the highest range in the Northern direction for the Quaternary aquifer whereas at 30° from the Northern direction for the Tertiary aquifer for α-HCH. The results of range and sill for various directions using Gaussian model is presented in Table 6. Overall, there is the indication that prominent α-HCH concentration flows towards the North direction in both the type of aquifers, with a slight deviation towards east direction in case of the Tertiary aquifer.
Season wise variogram modeling for α-HCH data
To analyze seasonal variability in the flow direction, the experimental variogram was modeled using the data set of α-HCH for hydrological summer and winter seasons. The result for summer shows that the range is highest in the North direction in both Quaternary and Tertiary aquifers, as shown in Table 7.
Again, modeling the experimental variogram for the set of data for hydrological winter season depicted the range to be highest at the 60° from North in the Quaternary aquifer while in the direction of 120° from the North as shown in Table 8.
Year-wise directional variogram modeling for α-HCH data
To analyze the prominent groundwater flow direction and to compare it with the simulated groundwater flow direction based on the hydrogeological model, variogram modeling was carried out for α-HCH for the years 2005 and 2006. The result again showed the prominent flow in the northern direction for the Quaternary aquifer while at 30° from North in the Tertiary aquifer as shown in Tables 9 and 10.
The overall flow direction analysis points that the predicted α-HCH spreading direction is northwards. This has been verified approximately by the contaminant flow direction from particle tracks for α-HCH obtained through hydrogeological modeling for the Quaternary and Tertiary aquifers.
Specifically, the year-wise analysis of α-HCH contaminant flow direction based on experimental variogram modelling predicted a prominent flow direction towards the North in 2006 which verified the groundwater and contaminant flow direction observed from the hydrogeological modeling. Thus, flow direction result from the experimental variogram modeling was verified by the groundwater and contaminant flow direction observed using the hydrogeological model. The contaminant flow direction was also found to be northwards in the analysis of particle tracks for α-HCH from the hydrogeological model for Quaternary and Tertiary aquifers (Fig. 11).
Figure 11 clearly shows that the contaminant flow direction shows slight changes but the overall flow direction is headed towards the north.
Improving groundwater monitoring strategies
With the application of hydrogeological modeling, the LTM network was optimized. With this optimization methodology, the monitoring network can be optimized and the existing strategies for monitoring can be improved to reduce the hassle as well as economic burden for the policy makers. Table 11 outlines the examples of 15 such wells that were assigned spatially and/or temporally redundant/essential on the basis of outcomes from hydrogeological modeling.
Discussion
The hydrogeological modeling has been used to predict the overall attributes and scenario of ground water in the study area. Different hydrogeological models attempt to take into account the flow velocity, heterogeneity and other peculiarities associated with groundwater system (Bakalowicz 2005). Despite substantial work on groundwater flow and transport models for various applicable purposes (Van Genuchten 1978; Anderson and Cherry 1979; Tripathi 1991), works on the use of such procedures for groundwater quality monitoring network optimizations with transient state of plumes are comparatively sparse (Datta et al. 2009). Groundwater monitoring network optimization methods are greatly challenged besides the problems associated with data availability. Though quite a number of methods for optimization exists, most of them fail to incorporate hydrogeological characteristics and the intricate relationship that they have on optimization methods (Loaiciga 1992).
One of the greatest challenges facing pertinent planning and implementation of groundwater monitoring strategies is the mere lack of data from required sampling locations (Beck 1987; Harmel et al. 2009). This study has attempted to find contaminant flow path lines to assign the level of importance to the existing monitoring wells with respect to potential monitoring well locations. The model has been used to account for the unmonitored concentrations at potential monitoring location for the purpose of spatiotemporal optimization of the monitoring network. Of its kind, Bashi-Azghadi and Kerachian (2009) used monitored data and hydrogeological model to locate monitoring wells in groundwater systems so as to identify unknown source of pollution.
The result from the spatial optimization using the model indicates that 6.49 % of existing wells in the Quaternary aquifer and 3.92 % of those in the Tertiary aquifer were redundant. As the resultant contaminant flow path lines were very narrow 3-D lines, overlying the existing monitoring wells in such lines got only few existing wells to be positioned on the same path line. Increasing the width of the line gradually within a defined buffer zone of 0–100 m around the particle track resulted higher number of redundant wells as given in Table 4. For instance, with a buffer zone width of 100 m around the particle track, the LTM network optimization result showed 31.38 % of wells in the Quaternary aquifer and 20.41 % of the wells in Tertiary aquifer to be redundant (Fig. 9). Further increment of width of particle track from 100 m will result in higher redundant wells; however, this would lead to uncertainties in monitoring network in the real world scenario.
Another issue of utmost importance was the depth of sampling for the essential monitoring wells (Thakur 2013). This research studied the variation of contaminant concentration with vertical profile of the model and from the analysis; it is recommended that the sampling depth should be at the particular depths where temporal fluctuation, observed in the visualization of vertical contaminant profile. It is important because pollutants in groundwater may spread to uncontaminated areas and endanger receptors like surface water and drinking water wells according to the site-specific hydrologic regime (Heidrich et al. 2004).
Again, the temporal optimization of monitoring network presents a number of wells with different variable recommended sampling frequencies as shown in Table 5 and their locations portrayed in Fig. 10. The results were the function of simulated groundwater velocity, which in turn depends on the initial and boundary conditions of the model and the transport material (Gossel et al. 2004; Gossel 2011). For enhanced temporal optimization as well as better recommendations for temporal sampling interval, it is important that the model has to be calibrated and validated with time.
In this particular optimization of the monitoring network, a reference value of contaminant concentration of 100 mg/L was used. A comparative analysis of contaminant scenario can be made through analyzing the concentration at the source and the spread of this ideal concentration through various methods in the model environment with that of observed contaminant scenario to make comparative analysis of possible scenarios of contaminant in the real world.
Model 1 was used for general optimization in this research without special consideration to the contaminants source and time. However, model 2 was used for prognostic optimization in which spatial location of the well was taken into account which is considered when the optimization aims to ignore the contaminant source but track the present and future contaminant location. Similarly, model 3 was used when special consideration to specific contaminant sources was required. The high-resolution digital 3D model improves the hydrogeological modeling results which serve to be the basic requirement for groundwater modeling and investigations on environmental risk and impact assessment and pathway exposure route analysis of the complex geological and groundwater situations (Wycisk et al. 2009).
Prominent groundwater and contaminant flow direction are revealed from the data sets of α-HCH, determined using the experimental variogram. The analysis from the period of January 2003 to February 2009 shows the flow direction of α-HCH to be north and 30° from the north in the Quaternary and the Tertiary aquifers, respectively. The deviation of flow direction in the Tertiary aquifer relates to the impacts of historical shift in the groundwater flow direction in the study area. Seasonal analysis, again shows preferential flow direction towards north for both aquifers in hydrological summer season whereas 60° from north in the Quaternary aquifer and 120° from north in the Tertiary aquifer in the winter season. This seasonal variation in the flow direction is strongly influenced by the location of the contaminant source, and the seasonal fluctuation in the water level in Mulde river and surrounding water bodies (Thakur et al. 2011b).
Each component of monitoring network needs to be improved for the overall improvement of monitoring network in the study area. Depending upon groundwater and monitoring status, the improvement objectives could account for enhancement in understanding of monitoring network, legal requirements, or socio-economic aspect of monitoring (Thakur et al. 2011a). The monitoring strategy is based on groundwater monitoring effort, reduction of uncertainties, socioeconomic needs, legal requirements, etc. With the established outcomes from this study, the monitoring network can be substantially optimized and the existing strategies for monitoring can be modified in the view of multiple purpose of overcoming the present difficulty in maintaining immense number of monitoring wells. Similarly, since the research also portrays the monitoring needs for the unmonitored sites, the outcome can be used to develop improved monitoring network strategies with the incorporation of such sites for effective strategies.
Conclusion and recommendations
The presented research helps to establish a new approach and improve methods for optimizing groundwater monitoring network on the basis of hydrogeological modeling. Meanwhile, this has been tested using the methods in the research area.
Existing monitoring network can be strategically optimized using hydrogeological methods without losing essential information from the monitoring network. Since data unavailability or its limitation can sometimes pose hindrance at many circumstances, the application of hydrogeological model opens the possibility for optimization in such situation. This study presents the method for incorporating unmonitored concentrations at different potential monitoring locations to optimize the monitoring network using a hydrogeological model. Calibration and validation of the model according to the site conditions, was meant to strengthen the reliability of the results. Monitoring network optimization using hydrogeological model is eased by prior existence of a hydrogeological model.
The spatial optimization gave an account of spatial redundancy in the existing monitoring network while the temporal optimization using simulated groundwater flow velocity recommended appreciable sampling frequencies at potential sampling locations. This modeling approach, used for analytical optimization of monitoring network gives the results that can be interactively visualized since it gives 3-D model visualization. In this study, at a particular contaminated megasite, a convincing result has been obtained for the prognostic spatiotemporal optimization.
Again, the results obtained for the flow direction from hydrogeological modeling was verified by the experimental variogram modeling from available α-HCH data from the year 2003–2009, hence increasing the reliability of the model.
However, the use of this model-based method is only recommended in the areas where there is pre-existence of a calibrated and validated hydrogeological model. In areas where not enough real observed data are available, a hydrogeological model and particle tracking method can be used for the monitoring network optimization. Again, it is recommended that the expert knowledge about the present scenario and dynamic condition of the specific location should be combined with the outcomes of this study to plan for appropriate monitoring strategies.
References
Anderson MP, Cherry JA (1979) Using models to simulate the movement of contaminants through groundwater flow systems. Crit Rev Environ Sci Technol 9(2):97–156
Ashraf A, Ahmad Z (2008) Regional groundwater flow modelling of Upper Chaj Doab of Indus Basin, Pakistan using finite element model (Feflow) and geoinformatics. Geophys J Int 173(1):17–24
Avtar R, Thakur JK et al (2012) Geospatial technique to study forest cover using ALOS/PALSAR data. Geospatial Techniques for Managing Environmental Resources. Thakur JK, Singh SK, Ramanathan AL, Prasad MBK, Gossel W, Springer Netherlands: 139–151
Bakalowicz M (2005) Karst groundwater: a challenge for new resources. Hydrogeol J 13(1):148–160
Bashi-Azghadi SN, Kerachian R (2009) Locating monitoring wells in groundwater systems using embedded optimization and simulation models. Sci Total Environ 408(10):2189–2198
Beck MB (1987) Water quality modeling: a review of the analysis of uncertainty. Water Resour Res 23(8):1393–1442
Borsdorf H, Rammler A et al (2001) Rapid on-site determination of chlorobenzene in water samples using ion mobility spectrometry. Anal Chim Acta 440(1):63–70
Chen C-S (1987) Analytical solutions for radial dispersion with cauchy boundary at injection well. Water Resour Res 23(7):1217–1224
Cheng AHD, Cheng DT (2005) Heritage and early history of the boundary element method. Eng Anal Bound Elem 29(3):268–302
Datta B, Chakrabarty D et al (2009) Optimal dynamic monitoring network design and identification of unknown groundwater pollution sources. Water Resour Manage 23(10):2031–2049
Diersch H-JG (1998) Treatment of free surfaces in 2D and 3D groundwater modeling. Math Géologie 2:17–43
Diersch H (2009) WASY Software FEFLOW 5.4 User’s Manual. DHI-WASY, Berlin
Diersch H-JG (2014) Fundamental concepts of finite element method (FEM). FEFLOW, Springer, pp 239–404
Diwakar J, Thakur JK (2011) Groundwater monitoring scenario: methods for improving groundwater monitoring strategies. ARSOlux workshop: a practical water test for detecting arsenic in drinking water, Kathmandu, Nepal
Ebraheem AM, Garamoon HK et al (2003) Numerical modeling of groundwater resource management options in the East Oweinat area, SW Egypt. Environ Geol 44(4):433–447
Ebraheem AM, Riad S et al (2004) A local-scale groundwater flow model for groundwater resources management in Dakhla Oasis, SW Egypt. Hydrogeol J 12(6):714–722
Elango L, Stagnitti F et al (2004) A review of recent solute transport models and a case study. environmental sciences and environmental computing. Vol. II. P. Zannetti. Fremont, CA 94539, USA, The EnviroComp Institute
Gossel W (2011) Interfaces in coupling of hydrogeological modeling systems. Shaker Verlag, Aachen
Gossel W, Ebraheem AM et al (2004) A very large scale GIS-based groundwater flow model for the Nubian sandstone aquifer in Eastern Sahara (Egypt, northern Sudan and eastern Libya). Hydrogeol J 12(6):698–713
Gossel W, Stollberg R et al (2009) Regionales Langzeitmodell zur Simulation von Grundwasserströmung und Stofftransport im Gebiet der Unteren Mulde/Fuhne. Grundwasser 14(1):47–60
Harmel R, Smith D et al (2009) Estimating storm discharge and water quality data uncertainty: a software tool for monitoring and modeling applications. Environ Model Softw 24(7):832–842
Heidrich S, Schirmer M et al (2004a) Regionally contaminated aquifers - toxicological relevance and remediation options (Bitterfeld case study). Toxicology 205(3):143–155
Heidrich S, Weiß H et al (2004b) Attenuation reactions in a multiple contaminated aquifer in Bitterfeld (Germany). Environ Pollut 129(2):277–288
Hubert T (2005) Vergleichende 3D-Modellierung eines geologischen Strukturmodells am Beispiel einer industrie- und bergbaugeprägten Region—Bitterfeld. Diploma, Martin Luther University Halle-Wittenberg
Kollat JB, Reed PM (2007) A computational scaling analysis of multiobjective evolutionary algorithms in long-term groundwater monitoring applications. Adv Water Resour 30(3):408–419
Loaiciga H, Charbeneau R et al (1992) Review of ground-water quality monitoring network design. J Hydraul Eng 118(1):11–37
Meyer PD, Brill ED (1988) A method for locating wells in a groundwater monitoring network under conditions of uncertainty. Water Resour Res 24(8):1277–1282
Mitchell AR, Griffiths DF (1980) The finite difference method in partial differential equations. John Wiley
Neupane M, Thakur JK et al (2014) Arsenic aquifer sealing technology in wells: a sustainable mitigation option. Water Air Soil Pollut 225(11):1–15
Paschke A, Vrana B et al (2006) Comparative application of solid-phase microextraction fibre assemblies and semi-permeable membrane devices as passive air samplers for semi-volatile chlorinated organic compounds. A case study on the landfill “Grube Antonie” in Bitterfeld, Germany. Environ Pollut 144(2):414–422
Petelet-Giraud E, Négrel P et al (2007) Geochemical and isotopic constraints on groundwater-surface water interactions in a highly anthropized site. The Wolfen/Bitterfeld megasite (Mulde subcatchment, Germany). Environ Pollut 148(3):707–717
Prickett T (1975) Modelling techniques for groundwater evaluation. Adv Hydrosci 10:1–143
Reed P, Minsker BS et al (2001) A multiobjective approach to cost effective long-term groundwater monitoring using an elitist nondominated sorted genetic algorithm with historical data. J Hydroinf 3(2):71–89
Singh P, Thakur JK et al (2011) Assessment of land use/land cover using Geospatial Techniques in a semi arid region of Madhya Pradesh, India. Geospatial Techniques for Managing Environmenal Resources. Thakur JK, Singh SK, Ramanathan A, Prasad MBK, Gossel W. Heidelberg, Germany, Springer and Capital publication: pp 152–163
Singh V, Woolhiser D (2002) Mathematical modeling of watershed hydrology. J Hydrol Eng 7(4):270–292
Singh P, Thakur JK et al (2013) Delineating groundwater potential zones in a hard-rock terrain using geospatial tool. Hydrol Sci J 58(1):213–223
Software G (2011) “Surfer 11.” Retrieved 5th Dec., 2011, from http://www.goldensoftware.com/products/surfer
Srivastava PK, Singh S et al (2012) Modeling impact of land use change trajectories on groundwater quality using remote sensing and GIS. Environ Eng Manage J
Stollberg R (2013) Groundwater contaminant source zone identification at an industrial and abandoned mining site: a forensic backward-in-time modelling approach. Dr. nat. sc., Martin Luther University
Stollberg R, Gossel W et al (2009) Source and pathway identification of groundwater contaminants using a backward modeling technique. 2nd International FEFLOW User Conference, Potsdam, Germany
Thakur JK (2013) Methods in groundwater monitoring: strategies based on statistical, geostatistical, and hydrogeological modelling and visualization. Dr. nat. sc., Martin Luther University
Thakur JK (2015) Optimizing Groundwater Monitoring Networks Using Integrated Statistical and Geostatistical Approaches. Hydrology 2(3):148
Thakur JK, Gossel W et al (2011a) Improving groundwater monitoring strategies based on groundwater monitoring network optimization. TASK—the Centre of Competence for Soil, Groundwater and Site Revitalisation. Liepzig, Germany
Thakur JK, Gossel W et al (2011b) Optimizing long term groundwater monitoring network in a complex contaminated site. HIGRADE Conference, Leipzig, Germany, Helmholtz Centre for Environmental Research (UFZ)
Tripathi VS (1991) A model for simulating transport of reactive multispecies components: model development and demonstration. Water Resour Res 27(12):3075–3094
UIZ (2015) Environmental Monitoring, Analysis and Interactive Visualization-EMAIV. http://uizentrum.de/en/environmental-monitoring-analysis-and-interactive-visualization-emaiv
van Geer FC, Bierkens MFP et al (2006) Groundwater monitoring strategies. Encyclopedia of hydrological sciences. John Wiley & Sons, Ltd
Van Genuchten MT (1978) Simulation models and their application to landfill disposal siting: a review of current technology. Proceedings Fourth Annual Hazardous Waste Management Symposium, Land Disposal of Hazardous Wastes”, Southwest Research Institute and USEPA, San Antonio, Texas
Wollmann A (2004) Geologische Bearbeitung einer ehemaligen Bergbau- und Industriefolgelandschaft Bitterfeld/Wolfen. Diplomarbeit und Diplomkartierung, Martin-Luther-Universität Halle-Wittenberg
Wollmann A (2008) Geologisches 3D-Rauminformationssystem. Verlag Dr. Muller
Wycisk P, Hubert T et al (2009) High-resolution 3D spatial modelling of complex geological structures for an environmental risk assessment of abundant mining and industrial megasites. Comput Geosci 35(1):165–182
Acknowledgments
The presented work is funded by a Helmholtz PhD scholarship of the Centre for Environmental Research—UFZ in collaboration with the Martin Luther University Halle-Wittenberg, Germany. Existing 3-D geological model of 64 km2 and a 3-D hydrogeological model of 320 km2 were available from the Department of Hydrogeology and Environmental Geology, Martin Luther University, Halle (Saale), Germany. This work has been possible because of kind co-operation and support from the Department of Hydrogeology and Environmental Geology, Institute of Geosciences and Geography, Martin Luther University, Halle (Saale), Germany.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Thakur, J.K. Hydrogeological modeling for improving groundwater monitoring network and strategies. Appl Water Sci 7, 3223–3240 (2017). https://doi.org/10.1007/s13201-016-0469-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13201-016-0469-1