Abstract
This study is an attempt to quantify the impact of climate change on the hydrology of Armur watershed in Godavari river basin, India. A GIS-based semi-distributed hydrological model, soil and water assessment tool (SWAT) has been employed to estimate the water balance components on the basis of unique combinations of slope, soil and land cover classes for the base line (1961–1990) and future climate scenarios (2071–2100). Sensitivity analysis of the model has been performed to identify the most critical parameters of the watershed. Average monthly calibration (1987–1994) and validation (1995–2000) have been performed using the observed discharge data. Coefficient of determination (\(R^{2}\)), Nash–Sutcliffe efficiency (ENS) and root mean square error (RMSE) were used to evaluate the model performance. Calibrated SWAT setup has been used to evaluate the changes in water balance components of future projection over the study area. HadRM3, a regional climatic data, have been used as input of the hydrological model for climate change impact studies. In results, it was found that changes in average annual temperature (+3.25 °C), average annual rainfall (+28 %), evapotranspiration (28 %) and water yield (49 %) increased for GHG scenarios with respect to the base line scenario.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Global temperature is raising due to accumulation of greenhouse gases in the atmosphere and affecting the natural and managed ecosystems (Xie et al. 2008). The climatic variability can affect the precipitation pattern and other climatic variables. The most important impact of climate change will be changes in regional and local water availability (Evan et al. 2012; Poulin et al. 2011; Yadav et al. 2010). Water availability is one of the vital components and responsible for ecosystem, human livelihood, crop production and hydroelectric power production (Grabow et al. 2013; Johnston and Smakhtin 2014; Mialhe et al. 2015). For example, larger reservoir spillways and drainage waterways will be required where runoff is expected to increase, and higher water supply storage needed where runoff is expected to decrease (Sethi et al. 2015; Tiwari and Rai 2015; Tiwari et al. 2015). The impacts of climate change on hydrology of watersheds are usually evaluated by defining scenarios for changes in climatic inputs to a hydrological model and these scenarios based on the futuristic emissions of greenhouse gases (Gosain et al. 2006; Hossain 2014; Johnston and Smakhtin 2014; Srinivasan et al. 1998). The Intergovernmental Panel for Climate Change (IPCC) Special Report on Emissions Scenarios (SRES) developed new emission scenarios based on emissions of greenhouse gases (Girod et al. 2009; Solomon 2007). Emission scenario projections are developed based on the driving forces like socio-economic development, population growth and GHG emission (McGuire et al. 2001; Willems and Vrac 2011). Evaluation of impact of climate change on hydrology of catchment is very important for the policy makers to mitigate the impact and implementation for the coping strategies (Delgado et al. 2010; Fischer et al. 2007). Hydrologic cycle affects the surface water runoff and ground water recharge (Holman 2005; Zhu 2013). Ficklin et al. (2009) evaluated the climate change impact on water resources within agriculture systems of San Joaquin watershed, California (USA). A semi-distributed hydrological model, soil and water assessment tool (SWAT) was used for the hydrology and climate change impact studies. Results of the study implied that changes in carbon dioxide (CO2) and climatic parameters (temperature, precipitation) significantly affect the water yield, evapotranspiration and other components of hydrological cycle. Gosain et al. (2006) evaluated the 12 river basins of the India using SWAT for control or present and GHG (greenhouse gases) or future climate scenario of simulated weather data of HadRM2. At the initial analysis, severity of drought and intensity of flood for country have been analyzed under the GHG scenario. Neupane and Kumar (2015) investigated the effects of potential land use change and climate variability on hydrologic processes of Big Sioux River (BSR) watershed, North Central region of USA. Future climate change projections have been simulated using temperature and precipitation data derived from Special Report on Emission Scenarios (SRES) (B1, A1B and A2) for end twenty-first century. Liu et al. (2015) analyzed the effects of land use change and climate variability on the upper Naoli River watershed, China, using SWAT hydrological model. In results, it has been found that the stream flow is significantly affected by the combined effects of land use change and climate variability. Murty et al. (2014) applied SWAT model on Ken basin (India) to predict the water balance components. The hydrological studies were carried out for 25 years’ (1985–2009) time period.
In this paper, SWAT, a semi-distributed hydrological model has been used to evaluate the changes in water balance components and impact of the climate change on watershed. Calibration and validation of the model have been performed for the study area as shown in Fig. 1. Hydrological studies were carried out at the regional scale for long-term scale of 30 years. Future climatic projection (2071–2100) for the study area was computed, based on the IPCC Hadley centers regional climate model (HadRM3) data for A2 and B2 GHG scenarios. Water balance components based on GHG scenario were compared with the historical value to evaluate the percentage changes of the study area. The methodology processes have been shown in Fig. 2.
Study area
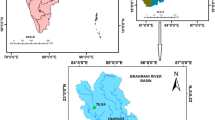
For the present study, model run is done on Armur watershed belonging to the river system of Godavari, India (Fig. 1). The total catchment area of the watershed is 20,319 hectares. Armur mandal is situated in Nizamabad district under the state of Telangana (India). The total geographical area of the district is 7956 Km2. The district is located in the northwestern part of the state bordering Maharashtra state. It lies between 18°05″00′ and 19°00″00′ north latitudes and 77°32″00′ and 78°40″00′ east longitudes. Topography of Armur is sloping from northeast to southwest. It has about 10 m of low and high altitudes difference between areas (375.00–365.00 m above m.s.l.).
There are four seasons categorized in a year: winter (Jan–Feb), summer (March–May), southwest monsoon (June–September) and northeast monsoon (October–December).The annual rainfall in the district is around 1000 mm. The average minimum and maximum temperature have been found to be 13.7 °C (winter) and 39.9 °C (summer), respectively (Fig. 1).
Data
Simulation of the river basin requires certain type of data before simulation is done. The data required by SWAT for basin simulation are
Digital elevation model
Shuttle radar topographic mission (SRTM) has provided digital elevation data (DEMs) of 90 m resolution. The downloaded digital elevation model from SRTM has projection system of WGS_1984_UTM, Zone_45 N at 90 m resolution and the position of study area is maximum, latitude and longitude are 78000′00″N and 18000′00″E, minimum 79000′00″N and 19000′00″E, respectively.
Land cover/land use
1 km grid cell size and taken from University of Maryland Global Land Cover Facility.
Soil map
FAO digital soil map of the world having a scale of 1:5,000,000.
Weather data
High-resolution (1° latitude × 1° longitude) daily gridded temperature data set for the period 1969–2005 and (0.5° × 0.5°) gridded daily rainfall data for the period 1971–2005 over Indian region from Indian Meteorological Department (IMD) Pune, India.
HadRM3 simulated weather data
The Hadley’s center regional climate model, HadRM3 provided a revised version of climate change simulation at a spatial resolution of 0.44° × 0.44°. The model comprises of three ensemble members for the medium-to high-emission scenarios, i.e. 3 × 30 year of daily data for the control (1961–1990) and future perturbed (2071–2100) runs. The GHG scenario (A2 and B2) and baseline scenarios were generated for the maximum temperature, minimum temperature, rainfall, relative humidity, solar radiation and wind speed.
Methodology
SWAT model
The AVSWAT (SWAT extension of ArcView GIS), a distributed hydrologic model has been used for the watershed. The model has potential to predict land management practices, sediment and agricultural chemical yields. Catchments with varying soils, land use and management conditions can be estimated for long time period (Srinivasan et al. 1998). To satisfy this objective, model requires specific climatic input parameters as precipitation, temperature, solar radiation, relative humidity and wind speed. Besides the climatic parameters, other information such as topography map or DEM, soil properties, vegetation and land management practices occurring in the watershed are required for model setup (Santhi et al. 2006; Srinivasan et al. 1998).
In order to setup the model, the digital elevation model, land use/land cover and soil map were projected into common projection system. Model has capability to delineate the DEM into watershed or basin and divided into sub-basin. The layers of land use/land cover, soil, map and slopes categories were overlaid and reclassified into hydrological response unit (HRUs). Hydrologic response units (HRUs) have been defined as the unique combination of specific land use, soil and slope characteristics (Arnold et al. 2012). The model estimates the hydrologic components such as evapotranspiration, surface runoff, peak rate of runoff and other components on the basis of each HRUs unit. Water is then routed from HRUs to sub-basin and sub-basin to watershed (Tripathi et al. 2004). The equation of mass balance performed at the HRU level is given as follows:
where \(S_{t}\) is the final storage (mm), \(S_{o}\) is the initial storage in day \(i\) (mm), \(t\) is the time (days), \(R_{\text{day}}\) is the rainfall (mm/day), \(Q_{\text{surf}}\) is the surface runoff (mm/day), \(E_{a}\) is evapotranspiration (mm/day), \(W_{\text{seep}}\) is seepage rate (mm/day) and \(Q_{\text{gw}}\) is return flow (mm/day).
In order to estimate the surface runoff, there were two methods available: SCS curve number (Soil Conservation Service) and Green and Ampt infiltration method. In this study, the SCS curve number method was used to estimate surface runoff. The SCS curve number is described by the following equation:
where \(Q_{\text{surf}}\) is accumulated runoff or rainfall excess (mm/day), \(R_{\text{day}}\) is the rainfall depth (mm/day) and \(S\) is the retention parameter (mm). The retention parameter is defined by the following equation:
The SCS curve number is a function of the soil’s permeability, land use and antecedent soil water conditions (Arnold et al. 2012). Hargreaves method was used for estimation of potential evapotranspiration (PET):
where \(\lambda\) is the latent heat of vaporization (MJ/kg), \(E_{o}\) is the potential evapotranspiration (mm/d) and \(H_{o}\) is the extraterrestrial radiation (MJ/m2/d). \(T_{ \hbox{max} }\), \(T_{ \hbox{min} }\), and \(T_{\text{avg}}\) are the maximum, minimum, and mean temperature, respectively, for a given day (°C).
Watershed delineation
Using the ArcGIS, digital elevation model (DEM) was used to generate the stream network of the watershed and identify the outlet points for a given threshold value. Automatic delineation delineates the main watershed into 14 sub-watersheds (Fig. 3). Land use/land cover of study area has been shown in Fig. 4. Land use and soil grids are then overlaid and the basic units of modeling (Hydrologic Response Unit, HRUs) are extracted. In the present study, HRUs are defined by taking all land uses and soil type occupying 10 % or more of sub-basins into account. Areas of the minor land uses and soil type (<10 % of a sub-basin) were re-allocated to major land uses to reflect 100 % sub basin areas.
Results and discussion
Calibration and validation of the model
Calibration is tuning of model parameters based on checking against observation to ensure the same response over time. In this process, model parameters varied until recorded flow patterns were accurately simulated. For this study, the manual calibration was applied (Green and Vangriensven 2008; Roy et al. 2014; Yang et al. 2007; Zhang et al. 2009). The steps followed were based on the recommendations given in the SWAT user manual (Arnold et al. 2012). Calibration was commenced by the monthly average of surface runoff volume (Benaman et al. 2005; Cao et al. 2006).
The catchment so taken for the study is an ungauged one, so no observed discharge data were available for the purpose of model calibration and validation. The transposed observed discharge data from a gauged catchment (Gandlpet) adjacent to the study area with similar physiographic characteristics was taken to calibrate the model parameter. For model calibration purpose, observed transposed discharge data of the catchment for the period of 1987–1994 has been taken. Subsequently, calibrated parameters have been used to validate the model for the period of 1995–2000 (Table 1).
Observed and simulated average monthly flow for calibration and validation period have been shown in Fig. 5 and 6, respectively. Several statistics such as mean, standard deviation, coefficient of determination (R 2), Nash–Sutcliffe efficiency (ENS) and prediction efficiency (PE) have been computed to evaluate the model predictions against the observed values.
Coefficient of determination (\(R^{2}\)) measures the dispersion between observed value and simulated value from model:
where \(Q_{\text{obs}}\) is the observed discharge (m3/s) and \(Q_{\text{sim}}\) is the simulated discharge (m3/s) from model. The range of R 2 lies between 0 and 1. Value of \(R^{2}\), 0 and 1 indicates no correlation and perfect correlation, respectively, between observed and simulated values. Nash–Sutcliffe efficiency (ENS) values lies between −∞ and 1. ENS values, 1 indicates that the perfect match, whereas 0 value indicates that simulated values are accurate as mean of the observed values.
Sensitivity analysis
The sensitivity analysis was carried out for a period of 6 years and out of 26 parameters only 10 of them revealed meaningful effect on the simulated flow as shown in Fig. 7. These sensitive parameters were considered for model calibration (Muleta and Nicklow 2005; Setegn et al. 2010). The remaining parameters had no significant effect on stream flow simulations. Changes in their values do not cause significant changes in the model output.
The sensitivity analysis results are shown in Fig. (7). Flow calibration was performed for 8 years, from January 1987 to December 1994. Descriptions of some critical sensitive parameters were given in Table 2. Manipulation of sensitive parameter values was of carried out within the allowable ranges (Table 3).
Climate change assessment
Hadley center’s regional climatic model (RCM) data were analyzed to study the variation induced in the climate parameters through the GHG scenarios (Chen et al. 2011; Ghosh and Mujumdar 2008; Willems and Vrac 2011). Long term variations in temprature (maximum, minimum and average) have been shown in Fig. 8 and rainfall variations shown in Fig. 9. The baseline (1961–1990) linear trend of the average surface minimum temperature was computed as 0.09 °C/year. The GHG (2071–2100) linear trend of the average minimum temperature was 0.016 and 0.018 °C/year for A2 and B2 scenarios, respectively. With reference to baseline scenario, the average minimum temperature increased by 3.07 and 3.09 °C based on A2, B2 scenarios, respectively.
For baseline scenario (1961–1990) and GHG (2071–2100) A2, B2 scenario linear trend of the average surface maximum temperature is 0.042, 0.074 and 0.001 °C/year, respectively. Figure 8 also shows, with respect to baseline scenario, that average minimum temperature increased by 3.25 and 3.29 °C in the consideration of A2, B2 scenarios, respectively.
Assessment of model output
HadRM3 simulated daily weather data of baseline (1960–1990) and GHG scenarios (2071–2100) were used to run the model. Results from the model have been analyzed on annual and monthly basis. Considering the benchmark of baseline period, percentage changes in water balance components for future scenario have been shown in Fig. 10 (% change in rainfall), Fig. 11 (% change in evapotranspiration), and Fig. 12 (% change in water yield) on annual basis, whereas monthly percentage changes have been shown in Fig. 13 and Fig. 14 for A2 and B2 scenario.
Results based on annual studies for baseline (1961–1990) period indicate that the maximum value of rainfall, evapotranspiration and water yield are 1854 mm (1981), 698 mm (1970) and 1232 mm (1981), respectively. The minimum values are 722 mm (1986), 451 mm (1961) and150 mm (1987) for rainfall, evapotranspiration and water yield, respectively. Considering the benchmark of average rainfall (for baseline period), maximum rainfall has increased by 86 % and minimum rainfall decreased by 32 % corresponding to A2 scenario. In the same time, for B2 scenario maximum rainfall has increased by 22 % and minimum rainfall decreased by 12 %. However, it has been noticed that frequency of rainfall is decreasing but average rainfall has increased by 28 % and 29.3 % for A2 and B2 scenarios, respectively. The minimum rainfall has increased by 17.70 % and 41.4 % for A2 and B2 scenarios with respect to the minimum rainfall of the baseline scenario.
The maximum and minimum evapotranspiration values of A2 scenario have changed by +39 % and –12 % respectively, against the average evapotranspiration of baseline. For B2 scenario, maximum and minimum evapotranspiration values have changed by +28 % and –10 %, with reference to the average evapotranspiration of baseline. Average value of evapotranspiration has increased by 14 % for A2 scenario and 28 % for B2 scenarios, with respect to the average evapotranspiration value of baseline. Estimated value of maximum evapotranspiration has found to be increased by 18.6 % and 12.6 % for A2 and B2 scenarios respectively, comparing with the maximum evapotranspiration of the baseline. Minimum evapotranspiration has increased by 38.4 % and 22.6 % for A2 and B2 scenarios, with respect to minimum evapotranspiration of the baseline.
Comparing with the average water yield of baseline, maximum water yield will be increasing by 162 % for A2 and 238 % for B2 scenarios, and minimum water yield is decreasing by 66 % and 30 % for A2 and B2 scenarios, respectively. Average water yield has increased by 43 % for A2 and 49 % for B2 scenarios respectively, with respect the average value of baseline.
From Fig. 14, it has been noticed that mean monthly value for water yield increased by 35 mm for A2 scenario (2071–2100) with respect to base line scenario (1961–1990). Mean monthly value for water yield increased by 72 mm for B2 scenario (2071–2100) with respect to base line scenario (1961–1990). In the monsoon season rainfall increased by 23.77 and 24.55 %, evapotranspiration increased by 14 and 6 % and water yield increased by 60 and 72 % times for A2 and B2 Scenario, respectively, with respect to the average value of base line scenario.
Conclusion
This paper has different aspects related to hydrological modeling studies: (1) successfully applied the SWAT model setup for watershed (2) calibrations and validation have been carried out for the ungaged catchment using the observed flow data of the adjacent gaged catchment. Several evaluation parameters such as standard deviation, coefficient of determination (R 2), Nash–Sutcliffe prediction efficiency (ENS) and prediction efficiency (PE) were used to evaluate the model predictions against the observed values (3) computed the water balance component of the watershed in context of climate change. (4) In the monsoon season, rainfall, evapotranspiration and water yield increased by significant amount for GHG scenario (A2 and B2) respectively with reference to the base line scenario (5) this study will be very useful for decision-makers to assess the benefits best management practices at the watershed level.
References
Arnold JG, Moriasi DN, Gassman PW, Abbaspour KC, White MJ, Srinivasa, Jha MK (2012) SWAT: model use, calibration, and validation. Trans ASABE 55(4):1491–1508
Benaman J, Shoemaker CA, Haith DA (2005) Calibration and validation of soil and water assessment tool on an agricultural watershed in upstate New York. J Hydrol Eng 10(5):363–374
Cao W, Bowden WB, Davie T, Fenemor A (2006) Multi‐variable and multi‐site calibration and validation of SWAT in a large mountainous catchment with high spatial variability. Hydrol Process 20(5):1057–1073
Chen J, Brissette FP, Leconte R (2011) Uncertainty of downscaling method in quantifying the impact of climate change on hydrology. J Hydrol 401(3–4):190–202
Delgado JM, Apel H, Merz B (2010) Flood trends and variability in the Mekong river. Hydrol Earth Syst Sci 14(3):407–418
Evan K, Subimal G, Auroop RG (2012) Evaluation of global climate models for Indian monsoon climatology. Environ Res Lett 7(1):014012
Ficklin DL, Luo Y, Luedeling E, Zhang M (2009) Climate change sensitivity assessment of a highly agricultural watershed using SWAT. J Hydrol 374(1):16–29
Fischer EM, Seneviratne SI, Lüthi D, Schär C (2007) Contribution of land‐atmosphere coupling to recent European summer heat waves. Geophys Res Lett 34(6):L06707
Ghosh S, Mujumdar PP (2008) Statistical downscaling of GCM simulations to streamflow using relevance vector machine. Adv Water Resour 31(1):132–146
Girod B, Wiek A, Mieg H, Hulme M (2009) The evolution of the IPCC’s emissions scenarios. Environ Sci Policy 12(2):103–118
Gosain A, Rao S, Basuray D (2006) Climate change impact assessment on hydrology of Indian river basins. Curr Sci 90(3):346–353
Grabow GL, Ghali IE, Huffman RL, Miller GL, Bowman D, Vasanth A (2013) Water application efficiency and adequacy of ET-based and soil moisture-based irrigation controllers for turfgrass irrigation. J Irrig Drain Eng 139(2):113–123
Green C, Vangriensven A (2008) Autocalibration in hydrologic modeling: using SWAT2005 in small-scale watersheds. Environ Model Softw 23(4):422–434
Holman IP (2005) Climate change impacts on groundwater recharge- uncertainty, shortcomings, and the way forward? Hydrogeol J 14(5):637–647
Hossain F (2014) Paradox of peak flows in a changing climate. J Hydrol Eng 19(9):02514001
Johnston R, Smakhtin V (2014) Hydrological modeling of large river basins: how much is enough? Water Resour Manage 28(10):2695–2730
Liu GH, Luan ZQ, Yan BX, Guo YD, Wang ZX (2015) Response of hydrological processes to land use change and climate variability in the upper Naoli River watershed, northeast China. Water Resour 42(4):438–447
McGuire AD, Sitch S, Clein JS, Dargaville R, Esser G, Foley J, Heimann M, Joos F, Kaplan J, Kicklighter DW, Meier RA, Melillo JM, Moore III B, Prentice IC, Ramankutty N, Reichenau T, Schloss A, Tian H, Williams LJ, Wittenberg U (2001) Carbon balance of the terrestrial biosphere in the twentieth century: analyses of CO2, climate and land use effects with four process-based ecosystem models. Gl Biogeochem Cycl 15(1):183–206
Mialhe F, Gunnell Y, Ignacio JAF, Delbart N, Ogania JL, Henry S (2015) Monitoring land-use change by combining participatory land-use maps with standard remote sensing techniques: showcase from a remote forest catchment on Mindanao, Philippines. Int J Appl Earth Obs Geoinf 36:69–82
Muleta MK, Nicklow JW (2005) Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. J Hydrol 306(1–4):127–145
Murty P, Pandey A, Suryavanshi S (2014) Application of semi-distributed hydrological model for basin level water balance of the Ken basin of Central India. Hydrol Process 28(13):4119–4129
Neupane RP, Kumar S (2015) “Estimating the effects of potential climate and land use changes on hydrologic processes of a large agriculture dominated watershed. J Hydro Part 529(Part 1):418–429
Poulin A, Brissette F, Leconte R, Arsenault R, Malo J-S (2011) Uncertainty of hydrological modelling in climate change impact studies in a Canadian, snow-dominated river basin. J Hydrol 409(3–4):626–636
Roy DP, Wulder MA, Loveland TR, Woodcock CE, Allen RG, Anderson MC, Helder D, Irons JR, Johnson DM, Kennedy R, Scambos TA, Schaaf CB, Schott JR, Sheng Y, Vermote EF, Belward AS, Bindschadler R, Cohen WB, Gao F, Hipple JD, Hostert P, Huntington J, Justice CO, Kilic A, Kovalskyy V, Lee ZP, Lymburner L, Masek JG, McCorkel J, Shuai Y, Trezza R, Vogelmann J, Wynne RH, Zhu Z (2014) Landsat-8: science and product vision for terrestrial global change research. Remote Sens Environ 145:154–172
Santhi C, Srinivasan R, Arnold JG, Williams JR (2006) A modeling approach to evaluate the impacts of water quality management plans implemented in a watershed in Texas. Environ Model Softw 21(8):1141–1157
Setegn SG, Srinivasan R, Melesse AM, Dargahi B (2010) SWAT model application and prediction uncertainty analysis in the Lake Tana Basin, Ethiopia. Hydrol Process 24(3):357–367
Sethi R, Pandey BK, Krishan R, Khare D, Nayak P (2015) Performance evaluation and hydrological trend detection of a reservoir under climate change condition. Model Earth Syst Environ. 1(4):1–10
Solomon S (2007) Climate change 2007-the physical science basis: Working group I contribution to the fourth assessment report of the IPCC. Cambridge University Press, Cambridge
Srinivasan R, Ramanarayanan TS, Arnold JG, Bednarz ST (1998) Large area hydrologic modeling and assessment part II: model application1. JAWRA Journal of the American Water Resources Association 34(1):91–101
Tiwari H, Rai SP (2015) Discharge and sediment time series: uncertainty analysis using the maximum likelihood estimator and artificial neural network. J Water Res Environ Eng 1(1):1–9
Tiwari H, Rai SP, Kumar D, Sharma N (2015) Rainfall erosivity factor for India using modified Fourier index. J Appl Water Eng Res 1–9
Willems P, Vrac M (2011) Statistical precipitation downscaling for small-scale hydrological impact investigations of climate change. J Hydrol 402(3–4):193–205
Xie SP, Okumura Y, Miyama T, Timmermann A (2008) Influences of Atlantic Climate Change on the Tropical Pacific via the Central American Isthmus*. J Clim 21(15):3914–3928
Yadav RK, Rupa Kumar K, Rajeevan M (2010) Climate change scenarios for Northwest India winter season. Quatern Int 213(1–2):12–19
Yang J, Reichert P, Abbaspour KC, Yang H (2007) Hydrological modelling of the Chaohe Basin in China: statistical model formulation and Bayesian inference. J Hydrol 340(3–4):167–182
Zhang X, Srinivasan R, Bosch D (2009) Calibration and uncertainty analysis of the SWAT model using Genetic Algorithms and Bayesian Model Averaging. J Hydrol 374(3–4):307–317
Zhu J (2013) Impact of climate change on extreme rainfall across the United States. J Hydrol Eng 18(10):1301–1309
Acknowledgments
The authors wish to thank Indian Institute of Technology, Delhi (IIT D), as well as Indian Institute of Technology, Roorkee (IIT R), for providing the needful space and resources during the study. This work was financially supported by the Ministry of Human Resources and Development, New Delhi, and the Department of Science and Technology, New Delhi.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pandey, B.K., Gosain, A.K., Paul, G. et al. Climate change impact assessment on hydrology of a small watershed using semi-distributed model. Appl Water Sci 7, 2029–2041 (2017). https://doi.org/10.1007/s13201-016-0383-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13201-016-0383-6