Introduction

Agriculture, hydroelectricity and industrial sector derive their water resource indirectly from Summer Monsoon rainfall in the month of June–September. The irony is that the same Monsoon often cause flood in many parts of the country like Assam, Bihar and Uttar Pradesh. The worst drought years were 1877, 1899, 1911, 1918, 1920, 1951, 1965 and 1972 and the worst flood years were 1892, 1933, 1961 and 1983 when many subdivisions reported extremely low and excess rainfall, respectively (Parthasarathy et al. 1987). 1988, 1994, 1998, 2000, 2005, 2008, 2009, 2010, 2013 and 2014 can also be regarded as flood years in India. Assam, the state which lies in Brahmaputra River floodplains has been experiencing flood annually since 1998. Floods in Ganga River have been very common and their cause is attributed to heavy downpour in upper reaches in Uttarakhand district and in the floodplains. Ganga Flood Control Commission was established in 1972 to look into the causes and sort out the flooding problem by suggesting structural measures. The National Flood Control Program was launched in the country in 1954. Since then a good progress has been made in the flood protection measures. About one-third of the flood prone area had been afforded reasonable protection. Besides, many steps were undertaken in planning, implementation and performance of flood warning, protection and control measures (CWC 2007). On an average 32.92 million people are affected by floods every year in India (Report 2011).

Attempts of flood frequency analysis have been made for deltaic region (Jha and Bairagya 2011) and Middle subzone 1(f) of Ganga basin (Kumar et al. 2003). They have adopted the normal, lognormal, gumbel maximum value and Log Pearson type III probability distribution functions to find the flood frequency for different return periods. Now-a-days the L-moment approach is widely used for developing regional flood frequency relationships (Hosking and Wallis 1997). There is a need of data on flood magnitudes and their frequencies for designing of hydraulic structures like dams, spillways, culverts, urban drainage systems; also for road and railway bridges, flood plain zonation, etc. (Kumar et al. 2003). Singo et al. (2013) used similar approach to find that the Log Pearson type III best fits the model to find the flood intensity of different return period in flood prone Luvuvhu River Catchment (LRC) of South Africa.

There are many frequency models which are now used for determining hydrologic frequency of flood. Probabilistic model rely on the use of existing data to forecast future scenario and deterministic model rely on the different physical parameters to bring out the result and verify it with the existing data to develop a best fit model. Probabilistic approach is commonly practiced in hydrology (Helsel and Hirsch 2010). Within probabilistic models, the two most popular are Gumbel maximum value and Log Pearson type III distribution.

The development of model for hydrological data is driven by the pattern that one obtains through fitting of various equations into an orderly arrangement of data. Overtime the hydrological models have become more complex with the advent of new theories in mathematical sciences. But in terms of result they are more reliable than before. The most common distribution that have been explored here are: Lognormal 3P, Generalised Extreme Value, Log Pearson type III and Gumbel distribution. These distributions are finally tested to find which one gives the best results and can be utilized for modelling flood hazards in that area.

Log Pearson type III distribution has found very wide use in hydrological sciences, especially in flood frequency analysis. Bernard Bobee discussed its limitation and utilization in his paper in 1975. This method retains the original data and it gives better fit over other distribution for long return period. Similar studies have shown that GEV distribution is a more acceptable distribution over Log Pearson type III (Vogel et al. 1993). Nazemi et al. (2011) corroborated this fact by his studies in Saskatoon city of Saskatchewan in Canada. Environmnent Canada (EC) prefers to use Gumbel distribution with the method of moments (MOM) for precipitation analysis.

The lognormal, GEV, EV1 and LP3 distributions are explained here along with their advantages and disadvantages. A random variable x (variate) is said to be in log-normal distribution if the logarithmic values of x is distributed normally, as derived using central limit theorem. The mean and the standard deviation are the two parameters here and third frequency factor is derived from the exceedance probability value. GEV (Generalized Extreme Value Distribution) is a continuous probability distribution method that uses three parameters: location, scale and shape. The shift of a distribution in a particular direction is explained by location parameter, spreading out of the distribution is explained by the scale parameter similar to kurtosis and tails of each distribution is governed by the shape parameter like skewness. For shape parameter (k) = 0, Gumbel or EV1 distribution is applicable, for k > 0, EV2 or Frechet is applicable, and for k < 0 EV3 or Weibull is applicable. In general, GEV which has more parameters will be able to model the input data more accurately than a distribution with a lesser number of parameters. GEV is also good for sample size greater than 50 (Cunnane 1989). Cunnane also found that 3–4 parameter distributions have less bias. Gumbel Distribution (EV1) uses 2 parameters, location (ξ) and scale (α) and is used for all Precipitation Frequency Analysis in Canada. The LP3 distribution is also referred to as the Gamma distribution. The LP3 distribution is complex due to 2 interacting shape parameters (Stedinger and Griffis 2007).

The parameter estimation is done by using many ways, viz. by maximum likelihood estimators, method of moments (MOM) or by methods of L-Moments. L-Moments are based on probability-weighted moments (PWMs), for the data arranged in ascending order. The MOM technique is good for limited range of parameters, whereas L-Moments can be more widely used, and are unbiased (Rowinski et al. 2001).

Study area and data availability

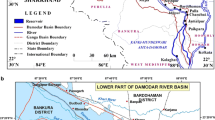
The yearly discharge data from two locations on the Ganga River have been used here, one at Haridwar and the other located 145 km downstream at Garhmukteshwar. Haridwar site is located at 78.165°E longitude and 29.942°N latitude and Garhmukteshwar site is located at 78.148°E longitude and 28.758°N latitude (Fig. 1). The maximum yearly discharge data of Haridwar is taken from the book authored by Professor H.M. Raghunath, Hydrology Principles, Analysis and Design. This data is from 1885 to 1971. The yearly discharge data of Garhmukteshwar (1970–2010) has been obtained through proper channel from CWC (Central Water Commission), and since the data is restricted by the Indian Government due to international character of Ganga River, it has not been shown here; only the graph is shown (Fig. 2). The data of Haridwar is also shown along with the Summer Monsoon rainfall data of Eastern U.P. region which is the region where Haridwar falls, to show how well the rainfall peaks match with that of discharge (Fig. 3). The lognormal values help in synchronizing the data of rainfall and discharge which are in different units. The rainfall data is used from the work of Parthasarathy et al. 1987.

Fig. 1
figure 1

Study area with two gauging sites on Ganga River

Full size image
Fig. 2
figure 2

Graphs showing yearly maximum discharge variation in both the stations

Full size image
Fig. 3
figure 3

Graph showing log values of Summer Monsoon rainfall and yearly discharge

Full size image

Methodology

Generalized Extreme Value distribution is done on the L-Moments approach and MOM is used in LP3 and EV1. PWMs are needed to find L-Moments. The data is first arranged in ascending order, and then following equations are used to calculate PWMs: M100, M110, M120 and M130 (Cunnane 1989).

$${\text{M}}100 = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} Q_i$$
(1)
$${\text{M}}110 = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \frac{i - 1}{n - 1}Q_i$$
(2)
$${\text{M}}120 = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \frac{(i - 1)(i - 2)}{{\left( {n - 1} \right)(n - 2)}}Q_i$$
(3)
$${\text{M}}130 = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \frac{{\left( {i - 1} \right)\left( {i - 2} \right)(i - 3)}}{{\left( {n - 1} \right)\left( {n - 2} \right)(n - 3)}}Q_i$$
(4)

in which N is the sample size, Q is the data value, and i is the rank of the value in ascending order. The L-Moments are then calculated as follows (Cunnane 1989):

$$\lambda_1 = {\text{ L1 }} = {\text{M}}_{ 100}$$
(5)
$$\lambda_2 = {\text{ L2 }} = 2 {\text{M}}_{ 1 10} - {\text{ M}}_{ 100}$$
(6)
$$\lambda_3 = {\text{ L3 }} = 6 {\text{M}}_{ 1 20} - {\text{ 6M}}_{ 1 10} + {\text{ M}}_{ 100}$$
(7)
$$\lambda_4 = {\text{ L4 }} = 20{\text{M}}_{ 1 30} - { 3}0{\text{M}}_{ 1 20} + {\text{ 12M}}_{ 1 10} - {\text{ M}}_{ 100}$$
(8)

The L-moments are further used to derive variation coefficient L-CV (τ2), symmetry coefficient L-Skewness (τ3) and peakedness coefficient L-Kurtosis (τ4) as follows, (Hosking and Wallis 1997):

$$\tau_2 { } = {\text{L2}}/{\text{L1 }}\left( {{\text{L}} - {\text{CV}}} \right)$$
(9)
$$\tau_3 { } = {\text{ L3}}/{\text{L2 }}\left( {{\text{L}} - {\text{Skewness}}} \right)$$
(10)
$$\tau_4 { } = {\text{ L4}}/{\text{L2 }}\left( {{\text{L}} - {\text{Kurtosis}}} \right)$$
(11)

Generalized Extreme Value (GEV) distribution uses three parameters: ξ, the location parameter, α, the scale parameter and κ, the shape parameter. The parameters are defined from (Hosking and Wallis 1997) as:

$$\kappa = 7.8590{\text{c }} + 2.9554{\text{c}}^{2}$$
(12)
$${\text{in which}}\,c = \frac{2}{3 + \tau_3} - \frac{\ln 2}{\ln 3}$$
(13)
$$\xi = \lambda 1 - \frac{{\left\{ {1 {-} \varGamma \left( {1 + k } \right)} \right\}}}{k}$$
(14)

in which Γ = the gamma function.

Finally the return period discharge is calculated using the following formulae:

$$Qt = \xi + ( \alpha /k)\{ 1{-\!\!-}{ \log }( (T - 1)/T ) )k$$
(15)

in which T is the desired return period in years.

Step by step GEV performed in excel (Millington et al. 2011) is as follows :

  1. (a)

    Firstly, sort the data set by ordering all of the data points in ascending order (lowest to highest)

  2. (b)

    Calculate the 4 PWM’s (M100, M110, M120, M130)

  3. (c)

    Calculate the 4 L-Moments (λ1, λ2, λ3, λ4) using the PWMs

  4. (d)

    Calculate k, the shape parameter

  5. (e)

    Calculate ξ, the location parameter and α, the scale parameter

  6. (f)

    Using the desired return period, apply all parameters to the Return Period equation to calculate the discharge value.

The US Water Resources Council (1967) adopted the Log-Pearson Type-III distribution. The procedure is to first convert the data to logarithms and calculate the following (Raghunath 2006):

$${\text{Mean}} \,\, \overline{\log x } = \frac{\mathop \sum \nolimits \log x }{n}$$
(16)
$${\text{Standard deviation}}: \, \sigma_{\log x} = \sqrt {\frac{{\mathop \sum \nolimits \left( {{ \log }x - \overline{{{ \log }x}} } \right)^{2} }}{n - 1}}$$
(17)
$${\text{Skew coefficient}}: \, g \, = \frac{{n\mathop \sum \nolimits \left( {\log x - \overline{\log x} } \right)^{3} }}{{\left( {n - 1} \right)\left( {n - 2} \right)(\sigma \log x)^{3} }}$$
(18)

The values of x for various recurrence intervals are computed from,

$$\log x = \overline{\log x} + K \sigma \log x$$
(19)

The frequency factor K is obtained from the following Table 1 for the computed value of ‘g’ and the desired recurrence interval.

Table 1 Table of frequency factor ‘K’ for LogPearson III distribution
Full size table

Gumbel’s method by V.T. Chow is used. The equation is

$$Qt = a + bXt$$
(20)
$${\text{where}},X_t = \log \left( {\log \left( {\frac{T}{T - 1}} \right)} \right)$$
(21)

a, b = parameters estimated by the method of moments. The following equations are derived from the method of least squares.

$$\sum Q = an + b\sum {X_t}$$
(22)
$$\sum {(QXt)} = a\sum {X_t} + b\sum {X_t^{2} }$$
(23)

Now, ‘a’ and ‘b’ can be solved.

In this method, a plotting position has been assigned for each value of Q when arranged in the descending order. For example, if an annual flood peak Q T has a rank m, its plotting position

$$T = \frac{n + 1}{m}$$
(24)

From Eq. (21),

$$X_t = \log \left( {\log \left( {\frac{n + 1}{n + 1 - m}} \right)} \right)$$
(25)

We substitute the values and solve the equations for getting ‘a’ and ‘b’, finally to get Qt.

The three parameter lognormal (TPLN) distribution is used as the fourth method of distribution. Properties of this distribution are discussed by Aitchison and Brown (1957), and Johnson and Kotz (1970). For a random variable X, if Y = ln(X − a) has a normal distribution then X will have a lognormal distribution whose probability density function (pdf) can be expressed as

$$f\left( x \right) = \frac{1}{{\left( {x - a} \right)c\sqrt {2\pi } }}\exp \left[ {\frac{{ - [\ln \left( {x - a} \right) - b]^{2} }}{{2c^{2} }}} \right]$$
(26)

where ‘a’ is a positive quantity defined as a lower boundary, and ‘b’ and ‘c 2’ are the form and scale parameters of the distribution. ‘b’ is equal to the mean and ‘c 2’ is equal to the variance of log values. The cumulative distribution function (cdf) of the TPLN is an integral function from x to a of f(x) (Singh 1998). The cdf obtained from EasyFit software is used to calculate the Annual Exceedance Probability (AEP), or the probability that the event is excelled or equaled in any single year. This is calculated as (1 − P). Return period is calculated as inverse of AEP. Then finally the Qt for a return period ‘t’ is obtained using the logarithmic relation between return period and discharge values.

Goodness of fit tests

Climatic datasets are analyzed using different distribution techniques and to find which one is most reliable, we use the goodness of fit tests. These tests are:

  1. 1.

    The Anderson–Darling (AD) and

  2. 2.

    Kolmogorov–Smirnov (KS)

Solaiman 2011 described all test statistics. The goodness of fit tests was carried out using EasyFit, available at http://www.mathwave.com/easyfit-distribution-fitting.html.

Anderson–Darling Test

The Anderson–Darling test compares an observed CDF to an expected CDF. The Anderson–Darling test gives more weight to the tail of the distribution than KS test. The test hypothesis is rejected if the AD statistic is greater than a critical value of 2.5018 at a given significance level α = 0.05. The AD test statistic (A 2) is:

$$A^{2} = - n {-}\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {2i - 1} \right) . \left[ { \text{ln} F \left( {xi} \right) + \ln \left( {1 - F \left( {xn - i + 1} \right)} \right)} \right]$$
(27)

Kolmogorov–Smirnov Test

The Kolmogorov–Smirnov test statistic is based on the greatest vertical distance from the empirical and theoretical CDFs. Similar to the AD test statistic, a hypothesis is rejected if the KS statistic is greater than the critical value 0.1255 at a chosen significance level α = 0.05.

The samples are assumed to be from a CDF F(x). The test statistic (D) is:

$$D = { \hbox{max} }\left( {F\left( {xi} \right){-} \frac{i - 1}{n},\frac{i}{n}{-} F\left( {xi} \right)} \right)$$
(28)

Log Normal, Log Pearson type III, Gumbel EV1 (Ven T Chow method) and Generalised Extreme Value (L Moments method) as discussed above were used to calculate maximum discharge for return period of 2, 5, 10, 25, 50, 100 and 200 years in Ganga river at the discharge site of Haridwar and Garhmukteshwar.

Results and discussion

The following table (Table 2) shows the outcome of the various distributions. The entire process was executed in Microsoft Excel 2007. The graph in Figs. 4 and 5 shows the comparison of discharge calculated by different distributions. It comes out that for both Haridwar and Garhmukteshwar discharge sites; GEV gives maximum values, followed by Gumbel, Log Pearson III and Lognormal 3P at last. To find statistically which distribution best fits the discharge data and gives the best output in terms of return period, the available data was processed in Easyfit software. Easyfit software compares the three Goodness of Fit (GOF) tests. According to the theory discussed before, the statistic is calculated from Kolmogorov–Smirnov test, Anderson–Darling test and Chi-Squared test (Tables 3, 4). The Chi-Squared test determines if a sample comes from a given distribution. It is not considered a high power statistical test and is not so useful (Cunnane 1989). So, the Chi-square has not been adopted here for GOF test.

Table 2 Final result showing the return period discharge values expected through four distribution methods
Full size table
Fig. 4
figure 4

Bar graph showing the comparison of outcome of four distribution for Haridwar data

Full size image
Fig. 5
figure 5

Bar graph showing the comparison of outcome of four distribution for Garhmukteshwar data

Full size image
Table 3 Goodness of fit test for Haridwar data
Full size table
Table 4 Goodness of fit test for Garhmukteshwar data
Full size table

The critical value at α = 0.05, i.e. 95 % confidence level for all three test is shown in the table (Table 3, 4). This value decides which distribution is to be rejected from the study. We see that all the distributions are accepted with no rejection statistically. The other fact that is brought out is the significance of the distribution. Ranking is given on the difference between statistic value and the critical value. Lognormal (3P) is given ranking 1 in case of Haridwar data and Gumbel is given ranking 1 in case of Garhmukteshwar data. The sample size in terms of number of years is high for Haridwar i.e. 87 (1885–1971) and low for Garhmukteshwar, i.e. 42 (1971–2013). The present study is corroborated by the previous similar studies on latest data done by Kumar et al. (2003) where GEV (L moments method) was found to be robust for Middle Ganga subzone (1f) and Singo et al., where Gumbel distribution and Log Pearson 3 gave good results for steep Luvuhu river catchment. Haridwar is analogous to Luvuhu as it lies in foothills and Garhmukteshwar is very close to Middle Ganga subzone (1f).

So we can conclude that Gumbel is good for low sample size and Lognormal (3P) gives good result for large sample size (Table 4). Log Pearson III is placed at poor ranking in Garhmukteshwar data which supports the fact that Log Pearson III is not good for small sample size, and Gumbel is better than this. Now, the question arises, why discharge is less at Garhmukteshwar, though it is downstream of Haridwar and theoretically the discharge increases downstream. The answer can be easily given from the fact that there is significant withdrawal of river water via canal at Bijnor barrage which lies in between Haridwar and Garhmukteshwar. Bijnor barrage is also known as Madhya Ganga canal project which started in 1976. Also there are no perennial tributaries which come and join in between. So, naturally the discharge level goes down at Garhmukteshwar, which has discharge data after 1970. This underlines the methodological limitations of statistical distributions which primarily rely on the fact that the flow in a river is not altered through unnatural ways and the data availability is continuous and of long duration at every station along the river. Ironically, such conditions are hard to find for any river and field data availability is also scarce for such rivers due to the legal and technical issues involved.

Conclusion

The present study has been done on the data available for Upper Ganga region, and is important because of dearth of data availability, for the Ganga River. The floodplain of Ganga River is facing danger of encroachment by illegal construction. The future scope of the present work is that the values of return period flood can be used to construct the flood hazard zones and define the river space. This river space is to be preserved for the sake of ecology, riparian vegetation and nutrient recycling during floods. It signifies the horizontal connectivity in a fluvial system.

The statistical approaches have been used widely to fit the data and predict the values for return period by many authors. The study has shown that the recent technique of GEV distribution that uses L-Moments does not fits well with the discharge data of Ganga in Haridwar for long term data but Log normal (3P) fits and prove more reliable for flood frequency analysis. Goodness of fit tests validated that Gumbel EV1 distribution stand high in ranking for short term data of Garhmukteshwar at 145 km downstream. The comparison of return period discharge further proves that Log normal (3P) gives more practical result if we have more historical data, with values neither overshooting nor undershooting.