Abstract
Identification of pollutant sources for river pollution incidents is an important and difficult task in the emergency rescue, and an intelligent optimization method can effectively compensate for the weakness of traditional methods. An intelligent model for pollutant source identification has been established using the basic genetic algorithm (BGA) as an optimization search tool and applying an analytic solution formula of one-dimensional unsteady water quality equation to construct the objective function. Experimental tests show that the identification model is effective and efficient: the model can accurately figure out the pollutant amounts or positions no matter single pollution source or multiple sources. Especially when the population size of BGA is set as 10, the computing results are sound agree with analytic results for a single source amount and position identification, the relative errors are no more than 5 %. For cases of multi-point sources and multi-variable, there are some errors in computing results for the reasons that there exist many possible combinations of the pollution sources. But, with the help of previous experience to narrow the search scope, the relative errors of the identification results are less than 5 %, which proves the established source identification model can be used to direct emergency responses.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In the past a few decades, thousands of water pollution incidents caused by accident or illegal emissions happened all over the world. Such as Tuojiang River pollution incident happened in 2004, Songhua River benzene pollution incident happened in 2005, Colorado River pollution incident happened in 2015, and so on. The pollution incident refers to a large amount of pollutant leaked into the water suddenly, resulting in a rapid increase in pollutant concentrations, which may serious impact on the safety of water supply. When water pollution incidents occur, the recognition of pollution sources (including source location and amount of pollutant) is a primary task in emergency response, which has attracted the attention of many researchers and governors. Xue and Wang identified the source location of a water pollution incident successfully by adopting the ‘monitoring-judging’ method (Xue and Wang 1997). With the help of an established pollution source database created by government agencies, Wang proposed the “Fingerprint Method” for identification of the source location of the pollution incident (Wang et al. 2009). Combining a one-dimensional water quality model in rivers with a geostatistical method, Fulvio inversely analyzed the pollutant amount on where the pollution source location was known (Fulvio et al. 2005). With the combination of a two-dimensional river water quality model and Adjoint Method, Nikolaos and Michael used an optimization procedure to predict the position of the pollution sources and the amount of pollutant (Nikolaos and Michael 1996). Combining MODFLOW and MT3DMS and BL-PDF, Neupauer and Wilson developed a groundwater pollution source identification model (Roseanna and Neupauer 2004). With the combination of the two-dimensional water quality mathematical model in rivers and BL–PDF, Cheng and Jia proposed a surface water pollution source inversion model (Cheng and Jia 2010). With the combination of water quality model and a Bayesian estimation method, Zhu obtained the location probability distribution of pollution source (Zhu et al. 2009). The inversion problem of water pollution sources is also studied by the researchers in the field of mathematics. Based on mathematical theory, the uniqueness of the pollution source (single source) position has been proved (Wang and Xu 2006), and the related identification method has been given (Wang and Qiu 2008).
To figure out the source for a pollution incident is of great difficult. Traditional identification models relied excessively on monitoring data, and are laborious and data intensive (Cheng and Jia 2010). With the high requirement for topographical, hydrological, water quality data, and needing a lot of incident environmental monitoring data as support, the methods that use numerical water quality models method may affect the efficiency. The recognition of pollution sources with the aid of an optimization algorithm combined with mathematical analysis methods is simple, practical and has been widely applied (Cao et al. 2010; Yin et al. 2011). Meanwhile, with the ability for global searching, robustness and high efficiency, the Genetic Algorithm (GA) is widely used on the inverse problems in the aquatic environment (Singh and Datta 2006). Combining GA and the mathematical analysis method, this paper proposed a pollution source identification model of sudden water pollution incidents in small straight rivers, which can concisely and effectively deal with the problem of the pollution source determination.
Water quality equations and its analytic solution
The motion and transportation process for pollutant in the river channel can be described as convection and diffusion processes, so the water quality equations are called as convection and diffusion equations. The three-dimensional equation is as follows (Wang and Shen 2005; Li et al. 2015):
where, C is the concentration of pollutant caused by the pollution incident (mg/L); t is the time (s); x, y, z are the lateral, transverse and vertical coordinates (m); u, v, w are the flow velocity in the above three coordinates, respectively (m/s); E x is the diffusion coefficient, (m2/s); K is the comprehensive decay coefficient, (1/s); S is the source item. In general, the concentration field can be computed by numerically models with Eq. (1). However, river terrain and hydrological data are usually insufficient where accident emergencies occur. Therefore, especially for small rivers, the three-dimensional convection–diffusion equation in rivers can be simplified as: (1) A river, whose discharge is less than 50 m3/s, bend coefficient is less than 1.5 and water width is less than 100 m, can be assumed as small straight river (Ni and Wang 2000). For those rivers, the river courses can be assumed as homogeneous channel and the flow can be assumed as constant (Liu 2005). (2) Comparing to the quantity and concentration of pollutants leaked into the river, the background concentrations at two endpoints could be ignored, and the initial concentration could be assumed to be zero as well. (3) For a small river, the pollutant is considered to mix homogeneously across the transverse section, and have a constant attenuation. Therefore, the concentration distribution along the river can be simplified as the following one-dimensional convection–diffusion equations (Jiang and Wang 1997; Liu 2005; Abderrezzak et al. 2015):
where l is the river length (m); M i represents pollutant amount of the corresponding pollution source, (g/s); δ is the Dirac Function; x i is the location (coordinate) of the pollution source, (m); q is the number of pollution sources in the incident.
When the location x i of pollution sources and the amount of pollutant M i released into the river are known, solving the distribution C(x, t) of pollutant concentration in the river at different times is known as the “forward problem” for pollutant concentration simulation. With this “forward problem”, we can simulate and predict the effect degree and scope of a water pollution incident. On the other hand, when the concentration monitoring values at different places at a particular time or the monitoring values at a place at different times are given, we need to find out the pollution source position or the pollutant amount, which is known as an “inverse problem”. In the process of solving an “inverse problem”, the first step is to build the optimization object function of the “inverse problem” by applying the solution of the “forward problem”. So we should use an appropriate method to solve Eq. (2). As we can see, the partial differential Eq. (2) belongs to the linear convection–diffusion equations. Some researchers used the method for combining Fourier transform with Laplace transform method (Kumar et al. 2010; Feng 2012), and others have used separation of variables to solve the equations (Min et al. 2004; Wu et al. 2008). Finally, it is concluded that the water quality equation’s analytical solution of a river pollution incident is as follows:
Supposing the experimental river length l is 1000 m, the flow velocity u is 0.1 m/s, the diffusion coefficient E x is 5.0 m2/s, and the comprehensive attenuation coefficient K is 0.00001/s, and the pollutant concentration can be calculated using the above Eq. (3). There are two supposed conditions: (1) a single pollutant source incident happens with the position x = 500 m and amount M = 3.0 g/s; (2) double pollutant sources incident occur with the position x 1 = 300 m, amount M 1 = 3.0 g/s, x 1 = 500 m, amount M 1 = 5.0 g/s, respectively. Hydrodynamic and pollution source characteristics parameters of the supposed conditions are listed in Table 1.
Calculating the infinite series from n = 1 to n = 1000 to obtain the pollutants concentration approximately at each moment, under the two kinds of working conditions, concentration distribution at each moment along the river channel is shown in Fig. 1, and concentration distribution of each section changing in time is shown in Fig. 2. As can be seen, the pollution causes the pollutant concentration jump in the adjacent river sections. And for a special position, the concentration increases at first and then tends to be stable, which did respond the truth
Genetic algorithm and the identification model of accident pollution source
Basic genetic algorithm
The basic genetic algorithm (BGA) is a kind of intelligent optimization method proposed by Holland (Holland 1975), which imitated the natural genetic phenomena of selection, crossover and mutation processes in nature. Jong carried out a great quantity of optimization tests with numerical functions using Holland’s theory, which proofed BGA is an effective and efficient stochastic search method (Jong 1975). In the 1990s, BGA were widely used in the scope of engineering with the publication of ‘Hand book of Genetic Algorithm’, such as reservoir operation optimization (Jothiprakash and Shanthi 2006), numerical model parameter optimization (Tang et al. 2010), inverse problem research (Dai and Wang 2006), and so on.
BGA starts from an initial population that contains a number of individuals, and then new individuals are produced to be better adapted to the environment with random selection, crossover and mutation. The best individual is eventually achieved by a number of evolution steps (generations). Every individual in a population is a feasible solution for the optimization problems, and the best individual is the optimal solution of the optimization problem. Compared with the other optimization algorithms, BGA has the following advantages: (1) the optimization objective function can be either a continuous function or a discrete function (Tang et al. 2010); (2) has the property of global search and automatic convergence to the optimal solution; (3) robust in dealing with complex nonlinear problems; (4) the principle is simple, easy to understand, versatile and highly maneuverable. Many improvements have been made to the BGA considering its wide application, including a niche technology of crossover operation (Srinivas and Patnaik 1994), uniform mutation operation method (Xin et al. 2009) and adaptive algorithm of crossover and mutation probability (Li et al. 2004; Yu et al. 2013).
Pollutant source identification model
It can be seen from the pollutant concentration Eq. (2) that solving C (x, t) depends on the location x i of sudden water pollution incident and the amount of pollutants M i . Therefore, different x i and M i decide different pollutant concentration distributions. By setting up a monitoring cross section on an experimental river at time T and obtaining the concentration distribution \(\overline{C} (\overline{x}_{i} ,T)\) of the pollutant, where, i is the number of the monitoring section, \(\overline{x}_{i}\) is the position coordinates of the ith monitoring section, then the pollution source inversion problem can be transformed into an optimization problem of a linear discrete function as follows:
If we obtain the x i and M i which are the closest to calculated values and measured values by optimal Eq. (4), and the location of incident pollution sources and pollutants amount are consequently confirmed. This optimization search process can be completed by the basic genetic algorithm. Hence, a pollution source identification model of a sudden water pollution incident based on the basic genetic algorithm can be established through the following steps:
-
1.
Determining the parameters of the basic genetic algorithm, including the gene number N g of individuals, and the value scope of the gene, the crossover probability p c, the mutation probability p m, the number of individuals in a population (population size) I m, and the maximum evolution step T m, among which the number of genes N g is determined by the number of optimization variables. Take a single source identification problem as an example, if only the position or the amount need to be identified, the N g = 1, else if both the position and amount needs to be optimized, the N g = 2. The crossover probability, mutation probability and the population size are determined by experience (Zhang et al. 2009).
-
2.
Determining the gene encoding. Since a water pollution incident may have q sources, and each source will have two optimization variables. So the number of optimization variables is 2q. If we use binary encoding method, a dozen of gene may only represent an individual, which may waste a lot of storage space. So we choose the floating-point real number coding method which means the number of the gene is 2q, accordingly. A floating-point real number coding method is adopted for the convenience of encoding and decoding. In the basic genetic algorithm, the genes of kth individual in the population is \(X^{k} = (x_{i}^{k} ,M_{i}^{k} )\), where \(x_{i}^{k}\) is the position and \(M_{i}^{k}\) represents pollutant amount for the ith pollution source.
-
3.
Generating initial population \(x_{i}^{k} = x_{i,\hbox{min} } + {\text{rand}}(x_{i,\hbox{max} } - x_{i,\hbox{min} } )\),\(M_{i}^{k} = M_{i,\hbox{min} }\, + {\text{rand}}(M_{i,\hbox{max} } - M_{i,\hbox{min} } )\), where rand is a random function which creates a number between 0 and 1; x i,min and x i,max are the lower limit and upper limit for the position of the ith pollution source. M i,min and M i,max are the lower limit and upper limit for the pollutant amount of the ith pollution source.
-
4.
Establishing the optimal objective function (fitness function of basic genetic algorithm). Because the basic genetic algorithm can only make the individual evolve towards the increasing fitness values, while Eq. (4) requires optimization variables changing in the decreasing direction of the objective function value, thus it is necessary to modify the objective function to the fitness function (Tang et al. 2010):
$$F = {1 \mathord{\left/ {\vphantom {1 {\left[ {C(x_{i} ,M_{i} ,\overline{x}_{i} ,T) - \overline{C} (\overline{x}_{i} ,T)} \right]^{2} }}} \right. \kern-0pt} {\left[ {C(x_{i} ,M_{i} ,\overline{x}_{i} ,T) - \overline{C} (\overline{x}_{i} ,T)} \right]^{2} }}$$(5) -
5.
Optimization operation. The operators of selection, crossover and mutation are applied to the initial population, and it stops when the Genetic Algorithm converges or reaches the maximum evolution step. The best individual of the latest population represents the positions x i and pollutant amount M i .
With this, a pollutant source identification model of pollutant incidents based on BGA has been established, and the working flow chart of the model is shown in Fig. 3.
Tests of pollutant source identification model
Single variable identification for single source
In the reality, after some sudden water pollution incident happens, we may know the location of the pollutant incident by investigation with other methods, such as Chinese national pollution source information database (MEP 2010). But, we do not know the pollutant amount discharged into river. Under this condition, the pollutant amount is the optimization variable. Water pollution incident happened at Fujiang, China, in 2011 belongs to this situation (Wang et al. 2012). On the other hand, the pollutant amount can be figure out easily or the incident perpetrator know the amount of pollutant, but we cannot obtain relate information about pollution source position, so the position is the optimization variable. To forecast the pollution information and carry out rescue measures, using the established identification model of pollution source to identify the pollutant amount into river or pollutant source position is of great importance.
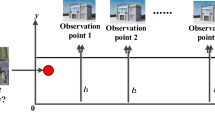
Take the following water pollution incident as an example, where the hydrodynamic parameters of the test river section are the same as in Table 1 (single source condition), the pollutant amount is 3.0 g/s and the pollution source location is at 500 m. For the sake of contrast analysis, the analytic solution to the “forward problem” at t = 4000 s is selected as the field monitoring value \(\overline{C} (\overline{x}_{i} ,T)\), and the monitoring sections (data collection points) are shown as Figs. 4 and 5, the “field monitoring data” are shown in Table 2.
Considering the fact that the population size I m of the basic genetic algorithm has significant influence on the identification model, different computing conditions are set with different population sizes. The other parameters of computing conditions for BGA are shown in Table 3. The identification results of pollutant amount or the position of sources are shown in Table 4. As we can see from Table 4, this novel identification model based on the basic genetic algorithm has a relatively higher precision: the relative error between identification results of pollutant amount and analytic results varied from −1.7 to 5.0 %, and the relative error between identification results of source position and analytic results varied from 0 to −1.6 %. Since the crossover probability parameter p m has been set as 0.8, so crossover operation is more fully undertaken with increasing population size, the “premature” phenomenon can be avoided and the model converges faster. When population size is set as 10, the model identification result and analytic result are exactly the same, where the relative error is 0.
Multi-variable identification for single source
For the other water pollution incidents, we not only do not know the locations of the pollution sources, but also do not know the pollutant amount discharged into the river, so we need to identify these two variables at the same time, which is a multi-variable identification for single source problems. Ammonia nitrogen pollution incident happened at Hanjiang, China, in 2014 belongs to this situation. (http://finance.sina.com.cn/consume/puguangtai/20140425/092218920579.shtml).
Continuing with the above water pollution incident as an example, where the hydrodynamic parameters of the test river section are the same as Table 1, the pollutant amount is 3.0 g/s and the pollution source location is at 500 m. For the sake of contrast analysis, the analytic solution to the “forward problem” at t = 4000 s is selected as the field monitoring value, and the monitoring sections (data collection points) are shown in Figs. 4 and 5, “field monitoring data” are shown in Table 2. An identification model is established to carry out a test experiment for the pollutant source position and the pollutant amount synchronously. Computing parameters of the source identification model are shown in Table 5. The computing results are shown in Table 6. Obviously, the pollution source location is 500 m calculated by the identification model (relative error is 0.0 %), pollutant total amount is 2.90 g/s (relative error is 2.34 %), which implies the precision is dropping in an acceptable range (relative error less than ±10 %). The model converged when calculated to the 20th generation, and the profile curve of fitness value changing along with the evolution steps is shown in Figs. 4 and 5.
Single variable identification for double sources
Although the probability of occurrence in practice is small, to test the applicability of the established identification model, taking a water pollutant incident with double sources as an example where pollutant amounts are 3.0 and 5.0 g/s, pollution sources’ positions are 300 and 500 m, respectively. Analytic solution at t = 4000 s of “forward problem” is still used as the monitoring value \(\overline{C} (\overline{x}_{i} ,T)\) for the “inverse problem”. The analytic results are shown in Table 7. On this basis, the identification model of a single variable (pollutant amounts or source positions) for multi-sources is established. The computing results are shown in Table 8. When the positions of double sources are known, computing results of pollutant amounts are 2.85 and 5.02 g/s, the relative errors are −5.0 and 0.4 %, respectively. When the pollutant amounts of double sources are known, the computing results of source positions are 310 and 496 m, the relative errors are, respectively, 3.3 and −0.8 %. So the precision is in an acceptable range (relative error less than ±10 %).
Multi-variable identification for double sources
If the amounts and the positions are not both known, continuing with the sudden water pollutant incident of double sources as an example where pollutant amounts are 3.0 and 5.0 g/s, and pollutant source locations are 300 and 500 m. The analytic results at t = 4000 s are still used as monitoring data \(\overline{C} (\overline{x}_{i} ,T)\). The identification results of pollutant amounts and positions are shown in Table 9. If without any experience to narrow the search scope of the positions or the amounts, the model is thoroughly unable to identify the pollution sources, with the computing positions x 1 = 520 and x 2 = 295, and the computing amounts M 1 = 9.15 and M 2 = 2.40, which draws a wrong results. However, if narrowed the positions x 1, x 2 to [100, 600] and the amounts M 1, M 2 to [1.0, 6.0], identification results of pollution source positions for double point sources are 293 and 511 m, the relative errors are −2.3 and 2.2 %, identification results of pollutant amounts are 2.93 and 5.22 g/s, the relative errors are −2.3 and −4.4 %, respectively. The model converges at an evolution step of 145, and the profile curve of fitness value changing along with the evolution steps is shown in Fig. 6.
Conclusions
-
1.
To supply some help in the rescue of pollution incidents, coupling the BGA with the analytical solution of a one-dimensional convection–diffusion equation, a sources identification model for water pollution incidents in small straight rivers is established. Tests imply that for both single variable and multi-variables for single pollutant source, the inversion results are well satisfied when the population size is large enough, such as 10. The relative errors are less than 5 %.
-
2.
For the pollutant source identification of multiple point sources in a water pollution incident, there exists certain error even mistake, because this kind of “inverse problem” is a so called “ill-posed problem” mathematically, which does not have a unique solution. So in this situation, we need some more previous experience to narrow the search scope of the BGA.
-
3.
For the sources identification of a sudden water pollution incident, a water quality monitoring work is a necessary. The water quality monitoring scheme proposed in this paper is to set multiple monitoring points in the affected river section, and obtain the \(\overline{C} (\overline{x}_{i} ,T)\) in the same time. In fact, the field monitoring scheme can also be a single monitoring point and acquiring data \(\overline{C} (X,t_{i} )\) by continuous time. According to the numerical testing, ideal results can be obtained under both these conditions.
References
Abderrezzak KEK, Ata R, Zaoui F (2015) One-dimensional numerical modeling of solute transport in streams: the role of longitudinal dispersion coefficient. J Hydrol 527:978–989
Cao XQ, Song JQ, Zhang WM, Zhang LL (2010) MCMC method on an inverse problem of source term identification for convection–diffusion equation. Chin J Hydrodyn 25(2):127–136
Cheng WP, Jia YF (2010) Identification of contaminant point source in surface waters based on backward location probability density function method. Adv Water Resour 33:397–410
Dai HC, Wang LL (2006) Study and application of inverse problem on hydraulics. J Sichuan Univ (Engineering Science Edition) 38(1):15–19
Feng AZ (2012) An analytical solution to constant coefficients advection-diffusion equation in the semi-infinite domain. J Shaoyang Univ Sci Technol 9(1):19–22
Fulvio B, Roberto R, Luca R (2005) Source identification in river pollution problems: a geostatistical approach. Water Resour Res 41(7):23–30
Holland JH (1975) Adaptation in natural and artificial systems. An introductory analysis with application to biology, control, and artificial intelligence. The MIT Press, Cambridge
Jiang ZJ, Wang JH (1997) Study and modification on one dimensional water quality model in natural rivers. J Hunan Univ 24(6):90–94
Jong D (1975) Analysis of the behavior of a class of genetic adaptive systems. College of Literature, Science, and the Arts, The University of Michigan
Jothiprakash V, Shanthi G (2006) Single reservoir operating policies using genetic algorithm. Water Resour Manag 20(6):917–929
Kumar A, Kumar N, Kumar JD (2010) Analytical solutions to one-dimensional advection–diffusion equation with variable coefficients in semi-infinite media. J Hydrol 380(3):330–337
Li J, Feng ZP, Tsukamoto H (2004) Hydrodynamic optimization design of low solidity vaned diffuser for a centrifugal pump using genetic algorithm. J Hydrodyn Ser B 16(2):186–193
Li KQ, Li Z, Li Y, Zhang LJ, Wang XL (2015) A three-dimensional water quality model to evaluate the environmental capacity of nitrogen and phosphorus in Jiaozhou Bay, China. Mar Pollut Bull 91:306–316
Liu SY (2005) Simple simulation of river pollutant diffusion with one-dimensional water quality model. Water Transp Manag 27(4):33–35
Min T, Zhou XD, Zhang SM, Feng MQ (2004) Genetic algorithm to an inverse problem of source term identification for convection–diffusion equation. J Hydrodyn 19(4):520–524
Ministry of Environmental Protection of the People’s Republic of China (MEP) (2010) The first national pollution source census bulletin. http://www.zhb.gov.cn/gkml/hbb/bgg/201002/t20100210_185698.htm. Accessed 18 Nov 2015
Ni JR, Wang SJ (2000) On straight river. Shuili Xuebao 12:14–20
Nikolaos DK, Michael P (1996) Site and optimization of contaminant sources in surface water system. J Environ Eng 122:917–923
Roseanna M, Neupauer JLW (2004) Numerical implementation of a backward probabilistic model of ground water contamination. Groundwater 42(2):175–188
Singh RM, Datta B (2006) Identification of groundwater pollution sources using GA-based linked simulation optimization model. J Hydrol Eng 11:101–109
Srinivas M, Patnaik LM (1994) Adaptive probabilities of crossover and mutation in genetic algorithm. IEEE Trans Syst Man Cybernet 24(4):656–667
Tang HW, Xin XK, Dai WH, Xiao Y (2010) Parameter identification for modeling river network using a Genetic Algorithm. J Hydrodyn Ser B 22(2):246–253
Wang ZW, Qiu SF (2008) Stability and numerical simulation of pollution point source identification in a watershed. Chin J Hydrodyn 23(4):364–371
Wang SD, Shen YM (2005) Three high-order splitting schemes for the 3D transport equation. Appl Math Mech 26(8):921–928
Wang ZW, Xu DH (2006) Uniqueness and numerical methods for point source pollution of watershed. J Ningxia Univ (Natural Science Edition) 27(2):124–129
Wang L, Wang Y, Wu CD, Xie QJ (2009) Pollution source fingerprinting system of accident water pollution based on GIS in chemical area. Environ Sci Technol 22(6):57–60
Wang Y, Wu SB, Wang CL, Liu YC (2012) Emergency monitoring and analysis for ‘721’ water contamination incident in Fujiang River. Yangtze River 43(12):64–67
Wu ZK, Fan HM, Chen XR (2008) The numerical study of the inverse problem in reverse process of convection–diffusion equation with adjoint assimilation method. J Hydrodyn 23(2):121–125
Xin XK, Xiao Y, Zhu XD, Cao G, Lv SQ (2009) BP neural network based on DGA and its application in one-dimensional river network simulation. Adv Sci Technol Water Resour 29(32):9–13
Xue GP, Wang C (1997) The determination of source for drinking water pollution accident. Admin Tech Environ Monit 9(6):20–22
Yin FL, Li GS, Jia GZ (2011) An inverse problem of determining magnitudes of multi-point sources in the diffusion equation. J Shandong Univ Technol Sci Technol 25(2):1–5
Yu H, Fan Z, Du HD (2013) The optimal retrieval of ocean color constituent concentrations based on the vibrational method. J Hydrodyn Ser B 25(1):62–71
Zhang GL, Liu XX, Zhang T (2009) The impact of population size on the performance of GA. In: Proceeding of 2009 international conference on machine learning and cybernetics, pp 1866–1870
Zhu S, Liu GH, Wang LZ, Mao GH, Cheng WP, Huang YF (2009) A Bayesian approach for the identification of pollution source in water quality model coupled with hydrodynamics. J Sichuan Univ (Engineering Science Edition) 41(5):30–35
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 51309031) and the “Chinese 12th Five-Year Science and Technology Support Program” (Grant No. 2012BAC06B00).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, Sp., Xin, Xk. Pollutant source identification model for water pollution incidents in small straight rivers based on genetic algorithm. Appl Water Sci 7, 1955–1963 (2017). https://doi.org/10.1007/s13201-015-0374-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13201-015-0374-z