Introduction

Groundwater is a primary life-giving resource. Its availability is an essential component in socio-economic development, human evolution, poverty reduction, and ecological diversity. Groundwater often provides a reliable source of water where surface water is unavailable or inadequate. Thus, it is essential to manage groundwater resources in sustainable mode to ensure its quality and quantity for a long period. To properly manage and protect groundwater reservoirs, especially shallow water-bearing layers, it is necessary to delineate areas where groundwater may be more vulnerable to pollution. Analysis of aquifer vulnerability is an important tool for groundwater management and provides basic information for facilitating proper planning and protection of groundwater resources (Majandang and Sarapirome 2013). The term vulnerability is defined as the degree to which human or environmental systems are likely to experience harm due to perturbation of stress, and can be identified for a specified system, hazard, or group of hazards (Popescu et al. 2008). In groundwater hydrology, vulnerability assessments typically describe the susceptibility of the water table, a particular aquifer, or water well to contaminants that can reduce the groundwater quality (Liggett and Talwar 2009). Two terms are used to describe groundwater vulnerability: intrinsic and specific. Intrinsic vulnerability is the natural susceptibility to contamination based on the physical characteristics of the environment. On the other hand, specific vulnerability is defined as an accounting for the transport properties of a particular contaminant or a group of contaminants through the subsurface. In general, three different methods can be used to assess groundwater vulnerability namely, index and overly, statistical, and process-based methods. In overly and index methods, factors which are believed to have an influence on the movement of pollutants such as geology, soil, slope, hydraulic conductivity are mapped. These factors are assigned weights and rates depending on their importance on controlling pollutants movement. The resultant maps are linearly summed to produce a map of vulnerability index of an area. The groundwater vulnerability produced by such methods is generally qualitative and relative. Several overly and index methods have been developed. The most common are the DRASTIC (Aller et al. 1987), the GOD (Foster 1987), the AVI (Van Stempvoort et al. 1993), the SINTACS (Civita 1994), and the EPIK (Doerfliger and Zwahlen 1997). The process-based models use simulation models to estimate time of travel, concentration of contaminant, and duration of contamination to quantify areas of high and low susceptibility to pollution. Some of these models are designed to simulate migration of contaminants through unsaturated zone, saturated zone, and unsaturated–saturated zones. Process-based models are not commonly used to assess vulnerability because they are constrained by data shortage, computational difficulty, and the expertise required to implement them. Statistical methods are used to quantify the risk of groundwater pollution by determining the statistical dependence between observed contamination and observed land uses that are potential source of contamination (Harter and Walker 2001). Once the statistical relationship is attained, the model can be used to predict the probability of contamination risk. The main advantage of this method is that the statistical significance can be explicitly calculated. There are only few studies that have used these methods to quantify groundwater vulnerability around the world. For example, Arthur et al. (2007) implemented a Bayesian-probabilistic weights-of-evidence (WOE) technique to generate a series of maps reflecting the relative aquifer vulnerability of Florida’s principle aquifer system in United States of America (USA). They used WOE to explore the relationship between several evidential hydrogeological themes (such as soil hydraulic conductivity, density of karst features, thickness of aquifer confinement, and hydraulic head difference) and ambient groundwater parameters in wells that reflect relative degree of vulnerability. The same technique was used by Masetti et al. (2007) to assess aquifer vulnerability to occurrence of elevated nitrate concentration in the Province of Milan (northern Italy). Uhan et al. (2010) used outputs of three models (GROWA, SWAT, and FEFLOW) as evidential themes for assessing aquifer vulnerability for nitrate concentrations using WOE technique in Lower Savinja Valley (Slovenia). They concluded that WOE model was capable to indicate regional groundwater nitrate distribution and enable spatial prediction of the probability for nitrate groundwater concentrations. Mair and El-Kadi (2013) successfully applied bivariate logistic regression technique (LR) to assess the groundwater vulnerability to contamination in Hawaii, USA. Sorichetta et al. (2013) used multivariate WOE and LR methods for assessing groundwater vulnerability in the Milan District, Italy. They concluded that these methods were suitable for evaluating aquifer vulnerability for nitrate contamination.

The Dempster–Shafer theory (DST) of evidence (also known as evidential belief functions EBF’s) is a generalization of the Bayesian theory of subjective probability. It has a relative flexibility to accept uncertainty and the ability to combining beliefs from multiple source of evidence (Thiam 2005). In Earth sciences, the application of this method is still limited. This method has been used for mineral potential mapping (Moon 1990; An et al. 1992; Carranza and Hale 2003; Carranza et al. 2005), landslide susceptibility (Park 2011; Mohammady et al. 2012; Bui et al. 2012; Lee et al. 2012; Pourghasemi et al. 2013), and groundwater potential mapping (Nampak et al. 2014; Mojaji et al. 2014).

To our knowledge, application of this method for assessing aquifer vulnerability for nitrate contamination has never been investigated. Due to the high mobility and solubility, nitrate NO −3 always exists in groundwater under oxidizing conditions (Almasri and Ghabayen 2008). In general, source of nitrate in groundwater can be classified into point and non-point sources (Alagha et al. 2013). The non-point source of nitrate includes fertilizer, manures, and return flows from irrigation, while the point sources include septic system and cesspits. Groundwater contamination by nitrate causes many diseases such as methemoglobinemia, which at severe cases may result in brain damage and death (Cissé and Mao 2008). Thus, the main objective of this study is to evaluate the applicability of the DST for GIS-based aquifer vulnerability analysis. A case study of the Galal Badra area in central Iraq was conducted to explore the application of this method for assessing specific aquifer vulnerability.

The basic principles of DST

The DST is a generalization of the Bayesian theory of subjective probability. Whereas the Bayesian theory requires probabilities for each question of interest, DST allow us to base degrees of belief for one question on probabilities for a related question (Dempster 1968). The detailed mathematical description of the DST is outside of this study, only a brief description of the theory synthesized from works of An et al. (1992), Carranza and Hale (2003), and Park (2011) was reviewed here.

A frame of discernment, for an event propositions exist such that Θ = {A1, A2,…,An} which is a set of mutually exclusive and exhaustive proposition, is first established. Then, a mass function [m(A)] assigns belief committed to each proposition as shown below.

$$ m = 2^{\varTheta } \to \left[ {0,1} \right] $$
(1)

with

$$ m\left( \varphi \right) = 0 $$
(2)

and

$$ \sum\limits_{A \subset \varTheta } {m\left( A \right) = 1}, $$
(3)

where φ is the empty set and A is a subset of Θ. The function m is a measure of belief committed to each possibility (Wally 1987). The belief (Bel) and plausibility (Pls) functions are defined based on the mass functions as follows:

$$ {\text{Bel}}\left( H \right) = \sum\limits_{A \subset H}^{{}} {m\left( A \right)} $$
(4)
$$ {\text{Pls}}\left( H \right) = \sum\limits_{A \cap H \ne \varphi }^{{}} {m\left( A \right)} $$
(5)

where for every H ⊂ Θ, Bel(H) is a measure of the total amount of beliefs committed exactly to every subset of H by m. Pls(H) represents the degree to which the evidence remains plausible (Park 2011).

According to An et al. (1992), Eqs. (4) and (5) represent the lower and upper probabilities. These probabilities have the following properties:

$$ {\text{Bel}}\left( H \right) \le {\text{Pls}}\left( H \right) $$
(6)
$$ {\text{Pls}}\left( H \right) = 1 - {\text{Bel}}\left( {\bar{H}} \right) $$
(7)

where \( \bar{H} \) is the negation of H. \( Bel\left( {\bar{H}} \right) \) is called the disbelief function.

The difference between Pls(H)and Bel(H) indicates the degree of uncertainty. When the degree of uncertainty equals 0, then \( {\text{Bel}}\left( H \right) + {\text{Bel}}\left( {\bar{H}} \right) = 1 \), which is a Bayesian probability (An et al. 1992).

The core part of the application of the DST to assess specific aquifer vulnerability is to define mass functions using quantitative relationship between the well locations having elevated nitrate concentrations (>3 mg/L) and factors which control aquifer vulnerability such as depth of groundwater table, hydraulic conductivity, slope, soil, land use land cover. The mass functions in this study were derived from likelihood ratio functions. Suppose that there are ℓ multiple spatial thematic layers in an area where wells with elevated nitrate concentration existed, then each thematic layer is regarded as evidence E i (i = 1, 2, …, ℓ) for the target proposition T p . If E ij is the jth class attribute of the evidence E ij and frequency distribution function of positive and opposite target prepositions, the likelihood ratio is (Park 2011)

$$ \lambda \left( {T_{p} } \right)_{{E_{ij} }} = \frac{{\frac{{N\left( {L \cap E_{ij} } \right)}}{N\left( L \right)}}}{{\frac{{N\left( {E_{ij} } \right) - N\left( {L \cap E_{ij} } \right)}}{N\left( A \right) - N\left( L \right)}}} $$
(8)

where N(L ∩ E ij ): number of wells that occurred in E ij

N(L) total number of existed wells with elevated nitrate concentrations in the study area

N(E ij ) number of pixels in E ij

N(A) total number of pixels in the study area.

The Bel function can be calculated as

$$ {\text{Bel}} = \frac{{\lambda \left( {T_{p} } \right)_{{E_{ij} }} }}{{\sum {\lambda \left( {T_{p} } \right)_{{E_{ij} }} } }}. $$
(9)

The likelihood ratio for supporting the opposite target proposition is calculated as

$$ \lambda \left( {\bar{T}_{p} } \right)_{{E_{ij} }} = \frac{{\frac{{N\left( L \right) - N\left( {L \cap E_{ij} } \right)}}{N\left( L \right)}}}{{\frac{{N\left( A \right) - N\left( L \right) - N\left( {E_{ij} } \right) + N\left( {L \cap E_{ij} } \right)}}{N\left( A \right) - N\left( L \right)}}}. $$
(10)

The Dis function is calculated as

$$ {\text{Dis}} = \frac{{\lambda \left( {\bar{T}_{p} } \right)_{{E_{ij} }} }}{{\sum {\lambda \left( {\bar{T}_{p} } \right)_{{E_{ij} }} } }}. $$
(11)

The uncertainty (Unc) and plausible (Pls) values are obtained using Eqs. (12) and (13)

$$ {\text{Unc}} = 1 - {\text{Dis}} - {\text{Bel}} $$
(12)
$$ Pls = 1 - Dis. $$
(13)

The values of Bel and Pls range between 0 and 1.

Once the mass functions are calculated for all the used factors, the Dempster’s rules of the combination is used to obtain the four integrated mass functions (Dempster 1968). These rules have both commutative and associative attributes such that different groupings or orderings of evidence combinations do not affect the final results (George and Pal 1996 in Mogaji et al. 2014). The Dempster’s rules for combining the two used factor maps A and B are as follows (Carranza et al. 2005; Mogaji et al. 2014):

$$ {\text{Bel}}_{X} { = }\frac{{{\text{Bel}}_{A} {\text{Bel}}_{B} {\text{ + Bel}}_{A} {\text{Unc}}_{B} {\text{ + Bel}}_{B} {\text{Unc}}_{A} }}{\beta } $$
(14)
$$ {\text{Dis}}_{X} { = }\frac{{{\text{Dis}}_{A} {\text{Dis}}_{B} {\text{ + Dis}}_{A} {\text{Unc}}_{B} {\text{ + Dis}}_{B} {\text{Unc}}_{A} }}{\beta } $$
(15)
$$ {\text{Unc}}_{X} { = }\frac{{{\text{Unc}}_{A} {\text{Unc}}_{B} }}{\beta } $$
(16)
$$ {\text{Pls}}_{X} {\text{ = Unc}}_{X} {\text{ + Bel}}_{X}, $$
(17)

where

Bel X Lower degree of belief for each layer of parameters type of range

Dis X Degree of disbelief for each layer of parameters type or range

Unc X Degree of uncertainty for each layer of parameters type or range

X The A, B, …, E denoting each parameters types.

The denominator β is called the normalization factor. It is also called the degree of conflict, which measures the conflict between the pieces of evidence (George and Pal 1996). The β is written mathematically as

$$ \beta = 1 - {\text{Bel}}_{A} {\text{Dis}}_{B} - {\text{Dis}}_{A} {\text{Bel}}_{B}. $$
(18)

The study area

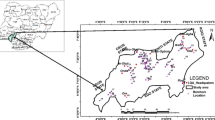
The study area extends over an area of 657 km2 and lies between 32°59′31.43″ and 33°12′30.00″ latitude and 45°50′52.22″ and 46°12′42.68″ longitude in the northeastern Wasit governorate at central east part of Iraq, Fig. 1. It is bounded by Iraqi–Iranian borders (Hamrin hills) from the east, wadi Galas from north, and hor Al-Shiwach from east and south. The main cities within the study area are Badra, Zurbatiyah, and Jassan. Badra city is located in the central part of the area while Zurbatiyah and Jassan are located 12 and 20 km in the north and south of the Badra city, respectively. Relief is low with only a few isolated hills rising above the general level of the plain in the east (Parsons 1956). Elevation in the study area ranges from 6 to 691 m with an average of ~45 m above mean sea level. The climate of the study area is characterized by hot, dry summer, cold winter, and a pleasant spring and fall. Approximately 90 % of the annual rainfall occurs between November and April, most of it in the winter months from December to March. The remaining 6 months are dry and hot. According to the recorded meteorological data in Badra station (north of the study area) for the period (1994–2013), the monthly maximum, minimum, and average temperatures are 37.8, 10.4, and 24.56 °C, respectively. The area receives an average mean annual rainfall of approximately 212 mm/year with uneven rainfall distribution between plain and mountain parts. The major stream in the study area is Galal Badra River. The mean monthly discharge of this river is 2.5 and 1000 m3/s in drought and flood period, respectively (Al-Shammary 2006). Due to the prolonged drought conditions and intermittent nature of the streams in the study area, most of the farmers depend on the groundwater for their irrigation needs.

Fig. 1
figure 1

Location map of the study area

Full size image

Rocks in the study area range in age from Middle Miocene to Recent. In the western portion, the younger rocks are exposed and increasingly become old to the east. Most of the area is covered by rocks of alluvial and lacustrine origin, Pliocene or younger in age. The stratigraphic succession is composed of Fatha, Injana, Muqdadiyah formations in addition to the Quaternary deposits. The Quaternary deposits mainly consist of mixture of gravel, sand, silt, and conglomerates of post Pliocene deposits. A brief description of these units is provided in Table 1. Approximately 80 % of the study area is covered with Quaternary deposits. Tectonically, the platform of the Iraqi territory is divided into two basic units, the stable and unstable shelf (Jassim and Goff 2006). The stable shelf is characterized by reduced thickness of the sedimentary cover and by the lack of folding, while the unstable shelf has a thick and folded sedimentary cover. The folds are arranged in narrow long anticlines and broad flat synclines (Al-Sayab et al. 1982). The greater parts of the study are located in the stable shelf (Mesopotamian plain) and only a small part extends over the unstable shelf close to the Iraqi–Iranian border (folded zone). There are many folds and faults in the study area. The bigger one is Shbichia–Najaf fault.

Table 1 Description of the lithological units in the study area
Full size table

Two major aquifer systems exist within the study area. The first one represents the shallow unconfined aquifer consisting mainly of layers of sand, gravel with overlapping clay, and silt (Al-Abadi 2015b). This hydrogeological unit is located within the Quaternary lithological layers. The second hydrogeological unit is Muqdadiyah water-bearing layer. The aquifer condition of this unit is confined/semi-confined. The regional groundwater flow is from northeast to southwest. The hydraulic characteristic of the two units was estimated by Al-Shammary (2006) by means of pumping test. For the unconfined aquifer, the hydraulic conductivity, transmissivity, and specific yield were 6.3 m/d, 228.43 m2/d, and 0.042, respectively. For the confined aquifer, the values were 3.5 m/d, 81.07 m2/d, and 0.0017 for hydraulic conductivity, transmissivity, and storage coefficient, respectively.

Generating of evidential thematic layers

To assess aquifer vulnerability for nitrate contamination in the study area, two main steps were implemented. In the first step, an inventory of wells with elevated nitrate concentrations was prepared. The nitrate levels in most ambient groundwater in Iraqi aquifers are very low, generally much less than 1 mg/L (Jabar Al-Saydi, Expert, Head of Groundwater Commission of Groundwater/Basra Branch, personal communication). Therefore, the presence of nitrate in groundwater greater than 3 mg/L usually reflects the impact of human activities on well water quality. The total number of wells in the interested area is 102. From these, 63 wells with elevated nitrate concentration (3 mg/L) were selected. The 63 wells were randomly partitioned into two sets, 44 wells (70 %) for training and 19 wells (30 %) for testing. In the second step, the evidential thematic layers of five factors influencing groundwater vulnerability were selected and mapped depending on the availability of data and literature review. These layers were depth of groundwater level, hydraulic conductivity, slope percentage, soil, and land use land cover (LULC). The sources of these layers are explained in Table 2. All evidential thematic layers were prepared as raster with 30 × 30 m cell size using different types of tools in ArcGIS 10.2 commercial software such as Geostatistical extension, Spatial Analyst extension, Image Classification tool, and ArcTool box.

Table 2 Information and sources of data used in this study
Full size table

Depth of groundwater represents the depth of groundwater levels, both for confined or unconfined aquifer with comparison to the ground surface. Its value is important because it determines the thickness of material through which a contaminant must travel before reaching water-bearing layers. In addition, attenuation capacity increases as the depth to groundwater increases. The presence of confining layers (low permeability layers) limits the travel of pollutants into an aquifer (Aller et al. 1987). Deeper water levels imply lesser chance for contaminants to enter (Piscopo 2001). The data used for drawing groundwater depths for the shallow aquifer in the study area were taken from the General Commission of Groundwater/Wasit Branch, Iraq, and Al-Shammary (2006) work, Table 3. The data include locations of the wells, well depths, groundwater depths (m), and hydraulic conductivities (m/s). The well locations covered the interested region and beyond, Fig. 2, and were different from the data used for the rest of the analysis. The minimum, maximum, and average depth of groundwater are 16, 162, and 65.98 m, respectively. The spatial distribution of the groundwater depth is shown in Fig. 3. Ordinary kriging technique in geostatistical extension of ArcGIS 10.2 was used to interpolate groundwater depths data after a comprehensive exploratory data analysis, i.e., investigate the data normality and trend detection. The greater part of the study area (about 69 %) has a groundwater depth greater than 30 m which implies that the aquifer systems are relatively protected from contamination at the ground surface. The groundwater depth map, Fig. 3, shows that the central part of the study area has a relatively shallow depth while the eastern parts have a greater depth. The groundwater depths increases from the west toward the east corresponding with the elevation increase in the same direction. To use the map of groundwater depth in further analysis, the raster map of this factor is classified into five categories based on the Jenks (natural break) classification system. Selection of this classification scheme is based on literature reviews and author’s experience of study area and its condition (Al-Abadi 2015a).

Table 3 Data used for constructing maps of groundwater depth and aquifer hydraulic conductivity
Full size table
Fig. 2
figure 2

Locations of wells used to produce maps of groundwater depths and hydraulic conductivity

Full size image
Fig. 3
figure 3

Spatial distribution of groundwater depths in the study area

Full size image

Hydraulic conductivity is defined as the rate at which the aquifer materials transmit water, which in turn, controls the rate at which groundwater will flow under a given hydraulic gradient. The rate at which the groundwater flows also controls the rate at which a contaminant moves away from the point at which it enters the aquifer system. Higher rates represent higher susceptibility to contamination. Evidential thematic layer of the hydraulic conductivity was prepared based on data provided by Al-Shammary (2006), Table 3 and Fig. 4. The hydraulic conductivity values were also interpolated using ordinary kriging interpolation technique and then reclassified into five categories using Jenks scheme too. Figure 4 shows that the 77 % of the total study area have low hydraulic conductivities with an average of 4.3 m/day.

Fig. 4
figure 4

Spatial distribution of hydraulic conductivity over the study area

Full size image

Slope is a rise or fall of land surface. It is an important factor for groundwater vulnerability assessment because it controls the likelihood that pollutants will runoff or remain on the surface to allow contaminants' percolation to the saturated zone. Slopes that provide a greater opportunity for contaminants to infiltrate will be associated with higher groundwater pollution potential (Aller et al. 1987). Slope also influences soil development, and therefore, has an impact on contaminants attenuation (Babiker et al. 2005). To prepare thematic layer of slope, the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Global Digital Elevation Model (GDEM) (http://gdem.ersdac.jspacesystems.or.jp/search.jsp) was used. The ASTER-GDEM was developed by the Ministry of Economy of Japan and the United States National Aeronautics and Space Administration (NASA). The spatial resolution of the ASTER-GDEM is approximately 30 m. Four tiles were downloaded from the previous web location, merged to new mosaic raster, clipped for the study area, reprojected using UTM WGS 1984 38 N projected coordinate system, and fill sinks. The treated raw DEM was then used to derive slope raster using Spatial Analyst extension of ArcGIS 10.2. The resulting raster values were then classified into five categories: 0–2 % (23 %), 2–8 % (51 %), 8–12 % (15 %), 12–18 % (8 %), and >18 % (3 %), Fig. 5. The greater part of the study area (about 74 %) has low slope values (0–8 %), indicating that the area is sensitive to contamination on the ground surface.

Fig. 5
figure 5

Slope (%) in the study area

Full size image

Soil refers to the uppermost portion of the unsaturated zone characterized by significant biological activities. Soil has an impact on the amount of recharge, which can infiltrate to the groundwater, and hence contaminants' movement (Piscopo 2001). The presence of fine-textured material such as silt and clay can decrease relative soil permeability and restrict contaminants' migration (Aller et al. 1987). The attenuation processes such as biodegradation, filtration, sorption, and volatilization may be significant if the soil zone is thick enough. Soils are classified into four hydrologic soil groups (HSG’s) to indicate the minimum rate of infiltration for bare soil after prolonged wetting. The four hydrologic soils groups are A, B, C, and D, where A generally has the greatest infiltration rate (smallest runoff potential) and D has the smallest infiltration rate (greatest runoff potential). The HSG map of the study area was prepared by digitizing the hard copy of the soil map of Iraq and few soil textures available in the work of Al-Shammary (2006), Fig. 6. From this map, it is obvious that the major portion of the study area (about 65 %) has high infiltration rate (A and B groups).

Fig. 6
figure 6

HSG in the study area

Full size image

Land cover defines the biophysical state of the earth’s surface and immediate subsurface, thus embracing the soil, material, vegetation, and water status. Land use on the other hand is a description of how people utilize land and socio-economic activity. There are two primary methods for capturing information on LULC: analysis of remotely sensed imagery and filed survey. The LULC map in this study was prepared using remote sensing data of Landsat 8. The raw image acquired in 6/2/2015 was first download from the official web site of USGS (United State of Geological Survey) (http://earthexplorer.usgs.gov/). Seven bands of the raw image (bands 1–7) were merged to create new raster, enhance radiometry, clipped for the study area, and then classified using supervised maximum likelihood approach by Image Classification tool in ArcGIS 10.2. Four LULC classes were found in the study area after being compared with ground truth: urban, agriculture, barren, and shrub, Fig. 7. The Barren and Shrub classes encompassed an area of 595 km2 (90 %). Only 62 km2 of the study area (10 %) was covered by urban and agricultural classes.

Fig. 7
figure 7

LULC categories in the study area

Full size image

Results and discussion

As previously mentioned, the five evidential thematic layers were prepared as raster comprising of 30 × 30 m cell size. The number of wells per each class of a specific thematic layer was determined through multi-stage procedure. In the first stage, the evidential theme was reclassified. After that, it was converted to polygon. The resultant polygon was interested with training wells layer using tabulate intersection command to produce a table containing the number of wells for each class in the specific evidential thematic layer. The total number of pixels of the study area and the number of pixels of each class of a factor were determined directly from the attribute tables of a reclassified raster layer. The attribute table for each reclassified raster layer has a column from which the number of pixels of each class is directly determined. Summation of the pixels for all classes gives the total number of pixels of the study area.

The Bel, Dis, Unc, and Pls functions of the DST are summarized in Table 4. The detail procedure to calculate these functions is given in the previous section; an example of calculation is presented here for groundwater depth class 2; the number of wells in the class (=26), total number of training boreholes in the study area (=44), number of pixels in the considered class (=374,255), total number of pixels in the study area (730,180). Therefore,

Table 4 Values of DS mass functions for classes of groundwater vulnerability factors
Full size table
$$ \lambda \left( {T_{p} } \right)_{{{\text{class}}\, 2}} = {{\left( {{{26} \mathord{\left/ {\vphantom {{26} {44}}} \right. \kern-0pt} {44}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{26} \mathord{\left/ {\vphantom {{26} {44}}} \right. \kern-0pt} {44}}} \right)} {\left[ {{{374255 - 26} \mathord{\left/ {\vphantom {{374255 - 26} {\left( {730180 - 44} \right)}}} \right. \kern-0pt} {\left( {730180 - 44} \right)}}} \right] = 1.15}}} \right. \kern-0pt} {\left[ {{{374255 - 26} \mathord{\left/ {\vphantom {{374255 - 26} {\left( {730180 - 44} \right)}}} \right. \kern-0pt} {\left( {730180 - 44} \right)}}} \right] = 1.15}} $$
$$ \lambda \left( {\bar{T}_{p} } \right)_{{{\text{class}}\, 2}} = {{\left( {{{\left( {44 - 26} \right)} \mathord{\left/ {\vphantom {{\left( {44 - 26} \right)} {44}}} \right. \kern-0pt} {44}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\left( {44 - 26} \right)} \mathord{\left/ {\vphantom {{\left( {44 - 26} \right)} {44}}} \right. \kern-0pt} {44}}} \right)} {\left( {{{\left( {\left( {730180 - 44 - 374255} \right) + 26} \right)} \mathord{\left/ {\vphantom {{\left( {\left( {730180 - 44 - 374255} \right) + 26} \right)} {\left( {730180 - 44} \right)}}} \right. \kern-0pt} {\left( {730180 - 44} \right)}}} \right) = 0.84}}} \right. \kern-0pt} {\left( {{{\left( {\left( {730180 - 44 - 374255} \right) + 26} \right)} \mathord{\left/ {\vphantom {{\left( {\left( {730180 - 44 - 374255} \right) + 26} \right)} {\left( {730180 - 44} \right)}}} \right. \kern-0pt} {\left( {730180 - 44} \right)}}} \right) = 0.84}}. $$

The other λ(T p ) for 1, 3, 4, and 5 classes were 1.07, 0.88, 0.30, and 0, respectively. Thus, \( \sum \lambda \left( {T_{p} } \right)_{\text{slope}} = 3.41 \). The Bel function was then calculated using Eq. 9 as

$$ {\text{Bel}} = \frac{1.15}{3.41} = 0.34. $$

The values of \( \lambda \left( {\bar{T}_{p} } \right) \) for classes 1, 3, 4, and 5 were 0.98, 1.02, 1.06, and 1.02, respectively. Therefore, \( \sum {\lambda \left( {\bar{T}_{p} } \right)_{\text{slope}} } = 4.92 \). The Dis function were calculated from Eq. 11

$$ {\text{Dis}} = \frac{0.84}{4.92} = 0.171. $$

The Unc and Pal functions was calculated using Eqs. 12 and 13

$$ {\text{Unc}} = 1 - 0.34 - 0.171 = 0.49 $$
$$ {\text{Pls}} = 1 - 0.171 = 0.83. $$

For the groundwater depth factor, high Bel (0.41) and low Dis (0.33) values were found in the ranges of 41.7–65.7 m and 65.7–92.67 m which indicate that these classes have positive associations with aquifer vulnerability. The remaining classes have minor effect on vulnerability due to low values of Bel and high values of Dis. In the case of hydraulic conductivity, the range of 13.49–25.63 has the highest Bel value (0.62) and the lowest Dis value (0.20) indicating the highest probability of contamination by nitrate. The other classes have relatively low Bel values indicating that these classes play a minor role in the control of contamination processes in the study area. For the slope factor, slope angle in the range of 20–30 % has the highest Bel and the lowest Dis values indicating the highest probability of contamination, followed by slope range of 0–2 % and then of 8–12 %. For the remaining slope ranges, Bel values are low referring to the low probability of contamination by nitrate. For the soil factor, the highest values of Bel and the lowest values of Dis are associated with A and B groups. These groups have higher infiltration rates and thus they are more vulnerable to contamination. The low Bel and high Dis values for other groups indicate that the probability of contamination is low. In the case of LULC, there are high Bel and low Dis values for urban and agricultural categories, reflecting the high probability of contamination by nitrate for these categories. High probability of contamination in these LULC is due to increase in human activity and population growth. As the high value of Bel is correlated with urban and agricultural cause, the major sources of nitrate in the groundwater may be latrines and manures.

The integrated results are shown in Fig. 8. Comparison between the belief map, Fig. 8a, and the disbelief map, Fig. 8b, exhibits that belief values are high for the area where disbelief values are low and vice versa. The areas with high belief and low disbelief indicate high vulnerability for contamination by nitrate. The uncertainty map shows lack of information support uncertainty for vulnerability. As indicated from comparison between Fig. 8c and Fig. 8a, the uncertainty values are high in areas with low values of Belief. On the other hand, the plausibility map, Fig. 8d, shows high values for areas where both belief and uncertainty values are high. The integrated belief function map was used in this study as groundwater vulnerability index (GVI). The pixel values of GVI were reclassified into five categories: very low, low, moderate, high, and very high using Jenks classification scheme, Table 5 and Fig. 9. The very low–low zones cover 32 % (209 km2). These classes mainly concentrate in the eastern parts of the study area and occupy small zone in the central part. The moderate zone extends over an area of 42 % (279 km2) and mainly encompasses the western part of the study area. The high–very high zones cover 26 % (170 km2) and these zones concentrate in the central part of the study area. The results indicate that the aquifer systems in the study area are moderately vulnerable to contamination by nitrate; thus it needs a wise plan to protect groundwater quality.

Fig. 8
figure 8

Integrated BEF map a Bel, b Dis, c Unc, and d Pls

Full size image
Table 5 Areas covered by GVI classes
Full size table
Fig. 9
figure 9

GVI classes in the study area

Full size image

The next step in the analysis is to validate the results. Any predictive model (deterministic or stochastic) requires validation before it is used in prediction purposes. Without validation process the model will have no scientific significance (Chung and Fabbri 2003). In this context, the receive operating characteristic (ROC) curve is usually used for examining the quality of deterministic and probabilistic detection and forecast system (Swets 1988). The area under the ROC curve (AUC) characterizes the quality of a forecast system by describing the system's ability to anticipate correctly the occurrence or non-occurrence of pre-defined “event” (Negnevitsky 2002). The quantitative–qualitative relationship between AUC and prediction accuracy is given in Table 6. The AUC was obtained for both the training (success rate) and testing (prediction rate) using ROC module in IDRISI software, Fig. 10. The success rate is important to explain how well the resulting GVI map classified the area of existing borehole locations. The success rate results were obtained by comparing the training well locations (32) with the GVI map. The AUC was 0.86. On the other hand, the prediction rate used a measure of performance as a predictive rule (Yesilnacar and Topal 2005; Pradhan et al. 2010a). It has only used the testing data set to explore the predictive capability of the model. The AUC for prediction rate was 0.77. These results indicate that DS has good capability (Table 6) to delineate groundwater vulnerability zones in the study area.

Table 6 The relation between AUC and model prediction accuracy (after Yesilnacar (2005))
Full size table
Fig. 10
figure 10

Validation results using ROC technique

Full size image

Conclusions

Groundwater is a very important renewable resource for drinking, agricultural, industrial, and other purposes. Therefore, it is vital that the use of groundwater should be carefully managed in terms of both quantity and quality. In recent years, delineation of areas that are more vulnerable to contamination is an essential step for managing aquifer system. In this study, the vulnerability of shallow aquifer for nitrate contamination in Galal Badra basin, east of Iraq was evaluated using DST of evidence in GIS framework. In the first stage of this study, an inventory map of the wells locations with elevated nitrate concentrations was prepared. After that, these wells were split into two sets: training and testing. In the second stage, the evidential thematic layers were prepared. Five factors namely groundwater depth, hydraulic conductivity, slope, soil, and LULC were selected for modeling the relationship between training well locations and factor classes using mass functions of DS method. The Bel function was combined according to Dempster rules to produce aquifer vulnerability index of the study area. The results of application of the method were validated using ROC. The prediction of the model was 87 % for success rate and 77 % for prediction rate. So, the performance of the map made using DST was good. The results of this study could be used by planners and decision makers to protect groundwater aquifer in the study area. The prediction accuracy of the method could be increased by adding other thematic layers if they are available or by combining multi-methods to produce more accurate picture of the vulnerability status in the study area.