Abstract
An attempt has been made to develop water quality index (WQI), using six water quality parameters pH, dissolved oxygen, biochemical oxygen demand, electrical conductivity, nitrate nitrogen and total coliform measured at three different stations along the Sabarmati river basin from the year 2005 to 2008. Rating scale is developed based on the tolerance limits of inland waters and health point of view. Weighted arithmetic water quality index method was used to find WQI along the stretch of the river basin. It was observed from this study that the impact of human activity and sewage disposal in the river was severe on most of the parameters. The station located in highly urban area showed the worst water quality followed by the station located in moderately urban area and lastly station located in a moderately rural area. It was observed that the main cause of deterioration in water quality was due to the high anthropogenic activities, illegal discharge of sewage and industrial effluent, lack of proper sanitation, unprotected river sites and urban runoff.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
The Sabarmati River is a well-known river in western India and is approximately 371 km in length. The Sabarmati River starts its journey in the Aravalli Range of Udaipur district in the state of Rajasthan in India. In the beginning of the course, it is also known as Wakal River. The majority course of the river flows in the state of Gujarat, India.
Relevant studies on water quality index (WQI) and its modeling were reviewed. WQI is valuable and unique rating to depict the overall water quality status in a single term that is helpful for the selection of appropriate treatment technique to meet the concerned issues (Tyagi et al. 2013).Water quality indices are tools to determine conditions of water quality. Creating the WQI involves three main steps (US EPA 2009): (1) obtain measurements on individual water quality indicators (2) transform measurements into “subindex” values to represent them on a common scale (3) aggregate the individual subindex values into an overall WQI value. Various researchers have attempted to develop water quality index based on five types of WQI aggregation functions:
(a) arithmetic aggregation function, (b) multiplicative aggregation function, (b) geometric mean, (c) harmonic mean, and (d) minimum operator.
Horton 1965 used the arithmetic aggregation function for the WQI. He selected 10 most commonly measured water quality variables for his index including dissolved oxygen (DO), pH, coliforms, specific conductance, alkalinity, and chloride. The arithmetic weighing of the water quality variables was multiplied with the temperature and “obvious pollution” to obtain the sum aggregation function from which the overall water quality index was found out. The index weight ranged from 1 to 4. Similar to Horton (1965), Brown et al. (1970) also employed basic arithmetic weighting, although without the multiplicative variables. This effort was supported by the National Sanitation Foundation (NSF) in which the water quality variables were chosen using the Delphi method (Dalkey 1968), which generates results from the convergence of expert’s opinions. The NSF WQI used logarithmic transforms to convert water quality variable results into subindex values.
Dinius (1987), developed a index based on multiplicative aggregation having decreasing scale, with values expressed as a percentage of perfect water quality corresponding to 100 %. Similar work was carried out by Helmer and Rescher 1959, Dalkey and Helmer 1963 by introducing changes to Delphi method (Dalkey 1968). Brown et al. (1972), Bhargava et al. (1998), Dwivedi et al. (1997), Landwehr and Deininger (1976) gave multiplicative form of the index where weights to individual parameters were assigned based on a subjective opinion based on the judgment and critical analysis of the author. Dee et al. (1973) proposed a system for evaluating the environmental impact of large scale water resources projects.
McClelland (1974) introduced the geometric mean form of weighting to the WQI. McClelland was concerned that the arithmetic mean lacked sensitivity to low value parameters, a characteristic later deemed “eclipsing.” McClelland instead proposed the weighted geometric mean. Later researchers (Landwehr and Deininger 1976; Walski and Parker 1974; Bhargava 1983; Dinius 1987) have also employed a weighted geometric mean for aggregation.
Dojlido et al. 1994 used the harmonic mean to find the WQI. This mean does not use weights for the individual indicators. Dojlido et al. (1994) found that it was more sensitive to the most impaired indicator than the arithmetic or harmonic means, reducing eclipsing, while still accounting for the influence of other indicators (Walsh and Wheeler 2012). Other indices based on harmonic means are Canadian Council of Ministers of the Environment Water Quality Index (CCMEWQI) and British Columbia water quality index. The CCMEWQI compares observations to a benchmark instead of normalizing observed values to subjective rating curves, where the benchmark may be a water quality standard or site specific background concentration (CCME 2001; Khan et al. 2003; Lumb et al. 2006).British Columbia water quality index was developed by the Canadian Ministry of Environment in 1995 as increasing index to evaluate water quality. This index is similar to CCMEWQI where water quality parameters are measured and their violation is determined by comparison with a predefined limit. It provides possibility to make a classification on the basis of all existing measurement parameters (Bharti and Katyal 2011).
Smith et al. (1987a, b) developed an index based on minimum operator for four water uses i.e., contact as well as non-contact. It is a hybrid of the two common index types and is based on expert opinion as well as water quality standards. The selection of parameters for each water class, developing subindices, and assigning weightages were all done using Delphi. The minimum operator technique was used to obtain the final index score (Bharti and Katyal 2011):
where I min equals the lowest subindex value.
In general, water quality indices are divided into five main groups (Sobhani 2003):
-
(A)
Public indices: in this category, the indices ignore the kind of water consumption in the evaluation process, such as NSFWQI, Horton (Ott 1978; Horton 1965).
-
(B)
Specific consumption indices: in this category, classification of water is conducted on the basis of the kind of consumption and application (drinking, industrial, ecosystem preservation, etc). The most important and applicable of these indices are the Oconer, Oregan and British Columbia indices (DEQ 2003).
-
(C)
Statistical indices: in these indices statistical methods are used and personal opinions are not considered.
-
(D)
Designing indices: this category is an instrument aiding decision and planning in water quality management projects.
In this study, the weighted arithmetic mean method for WQI is used.
Water quality index by weighted arithmetic mean method WQIA can be found out by the following formula:
where W i is the unit weight of each parameter, q i is the 0–100 subindex rating for each variable and n is the number of subindices aggregated.
The advantages of weighted arithmetic mean method used in this study are (Tyagi et al. 2013).
-
1.
This method incorporates data from multiple water quality parameters into a mathematical equation that rates the health of water body with number.
-
2.
Less number of parameters required in comparison to all water quality parameters for particular use.
-
3.
Useful for communication of overall water quality information to the concerned citizens and policy makers.
-
4.
Reflects the composite influence of different parameters i.e., important for the assessment and management of water quality.
Methodology
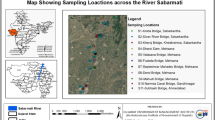
The methodology involves the development of Water Quality Index model to estimate d/s surface water quality at three stations on the Sabarmati River: 1. Station-1 (S1) V. N Bridge, at Ahmedabad 2. Station-2 (S2) Shedhi at Kheda and 3. Station-3 (S3) Kheroj bridge at Sabarkantha.
Water quality index model
The Water Quality Index model developed in the present study consists of 5 steps:
-
1.
Selection of parameters for measurement of water quality.
-
2.
Development of a rating scale to obtain the rating (V r ).
-
3.
Estimating the unit weight of each indicator parameter (W i ) by considering the weightage of each parameter.
-
4.
Determining the subindex value (W i × V r ).
-
5.
Aggregating the subindices to obtain the overall WQI.
The above steps are elaborately discussed below:
Selection of parameters for measurement of water quality
The evidence of high organic pollution in the Sabarmati river basin is considered as a basis of selecting the water quality parameters viz. pH, DO, BOD, electrical conductivity (EC), nitrate nitrogen, total coliform as significant indicator parameters of surface water quality in the present study.
Effect of pH
The pH is a measure of the acidic or alkaline conditions of the water. When the water is used for drinking purpose, the pH level of the water has an important effect on all body chemistry, health and disease because human body consists of 50–60 % water. The pH level of our body fluid should be in the range 7–7.2. If pH is less than 5.3, assimilation of vitamins or minerals is not possible; hence, it should be above 6.4. If pH is greater than 8.5, causes the water taste bitter or soda-like taste. If the pH is greater than 11, causes eye irritation and exacerbation of skin disorder. pH in the range of 10–12.5 cause hair fibers to swell. pH in the range 3.5–4.5 affects the fish reproduction. (Avvanavar and Shrihari 2008; Leo and Dekkar 2000).
Effect of dissolved oxygen
The amount of DO present in surface waters depends on water temperature, turbulence, salinity, and altitude Natural waters in equilibrium with the atmosphere will contain DO concentrations ranging from about 5 to 14.5 mg O2 per liter. The DO concentration present in water reflects atmospheric dissolution, as well as autotrophic and heterotrophic processes that, respectively, produce and consume oxygen. DO is the factor that determines whether biological changes are brought by aerobic or anaerobic organisms. Thus, dissolved–oxygen measurement is vital for maintaining aerobic treatment processes intended to purify domestic and industrial wastewaters. A rapid fall in the DO indicates a high organic pollution in the river. The optimum value for good water quality is 4 to 6 mg/l of DO, which ensures healthy aquatic life in a water body (Sawyer et al. 1994; Leo and Dekkar 2000; Burden et al. 2002; De 2003).
Effect of biological oxygen demand
Biochemical oxygen demand (BOD) determines the strength in terms of oxygen required to stabilize domestic and industrial wastes. For the degradation of oxidizable organic matter to take place minimum of 2–7 mg/l of DO level is to be maintained at laboratory experimentation or should be available in the natural waters (De 2003).
Effect of total dissolved solids/electrical conductivity
Total dissolved solids (TDS) is the amount of dissolved solids (i.e., salts) in the water. TDS can be measured indirectly by measuring the EC. The more dissolved salts in the water, the more electricity the water will conduct. EC is the ability of the water to conduct an electrical current. Conductivity is important because it directly affects the quality of the water used for drinking and irrigation. Waters with higher solids content have laxative and sometimes the reverse effect upon people whose bodies are not adjusted to them and cause the water to have an unpleasant mineral taste. TDS consists of oxygen-demanding wastes, disease-causing agents, which can cause immense harm to public health. The presence of synthetic organic chemicals (fuels, detergents, paints, solvents, etc) imparts objectionable and offensive tastes, odors and colors to fish and aquatic plants even when they are present in low concentrations (Sawyer et al. 1994; Leo and Dekkar 2000). Dissolved ions affect the pH of water, which in turn may influence the health of aquatic species.
Effect of nitrate nitrogen
Excess nitrate nitrogen can cause eutrophication of surface waters due to overstimulation of growth of aquatic plants and algae. It causes anaerobic conditions in the water bodies leading to fish kills, and can even “kill” a lake by depriving it of oxygen. High levels of Nitrate nitrogen can cause the respiration efficiency of fish and aquatic invertebrates to lower down, leading to a decrease in animal and plant diversity, and affects use of the water for fishing, swimming, and boating. High levels of Nitrate nitrogen in water can cause serious health hazards. The acute health hazard associated with drinking water with elevated levels of nitrate occurs when bacteria in the digestive system transform nitrate to nitrite. The nitrite reacts with iron in the hemoglobin of red blood cells to form methemoglobin, which lacks the oxygen-carrying ability of hemoglobin. This creates the condition known as methemoglobinemia (sometimes referred to as “blue baby syndrome”), in which blood lacks the ability to carry sufficient oxygen to the individual body cells. Infants under 1 year of age have the highest risk of developing methemoglobinemia from consuming water with elevated levels of nitrate.
Development of a rating scale to obtain the rating (V r )
Rating scale (Table 1) was prepared for range of values of each class. The rating varies from 0 to 100 and is divided into five classes. The subindex rating (V r ) = 0 implies that the concentration of the parameter in water remained exceeded by the standard maximum permissible limits and water is highly polluted. The rating (V r ) = 100 denotes the excellent water quality since the parameter remained within the prescribed permissible limit for drinking water and water is clean. The other ratings fall between these two extremities and are V r = 40, V r = 60, and V r = 80 standing for excessively polluted, moderately polluted and slightly polluted, respectively. Accordingly, 5 classes are proposed, (class 1–5). This scale is modified version of rating scale given by Tiwari and Mishra (1985).
The concentrations ranges of these parameters in the given classes are defined with due consideration of Central Pollution Control Board (CPCB) of India standards/criteria and Indian Standards (IS) 10500. For parameters and classes not included in the CPCB standards, reference was made to the standards defined by other agencies. The proposed classification along with ranges of concentrations of these parameters is given in Table 1. The basis for selecting the concentration levels for each of the parameters under consideration in the above classes is detailed below.
pH
Central Pollution Control Board (CPCB, ADSORBS/3/78–79), has given pH range 6.5–8.5 for classes A, B, D, and E. and 6–9 for class C. Considering the similar classification for pH for this study, pH ranges for classes 1–5 are allotted in increasing or decreasing geometric progression and are shown in Table 1.
Dissolved oxygen (DO)
The maximum concentration of oxygen that can dissolve in water is the function of water temperature, and therefore may vary from place to place and time to time. In India average tropical temperature is 27 °C. The corresponding average DO saturation concentration reported is 8 mg/l (Metcalf and Eddy 1972).
Central Pollution Control Board (CPCB, ADSORBS/3/78–79), has defined DO values 6, 5, 4, and 4 mg/l for classes A, B, C, and D, respectively. Considering the classification in the similar guideline for DO for this study, the DO ranges for classes 1–5 are allotted in decreasing progression and are shown in Table 1.
Biochemical oxygen demand (BOD)
Reference is taken from primary water quality criteria for various uses of fresh waters laid down by the Central Pollution Control Board (CPCB). The maximum value of BOD is given by CPCB as 3 mg/l for class B and C. European Community freshwater fish water quality standards indicate Guide Level and Maximum admissible Level of BOD as 3 and 6 mg/l, respectively, which indicate recreational use. The classes 1 and 2 are taken as per this standard in this study. The concentration ranges above this standard are assigned the classes 3, 4, 5 in this study as moderately Polluted, excess Polluted and severely Polluted for higher concentrations.
Total coliform
WHO guideline specifies coliform action level in drinking water as absent/100 ml. Hence class 1 has been given a range of total coliform as 0–5 MPN/100 ml in this study.
CPCB has classified the total coliform organism count 50, 500 MPN/100 mL, (maximum) in classes A, B, respectively, and the same has been retained in this study as classes 2 and 3, respectively. A count of 10,000 (MPN/100 mL) has been indicated as Maximum Admissible Level in European Community (EC) bathing water standards. This value is assigned to class 4 (500–10,000) in this study indicating excess Polluted water quality, making the criteria more stringent. Coliform count more than 10,000 obviously indicates severe pollution, and therefore it is considered in class 5 for this study.
Nitrate nitrogen
In CPCB Standard concentration 20 and 50 mg/l are given for class A and C water. Hence a range is assigned to class 1 (0–20) indicating clean and class 2 (20–50) indicating slight pollution in this study. Nitrate nitrogen at or below 90 mg/l have no adverse effect on warm water fish (Train 1979). Therefore, concentration range of 100–200 and >200 mg/l are considered for class 4 and class 5 of water, respectively, for this study.
Electrical conductivity
Since CPCB guidelines do not mention the concentration limits for class A, B, and C for the parameter EC, the reference is taken from IS Standards for drinking water and European community Standards. According to IS standards, the limits of EC are 300 micromhos/cm for drinking water; EC Specifies guide level of 400 micromhos/cm. Hence, value >300 micromhos/cm indicates severe pollution, and therefore, it is considered in class 5. Other classes are given in geometrical progression, as class 1, 2, 3, and 4.
Estimating the unit weight of each indicator parameter (W i ) by considering the weightage of each parameter
Weightage of each parameter
Weighing means the relative importance of each water quality parameter that play some significant role in overall water quality and it depends on the permissible limit in drinking water set by National and International agencies viz., WHO, IS-10500, etc. Those parameters, which have low permissible limits and can influence the water quality to a large extent even fluctuate a little, allocate high weighing while parameter having high permissible limit and are less harmful to the water quality allocate low weighing. The intended use of water is considered for this study is as per class B and C i.e, outdoor bathing Organized (B), drinking water source with conventional treatment followed by disinfections (C). Hence, the weightage is assigned with respect to class 1 and 2 of Table 1. Weightage of parameter is inversely proportional to its permissible limits, i.e, weightage of parameter I = 1/S i , where S i = maximum permissible limits of the parameter. The map of Sabarmati river basin with the locations of the stations under study is shown in Fig. 1.
Unit weight of each parameter
The unit weight (W i ) of each parameter is proportional to the weightage of each parameter. i.e, W i ά 1/S i or W i = K/S i where \(K = { 1}/\sum\nolimits_{i = 1}^{n} {1/S_{i} }\) where K is the constant of proportionality; W i is the unit weight of the parameter; n is the number of water quality parameters.
The unit weight of each parameter calculated are shown in Table 2.
Determining the subindex value (W i × V r )
The subindex value is determined by multiplying its unit weight with its rating obtained from Table 1
Aggregating the subindices to obtain the overall water quality index (WQI)
WQI is the sum of product of rating (V r ) and unit weight (W i ) of all the parameters
Data collection
The data for water quality parameters as indicators for the measurement of water quality index, from year 2005 to the year 2008 have been made available for three stations on the river i.e, Station-1 (S1) V. N Bridge, at Ahmedabad, Station-2 (S2) Shedhi at Kheda and Station-3 (S3) Kheroj bridge at Sabarkantha from Central Pollution Control Board, India (CPCB, India) (website: www.cpcb.nic.in). Table 3 gives the quarterly data of Sabarmati river water quality at the Stations.
Results and discussions
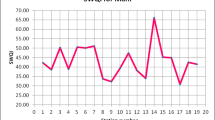
The water quality indices obtained for the three stations are shown in Table 4 and graphically in Fig. 2. Table 5 shows the scale of water quality based on WQI.
Water quality of Sabarmati River
In the present study, principle pollution indicator DO showed a large variation for station S1. For S1, the DO dropped to as low as 0 mg/l for all the years mostly in the month of April. This suggests addition of high organic load at this station due to the discharge of domestic sewage and industrial wastewater in the river. In summer, the temperature of the stream increases. With the increase in temperature, the solubility of oxygen in waters decreases. Also the temperature affects the metabolism, growth and reproduction of bacteria responsible for the biodegradation of the organic matter in water. The rate of biodegradation and biological activity increases with the increase in temperature. Hence, the oxygen demand in the water increases. At S1, high organic pollution, low flow in the summer coupled with increased temperature caused a zero DO level. At stations S2 and S3, DO levels for most of the months was found sufficient for aquatic life survival. The minimum DO observed for S2 was in July, 2006 (0.5 mg/l) and for S3 in July, 2007 (2.4 mg/l).This sudden lowering of DO at these stations may be attributed to organic pollution caused by discharge of domestic sewage and industrial waste water in the river during this period. In the present study, the pH ranged from 6.5 to 8.9. A narrow variation of pH is observed for all stations. This may be due to low variation of free CO2 during these periods (Jayaprakash 1988).
EC is a measure of TDS in water. In this study, EC values are comparatively low at station S3. This may be due to the land cover pattern here i.e, semi-green area and forest area thereby less soil erosion of the top soil (Avvanavar and Shrihari 2008). Stations S1 and S2 show high EC values mostly in the month of April. This may be due to sewage discharges and anthropogenic activities along the river banks at these stations in the summer months. It is noticed that the stations of downstream region have higher TDS values compared to the upstream ones (Jayaprakash 1988).
Nitrate-Nitrogen levels for all the three stations S1, S2, and S3 are found to be low, at S1, 0–2.5 mg/l, at S2, 0.1–5.1 mg/l, at S3, 0.2–2.5 mg/l for all the years. There is no significant increase in the Nitrate-Nitrogen levels at these stations in the monsoon period. This suggests that the natural occurring sources may be the cause of low Nitrate-Nitrogen levels in these stations.
In this study, most probable number (MPN) was found to be very high at S1 i.e, ranging from 43,000 to 15,00,000 per 100 ml. These variations in MPN values may be due to discharge of untreated or partially treated domestic sewage in the river at this station. At S2 and S3, the highest MPN values are observed mostly in the month of July and October for all the years. This shows mixing of sewage with rain and then entering river as runoff. Another source of fecal contaminants may be human and animal activities along the banks of the river.
At station S1, high variation was observed in BOD values (2–293) mg/l.Highest values of BOD are reported in the month of April at S1 for most of the years. Also, as reported earlier the DO levels are 0 mg/l during this period because of increased oxygen demand at high temperatures in summer. At S2, the BOD values range from (7 to 19) mg/l, with maximum values observed in the month of July for most of the years. For S3, the BOD values range from (3 to 12) mg/l. During monsoon, the sewage treatment plants receive a high quantum of sewage which sometimes exceeds their treatment capacity. Hence, untreated or partially treated sewage is discharged into the river leading to increased BOD values observed at S2 and S3 mostly in the monsoon periods.
Water quality index
Water Quality Index allows for a general analysis of water quality on many levels that affect a stream’s ability to host life and whether the overall quality of water bodies poses a potential threat to various uses of water (Akkaraboyina and Raju 2012). From Table 4, the average WQI of S1 ranges from 42.71 to 56.43, S2 ranges from 80.75 to 86.34 and S3 ranges from 85.67 to 95.08. From Table 5, water quality at S1 is bad, at S2 is good and at S3 is good–excellent. S1 is located in a highly urban area, while S2 is located in a moderately urban area and S3 is located in a moderately rural area. WQI values at these stations indicate that water quality deteriorates as river flows from rural to urbanized area.
Conclusions
In the present study, all the water quality parameters showed variation at the three monitoring stations along the Sabarmati River. A narrow variation of pH was observed for all the stations. DO was found 0 mg/l at S1 and low DO values were also observed at S2 and S3. High variations of BOD were found at S1. Stations at downstream region i.e, S1 and S2 showed high EC values than S3 which is located on the upstream region. Nitrate–Nitrogen levels were found to be low for all the three stations S1, S2, and S3. MPN was found to be very high at S1 compared to S2 and S3. The water quality index at S1 was lowest followed by S2 and lastly S3. The main cause of deterioration in water quality at these three monitoring stations was due to the high anthropogenic activities, illegal discharge of sewage and industrial effluent, lack of proper sanitation, unprotected river sites, and urban runoff.
There is a need of regular and detailed water quality monitoring of the Sabarmati River which is presently carried out by the state pollution control board. There is a need to the identify changes or trends in water quality over time and space, to obtain necessary information to design specific pollution prevention programs and to determine whether goals such as compliance with pollution regulations or implementation of effective pollution control actions are being met.
References
Akkaraboyina M, Raju B (2012) A Comparative Study of Water Quality Indices of River Godavari. Int J Eng Res Dev 2(3):29–34
Avvanavar SM, Shrihari S (2008) Evaluation of water quality index for drinking purposes for river Netravathi. Environ Monit Assess 143:279–290
Bhargava DS (1983) Use of a water quality index for river classification and zoning of the Ganga River. Environ Pollut (Ser B) 6:51–67
Bhargava DS, Saxena BS, Dewakar A (1998) A study of geo-pollutants in the Godavary river basin in India, Asian Environment. IOS Press, Amsterdam, pp 36–59
Bharti N, Katyal D (2011) Water quality indices used for surface water vulnerability assessment. Int J Environ Sci 2(1):154–173
Brown RM, McClelland NI, Deininger RA, Tozer RG (1970) Water quality index—do we dare? Water Sew Works 117(10):339–343
Brown RM, McClelland NI, Deininger RA, O’Connor MF (1972) A water quality index—crashing the psychological barrier. In: Indicators of environmental quality
Burden FR, Mc Kelvie I, Forstner U, Guenther A (2002) Environmental monitoring handbook. Mc graw-Hill Handbooks, New York, pp 3.1–3.21
CPCB, ADSORBS/3 1978–1979) Scheme for zoning and classification of Indian Rivers: estuaries and coastal waters. CPCB website: www.CPCB.nic.in
Dalkey NC (1968) DELPHI. The Rand Corporation, Santa Monica
Dalkey NC, Helmer O (1963) An experimental application of the Delphi method to the use of experts. Manag Sci 9(3):458–467
De AK (2003) Environmental chemistry, 5th edn. New Age International Publisher, New Delhi, pp 190, 215, 242–244
Dee N, Baker J, Drobny N, Duke K, Whitman I, Fahringer D (1973) An environmental evaluation system for water resource planning. Water Resour Res 9(3):523–535
DEQ (2003) The Oregon Department of Environmental Quality. http://www.deq.state.or.us/lab/WQM/WQI/Wqimain.htm
Dinius SH (1987) Design of an index of water quality. Water Res Bull 23(5):833–843
Dojlido J, Raniszewski J, Woyciechowska J (1994) Water quality index-application for river in Vistula River Basin in Poland. Water Sci Technol 30(10):57–64
Dwivedi S, Tiwari IC, Bhargava DS (1997) Water quality of the river Ganga at Varanasi. Inst Eng Kolkata 78:1–4
Helmer O, Rescher N (1959) On the epistemology of the inexact science. Manag Sci 6:25–53
Horton RK (1965) An index number system for rating water quality. J Water Pollut Control Fed 37(3):300–306
Indian Standard Specification for Drinking Water (1983) IS-10500-1983. Indian Standards Institution, New Delhi, Gr 6
Jayaprakash RI (1988), A study of the environmental biology of Netravathi river system. Thesis (Ph.D.) Mangalore University, pp 1–7, 9–14, 16–20, 25–27, 30–32, 106–107,113–114
Khan F, Husain T, Lumb A (2003) Water quality evaluation and trend analysis in selected watersheds of the atlantic region of Canada. Environ Monit Assess 88(1):221–248
Landwehr JM, Deininger RA (1976) A comparison of several water quality indices. J Water Pollut Control Fed 48(5):954–958
Leo ML, Dekkar M (2000) Hand book of water analysis (1–25,115–117, 143, 175, 223–226, 261, 273, 767). Marcel Dekker, New York
Lumb A, Halliwell D, Sharma T (2006) Application of CCME water quality index to monitor water quality: a case of the Mackenzie River basin, Canada. Environ Monit Assess 113:411–429
McClelland NI (1974) Water quality index application in the Kansas River Basin. EPA-907/9-74-001. US EPA Region VII. Kansas City, MO
Metcalf, Eddy (eds) (1972) Wastewater engineering: collection, treatment and disposal. McGraw Hill, New York, p 740
Ott WR (1978) Environmental indices: theory and practice. Ann Arbor Science Publishers, Ann Arbor
Sawyer CN, Mc Carthy PL, Parkin GF (1994) Chemistry for environmental engineering, 4th edn. Mc Graw-Hill International Edition, New York, pp 365–577
Smith RA, Alexander RB, Wolman MG (1987a), Analysis and interpretation of water-quality trends in major U.S. rivers, 1974–81. U.S. Geological Survey Water-Supply Paper 2307
Smith RA, Alexander RB, Wolman MG (1987b) Water-quality trends in the Nation’s rivers. Science 235:1607–1615
Sobhani N (2003) The review on water quality index methods and their applications on Zoning of Karoon River. Thesis (M.Sc), Environmental Faculty, Science and Industry University
Tiwari TN, Mishra M (1985) A preliminary assignment of water quality index to major rivers. Ind J Environ Protect 5:276
Train RE (1979) Quality Criteria for Water. U.S. Environmental Protection Agency, Washington, DC, pp 16, 17, 109
Tyagi S, Sharma B, Singh P, Dobhal R (2013) Water quality assessment in terms of water quality index. Am J Water Resour 1(3):34–38
US EPA (2009). Environmental impact and benefits assessment for final effluent guidelines and standards for the construction and development category. Office of Water, Washington, DC. EPA-821-R-09-012
Walsh P, Wheeler W (2012) Water quality index aggregation and cost benefit analysis. U.S. Environmental Protection Agency, Working Paper, 12-05
Walski TM, Parker FL (1974) Consumer’s water quality index. J Environ Eng ASCE 100:593–611
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shah, K.A., Joshi, G.S. Evaluation of water quality index for River Sabarmati, Gujarat, India. Appl Water Sci 7, 1349–1358 (2017). https://doi.org/10.1007/s13201-015-0318-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13201-015-0318-7