Abstract
The potential of using three different data-driven techniques namely, multilayer perceptron with backpropagation artificial neural network (MLP), M5 decision tree model, and Takagi–Sugeno (TS) inference system for mimic stage–discharge relationship at Gharraf River system, southern Iraq has been investigated and discussed in this study. The study used the available stage and discharge data for predicting discharge using different combinations of stage, antecedent stages, and antecedent discharge values. The models’ results were compared using root mean squared error (RMSE) and coefficient of determination (R 2) error statistics. The results of the comparison in testing stage reveal that M5 and Takagi–Sugeno techniques have certain advantages for setting up stage–discharge than multilayer perceptron artificial neural network. Although the performance of TS inference system was very close to that for M5 model in terms of R 2, the M5 method has the lowest RMSE (8.10 m3/s). The study implies that both M5 and TS inference systems are promising tool for identifying stage–discharge relationship in the study area.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The reliable estimation of river flow rate (discharge) is a prerequisite and crucial component for hydrological applications and analyses. Because of the dynamic nature of hydrological system, direct measurements of discharge are typically time consuming, costly and even impossible, especially during flood. Therefore, most discharge records are derived from converting the measured water levels (stages) to discharges by a functional relationship that is expressed as a rating curve. A calibrated stage–discharge rating offers an easy, cheap, and fast technique to estimate discharge (World Meteorological Organization 1980; Kennedy 1984; Herschy 1999). Stage–discharge rating is generally treated as the following power curve (Herschy 1999):
where Q is the discharge; H is the stage; α is an index exponent; a and b are constants (depending on the study area).
Unfortunately, the functional relationship between stage and discharge is complex, time-varying, and cannot always captured by simple rating curve, even with the help of traditional modeling techniques such as polynomial regression or autoregressive integrated moving average ARIMA technique (Bhattacharya and Solomatine 2000). Many research attempts to establish this relation via data-driven techniques such as artificial neural networks ANNs (Tawfik et al. 1997; Bhattacharya and Solomatine 2000; Sudheer and Jain 2003; Bisht et al. 2010), decision trees (Bhattacharya and Solomatine 2003; Ghimire and Reddy 2010; Ajmera and Goyal 2012), support vector machine (Aggarwal et al. 2012), wavelet-regression model (Kişi 2011), Takagi–Sugeno fuzzy inference system (Lohani et al. 2006), and evolutionary-based data-driven models (Ghimire and Reddy 2010; Azamathulla et al. 2011). The results approve that these techniques are very efficient and reliable.
The aim of this study is to investigate the potential of the different data-driven models (artificial neural networks, fuzzy inference system, and M5 decision trees) to emulate stage–discharge rating curve of the Gharraf River at Hay, south of Iraq. Daily records of the stage and discharge are available for this river at Hay station for the period from April 2005 to May 2006. The performance of these techniques was compared and the best one with smaller estimation error selected for future estimation of discharge from available data of previous discharge and stage values.
Modeling techniques
Artificial neural networks
Artificial neural networks (ANNs) are massively parallel systems composed of many processing elements connected by links of variable weights. Given sufficient data and complexity, ANNs can be trained to model any relationship between a series of independent and dependent variables. For this reason, ANNs are considered to be universal approximates and have been successfully applied to a wide variety of problems that are difficult to understand, define and quantify. There are many different types of ANNs based on topology. One of the many ANN paradigms, the Multilayer Perceptron (MLP) network, is by far the most popular (Lippmann 1987). The MLP is layered feedforward network which is typically trained with static backpropagation (BP) algorithm. MLP is capable of approximating any measurable function from one finite-dimensional space to another within a desired degree of accuracy (HornikK and White 1989). The MLP network consists of layers of parallel processing nodes. Each layer is fully connected to the preceding layer by interconnection strength, or weights, w. Figure 1 presents a three-layer MLP neural network consisting of layers i, j, and k, with interconnection weights w ij and w jk between layers of neurons. Each neuron in a layer receives and processes weighted input from a previous layer and transmits its output to nodes in the following layer through links. The connection between ith and jth neuron is characterized by the weight coefficient w ij and the ith neuron by the threshold coefficient ϑ i . The weight coefficient reflects the degree of importance of the given connection in the network. The output value of the ith neuron xi is computed as follows: (Haykin 1994)
with
where f(ξ i ) is the activation function. The threshold coefficient can be understood as a weight coefficient of the connection. With formally added neuron j, where x j = 1, sigmoid shape activation functions are normally defined as:
The backpropagation algorithm works by computing the error between the network output and the corresponding target value and propagating this backward through the network to update the weights. The weight updates are calculated based on:
Where η and μ are the learning and momentum rates, respectively. E is the error, or objective function, and Δw ij (t) and Δw ij (t–1) are– the weight increments between nodes i and j for iterations t and t–1. A detailed description of this algorithm can be found in Fausett (1994) and Haykin (1994).
M5 decision tree
A decision tree is a logical model represented as a binary (two-way split) tree that shows how the values of a target (dependent) variable can be predicted using the values of a set of predictor (independent) variables. There are basically two types of decision trees: (1) classification trees which are the msost commonly used to predict a symbolic attribute (class) (2) regression trees which are used to predict the value of a numeric attribute Witten and Frank (2005). If each leaf in the tree contains a linear regression model, which is used to predict the target variable at that leaf, then it is called a model tree.
The M5 model tree algorithm was originally developed by Quinlan (1992). Detailed description of this technique is beyond the scope of this paper. It can be found in Witten and Frank (2005). A short description of this technique follows. The M5 algorithm constructs a regression tress by recursively splitting the instance space using tests on a single attributes that maximally reduce variance in the target variable. Figure 2 illustrates this concept. The formula to compute the standard deviation reduction (SDR) is (Quinlan 1992):
Examples of M5 model. 1–6 are linear regression models [modified after Solomatine and Xue (2004)]
where T represents a set of example that reaches the node; T i represents the subset of examples that have the ith outcome of the potential set; and sd represents the standard deviation.
After the tree has been grown, a linear multiple regression is built for every inner node using the data associated with that node and all the attributes that participate for tests in the subtree to that node. After that, every subtree is considered for pruning process to overcome the overfitting problem. Pruning occurs when the estimated error for the linear model at the root of a subtree is smaller or equal to the expected error for the subtree. Finally, the smoothing process is employed to compensate for the sharp discontinuities between adjacent linear models at the leaves of the pruned tree.
Fuzzy logic
The term “fuzzy logic” has in fact two distinct meanings. In a narrow sense, it is viewed as a generalization of classical multi-valued logics (Demicco and Klir 2001). In a broad sense, fuzzy logic is viewed as a system of concepts, principles, and methods for dealing with modes of reasoning that are approximate rather than exact Fig. 1. The fuzzy logic system is a cognitive artificial intelligence scientific technique developed in 1965 by Professor Lotfi Zadeh of the Department of Computer Science, University of California, Berkeley, USA. It provides a means of representing uncertainties and vagueness that characterize human perception, judgmental reasoning, and decision (Emami et al. 2000). The generation of a fuzzy model is based on expert knowledge and historical data Fig. 2. Fuzzy inference is the process of formulating the mapping from a given input to an output equation using fuzzy logic, and then the mapping provides a basis from which decisions can be made or discerned. The fuzzy inference system (FIS) consists of four main interconnected components (Fig. 3): rules, fuzzifier, inference engine, and output processor. Once the rules have been established, a fuzzy logic system can be viewed as a map from inputs to outputs. The rules are the heart of a FIS and can be expressed as a collection of IF–THEN statements. The IF part of a rule is antecedent and the THEN part is consequent. Depending on the particular structure of the consequent proposition, three main types of fuzzy models are distinguished as: (1) Linguistic (Mamdani-Type) fuzzy model (Zadeh 1973; Mamdani 1977), (2) Fuzzy relational model (Pedrycz 1984; Yi and Chung 1993), (3) Takagi–Sugeno (TS) fuzzy model (Takagi and Sugeno 1985). In this paper, the TS fuzzy model is employed to emulate stage–discharge rating curve, so a brief description of this method is outlined below.
In the TS fuzzy inference system, the rule consequents are usually taken to be either crisp numbers or linear functions of the inputs (Lohani et al. 2006)
where x ∊ ℜn is the antecedent and y i ∊ ℜ is the consequent of the ith rule. In the consequent, a i is the parameter vector and b i is the scalar offset. The number of rules is denoted by M and A i is the (multivariate) antecedent fuzzy set of the ith rule defined by the membership function
The fuzzy antecedent in the TS model is defined as an and-conjunction by means of the products operator Wolfs and Willems (2013)
where x j is the jth input variable in the p dimensional input data space, and μ ij the membership degree of x j to the fuzzy set describing the jth premise part of the ith rule. μ i (x) is the overall truth value of the ith rule.
Where u i is the normalized degree of fulfillment of the antecedent clause of rule R i (Setnes 2000)
The y i s are called consequent functions of the M rules and defined by:
where W ij are the linear weights for the ith rule consequent function.
The study area and data description
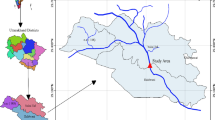
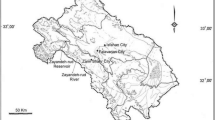
The Gharraf River system is located in Mesopotamian plain, southern Iraq (Fig. 4). The drainage area of this system is 435,052 × 106 m2. The river begins in the Kut Barrage and runs south between the great Euphrates and Tigris Rivers, and ends in Al-Hammer marsh land in Nassyria city. The main length of the river is approximately 230 km. The Gharraf area is characterized by hot and dry summer and cold and wet winter. The climate of the area is classified as semi-arid one. The course of the Shatt Al Gharraf can be subdivided according to the conditions that governed its development as follows (Iraqi Ministries of Environment, Water resources, Municipalities and Public works 2006): (1) The Hay Delta, which ends at Kalaat Sukkar in which expansion can take place, (2) The Rafai gully extends to about 10 km upstream of Bada’a in which flow is restricted, no lateral expansion being possible, (3) The Bada’a Delta is the most recent region of expansion on the left bank towards the Hor Abu Ijul, Hor H’weynah and Hor Ghamukah depressions, and (4) The Shattrah and Kasser–Ibrahim Deltas are the regions of expansion at the end of the Rafai gully.
The daily averages of stage and discharge data for the Hay station on the Gharraf River were used in this study. The observed data covers the period from April 2005 to May 2006. In Iraq, it is difficult to obtain enough time series to build data-driven models; hence, approximately 1 year was used. The available data was arbitrary divided into two parts sets: 66 % for training and 34 % for testing for all models developed in this study. The statistical parameters of the used data are given in Table 1. In this table, N, Min., Max., \(\bar{x}\), Me, s, C v, and K s refer to total number of data, minimum, maximum, arithmetic average, standard deviation, coefficient of variation, and coefficient of skewness, respectively. From Table 1, one could conclude that variation of discharge values is higher than that for stage. The maximum values of stage in testing set are higher than that for training set, this may cause difficulty to estimate discharge at extreme values. One the other hand, the maximum and minimum values of discharge in testing set fall within the range in training test. This may overcome the problem of estimation extreme discharge values which previously mention.
Performance criteria for the developed models
The performance of the various data-driven models was evaluated by means of errors statistics criteria such as root mean squared error (RMSE) and coefficient of determination (R 2). The mathematical formulation of these criteria is outlined below:
-
(a)
Root mean square error (RMSE)
$${\text{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^{n} {\left( {Q_{i} - \hat{Q}_{i} } \right)}^{2} }}{n}}$$(13)where Q i is the measured discharge and \(\hat{Q}\) is the simulated discharge, n is the number of observations (instants). As the value of this criterion approaches zero, the better fit between observed and modeled data is obtained.
-
(b)
Coefficient of determination
$$R^{2} = 1 - \frac{\text{SSE}}{{{\text{SS}}y}}$$(14)where \({\text{SSE }} = \sum\limits_{i = 1}^{n} {\left( {Q_{i} - \hat{Q}_{i} } \right)^{2} }\) \({\text{SSy }} = \sum\limits_{i = 1}^{n} {\left( {Q_{i} - \bar{Q}_{i} } \right)^{2} }\) where \(\bar{Q}\) is the arithmetic mean of the observed Q. The better the fit, the closer R 2 is to ± 1.
Applications of the techniques
Artificial neural networks
In this study, feedforward neural network (MLP) with backpropagation algorithm was employed for developing ANN models. The popularity of MLP in hydrological application (Zhang and Govindaragju 2003; Leahy et al. 2008) is the main reason for selecting this network. Although, the architecture of MLP can have many hidden layers, works by Cybenco (1989) and Coulibaly et al. (1999) have shown that a single hidden layer is sufficient for the MLP to approximate any complex non-linear function. For all the developed models, the Levenberg–Marquardt algorithm was applied to train the networks. The logistic sigmoid transfer function is used in the hidden layer and a linear one in the output layer for the all the developed networks. The early stopping method was selected to overcome overfitting problem. Demo version of Alyuda NeuroIntelligent commercial software was used in this study to build different neural networks. NeuroIntelligence is a neural network software for experts. It is used to apply neural networks to solve real-world forecasting, classification and function approximation problems. It is full-packed with proven techniques for neural network design and optimization. To ensure that each variable is treated equally in the models, all the input and output data were automatically normalized into the range [−1, 1]. The default values of learning rate (0.1) and momentum rate (0.1) were used for building network models. The number of nodes in the hidden layer for each developed models were determined by trial and error procedure considering the need to derive reasonable results.
The study examined various combinations of river stage H t with specified lag times H t−1 and H t−2 and the antecedent discharges Q t−1 and Q t−2 as inputs to the ANN models to evaluate the degree of effect of each of these variables on output variable Q t . The input combinations evaluated in the present study are shown in Table 2. The same variable input combinations were also used for M5 and TS fuzzy inference system techniques. Also, to reduce network error, different numbers of iterations for the best network were examined. These tests were conducted to verify whether an increase iteration numbers could reduce error rate or not.
M5 decision trees
For building M5 models, Weka 3.6 software was used. Weka is open-source machine learning/data mining software written in Java Witten and Frank (2005). The software contains a comprehensive set of pre-processing tools, learning algorithms and evaluation methods. For this study, the parameters of M5 algorithm were set to their default values; pruning factor 4.0 and smoothing option. The software was available on http://www.cs.waikato.ac.nz/~ml.
TS fuzzy inference system
A fuzzy toolbox in MATLAB 2012a software was used for building fuzzy models. Membership functions were extracted via subtractive clustering method. Subtractive clustering method (Chiu 1994) is an extension of the mountain clustering method, where data points (not grid points) are considered as the potential candidates for cluster centers. It uses the positions of the data points to calculate the density function, thus reducing the number of calculations significantly. Since each data point is a candidate for cluster centers, a density measure at data point x i is defined as (Chiu 1994)
where r a is a positive constant representing a neighborhood radius. Therefore, a data point will have a high density value if it has many neighboring data points. A trial and error procedure was used to assign a suitable value of calculus radius. After many trials the best result was 0.2. Three Gaussian membership functions were extracted for each model, which were labeled as low, medium, and high. The same labels were used for Q t . Default values of the TS inference system were used in this study.
Results and discussions
The RMSE and R 2 statistics of each ANN model in testing period are given in Table 3. The ANN model whose inputs were H t−1, H t , Q t−2, and Q t−1 (input combination 4) with [4 15 1] architecture has the smallest RMSE (9.91 m3/s) and the highest R 2 (0.82). As shown in Table 3, using only the stage H t (input combination 1) gives poor estimate with the RMSE (21.99) and R 2 (0.05). Among the ANN models, whose inputs were the antecedent discharges (input combinations 2, 3, 4, and 5), the ANN model with Q t−1 has the biggest RMSE (12.06 m3/s) and the lowest R 2 (0.67). This emphasizes that the Q t is mostly dependent on the antecedent discharge values. Among the ANN models, whose inputs were the antecedent stages (input combinations 3, 4, and 5), the ANN model with inputs H t−2, H t−1, and H t has the biggest RMSE (12.03 m3/s) and the lowest R 2 (0.72). In general, all the developed ANN models except ANN-1 and ANN-2 with [2 3 1] have good capabilities to emulate stage–discharge relationship because they have reasonable RMSE and R 2. Table 3 also shows that the increasing of hidden nodes brought slightly better performance for the developed models. The Q t estimates of the best performance models are also represented graphically in Fig. (5). It is obviously seen from these figures that measured and estimated discharge was reasonably good. All the figures show that the estimated discharge Q t for all the developed models was underestimated especially with the lowest values of discharge.
Table 4 presents the statistical performances of M5 decision tree models in which the model whose inputs were Ht and Q t−2 (input combination 2) was the best model among all other developed models with lowest RMSE and R 2, 8.10 and 0.88, respectively. The other models also perform best except the MT1 with single input H value. Figure 6 shows a graphical comparison between measured and estimated discharges. It is obvious from Fig. 5 that the MT2-5 four models have very good agreement between measured and estimated discharges for both low and high values. For the MT5 model, the following rule was extracted from M5 algorithm:
LM num: 1
LM num: 2
LM num: 3
For the MT2 with minimal input data (input combinations 2), the following tree was extracted:
LM num: 1
The statistical performance of TS inference system is shown in Table 5. Results of this data-driven model were similar to that of M5 model. The TS2 with two inputs parameter, i.e., H and Qt−1 was the best among the other models with lowest RMSE (8.17) and R 2 (0.88). The worst model was the model whose input was stage only Fig. 6. The other three models (TS3-5) also perform very well where both high and low values were reasonably predicted (Fig. 7). The TS2 was selected in this study a candidate for comparison with other data-driven models because it has minimal input data and perform the best for all other developed models as mentioned previously. The membership editor and fuzzy rules for this model are shown in Figs. 8, 9, respectively. Three simple fuzzy rules were generated for this model. These are:
The TS inference system for this model is illustrated in Fig. 10.
The comparison between the three data-driven best models is presented in Table 6. The best data-driven model for estimating Qt was M5 model tree. Although, the performance of TS inference system was very close to that for M5 model in terms of R 2, the M5 method has the lowest RMSE (8.10 m3/s). Results also reveal that the M5 model performed better than the ANN model for both low and high discharge predictions. The complex structure of ANN and the many parameters which must be assigned for successful training make the ANN a second priority when compared with the simple structure and very fast training M5 algorithm. The generated tree structure with linear models on the leaves bears another benefit for this technique; it was very easy to understand even from those people who are unfamiliar with hydrology. The same results were obtained by Ajmera and Goyal (2012) when they compared between ANN and M5 techniques for mimic flow rating curve. The results of this study agree with Ajmer and Goyal (2012) and added another comparison, i.e., between TS inference system and M5 which enhance the capability of M5 model for emulating stage–discharge relationship. The results also indicated that TS and MT models that used only two variables (Q t−1 and H) were very good for predicting Q t for the study area.
Conclusions
The abilities of the artificial neural networks, M5 decision trees, and Takagi and Sugeno fuzzy inference techniques for emulating stage–discharge relationship for Gharraf River system, southern Iraq have been investigated and discussed in this study. The study demonstrated that modeling of this relationship is possible through using these techniques. The M5 decision tree technique models with minimal data, i.e., current stage and one antecedent discharge, perform better than that ANN models and TS inference engine. The root mean squared error and correlation of determination for best M5 model were (8.17 m3/s) and (0.88), respectively. The best M5 and TS models were able to predict discharge on both high and low values. Most of the developed ANN models were slightly capable to predict the discharge but most predictions were underestimating. All the developed models with stage as a single input failed to mimic stage–discharge relationship. This implies that antecedent discharges were needed for better relationship at this area. The study used data from one station and further studies using more data may enhance the results obtained by this study.
References
Aggarwal SK, Goel A, Singh VP (2012) Stage and discharge forecasting by SVM and ANN techniques. Water Resour Manag. doi:10.1007/s11269-012-0098-x
Ajmera TK, Goyal MK (2012) Development of stage-discharge rating curve using model tree and neural networks: an application of Peachtree Creek in Atlanta. Expert Syst Appl 39:5702–5710
Azamathulla HM, Ghani AA, Leow CS, Chang CK, Zakaria NA (2011) Gene-expression programming for the development of a stage-discharge curve of the Pahang River. Water Resour Manag 25:2901–2916
Bhattacharya B, Solomatine DP (2000) Application of neural network in stage discharge relationship. In: Proceedings of the international conference of hydroinformatics, Iowa, USA
Bhattacharya B, Solomatine DP (2003) Neural networks and M5 model trees in modeling water level-discharge relationship for an Indian river. ESAN’2003 In: Proceedings-European Symposium on Artificial Neural Network Belgium
Bisht DC, Raju MM, Joshi MC (2010) ANN based river stage-discharge modeling for Godavari River, India. Comput Model New Technol 14:48–62
Chiu SL (1994) Fuzzy model identification based on cluster estimation. J Intell Fuzzy Sys 2:267–278
Coulibaly P, Anctil F, Bobée B (1999) Prévision hydrologique par réseaux de neurons artificiels: état de I’art. Can J Civ Eng 26:293–304
Cybenco G (1989) Approximation by superposition of a sigmoidal function. Math Control Signals Syst 2:303–314
Demicco RV, Klir GJ (2001) Stratigraphic simulations using fuzzy logic to model sediment dispersal. J Pet Sci Eng 31:135–155
Emami MR, Goldenberg AA, Tűrksen IB (2000) Fuzzy-logic control of dynamic systems: from modeling to design. Eng Appl Artif Intell 13:47–69
Fausett L (1994) Fundamentals of neural network, architectures, algorithms, and applications. A Simon and Schuster Company, USA
Ghimire BN, Reddy MJ (2010) Development of stage-discharge rating curve in river using genetic algorithm and model tree. International Workshop Advanced in Statistical Hydrology, Italy
Haykin S (1994) Neural networks a comprehensive foundation. Macmillan College Publishing Company Inc, New York
Herschy RW (1999) Hydrometry: principle and practice. Wiley, New York
HornikK Stinchcomebe M, White H (1989) Multi-layer feedforward networks are universal approximators. Neural Networks 2:359–366
Iraqi Ministries of Environment, Water resources, Municipalities and Public works (2006) Overview of present conditions and current use of the water in the marshlands area. vol. I Italy
Kennedy EJ (1984) Discharge rating at gaging stations. US Geol. Survey techniques of water resources investigation Book 3, Chapter A10
Kişi O (2011) Wavelet regression model as an alternative to neural networks for river stage forecasting. Water Resour Manag 25:579–600
Leahy P, Kiely G, Corcoran G (2008) Structural optimization and input selection of an artificial neural network for river level prediction. J Hydrol 355:192–201
Lippmann RP (1987) An introduction to computing with neural nets. IEEE ASSP Magazine 4–22
Lohani AK, Goel NK, Bhatia KK (2006) Takagi-Sugeno fuzzy inference system form modeling stage-discharge relasionship. J Hydrol 331:146–160
Mamdani EH (1977) Application of fuzzy logic to approximate reasoning using linguistic systems. Fuzzy Sets Syst 26:1182–1191
Pedrycz W (1984) An identification algorithm in fuzzy relational systems. Fuzzy Sets Syst 13:153–167
Quinlan JR (1992) Learning with continuous classes. In: Proceedings A192, 5th Australian Join Conference on Artificial Intelligence, Singapore. pp 343–348
Setnes M (2000) Supervised fuzzy clustering for rule extraction. IEEE Transactions Fuzzy Syst 8(4):416–424
Solomatine DP, Xue Y (2004) M5 model trees and neural networks: application to flood forecasting in the upper reach of the Huai River in China. J Hydrol Eng 9:491–501
Sudheer KP, Jain SK (2003) Radial basis function neural network for modeling rating curves. J Hydrol Eng 8:161–162
Takagi T, Sugeno M (1985) Identification of systems and its application to modeling and control. Insti. Elect Electron Eng Trans Syst Man Cybern 15:116–132
Tawfik M, Ibrahim A, Fahmy H (1997) Hysteresis sensitive neural network for modeling rating curves. J Comput Civ Eng 11:201–211
Witten IH, Frank E (2005) Data mining. Morgan Kaufmann, USA
Wolfs V, Willems P (2013) A data driven approach using Takagi—Sugeno models for computationally efficient lumped floodplain modeling. J Hydrol 503:222–232
World Meteorological Organization (1980) Manual on stream gauging, vol. II: computation of discharge. Operational hydrology report No. 13, WMO
Yi SY, Chung MJ (1993) Identification of fuzzy relational model and its application to control. Fuzzy Sets Syst 59:25–33
Zadeh LA (1973) Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans Syst Man Cyber 1:28–44
Zhang B, Govindaragju R (2003) Geomorphology-based artificial neural networks (GANNs) for estimation of direct runoff over watersheds. J Hydrol 273:18–34
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Al-Abadi, A.M. Modeling of stage–discharge relationship for Gharraf River, southern Iraq using backpropagation artificial neural networks, M5 decision trees, and Takagi–Sugeno inference system technique: a comparative study. Appl Water Sci 6, 407–420 (2016). https://doi.org/10.1007/s13201-014-0258-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13201-014-0258-7