Abstract
Two multivariate statistical technologies, factor analysis (FA) and discriminant analysis (DA), are applied to study the river and groundwater hydrochemistry and its controlling processes in the Sanjiang Plain of the northeast China. Factor analysis identifies five factors which account for 79.65 % of the total variance in the dataset. Four factors bearing specific meanings as the river and groundwater hydrochemistry controlling processes are divided into two groups, the “natural hydrochemistry evolution” group and the “pollution” group. The “natural hydrochemistry evolution” group includes the salinity factor (factor 1) caused by rock weathering and the residence time factor (factor 2) reflecting the groundwater traveling time. The “pollution” group represents the groundwater quality deterioration due to geogenic pollution caused by elevated Fe and Mn (factor 3) and elevated nitrate (NO3 −) introduced by human activities such as agriculture exploitations (factor 5). The hydrochemical difference and hydraulic connection among rivers (surface water, SW), shallow groundwater (SG) and deep groundwater (DG) group are evaluated by the factor scores obtained from FA and DA (Fisher’s method). It is showed that the river water is characterized as low salinity and slight pollution, and the shallow groundwater has the highest salinity and severe pollution. The SW is well separated from SG and DG by Fisher’s discriminant function, but the SG and DG can not be well separated showing their hydrochemical similarities, and emphasize hydraulic connections between SG and DG.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
The Sanjiang Plain, as a part of the Songhua River basin, is located in the northeast part of China, and it is one of the biggest and most important grain production bases in China. Large areas of wetlands have been exploited into crop lands since 1950s. In 2005, the area of crop lands was about 55,688 km2, three times than that in 1954 (Song et al. 2008). On one hand, agriculture boom and development of cities have increased the demand of freshwater, on the other hand, the local surface water and groundwater quality have been deteriorated by the discharge of domestic and agricultural sewage. Elevated nitrate have been found both in rivers and shallow groundwater in the Sanjiang Plain (Cao et al. 2012). Another problem existing in the study area is the geogenic pollution caused by elevated Fe and Mn ranging from 0.3–24 to 0.2–0.4 mg/L, respectively (Yang et al. 2008), which have exceeded the drinking water sanitary standard (DWSS) of China (0.3 mg/L for Fe and 0.1 mg/L for Mn). Recent years, for the deterioration of shallow groundwater quality, well depths in some rural areas have reached from 50 m to almost 100 m. Extractions of deep groundwater may lead to pollutants transporting vertically from shallow groundwater to deep groundwater, resulting in a more serious problem to be dealt with. Therefore, it is necessary to identify the hydraulic connections among different water bodies such as rivers (SW), shallow groundwater (SG) and deep groundwater (DG).
Cao et al. (2012) have given a detailed analysis of the characteristics of nitrate in major rivers and aquifers of the Sanjiang Plain, but there are no reports found about the analysis of regional hydrochemical characteristics. Multivariate analysis, such as factor analysis (FA), discriminant analysis (DA) and cluster analysis (CA), aiming to interpret the governing processes through data reduction and classification, are recognized as powerful tools to deal with the increasing number of hydrochemical parameters. They have been effectively and widely applied to assessment of surface water quality (Panda et al. 2006; Shrestha and Kazama 2007; Yidana et al. 2008, 2010), evaluation of the hydrogeochemical characteristic of groundwater (Cloutier et al. 2008; Papatheodorou et al. 2007; Yidana et al. 2010) and identification of groundwater contaminations (Dragon 2006; Kim et al. 2009; Zhou et al. 2007).
In this paper, two multivariate statistical analysis methods including FA and DA have been applied (1) to analyze the general characteristics of surface water (rivers) and groundwater hydrochemistry and their controlling factors; (2) to discriminate the hydrogeochemical difference among the SW, SG and DG; and (3) to deduce the hydraulic connectivity of these three water bodies based on hydrochemical similarities.
Study area
General descriptions
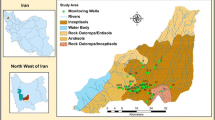
The Sanjiang Plain (129°46′42″–135°05′10″E, 46°06′30″N–48°28′06″N) is the alluvial plain within the Songhua River basin, northeast part of the Heilongjiang Province, China. The Xiao Xing Anling Mountains with a maximum elevation of 1,429 m above mean sea level and Wandashan Mountain with a maximum elevation of 831 m are found along the west side and southwest side of the study area. The north, east and southeast boundaries of the study area are the Heilong River, the Wusuli River and the Naoli River, respectively. The Songhua River and Naoli River flow through the plain and confluents with the Heilong River and Wusuli River, respectively (Fig. 1). The Sanjiang Plain has a generally flat topography declining from the southwest to the northeast with a slope gradient of about 1:5,000–1:10,000 except for some highlands in the center of the plain.
The study area located in temperate continental monsoon zone with annual mean temperature of 1.9 °C, the mean temperature in July and January is 22 and −21 °C, respectively (Sun and Song 2008). The annual precipitation is 500–650 mm, about 65 % of which occurring from June to August.
Geology and hydrogeology
The aquifers mainly consist of quaternary alluvial deposits, principally sandy gravels, medium and fine sands, sandy clays and silts. Underlain and surrounded by structurally disturbed base rocks of pre-Quaternary and older epochs, the thickness of aquifer varies from 50 to 300 m. Generally speaking, the thickness of sediments around the Suibin city in the west part of the study area is about 300 m and the size of deposits is coarser than other parts. The sediment around the line of Tongjiang-Fujin-Shuangyashan is mainly medium sands in a range of 50–100 m in thickness and the pre-Quaternary rocks crop out can be found beside the Fujin area (Yang et al. 2008). Vertically, the grain size of quaternary deposits in the layer above 60 m in depth is coarse, constituting the main aquifer in Sanjiang plain. Based on the 14C (Yi and Wang 2004) and CFCs (Cao et al. 2013) age dating results, the groundwater samples in this study have been classified into shallow groundwater and deep groundwater samples with sampling depth smaller than 50 m and larger than 50 m, respectively.
Materials and methodology
Sample collection, chemical analysis and data preparation
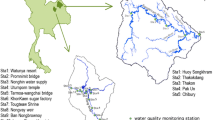
34 groundwater water samples and 23 surface water samples were collected in the study area in September 2007 and September 2009 (Fig. 1). Field parameters pH, temperature (T), electrical conductivity (EC), redox potential (ORP) and dissolved oxygen (DO) of samples were measured by portable equipments (Horiba, Japan), and alkalinity was determined using the acid neutralizing titration on site. Samples were immediately filtered through a 0.45 μm filter and filled in two preclean 100 ml bottles at each site for major ion analysis. All samples were brought back to the laboratory and stored under a temperature of 4 °C. Cations such as K+, Na+, Ca2+ and Mg2+, total Fe, Mn, Al, and dissolved silica (SiO2) were analyzed by ICP-OES chromatography with the limit of detection (LOD) of 0.05 mg/L. Anions such as Cl−, SO4 − and NO3 − were analyzed by ion chromatography (SHIMADZU LC-10AD) with the LOD of 0.01 mg/L. Charge balance error of the water samples is <5 % which is within the limits of acceptability.
Multivariate statistical analysis
Multivariate statistical analysis requires that the observations conform to normal distribution and the data transforms, such as log-transform (Cloutier et al. 2008), rank-ordered (Miller et al. 1997) and normalization (Ravichandrana et al. 1996; Ruiz et al. 1990), are carried out before doing multivariate statistical analysis. In this study, the normality of variables was checked by one-sample K–S test. When data do not follow normal distribution, log-transform was selected to improve the data normality. ORP and Al have been removed from the multivariate statistical analysis, because the normality improvements of these two parameters were poor after the log-transformation. All the statistical analyses were conducted by the PASW Statistics 18.
Factor analysis
Factor analysis is a generic term used to describe a number of methods designed to analyze interrelationships within a set of variables or objects (Reyment and Joreskog 1996). As a kind of dimension reduction technology in multivariate analysis, factor analysis can effectively reduce numerous data into few variables, the so-called factors. The underlying but unobservable or the latent processes which can not be directly revealed by the raw dataset could be determined through the use of factors and help to draw a more clear interpretation of the system. Factor analysis can be applied to the variables (R-mode) or to the cases (Q-mode). Here, main purpose is set to identify the hydrochemical characteristics and the involved controlling factors. So the R-mode which is dealing with the variables analysis is selected.
The principle component method was applied to calculate the factor loading matrix. The number of factors were defined according to the criterion that only factors that account for variances >1 (eigenvalue-one criterion) should be included. The rationale for this criterion is that any component should account for more variance than any single variable in the standardized test score space (de Andrade et al. 2008). Varimax procedure (Carroll 1953) was used for the rotation of the retaining factors to yield an insight and informative interpretation or a more “simple structure” of the factor loading matrix. The terms ‘strong’, ‘moderate’, and ‘weak’ as applied to factor loadings refer to absolute loading values of ≥0.75, 0.75–0.50 and 0.50–0.30, respectively (Liu et al. 2003). The factor scores were computed by the regression method which has the advantage of being the simplest technique and is easy to apply (Hardle and Simar 2007). Dalton and Upchurch (1978) have shown that factor scores for each sample could be related to intensity of the process described by the factor. It is pointed out that extreme positive factor scores (≥1) reflected areas most affected and negative scores (≤−1) reflected areas unaffected by the process represented by the factor, while near-zero scores reflected areas affected to an average degree of the process.
In addition, the usefulness of factor scores could be summarized as two points (Reyment and Joreskog 1996). The first of these is that in general there will be fewer factors than original variables. Fewer maps or diagrams were needed for illustrating the spatial distribution of the variables or parameters and relationship between them. The second point is that for an orthogonal solution, the factor scores (“new” variables) will be uncorrelated, an important feature in using other statistical procedures, such as discriminant analysis and cluster analysis.
Discriminant analysis
Discriminant analysis is used in situations where the groups are known as a priori. The priori groups correspond to natural classifications or groups known from history or prior knowledge and also could have been formed by a cluster analysis performed on past data (Hardle and Simar 2007). In this study, the Fisher’s discriminant method was used. Fisher’s suggestion was to find the linear combination of datas which maximizes the ratio of the between-group-sum of squares to the within-group-sum of squares (Hardle and Simar 2007). The linear discriminant functions (LDF) is given by Eq. 1:
where L denotes LDF; p is the number of parameters used to classify a set of data into a given group; a j is the weight coefficient assigned to a given selected parameter y j .
Results
Characteristics of general hydrochemistry
The statistical summaries of hydrochemical parameters for surface water (SW), shallow groundwater (SG) and deep groundwater (DG) in the Sanjiang Plain are listed in Table 1. The average of pH is about 8.10 for surface water, which is more alkaline than that of shallow (7.44) and deep groundwater (7.45). The shallow groundwater has the highest EC with an average of 444 μs/cm, and the lowest EC is observed in the surface water with an average of 153 μs/cm.
Both surface water and groundwater are Ca-HCO3 type. Prevalent cations are Ca2+ > Na+ > Mg2+ > K+. The average concentrations of Ca2+ are 21, 55 and 39 mg/L for SW, SG and DG, respectively. HCO3 − is the dominate anion and is followed by SO4 2− and Cl−. Generally speaking, averages of the major ions were within acceptable ranges for domestic and irrigation uses. However, there are a few samples of elevated concentrations of NO3 −, Fe and Mn suggesting local pollution in water environments. The max value of NO3 − in the shallow groundwater is about 153 mg/L, three times the standard value (50 mg/L, DWSS). Average concentrations of Fe are 2.42 mg/L (SW), 4.23 mg/L (SG) and 5.04 mg/L (DG), respectively, which have exceeded the standard value of 0.30 mg/L in DWSS.
Factor analysis
The total dataset except for the parameters of Al and ORP was analyzed by R-mode factor analysis, and the result is showed in Table 2. Five factors which explain 79.65 % of the total variance are obtained based on the criteria for factor selection (eigenvalues >1.0). Communalities for the parameters are high (>0.70) for almost all variables except for Cl− (0.60), SO4 2− (0.68) and SiO2 (0.66), and it indicates that the five-factor model explains the variability of almost all variables and can be used to indicate dominant processes controlling the local hydrochemistry without losing significant characteristics.
Factor 1 explains 29.49 % of the total variance and has strong positive loadings on EC, Na+, Ca2+, Mg2+ and HCO3 −, moderate positive loadings on Cl− and K+. Factor 2 explains 18.13 % of the total variance of the dataset and shows a significant bipolar characteristic. It has strong positive loadings on T and DO, and the negative pole has a strong loading on SiO2. Factor 3 explains 12.57 % of the total variance of the dataset and shows strong positive loadings on Fe and Mn. Factor 4 explains 9.74 % of the total variance and has a strong positive loading on K+. Factor 5 explains 9.73 % of the total variance and has a positive loading on NO3 − and a moderate loading on SO4 2−.
Discriminant analysis
The Fisher’s discriminant function was used to discriminate whether there is a significant hydrochemical difference and hydraulic connections between SW, SG and DG. Instead of the raw data set, here the factor scores obtained in the factor analysis were used as the input predictors. As mentioned above, the factor scores are orthogonal solutions so they are independent variables. This point is of benefit to carry out the discriminant analysis because colinearity of predictors will inflate the importance of some variables in their discriminant potentials. The number of Fisher’s discriminant functions is related with the number of groups and number of predictors, and here two functions were identified and the function coefficients are displayed in Table 3.
Discussion
Processes controlling the regional hydrochemistry
Based on the factor loadings, the five factors are divided into two groups, which represent two important geochemical processes controlling the regional hydrochemistry. The group 1 includes the factor 1 and factor 2, and the group 2 contains the factor 3 and factor 5. Factor 4 with strong loading on K+ have no significant meaning and is eliminated from the following analysis. The chemical parameters EC, Na+, Ca2+, Mg2+ and HCO3 − associated with factor 1 connote salinity enhancement caused by mineral dissolution (Yidana et al. 2008; Jang 2010), and is defined as “salinity” factor contributing to most of the TDS for water samples. It is also the most important process controlling the regional hydrochemistry due to its highest eigenvalue and ratio explaining the total variance.
In the cation Gibbs (1970) plot the water compositions are displayed as a function of the dominance of end-member components Na+ at one end and Ca2+ at the other. The relative fractions for cations and anions are plotted against the total dissolved solids (TDS) on a logarithmic axis. Rock weathering and dissolution are apparently the dominant process influencing groundwater hydrochemistry in the study area (Fig. 2). But some of shallow groundwater showed a slight deviation from domain controlled by rock weathering and dissolution and branched into the seawater controlling domain which indicated that the shallow groundwater had been further salinized due to evaporation.
Gibbs (1970) plot for cations
Factor 2 has strong positive loadings on T and DO, and the negative pole has a strong loading on SiO2. This factor is defined as “residence time” factor, which is reflecting the traveling time and the evolution of redox conditions for both surface water and groundwater. Yi (2001) reported that groundwater SiO2 concentrations increase with sampling depths and the SiO2 can be recognized as a residence time indicator in the Sanjiang Plain. The negative correlation between SiO2 concentrations and DO (Fig. 3) implies that DO is consumed when the surface water recharge into the groundwater, and results in reducing environment for the groundwater with long residence time. The combination of factor 1 and 2 is recognized as the representative of natural hydrochemistry evolution processes (rock weathering and consumption of DO by organic matters) in the study area.
Factor 3 with high positive loadings on Fe and Mn is defined as “geogenic pollution” factor. Factor 5 with high positive loading on NO3 − and a moderate loading on SO4 2− is recognized as “anthropogenic pollution” factor, which is usually identified in the urban-, industry-, and agriculture-intensive areas due to the domestic wastewater discharge and agricultural activities (Dragon 2006; Lambrakis et al. 2004). The appearance of both NO3 − and SO4 2− in factor 5 implies the same sources for these two elements N and S. Major sources of NO3 − come from fertilizer (chemical fertilizer and manure) and have been identified by Cao et al. (2012) by applying nitrogen isotope tracing tools. Papatheodorou et al. (2006) summarized three possible sources of SO4 2− in groundwater and surface waters as atmospheric deposition, sulfate-bearing fertilizers and bacterial oxidation of sulfur compounds. In this study, considering that SO4 2− appeared both in factor 5 with NO3 −, it implies that SO4 2− also presented a similar source with NO3 −, coming from the use of fertilizers such as ammonium sulfate with major element of N and S. The combination of factor 3 and factor 5 is recognized as the “pollution” group which indicates major processes deteriorating the regional groundwater quality.
Hydrochemical differences
Hydrochemical differences have been detected among SW, SG and DG from Table 1. The natural hydrochemistry evolution processes and pollutions discussed in section “Processes controlling the regional hydrochemistry” are treated as two major reasons resulting in these differences. Here the factor scores are employed to quantify these differences. Surface water and groundwater samples are well separated by scores of the factor 1 and 2 (Fig. 4). Surface water is located in the left upper quadrant with factor 1 scores ≤0 and factor 2 scores ≥0. It implies that influence of rock weathering is lower in the surface water comparing to groundwater due to relative short residence time. In addition, contacting with air makes surface water have oxic conditions and high factor 2 scores.
Most of groundwater samples (SG and DG) are located in the lower half of Fig. 4 with factor 2 scores ≤0, implying that groundwater begins to enter into anoxic zones due to DO consumptions by organic matters without supply. The SG and DG mix together and are not well separated by factor 1 and 2, showing that their hydrochemistry are controlled by similar processes, here mainly referring to water–rock interactions. However, some “extremely affected” samples (mainly SG) with factor 1 score higher than +1 are characterized as high salinity because of the influence of evaporations, and some DG samples with factor 2 score lower than −1 implies enhance silicate weathering due to its long residence time.
Figure 5 presents the plot of factor scores for factor 3 and 5 to explain the hydrochemical differences caused by pollutions. Most of the SW and DG samples are confined by factor scores ranging from −1 to 1 showing that slight contaminations of surface water and deep groundwater. Specifically, the SW samples mainly located in the upper half of Fig. 5 with relative high factor 5 scores show that the major pollutant is NO3 −, while for the DG, which are located in the lower half, have elevated Fe and Mn as the major pollutants. Comparing with SW and DG, SG is vulnerable to contaminations because groundwater table is shallow and the pollutants are easily passing through the unsaturated zones to recharge groundwater. Most of the SG samples locate out of the square bonded by the dot lines in Fig. 5 indicating serious pollutions caused by elevated NO3 −, Fe and Mn.
Hydraulic connections revealed by hydrochemistry
In the Sanjiang Plain, many wells with depth deeper than 50 m have been dug for water supply due to the contamination of shallow groundwater. It is necessary to identify the hydraulic connections among SW, SG and DG, because extractions of deep groundwater may lead to pollutants transporting vertically from shallow groundwater to deep groundwater, and the contamination of deep groundwater is a more serious problem to be dealt with. In this study, the hydraulic connection is identified by evaluating the hydrochemistry similarity according to discriminant analysis.
The magnitudes of the coefficients given by Fisher’s discriminant function directly show the importance of corresponding predictors and their contributions to discriminate the three groups (Table 3). For the discriminant function 1, the residence time factor (factor 2) with the largest coefficient 1.13 has the most substantial differentiating ability for discriminate scores and it is followed with the “salinity” factor (factor 2) which shows the second largest discriminate ability. Obviously, the function 1 discriminate the SW, SG and DG from the point view of natural hydrochemistry evolution. For the discriminant function 2, the “anthropogenic pollution” factor (factor 5) shows its largest coefficient of 0.79 and the “geologic pollution” factor (factor 3) has the second largest coefficient with a value of −0.43, and this function discriminates the three groups by the pollution indicators. Similar result is also confirmed by the structure matrix which shows the absolute correlation between each variable and any discriminant function.
The surface water (SW) is well separated with the groundwater samples (SG and DG) in the function 1 dimension, but for the SG and DG, samples gather together and cannot be well separated in both function 1 and function 2 dimension (Fig. 6). Specifically, the correct classification ratio for SW, SG and DG were 95.7, 54.2 and 63.6 %, respectively by applying the discriminant functions (Table 4). Moreover, 41.7 % of shallow groundwater samples are misclassified into deep groundwater group, while 36.4 % of deep groundwater samples are misclassified into shallow groundwater group. The poor discriminant ability for the SG and DG shows their hydrochemical similarities, and emphasized that tight hydraulic connections existed between SG and DG.
Conclusion
In the Sanjaing Plain, one of the most important grain production bases in China, water resources security has been recognized as a warranty of food security. Water pollution due to human activities threatens the regional water security, so in this paper, the major ion and pollutants hydrochemistry for both surface water and groundwater was studied by two multivariate analysis methods, factor analysis (FA) and discriminant analysis (DA), aiming to well understand the processes controlling the regional hydrochemistry, hydrochemical difference among SW, SG and DG, and hydrological connections for the three water bodies.
Factor analysis identified five factors accounting for 79.65 % of the total variance in the dataset. Two main factor groups were recognized as the main process controlling the regional hydrochemistry. The first factor group named “natural hydrochemistry evolution” consists of the “salinity” factor and “residence time” factor, and the second group revealing the “water pollution” is the combination of the “geogenic pollution” factor and “anthropogenic pollution” factor. Factor scores show the hydrological differences for SW, SG and DG. The surface water is characterized as having relative low salinity, slight contaminations and an oxygen-enriched state. The shallow groundwater has relative high TDS due to groundwater evaporation and is severely polluted with elevated nitrate, Fe and Mn. The deep groundwater has moderate TDS due to water–rock interaction during long residence time, and its major pollutants are Fe and Mn.
Fisher’s discriminant method was used to discriminate the hydrochemical differences between SW, SG and DG, and shows that the factor group of “natural hydrochemistry evolution” had the most substantial discriminant ability for the surface water and groundwater. Poor discriminant ability for the shallow groundwater and deep groundwater reveals their hydrochemical similarity, indicating hydraulic connections between SG and DG.
References
Cao Y, Tang C, Song X, Liu C, Zhang Y (2012) Characteristics of nitrate in major rivers and aquifers of the Sanjiang Plain, China. J Environ Monit 14(10):2624–2633
Cao Y, Tang C, Song X, Liu C, Zhang Y (2013) Residence time as a key for comprehensive assessment of the relationship between changing land use and nitrates in regional groundwater systems. Environ Sci: Process Impacts 15(4):876–885
Carroll JB (1953) An analytical solution for approximating simple structure in factor analysis. Psychometrika 18(1):23–38
Cloutier V, Lefebvre R, Therrien R, Savard MM (2008) Multivariate statistical analysis of geochemical data as indicative of the hydrogeochemical evolution of groundwater in a sedimentary rock aquifer system. J Hydrol 353(3):294–313
Dalton MG, Upchurch SB (1978) Interpretation of hydrochemical facies by factor analysis. Ground Water 16(4):228–233
de Andrade EM, Palácio HAQ, Souza IH, de Oliveira Leão RA, Guerreiro MJ (2008) Land use effects in groundwater composition of an alluvial aquifer (Trussu River, Brazil) by multivariate techniques. Environ Res 106(2):170–177
Dragon K (2006) Application of factor analysis to study contamination of a semi-confined aquifer (Wielkopolska Buried Valley aquifer, Poland). J Hydrol 331(1):272–279
Gibbs RJ (1970) Mechanisms controlling world water chemistry. Science 170(3962):1088–1090
Hardle W, Simar L (2007) Applied multivariate statistical analysis. Springer Verlag, Berlin
Jang C-S (2010) Applying scores of multivariate statistical analyses to characterize relationships between hydrochemical properties and geological origins of springs in Taiwan. J Geochem Explor 105(1):11–18
Kim K-H, Yun S-T, Choi B-Y, Chae G-T, Joo Y, Kim K, Kim H-S (2009) Hydrochemical and multivariate statistical interpretations of spatial controls of nitrate concentrations in a shallow alluvial aquifer around oxbow lakes (Osong area, central Korea). J Contam Hydrol 107(3):114–127
Lambrakis N, Antonakos A, Panagopoulos G (2004) The use of multicomponent statistical analysis in hydrogeological environmental research. Water Res 38(7):1862–1872
Liu C-W, Lin K-H, Kuo Y-M (2003) Application of factor analysis in the assessment of groundwater quality in a blackfoot disease area in Taiwan. Sci Total Environ 313(1):77–89
Miller C, Denis J, Ator S, Brakebill J (1997) Nutrients in streams during baseflow in selected environmental settings of the Potomac River Basin. J Am Water Resour Assoc 33(6):1155–1171
Panda UC, Sundaray SK, Rath P, Nayak BB, Bhatta D (2006) Application of factor and cluster analysis for characterization of river and estuarine water systems–a case study: Mahanadi River (India). J Hydrol 331(3):434–445
Papatheodorou G, Demopoulou G, Lambrakis N (2006) A long-term study of temporal hydrochemical data in a shallow lake using multivariate statistical techniques. Ecol Model 193(3):759–776
Papatheodorou G, Lambrakis N, Panagopoulos G (2007) Application of multivariate statistical procedures to the hydrochemical study of a coastal aquifer: an example from Crete, Greece. Hydrol Process 21(11):1482–1495
Ravichandrana S, Ramanibai R, Pundarikanthan NV (1996) Ecoregions for describing water quality patterns in Tamiraparani basin, South India. J Hydrol 178(1–4):257–276
Reyment RA, Joreskog KG (1996) Applied factor analysis in the natural sciences. Cambridge Univ Press, Cambridge
Ruiz F, Gomis V, Blasco P (1990) Application of factor analysis to the hydrogeochemical study of a coastal aquifer. J Hydrol 119(1):169–177
Shrestha S, Kazama F (2007) Assessment of surface water quality using multivariate statistical techniques: a case study of the Fuji river basin, Japan. Environ Model Softw 22(4):464–475
Song K, Liu D, Wang Z, Zhang B, Jin C, Li F, Liu H (2008) Land use change in Sanjiang Plain and its driving forces analysis since 1954. Acta Geographica Sinica 63(1):93
Sun L, Song C (2008) Evapotranspiration from a freshwater marsh in the Sanjiang Plain, Northeast China. J Hydrol 352(1):202–210
Yang X, Yang W, Zhang F, Chu Y, Wang Y (eds) (2008) Investigation and assessment of groundwater resources potential and eco-environment geology in Sanjiang Plain. Geology Press of China
Yi X (2001) Metasilicic acid groundwater in the Sanjiang Plain. Ground Water 23(3):146–149
Yi X, Wang Z (2004) Shallow groundwater system in Sanjiang Plain. Ground Water 26(1):17–37
Yidana SM, Ophori D, Banoeng-Yakubo B (2008) A multivariate statistical analysis of surface water chemistry data: the Ankobra Basin, Ghana. J Environ Manage 86(1):80–87
Yidana SM, Banoeng-Yakubo B, Akabzaa TM (2010) Analysis of groundwater quality using multivariate and spatial analyses in the Keta Basin, Ghana. J Afr Earth Sci 58(2):220–234
Zhou F, Huang GH, Guo H, Zhang W, Hao Z (2007) Spatio-temporal patterns and source apportionment of coastal water pollution in eastern Hong Kong. Water Res 41(15):3429–3439
Acknowledgments
This work was funded by the Main Direction Program of Knowledge Innovation of Chinese Academy of Sciences: Study on water cycle, water resource carrying capacity and optimization configuration (No. KZCX2-YW-Q06-1). Bing Zhang, Peng Wang and Xin Liu (Chinese Academy of Sciences) provided valuable information and logistical assistance.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Cao, Y., Tang, C., Song, X. et al. Identifying the hydrochemical characteristics of rivers and groundwater by multivariate statistical analysis in the Sanjiang Plain, China. Appl Water Sci 6, 169–178 (2016). https://doi.org/10.1007/s13201-014-0215-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13201-014-0215-5