Introduction

Durian (Durio zibethinus), locally referred to as the “king of fruits” is a dicotyledonous tropical seasonal plant species belonging to the member of family Bombacaceae and genus of Durio (Brown 1997). Its shape is typically ranging from ovoid to nearly round-shaped, featured by a distinctive, strong, pungent and penetrating odor. The edible aril is enveloped in a green to yellowish brown semi-woody rind, with a spike-like spine and sharply pointed pyramidal formidable thorns (Subhadrabandhu and Kesta 2001). Durian tree (25–50 m in height) thrive well in a warm and humid climate, ideally in the temperature range from 25 to 30 °C and evenly distributed rainfall rate between 1.5 and 2 months/year. Its flowers are produced in 3–30 clusters, with each flower having a calyx (sepals) and five (rarely four or six) petals (Voon et al. 2007). Today, its growth has been phenomenal in the global trade market, forecasted a total world’s harvest of 1.4 Mt, dominated by its major producers, Thailand (781 kt), Malaysia (376 kt), Indonesia (265 kt), followed by Philippines (Davao Region), Cambodia, Laos, Vietnam, Myanmar, India, Sri Lanka, Florida, Hawaii, Papua New Guinea, Madagascar, and Northern Australia. Meanwhile, China (65 kt), Singapore (40 kt) and Taiwan (5 kt) are among the key importers accounting for 65 % of the total exports from the top supplying countries. Despite its prolific implementations in food manufacturing industries, such exertions are hampered by the massive generation of durian residues, chiefly in the form of durian shells, seeds, peels and rinds, which constitute 70 % of the entire fruit (Amiza et al. 2004). In the common practice, durian residues are burned or sent to the landfills, without taking care neither of the surrounding environment, nor considering any precaution to prohibit the percolation of contaminants into the underlying water channels. Lately, environmental rules and regulations concerning pollution from agricultural waste streams by regulatory agencies are more stringent and restrictive; inevitably affecting the design, planning, and operation of the durian processing industry. This has inspired a developing exploration to establish a leading selective, reliable and durable alternative for judicious utilization of these pollutants called durian residues.

Methyl red (MR) dye is a commonly used mono-azo dye in laboratory assays, textiles and other commercial products; however, it may cause eye and skin sensitization (Chung et al. 1981) and pharyngeal or digestive tract irritation if inhaled or swallowed (So et al. 1990). Furthermore, MR is mutagenic under aerobic conditions: it undergoes biotransformation into 2-aminobenzoic acid and N,N′-dimethyl-p-phenylene diamine (Wong and Yuen 1998; Vijaya and Sandhya 2003; Jadhav et al. 2008). It became imperative to develop low-cost adsorbent for the removal of MR dye from wastewater before being discharged into receiving water body. The main objective of this work is to evaluate the adsorption performance of locally derived adsorbent from durian seeds for the removal of MR dye from aqueous solutions. Adsorption equilibrium and kinetics were determined. Eight different isotherm equations were employed to quantify the adsorption equilibrium. The effects of solution pH, initial dye concentration and temperature on MR dye adsorption were also examined.

Materials and methods

Activated carbon preparation

Durian fruits (DS) were purchased from a local market in Parit Buntar area, Perak, Malaysia. The fruit was de-husked (the rind was cut open), by cutting along the suture on the back of the lobules. Durian seeds were removed, cleaned and rinsed thoroughly with distilled water. It was then dried to constant weight and stored in an air-tight container for further use. 10 g of durian seed was placed in a vertical tubular reactor. Nitrogen gas was purged into the reactor to create inert condition. The flow rate of nitrogen gas and the heating rate were held at 150 cm3/min and 10 °C/min, respectively. The temperature was ramped from room temperature to 700 °C and held for 1 h. Then the reactor was cooled down to room temperature. The char produced was stored in air-tight container for further treatment. The char produced was then impregnated. The impregnation ratio (IR) was calculated using;

$$ {\text{IR}} = \,\,\frac{{w_{\text{c}} }}{{w_{0} }}, $$
(1)

where w KOH is the dry weight (g) of potassium hydroxide pellet and w char is the dry weight (g) of char. The char and KOH powder (depending on the IR) were mixed together with deionized water in a 250-mL beaker. The mixture was stirred thoroughly until it dried in an oven overnight at 105 °C for dehydrating purpose. The KOH impregnated char was placed inside the vertical tubular reactor for activation process. The system was purged under nitrogen flow of 150 cm3/min. The temperature was ramped from ambient temperature to the activation temperature of 800 °C at heating rate of 10 °C/min. Once the desired activation temperature was reached, the gas flow was switched to carbon dioxide at flow rate of 150 cm3/min to complete the activation process. Then, the reactor was cooled to room temperature under nitrogen flow. The sample was washed with 0.1 M HCl. It was further washed with deionized water several times until the pH of the washing solution reached 6.5–7. The pH was measured using pH meter (Model Delta 320, Mettler Toledo, China). Filter paper and filter funnel were used in the washing process. The washed sample was kept in an oven at 105 °C for 12 h. The dried sample which was the activated carbon (DSAC) was stored in air-tight containers for further characterization and adsorption studies. The DSAC yield was calculated using the equation.

$$ {\text{Yield}}\;\left( \% \right) = \frac{{w_{\text{KOH}} }}{{w_{\text{char}} }}\;{ \times }100, $$
(2)

where w c and w 0 are the dry weight of DSAC (g) and the dry weight of precursor (g), respectively.

Adsorbate used

Methyl red (MR) dye was used as adsorbate to determine the adsorption performance of the prepared activated carbon. The properties of MR dye used are listed in Table 1.

Table 1 Properties of methyl red (Sigma-Aldrich, 2012)
Full size table

Preparation of synthetic methyl red dye solution

0.2 g of Methyl red dye was dissolved in 600 mL of 95 % ethanol. Sufficient deionized water was added with constant stirring to make it up to 1,000 mL mark. Other solutions used for the experiment are prepared from the stock solution using serial dilution.

Batch equilibrium studies

The effects of initial dye concentration, contact time, solution temperature and solution pH on the adsorption uptake for adsorption of MR dye on DSAC were studied. Sample solutions were withdrawn at intervals to determine the residual concentration using UV–visible spectrophotometer at the maximum wavelength of 410 nm. The amount of dye adsorbed at equilibrium, q e (mg/g) was calculated as:

$$ q_{\text{e}} = \frac{{(C_{ 0} - C_{\text{e}} )V}}{W}, $$
(3)

where C 0 and C e (mg/L) are the liquid-phase concentrations of adsorbate at initial and at equilibrium, respectively. V is the volume of the solution (dm3) and W is the mass (g) of DSAC used.

Effect of initial adsorbate concentration and contact time

100 mL of MR dye solution with known initial concentration was put in a series of 250-mL Erlenmeyer flasks. The amount of adsorbent that was added to each flask was fixed at 0.1 g. The flasks were placed in an isothermal water bath shaker (Model Protech, Malaysia) at constant temperature of 30 °C, with rotation speed of 120 rpm, until equilibrium point was reached. Samples are withdrawn at intervals to determine the residual concentration of the dye at 410 nm wavelength using an UV–visible spectrophotometer.

Effect of solution pH

Solution pH was studied by varying the initial pH of solution from 2 to 12. The pH was adjusted by 0.1 M NaOH or 0.1 M HCl and measured using a pH meter. The adsorbent dosage, rotation speed, solution temperature and initial dye concentration were fixed at 0.1 g, 120 rpm, 30 °C and 100 mg/L, respectively.

Adsorption isotherm studies

This was carried out by fitting the equilibrium data to the Langmuir, Freundlich, Temkin, Dubinin–Radushkevich, Sips, Vieth–Sladek, Brouers–Sotolongo and Radke–Prausnitz isotherms. The applicability and suitability of the isotherm equation to the equilibrium data were compared by judging the values of the correlation coefficients, R 2 and Δq e. Linear regression was carried out using Microsoft Excel spreadsheet with Solver add-in to determine the isotherm parameters.

Langmuir isotherm

This model depends on the assumption that intermolecular forces decrease rapidly with distance and consequently help to predict the existence of monolayer coverage of the adsorbate on the outer surface of adsorbent. The linear form of Langmuir isotherm equation (Langmuir 1918) is given by:

$$ \frac{{C_{\text{e}} }}{{q_{\text{e}} }} = \frac{1}{{Q_{0} K_{\text{L}} }} + \frac{1}{{Q_{0} }}C_{\text{e}} , $$
(4)

where C e is the equilibrium concentration of the adsorbate (mg/L), q e is the amount of adsorbate adsorbed per unit mass of adsorbent (mg/g), Q 0 is the maximum monolayer adsorption capacity of the adsorbent (mg/g) and K L is the Langmuir adsorption constant related to the free energy adsorption (L/mg). The constant value can be evaluated from intercept and slope of the linear plot of experimental data of (C e/q e) versus C e. The essential characteristics of Langmuir equation can be expressed in terms of dimensionless separation factor, R L, defined as:

$$ R_{\text{L}} = \frac{1}{{(1 + K_{\text{L}} C_{0} )}} , $$
(5)

where C 0 is the highest initial solute concentration whereas R L value implies the adsorption is unfavorable (R L > 1), linear (R L = 1), favorable (0 < R L < 1), or irreversible (R L = 0).

Freundlich isotherm

The Freundlich model is an empirical equation based on adsorption on heterogeneous surface or surface supporting sites of varied affinities. It is assumed that the stronger binding sites are occupied first and that the binding strength decreases with the increasing degree of site occupation. The Freundlich isotherm (Freundlich 1906) is expressed as

$$ \log q_{\text{e}} = \, \log K_{\text{F}} + \, \left( {1/n} \right) \, \log C_{\text{e}} , $$
(6)

where q e is amount of adsorbate adsorbed per unit mass of adsorbent (mg/g); k F is Freundlich isotherm constant (mg/g) (L/mg)1/n), which indicate the relative adsorption capacity of the adsorbent related to the bonding energy; C e is equilibrium concentration of the adsorbate (mg/L) and n F is the heterogeneity factor representing the deviation from linearity of adsorption and is also known as Freundlich coefficient. If the plot of (log q e) against (log C e) gave straight line, it indicates that the Freundlich isotherm fit the adsorption data. Other constants can be calculated from the slope (1/n) and intercept (log K F) of the linear plot of experimental data. The slope of 1/n ranging between 0 and 1 is a measure of adsorption intensity, becoming more heterogeneous as its value gets closer to zero.

Temkin isotherm

Temkin isotherm contains a factor that explicitly takes into account the adsorbent–adsorbate interactions. This model assumes that the heat of adsorption of all the molecules in the layer would decrease linearly with coverage due to adsorbent–adsorbate interactions. The Temkin model (Temkin and Pyzhev 1940) is expressed as:

$$ q_{\text{e}} = B \;{ \ln }\;A_{t} + B\; { \ln }\;C_{\text{e}} , $$
(7)

where B is RT/b constant related to the heat of adsorption (L/mg); q e is amount of adsorbate adsorbed at equilibrium (mg/g); C e is equilibrium concentration of adsorbate (mg/L); T is absolute temperature; R is universal gas constant (8.314 J/mol K) and A t is equilibrium binding constant (L/mg). A graph of plot of q e versus ln C e will yield both value of slope, B and intercept, A t .

Dubinin–Radushkevich isotherm

Dubinin–Radushkevich isotherm is an empirical model initially for the adsorption of subcritical vapors onto micropore solids following pore filling mechanism. It is applied to distinguish the physical and chemical adsorption for removing a molecule from its location in the adsorption space to the infinity, which can be expressed as (Dubinin and Radushkevich 1947):

$$ q_{\text{e}} = q_{\text{s}} \exp \left( { - B_{\text{DR }} \varepsilon^{2} } \right) $$
(8)

where ε can be correlated:

$$ \varepsilon = RT\;\ln \left[ {1 + \frac{1}{{C_{\text{e}} }}} \right] $$
(8a)
$$ E = \frac{1}{{\sqrt {2B_{\text{DR}} } }}, $$
(8b)

where R, T and C e represent the gas constant (8.314 J/mol K), absolute temperature (K) and adsorbate equilibrium concentration (mg/L), respectively. The value of B DR was then used to estimate free energy E of adsorption per molecule of the sorbate when it is transferred to the surface of the solid from infinity in the solution. A plot of ln q e versus ε 2 will yield a straight line where B DR and q s are obtained from the slope and intercept.

Sips isotherm

Sips isotherm model is a combined form of Langmuir and Freundlich expressions deduced for predicting the heterogeneous adsorption systems and circumventing the limitation of the rising adsorbate concentration associated with Freundlich isotherm model. At high adsorbate concentration, it predicts monolayer adsorption characteristics of Langmuir, while in low adsorbate concentration, it reduces to Freundlich isotherm. The Sips model expressed as (Sips 1948):

$$ q_{\text{e}} = \frac{{Q_{\text{m}} \left( {k_{\text{s}} C_{\text{e}} } \right)^{{m_{\text{s}} }} }}{{1 + \left( {k_{\text{s}} C_{\text{e}} } \right)^{{m_{\text{s}} }} }} , $$
(9)

where k s is Sips isotherm model constant and m s is Sip’s isotherm model exponent.

Vieth–Sladek isotherm

The Vieth–Sladek isotherm is given by the following equation (Vieth and Sladek 1965)

$$ q_{\text{e}} = K_{\text{vs}} C_{\text{e }} + \frac{{Q_{\text{m}} B_{\text{vs}} C_{\text{e}} }}{{1 + B_{\text{vs}} C_{\text{e}} }} , $$
(10)

where q e is the adsorbed amount at equilibrium (mg/g); C e is the adsorbate equilibrium concentration (mg/L); Q m is maximum adsorption capacity, K vs and B vs are Vieth–Sladek constants. The Vieth–Sladek isotherm is used for estimating diffusion rates in solid materials from transient adsorption.

Brouers–Sotolongo isotherm

The Brouers–Sotolongo (Brouers et al. 2005) model is expressed as:

$$ q_{\text{e}} = Q_{\text{m}} \left( {1 - \exp \left( { - K_{\text{BS}} \left( {C_{\text{e}} } \right)^{{\alpha_{\text{BS}} }} } \right)} \right), $$
(11)

where k BS and α BS are Brouers–Sotolongo constant. The exponent is a measure of the width of the adsorption energy distribution and energy heterogeneity of the sorbent surface.

Radke–Prausnitz isotherm

The Radke–Prausnitz model (Radke and Prausnitz 1972) isotherm can be represented as:

$$ q_{\text{e}} = \frac{{k_{\text{RP}} Q_{\text{m}} C_{\text{e}} }}{{(1 + k_{\text{RP}} C_{{{\text{e}})}}^{{m_{\text{RP}} }} }} $$
(12)

where q e is the adsorbed amount at equilibrium (mg/g), q mRP is the Radke–Prausnitz maximum adsorption capacity (mg/g), C e is the adsorbate equilibrium concentration (mg/L), K RP is the Radke–Prausnitz equilibrium constant and m RP is the Radke–Prausnitz model exponent. Radke–Prausnitz model will be converted to another model under certain condition. At low concentration, if the value of exponent’s m RP is equal to unity, the model of Radke–Prausnitz is reduced to the Langmuir model. While, if liquid-phase concentration is high, the model of Radke–Prausnitz is converted to the Freundlich.

Batch kinetic studies

This procedure is similar to that of batch equilibrium studies. The difference is that the absorbent–absorbate solution was taken at preset time intervals and the concentration of the solution was measured. The amount adsorbed at time t, q t (mg/g), was calculated using Eq. 13

$$ q_{t} = \frac{{\left( {C_{0} - C _{t} } \right)V}}{W}, $$
(13)

where C o and C t (mg/L) are the liquid-phase concentrations of adsorbate at initial and at any time t, respectively. V is the volume of the solution and W is the mass of adsorbent used. The adsorption kinetics of dye on adsorbent was investigated using pseudo-first-order model, pseudo-second-order model, Avrami, and Elovich models, respectively.

Pseudo-first-order kinetic model

The pseudo-first-order kinetic model equation is generally expressed as follows (Lagergren 1898):

$$ \ln \left( {q_{\text{e}} - q_{t} } \right) = { \ln }\;q_{\text{e}} - k_{1} t, $$
(14)

where q e is the amount of adsorbate adsorbed at equilibrium, (mg/g), q t is the amount of solute adsorb per unit weight of adsorbent at time t, (mg/g), k 1 is the rate constant of pseudo-first-order adsorption (1/h). A plot of ln (q e − q t ) versus t gives a straight line with slope of k 1 and intercept of ln q e.

Pseudo-second-order kinetic model

The pseudo-second-order equation can be expressed as (Ho and McKay 1999):

$$ \frac{t}{{q_{t} }} = \frac{1}{{k_{2} q_{\text{e}}^{2} }} + \frac{1}{{q_{\text{e}} }}t $$
(15)

The constant k 2 is used to calculate the initial adsorption rate, h, at t = 0, as follows:

$$ h \, = \, k_{2} q_{\text{e}}^{2} $$
(15a)

Thus the rate constant k 2, initial adsorption rate h and predicted q e can be calculated. The linear plot of t/q e versus t gives 1/q e as the slope and 1/k 2 q 2e as the intercept.

Elovich kinetic model

The simplified Elovich equation expressed as (Aharoni and Unganish 1976):

$$ q_{t} = \frac{1}{\beta }\ln \left( {\alpha \beta } \right) + \frac{1}{\beta }\ln t, $$
(16)

where α is the initial desorption rate [mg/(g min)] and β is the desorption constant (g/mg) during any experiments. Plot of q t versus ln t gave a linear relationship with slope of 1/β and an intercept of (1/β) ln (αβ). The 1/β value reflects the number of sites available for adsorption whereas the value of 1/β ln (αβ) indicates the adsorption quantity when ln t equal to zero.

Avrami kinetic model

The Avrami equation is used to verify specific changes of kinetic parameters as functions of the temperature and reaction time. It is also an adaptation of kinetic thermal decomposition modeling (Avrami 1940).

The Avrami kinetic model is expressed as:

$$ q_{t} = q_{\text{e}} \left\{ {1 - \exp \left[ { - \left( {K_{\text{AV}} t} \right)} \right]^{{n_{\text{AV}} }} } \right\}, $$
(17)

where q t is the adsorption fraction at time t, k Av is the adjusted kinetic constant, and n Av is another constant, which is related to the adsorption mechanism. n value can be used to verify possible interactions of the adsorption mechanisms in relation to the contact time and the temperature.

Validity of kinetic model

The applicability and fitting of the isotherm equation to the kinetic data was compared by judging from the R 2 values and the normalized standard deviation Δq (%) calculated from Eq. 18. The normalized standard deviation, ∆q (%) was used to verify the kinetics model used to describe the adsorption process. It is expressed as:

$$ \Updelta q = 100\,{\frac{{\sqrt {\sum [(q_{\exp } - q_{\text{cal}} )/q_{\exp } ]^{2}} }}{n - 1}} , $$
(18)

where n is the number of data points, q exp and q cal (mg/g) are the experimental and calculated adsorption capacity values. Lower value of ∆q indicates good fit between experimental and calculated data.

Adsorption thermodynamics

The experimental data obtained from batch adsorption studies performed earlier were analyzed using the thermodynamic equations as expressed by Eqs. 19a and 19b.

$$ \Updelta G = - RT\;\ln K_{\text{L}} $$
(19a)
$$ \ln K = \frac{\Updelta S}{R} - \frac{\Updelta H}{RT} $$
(19b)

ΔG was calculated using Eq. 19a. The values of ΔH and ΔS can be obtained, respectively, from the slope and intercept of Van’t Hoff plot of ln K L versus 1/T (Eq. 19b). Values of K L may be calculated from the relation ln q e/C e at different solution temperatures of 30, 45 and 60 °C, respectively. Arrhenius equation has been applied to evaluate the activation energy of adsorption representing the minimum energy that reactants must have for the reaction to proceed, as shown by following relationship:

$$ \ln k_{2} = \ln A - \frac{{E_{\text{a}} }}{RT}, $$
(19c)

where k 2 is the rate constant obtained from the pseudo-second-order kinetic model, (g/mg h), E a is the Arrhenius activation energy of adsorption, (kJ/mol), A is the Arrhenius factor, R is the universal gas constant (8.314 J/mol K) and T is the absolute temperature. When ln k 2 is plotted against 1/T, a straight line with slope of −E a /R is obtained.

Adsorption mechanism

The adsorption mechanisms of MR dye on the adsorbent were investigated using intraparticle diffusion and Boyd models represented by Eqs. 20 and 21 respectively. The applicability and fitting of the model throws more light into the mechanism of MR dye adsorption onto DSAC prepared.

Intraparticle diffusion model

Intraparticle diffusion model (Weber and Morris 1962) is expressed as shown in Eq. 20

$$ q_{t} = k_{\text{pi}} t^{\frac{1}{2}} + C_{\text{i}} , $$
(20)

where C i is the intercept and k pi (mg/g h1/2) is the intraparticle diffusion rate constant, which can be evaluated from the slope of the linear plot of q t versus t 1/2. The q t is the amount of solute adsorb per unit weight of adsorbent per time, (mg/g), and t 1/2 is the half-adsorption time, (g/h mg). The intercept of the plot reflects the boundary layer effect. The larger the intercept, the greater the contribution of the surface adsorption in the rate-controlling step. If the regression of q t versus t 1/2 is linear, and passes through the origin, then intraparticle diffusion is the sole rate-limiting step. If the linear plots at each concentration did not pass through the origin, it indicates that the intraparticle diffusion was not only rate-controlling step (Wu et al. 2005).

Boyd model

To identify the slowest step in the adsorption process, Boyd kinetic equation (Boyd et al. 1947) was applied, it is expressed as:

$$ F = 1 - \frac{6}{{\pi^{2} }}{\text{e}}^{{B_{t} }} $$
(21)
$$ F = \frac{{q_{t} }}{{q_{e} }} $$
(21a)

where q t is the amount of the adsorbate adsorbed at time t (mg/g), F is the fraction of adsorbate adsorbed at time t and B t is the mathematical function of F. Equation 21 can be rearranged by taking the natural logarithm to obtain the following equation:

$$ B_{t} = \, - 0.4977{-}\ln \left( {1 \, {-}F} \right). $$
(21b)

Results and discussions

Characterization of prepared adsorbent

Surface area and pore characteristics

The Brunauer, Emmett and Teller (BET) surface area, mesopore surface area, total pore volume and average pore diameter of DSAC are shown in Table 2. The surface area of DSAC was 980.62 m2/g with high pore volume of 0.528 cm3/g. The average pore diameter is 3.40 nm. According to IUPAC classification (IUPAC 1972), DSAC belongs to the mesopore region which has significant mesopores suitable for MR dye adsorption. A similar result was obtained in the removal of MG dye using Cocos nucifera shell-based activated carbon (Bello and Ahmad 2012)

Table 2 Surface area and pore characteristics of different precursors from durian seed
Full size table

The surface area of DSAC prepared was comparable with other AC obtained from the literature. The physiochemical activation process had contributed to the high surface area and total pore volume of the prepared DSAC. The DSAC expansion porosity is associated with gasification reaction (Basta et al. 2009). The diffusion of carbon–KOH and CO2 molecules into the pore promotes reactions which developed more pores in the DSAC. The KOH melts and its oxide component reacts with carbon dioxide, which assist to the enhancement of the surface area of the samples. This result was in agreement with the findings of (Ahmad and Alrozi 2011) which reported the BET surface area, total pore volume and average pore diameter of the rambutan peel based AC as 908.35 m2/g, 0.52 cm3/g and 2.63 nm, respectively, thus confirming that the combination of both chemical and physical activating agents of KOH and CO2 promotes the formation of mesopores and enhance the surface area of DSAC.

Proximate analysis

The precursors were found to be rich in moisture and volatile matter. However, the moisture and volatile content were found to decrease significantly from precursor to activated carbon. During carbonization and activation processes, organic substances become unstable as a result of the heat causing the molecules to break their bonds and linkages. During activation step, the volatile matter is released as gas and liquid products evaporates off leaving the material with high carbon content (Ahmad and Alrozi 2010). Proximate analysis clearly indicates that the physiochemical activation has successfully increased the fixed carbon content and decreased the volatile matter (Table 3).

Table 3 Proximate analysis of the precursor, char and activated samples
Full size table

Surface chemistry

Table 4 shows the assignment of absorption bands for FTIR spectrum of DSAC (Fig. 1). The spectrum of the samples shows the presence of the several functional groups. These spectra revealed either a reduction, disappearance or broadening of the peaks after the process of impregnation.

Table 4 FTIR spectrum band assignment for DS, DS char and DSAC
Full size table
Fig. 1
figure 1figure 1

FTIR spectrums; a DS; b DS char; c DSAC (before); d DSAC (after)

Full size image

The long bandwidth around 3,601–3,861 cm−1 indicated that the main functional groups found on DS were O–H stretching vibration of hydroxyl functional groups including hydrogen bonding. Other major peaks detected at bandwidths of 2,399–2,102, 1,732–1,901, 1,635 and 1,361 cm−1 were respectively attributed to C≡C stretching of alkyne group, vibration of carboxylic C=O stretching of lactones, ketones, and carboxylic anhydrides, C=C of aromatic ring and C–H stretching in alkanes or alkyl group. The disappearance of ether and phenol in the DSAC samples shows that these functional groups are thermally unstable. DS exhibits the peaks at band position 1,635 cm−1, which was assigned to aromatic group but disappeared in DS char and DSAC. Aromatic group disappeared due to oxidative degradation of aromatic rings during chemical impregnation and heating stage. The medium peaks around 1,014 and 867–590 cm−1 found on the spectrums were due to the presence of C–O groups stretching in ester, ether or phenol group and C–H out-of-plane bending in benzene derivatives, respectively. A similar result was obtained in the preparation of activated carbon from cherry stones by chemical activation with ZnCl2 (Olivares et al. 2006). The spectrum after adsorption shows that most of the functional groups were involved in the adsorption process; a greater number of them disappeared after adsorption (Fig. 1d).

Surface morphology

The surface morphology of DS and DSAC are shown in Fig. 2. The surface structures of both precursors were rough and uneven. DSAC has several pores due to the modification using activating agent. A significant pore structure exists with a series of rough cavities distributed over the surface of DSAC. This was due to the breakdown of the lignocellulosic material at high temperature followed by evaporation of volatile compounds leaving samples with well-developed pores. During activation process, the C–KOH reaction rate was increased, thus resulting in carbon ‘burn off’ thereby developing good pores on the sample. The C–KOH reaction also increased the porosity of DSAC as well as creating new pores due to loss of volatile components, carbon in the form of CO and CO2 (Auta and Hameed 2011). The physiochemical treatment was able to produce porous adsorbent thus increasing the surface area. Kilic et al. (2011) found out that the KOH assists in widening the porosity of tobacco residue AC. The tobacco residue was found to have very little porosity, whereas the surface structure of TRAC was full of cavities. Physiochemical activation produces porous adsorbent resulting in increased uptake in the adsorption of MR dye.

Fig. 2
figure 2

SEM micrographs of a DS (×2,000); b DSAC (×2,000)

Full size image

Batch adsorption studies

The effect of initial MR dye concentration and contact time

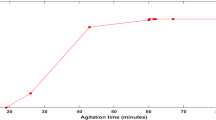
Figure 3 shows the effect of contact time and initial MR dye concentrations (25–500 mg/L) on the amount of MR dye adsorbed per gram of DSAC. From Fig. 3, it was observed that the amount of dye uptake is increased with increasing contact time at all initial dye concentrations. Furthermore, the amount of dye adsorbed is increased with the increase in initial dye concentration. For the first 6 h, the adsorption uptake was rapid then it proceeds at a slower adsorption rate and finally it attains saturation at 22 h. These observations show that the initial dye concentration has no effect on the required time for equilibrium. Thus, up to 70–80 % of the total amount of dye uptake was found to occur in the first stage. The higher adsorption rate at the initial period may be due the availability of vacant sites at the initial stage that is because of the increase in the concentration gradients between adsorbate in solution and adsorbate on the adsorbent surface. As time proceeds, the dye concentration is reduced due to the accumulation of dye particles in the vacant sites, leading to a decrease in the adsorption rate at later stages (Vadivelan and Kumar 2005). A similar result was obtained in the adsorption of MB dye using periwinkle shells (Bello et al. 2008). The curves were single, smooth and continuous, indicating monolayer coverage of dye on the surface of adsorbent (Namasivayam et al. 1993).

Fig. 3
figure 3

MR dye adsorption uptakes on DSAC versus adsorption time at various initial concentrations at 30 °C

Full size image

Effect of solution temperature on MR dye adsorption

The adsorption of MR dye on DSAC was investigated as a function of temperature and maximum dye removal was obtained at 60 °C. Experiments were performed at different temperatures (30–60 °C) for initial MR dye concentrations of 25–500 mg/L. The amount of MR dye adsorbed increased from 21.26 to 313.47 mg/g (30 °C), 22.72–326.35 mg/g (45 °C) and 23.88–350.27 mg/g (60 °C) for the initial MR dye concentrations of 25-500 mg/L, respectively, with the rise in temperature from 30 to 60 °C (Fig. 4). This is mainly due to the increased surface activity suggesting that adsorption between MR dye and DSAC was an endothermic process. Similar result was obtained in the adsorption of eosin dye using groundnut hull-based activated carbon (Bello et al. 2012).

Fig. 4
figure 4

Effect of solution temperature on MR dye adsorption onto DSAC

Full size image

Effect of pH on MR dye adsorption

The pH value of aqueous solution may affect the surface charge of the adsorbent and the functional groups on the adsorbate. The effect of pH on adsorption of MR dye was studied in pH range 2.0–12.0, this is shown in Fig. 5. From Fig. 5, a higher percentage removal was observed at pH range 2–6 (89–92 %). There was a gradual drop in percentage removal from pH 6 to 7 (92–90 %). Above pH 7, there was a sharp reduction in the percentage of MR dye adsorbed (90–30 %). This trend can be attributed to the electrostatic attraction between the negatively charged dye and the positively charged surface of the adsorbent at pH 2–6. Increase in solution pH increases the number of hydroxyl groups, thus, decreases the number of positively charged sites and reduces the attraction between MR dye and the adsorbent surface. Thus, as pH is increased, the surface functional groups of the adsorbent deprotonates which results in a decrease in surface charge density and is unable to exert any electrostatic effect toward anionic species (Saad et al. 2007). Similar result was obtained in the adsorption of anionic dyes on ammonium-functionalized MCM-41 (Qin et al. 2009).

Fig. 5
figure 5

Effect of initial pH on MR dye removal

Full size image

Adsorption isotherms

Equilibrium relationship between the amounts of MR dye adsorbed on the surface of DSAC could be established through adsorption isotherms (Bulut et al. 2008). Eight different isotherms: Langmuir, Freundlich, Temkin, Dubinin–Radushkevich, Sips, Vieth–Sladek, Brouers–Sotolongo and Radke–Prausnitz models were chosen to fit the experimental equilibrium data. Figure 6 shows the plots of the linearized equation isotherm parameters for MR dye removal at 30 °C. Similar plots were obtained for the adsorption systems at 45 and 60 °C, respectively (figure not shown). The values of the maximum amount adsorbed (Q m), correlation coefficient (R 2), and the other parameters for all the isotherms are shown in Table 5. For the Langmuir isotherm, the Q m value of 384.62 mg/g was obtained and the value of R 2 of 0.948 shows good fitting of this isotherm to the experimental data (Table 5). The separation factor (R L), an important parameter of the Langmuir isotherm, was 0.317 (average of six concentrations) indicates favorable adsorption of DSAC-MR system. The decrease in R L with an increase in the initial concentration indicates that the adsorption is more favorable at high concentrations (figure not shown). For the Freundlich isotherm, the values of n F = 1.32 and 1/n F = 0.756 indicate that both the physical process and the normal Langmuir isotherm are favorable. The fitting of the Freundlich isotherm to the experimental data is (R 2 = 0.999). For the Temkin isotherm, the constant B is related to the heat of adsorption, and the positive value found (B = 58.031) indicates an endothermic process. The fit to experimental data (R 2 = 0.9147).

Fig. 6
figure 6

Plots of a Langmuir, b Freundlich, c Temkin, d Dubinin–Radushkevich, e Radke–Prausnitz, f Sips, g Vieth–Sladek, h Brouers–Sotolongo isotherms for MR dye adsorption on DSAC

Full size image
Table 5 Isotherm values for the adsorption of MR dye onto DSAC at 30 °C
Full size table

The Sips isotherm is a combination of the Langmuir and Freundlich isotherms. The value of Q m = 372.46 mg/g found for the Sips isotherm is almost the same as value of Q m for Langmuir isotherm. Similarly, the Vieth–Sladek isotherm showed a Q m equal to 349.99 mg/g, which was the lowest value among the isotherms that allow calculating this parameter. The fit of the Sips isotherm (R 2 = 0.988), the Vieth–Sladek isotherm (R 2 = 0.959). The Brouers–Sotolongo isotherm shows a Q m value (401.65 mg/g) higher than that of Langmuir isotherm value. On the other hand, the Q m value equal to 443.96 mg/g found for the Radke–Prausnitz isotherm was the highest in all. The fits of the Radke–Prausnitz (R 2 = 0.971), Brouers–Sotolongo (R 2 = 0.949), and the D–R (R 2 = 0.836) isotherms to the experimental data are shown in Table 5. From the analysis of all the isotherms and the knowledge of the most important parameters (Q m and R 2), the isotherms can be arranged according to their capacity to predict their efficiency in predicting the experimental behavior of the DSAC-MR system. With respect to Q m (in descending order): Radke–Prausnitz > Brouers–Sotolongo Langmuir > Sips > Vieth–Sladek. With respect to R 2 (in descending order): Freundlich > Sips > Radke–Prausnitz > Vieth–Sladek > Brouers–Sotolongo > Langmuir > Tempkin > Dubinin–Radushkevich. The normalized standard deviation (∆q) measures the differences in the amount of dye taken up by the adsorbent predicted by the models and the one determined experimentally. According to Table 5, the (∆q) values of isotherm models ranged from 3.544 to 15.215. The Freundlich model presented the lowest ∆q, and the highest R 2 value. Therefore, considering the highest R 2 values and the lowest ∆q value, the Freundlich model is the most appropriate for the adsorption of the MR dye onto DSAC. The value of E obtained in D–R isotherm was found to be 5.00 kJ/mol (Table 5). Since E < 8 kJ/mol, it suggests that the adsorption mechanism is physical in nature (Helfferich 1962).

Kinetic modeling

Kinetic studies are carried out to understand the mechanism of adsorption process. The adsorbate molecules undergo different stages, while moving from bulk solution to the adsorbent surface such as migration of adsorbate molecules to the external surface of adsorbent particles, molecular and pore diffusion (Mane and Babu 2011). Adsorbate may face either single or combinations of these steps depending on several factors (Safa and Bhatti 2011; Mane and Babu 2011). Four kinetic models are applied to understand the adsorption mechanism. From the plots in Fig. 7, the pseudo-second-order kinetic models fit the data best when compared to the other kinetic models. The experimental data reported in Table 6 showed that the MR dye adsorption is in good agreement with the pseudo-second-order kinetic model having the highest R 2 value and lowest value of ∆q.

Fig. 7
figure 7

Linerized plots of a pseudo-first-order, b pseudo-second-order, c Avrami and d Elovich kinetic model for MR dye adsorption on DSAC at 30 °C

Full size image
Table 6 Kinetic model constant values for MR dye adsorption unto DSAC at 30 °C
Full size table

Adsorption thermodynamics

Thermodynamic parameters such as Gibbs free energy change (∆G), enthalpy change (∆H) and entropy change (∆S) are among the most important features involved in an adsorption system. The values of Gibbs free energy change (∆G), enthalpy change (∆H) and entropy change (∆S) were computed using Eqs. 19a and 19b, respectively. The positive values of ∆S (22.84 J/mol K) revealed the affinity of DSAC for the adsorbate being tested and increased randomness at the solid–solution interface during adsorption of MR dye onto the active sites of DSAC. The negative ∆G obtained for the adsorption of MR dye onto DSAC dictates spontaneous nature and feasibility of the adsorption process with high preference of MR dye onto DSAC (Table 7). The E a, i.e., the mean heat of adsorption value obtained is <8 kJ/mol. It is further confirming that the reaction follows a physisorption mechanism (Bello and Ahmad 2011).

Table 7 Thermodynamic parameters for the adsorption of MR dye onto DSAC at different temperatures
Full size table

Adsorption mechanisms

Adsorption rate is known to be controlled by several factors including (1) diffusion of the solute from the solution to the film surrounding the particle, (2) diffusion from the film to the particle surface (external diffusion), (3) diffusion from the surface to the internal sites (surface diffusion or pore diffusion) and (4) uptake which can involve several mechanisms such as physicochemical adsorption, ion exchange, precipitation or complexation (Gercel et al. 2007; Wu et al. 2001). Adsorption kinetics are usually controlled by different mechanisms, of which the most limiting ones are the diffusion mechanisms, including the initial curved portion, which is attributed to rapid external diffusion or boundary layer diffusion and surface adsorption, and the linear portion, i.e., a gradual adsorption stage due to intra-particle diffusion, followed by a plateau to equilibrium where the intra-particle diffusion starts to decrease due to the low concentration in solution as well as fewer available adsorption sites (Venkata et al. 2002). In the present study, non-linear plots were obtained, the first one is bulk diffusion, the second is external mass transfer resistance and the third is intra-particle mass transfer resistance. Mass transfer is governed by several relationships, taking into account the diffusion mechanisms and their related equations, the coupling between liquid and solid phases and the initial and boundary conditions. Therefore, it means that the rate of attainment to equilibrium may be particle-diffusion controlled (Yang and Al-Duri 2005). The rapid adsorption occurred within first 140 min. This is attributed to external surface adsorption, in which the adsorbate diffuses through the bulk solution to the external surface of the adsorbent or the boundary layer diffusion of MR dye molecules. Following the fast adsorption, there was a gradual adsorption stage, where intraparticle diffusion rate is rate controlling. Thereafter, adsorption became very slow and stable, approaching an equilibrium stage and maximum adsorption, i.e., a plateau profile. Similar findings were reported by Vimonses and coworkers, who studied the intra-particle diffusion mechanisms of three natural kaolin clays (Vimonses et al. 2009). The three stages can be determined by the intra-particle diffusion rate as referred to k p. The increase in q t versus t 1/2 profiles of MR dye adsorption by DSAC adsorbents was non-linear (Fig. 8). Such deviation from the origin shows that intra-particle transport is not the only rate-limiting step. It can be seen, however, that the second adsorption stage is characterized as the intra-particle diffusion, which is the rate-controlling step for the adsorption process of the modified DSAC. The plots did not pass through the origin, i.e., C ≠ 0. This further indicates that the intra-particle diffusion was involved in the adsorption process, but was not the only rate-controlling step. The extrapolation of the linear straight lines gives the intercepts C, which are proportional to the boundary layer thickness. The extent of thickness of boundary layer can be examined from the C value. The larger the C value is, the greater the effect of boundary layer can be (Özcan et al. 2005). The boundary layer also gives an insight into the tendency of the adsorbent to adsorb the dye or remain in solution. Since diffusion takes place, the boundary layer is looked upon as a viscous drag existing between the DSAC surface and the MR dye solution diffusing across its surface. Therefore, higher values of C, i.e., the boundary layer thickness, depict higher adsorption capacities (Table 8).

Fig. 8
figure 8

Plots of intraparticle diffusion model for MR dye adsorption on DSAC

Full size image
Table 8 Intraparticle diffusion model constants for adsorption of MR dye onto DSAC
Full size table

To further determine the actual rate-controlling step of the adsorption, the experimental data were analyzed using the expression given by Boyd et al. (1947), which can be calculated by the fraction of amount of MR dye adsorbed on DSAC. As shown in Fig. 9, plots B t versus t display linear profiles, but do not pass through the origin. These results further indicate that the external transport mainly controls the rate-limiting process of MR dye adsorption on the modified DSAC.

Fig. 9
figure 9

Boyd plots for adsorption of MR dye on DSAC at 30 °C

Full size image

Conclusion

This study revealed the potential of durian seed as an efficient precursor for the preparation of activated carbon. The well-developed porous structure, with the BET surface area and total pore volume of 980.62 m2/g and 0.528 cm3/g, respectively, enhances the adsorption process. Equilibrium studies showed that Freundlich isotherm model fit the adsorption data most, signifying that the MR dye adsorption does not form a monolayer on DSAC, it rather follows multilayer adsorption process. The pseudo-second-order kinetic model exhibited the best correlation for the experimental data. The mechanism of adsorption is controlled by both intra particle and film diffusion models. Thermodynamic parameters, i.e., the negative values of Gibbs energy and the positive value of enthalpy, indicated that the adsorption process is spontaneous and endothermic in nature.