Introduction

Soil moisture plays a key role in various hydrological, environmental and agricultural applications. It governs infiltration and surface runoff, since the hydraulic conductivity of soil depends upon the available water content in the soil. It also influences the plant evapotranspiration thereby making it an important component of water balance equation. Knowledge of spatial distribution of soil moisture is essential for predicting runoff at the catchment scale (Fitzjohn et al. 1998; Western et al. 1999, 2001) and in the design of irrigation scheduling (Blonquist et al. 2006; Vellidis et al. 2008). For optimum irrigation practices, it becomes essential to accurately estimate the soil moisture. Moreover, to model overland flow from a precipitation event over a catchment, the estimation of antecedent soil moisture is a prerequisite.

Various studies (Oevelen 1998; Feng et al. 2004; De Lannoy et al. 2006) have shown that hydrometeorological conditions, soil properties and land cover govern the presence of moisture in the unsaturated zone of soil. These studies (Anderson and Burt 1977, 1978; Beven and Kirkby 1979; Chorley 1980; Moore et al. 1988; Wood et al. 1990; 1993; Bárdossy and Lehmann 1998) have shown that soil moisture is highly variable both in space and time. The characteristics of spatial variability of soil moisture depend on the scale of observation (Lakhankar et al. 2010).

For estimation of soil moisture at catchment level using observed point observations of soil moisture data, various interpolation methods such as weighted average, inverse distance interpolation, spline interpolation and kriging can be employed (Bárdossy and Lehmann 1998; Thattai and Islam 2000). For the estimation of soil moisture at spatial scale using observed point observations of soil moisture data, various interpolation techniques such as weighted average, inverse distance interpolation, spline interpolation and kriging can be employed. Dynamic multiple linear regression technique was adopted by Wilson et al. (2005) to compute soil moisture using topographic attributes. Downer and Ogden (2003) estimated soil moisture using gridded surface subsurface hydrologic analysis (GSSHA) hydrologic model with a root mean square error of 0.1. Pandey and Pandey (2010) mapped soil moisture in Udaipur, India, applying ordinary kriging. The study concluded that the krigged values were consistent and true representative of soil moisture values. Said et al. (2008) have experimented with ANN method to estimate soil moisture in the Solani River catchment. However, application of geostatistical interpolation technique is new in the study area.

The aim of this paper is to evaluate the efficacy of geostatistical interpolation techniques and to estimate soil moisture at spatial level from the in situ observed soil moisture data at point locations. The selection of an estimation technique may be site specific. Therefore, an evaluation of the techniques may be necessary to identify the appropriate one to be adopted in the prediction model. In the present study, two interpolation techniques, namely, moving average and ordinary kriging, have been evaluated to estimate the soil moisture at spatial scale.

Study area

The study area is a part of the Solani River catchment in the vicinity of Haridwar district in Uttarakhand State of India. The area lies between 77.48°E, 29.45°N and 78.03°E, 29.55°N at an average elevation of 268 m above mean sea level. Location map of the study area is shown in Fig. 1. Average annual rainfall of the region is 1,170 mm and the temperature varies approximately from 1 °C in winter to 45 °C in the summer. Texture of soil influences the infiltration, surface runoff, evapotranspiration, interflow, and aquifer recharge. Study by Kumar et al. (2012) indicates that the type of soil in the catchment area is loam (US Bureau of Soil and PRA Classification) with an average proportion of 50–55 % of sand, 35–42 % silt and 8–15 % clay. Solani River is a seasonal tributary of the Ganges River. Besides Solani River, a few seasonal streams, Ratmau, and Pathri Rao, originating from Shivalik hills (lower Himalayan mountain range) play a significant role in enriching the land fertility in the study area. The study area constitutes three major land cover classes: built-up land, bare soil and vegetated land. A significant portion of the vegetated land is agricultural with perennial and seasonal crops. Sugarcane is the perennial crop in the area. The summer (period from June to September) crops are paddy, maize and cherry whereas the winter (period from October to March) crops are wheat, mustard and fodder crop berseem.

Fig. 1
figure 1

Location map of study area

Full size image

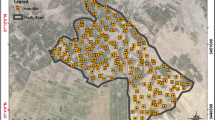
Field observations were collected during 10–12 Dec 2009 at 69 sample locations in the study area covering about 154 km2. The geographical coordinates of the sample points were recorded with the help of hand held global positioning system (GPS). Of the measured 69 locations, 52 samples were collected from the vegetated land covered with wheat, sugar cane, mustard and berseem crop. The wheat was in early growing stage, whereas the rest of the crops were at matured level. The remaining 17 locations correspond to bare soil fields. Out of 69 locations, 49 locations were considered for the model development whereas remaining 20 locations were kept for model validation. A due representation for vegetated and bare soil samples has been given in model development and its validation. Figure 2 depicts the geographical representation of the soil sampled locations.

Fig. 2
figure 2

Geographical representation of soil sampled locations

Full size image

The undisturbed soil samples were collected with the help of piston sampler from both bare soil and vegetated surfaces from the upper 0–10 cm thick soil layer. The samples were weighed and then oven-dried at 105 °C for 24 h to compute the volumetric soil moisture content. The observed volumetric soil moisture in the area varied from a minimum 3 % to a maximum of 43 %.

Methodology

A number of interpolation techniques have been used for the analysis of distribution of the soil moisture at spatial scale (Feng et al. 2004; Wilson et al. 2005; Lakhankar et al. 2010). The most common interpolation techniques are moving average, trend surface and kriging (Kratze et al. 2006). The applicability of these techniques depends upon various factors such as distribution of sampled data in the space, the type of surfaces to be generated and tolerance of estimation errors. Hence, an evaluation of these geostatistical techniques may help in arriving at the most appropriate technique for estimation of soil moisture estimation at spatial level in Indian conditions. In the present study, the performance of moving average and kriging geostatistical techniques has been evaluated in estimating soil moisture distribution in a part of Solani River catchment.

Moving average technique

In the present context, moving average operates upon computing weight factor for each observed soil moisture at a sample location considered within a limiting distance, also called as the search radius to estimate soil moisture. The locations lying beyond the specified search radius are not taken into account for the estimation. For each location within the search radius, the distances of all observed soil moisture locations are calculated to determine weight factors. The sampled locations are weighted during interpolation such that the influence of one location relative to the other declines with distance from the location at which the moisture is to be estimated. Hence, the locations closer to it will have larger weight than those obtained at locations farther from it. The soil moisture at a location may thus, be estimated as,

$$M_{\text{vc}} = \frac{{\sum\nolimits_{{i\text{ } = \text{ }1}}^{n} {W_{i} M_{\text{voi}} } }}{{\sum {W_{i} } }}$$
(1)

where n is the number of observed soil moisture locations within the search radius, \(W_{i}\) and \(M_{\text{voi}}\) are the weights assigned and the volumetric moisture content in percentage, respectively, at the ith location. The weight \(W_{i}\) for each observed soil moisture location may be computed as,

$$W_{i} = \frac{1}{{h_{\text{ri}}^{m} }} - 1$$
(2)

where \(m\) is the weight exponent, and \(h_{\text{ri}}\) is the relative distance of ith observed soil moisture location from the estimated soil moisture location. The \(h_{\text{ri}}\) is computed as,

$$h_{\text{ri}} = \frac{{h_{i} }}{{h_{l} }}$$
(3)

where \(h_{i}\) is the distance of ith observed soil moisture location from the estimated soil moisture location, and \(h_{l}\) is the search radius. The accuracy of estimation depends upon the search radius and the weight exponent. Therefore, several trials are conducted before arriving at the acceptable values for the search radius and weight exponents.

The RMSE between the observed and estimated soil moisture at validation locations is computed as,

$$\begin{gathered} {\text{RMSE = }} \sqrt { \frac{1}{p} \sum\limits_{{k\text{ } = \text{ }1}}^{p} {(M_{\text{vok}} - M_{\text{vck}} )^{2} } } \hfill \\ \hfill \\ \end{gathered}$$
(4)

where \(p\) is the number of locations considered for model validation and \(M_{\text{vo}}\), \(M_{\text{vc}}\) are the observed and estimated moisture contents at those locations respectively.

Kriging

Kriging is a geostatistical data interpolation technique based on the assumption that the data are spatially correlated. Ordinary kriging works on selected theoretical semi-variogram model used for computing semi-variance values at the points where soil moisture is to be estimated. A plot of the calculated semi-variance values against the distance (lags) is known as a semi-variogram. Increasing the lag distance of the semi-variance values consider average over more points, thus decreasing the fluctuations of the experimental semi-variogram. Several theoretical semi-variogram models are possible that include linear, spherical, circular, exponential and Gaussian (Teegavarapu and Chandramouli 2005) to fit over the experimentally constructed semi-variogram. The most suitable semi-variogram model may be found based on the RMS error between the semi-variance values obtained from experimentally observed data and the theoretical model predicted semi-variance values. Often the experimental semi-variogram values do not approach to zero at the origin and intersect the positive y-axis. This is due to the residual or spatially uncorrelated noise, which is also known as the nugget (Kitanidis 1997). The stabilized semi-variogram value is known as the sill, and the distance at which the semi-variogram values approach the sill is called the range.

The general expression to estimate the semi-variance is given as,

$$\gamma_{(h)} = \frac{1}{2n(h)}\sum\limits_{{hij\text{ } = \text{ }h}} {(M_{\text{voi}} - M_{\text{voj}} )^{2} }$$
(5)

where \(\gamma_{(h)}\) is the semi-variance defined over the observed data, \(M_{\text{voi}}\) and \(M_{\text{voj}}\) is the measured moisture at two locations lagged successively by the distance \(h\).

Spatial interpolation using kriging significantly depends on the semi-variogram model used. The appropriate semi-variogram model is usually obtained through experiments. In this study, three semi-variogram models, namely, spherical, Gaussian and exponential, stated in Eqs. (6) to (8), respectively, have been considered.

$$\gamma_{(h)} = C_{o} + C_{1} \left( {\frac{3\left| h \right|}{2a} - \frac{1}{2}\left( {\frac{\left| h \right|}{a}} \right)^{3} } \right)$$
(6)
$$\gamma_{(h)} = C_{o} + C_{1} \left( {1 - {\text{Exp}}( - )\left( \frac{h}{a} \right)^{2} } \right)$$
(7)
$$\gamma_{(h)} = C_{o} + C_{1} \left( {1 - {\text{Exp}}\left( { - \frac{h}{a}} \right)} \right)$$
(8)

The parameters, \(C_{0}\) and \(a\) denote nugget and range. The summation of \(C_{0}\) and \(C_{1}\) is referred to as sill and the sill value at range, \(a\), is the desired semi-variance.

In ordinary kriging, having obtained the most appropriate semi-variogram model, the soil moisture values \(M_{\text{vc}}\), at any location can be obtained as a weighted sum of the observed soil moisture values,

$$M_{\text{vc}} = W_{1} M_{\text{vo1}} + W_{2} M_{\text{vo2}} + W_{3} M_{\text{vo3}} + \ldots \ldots \ldots W_{n} M_{{{\text{vo}}n}}$$
(9)
$$M_{\text{vc}} \text{ } = \text{ }\sum\limits_{{i\text{ } = \text{ }1}}^{n} {W_{i} M_{\text{voi}} }$$
(10)

where \(W_{i}\) and \(M_{\text{voi}}\) are the weight and observed soil moisture at the ith location, and n is the number of locations within the limiting distance. The \(W_{i}\) are computed by solving the following equations,

$$\begin{gathered} W_{1} \gamma_{(h11)} + W_{2} \gamma_{(h12)} + W_{3} \gamma_{(h13)} + \ldots \ldots \ldots \ldots \ldots W_{n} \gamma_{(h1n)} = \gamma_{(hp1)} \infty \hfill \\ W_{1} \gamma_{(h21)} + W_{2} \gamma_{(h22)} + W_{3} \gamma_{(h23)} + \ldots \ldots \ldots \ldots \ldots W_{n} \gamma_{(h2n)} = \gamma_{(hp2)} \hfill \\ W_{1} \gamma_{(h31)} + W_{2} \gamma_{(h32)} + W_{3} \gamma_{(h33)} + \ldots \ldots \ldots \ldots \ldots W_{n} \gamma_{(h3n)} = \gamma_{(hp3)} \hfill \\ \ldots \ldots \ldots \ldots + \ldots \ldots \ldots \ldots + \ldots \ldots \ldots \ldots + \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots = \ldots \ldots \hfill \\ W_{1} \gamma_{(hn1)} + W_{2} \gamma_{(hn2)} + W_{3} \gamma_{(hn3)} + \ldots \ldots \ldots \ldots \ldots W_{n} \gamma_{(hnn)} = \gamma_{(hpn)} \hfill \\ \end{gathered}$$
(11)

and

$$\sum\limits_{i} {W_{i} } \text{ } = \text{ }1$$
(12)

The matrix form of Eqs. (11) and (12) is given as,

$$\left[ {\begin{array}{*{20}c} 0 & {\gamma_{(h12)} } & {\gamma_{(h13)} } & { \ldots \ldots \ldots } & {\gamma_{(h1n)} } \\ {\gamma_{(h21)} } & 0 & {\gamma_{(h23)} } & { \ldots \ldots \ldots } & {\gamma_{(h2n)} } \\ {\gamma_{(h31)} } & {\gamma_{(h32)} } & 0 & { \ldots \ldots \ldots } & {\gamma_{(h3n)} } \\ { \ldots \ldots \ldots } & { \ldots \ldots \ldots } & { \ldots \ldots \ldots } & { \ldots \ldots \ldots } & { \ldots \ldots \ldots } \\ \begin{gathered} \gamma_{(hn1)} \hfill \\ 1 \hfill \\ \end{gathered} & \begin{gathered} \gamma_{(hn2)} \hfill \\ 1 \hfill \\ \end{gathered} & \begin{gathered} \gamma_{(hn3)} \hfill \\ 1 \hfill \\ \end{gathered} & \begin{gathered} \ldots \ldots \ldots \hfill \\ 1 \hfill \\ \end{gathered} & \begin{gathered} 0 \hfill \\ 1 \hfill \\ \end{gathered} \\ \end{array} \begin{array}{*{20}c} 1 \\ 1 \\ 1 \\ { \ldots \ldots \ldots } \\ \begin{gathered} 1 \hfill \\ 0 \hfill \\ \end{gathered} \\ \end{array} } \right].\left[ {\begin{array}{*{20}c} {W_{1} } \\ {W_{2} } \\ {W_{3} } \\ \ldots \\ {W_{n} } \\ \lambda \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\gamma_{(hp1)} } \\ {\gamma_{(hp2)} } \\ {\gamma_{(hp3)} } \\ \ldots \\ {\gamma_{(hpn)} } \\ 1 \\ \end{array} } \right]$$
(13)

Where \(_{hpi}\) is the distance between the location p where soil moisture is to be estimated, and the location \(i\) where soil moisture is observed. \(\gamma_{(hik)}\) is semi-variance value for the distance between the locations i and k and \(W_{i}\) is the weight for point \(i\). \(\lambda\) is a Lagrange multiplier that is used to minimize the possible estimation error in kriging interpolation.

The limiting distance governs the selection of observed locations around a location considered to estimate the soil moisture. The limiting distance is usually taken as smaller than the range of the selected semi-variogram. Observed locations that lie beyond specified limiting distance are not considered in the interpolation of soil moisture.

Results and discussion

In this paper, an evaluation of soil moisture predicted by two geostatistical techniques, moving average and kriging, was carried out. The success of moving average method depends primarily upon two factors: (1) limiting distance and (2) weight of the exponent. A decrease in limiting distance improves the interpolation accuracy, whereas with the decrease in limiting distance the moving average method may fail to predict soil moisture in regions of scarce observed soil moisture locations. Figure 3a–d shows the estimated distribution of soil moisture using moving average method for limiting distance 1,000, 2,000, 3,000 and 4,000 m, respectively.

Fig. 3
figure 3

Spatial distribution of soil moisture estimated from moving average at limiting distance. a 1,000 m, b 2,000 m, c 3,000 m, d 4,000 m

Full size image

It can be seen from Fig. 3a that the method has failed to predict soil moisture at few places in case of small limiting distance. This is due to non-availability of observed sufficient soil moisture locations within the selected limiting distance. However, by increasing the limiting distance to 2,000 m and beyond, the moving average method is able to estimate the soil moisture over the entire study area. It can thus be concluded that for the effective application of moving average method, several experimental trials on limiting distance and weight exponent may therefore be necessary to obtain the optimal limiting distance and the weight exponent, which may also be case dependent.

Table 1 shows the RMSE between the observed soil moisture and the estimated soil moisture at 20 points locations considered to evaluate the interpolation. It can be seen from the table that the RMSE increases with the increase in the limiting distance 1,000–2,000 m. However, a further increase in limiting distance (i.e., 3,000 and 4,000 m) results in decrease in the RMSE. Nevertheless, for a given limiting distance, the impact of weight exponent on estimation of soil moisture appears insignificant, since the RMSE remains unchanged with the variation in weight exponent.

Table 1 Effect of limiting distance and weight exponent on estimated soil moisture using moving average technique
Full size table

In summary, it can be reiterated that the moving average method has limitation in selecting appropriate limiting distance as the user may have to determine it experimentally. To overcome this limitation, Kitanidis (1997) has proposed the use of ordinary kriging under the domain of semi-variogram model wherein the limiting distance may be taken as less than or equal to the range.

The ordinary kriging method uses semi-variogram model for interpolating point data. In this study, the observed volumetric soil moisture at 49 locations has been used to construct an experimental semi-variogram. Table 2 shows the semi-variance values of these locations at lag distances of selected 1,000 m chosen. It is evident from the table that as the distance between the points pairs increases to 3,000 m, the semi-variance increases. Beyond 3,000 m, these values fluctuate. Hence, pairs of locations beyond this distance are considered to be uncorrelated.

Table 2 Experimental semi-variance values at different lag distances
Full size table

The accuracy of ordinary kriging depends primarily upon the theoretical semi-variogram model employed to fit the experimental semi-variogram. Therefore, three theoretical semi-variogram models, namely, spherical, Gaussian and exponential models have been used in this study.

Different semi-variogram models have been tried over the experimentally constructed semi-variogram to determine the RMSE between the actual and model computed semi-variance values. Initial trials were made by fitting spherical, gaussian and exponential models over the experimentally constructed semi-variogram. Table 3 indicates that spherical model results in the least RMSE at distance 2,000 m.

Table 3 RMSE between actual and model computed semi-variance values
Full size table

It can also be seen that as the lag distance increases, the RMSE between the semi-variance values increases. The optimum lag distance has been found to be 2,000 m in case of spherical model.

Figure 4 shows the fit of the three semi-variogram models over the semi-variance values obtained from the experimental semi-variogram. From this figure, it can be seen that the spherical model adequately explains the variation of experimental semi-variance as compared to the other models for the dataset considered. Figure 4 also shows that at a range value of 2,800 m, this semi-variogram model stabilizes. Thus, by taking limiting distance equal or more than 2,800 m will result in a constant semi-variance value for all the points separated by a distance greater than 2,800 m.

Fig. 4
figure 4

Fitting of different theoretical semi-variogram models

Full size image

The parameters of spherical model (i.e., nugget and sill) have been used to estimate the soil moisture at each grid (i.e., pixel of size 30 m × 30 m) location to reflect the spatial distribution of soil moisture using ordinary kriging. The kriging is performed for the observed soil moisture values at 49 locations and the spherical semi-variogram model to generate the spatial distribution of soil moisture at limiting distances of 1,000, 2,000 and 2,700 m (Fig. 5a–c).

Fig. 5
figure 5

Spatial distribution of soil moisture using ordinary kriging at limiting distance. a 1,000 m, b 2,000 m, c 2,700 m

Full size image

It can be seen from Fig. 5a that kriging method also is unable to estimate soil moisture in regions where observed locations for interpolation are at a greater distance than the limiting distance. However, with the increase in the limiting distance to 2,000 m and beyond, the kriging method is able to estimate the soil moisture distribution entire area.

The RMSE between the estimated soil moisture and the observed soil moisture at the 20 independent locations considered to evaluate the interpolation model are given in Table 4. From Table 4, it can be seen that the RMSE increases with the increase in the limiting distance. The analysis shows that to select the appropriate semi-variogram model for kriging, several trials are required. The limiting distance chosen to krig soil moisture values depends upon the range of the semi-variogram model adopted, which is again a case specific.

Table 4 RMSE between the observed and the estimated soil moisture using ordinary kriging
Full size table

Conclusions

Spatial and temporal knowledge of soil moisture is important to effectively model the surface runoff from a river catchment. The moving average and kriging methods were employed to estimate soil moisture at spatial scale in a part of Solani River catchment. Observed soil moisture data at 49 sample locations points were used to estimate soil moisture spatial scale, whereas the soil moisture data at 20 locations were used to validate the results by computing RMSE between the observed and estimated soil moisture using the two methods.

For the dataset used, for small limiting distances, due to non-availability of sufficient observed soil moisture locations within the adopted limiting distance, the moving average method was not able to estimate the soil moisture in the region. The effect of variation in weight exponent was also found insignificant in this method. The kriging method was also unable to estimate soil moisture in regions where observed locations for interpolation were at a distance greater than the limiting distance. However, with the increase in the limiting distance to 2,000 m and beyond, the kriging method was able to estimate the soil moisture distribution entire area. Increase in the limiting distance beyond 1,000 m resulted in increase RMSE in both the cases. From the comparison of the two methods, the kriging appears to be a more practical method due to its dependency on data-constructed semi-variogram.