Adsorption of blue copper on a natural and electrochemically treated bentonite

Abstract

Kinetics and equilibrium studies of the adsorption of blue copper on a natural (NC) and electrochemically treated (EMC) bentonite, taken in different experimental conditions, were carried out. Changes of the dye uptake versus operating factors were evaluated using response surface methodology (RSM). The kinetics at 5–50 °C and pH < 10 obeyed the pseudo-first-order equation. Beyond pH 10, the pseudo-second-order equation also was suitable. The kinetics for NC was essentially controlled by external diffusion. However, both internal and external diffusion were the rate-limiting steps of the EMC kinetics. The NC isotherms were well described by the Langmuir model and the maximum uptake was around 21 mg/g. In the case of EMC, the Freundlich equation was rather fitting. Dye adsorption on both sorbents was a non-spontaneous process (2 < ΔG ⁰ _T  < 8 kJ/mol). According to the RSM results, pH had a negative impact on the dye adsorption and was the most influential factor in the case of EMC. For NC, the clay dose was rather the most important parameter.

Introduction

Dyestuffs in effluents engender water pollution and affect the photosynthesis process (Albanis et al. 2000). They can be successfully removed by commercial adsorbents (activated carbon and synthetic resins). However, these materials are expensive and very difficult to regenerate. Thus, low-cost adsorbents such as fly ash and mud (Wang et al. 2005), clays (Hajjaji et al. 2006; Atun et al. 2003; McKay et al. 1987), agricultural residues (Robinson et al. 2002), chitosan-based materials (Elwakeel et al. 2012; Elwakeel 2009) and diatomaceous earth (Al-Ghouti et al. 2003) were tested.

As anionic species, clay minerals especially those of the smectite group are able to remove cationic dyes from aqueous solutions (Gillman 2011; Crini 2006; Lagaly et al. 2006; Hajjaji et al. 2001; Yariv 2001). However, numerous dyes are anionic compounds and their spontaneous adsorption on clay minerals is limited if not impossible.

Much less attention has been paid to the adsorption of anionic dyes on electrochemically modified clays. The electrochemical treatment of clays may result in the change of particles polarization and the increase of porosity. Moreover, in the use of a sacrificial aluminum anode, cationic monomers and polymers might form in solution (Picard et al. 2000) and enter the interlayer space of swelling clay minerals. All these eventual phenomena could facilitate adsorption of anionic dyes on clay particles.

In this study, the kinetics of the adsorption of blue copper (anionic dye) on a natural and electrochemically treated bentonite was followed in different operating conditions. The influence of operating factors (pH, contact time, clay dose and temperature) on the adsorption process was assessed using response surface methodology. The adsorption isotherms for both sorbents were established, and thermodynamic data were determined.

Materials and experimental procedures

The basic raw clay, labeled NC, was from a Mio-Pliocene deposit sited at the east side of the high Atlas Mountain (Morocco) (Driouich 1993). It looked like a fuller’s earth and was used in rustic cosmetic preparations. Its fine fraction (equivalent spherical diameter <2 µm) represented 90 %. The specific surface area and cation exchange capacity determined using methylene blue (Hang and Brindley 1970) were 608 m²/g and 1.15 meq/g, respectively.

The electrochemical treatment of the clay was carried out using the experimental assembly represented in Fig. 1. An aqueous dispersion composed of bentonite (1 g/L) and NaCl (1 g/L) was placed in the electrochemical cell, consisting of a sacrificial aluminum anode, and experienced the current density 46.62 A/m² for 2 h. The test was realized at 25 °C and pH = 6–7. The as-treated dispersion was centrifuged at 4,000 rpm, and the sediment, labeled EMC, was washed with distilled water to remove Cl⁻, then oven-dried 24 h at 80 °C.

Fig. 1

Schematic representation of the experimental assembly used for the electrochemical treatment of the studied bentonite. 1 DC power supply, 2 ammeter, 3 voltmeter, 4 electrochemical cell, 5 anode, 6 cathode, 7 thermostat, 8 stirring apparatus, 9 pH-meter

The used blue copper (chemical formula: C₂₁H₁₆N₃S₄Na₃O₁₆Cu; purity: 98 %) was supplied by a small textile-dying plant located at El Jadida (Morocco). It was freely soluble in water, and its absorption band manifested at 560 nm.

For the kinetics experiments, 100 mL of an aqueous dispersion, composed of 25 mg/L of blue copper and 0.8 g of NC or 0.6 g of EMC, was placed in a thermostated bath (5, 15, 25 or 50 °C) and experienced a steady stirring. Samples were taken from the dispersion at regular time intervals and centrifuged at 6,000 rpm. The dye content in the supernatant was determined by means of a Spectronic 20 Genesys TM, operating at the wavelength 560 nm, and using a pre-established linear curve expressing the Beer’s law. The instantaneous amount of the adsorbed dye (q _t ; mg/g of adsorbent) was related to the measured dye concentration (C _t ; mg/L) as follows: q _t  = (C ₀ − C _t ) V/m [C ₀ initial dye concentration (mg/L), V volume of solution (L); m sorbent mass (g)]. The effect of pH on the adsorption kinetics was tested in the range 4–12. Droplets of H₂SO₄ (0.1 M) or NaOH (0.1 M) were occasionally added to maintain pH constant.

The equilibrium tests were carried out at different constant temperatures (5, 15, 25 and 50 °C). The characteristics of the used dispersions were similar to those mentioned in the kinetics study, except for the dye concentration, which was varied from 1 to 75 mg/L. The contact time was 1 h 30 min, largely exceeding the equilibrium time. The pH of solutions was naturally stabilized at 7.2 ± 0.1.

Adsorbents, before and after experiments, were analyzed by X-ray diffraction (XRD) and Fourier transform infrared (FT-IR). For XRD, a PHILIPS X’PertMPD diffractometer [generator voltage: 40 kV; tube current: 30 mA; scan step size: 0.02°; time/step: 2 s; anode: copper (Kα = 1.5418 Å)] was used. The FT-IR spectra were recorded with a Perkin Elmer spectrophotometer functioning in the range 4,000 and 400 cm⁻¹. For this purpose, thin pastilles composed of adsorbent and KBr (about 96 mass%) were shaped.

Model presentation

The equations expressing the variation of the dye uptake amount versus the operating factors (pH, contact time, clay dose and temperature) for both sorbents were established by adopting the following polynomial model, which was successfully applied in various studies (e.g., Ferreira et al. 2003; Khalfaoui et al. 2006; Liu et al. 2004):

$$\begin{gathered} Y = a_0 + a_1 X_1 + a_2 X_2 + a_3 X_3 + a_4 X_4 + a_{11} X^2_1 + a_{22} X^2_2 + a_{33} X^2_3 + a_{44} X^2_4 + a_{12} X_1 X_2 + a_{13} X_1 X_3 + \hfill \\ a_{14} X_1 X_4 + a_{23} X_2 X_3 + a_{24} X_2 X_4 + a_{34} X_3 X_4 \hfill \\ \end{gathered}$$

X ₁, X ₂, X ₃ and X ₄ are the coded variables associated to pH, contact time, clay dose and temperature, respectively. The coded variable X _i is related to the natural variable (x _i ) as follows: X _i  = (x _i  − x ⁰ _i )/∆x _i ; x ⁰ _i is the central value of the investigated range of x _i . ∆x _i is the variation step of x _i .

a ₀ is a constant; a ₁, a ₂, a ₃ and a ₃ are the weights of pH, contact time, clay dose and temperature, respectively. Coefficient a _ii can be considered as a curve-shape parameter, and a _ij expresses the interaction effect between x _i and x _j factors. The coefficients were determined by the least square regression using the Design-Expert software. For this purpose, 30 experiments included the replicated ones were realized.

The significance and the validity of the model were evaluated by the analysis of variance (ANOVA). The above software was used for the statistical data determination.

Results and discussion

Mineralogical and chemical characterization of the used sorbents

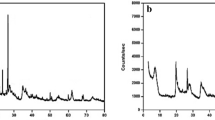
The studied raw clay (NC) was composed of montmorillonite, carbonates (calcite and dolomite), quartz and hematite (Fig. 2, NC) together with minor amounts of aliphatic organic compounds and kaolinite (Fig. 3). As a result of the electrochemical treatment, the intensities of the X-ray reflections of calcite, quartz and montmorillonite decreased when those of hematite almost vanished (Fig. 2, EMC). Quartz and montmorillonite experienced a partial dissolution and/or transformation into amorphous compounds. The basal distance of montmorillonite (d ₀₀₁) evolved from 14.21 to 14.98 Å. This slight swelling could be due to a limited intercalation of water molecules in the interlayer space (Holtzapffel 1985).

Fig. 2

X-ray diffraction patterns of the studied natural clay (NC), electrochemically modified clay (EMC), natural clay-blue copper (NC-D) and the electrochemically modified clay-blue copper (EMC-D) residues, and the blue copper (D). M montmorillonite, Q quartz, C calcite, Do dolomite, H hematite

Fig. 3

FT-Infrared spectra of NC, EMC, and NC-dye and EMC-dye residues. K kaolinite, M montmorillonite, W water, OM organic matter, C carbonates (calcite/dolomite), Q quartz

Considering the chemical compositions of NC and EMC (Table 1), it is derived that calcium, sulfur, potassium and iron were partially leached from the modified clay. Calcium was the most leachable element. It was essentially derived from dissolved calcite, which proportion was estimated to be 30 %.

Table 1 Elemental compositions (wt%) of the studied sorbents

Referring to the reported results dealing with the electrocoagulation processes using aluminum as a sacrificial electrode, species such as Al(OH)₃ and/or Al(OH) ⁻₄ could be formed in solution (Kobya et al. 2003; Picard et al. 2000). Based on the analytical data (Table 1) and the FT-IR analyses (Fig. 3), no aluminum-derivative species were present in the sediment, likely because of leaching or formation of a film at the anode surface.

Considering the amounts of silica in NC and EMC (Table 1) and seeing that the quartz amount decreased as a result of the electrochemical treatment, quartz partially transformed to amorphous silica, and the sediment of EMC manifested a homogeneous texture.

Effect of the adsorbent content on the dye uptake

The dye uptake by both adsorbents increased almost linearly with the increase of the adsorbent dose (Fig. 4), and the slopes of the curves were quasi-similar (2.4 mg L/g²). The uptake increase was linked to the accessibility to supplementary active sites. Nevertheless, beyond a threshold value of the clay dose (about 7.8 and 6.5 g/L of NC and EMC, respectively), the dye-retained amount remained quasi-constant. In such concentrated dispersions, the quasi-totality of additional potential adsorption sites was likely not accessible because of particles aggregation, due to the development of intense attractive electrostatic forces. The dye uptake was relatively high for EMC (Fig. 4), which suggested that the clay treatment produced new active adsorption sites.

Fig. 4

Variation of the dye uptake by NC and EMC versus sorbent dose

Kinetics study

Effects of contact time and temperature

Typical curves showing the evolution of the dye uptake at different temperatures versus contact time for NC and EMC are reported in Fig. 5. The adsorption process was fast for both sorbents and the equilibrium contact time was <25 min, except for the lowest operating temperature.

Fig. 5

Kinetics curves of dye adsorption on NC (at different temperatures)

The kinetics data were examined using the pseudo-first-order equation (Ln [(q _e − q _t )/q _e] = −kt; q _e and q _t are the uptake amounts at equilibrium and t instant; k is the rate constante) as well as the pseudo-second-order equation (1/(q _e − q _t ) = 1/q _e + kt; the parameters have the same meaning) (Ho and McKay 1998). The best fitting was observed by applying the pseudo-first-order equation. The rate constants and the fitting coefficients for tested temperatures are given in Table 2. It was derived that dye adsorption was more rapid for NC, except at the lowest temperature. It may be noted that the plot of Ln k ₁ = f(1/T) (not shown) did not follow a linear curve, indicating that the activation energy was not constant in the investigated range of temperatures.

Table 2 Pseudo-first-order rate constants and fitting coefficients related to the kinetics of the dye adsorption on NC and EMC realized at different temperatures

To have a deep insight into the kinetics process, the internal (Eq. 1) and external (Eq. 2) diffusion models (Al-Degs et al. 2006; Ho et al. 2000) were tested:

$$q_t = k_d t^{0.5}$$

(1)

k _d is the intra-particle diffusion rate (mg/g min^0.5).

$${\text{Ln}}({C_t /C_o }) = - k_f ({A/V})t$$

(2)

k _f is the external diffusion coefficient (cm/s), and A the external surface area to the volume (V) of solution.

The plots of Eqs. (1) and (2) using the kinetics data relevant to NC are shown in Fig. 6a. As the linear curves associated to the internal diffusion model (q _t  = f(t ^0.5)) did not go through the origin, the external diffusion was considered as the rate-limiting step (Al-Degs et al. 2006). The determined internal and external diffusion coefficients are reported in Table 3. Except for the highest temperature, the suitability of the external diffusion model was supported by the high values of the fitting coefficient (Table 3). In the case of EMC, the curves relevant to the intra-particle diffusion model passed by the origin (Fig. 6b), and the models suitability was evaluated by comparing the correlation coefficients values (Table 3). It was deduced that the rate-controlling step depended on temperature: at 323 K the intra-particle diffusion was the most influencing process. At 278 and 288 K, diffusion across the liquid boundary layer was rather the main controlling phenomenon. At 298 K, both diffusion mechanisms were comparable.

Fig. 6

Variations of the instantaneous uptake amount (q _t ) and Ln(C _t /C ₀), taken at different temperatures, against contact time for both considered sorbents

Table 3 Internal and external diffusion coefficients and correlation coefficients determined at different temperatures

Effect of pH

Adsorption kinetics curves plotted at different pH are shown in Fig. 7. The change of pH did not have an appreciable effect on the equilibrium time, but it affected the maximum uptake (Fig. 8). Beyond about 8.7, which was close to pH of NC, the maximum uptake declined. This could be linked to intense negative polarization of clay particles, and consequently to dye species repulsion. Details related to this process are reported hereafter.

Fig. 7

Kinetics curves of the dye adsorption on NC and EMC at different pH

Fig. 8

Change of the maximum uptake of the dye by NC and EMC versus pH

The plots of the aforementioned kinetics equations (not shown) and the correlation coefficient values (Table 4) allowed to deduce that the kinetics of the dye adsorption on both sorbents well followed the pseudo-first-order equation for pH < 10, and the rate constants for NC were slightly higher (Table 4). For pH = 10, the kinetics data related to NC and EMC might be rather described by both equations. For pH = 12, the well-fitting kinetic equation for the data of NC was the pseudo-second-order equation.

Table 4 Pseudo-first- and pseudo-second-order rate constants and fitting coefficients related to the kinetics of the dye adsorption on NC and EMC realized at different pH

Regardless the correlation coefficients in Table 5, and because the plots of q _t  = f(t ^0.5) related to NC did not pass through the origin, the intra-particle diffusion could not be the rate-controlling step. Thus, dye adsorption was essentially controlled by diffusion through the liquid film. For EMC, the curves q _t  = f(t ^0.5) and Ln(C _t /C _o) = f(t) together with R ² values (Table 5) showed that the kinetics was also controlled by film diffusion, but the transfer coefficient was slightly lower than that found for NC (Table 5).

Table 5 Internal and external diffusion coefficients and correlation coefficients determined at different pH

Modeling study

The experimental conditions of the runs arranged by the central composite design (CCD) and their corresponding experimental responses (Y _i,meas; mg/g) for both adsorbents are given in Table 6. The determined equations expressing the variation of the dye uptake amount versus the coded variables related to pH, contact time, clay dose and temperature are as follows:

$$\begin{gathered} Y_1 = \, + 14.53 \, - 2.03X_1 + 2.47X_2 + 3.46X_3 + 0.26X_4 - 0.42X_1 X_2 - 0.34X_1 X_3 - 0.67X_1 X_4 - 0.28 \hfill \\ X_2 X_3 - 0.74X_2 X_4 + 0.35X_3 X_4 - 0.22X_1^2 - 1.15X_2^2 - 0.99X_3^2 - 1.60X_4^2 \hfill \\ \end{gathered}$$

$$\begin{gathered} Y_2 = \, + 15.47 \, - 3.37X_1 + 2.75X_2 + 2.53X_3 + 0.70X_4 - 0.46X_1 X_2 - 0.20X_1 X_3 - 0.29X_1 X_4 - 1.10 \hfill \\ X_2 X_3 + 0.20X_2 X_4 + 0.89X_3 X_4 + 1.07X_1^2 - 0.51X_2^2 - 0.48X_3^2 - 1.04X_4^2 \hfill \\ \end{gathered}$$

Table 6 Central composite design matrix of four test variables in coded and natural variables, and measured responses (Y _i,meas) for NC and EMC sorbents

The accuracy of the model was checked based on the statistical data given in Table 7. The higher F values and correlation coefficients (Aleboyeh et al. 2008; Yetilmezsoy et al. 2009), and the smaller standard deviation (SD) allowed to confirm the model suitability. As a matter of fact, only 3.6 and 2.3 % of the variations of the dye uptake retention by NC and EMC respectively could not be explained by the model.

Table 7 Analysis of variance (ANOVA) for the adopted quadratic models and supplementary statistical data

Considering the Y ₁ equation, the influence of the test factors on the dye retention followed the order: clay dose > contact time > pH > T. In fact, the dye uptake enhanced much more with the increase of adsorption sites, which amount should rise with the increase of the clay dose. Nevertheless, there was a limit due to particles agglomeration. Also, but at a lesser degree, the dye-retained amount increased with the increase of the contact time. This may had a relation with the hindrance experienced by dye species to go through the boundary layer for reaching the active sites. Except for pH, the test factors had positive impacts on the uptake amount, i.e., dye fixation increased with the increase of the factors. The negative impact of pH could be explained by the fact that in alkaline solutions, abundant negative sites developed on the clay particles and repulsed the anionic dye species.

The interactions between the factors were antagonistic (Fig. 9a–e), except that manifested between temperature and clay dose, which was synergetic (Fig. 9f). The weights of the interactions were less significant as compared to those of the factors.

Fig. 9

Response surface plots related to the dye uptake by NC (hold values: pH = 8; T = 27.5 °C; C = 6 mg/L; t = 20.5 min)

In view of the algebraic values of the linear terms of the Y₂ equation, the nature of the effects (positive/negative) of the factors on the dye uptake by EMC were similar to those seen for NC, but the weights of the effects were different: pH > contact time > clay dose > T. The plots showing the interactions between the factors are given in Fig. 10. The unique difference with the NC case was the synergetic effect manifested between the contact time and temperature (Fig. 10e).

Fig. 10

Response surface plots related to the dye uptake by EMC (hold values: pH = 8; T = 27.5 °C; C = 6 mg/L; t = 20.5 min)

Isotherms and thermodynamic data

As shown in Fig. 11, the shapes of the adsorption isotherms of NC and EMC were quite different, and saturation of NC particles required lower dye contents (C _e < 20 mg/L). These let to think that interactions between dye species and adsorbents particles were dissimilar.

Fig. 11

Adsorption isotherms of NC and EMC sorbents

The plots (not shown) of the linear forms of the Langmuir equation [q _e = K _L C _e q _m/(1 + K _L C _e); q _e:equilibrium uptake (mg/g); q _m:maximum uptake (mg/g); K _L:Langmuir constant (L/mg)] and Freundlich equation (q _e = K _F (C _e)^1/n; q _e (mg/g); K _F (mg ^(n−1)/n/g Lⁿ) and n are constants) together with the values of the linear correlation coefficients (Table 8) allowed to deduce that NC isotherms were well described by the Langmuir model while those of EMC well fitted the Freundlich isotherm. Values of the models parameters are given in Table 8. The dye adsorption on both sorbents was favored since the equilibrium dimensionless parameter R _L (R _L = 1/(1 + K _L C _o), C _o: maximal initial concentration of dye) and the Freundlich constant (1/n) were <1 (Hall and Vermeylem 1966; Yeddou and Bensmaili 2005).

Table 8 Langmuir and Freundlich constants and fitting coefficients

The suitability of the models also was assessed by the Marquardt’s percent standard deviation (MPSD) (Porter et al. 1999):

$$100\left({\sqrt {\frac{1}{p - n}\sum_{i = 1}^p {[{\frac{{({q_{\text{e,meas}} - q_{\text{e,calc}} })_i^2 }}{{q_{\text{e,means}} }}}]} } }\right)$$

p : number of experimental measurements; n: number of isotherm parameters (2); q _e,_meas and q _e,_calc are the measured and calculated uptake amounts at equilibrium.

The MPSD values are reported in Table 9. In agreement with the above findings, the NC isotherms well followed the Langmuir equation. However, a discrepancy was observed for EMC results. Referring to MPSD values, the best fitting model for the isotherm at 298 K should be the Langmuir model, and the isotherm at 288 K could be described by both models.

Table 9 Marquardt’s percent standard deviation (MPSD) determined for Langmuir and Freundlich isotherms related to NC and EMC sorbents

As the NC isotherms obeyed the Langmuir model, the Gibbs free energy (ΔG ⁰ _T ) was calculated from the relation: ΔG ⁰ _T  = −R T Ln K _L [R: gas constant; T: temperature (K)]. The change of ΔG ⁰ _T versus temperature evolved linearly (Fig. 12), suggesting thus the heat (ΔH ⁰) and entropy (ΔS ⁰) of the adsorption process were almost constant in the considered range of temperatures. Given that ΔG ⁰ _T  = ΔH ⁰ − TΔS ⁰, it was derived that ΔH⁰ = −19.326 kJ/mol and ΔS⁰ = 0.0799 kJ/K mol. These results allowed deducing that dye adsorption was a non-spontaneous and exothermic process, and disorder increased as a result of the dye species fixation. Moreover, adsorption took place by physisorption (no chemical change happened) since ΔH⁰ < 40 kJ/mol (Shiau and Pan 2004).

Fig. 12

Variation of the Gibbs free energy of the adsorption process of blue copper on NC versus operating temperature

As NC isotherms followed the Langmuir model, dye species adsorbed on like sites of sorbent particles without interactions. Saturation happened as a monolayer of adsorbate formed. Likely because of the small thickness of the layer and the random distribution of dye species, the XRD pattern of the NC-Dye residue (Fig. 2) did not exhibit any peak associable to the dye, characterized by a well-crystallized structure (Fig. 2). However, in the case of the EMC-D residue, some X-reflections of the dye were identified (Fig. 2). In this respect, it could be mentioned that because of bands overlapping, the IR bands of the eventual tied species of the dye could not be distinguished (Fig. 3). It was believed that thicken layers of dye molecules were built around EMC particles. These results concurred with the isotherms modeling since it was shown that EMC isotherms followed the Freundlich equation, that is, adsorption happened on heterogeneous sites and dye layers built around solid particles. It seemed that, in the later case, active sites located on amorphous silica were involved in the adsorption process.

Because of their overall negative charges, dye species and clay particles should be the subject of repulsion, and adsorption should not occur. But, referring to the aforementioned kinetic study, the step relevant to the fixation of dye species on adsorbent particles was relatively rapid since the main controlling step was diffusion across the boundary liquid layer. Given the absence of exchangeable anion, adsorption likely happened, among others, on positive edge sites of the particles of montmorillonite. Considering the NC absorbent, the maximum retained amount as compared to CEC (q _m/CEC) did not exceed about 2 %.

Conclusions

• 1. The electrochemical treatment of bentonite resulted in a partial dissolution of montmorillonite and ancillary minerals. The basal spacing of the clay mineral was quasi-constant, and the common aluminum sacrificial anode-derivative species were not detected.

• 2. The dye adsorption increased with the rise of the clay content. It however remained unchanged as the clay dose exceeded 7.8 and 6.5 g/L of NC and EMC, respectively. Apparently, higher clay contents led to particles agglomeration.

• 3. In the range 5–50 °C, the adsorption kinetics data for both sorbents were well described by the pseudo-first-order equation. Divergences were observed in the kinetics rate-controlling steps.

• 4. The kinetics law varied with the change of pH, and the rate constants for NC were always higher. At 4 ≤ pH ≤ 12, diffusion through the liquid film around particles of the sorbents was the rate-limiting step.

• 5. The NC isotherms well fitted the Langmuir model, and adsorption proceeded by physisorption. The heat involved in this process was −19.326 kJ/mol. In the case of EMC, the isotherms well followed the Freundlich equation. However, this result was partially questionable by the use of the Marquardt’s percent standard deviation.

• 6. The adoption of the polynomial model and the use of RSM allowed to express the variation of the dye uptake amount against the coded variables related to pH, contact time, clay dose and temperature. In this respect, it may be concluded that apart from pH, the increase of the considered factors had positive impacts on the uptake amount. Moreover, the most interactions between the factors were antagonistic.