Introduction

Environmental pollution has become a global concern and attracts much attention. Water bodies are the most common natural resources that have been contaminated as a result of different human activities. One of the most important environmental problems related to water pollution throughout the world is the contamination of water bodies by heavy metal ions because of their toxic effects on the environment and human health (Akpor and Muchie 2010; Cavus and Gurdag 2008; Calmano and Förstner 1983).

Among many toxic metals, uranium is known to be one of the most toxic for human health mostly because of its radioactivity and carcinogenicity; thus its maximum level in drinking water recommended by the World Health Organization is 0.015 mg L−1. Uranium is released into the aqueous environment through different sources such as the acid drainage waters from uranium mines. The uranium concentration of acid drainage water from uranium mines was reported in the range 6–14 mg L−1. Moreover, uranium mining generates around one billion m3 of mill tailings with uranium concentration of nearly 40 mg kg−1.

Many studies and methods have been developed to eliminate U from aqueous solutions including ion-exchange resins, electrolytic or liquid extraction, electrodialysis, chemical precipitation, membrane filtration, and biosorption (Ahmed et al. 2008). The use of polymeric adsorbents is one of the most common methods. Many studies have reported the successful application of different polymers for the removal of U and these include sulfonated polyethylenimine, phosphonated polyethylenimine, polyvinylimidazole, polyacrylamide, polyacrylamidoglycolic, and polyacrylamidomethylpropanesulfonic acid (Martinot et al. 1997; Leroy et al. 2003). These polymers have largely been studied in batch sorption mode.

Although batch adsorption experiments provide important information on adsorption equilibrium characteristics and adsorption kinetics, the data obtained are not sufficient to provide accurate scale-up data required in the design of adsorption columns. Therefore, studies of column adsorption systems are needed, in which the most important parameter to be determined is the column breakthrough curves, that is useful for the determination of the operating life span of the fixed adsorbent bed (Bielicka-Daszkiewicz and Voelkel 2009; Naja and Volesky 2006; Chu 2004).

This study, therefore, was aimed at testing the performance of fixed-bed columns packed with PCPEI for the removal of U. Our previous study demonstrated that this polymer offers excellent potential for U removal using batch sorption experiments.

The breakthrough and exhaustion points were determined for fixed-bed columns packed with PCPEI used for the continuous adsorption of U from aqueous solutions. The system variables or parameters such as solution flow rate, inlet concentration and bed height were investigated.

Materials and methods

Materials

All the reagents and solutions were prepared using reagent-grade chemicals from Sigma Aldrich (South Africa) without further purification.

Cross-linked polyethylenimine (synthesis reported by Saad et al. 2011) and phosphorous acid were used for the synthesis of PCPEI. The U solutions were prepared from UO2(NO3)2·6 H2O. Adjustments of pH for the adsorption experiments were conducted using 1 mol L−1 solutions of HNO3 and NaOH. Deionized water (Millipore) was used for the preparation of all solutions.

Synthesis of phosphonated cross-liked polyethylenimine (PCPEI)

The synthesis of PCPEI was carried out according to the method reported by Saad et al. (2012). Cross-linked polyethylenimine, 2.5 g, was placed in 80 mL of 6 mol L−1 HCl. Phosphorous acid, 19.31 g, was added and the mixture was heated under reflux at 90 °C. Formaldehyde, 38 mL, was added drop wise over a period of an hour and the reaction was left over night. A pale, powdery, yellow solid was obtained, washed with abundant deionised water before drying in an air oven at 30 °C. The solid was then pulverised and sieved (<1 mm).

Fixed-bed column studies

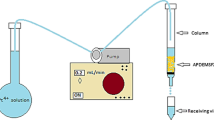
Figure 1 represents the schematic diagram of the fixed-bed adsorption system. Continuous flow adsorption studies were conducted in a column made of glass tube having an inner diameter of 1.5 cm and height of 12 cm. The column was packed with PCPEI. A layer of glass wool was placed at the bottom of the column to prevent loss of the adsorbent. A peristaltic pump (MASTERFLEX L/S, Heidolph 5201) was used to pump the standard metal solution (40 mg L−1 of U, at pH 2 and room temperature) downward through the column at a constant flow rate of 1 mL min−1. The concentration of 40 mg L−1 of U was chosen arbitrarily for the “worst case” scenario of U load in water emanating from gold mining activities around Johannesburg (Tutu et al. 2009). The effluent samples were collected at specified times and measured for the remaining metal concentration using ICP-OES (Spectro, Germany).

Fig. 1
figure 1

Fixed-bed adsorption system

Full size image

Effect of flow rate

The effect of feed flow rate on the adsorption of U onto PCPEI was investigated by varying the feed flow rate (1, 2, and 3 mL min−1) while maintaining a constant bed height of 4.5 cm and inlet concentration of 40 mg L−1.

Effect of inlet concentration

The effect of inlet concentration on the column performance was studied by varying the U concentration of 40, 70, and 100 mg L−1 while maintaining a constant adsorbent bed height and feed flow rate.

Effect of bed height

In the first stage, the bed height was changed (2.5, 3.2, and 4.5 cm) with amount of 1, 1.55, and 2 g, respectively. This to assess the height required for optimal removal while the inlet U concentration in the feed and the flow rate were held constants at 40 mg L−1 and 1 mL min−1, respectively.

Modelling of analytical results

The dynamic behaviour of the columns was predicted using Adams–Bohart, Thomas, and Yoon–Nelson models. These models are important when designing an efficient fixed-bed adsorption system with the optimum required conditions.

Adams–Bohart model

This model was established by Adams and Bohart to describe the relationship between (Ct/C0) and time. The Adams–Bohart model basically describes the initial part of the breakthrough curve and focusses on some characteristic parameters such as the maximum adsorption capacity (N0) and kinetic constant KAB (Aksu and Gonen 2004; Chowdhury et al. 2013). The mathematical equation of the model can be written as:

$$\ln {\kern 1pt} \left( { {\raise0.7ex\hbox{${C_{\text{t}} }$} \!\mathord{\left/ {\vphantom {{C_{\text{t}} } {C_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${C_{0} }$}}} \right) = K_{\text{AB}} C_{0} t - K_{\text{AB}} N_{0} \left( {{\raise0.7ex\hbox{$Z$} \!\mathord{\left/ {\vphantom {Z {U_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${U_{0} }$}}} \right)$$
(1)

where \({\text{C}}_{0}\) and Ct are the inlet and outlet adsorbate concentrations, respectively (mg L−1), Z is the bed height (cm), U0 is the superficial velocity (cm min−1), N0 is the saturation concentration (mg L−1), and KAB is the kinetic constant (L mg−1 min−1). The last two values can be calculated from the intercept and slope of the plot of ln \(\left( {C_{\text{t}} /C_{0} } \right)\) against time (t).

Yoon–Nelson model

This model was developed by in Yoon and Nelson 1984 to describe the adsorption breakthrough curves. The Yoon–Nelson model was derived based on the assumption that the rate of decrease in the probability of adsorption for each adsorbate molecule is proportional to the probability of adsorbate adsorption and the probability of adsorbate breakthrough on the adsorbent. It is a simple model that requires no detailed data concerning the type of the adsorbent and the physical properties of the adsorption bed (Aksu and Gonen 2004; Chowdhury et al. 2013). The linearised model for a single component system is expressed as:

$$\ln {\kern 1pt} \left( {\frac{{C_{\text{t}} }}{{C_{0} - C_{\text{t}} }}} \right) = K_{\text{YN}} t - {\mathbf{\mathcal{T}}}K_{\text{YN}}$$
(2)

where KYN is the rate constant (min−1);\({ \mathcal{T}}\) is the time required for 50 % adsorbate breakthrough (min) and t is the breakthrough time (min).

The values of KYN and \({\mathcal{T}}\) can be calculated from a plot of \({\text{ln }}\)\(\left( {C_{\text{t}} /C_{0} - Ct} \right)\) vs. \(t\) at different inlet concentrations, flow rates, and bed heights. If the theoretical model accurately characterizes the experimental data, this plot will result in a straight line with a slope of \(K_{\text{YN}}\) and intercept of \({\mathcal{T}}K_{\text{YN}}\) (Yoon and Nelson 1984).

Thomas model

This model is a general model that is widely used to describe column performance (Thomas 1994). The Thomas model is based on the assumption that the adsorption behaviour follows Langmuir kinetics and assumes that the rate driving forces obeys the second-order reversible reaction kinetics. The theoretical form of the model is given as:

$$\ln {\kern 1pt} \left( {\frac{{C_{0} }}{{C_{\text{t}} }} - 1} \right) = \frac{{K_{\text{Th}} Cq_{0} m}}{Q} - \frac{{K_{\text{Th}} C_{0} }}{Q} \left( {V_{\text{eff}} } \right)$$
(3)

where \(K_{\text{Th}}\) is the Thomas rate constant (mL mg−1 min−1), \(q_{0}\) is the equilibrium adsorbate uptake (mg g−1), m is the adsorbent amount in the column (g), \(V_{\text{eff}}\) is the volume of the solution (mL), and Q is the feed flow (mL min−1). The values of KTh and \(q_{0}\)can be calculated from the slope and intercept of the linear graph between \(\ln {\kern 1pt} \left( {C_{\text{t}} /C_{0} - 1} \right)\) vs. \(V_{\text{eff}}\) at different inlet concentrations, flow rates, and bed heights.

Results and discussion

Characterization of phosphonated cross-linked polyethylenimine

Fourier transform infrared spectroscopy was used to characterize the phosphonated derivative of cross-linked polyethylenimine (PCPEI) in order to confirm the introduction of the –PO3H2 chelating group. The FTIR spectrum is given in Fig. 2.

Fig. 2
figure 2

FTIR spectrum of CPEI and PCPEI

Full size image

The major peaks of importance on the IR spectrum of PCPEI are: 966.76 cm−1 indicating the presence of the P–OH bond; 1,060.34 cm−1 corresponding to the presence of the P–O bond; and 2,803.31 cm−1 signifying the presence of the PO–H bond. The difference in the strength of absorption bands for the stretching vibration of N–H before and after the phosphonation could be observed, with the phosphonated polymer yielding lower band strength. This could be attributed to the closure of some secondary amine sites during phosphonation of the polymer. The phosphonated polymer thus contains less secondary amine groups due to the reaction between these groups in CPEI and (–PO3H2) groups in phosphorous acid.

Effect of inlet concentration

The breakthrough curve presented in Fig. 3 shows the effect of initial concentration on the breakthrough curves using a bed height of 4.5 cm and flow rate of 1 mL min−1. As the figure shows, an earlier breakthrough point was reached at higher concentration (100 mg L−1), where the adsorbent was exhausted faster as compared to the lowest concentration (40 mg L−1).

Fig. 3
figure 3

Breakthrough curves for adsorption of U onto PCPEI for different inlet concentrations

Full size image

The breakthrough time was found to decrease with increasing adsorbate inlet concentration as the binding sites saturated quicker. A decrease in inlet concentration gave an extended breakthrough curve, indicating that a higher volume of solution could be treated. This could be explained by the fact that a lower concentration gradient caused a slower transport due to a decrease in diffusion coefficient or mass transfer coefficient.

Effect of flow rate

The effect of feed flow rate on the adsorption of U onto PCPEI was investigated by varying the feed flow rate (1, 2, and 3 mL min−1) while keeping a constant bed height of 4.5 cm and inlet concentration of 40 mg L−1 as shown in Fig. 4. The curve showed that at a higher flow rate the front of the adsorption zone quickly reached the top of the column, that is, the column was saturated early. A lower flow rate resulted in a longer contact time as well as shallow adsorption zone. At a higher flow rate a steeper curve with a relatively early breakthrough and exhaustion time resulted in less adsorption uptake.

Fig. 4
figure 4

Breakthrough curves for adsorption of U onto PCPEI for different flow rates

Full size image

Effect of bed height

Figure 5 shows the breakthrough curve obtained for the adsorption of U onto PCPEI for different bed heights of 2.5, 3.2, and 4.5 cm at a constant adsorbate feed flow rate of 1 mL min−1 and adsorbate inlet concentration of 40 mg L−1.

Fig. 5
figure 5

Breakthrough curves for adsorption of U onto PCPEI for different bed heights

Full size image

As Fig. 5 shows, the breakthrough time was found to increase with increasing bed height. Higher uptake was observed at a bigger bed height due to the increase in the amount of the adsorbent which provided more adsorption sites for the adsorption process to proceed. The increase in bed height increases the mass transfer zone. The mass transfer zone in a column moves from the entrance of the bed and proceeds towards the exit. Hence for the same influent concentration and fixed-bed system, an increase in bed height would create a longer distance for the mass transfer zone to reach the exit, subsequently, resulting in extended breakthrough time. For a bigger bed height, the increase of adsorbent mass would provide a larger surface area leading to an increase in the volume of the treated solution.

Application of Adams–Bohart model

Adams–Bohart model was applied to experimental data to describe the initial part of the breakthrough curves. A linear relationship was obtained between ln\(\left( {C_{\text{t}} /C_{0} } \right)\) and t by applying Eq. (1) to the experimental data for varying initial concentrations, flow rates and bed heights. \(K_{\text{AB}}\) and N0 values were calculated from the slope and intercept, respectively, and listed in Table 1 together with the correlation coefficients (R2).

Table 1 Adams–Bohart parameters for U sorption at different conditions
Full size table

From the table, it is observed that the kinetic constant (KAB) was influenced by the experimental conditions as it decreased with increasing inlet initial concentration and increased with increase in both flow rate and bed height. The sorption capacity (N0) increased for increasing initial concentration and bed height while it decreased with flow rate. This showed that the overall system kinetics was dominated by external mass transfer. However, the relatively poor correlation coefficient for initial concentration and flow rate reflects less applicability of this model.

Application of the Yoon–Nelson model

The column data were fitted to the Yoon–Nelson model to determine the rate constant (KYN) and the time required for 50 % adsorbate breakthrough (\({\mathcal{T}}\)). Application to the experimental data with respect to initial concentration, flow rate, and bed height enabled the determination of Yoon–Nelson model parameters (KYN and \({ \mathcal{T}}\)) from the slope and intercept of the graph between \(\ln {\kern 1pt} \left( {C_{\text{t}} /C_{0} - Ct} \right)\) against \(t\). The calculated values are given in Table 2.

Table 2 Yoon–Nelson parameters for U sorption at different conditions
Full size table

As Table 2 shows, both \(K_{\text{YN}}\) and \({\mathcal{T}}\) values decreased with increasing initial concentration and flow rate, but increased significantly with increase in bed height. These results are in agreement with some literature findings (Aksu and Gonen 2004; Chowdhury et al. 2013).

The values of KYN relate to the initial concentration, flow rate and bed height as follows:

KYN values are higher at low than at high initial concentration as result of the relationship between the rate, the rate constant and concentration [e.g. rate = KYN (U)]. At low flow rates, there is increased contact time, thus KYN is higher compared to at high flow rates. The effect of the bed height is similar to this in that for longer bed heights, there is increased contact time and hence higher values of KYN.

Application of Thomas model

Thomas model was applied to investigate the breakthrough behaviour of U on PCPEI. The values of the Thomas rate constant (KTh) and the equilibrium adsorbate uptake (q0) were calculated from the slope and intercept of the graph of \(\ln {\kern 1pt} \left( {\frac{{C_{0} }}{{C_{\text{t}} }} - 1} \right)\) against \(V_{\text{eff}}\) at different experimental conditions and listed in Table 3.

Table 3 Thomas model parameters for U sorption at different conditions
Full size table

As can be observed from the table, as the concentration increased, the value of \(K_{\text{Th}}\) decreased whereas the value of \(q_{0}\) increased. For both flow rate and bed height \(K_{\text{Th}}\) values showed a reverse trend, that is increased with increase in flow rate and bed height. The Thomas model is suitable for adsorption processes where the external and internal diffusions will not be the limiting step.

Conclusions

The adsorption of U from aqueous solution onto PCPEI was investigated in a continuous packed fixed-bed column mode. The breakthrough curves for column adsorption of U from solutions to PCPEI have been measured at various inlet U concentrations, flow rates and bed heights.

The results obtained showed that the sorption of U is dependent on the inlet concentration, flow rate, and bed height as the breakthrough time and U removal decreased with increasing flow rate and U concentration and increased with increasing the bed height. The results also indicated that better sorption process could be achieved with lower flow rates and lower concentrations of U solutions as well as long bed heights. This was achieved at flow rate of 1 mL min−1, initial concentration of 40 mg L−1, and bed height of 4.5 cm.

By adjusting the operating characteristics of the packed column, for example the flow rate, inlet U concentration, adsorbent amount (bed height), very rapid and efficient U uptake can be achieved for the system.

The Adams–Bohart, Thomas and Yoon–Nelson models were applied to experimental data to predict the breakthrough curves and to determine the column kinetic parameters. The initial region of the breakthrough curves was defined by the Adams–Bohart model at all inlet concentrations, flow rates and bed height studied while the full description of breakthrough was accomplished by the Thomas and Yoon–Nelson models. The model constants belonging to each model were determined by linear regression and were proposed for use in column design.

The overall performance of the column study demonstrated that PCPEI can be used in fixed-bed columns for removal of U by choosing the optimal running conditions which are (1 mL min−1 flow rate, 40 mg L−1 initial concentration, and 4.5 cm bed height) according to the findings of this study. Another configuration would be to pack the polymer into columns that can be placed in household containers (e.g. water jars) and left to contact with polluted water, allowing mass transfer of U to the adsorbents in the columns.