Introduction

Dyes are organic compounds consisting of two main groups of compounds, chromophores (responsible for the color of the dye) and auxochromes (responsible for intensity of the color) (Christie 2001). Dyes usually have a synthetic and complex aromatic structure, which makes them more stable and difficult to biodegrade (Sayan 2006). According to the color index (C.I.) which is managed by the society of dyers and colorists, currently more than 10,000 various types of dyes are synthesized and available in the world (Elkady et al. 2011). It is estimated that approximately 12 % of synthetic dyes are lost during manufacturing and processing operations, and 20 % of these lost dyes enter in the industrial wastewater (Chowdhury et al. 2011a). The dyes used in the textile industries include several structure varieties such as acidic, reactive, basic, disperse, azo, diazo, anthraquinone based and metal complex dyes (Banat et al. 1996).

Crystal violet (CV) or Gentian violet is widely used for dyeing of cotton and silk and in the manufacture of paints and printing inks (Chakraborty et al. 2011; Senthilkumar et al. 2010). It also finds application as a biological stain and is the active ingredient in Gram’s stain. The dye is used as a bacteriostatic agent in animal husbandry and veterinary practice and as an additive to poultry feed to inhibit propagation of mold, intestinal parasites and fungus (Senthilkumar et al. 2010; Kumar and Ahmad 2011). Being a protein dye, Crystal violet is also used on most types of adhesive tapes, because conventional powders adhere to the entire sticky side of the tape and are not selective to the latent prints (Ahmad 2009). A considerable amount of dye is lost during manufacturing and processing operations which ultimately enters the water resources through industrial wastewater. Crystal violet is poorly metabolized by microbes, is non-biodegradable and can persist in a variety of environments. Hence, it has been classified as a recalcitrant molecule (Chakraborty et al. 2011). The dye is highly cytotoxic and carcinogenic to mammalian cells. It can cause permanent injury to the cornea and conjunctiva (Chakraborty et al. 2011). Acute exposure to CV can cause skin irritation, irritation of the digestive tract and may also lead to respiratory and kidney failures (Saeed et al. 2010). Therefore, the treatment of effluents containing such dye is extremely necessary for the protection of both human and public health, as well as the natural environment.

Many treatment processes such as photocatalytic degradation (Sohrabi and Ghavami 2008; Saleiman et al. 2007), electrochemical degradation (Fan et al. 2008), cation exchange membranes (Wu et al. 2008), micellar enhanced ultra filtration (Zaghbani et al. 2008), adsorption/precipitation processes (Zaghbani et al. 2007), and Fenton-biological treatment (Lodha and Chaudhari 2007) have been applied for the removal of dyes from wastewater. Adsorption has been found to be superior to other techniques for removal of dyes from wastewater in terms of simplicity and flexibility of design, high selectivity and efficiency and high-quality treated effluent (Chowdhury and Saha 2013). Activated carbon is the most widely employed adsorbent for the removal of color from textiles due to its effectiveness and high adsorption capacity; however, its use is still limited because of high operating cost. The need for regeneration and difficulty of separation from wastewater after use are also major concerns associated with activated carbon (Weng et al. 2009). Conversely, biosorption defined as the removal of materials (organic compounds, metal ions, dye molecules, etc.) by inactive, non-living biomass (materials of biological origin) has emerged as an alternative low cost and eco-friendly technology (Farooq et al. 2010).

An economic sorbent is defined as the one which is abundant in nature, or is a by-product or waste from industry, has little or no economic value and requires little processing. Agricultural residues, also called lingo cellulosic biomass resources are defined as a biomass by-product from the agricultural system and include straws, husks, shell and stalks. These wastes can be divided into two groups: crop residues, which remain in the field after harvest, for example, cotton; agricultural residues, which are the by-products of the industrial processing of crops, for example, rice husk (Tunc et al. 2009). Several million tons of agricultural wastes are being disposed in the world every year through different ways such as incineration, land applications and land filling. Dye adsorption by these wastes may provide an attractive alternative treatment due to their low cost and readily availability (Farooq et al. 2010). A number of studies on removal of dye from aqueous solution using different low-cost materials such as Posidonia oceanic (L.) dead leaves (Cavas et al. 2011), peanut husk (Song et al. 2011), Capsicum annuum seeds (Akar et al. 2011), oil palm shell (Foo and Hameed), cotton seed hull (Qi et al. 2011), pine tree leaves (Deniz and Karaman 2011), waste tea activated carbon (Auta and Hameed 2011), Thespesia populena pods (Arulkumar et al. 2011), Ananas comosus (Chowdhury et al. 2011b), coffee husk-based activated carbon (Ahmad and Rahman 2011), palm kernel fiber (El-Sayed 2011), sugarcane bagasse (Zhang et al. 2011a), treated ginger waste (Kumar and Ahmad 2011), Mangifera indica (Alencar et al. 2012), Jujuba seeds (Reddy et al. 2012), wheat residue (Zhong et al. 2011), peanut hull (Tanyildizi 2011), Oryza sativa (Safa and Bhatti 2011), ground shell powder (Kumar et al. 2013), wheat straw (Zhang et al. 2011b), NaOH-modified rice husk (Chowdhury and Saha 2013), Dithiocarbamated symphoricarpus albus (Kara et al. 2012), cashew nut shell (Senthilkumar et al. 2010), rice straw (Chakraborty et al. 2011), tamarind seed powder (Patel and Vashi 2012), oil palm empty fruit bunch (Auta 2012) have been reported. Despite that many low-cost adsorbents have been studied for decontamination purposes, study on the Citrullus lanatus rind and Cyperus rotundus as economical sorbents for the treatment of wastewater is a win–win strategy because it not only converts the waste into a useful material but it also prevents on-site burning of the waste and saves disposal costs (Weng et al. 2009).

Most of the adsorption studies have been conducted in batch modes which are usually limited to the treatment of small quantities of wastewater (Upendra and Manas 2006). Moreover, batch operations are very easy to apply in the laboratory study, but less convenient for field applications (Hasan et al. 2010). The sorption capacity of the sorbent, obtained from batch equilibrium experiment, is useful in providing fundamental information about the effectiveness of sorbate–sorbent system. However, the data obtained under batch conditions are generally not applicable to most treatment system (such as column operations) where contact time is not sufficiently long for the attainment of equilibrium (Low and Lee 1991). Thus, it is necessary to ascertain the practical applicability of the sorbent in the continuous mode. In order to obtain basic engineering data, continuous flow system is an effective process suitable for large-scale wastewater volumes and cyclic sorption/desorption: fixed-bed reactor is a simple method for the determination of bed operation life span and regeneration time (Cheknane et al. 2012). Fixed-bed sorption is used to determine the experimental breakthrough curve. In fact, from the industrial point of view, the removal of dyes and/or colored compounds using the adsorption techniques performed in column systems is thought to be very useful due to the adaptability of column systems to versatile processes, low reagent handling and accordingly low operational cost coming out (Akar et al. 2011). Reports regarding the removal of pollutants in continuous mode using fixed-bed column are only a few (Batzias and Sidiras 2004).

Thus, the primary objective of this study was to evaluate the performances of Citrullus lanatus rind and Cyperus rotundus for Crystal violet removal from aqueous solution in dynamic flow system. The effects of important design parameters such as feed flow rate, column bed height and initial dye concentration were studied, and the obtained breakthrough curves were analyzed using Bed Depth Service Time (BDST) model, Thomas model and Yoon–Nelson model.

Materials and methods

Preparation of biosorbents

The biosorbent, Citrullus lanatus rinds, was collected from the local market, Tiruchirappalli, Tamil Nadu, India, as solid waste. The rinds were thoroughly washed with tap water and with distilled water to remove the dirt and earthy materials adhered to the surface. Then it was sliced, spread on trays and kept under hot sun for 5 days. The dried biomass was ground, sieved and stored in air tight container for further use.

The other sorbent, Cyperus rotundus, was collected from the local farmlands in Tiruchirappalli, Tamil Nadu, India. The biosorbent was first thoroughly washed with tap water and again with distilled water to remove the remaining dirt and any unwanted particles and then sun dried and subsequently oven dried at 60 °C for 24 h and ground to find powder. No other physical or chemical treatments were given to both the biosorbents prior to experiments. The sorbents were designated as CLR (Citrullus lanatus rind) and CR (Cyperus rotundus) in the further experiments.

Adsorbate

Crystal violet (CV) used in this study was procured from S.D. Fine-Chem. Ltd. (India) (CI 42555, MF: C25 H30CIN3) λmax: 579 nm) and used without further purification. Stock dye solution (1,000 mg L−1) was prepared by dissolving 1 g of the dye in 1 L of double distilled water. Experimental dye solution of different concentrations was prepared by diluting the stock solution with suitable volume of double distilled water.

Fixed-bed column studies

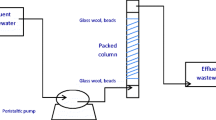
The continuous flow biosorption experiments were conducted in a glass column of internal diameter 2.5 cm and length 55 cm. The biosorbents were packed in the column between glass wool and glass beads, which prevented the wash out of CLR and CR. The particle size of both the sorbents was 150–300 μm with a bed depth of 30 cm. The filling weight of CLR and CR were 21.63 and 14.5 g, respectively and the packed density of CLR and CR in the column were 0.1469 and 0.0984 g cm−3, respectively. All the experiments were carried out at 303 ± 1 K. Before operation, the bed was rinsed with distilled water and left overnight to ensure a closely packed arrangement of particles with no void, channels, or cracks. A schematic of a fixed-bed column of the biosorbent for CV biosorption is shown in Fig. 1. Dye solution was fed through the fixed-bed column in a down flow mode. The samples were collected at specified time intervals, and the concentration of CV in the effluent was analyzed using UV/vis spectrophotometer. Operation of the column was stopped when the effluent CV concentration exceeded a value of 99.5 % of its initial concentration. The time for breakthrough appearance and shape of the breakthrough curves are very important characteristics for determining the operation and the dynamic response of an adsorption column. Therefore, breakthrough curves, i.e., \(\frac{{C_{t} }}{{C_{o} }}\) verses times were plotted. The breakthrough time (tb, the time at which dye concentration in the effluent reached 1 mg L−1) and bed exhaustion time (te, the time at which dye concentration in the effluent reached 99.5 % of initial dye concentration) were used to evaluate the breakthrough curves.

Fig. 1
figure 1

Schematic diagram of lab-scale column study

Full size image

Effect of flow rate, initial CV concentration and bed depth

For both the sorbents, three initial CV concentrations of 10, 15 and 25 mg L−1 and three flow rates of 10, 15 and 20 mL min−1 were investigated at a constant bed depth. The cumulative bed depths studied were 10, 20 and 30 cm.

Desorption study

For any adsorption process, the most important factors are the recovery of the adsorbent and the regeneration capacity of the adsorbent. Desorption was carried out by 1 N CH3COOH solution through the bed in the downward direction at a flow rate of 13 mL min−1, slightly less than the sorption flow rate 15 mL min−1.

Characterization of biosorbents

Fourier transform infrared (FTIR)

A qualitative and preliminary analysis of the main functional groups on the biosorbent surface that might be involved in dye binding can be identified by FTIR as each group has a unique energy absorption band. Therefore, FTIR spectra of CLR and CR, before and after biosorption of CV, were recorded with a FTIR spectrometer (Spectrum BX-II, PerkinElmer, USA). 0.001 g of dry sample was mixed with 0.5 g of spectroscopic grade potassium bromide powder in an agate pestle and mortar. The powder was then compressed into a thin KBr translucent disk under a pressure of 100 kg cm−2 for 8 min with the aid of a bench press. FTIR spectra were then recorded in the wave number range 400–4,000 cm−1.

Scanning electron microscopy (SEM)

The surface structure of the biosorbent, before and after biosorption, was analyzed by scanning electron microscope (S-300 N, Hitachi, Japan) at an electron acceleration voltage of 25 kV. Prior to scanning, the unloaded and dye-loaded CLR and CV samples were mounted on a stainless steel stab with double stick tape and coated with a thin layer of gold in a high-vacuum condition.

Theory

Modeling of column data

In the present study, the Bed Depth Service Time (BDST) model (Hasan et al. 2010), Thomas model (Han et al. 2008) and Yoon–Nelson model (Ramesh et al. 2011) were fitted to the dynamic flow experimental data performed in the fixed-bed column to predict the breakthrough curves and to determine the characteristic parameters of the column.

Bed depth service time (BDST) model

The BDST is a model for predicting the relationship between depths, X and service time t (Vijayaraghavan and Prabu 2006). This model states that the bed height and service time of a column bear a linear relationship. This model was derived based on the assumption that forces like intra particle diffusion and external mass transfer resistance are negligible and that the adsorbate is adsorbed onto the adsorbent surface directly (Han et al. 2008). This model is used only for the description of the initial part of the breakthrough curve, i.e., up to the breakpoint or 10–50 % of the saturation points (Kundu and Gupta 2006). This BDST model was focused on the estimation of characteristic parameters such as the maximum adsorption capacity and kinetic constant. The original BDST model was carried out by Bohart and Adams and given in Eq. (1) (Singh and Panat 2006)

$$\ln \left( {\frac{{C_{0} }}{{C_{B} }} - 1} \right) = \ln \;\left( {\exp \left[ {\frac{{KXN_{0} }}{v}} \right] - 1} \right) - KC_{0} t $$
(1)

A linear relationship between bed depth and service time is given by Eq. (2) (Goel et al. 2005)

$$t{ = }\frac{{N_{0} }}{{vC_{0} }}{\text{X}} - \frac{1}{{KC_{0} }}{ \ln }\;\left( {\frac{{C_{0} }}{{C_{B} }} - 1} \right){ \ln }\;{\text{C}}_{\text{o}} {\text{C}}_{\text{B}} - = \,{ \ln }\,({\text{eKx}}v{\text{N}}_{0} - 1- {\text{KC}}) $$
(2)

where C0 is the initial concentration of solute (mg L−1), C B the desired concentration of solute at breakthrough (mg L−1), K the adsorption rate constant (L−1 mg−1 h), N0 the adsorption capacity (mg L−1), X the bed depth of column (cm), v the linear flow velocity of feed to bed (cm h−1), t the service time of column under above conditions (h). Eq. (2) can be rewritten in the form of a straight line:

$$t\,{ = }\,a{\text{X}}\, - \,b $$
(3)

where a is the slope of BDST line \(\left( {a = \frac{{N_{0} }}{{vC_{0} }} } \right)\)and the intercept of this equation represened as Eq. (4).

$$b\,{ = }\,\frac{1}{{KC_{0} }}\ln \,\left( {\frac{{C_{0} }}{{C_{B} }}-1 } \right) $$
(4)

Thus, N0 and k can be evaluated from slope (a) and the intercept (b) of the plot of t versus X, respectively.

The critical bed depth (X0) is the theoretical depth of adsorbent sufficient to ensure that the outlet solute concentration does not exceed the breakthrough concentration (C B ) value at time t = 0. X0 can be calculated as Eq. (5) (Vijayaraghavan and Prabu 2006)

$$X_{0} \, = \,\frac{v}{{KN_{0} }}\ln \,\left( {\frac{{C_{0} }}{{C_{B} }}-1} \right) $$
(5)

The BDST model can be extended for the predication of a slope of the model at other flow rates. When the flow rate is changed from Q to a new value, Q′, the new value of slope (a1) is obtained by Eq. (6). However, the intercept remains unchanged because it depends on the inlet solute concentration, C0 (Taty-Costodes et al. 2005)

$${\text{a}}^{ 1} \, = \,\frac{aQ}{{Q^{1} }} $$
(6)

Thomas model

The Thomas model is one of the most general and widely used models to describe the behavior of sorption process in fixed-bed columns. The model is based on the assumption that the process follows Langmuir kinetics of sorption–desorption with no axial dispersion (Hasan et al. 2010). Its main limitation is that its derivation is based on second-order kinetics and considers that sorption is not limited by the chemical reaction but controlled by the mass transfer at the interface (Hasan et al. 2010). This discrepancy can lead to errors when this method is used to model sorption processes in specific conditions.

The model has the following form:

$$\frac{{C_{t} }}{{C_{0} }} = \frac{1}{{\left[ {1 + \exp \frac{{K_{T} (qm - C_{0} V)}}{r}} \right]}} $$
(7)

Substituting = t = V/r in Eq. (7), it becomes

$$\frac{{C_{t} }}{{C_{0} }} = \frac{1}{{\left[ {1 + \exp \left( {K_{T} \left\{ {\frac{qm}{r} - C_{0} t} \right\}} \right)} \right]}} $$
(8)

It can be rewritten as

$$KT\;\left( {\frac{qm}{r} - C_{0} t} \right) = \;{ \ln }\left( {\frac{{C_{t} }}{{C_{0} }} - 1} \right)$$

This is in the form of

$$Y\, = \,b-at $$
(9)

Having slope a = K T C0, intercept b = \(\frac{{K_{T} qm}}{r}\,\)where C t is effluent concentration (mg L−1), C0 is influent concentration (mg L−1), K T is Thomas rate constant (Lmin mg−1), q is the maximum biosorption capacity (mg g−1), m is mass of adsorbent (g), V is effluent volume (mL) and r is flow rate (mL min−1). The constants K T and q can be determined from a plot of ln (C t /C0−1) against t (Sivakumar and Palanisamy 2009)

Yoon Nelson model

This model is mathematically equivalent to the Thomas model, and it has also been applied to a range of concentrations in the effluent between the breakthrough and saturation time of the column (Martín-Lara et al. 2010). This model is based on the assumption that the rate of decrease in the probability of adsorption for each adsorbate molecule is proportional to the probability of adsorbate adsorption and probability of adsorbate breakthrough on the adsorbent. (Han et al. 2009) The linear form of Yoon and Nelson equation regarding a single-component system is expressed as

$${ \ln }\,\left( {\frac{{C_{t} }}{{C_{0} - C_{t} }}} \right) = \,K_{\text{YN}} {\text{t }} - \tau \,K_{\text{YN}} $$
(10)

where KYN is the Yoon–Nelson rate constant; τ is the time required for 50 % sorbate breakthrough and t is the breakthrough (sampling) time. The parameters KYN and τ may be determined from a plot of ln [C/(C0−C t )] versus sampling time (t). The derivation of Eq. (10) was based on the definition that 50 % breakthrough occurs at t = τ. Thus, the sorption bed should be completely saturated at t = 2τ. Owing to the symmetrical nature of breakthrough curves due to the Yoon–Nelson model, the mount of metal being sorbed in the fixed bed is half of the total metal entering the sorption bed within 2τ period. Hence, the following equation can be obtained for a given bed:

$$q_{\text{YN}} \, = \,\frac{{q_{\text{tot}} }}{M}\, = \,\frac{{\left( \frac{1}{2} \right)C_{0} \left( \frac{Q}{1000} \right)(2_{\tau } )}}{M }\, = \,\frac{{C_{0} Q_{\tau } }}{1000 M} $$
(11)

This equation also permits to determine the adsorption capacity of the column (qYN) as a function of bed height (Z), initial dye concentration (C0), flow rate (Q), biomass quantity in the column (M) and 50 % breakthrough time (τ) by using Yoon–Nelson model.

Results and discussion

Characterization of biosorbents

SEM analysis

SEM is one of the useful tools to examine the surface morphology of the biosorbent. SEM micrographs were taken before and after CV biosorption by CLR and CR. Figure 2 elucidates the surface structure of CLR and CR before and after CV biosorption. Before dye uptake, the CLR is characterized by irregular and porous surface (Fig. 2a). Following dye biosorption, pores are absent on the surface of CV-loaded CLR, suggesting biosorption of CV onto CLR (Fig. 2b). As can be seen from Fig. 2c, the CR biosorbent without contact with dye solution is a more fibrous material presenting some macro porous. The cavities of the fibrous materials were expanded, which should allow the diffusion of the dye molecules through the macro porous of the CR biosorbent. In addition, the appearance of a molecular cloud over the surface of dye-loaded biosorbent confirms the binding of dye ions to the functional groups present in CR.

Fig. 2
figure 2

SEM micrographs of raw and CV loaded CLR and CR

Full size image

FTIR analysis

The FTIR is an important tool to identify same characteristic functional groups, which are capable of adsorbing dye ions. The FTIR spectra of CLR and CR before and after biosorption of CV are shown in Fig. 3. The FTIR spectrum of CLR (before biosorption) shows several distinct and sharp absorption peaks (Fig. 3a). The peak positions are noticed at 3,929.84, 3,820.95, 3,706.86, 3,389.93, 3,285.60, 2,929.25, 2,239.66, 1,634.19, 1,430.29, 1,247.20, and 1,057.0 cm−1. The band at 3,929.84 cm−1 is due to O–H stretch vibration that is present on the biosorbent (Elkady et al. 2011). The band observed at about 2,929.25 cm−1 could be assigned to CH stretch shift (Hameed and El-Khaiary 2008). The peak present at 1,430.29 cm−1 represents the CH2 deformation (Hameed and El-Khaiary). The peak around 1,634.19 corresponds to C=O stretch (Hameed and Ahmad 2009). While the band at 1,247.20 cm−1 corresponds to Si–C stretch (Hameed et al. 2008), and the band at 1,057.0 cm−1 represents C–OH stretching vibration deformation (Tan et al. 2008). From Fig. 3b, after the biosorption of CV by CLR, it can be concluded that some of these peaks are shifted or disappeared and new peaks are also detected. These changes observed in the spectrum indicated the possible involvement of those functional groups on the surface of the CLR in sorption process.

Fig. 3
figure 3

FTIR spectrum of raw and CV loaded CLR and CR

Full size image

The FTIR spectra of CR before CV biosorption were performed in the range of 400–4,000 cm−1 to explore the surface characteristics of the biosorbent. Figure 3c illustrates the FTIR spectrum of the CR before CV biosorption. Cyperus rotundus consists of various functional groups on its surfaces. The main functional groups found were O–H stretching vibration of hydroxylic functional groups including hydrogen bonding which was detected at band width of 3,415–3,420 cm−1 (Mohd Azmier and Nazira Khabibor 2011). The intensities of peaks at 2,850 cm−1 were ascribed to –CH2 stretching vibrations (Tamer et al. 2010). The band at 1,590 cm−1 was attributed to –NH2 deformation (Dotto and Pinto 2011). In the FTIR of dye loaded CR (Fig. 3d), the broad and intense band ranging from 3,831 to 3,189 cm−1 can be ascribed to the hydrogen bonded –OH vibrations of the cellulosic structure of CR. The peaks at 2,980 and 714 cm−1 are due to –CH stretching vibration (Chowdhury et al. 2011a). The other prominent peaks are due to –NH2 and –C–O (1,631 and 1,367 cm−1, respectively). From the FTIR analysis, it is clear that the functional groups present on the surface of the biosorbents might involve in the dye sorption process.

Column studies

Effect of bed height

In order to determine the effect of bed height on the breakthrough curve, dye solution having influent CV concentration 25 mg L−1 and flow rate 10 mL min−1 was passed through the column by varying the bed height. The breakthrough curves obtained for CV biosorption onto CLR and CR at different bed heights are shown in Fig. 4a and b, respectively. From the figure, it was observed that the breakthrough time varied greatly with bed height. The breakthrough time increased from 9 to 30 h for CLR and 5 to 24 h for CR with increasing bed height from 10 to 30 cm. The mass of the sorbent forming the homogeneous fixed bed is proportional to the bed height, and as a result the number of sorption sites increases with the increase in bed height leading to a larger sorption capacity of the reactor (Hamdaoui 2006). The slope of the breakthrough curve decreased with increasing bed height which resulted in a broadened mass transfer zone. At lower adsorbent bed height, axial dispersion phenomenon predominated and reduced the diffusion of CV adsorbate (Foo and Hameed 2012). Higher uptake was observed at the highest bed height due to an increase in the surface area of the biosorbent, which provided more binding sites for the sorption (Vijayaraghavan et al. 2004). Also, as the bed height is increased, the dye molecules have more time to contact with the biosorbent resulting in higher dye removal efficiency (Saha et al. 2011)

Fig. 4
figure 4

Breakthrough curves for CV biosorption onto CLR and CR at different bed heights (flow rate = 10 mL min−1, initial dye concentration = 25 mg L−1)

Full size image

Effect of flow rate

Flow rate is an important parameter in evaluating the performance of a biosorption process, particularly for continuous treatment of wastewater on industrial scale (Saha et al. 2011). Therefore, the effect of flow rate on biosorption of CV by CLR and CR was studied by varying the flow rates from 10 to 20 mL min−1 and keeping the initial dye concentration 25 mg L−1 and bed height (30 cm) constant. The effect of flow rate on breakthrough performance at the above operating condition for CLR and CR is shown in Fig. 5a and b, respectively. From the figure it can be seen that, the breakthrough time as well as the biosorption efficiency of CLR and CR was lower at higher flow rate. As the flow rate increased from 10 to 20 mL min−1, the breakthrough time decreased from 30 to 8 h for CLR and 24 to 7 h for CR. This is due to the fact that at higher flow rate the contact time of the dye with the biosorbent surface is very short, and hence the dye molecules do not have enough time to capture the binding sites on the biosorbent surface or diffuse into the pores of the biosorbent, leaving the column before equilibrium occurs (Ahmad and Hameed 2010). However, the breakthrough curve became steeper when the flow rate was increased with which the breakthrough time and the dye removal efficiency decreased. But, when the flow rates were low, the external mass transfer controlled the process and it was also ideal for intra particle diffusion system. Thus, the lower flow rates, the more effective was the diffusion process and higher was the residence time of the sorbate, which ultimately resulted in high sorption capacity (Vijayaraghavan et al. 2004).

Fig. 5
figure 5

Breakthrough curves for CV biosorption onto CLR and CR at different flow rates (bed depth = 30 cm, initial dye concentration = 25 mg L−1)

Full size image

Effect of initial dye concentration

The effect of initial CV concentration (10, 15 and 25 mg L−1) on the biosorption of CV by CLR and CR at a constant bed height 30 cm and flow rate 20 mL min−1 is shown in Fig. 6a and b, respectively. From the figure it can be observed that, as the initial CV concentration increased from 10 to 25 mg L−1, the breakthrough and exhaustion time decreased considerably. In the biosorption of CV by CLR, the breakthrough time decreased from 34 to 8 h and exhaustion time decreased from 49 to 26 h; whereas in the biosorption of CV by CR, the breakthrough time and exhaustion time decreased from 26 to 7 h and 41 to 18 h, respectively. This is due to the fact that high dye concentration leads to quick saturation of the sorbent, which in turn leads to the earlier breakthrough and exhaustion time (Hasan et al. 2010). From the figure, it can also be seen that more favorable and steep breakthrough curves were obtained at high influent CV concentration. These results demonstrated that the change in concentration gradient affects the saturation rate and breakthrough time (Goel et al. 2005). This can also be explained by the fact that more sorption sites were being covered as the concentration of the dye increases (Han et al. 2009).

Fig. 6
figure 6

Breakthrough curves for CV biosorption onto CLR and CR at different initial dye concentration (bed depth = 30 cm, flow rate = 20 mL min−1)

Full size image

Application of Bed Depth Service Time (BDST) model

The experimental results obtained from CV biosorption in a column by CLR and CR were fitted to the BDST model to determine the biosorption capacities and kinetic constants. For this purpose, the service time, i.e., the exhaustion time of the column corresponding to bed height 10, 20, and 30 cm at three flow rates, i.e., 10, 15, and 20 mL min−1 at a constant influent CV concentration 25 mg L−1 were recorded. A plot of service time versus bed depth at different flow rates in the biosorption of CV by CLR and CR is shown in Fig. 7a and b, respectively. From the slope and intercept of these BDST plot, the BDST parameters viz. sorption rate constant (k), sorption capacity (N0), and critical bed depth (X0) were calculated and are listed in Table 1. High values of correlation coefficient (R2) (Table 1) showed that the variation of the service time with the bed depth is highly linear for all the systems, thus, indicating the validity of the BDST model when applied to the continuous column studies. The rate constant calculated from the intercept of the BDST plot characterizes the rate of solute transfer from the liquid phase to the solid phase (Hasan et al. 2010). It can be seen from the Table 1 that the values of the rate constant, k, were 0.03, 0.04, and 0.06 for CLR and 0.02, 0.03, and 0.05 for CR at flow rates 10, 15, and 20 mL min−1, respectively. The values of the rate constants showed an increasing trend with the increase in flow rate indicating that the overall system kinetics was dominated by external mass transfer in the initial part of the sorption in the column. In the biosorption of CV by CLR and CR, it has been found that the sorption capacity decreased with the increase in flow rate. The sorption capacity was reduced from 5.02 to 3.34 (mg cm3)−1 for CV biosorption by CLR and 4.54 to 2.39 (mg cm3)−1 for CV biosorption by CR. The values of k and N0 indicated that CLR and CR can be used as an efficient biosorbent for the removal of CV from aqueous solution. The values of the critical bed depth for CV biosorption by CLR and CR at different flow rates are given in Table 1. The value of critical bed depth was found to increase from 1.9 to 4.2 cm for CLR and 4.6 to 6.7 cm for CR as the flow rate increased from 10 to 20 mL min−1. The amount of CV biosorbed by CLR and CR in unit of mg g−1 can be calculated by dividing N0 with bulk density of CLR and CR in the column. This produced 34.15, 26.82, and 22.75 mg g−1 for CV biosorption by CLR and 46.14, 32.76, and 24.25 mg g−1 for CV biosorption by CR for flow rates of 10, 15 and 20 mL min−1 respectively.

Fig. 7
figure 7

Bed depth service time plot for CV biosorption onto CLR and CR (initial CV concentration = 25 mg L−1)

Full size image
Table 1 Bed depth service time (BDST) model parameters for the sorption of CV by CLR and CR
Full size table

Application of Thomas model

Thomas model was applied to the sorption kinetic data at three different flow rates, i.e., 10, 15, and 20 mL min−1 at an initial dye concentration of 25 mg L−1 and bed height of 10 cm for the sorption systems of CV by both CLR and CR. The Thomas rate constant (k T ) and the bed capacity (q0) were calculated from the slope and intercept of the plot between ln (C0/C t −1) versus t at different flow rates. The calculated values of k T and q0 along with the regression coefficients are presented in Table 2. The relatively high R2 values at all the operating conditions suggested that the Thomas model was suitable for describing the column biosorption data of CV by CLR and CR. As can be seen from the Table 2, at a constant depth of 10 cm, increased flow rate from 10 to 20 mL min−1 reduced the maximum CV biosorption capacity by CLR from 46.68 to 39.74 mg g−1 and from 53.79 to 43.85 mg g−1 by CR. This is due to the fact that, at a higher flow rate, the adsorption capacity was lower due to insufficient residence time of the solute in the column and diffusion of the solute into the pores of the adsorbent, and therefore the solute left the column before equilibrium occurred (Tan et al. 2008). The comparison of the experimental and predicted breakthrough curves obtained in the biosorption of CV by CLR and CR at different flow rates (10, 15 and 20 mL min−1) at a constant bed depth (10 cm) according to the Thomas model is shown in Fig. 8a and b, respectively. From the figure, it was clear that there was a good agreement between the experimental points and model predicted values.

Table 2 Parameters of Thomas model for the sorption of CV by CLR and CR
Full size table
Fig. 8
figure 8

Experimental and Thomas model predicted breakthrough curves at 10 cm depth for different flow rates (initial CV concentration = 25 mg L−1)

Full size image

Application of Yoon–Nelson model

Yoon–Nelson model was also applied to the column data obtained from CV biosorption by CLR and CR. Linear regression was performed, and the values of the parameters Yoon–Nelson constant (kYN) and τ (the time required for 50 % sorbate breakthrough) were determined from the plot of ln (C/C0-C t ) versus time. The value of these calculated parameters are presented in Table 3. It was found that the experimental data exhibited good fit to the model with R2, which was better in comparison to the Thomas model in both the cases (i.e., biosorption of CV by CLR and CR). The bed capacity was found to decrease with the increase in flow rate in the biosorption of CV by CLR and CR. The comparison of the experimental and predicted breakthrough curves obtained in the biosorption of CV by CLR and CR at different flow rates (10, 15 and 20 mL min−1) at a constant bed depth (10 cm) according to the Yoon–Nelson model is shown in Fig. 9a and b, respectively. From the figure, it was clear that there was a good agreement between the experimental points and model predicted values.

Table 3 Parameters of Yoon–Nelson model for the sorption of CV by CLR and CR
Full size table
Fig. 9
figure 9

Experimental and Yoon–Nelson model predicted breakthrough curves at 10 cm depth for different flow rates (initial CV concentration = 25 mg L−1)

Full size image

Column regeneration and reuse studies

The column with a bed depth of 10 cm and flow rate of 15 mL min−1 saturated with 25 mg L−1 of CV was selected for this study. Desorption was carried out by 1 N CH3COOH solution through the bed in the downward flow direction at a flow rate of 13 mL min−1, slightly less than the sorption flow rate 15 mL min−1. The concentration of CV was monitored after different time interval as shown in the Fig. 10. It was observed that desorption cycle took 8.5 h for CLR and 6 h for CR, after which further desorption was negligible. The maximum concentration of CV was obtained at a contact time of 30 min for CLR and 15 min for CR and recorded as 342 and 353 mg L−1 which were 13.7 and 14.12 times higher than influent CV concentration. The eluting solution was low in volume and high in concentration, which could help in easy handling and recovery and reuse of CV.

Fig. 10
figure 10

First cycle desorption profile of CV

Full size image

Comparison of sorption capacity of CLR and CR with other sorbents for the removal of CV in column mode

The use of low-cost, non-conventional sorbent for the removal of CV using column mode has not been paid much attention since now and thus very few literature is available on the sorption of CV using the continuous column mode and also the direct comparison of sorption capacity is difficult with other sorbents because of different applied experimental conditions. The comparison of sorption capacities of CLR and CR with other sorbents for the removal of CV in column mode is shown in Table 4. The results revealed that CLR and CR are promising biosorbents for the removal of CV from aqueous solution.

Table 4 Comparison of sorption capacity of CLR and CR with other sorbents for the removal of dye in column mode
Full size table

Conclusion

This study confirmed that the freely, locally and abundantly available agricultural wastes, Citrullus lanatus rind and Cyperus rotundus, could be used as an alternate to the commercial activated carbon for the removal of CV from aqueous solution. The sorption of CV was strongly dependent on the bed height, flow rate and initial dye concentration. An increase in bed height resulted in improved sorption performance. With the increase in flow rates, the uptake capacity was found to decrease. The increase in initial dye concentration resulted in higher uptake. A maximum uptake of 46.68 and 54.24 mg g−1 for CV biosorption by CLR and CR, respectively, was observed at 10 cm bed height, 10 mL min−1 flow rate and 25 mg L−1 initial dye concentration. The BDST model was used to predict the relationship between service time and bed height, which is essential in column process design. The experimental data fitted well to the BDST model. The bed sorption capacity (N0) was found to be 5.02 and 4.54 mg L−1 for CV biosorption by CLR and CR, respectively. The BDST model was also applied for the successful prediction of design parameters at different flow rates. Thomas and Yoon–Nelson models were also applied to the data, and the Yoon–Nelson model provided better descriptions of the experimental kinetic data in comparison to the Thomas model. Desorption studies were carried out by 1 N CH3COOH solution through the bed in the downward direction at a flow rate of 13 mL min−1. It was observed that desorption cycle took 8.5 h for CLR and 6 h for CR, after which desorption was negligible.