Introduction

Streamflow synthesis from ungauged catchments has long been recognized as a subject of scientific investigations. In this regard, many empirical, conceptual and physically based models were developed during the last century. Sherman (1932) first introduced the unit hydrograph model based on the rainfall and runoff data for gauged watershed as a means to develop a runoff hydrograph for any given storm hyetograph. The geomorphologic instantaneous unit hydrograph (GIUH) approach was initiated by Rodriguez-Iturbe and Valdes (1979) to relate rainfall–runoff process in ungauged basins. This was further developed by Valdes et al. (1979) and Rodriguez-Iturbe and Valdes (1979).

In the international front, various authors used the GIUH approach to formulate the rainfall–runoff transformation process under different conditions (Rodriguez-Iturbe et al.1982; Troutman and Karlinger 1985, Chutha and Dooge 1990; Sorman 1995). Wooding (1965) determined the geomorphology-based runoff hydrograph using the kinematic wave theory for flow on a catchment and along the stream, assuming the rainfall of constant intensity and finite duration. Yen and Lee (1997) derived the GIUH using the kinematic wave theory and stream-law ratios for computation of travel times for the overland and channel flows in a stream ordering sub-basin system.

In the national front, Bhaskar et al. (1997) derived the GIUH from the watershed geomorphologic characteristics, based on the approaches of Valdes et al. (1979) and Rodriguez-Iturbe and Valdes (1979), and used Nash instantaneous unit hydrograph (IUH) model to develop the gamma geomorphologic instantaneous unit hydrograph model (GGIUH) for Jira sub basin (under Mahanadi basin). Jain et al. (2000) applied geographical information system (GIS)-supported GIUH approach for the estimation of design flood for the Gambhiri sub-catchment (under Chambal basin) in India and reported the suitability of the approach for the estimation of the design flood particularly for the ungauged catchment. The derivation of the GIUH based on kinematic wave theory and geomorphologic parameters of the Gagas and Chaukhutia watersheds of the Ramanga catchment (under Ganga River basin in Uttaranchal, India) has been reported by Kumar and Kumar (2004) and Kumar and Kumar (2007). Sahoo et al. (2006) reported reasonably accurate computation of direct surface runoff hydrographs by the GIUH-based Clark and Nash models for Ajoy River (tributary of the Bhagirathi-Hugli—a distributary of the River Ganga) at Jamtara in India.

Again, physical, topographical and hydro-climatological features vary from river basin to river basin and to the best of our knowledge, no work related to (GGIUH) approach for computation of direct surface runoff hydrographs has been carried out for the Subarnarekha River basin which is the smallest of the fourteen major river basins of India and which drains sizeable portions of the three States of Jharkhand, Orissa and West Bengal in the eastern part of India. Therefore, it is appropriate to evaluate the GGIUH model for the basin of Dulung-Nala (an important tributary of the Subarnarekha River System in India).

Hence, the present study was carried out (1) to assess the performance of the GGIUH model (as developed by Bhaskar et al. 1997) for the basin of Dulung-Nala by computing the direct surface runoff hydrographs (DSRO) and (a) comparing them with observed DSRO hydrographs and with those derived by artificial neural network (ANN) model and (b) using statistical methods (in terms of probability density function) to identify the pattern replication ability of both the models; (2) to evaluate the effect of basin map scale (viz. 1:50,000 and 1:250,000) on the performance of the GGIUH model (which is based on geomorphological parameters of the basin).

It is worth mentioning that over the last two decades, neural networks have become very popular mathematical modeling tools in hydrology and water resources. The application of ANN modeling is widely reported in various hydrological literatures (Neelakantan and Pundarikanthan 2000; Ray and Klindworth 2000; Zhang and Govindaraju 2003; Ahmad and Simonovic 2005; Hong and Feng 2008; Zhang et al. 2008). Furthermore the use of the probability density function in hydrology has been found to be successful in solving many problems considering the hydrological laws and the quantity evaluation of the many characteristics of different hydrological regimes.

Study area

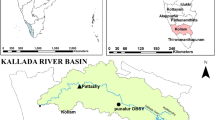
The Subarnarekha basin lying in eastern India is the smallest of the fourteen major river basins of India. It extends over 19,296 km2, covering 0.6% of geographical area of the country. The annual yield of water within the basin constitutes about 0.4% of the country’s total surface water resources. Dulung is its largest left bank tributary, having its origin in the forested uplands of western Midnapore. The basin of the Dulung, up to Phekoghat, measuring 802 km2 and lying between the latitudes 22°18′N and 22°37′N and longitudes 86°38′E and 87°E forms the study area for the present work (Fig. 1). Deep green area in Fig. 1 indicates forests and gray area indicates agricultural fields.

Fig. 1
figure 1

Location of the Basin of Dulung-Nala

Full size image

Data acquisition

The Survey of India toposheets (73J/10, 73J/14, 73J/15) (1:50,000) and 73J (1:250,000) were collected from the office of The Survey of India at Kolkata. Historical rainfall data spanning over the years 1995–2004 of the rain gauge stations (viz., Belpahari, Jhargram and Phekoghat) located in the basin (Fig. 1) were collected from the Dept. of Agriculture, GoWB. The discharge and flow velocity data at the Phekoghat gauging site (where stage is measured by water level stage recorder and flow velocity is measured by current meter) were collected for 1995–2004 from Central Water Commission, Govt of India, Bhubaneswar. The direct runoff which was estimated from the observed runoff data after deducting the baseflow was used to evaluate the Ф-index. The effective rainfall intensity was computed using this Ф-index. Sixteen isolated storm events (encompassing variety of sizes) were selected for study.

Methodology

GGIUH model

Rodriguez-Iturbe and Valdes (1979) presented a probabilistic description of the movement of runoff through the drainage network of the catchment. In this approach, the initial state probability of one drop of rainfall was expressed in terms of geomorphologic parameters as well as the transition probability matrix and the final probability density function (PDF) of droplets leaving the highest order stream into the trapping state yielded the GIUH.

Rodriguez-Iturbe and Valdes (1979) further suggested to assume a triangular instantaneous unit hydrograph (the GIUH) and specified the two most important characteristics of an IUH, the time to peak and peak of this hydrograph by the following expressions:

$$ q_{\text{p}} = 1.31\left( {R_{\text{L}} } \right)^{0.43} \left( {\tfrac{v}{{L_{\Omega } }}} \right) $$
(1)
$$ t_{\text{p}} = 0.44\left( {\tfrac{{L_{\Omega } }}{v}} \right)\left( {\tfrac{{R_{\text{B}} }}{{R_{\text{A}} }}} \right)^{0.55} \left( {R_{\text{L}} } \right)^{ - 0.38} $$
(2)

where LΩ is the length of the stream of highest order Ω; v is the expected peak velocity; qp is the peak flow; tp is the time to peak and RB, RL and RA are the Horton’s bifurcation ratio, length ratio and area ratio, respectively.

Rodriguez-Iturbe et al. (1979) rationalized that the peak velocity is a function of the effective rainfall intensity in order to derive qp and tp using Eqs. 1 and 2. Bhaskar et al. (1997) used the analytical from of the Nash IUH model (which is a two-parameter (n and k) gamma probability density function) along with Eqs. 1 and 2 and the relationship k = tp/(n − 1) for deriving the complete shape of the aforementioned GIUH and thus the gamma geomorphologic instantaneous unit hydrograph model (GGIUH) was developed. Singh (2004) used the following equation for deriving the ordinates of the GGIUH model-based unit hydrograph

$$ {\text{uh}}_{{g_{m} }} = \left( {5u_{{g_{m} }} + 8u_{{g_{m - 1} }} - u_{{g_{m - 2} }} } \right)\Updelta t/12 $$
(3)

where \( {\text{uh}}_{{g_{m} }} \) is the mth ordinate of the GGIUH model UH; \( {\text{u}}_{{g_{m} }} \) is the mth ordinate of the GGIUH model IUH; m = 3, 4, …, n.

The ordinates of the DSRO, obtained by the convolution of the \( {\text{uh}}_{{g_{m} }} \) with the excess rainfall hyetograph, is given by its discrete form as

$$ Q_{{c_{m} }} = \sum\limits_{t = 1}^{nr} {\left[ {EXR_{i} \times {\text{uh}}_{{g_{m - i + 1} }} } \right]} $$
(4)

where \( Q_{{c_{m} }} \) is mth ordinate of the computed direct surface runoff hydrograph; EXR i is excess rainfall intensity during the ith time step of duration \( \Updelta t; \)nr is the number of excess rainfall blocks of duration \( \Updelta t; \) and \( {\text{uh}}_{{g_{m} }} \) is the ordinate of the model UH.

Artificial neural network model

ANN is a flexible mathematical structure that is capable of identifying complex nonlinear relationships between input and output datasets. The ANN model of a physical system can be considered with n input neurons (x1, x2, …, x n ), h hidden neurons (z1, z2, …, z n ) and m output neurons (y1, y2, …, y n ). Let t j be the bias for neuron z j and f k for neuron y k . Let w ij be the weight of the connection from neuron x i to z j and beta is the weight of the connection z j to y k . The function that ANN calculates is

$$ y_{k} = g_{\text{A}} \left( {\sum {Z_{j} b_{jk} } + f_{k} } \right) \ldots \left( {j = 1- h} \right) $$
(5)

in which,

$$ z_{j} = f_{\text{A}} \left( {\sum {X_{i} W_{ij} + t_{j} } } \right) \ldots \left( {i = 1 - n} \right) $$
(6)

where gA and fA are the activation functions.

The development of an artificial neural network, as prescribed by ASCE (2000) follows the following basic rules,

  1. 1.

    Information must be processed at many single elements called nodes.

  2. 2.

    Signals are passed between nodes through connection links and each link has an associated weight that represents its connection strength.

  3. 3.

    Each of the nodes applies a non-linear transformation called as activation function to its net input to determine its output signal.

The numbers of neurons contained in the input and output layers are determined by the number of input and output variables of a given system. The size or number of neurons of a hidden layer is an important consideration when solving problems using multilayer feed-forward networks (Fig. 2). If there are fewer neurons within a hidden layer, there may not be enough opportunity for the neural network to capture the intricate relationships between indicator parameters and the computed output parameters. Too many hidden layer neurons not only require a large computational time for accurate training, but may also result in overtraining. A neural network is said to be “over-trained” when the network focuses on the characteristics of individual data points rather than just capturing the general patterns present in the entire training set. The network building procedure is divided into three phases which are described next in a broad way.

Fig. 2
figure 2

Basic methodology of model development by ANN

Full size image

Network building procedure

Selection of network topology

Neural networks can be of different types, like feed forward, radial basis function, time lag delay etc. The type of the network is selected with respect to the knowledge of input and output parameters and their relationship. Once the type of network is selected, selection of network topology is the next concern. Trial and error method is generally used for this purpose but many studies now prefer the application of genetic algorithm. Genetic algorithms are search algorithms based on the mechanics of natural genetic and natural selection. The basic elements of natural genetics—reproduction, crossover, and mutation—are used in the genetic search procedure (Majumdar et al. 2009).

Training phase

To encapsulate the desired input output relationship, weights are adjusted and applied to the network until the desired error is achieved. This is called as “training the network”.

Testing phase

After training is completed, some portion of the available historical dataset is fed to the trained network and known output is estimated out of them. The estimated values are compared with the target output to compute the MSE. If the value of MSE is less than 1%, the network is said to be sufficiently trained and ready for estimation. The dataset is also used for cross-validation to prevent overtraining during the training phase.

Generally 70% of the available dataset used for training and rest is equally divided for testing and validation purpose (15% each). In the present study 70, 15, and 15% were used, respectively, for training, testing and validation purpose.

For the present investigation, a linear equation of the relationship between peak discharge and the duration of the extreme event can be estimated by Eq. 8. The present problem used the pattern recognition ability of neural models to predict the constant α of Eq. 8.

A linear equation of any variable Y with X can be represented by,

$$ {{\alpha}}X + {{\beta}} = Y $$
(7)

where α and β are the linear constants, X is the independent variable and Y is the output predicted at an instant of X

Now, Eq. 7 can be rewritten as

$$ {{\alpha}}t + {{\beta}} = Q $$
(8)

where t is the time step and Q is the discharge at any instant t.

α was predicted by two sets of nonlinear data. This predicted α becomes the representative of nonlinearity between the Y and X datasets and when this α is used in the linear equation, the predicted X becomes a true representative of nonlinearity of the two datasets (Table 1). Now if the values of the constant are predicted with the help of observed dataset then a proper estimation of the constant will yield a better estimation of the discharge ordinate. The benefit of calibrative estimation approach is that the entire calibration is done in such a way that the observed dataset can be mapped and encoded as the representative of the existing nonlinearity.

Table 1 Input and output of ANN model
Full size table

Neural network model was prepared and trained with training algorithm Conjugate Gradient Descent (CGD) to compute discharge hydrograph using effective rainfall and observed discharge hydrograph as input for five storm events.

The correlation coefficient, standard deviation and mean square error were used to evaluate the efficiency of the training algorithm. After that, α was predicted for all the events and Q was estimated from Eq. 8.

Estimation of geomorphologic parameter

The boundary of the basin, stream network and elevation contours of the Dulung-Nala basin up to Phekoghat were mapped using Survey of India toposheets with scales of (1:50,000) and (1:250,000) using ArcGIS module of SMS 6.0—Surface Water Modeling System. The stream network and contours of the Dulung-Nala watershed were digitized and the vectorized maps were stored in shape files. Information on number of different orders of streams, stream length and corresponding basin area etc. were extracted from the vectorized maps. Strahler’s method of stream ordering was followed for ordering of streams. Horton’s laws were applied to estimate the geomorphologic parameters, viz., bifurcation ratio (RB), length ratio (RL), area ratio (RA), and length of highest order stream (LΩ) (Table 2) for use in Eqs. 1 and 2 for computing the time to peak and peak of the hydrograph.

Table 2 Geomorphological characteristics of the Dulung-Nala River basin
Full size table

Estimation of flow velocity

Rodriguez-Iturbe and Valdes (1979) in their studies have assumed that at any given instant during the storm, flow velocity can be taken as more or less constant throughout the catchment and have taken this flow velocity as the velocity corresponding to the peak discharge for a given rainfall–runoff event for the derivation of the GIUH. However, the peak discharge is not known for ungauged catchments. In such cases, the velocity may be estimated using relationship developed between velocity and excess rainfall in the following manner.

Assuming average excess rainfall intensity for a storm (with the assumption that storm will continue up to the time of equilibrium), the resulting equilibrium discharge may be given by the following equation: Qe = 0.2778 × ir × A where ir = P/Δt; P = depth of rainfall excess (in mm); A = catchment area in km2; and Δt = duration of excess rainfall.

Excess rainfall of constant intensity (ir), corresponding to observed discharge data was calculated using above equation. The observed velocity (V) corresponding to the above discharge data was also picked up from the dataset. From the pairs of such observed V and estimated ir, a relationship between ir and V was developed using power regression and this was used for flow velocity estimation.

Evaluation of the model

The model evaluation process included calibration, sensitivity analysis and validation. Critical parameters were identified by sensitivity analysis for the event of 16/8/2002 and the model was calibrated for the identified parameters.

The criteria for model evaluation involve the following:

  • Percentage error in simulated volume (PEV)

  • Percentage error in simulated peak (PEP), and

  • Net difference of observed and simulated time to peak (NDTP), as given below:

$$ {\text{PEV}} = \frac{{({\text{Vol}}_{\text{o}} - {\text{Vol}}_{\text{c}} )}}{{{\text{Vol}}_{\text{o}} }} \times 100 $$
(9)
$$ {\text{PEP}} = \frac{{(Q_{\text{po}} - Q_{\text{pc}} )}}{{Q_{\text{po}} }} \times 100 $$
(10)
$$ {\text{NDTP}} = (T_{\text{po}} - T_{\text{pc}} ) $$
(11)

Volo is the observed runoff volume (m3); Volc is the computed runoff volume (m3); Qpo is the observed peak discharge (m3/s); Qpc is the computed peak discharge (m3/s); Tpo is the time to peak of observed discharged (h); and Tpc is the time to peak of computed discharge (h). The prediction of overall performance of the model was assessed using Nash–Sutcliffe model efficiency (EFF) criterion (Nash and Sutcliffe 1970), recommended by ASCE Task Committee (1993)

$$ {\text{EFF}} = \frac{{\sum\limits_{i = 1}^{{n_{\text{o}} }} {\left( {Q_{\text{oi}} - \overline{Q}_{\text{o}} } \right)^{2} - \sum\limits_{i = 1}^{{n_{o} }} {\left( {Q_{\text{ci}} - Q_{\text{oi}} } \right)^{2} } } }}{{\sum\limits_{i = 1}^{{n_{\text{o}} }} {\left( {Q_{\text{oi}} - \overline{Q}_{\text{o}} } \right)^{2} } }} $$
(12)

where Qoi is ith ordinate of the observed discharge (m3/s); \( \overline{{Q_{\text{o}} }} \) is the mean of the ordinates of observed discharge (m3/s); Qci is ith ordinate of the computed discharge (m3/s).

After model prediction, the dataset was grouped into 10 classes. Each class represents the values that fall into the incremental domains which are determined by dividing the difference of highest and lowest data value with 10. The probability of these periods are plotted and matched with common distribution functions to identify the better matched one which was taken as the representative of the dataset. Predictions from the two models and actual data were used to identify the best fit density function.

Result and discussion

Morphometric analysis of the basin

The geomorphologic parameters were computed graphically by plotting number of streams, stream length and stream area versus the order of the stream and finding the slope of the best fit equation. The values of bifurcation ratio (RB), length ratio (RL), area ratio (RA) and length of highest order stream (LΩ) were estimated as RB = 3.5, RL = 2.2 and RA = 4.5, LΩ= 22.6 km and RB = 3.4, RL = 2.4, RA = 3.9 and LΩ = 22.1 for the two scales (1:250,000) and (1:50,000), respectively (Table 2). It may be noted that these ratios lie in the ranges of values observed for natural basins wherein RB ranges between 3 and 5, RL ranges between 1.5 and 3.5 and RA ranges between 3 and 6 (Smart 1972).

Velocity and effective rainfall intensity relationship

The following relationship was obtained between velocity and effective rainfall intensity

$$ V = 1.097i_{\text{r}}^{0.416} \left( {R^{2} = 0.9} \right)\quad {\text{for }}0.9 < i_{\text{r}} < 7 $$
(13)

where V is the flow velocity in m/s and ir is the excess rainfall intensity in mm/h. The above set of equations was used for determining the flow velocity corresponding to the average excess rainfall intensity of a particular storm event.

Calibration and sensitivity analysis of the model

The moderately high value of PEV (4.7%), high value of PEP (21.2%) and low value of Nash–Sutcliffe model efficiency (58.2%) for simulation of runoff with pre-calibrated model indicates the pre-calibrated model performance is poor.

Thus, in the present study critical parameters were identified by sensitivity analysis and the model was calibrated for the identified parameters

The results of the sensitivity analysis for peak discharge and runoff volume along with the calibrated parameters for the event of 16/8/2002 are shown in Table 3.

Table 3 Sensitivity analysis of calibrated parameters (n, RA, RB) of GGIUH model for the basin
Full size table

It is evident from Table 3 that both the peak discharge and runoff volume are more sensitive to the Nash model parameter n than to bifurcation ratio (RB), and area ratio(RA) as could be seen by either increasing or decreasing these parameters by ±1, ±5, ±10, ±15 and ±20%, respectively.

A change in the parameter n, RA and RB by 1–20% exhibited the peak discharge to vary from 1.1 to 27.2%, 3.4 to 21.2% and 3.4 to 21.6%, respectively. Corresponding runoff volume was found to vary from 0.3 to 12.5%, 2.1 to 2.6% and 2.2 to 2.7%, respectively.

The comparatively higher sensitivity of peak discharge to parameter n may be attributed to the fact that the parameter n representing number of reservoirs constituting the catchment is more dominant in yielding the peak discharge than the parameters RB and RA. Again, other watershed characteristics such as soil and land cover may also influence the results to some extent. The observed and simulated DSRO for the calibration event have been compared graphically as shown in Fig. 3.

Fig. 3
figure 3

Observed and calibrated DSRO hydrographs by GGIUH model for the event 16/8/2002

Full size image

It is evident from Fig. 3 that there is a close similarity in shape parameters of the hydrograph, such as peak discharge, time base and overall shape of the hydrograph. However, the time to peak of the predicted direct runoff hydrograph (DRH) occurred 2 h before that of the observed one. The low PEV, PEP and NDTP values (2.5%, 10.6% and 0) and the high value (79.1%) of the Nash–Sutcliffe model efficiency (EFF) for the storm event indicate that the model can be well adopted for simulation of direct runoff.

Thus the results indicate that overall prediction of DSRO by the GGIUH model during the calibration period is satisfactory and therefore may be accepted for further analysis.

Verification of the model

The calibrated model was then used for the estimation of DSRO for twenty storm events. The performance measures for all the events are shown in the Table 4.

Table 4 Performance measures of GGIUH model for storm events (basin map scale 1:50,000)
Full size table

The observed and simulated DSRO for four events were compared graphically as shown in Figs. 4, 5, 6 and 7.

Fig. 4
figure 4

Observed and simulated DSRO hydrographs by GGIUH model for two basin map scales for the event 6/9/2002

Full size image
Fig. 5
figure 5

Observed and simulated DSRO hydrographs by GGIUH model for two basin map scales for the event 21/7/1999

Full size image
Fig. 6
figure 6

Observed and simulated DSRO hydrographs by GGIUH model for two basin map scales for the event 16/8/1999

Full size image
Fig. 7
figure 7

Observed and simulated DSRO hydrographs by GGIUH model for two basin map scales for the event 14/9/1994

Full size image

It is observed from Table 4 that PEV, PEP and NDTP values vary from (2.9–20.9%), (0.1–20.8%) and (−1 to 3 h; only for the event of 25/7/1999 the deviation was 4 h), respectively, indicating a close agreement between observed and simulated runoff. The prediction limits for the simulation model for peak discharge and runoff volume have been found to be within ±20% (which is considered as acceptable levels of accuracy for simulations models) from measured values. The reasonably high (74.2–95.1%) values of the Nash–Sutcliffe model efficiency (EFF) show satisfactory performance of the model. A close similarity in peak discharge, time base and overall shape of the hydrographs are evident from Figs. 4, 5, 6 and 7.

The result is in agreement with an earlier study carried out for Chaukhutia watershed in India by Kumar and Kumar (2007), for Ajoy River basin in India by Sahoo et al. (2005), for Gagas watershed of Ram Ganga River, India by Kumar and Kumar (2004) and by Bhaskar et al. (1997) for Jira River subcatchment in eastern India.

Thus, the results confirm that GGIUH model predicts fairly well the peak discharge, time to peak and time base and runoff volume of the DRH for various storm events of the studied basin with marginal deviation as discussed earlier.

Since the GGIUH model utilizes only geomorphologic parameters of the basin and does not require the flow data, this model can be applied for predicting DRH for ungauged basins.

Comparative performance analysis of GGIUH model for two topographic map scales of 1:50,000 and 1:250,000

The DSRO hydrographs were computed using the GGIUH model at two map scales (viz. 1:50,000 and 1:250,000) in order to study the effect of the basin map scale on the performance of the GGIUH based model. The peak (QP) and time to peak (TP) of the direct surface runoff hydrographs of observed and as derived by the GGIUH model for the map scales 1:250,000 and 1:50,000 are shown in Table 5.

Table 5 Peak discharge and time to peak of the observed and the GGIUH model DSRO hydrographs at two basin map scales 1:250,000 and 1:50,000
Full size table

It is observed that the peak flow (qp) as estimated by the model is higher (ranges between 7.1 and 20.3%) at map scale 1:50,000 than that at map scale 1:250,000. While Time to peak (tp) as estimated by the model is lower (ranges between 0 and 16.7%) at map scale 1:50,000 than that at map scale 1:250,000.

It is revealed from Tables 4 and 6 that the EFF, NDTP and PEP are almost same for both the map scales. However, PEV is slightly lower for basin map scale 1:50,000 than that of 1:250,000. These results indicate that the GGIUH model yields comparable performance for the two map scales. Hence, a lower map scale of 1:250,000 can also be used to estimate the DSRO hydrographs for ungauged basin with reasonable accuracy.

Table 6 Performance measures of GGIUH model for storm events (basin map scale 1:250,000)
Full size table

It may be noted that Sahoo et al. (2005) in course of their study in Ajoy River basin in India concluded that smaller basin map scales can be used to estimate geomorphological parameters and correspondingly DSRO hydrographs.

Comparative performance analysis of GGIUH model and ANN

The neural network model trained with CGD algorithm has been used to predict DSRO hydrographs for various storm events. The DSRO predicted by ANN and GGIUH were compared and shown in Figs. 8, 9, 10 and 11.

Fig. 8
figure 8

DSRO hydrographs simulated by GGIUH model and ANN model for the event 6/9/2002

Full size image
Fig. 9
figure 9

DSRO hydrographs simulated by GGIUH model and ANN model for the event 21/7/1999

Full size image
Fig. 10
figure 10

DSRO hydrographs simulated by GGIUH model and ANN model for the event 11/10/1995

Full size image
Fig. 11
figure 11

DSRO hydrographs simulated by GGIUH model and ANN model for the event 14/9/1994

Full size image

It is evident from the figures that both the models have predicted the hydrograph characteristics uniformly, where slope of both GGIUH and ANN predicted hydrographs were found to be nearly equal for rising as well as recession curve, though a significant difference in time to peak was observed for both the hydrographs.

The performance measures of GGIUH model with respect to predicted discharge hydrograph by ANN model for 16 storm events are shown in the Table 7.

Table 7 Performance measures of GGIUH model with respect to ANN model for storm events
Full size table

It is observed from Table 7 that PEV, PEP and NDTP values range between 0.9 and 29.3%, 2.5 and 17.8% and 0 and 3 h, respectively, which indicates a good correlation between runoff computed by both ANN and GGIUH models. It may be noted that ‘Time to Peak discharge’ as estimated by both the models was found to be identical for the event of 23/6/1999. The reasonably high (73.9–88.8%) values of the Nash–Sutcliffe model efficiency (EFF) further supports this fact.

It may be noted that the distribution pattern of observed dataset was found to be same as the distribution pattern of dataset estimated by the GGIUH model for five events (Table 8). In the case of ANN model, the distribution patterns of observed and estimated datasets were found to be dissimilar for fifteen among sixteen events considered (Table 8). This establishes the superiority of the GGIUH model over ANN model.

Table 8 Probability distribution function (PDF) for observed data, GGIUH and ANN model
Full size table

Conclusion

Based on the previous work of Bhaskar et al. (1997) and Singh (2004), a gamma geomorphologic instantaneous unit hydrograph (GGIUH) model was developed for prediction of direct runoff from the catchment of the Dulung-Nala (the largest left bank tributary of the Subarnarekha River System) at Phekoghat station in the state of West Bengal in the eastern part of India.

The peak discharge and runoff volume were found to be quite sensitive to GGIUH model parameters viz., n, RA and RB. A change in these parameters by 1–20% resulted in the peak discharge to vary from 1.1 to 27.2%, 3.4 to 21.2% and 3.4 to 21.6%, respectively. On the other hand, for the same changes in the same three parameters, runoff volume was found to vary from 0.3 to 12.5%, 2.1 to 2.6% and 2.2 to 2.7%, respectively. Based on this sensitivity analysis, the calibration of the model was carried out for these parameters.

The Nash–Sutcliffe model efficiency (EFF) criterion, percentage error in volume (PEV), the percentage error in peak (PEP), and net difference of observed and simulated time to peak (NDTP) which were used for performance evaluation of the model for 16 storm events, have been found to range from 74.1 to 95.1%, 2.9 to 20.9%, 0.1 to 20.8% and −1 to 3 h (only for the event of 25/7/1999 the deviation was 4 h) respectively, indicating a good performance of the calibrated GGIUH model for prediction of runoff hydrograph.

Again, ANN models were prepared and trained with three different training algorithms to predict discharge hydrograph using observed rainfall and discharge hydrograph.

Analysis of performance measures of GGIUH model, with respect to predicted discharge hydrograph by ANN model, reveals that the PEV, PEP, NDTP and EFF values range between 0.9 and 29.3%, 2.5 and 17.8%, 0 and 3 h and 73.9 to 88.8%, respectively, indicating comparable performance of both ANN and GGIUH models.

Further, DSRO hydrographs computed using the GGIUH model at two map scales (viz. 1:50,000 and 1:250,000) were found to yield comparable performance indicating suitability of using lower map scale to estimate the DSRO hydrographs. Thus, lower map scales may also be employed for extraction of geomorphological parameters in case of non-availability of larger map scales (1: 50,000). This would further minimize the extent of labor and time involvement in estimating parameters and this has a practical relevance to field engineers. In a study in the Ajoy River basin in India, Sahoo et al. (2005) reported that smaller basin map scales may be used to estimate DSRO with reasonable accuracy. As GGIUH model was found to predict the event distribution pattern more efficiently than the ANN model, the supremacy of the former over latter is evident. Thus, the GGIUH model which does not use historical runoff data can be used for the prediction of design floods from ungauged basins.