Skip to main content
SpringerLink
Log in

Estimating the reliability of complex systems using various bounds methods

  • ORIGINAL ARTICLE
  • Published:
International Journal of System Assurance Engineering and Management Aims and scope Submit manuscript

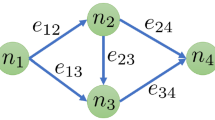
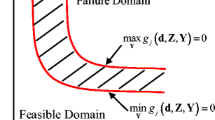
Abstract

The precise two-terminal reliability calculation becomes more difficult when the numeral of components of the complex system increases. The accuracy of approximation methods is often adequate for expansive coverage of practical applications, while the algorithms and computation time are typically simplified. As a result, the reliability bounds of two-terminal systems and estimation methods have been established. Our method for determining a complex system's reliability lower and upper bounds employs a set of minimal paths and cuts. This paper aims to present a modern assessment of reliability bounds for coherent binary systems and a comparison of various reliability bounds in terms of subjective, mathematical, and efficiency factors. We performed the suggested methods in Mathematica and approximated their interpretation with existing ones. The observed results illustrate that the proposed Linear and Quadratic bounds (LQb) constraint is superior to Esary-Proschan (EPb), Spross (Sb), and Edge-Packing (EDb) bounds in the lower bond, and the EDb bound is preferable to other methods above in the upper bond. This modification is attributed to sidestepping certain duplicative estimations that are part of the current methods. Given component test data, the new measure supplies close point bounds for the system reliability estimation. The Safety–Critical-System (SCS) uses an illustrative model to show the reliability designer when to implement certain constraints. The numerical results demonstrate that the proposed methods are computationally feasible, reasonably precise, and considerably speedier than the previous algorithm version. Extensive testing on real-world networks revealed that it is impossible to enumerate all minimal paths or cuts, allowing one to derive precise bounds.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Abbreviations

Sb:

Spross bound

EPb:

Esary-proschan bound

EDb:

Edge-packing bound

LQb:

Linear and quadratic bound

SCS:

Safety–critical system

i. i. d.:

Independent and identically distributed

\({x}_{i}\) :

A system component

\(\overline{{x }_{i}}\) :

The complement of component \({x}_{i}\) such that \(\overline{{x }_{i}}=1-{x}_{i}\)

\(Pr({x}_{i})\) :

The Probability of component \({x}_{i}\) such that \(Pr\left({x}_{i}\right)={r}_{i}\)

\({r}_{i}\) :

The reliability of component \({x}_{i}\)

\({q}_{i}\) :

The unreliability of component \({x}_{i}\)

\({\varvec{X}}\) :

The vector of all component \({x}_{i}\) of the system

\({\varvec{P}}\) :

The vector of all minimal path \({P}_{i}\) of the system

\({\varvec{D}}{\varvec{P}}\) :

The vector of all disjoint minimal path \(D{P}_{i}\) of the system

\({\varvec{C}}\) :

The vector of all minimal cut \({C}_{i}\) of the system

\({\varvec{D}}{\varvec{C}}\) :

The vector of all disjoint minimal cut \(D{C}_{i}\) of the system

\(IM\) :

Incidence matrix of the system

\(CM\) :

Minimal cut matrix of the system

\({R}_{Exact}\) :

The exact reliability of the system

\({Q}_{Exact}\) :

The exact unreliability of the system

\({R}_{LB}\) :

The reliability lower bound of the system

\({R}_{UB}\) :

The reliability upper bound of the system

\({B}_{j,r}\) :

The Boolean product of \({x}_{i}\) and \(\overline{{x }_{i}}\) for some \({P}_{i}\) or \({C}_{i}\)

\({A}_{j,i}\) :

Sets {\({B}_{j,r}\)} of disjoint products derived from \({P}_{i}\) or \({C}_{i}\)

\({\alpha }_{i}\) :

Portion that are obtained successively from

\({A}_{j,i}\) :

For minimal path \({P}_{i}\)

\({\beta }_{j}\) :

Portion that are obtained successively from

\({A}_{j,i}\) :

For minimal cut \({C}_{j}\)

\(\mu \left(g\right)\) :

A specified lower bound for a spross bound method

\(\gamma \left(h\right)\) :

A specified upper bound for a spross bound method

References

  • Aggarwal K (1993) Reliability engineering (Vol 3). Springer Science and Business Media

  • Babaei M, Rashidi-baqhi A (2022) Universal generating function-based narrow reliability bounds to evaluate reliability of project completion time. Reliab Eng Syst Saf 218:108121

    Article  Google Scholar 

  • Beichelt F, Sproß L (1989) Bounds on the reliability of binary coherent systems. IEEE Trans Reliab 38(4):425–427

    Article  MATH  Google Scholar 

  • Beichelt F (2012) Reliability and maintenance: networks and systems. Chapman and Hall/CRC

  • Colbourn CJ (1988) Edge-packings of graphs and network reliability. In: Annals of Discrete Mathematics 38 pp 49–61, Elsevier

  • Datta E, Goyal N (2023) An efficient sum of disjoint product method for reliability evaluation of stochastic flow networks using d-MPs. Int J Syst Assur Eng Manage pp 1–19

  • Datta E, Goyal NK (2017) Sum of disjoint product approach for reliability evaluation of stochastic flow networks. Int J Syst Assur Eng Manage 8:1734–1749

    Article  Google Scholar 

  • Esary JD, Proschan F (1963) Coherent structures of non-identical components. Technometrics 5(2):191–209

    Article  MathSciNet  MATH  Google Scholar 

  • Gertsbakh I, Shpungin Y (2011) Network reliability and resilience. Springer Science and Business Media

  • Hassan ZAH, Mutar EK (2017b) Geometry of reliability models of electrical system used inside spacecraft. 2017b Second Al-Sadiq International Conference on Multidisciplinary in IT and Communication Science and Applications (AIC-MITCSA)

  • Hassan ZA, Mutar EK (2017a) Evaluation the reliability of a high-pressure oxygen supply system for a spacecraft by using GPD method. Al-Mustansiriyah J Coll Educ 2(2):993–1004

    Google Scholar 

  • Hassan ZAH, Udriște C (2015) Equivalent reliability polynomials modeling EAS and their geometries. Ann West Univ Timisoara-Math Comput Sci 53(1):177–195

    Article  MathSciNet  MATH  Google Scholar 

  • Horváth Á (2013) The cxnet complex network analyser software. Acta Polytech Hungarica 10(6):43–58

    Google Scholar 

  • Jin T, Coit DW (2003) Approximating network reliability estimates using linear and quadratic unreliability of minimal cuts. Reliab Eng Syst Saf 82(1):41–48

    Article  Google Scholar 

  • Jula N, Costin C (2012) Methods for analyzing the reliability of electrical systems used inside aircrafts. In: Recent Advances in Aircraft Technology. IntechOpen

  • Kaushik B, Banka H (2015) Performance evaluation of approximated artificial neural network (AANN) algorithm for reliability improvement. Appl Soft Comput 26:303–314

    Article  Google Scholar 

  • Kuo W, Zuo MJ (2003) Optimal reliability modeling: principles and applications. John Wiley and Sons

    Google Scholar 

  • Malik S, Chauhan S, Ahlawat N (2020) Reliability analysis of a non series–parallel system of seven components with Weibull failure laws. Int J Syst Assur Eng Manage 11(3):577–582

    Article  Google Scholar 

  • Marichal J-L (2016) Structure functions and minimal path sets. IEEE Trans Reliab 65(2):763–768

    Article  Google Scholar 

  • Mi J, Li Y-F, Peng W, Huang H-Z (2018) Reliability analysis of complex multi-state system with common cause failure based on evidential networks. Reliab Eng Syst Saf 174:71–81

    Article  Google Scholar 

  • Mutar EK (2020) Matrix-based minimal cut method and applications to system reliability. Adv Sci Technol Eng Syst J 5(5):991–996

    Article  Google Scholar 

  • Mutar EK, Hassan Z (2017) On the geometry of the reliability polynomials. University of Babylon

  • Mutar EK, Hassan ZAH (2022) New properties of the equivalent reliability polynomial through the geometric representation. In: 2022 International Conference on Electrical, Computer and Energy Technologies (ICECET)

  • Mutar EK (2022a) Analytical method of calculating reliability sensitivity for space capsule life support systems. Math Probl Eng 2022a

  • Mutar EK (2022b) Path tracing method to evaluate the signature reliability function of a complex system. J Aerosp Technol Manage 14

  • Mutar EK (2022c) Reliability analysis of complex safety-critical system with exponential decay failure laws the 6th international conference on SRS

  • Mutar EK (2022d) Signature of electrical system reliability used inside aircraft IEEE 27th pacific rim international symposium on dependable computing (PRDC)

  • Pyzdek T, Keller PA (2003) Quality engineering handbook. CRC Press

    Book  Google Scholar 

  • Rai S, Veeraraghavan M, Trivedi KS (1995) A survey of efficient reliability computation using disjoint products approach. Networks 25(3):147–163

    Article  MATH  Google Scholar 

  • Rausand M (2014) Reliability of safety-critical systems: theory and applications. John Wiley and Sons

    Book  MATH  Google Scholar 

  • Rodionov A, Rodionova O (2013) Exact bounds for average pairwise network reliability. In: Proceedings of the 7th International Conference on Ubiquitous Information Management and Communication

  • Romero P (2021) Universal reliability bounds for sparse networks. IEEE Trans Reliab 71(1):359–369

    Article  Google Scholar 

  • Sebastio S, Trivedi KS, Wang D, Yin X (2014) Fast computation of bounds for two-terminal network reliability. Eur J Oper Res 238(3):810–823

    Article  MathSciNet  MATH  Google Scholar 

  • Sharma M (2014) Reliability analysis of a non-series parallel network in fuzzy and possibility context. Int J Educ Sci Res Rev 1(2):40–46

    Google Scholar 

  • Soh S, Rai S (1993) Experimental results on preprocessing of path/cut terms in sim of disjoint products technique. IEEE Trans Reliab 42(1):24–33

    Article  MATH  Google Scholar 

  • Todinov MT (2013) Flow networks: analysis and optimization of repairable flow networks, networks with disturbed flows, static flow networks and reliability networks. Newnes

    MATH  Google Scholar 

  • Wang Z, Zhang J, Huang T (2021) Determining delay bounds for a chain of virtual network functions using network calculus. IEEE Commun Lett 25(8):2550–2553

    Article  Google Scholar 

  • Xiao Z, Xu X, Xing H, Luo S, Dai P, Zhan D (2021) RTFN: a robust temporal feature network for time series classification. Inf Sci 571:65–86

    Article  MathSciNet  Google Scholar 

  • Xiao Z, Zhang H, Tong H, Xu X (2022) An efficient temporal network with dual self-distillation for electroencephalography signal classification. In: 2022 IEEE International Conference on Bioinformatics and Biomedicine (BIBM)

  • Xing H, Xiao Z, Zhan D, Luo S, Dai P, Li K (2022) SelfMatch: robust semisupervised time-series classification with self-distillation. Int J Intell Syst 37(11):8583–8610

    Article  Google Scholar 

  • Yang DY, Frangopol DM (2020) Life-cycle management of deteriorating bridge networks with network-level risk bounds and system reliability analysis. Struct Saf 83:101911

    Article  Google Scholar 

  • Zhu H, Zhang C (2019) Expanding a complex networked system for enhancing its reliability evaluated by a new efficient approach. Reliab Eng Syst Saf 188:205–220

    Article  Google Scholar 

Download references

Funding

No funding is required for the completion of this study.

Author information

Authors and Affiliations

  1. Department of Mathematics, Directorate of Education Babylon, Babylon, 51005, Iraq

    Emad Kareem Mutar

Authors
  1. Emad Kareem Mutar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Emad Kareem Mutar.

Ethics declarations

Conflict of interest

There are no conflicts of interest present that would affect the publication of this manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The following code allows the efficient computation of the IM ( in Eq. (3)) and CM ( in Eq. (4)) by using the MATHEMATICA software. Algorithms prepared by the author have been employed to find matrices in Eqs. (19) and (20).

figure a
figure b

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mutar, E.K. Estimating the reliability of complex systems using various bounds methods. Int J Syst Assur Eng Manag 14, 2546–2558 (2023). https://doi.org/10.1007/s13198-023-02108-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13198-023-02108-7

Keywords

Search

Navigation