1 Introduction

In designing a life test to investigate the lifetime distribution of a certain product, information on future observations can help us in determining the cost of the testing process and whether actions are needed to redesign the test (Valiollahi et al. 2017). Manufacturers can predict the number and times of future failures of a product using the past record of failures. Such predictions are useful to quantify future warranty costs and insure that a sufficient number of spare parts is available.

Prediction helps in developing plans and reduce the probability of risks in future. In manufacturing companies, financial managers need prediction bounds on the costs of future warranty (Meeker and Escobar 1998). Prediction gives managers the ability to make informed decisions and develop data-driven strategies. Therefore, it is necessary to develop point and interval predictors for future failure times.

Several studies have been conducted in the literature to study point and interval predictors for various types of lifetime distributions under a variety of experimental conditions. For example, Asgharzadeh et al. (2015) considered prediction of future failures for the two parameter Weibull random variable under hybrid censoring. They obtained three classical point predictors, namely the MLP, the BUP, and the CMP in addition to a Bayesian point predictor. Moreover, Valiollahi et al. (2017) have studied prediction based on censored samples from the generalized exponential distribution. Similar work on prediction for future failures from the exponential distribution can be found in Lawless (1971) and Ebrahimi (1992). The Weibull case was considered by Kundu and Raqab (2012). The one and two sample Bayesian prediction problems with hybrid censored data were considered by Shafay et al. (2012). Classical and Bayesian prediction in the Bur III model were discussed by Singh et al. (2019). ChauPattnaik et al. (2021) discuss component based reliability prediction using Markov chains techniques. Prediction of remaining useful life in some distributions was investigated using Artificial neural networks (ANN) by Farsi and Hosseini (2019).

It appears that little attention was given to developing and comparing the performance of point and interval predictors for future failures in the loglogistic model when the data are both left censored and right hybrid censored. In this paper, we developed various types of point predictors as well as prediction intervals. Using simulation techniques, the bias and mean squared error performance of the point predictors was investigated. The prediction intervals where compared based on their observed coverage probabilities and estimated expected interval lengths. The application of the methods studied in tis paper to real data was discussed using two examples.

The log-logistic distribution is an important statistical model with several applications in various fields. It is used in modeling population growth as first suggested by Verhulst (1838). It is known as the Fisk distribution in economic literature after Fisk (1961) where it was use for studying income inequality. In addition, it has several applications in reliability and life testing studies and sometimes used instead of the log-normal distribution as it is right skewed and has an increasing hazard rate function, it has heavier tail than the lognormal and its cumulative distribution functionand hazard function are available in simple closed forms, see Tahir et al (2014) and Akhtar and Khan (2014). The probability density, the cumulative distribution, and the reliability functions are given by (Lawless, 2003)

$$f\left(t\right)=\left\{\begin{array}{c}\frac{\alpha \beta (\alpha {t)}^{\beta -1}}{(1+{({\alpha t)}^{\beta })}^{2}} t\ge 0,\alpha >, \beta >0 ,\\ 0 otherwise\end{array}\right.$$
(1)
$$F\left(t\right)=P\left(T\le t\right)=\frac{{(\alpha t)}^{\beta }}{1+{(\alpha t)}^{\beta }} ,$$
(2)
$$S\left(t\right)=1- F\left(t\right)=1-\frac{{\left(\alpha t\right)}^{\beta }}{1+{\left(\alpha t\right)}^{\beta }}=\frac{1}{1+{\left(\alpha t\right)}^{\beta }} ,$$
(3)

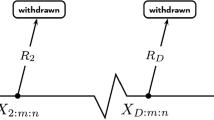
The hybrid censoring scheme is as follows: Assume that \(n\) units are put on test, the researcher terminates the experiment either when \(m<n\) units fail or when a certain time \(\tau\) for the experiment is reached. If \({X}_{m}\) is the time of the \({m}^{th}\) failure the life test will be stopped at time \({T}^{*}=\mathrm{min}({X}_{m},\tau )\). When \(n\) units are put on life test, and \(r\) out of \(n\) units have failure time less than a certain time \({t}_{0}\), the available information about the \(m\) units is that \(0\le {t}_{i}\le {t}_{0}\), \(i=1,\dots ,r\) where \({t}_{i}\) is the failure time of the \({i}^{th}\) unit. The failure times of the \(r\) units, \({t}_{1},\dots , {t}_{r}\) are left censored.

The remaining part of the paper is structured as follows. In Sect. 2, the likelihood equations are derived. In Sect. 3, predictive likelihood equations are obtained in addition to the point predictors. In Sect. 4, the prediction intervals are derived. In Sect. 5, we performed simulations to compare the performance of different predictors. An illustrative example based on real data is given in Sect. 6 . The conclusions and suggestions for further study are presented in the final section.

2 Likelihood construction and the maximum likelihood estimator

Now we will construct the likelihood function in the log-logistic case assuming a hybrid censored sample that include possibly left censored observations. Similar likelihood construction were considered by other authors in other situations including Ahmadi et al. (2012) for the proportional hazards model and Kundu and Mitra (2016) for the Weibull distribution. Assume that \(n\) units are placed on life test, assume that \(r\) units are left censored at time\({t}_{0}\). The contribution to the likelihood from a left censored observation is \({L}_{i}\left(\alpha ,\beta \right)=\frac{{\left(\alpha {t}_{0}\right)}^{\beta }}{1+{\left(\alpha {t}_{0}\right)}^{\beta }}\) and hence the Likelihood based on the left censored observations is \(\prod_{i=1}^{r}\frac{{\left(\alpha {t}_{0}\right)}^{\beta }}{1+{\left(\alpha {t}_{0}\right)}^{\beta }}= \frac{{\left(\alpha {t}_{0}\right)}^{r\beta }}{{\left(1+{\left(\alpha {t}_{0}\right)}^{\beta }\right)}^{r}.}\) Now we will consider hybrid censoring, we have two cases:

Case 1: There are \(m\) units with corresponding failure times: \({t}_{r+1},{t}_{r+2},{t}_{r+3},\dots ,{t}_{r+m}\) where \({t}_{i}<\tau\) for all \(i=r+1,\dots ,r+m\).

Case 2: We obtained \(s\) failures before time \(\tau\) with failure times: \({t}_{r+1},{t}_{r+2},{t}_{r+3},\dots ,{t}_{r+s}\) where \(s<m\) and \({t}_{r+s}<\tau <{t}_{r+s+1}\).

The hybrid censoring scheme is given in Figure 1 in Kundu and Pradhan (2009). A description of time terminated and failure terminated censoring types is given in several sources including Kececioglu (1991).

Combining the two cases as follows: Let \(d\) be the number of observed failures and \({\tau }^{*}\) be the experiment termination time, we have

$$d = \left\{ {\begin{array}{*{20}c} {m\,\,case\,\,1} \\ {s\,\,case\,\,2} \\ \end{array} } \right.$$
$$\begin{gathered} \tau ^{*} = \left\{ \begin{gathered} t_{{r + m}}\,\,case\,\,1 \hfill \\ \tau \,\,case\,\,2 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \end{gathered}$$

The \(d\) observations contribution to the likelihood is \(\prod_{i=r+1}^{r+d}f({t}_{i})=\prod_{i=r+1}^{r+d}\frac{\alpha \beta {\left(\alpha {t}_{i}\right)}^{\beta -1 }}{(1+{\left({\alpha {t}_{i})}^{\beta }\right)}^{2}}.\) The \(n-(r+d)\) censored data contribution to the likelihood is \({\left(1-F\left({\tau }^{*}\right)\right)}^{n-(r+d)}\).

The full likelihood function for both cases is

$$\begin{gathered} \left( {\alpha ,\beta } \right) = \frac{{\left( {\alpha t_{0} } \right)^{{r\beta }} }}{{\left( {1 + \left( {\alpha t_{0} } \right)^{\beta } } \right)^{r} }} \cdot \mathop \prod \limits_{{i = r + 1}}^{{r + d}} \frac{{\alpha \beta \left( {\alpha t_{i} } \right)^{{\beta - 1~}} }}{{(1 + \left( {\alpha t_{i} )^{\beta } } \right)^{2} }} \cdot \left\{ {\left( {\frac{1}{{1 + \left( {\alpha \tau ^{*} } \right)^{\beta } }}} \right)^{{n - \left( {r + d} \right)}} } \right\} \hfill \\ = \frac{{\left( {\alpha t_{0} } \right)^{{r\beta }} }}{{\left( {1 + \left( {\alpha t_{0} } \right)^{\beta } } \right)^{r} }} \cdot \mathop \prod \limits_{{i = r + 1}}^{{r + d}} \frac{{\alpha \beta \left( {\alpha t_{i} } \right)^{{\beta - 1~}} }}{{(1 + \left( {\alpha t_{i} )^{\beta } } \right)^{2} }}~ \cdot \left\{ {\left( {1 + \left( {\alpha \tau ^{*} } \right)^{\beta } } \right)^{{\left( {r + d} \right) - n}} } \right\} \hfill \\ \end{gathered}$$
(4)

The Log-Likelihood function is

$$\ln L\left( {\alpha ,\beta } \right) = r\beta \ln (\alpha t_{0} ) - r\ln (1 + \left( {\alpha t_{0} )^{\beta } } \right) + \mathop \sum \limits_{i = r + 1}^{i = r + d} \ln (\alpha \beta (\alpha t_{i} )^{\beta - 1} ) - 2\mathop \sum \limits_{i = r + 1}^{i = r + d} \ln ((1 + \left( {\alpha t_{i} )^{\beta } } \right) - \left( {n - \left( {r + d} \right)} \right)\ln (1 + \left( {\alpha \tau^{*} )^{\beta } } \right),$$
(5)

The log-likelihood function derivatives are given by

$$\frac{\partial L}{\partial \alpha }=\frac{r\beta }{\alpha }-\frac{r\beta ({\alpha {t}_{0})}^{\beta }}{\alpha \left(1+{\left(\alpha {t}_{0}\right)}^{\beta }\right)}+\frac{d\beta }{\alpha }-2\sum_{i=r+1}^{i=r+d}\frac{\beta {\left(\alpha {t}_{i}\right)}^{\beta }}{\alpha \left(1+{\left(\alpha {t}_{i}\right)}^{\beta }\right)}-\frac{\left(n-\left(r+d\right)\right)\beta {\left(\alpha {\tau }^{*}\right)}^{\beta }}{\alpha \left(1+{\left(\alpha {\tau }^{*}\right)}^{\beta }\right)} .$$
(6)
$$\frac{\partial L}{{\partial \beta }} = r\ln \left( {\alpha t_{0} } \right) - \frac{{r(\alpha t_{0} )^{\beta } \ln \left( {\alpha t_{0} } \right)}}{{\left( {1 + \left( {\alpha t_{0} } \right)^{\beta } } \right)}} + \mathop \sum \limits_{i = r + 1}^{i = r + d} \frac{{1 + \beta \ln \left( {\alpha t_{i} } \right)}}{\beta } - 2\mathop \sum \limits_{i = r + 1}^{i = r + d} \frac{{\left( {\alpha t_{i} } \right)^{\beta } \ln (\alpha t_{i} )}}{{\left( {1 + \left( {\alpha t_{i} } \right)^{\beta } } \right)}} - \frac{{\left( {n - \left( {r + d} \right)} \right)\left( {\alpha \tau^{*} } \right)^{\beta } \ln (\alpha \tau^{*} )}}{{\left( {1 + \left( {\alpha \tau^{*} } \right)^{\beta } } \right)}}$$
(7)

It is clear that the maximum likelihood estimator can’t be obtained explicitly. Therefore, numerical techniques can be used like the Newton Raphson technique or the Expectation–Maximization algorithm of Dempster et al. (1977) to find the MLEs.

3 Point prediction of future observations

We consider prediction of \(Y={T}_{p+(r+d)}\) where \(p=1,\dots ,n-(r+d)\) based on \(T=({T}_{r+1},\dots ,{T}_{r+d})\). Due to the Markov property for censored order statistics (Aggarwala and Balakrishnan 1998), \(Y|T=t\) has the same distribution as the \({p}^{th}\) order statistic of a sample of size \(n-(r+d)\) from the distribution \(G\left(y\right)=\frac{F\left(y\right)-F({\tau }^{*})}{1-F({\tau }^{*})}\) for all \(y>{\tau }^{*}\). The density function is \(g\left(y\right)=\frac{d}{dy}G\left(y\right)=\frac{f(y)}{1-F({\tau }^{*})}\). Therefore, the conditional density of \(Y={T}_{p+(r+d)}\) given \(T=t=({t}_{r+1},\dots ,{t}_{r+d})\) for all \(y>{\tau }^{*}\) is given by (Valiollahi et al. 2017):

$$f\left( {y|t} \right) = \frac{{\left( {n - \left( {r + d} \right)} \right)!}}{{\left( {p - 1} \right)!\left( {n - \left( {r + d} \right) - p} \right)!}}\left( {G\left( y \right)} \right)^{p - 1} \left( {1 - G\left( y \right)} \right)^{{n - \left( {r + d} \right) - p}} g\left( y \right)$$

Replace \(G\left(y\right) with \frac{F\left(y\right)-F({\tau }^{*})}{1-F({\tau }^{*})} and g\left(y\right) with \frac{f(y)}{1-F({\tau }^{*})}\), we get:

$$\begin{gathered} \left( {y|t} \right) = p\left( {\begin{array}{*{20}c} {n - \left( {r + d} \right)} \\ p \\ \end{array} } \right)\left[ {\left( {\alpha y} \right)^{\beta } - \left( {\alpha \tau ^{*} } \right)^{\beta } } \right]^{{p - 1}} \hfill \\ \left( {1 + \left( {\alpha y} \right)^{\beta } } \right)^{{ - n + \left( {r + d} \right) - 1}} \cdot \left( {1 + \left( {\alpha \tau ^{*} } \right)^{\beta } } \right)^{{n - \left( {r + d} \right) - p + 1}} \hfill \\ \,\, \cdot \alpha \beta (\alpha y)^{{\beta - 1}} , \hfill \\ \end{gathered}$$
(8)

for all \(y>{\tau }^{*}\), \(p=1,\dots ,n-(r+d)\).

3.1 The maximum likelihood predictor

Referring to Asgharzadeh et al. (2015), the predictive likelihood function (PLF) of \(Y and (\alpha ,\beta )\) is given by

$$L\left(y,\alpha ,\beta |t\right)=f(y|t,\alpha ,\beta )\cdot g(t|\alpha ,\beta )$$

where \(f(y|t,\alpha ,\beta )\) is the conditional density of \(Y\) and \(g(t|\alpha ,\beta )\) is the likelihood function of the log-logistic distribution. Hence,

$$L\left(y,\alpha ,\beta \right)=p\left(\begin{array}{c}n-\left(r+d\right)\\ p\end{array}\right){\left[{\left(\alpha y\right)}^{\beta }-{\left(\alpha {\tau }^{*}\right)}^{\beta }\right]}^{p-1}{\left(1+{\left(\alpha y\right)}^{\beta }\right)}^{-n+\left(r+d\right)-1}{\left(1+{\left(\alpha {\tau }^{*}\right)}^{\beta }\right)}^{n-\left(r+d\right)-p+1}\alpha \beta ({\alpha y)}^{\beta -1}\frac{{\left(\alpha {t}_{0}\right)}^{r\beta }}{{\left(1+{\left(\alpha {t}_{0}\right)}^{\beta }\right)}^{r}}\prod_{i=r+1}^{r+d}\frac{\alpha \beta {\left(\alpha {t}_{i}\right)}^{\beta -1 }}{(1+{\left({\alpha {t}_{i})}^{\beta }\right)}^{2}} \left\{{\left(1+{\left(\alpha {\tau }^{*}\right)}^{\beta }\right)}^{\left(r+d\right)-n}\right\}$$
(9)
$$\mathrm{ln}\,\,L\left(y,\alpha ,\beta \right)=\left(p-1\right)\mathrm{ln}\left[{\left(\alpha y\right)}^{\beta }-{\left(\alpha {\tau }^{*}\right)}^{\beta }\right]+(\left(r+d\right)-n-1)\mathrm{ln}(1+{\left(\alpha y\right)}^{\beta })+(1-p).\mathrm{ ln}\left(1+{\left(\alpha {\tau }^{*}\right)}^{\beta }\right)+\left(d+1\right)\mathrm{ln}\left(\alpha \beta \right)+\left(\beta -1\right)\mathrm{ln}\left(\alpha y\right)+r\beta \mathrm{ln}\left(\alpha {t}_{0}\right)-r\mathrm{ln}\left(1+{\left(\alpha {t}_{0}\right)}^{\beta }\right)+(\beta -1)\sum_{i=r+1}^{i=r+d}\mathrm{ln}\left(\alpha {t}_{i}\right)-2\sum_{i=r+1}^{i=r+d}\mathrm{ln}(1+{\left(\alpha {t}_{i}\right)}^{\beta })$$
(10)

It follows that

The maximum likelihood predictor (MLP) is the value ( \(\stackrel{\sim }{{Y}_{MLP})}\) in the maximizer of this function. Theerfore we obtain the derivatives of the log predictive likelihood as follows:

$$\frac{\partial \mathrm{ln}L\left(y,\alpha ,\beta \right) }{\partial y}=\frac{1}{y}\left[\frac{\left(p-1\right)\beta {\left(\alpha y\right)}^{\beta }}{{\left(\alpha y\right)}^{\beta }-{\left(\alpha {\tau }^{*}\right)}^{\beta }}+\frac{\left(r+d-n-1\right)\beta {\left(\alpha y\right)}^{\beta }}{1+{\left(\alpha y\right)}^{\beta }}+\beta -1\right]$$
(11)
$$\frac{\partial \mathrm{ln}L\left(y,\alpha ,\beta \right)}{\partial \alpha }=\frac{\beta }{\alpha }\left(\left(p-1\right)+\frac{\left(r+d-n-1\right){\left(\alpha y\right)}^{\beta }}{1+{\left(\alpha y\right)}^{\beta }}+\frac{\left(1-p\right){\left(\alpha {\tau }^{*}\right)}^{\beta }}{1+{\left(\alpha {\tau }^{*}\right)}^{\beta }}+\left(d+r+1\right)-\frac{r{\left(\alpha {t}_{0}\right)}^{\beta }}{1+{\left(\alpha {t}_{0}\right)}^{\beta }}-2\sum_{i=r+1}^{i=r+d}\frac{{\left(\alpha {t}_{i}\right)}^{\beta }}{1+{\left(\alpha {t}_{i}\right)}^{\beta }}\right)$$
(12)
$$\frac{\partial \mathrm{ln}L\left(y,\alpha ,\beta \right)}{\partial \beta }=\left(p-1\right)\frac{{\left(\alpha y\right)}^{\beta }\mathrm{ln}\left(\alpha y\right)-{\left(\alpha {\tau }^{*}\right)}^{\beta }\mathrm{ln}\left(\alpha {\tau }^{*}\right)}{{\left(\alpha y\right)}^{\beta }-{\left(\alpha {\tau }^{*}\right)}^{\beta }}+\left(r+d-n-1\right)\frac{{\left(\alpha y\right)}^{\beta }\mathrm{ln}\left(\alpha y\right)}{1+{\left(\alpha y\right)}^{\beta }}+\left(1-p\right)\frac{{\left(\alpha {\tau }^{*}\right)}^{\beta }\mathrm{ln}\left(\alpha {\tau }^{*}\right)}{1+{\left(\alpha {\tau }^{*}\right)}^{\beta }}+ \frac{(d+1)}{\beta }+\mathrm{ ln}\left(\alpha y\right)+r\mathrm{ln}(\alpha {t}_{0})-\frac{r{\left(\alpha {t}_{0}\right)}^{\beta }\mathrm{ln}\left(\alpha {t}_{0}\right)}{1+{\left(\alpha {t}_{0}\right)}^{\beta }}+\sum_{i=r+1}^{i=r+d}\mathrm{ln}(\alpha {t}_{i})-2\sum_{i=r+1}^{i=r+d}\frac{{\left(\alpha {t}_{i}\right)}^{\beta }\mathrm{ln}\left(\alpha {t}_{i}\right)}{1+{\left(\alpha {t}_{i}\right)}^{\beta }}$$
(13)

Solving the predictive likelihood equations will give the maximum likelihood predictor of Y ( \(\stackrel{\sim }{{Y}_{MLP})}\)

3.2 The best unbiased predictor

A predictor could be obtained using the conditional distribution of \(Y={T}_{p+(r+d)}\) given \(T=({T}_{r+1},\dots ,{T}_{r+d})\), see Valiollahi et al. (2019). This predictor \({Y}_{Cond}\) is the best unbiased predictor (BUP) of \(Y\). It is given by: \({Y}_{Cond}=E\left(Y|T\right)=\underset{{\tau }^{*}}{\overset{\infty }{\int }}yf\left(y|t,\alpha ,\beta \right)dy\) where \({\tau }^{*}\) is the experiment termination time. It follows that

$$Y_{{Cond}} = ~\mathop \smallint \limits_{{\tau ^{*} }}^{\infty } y \cdot p\left( {\begin{array}{*{20}c} {n - \left( {r + d} \right)} \\ p \\ \end{array} } \right) \cdot \left[ {\left( {\alpha y} \right)^{\beta } - \left( {\alpha \tau ^{*} } \right)^{\beta } } \right]^{{p - 1}} \cdot \left( {1 + \left( {\alpha y} \right)^{\beta } } \right)^{{ - n + \left( {r + d} \right) - 1}} \cdot \left( {1 + \left( {\alpha \tau ^{*} } \right)^{\beta } } \right)^{{n - \left( {r + d} \right) - p + 1}} \cdot \alpha \beta (\alpha y)^{{\beta - 1}} \cdot dy = p\left( {\begin{array}{*{20}c} {n - \left( {r + d} \right)} \\ p \\ \end{array} } \right) \cdot \left( {1 + \left( {\alpha \tau ^{*} } \right)^{\beta } } \right)^{{n - \left( {r + d} \right) - p + 1}} \cdot I_{1} ,$$

where \(I_{1} = \mathop {\mathop \smallint \limits^{\infty } }\limits_{{\tau ^{*} }} y \cdot \left[ {\left( {\alpha y} \right)^{\beta } - \left( {\alpha \tau ^{*} } \right)^{\beta } } \right]^{{p - 1}} \cdot \left( {1 + \left( {\alpha y} \right)^{\beta } } \right)^{{ - n + \left( {r + d} \right) - 1}} \cdot \alpha \beta (\alpha y)^{{\beta - 1}} \cdot dy,\)

Using the binomial theorem we obtain

$$\left[ {\left( {\alpha y} \right)^{\beta } - \left( {\alpha \tau ^{*} } \right)^{\beta } } \right]^{{p - 1}} = \sum\limits_{{k = 0}}^{{p - 1}} {\left( {\begin{array}{*{20}c} {p - 1} \\ k \\ \end{array} } \right)} \left( { - 1} \right)^{{p - 1 - k}} \cdot \left( {\left( {\alpha y} \right)^{\beta } } \right)^{k} \cdot \left( {\left( {\alpha \tau ^{*} } \right)^{\beta } } \right)^{{p - 1 - k}} ,I_{1} = \sum\limits_{{k = 0}}^{{P - 1}} {\left( {\begin{array}{*{20}c} {p - 1} \\ k \\ \end{array} } \right)} \left( { - 1} \right)^{{p - 1 - k}} \cdot \left( {\left( {\alpha \tau ^{*} } \right)^{\beta } } \right)^{{p - 1 - k}} \cdot \beta \smallint _{{\tau ^{*} }}^{\infty } \left( {\left( {\alpha y} \right)^{\beta } } \right)^{{k + 1}} .\left( {1 + \left( {\alpha y} \right)^{\beta } } \right)^{{ - n + \left( {r + d} \right) - 1}} dy,$$

Let \(t=\frac{1}{1+{\left(\alpha y\right)}^{\beta }}\) then \({\left(\alpha y\right)}^{\beta }=\frac{1-t}{t}\) and \(1+{\left(\alpha y\right)}^{\beta }=\frac{1}{t}\) and \(dy=\frac{-dt}{\alpha \beta {\left(\alpha y\right)}^{\beta -1}{t}^{2}}\) as \(y={\tau }^{*},t=\frac{1}{1+ {\left(\alpha {\tau }^{*}\right)}^{\beta }}\), as \(y\to \infty , t \to 0\) and the integral \({I}_{2}=\underset{{\tau }^{*}}{\overset{\infty }{\int }}{\left({\left(\alpha y\right)}^{\beta }\right)}^{k+1}\cdot {\left(1+{\left(\alpha y\right)}^{\beta }\right)}^{-n+\left(r+d\right)-1}dy\) will become

$$I_{2} = \frac{1}{{\alpha \beta }} \cdot \mathop {\mathop \smallint \limits^{{\frac{1}{{1 + \left( {\alpha \tau ^{*} } \right)^{\beta } }}}} }\limits_{0} \left( t \right)^{{n - \left( {r + d} \right) - k - 1 - \frac{1}{\beta }}} \cdot \left( {1 - t} \right)^{{k + \frac{1}{\beta }}} dt,Y_{{Cond}} = p\left( {\begin{array}{*{20}c} {n - \left( {r + d} \right)} \\ p \\ \end{array} } \right) \cdot \left( {1 + \left( {\alpha \tau ^{*} } \right)^{\beta } } \right)^{{n - \left( {r + d} \right) - p + 1}} \cdot \sum\limits_{{k = 0}}^{{p - 1}} {\left( {\begin{array}{*{20}c} {p - 1} \\ k \\ \end{array} } \right)} \left( { - 1} \right)^{{p - 1 - k}} \cdot \left( {\left( {\alpha \tau ^{*} } \right)^{\beta } } \right)^{{p - 1 - k}} \cdot \frac{1}{\alpha } \cdot \mathop {\mathop \smallint \limits^{{\frac{1}{{1 + \left( {\alpha \tau ^{*} } \right)^{\beta } }}}} }\limits_{0} \left( t \right)^{{n - \left( {r + d} \right) - k - 1 - \frac{1}{\beta }}} \cdot \left( {1 - t} \right)^{{k + \frac{1}{\beta }}} dt,$$
(14)

We can replace \(\alpha\) and \(\beta\) by their MLEs to obtain \({Y}_{Cond}.\) Note that, \({I}_{2}\) can be expressed as \(\frac{1}{\alpha \beta }\bullet B(\frac{1}{1+ {\left(\alpha {\tau }^{*}\right)}^{\beta }};n-\left(r+d\right)-k-\frac{1}{\beta },k+\frac{1}{\beta }+1)\) where \(B(z;a,b)\) is the incomplete beta function: \(B\left(z;a,b\right)=\underset{0}{\overset{z}{\int }}{\left(t\right)}^{a-1}\cdot {\left(1-t\right)}^{b-1}dt\) for \(0\le z<1\).

3.3 The conditional median predictor

Another predictor is the conditional median predictor \({Y}_{med}\). It is defined as \({Y}_{med}\) satisfying

$$P\left(Y\le {Y}_{med}|T=\left({T}_{r+1},\dots ,{T}_{r+d}\right)\right)=P\left(Y\ge {Y}_{med}|T=\left({T}_{r+1},\dots ,{T}_{r+d}\right)\right),$$

(Valiollahi et al., 2017). Consider the distribution of \(B\left(y\right)=\frac{F\left(y\right)-F({\tau }^{*})}{1-F({\tau }^{*})}\) where \(F\) is the cumulative distribution function of the log-logistic distribution.

$$B\left( y \right) = \left( {\frac{{\left( {\alpha y} \right)^{\beta } }}{{1 + \left( {\alpha y} \right)^{\beta } }} - \frac{{\left( {\alpha \tau^{*} } \right)^{\beta } }}{{1 + \left( {\alpha \tau^{*} } \right)^{\beta } }}} \right) \cdot \frac{1}{{1 - F\left( {\tau^{*} } \right)}} = \left( {\frac{{\left( {\alpha y} \right)^{\beta } }}{{1 + \left( {\alpha y} \right)^{\beta } }} - \frac{{\left( {\alpha \tau^{*} } \right)^{\beta } }}{{1 + \left( {\alpha \tau^{*} } \right)^{\beta } }}} \right) \cdot \left( {1 + \left( {\alpha \tau^{*} } \right)^{\beta } } \right) = \frac{{\left( {\alpha y} \right)^{\beta } - \left( {\alpha \tau^{*} } \right)^{\beta } }}{{1 + \left( {\alpha y} \right)^{\beta } }}$$

Following Asgharzadeh et. A. (2015), \(B\left(y\right)\) can be considered as having a Beta distribution \(B(p,n-r-d-p+1)\). Consider:

$$P\left(Y\le {Y}_{med}|T=\left({T}_{r+1},\dots ,{T}_{r+d}\right)\right)=P\left(\frac{{\left(\alpha Y\right)}^{\beta }-{\left(\alpha {\tau }^{*}\right)}^{\beta }}{1+{\left(\alpha Y\right)}^{\beta }} \le \frac{{\left(\alpha {Y}_{med}\right)}^{\beta }-{\left(\alpha {\tau }^{*}\right)}^{\beta }}{1+{\left(\alpha {Y}_{med}\right)}^{\beta }}|T=({T}_{r+1},\dots ,{T}_{r+d})\right),$$

Equivalently, \(P\left(B\le \frac{{\left(\boldsymbol{\alpha }{Y}_{med}\right)}^{{\varvec{\beta}}}-{\left(\boldsymbol{\alpha }{{\varvec{\tau}}}^{\boldsymbol{*}}\right)}^{{\varvec{\beta}}}}{1+{\left(\boldsymbol{\alpha }{Y}_{med}\right)}^{{\varvec{\beta}}}}\right)=0.5\) and hence \(\frac{{\left(\boldsymbol{\alpha }{Y}_{med}\right)}^{{\varvec{\beta}}}-{\left(\boldsymbol{\alpha }{{\varvec{\tau}}}^{\boldsymbol{*}}\right)}^{{\varvec{\beta}}}}{1+{\left(\boldsymbol{\alpha }{Y}_{med}\right)}^{{\varvec{\beta}}}}=\) Med \((B)\). Therefore,

\({Y}_{med}=\frac{1}{\alpha }{\left[\frac{\mathrm{Med}\left(B\right)+{\left(\boldsymbol{\alpha }{{\varvec{\tau}}}^{\boldsymbol{*}}\right)}^{{\varvec{\beta}}}}{1-\mathrm{Med}\left(B\right)}\right]}^{\frac{1}{\beta }}\). (15).

Where the unknown parameters are substituted by their MLEs.

4 Prediction intervals

We consider deriving prediction intervals for \(Y={T}_{p+(r+d)}\) based on the data \(T=({T}_{r+1},\dots ,{T}_{r+d})\). Let \(Z=B\left(y\right)=\frac{{\left(\boldsymbol{\alpha }{\varvec{y}}\right)}^{{\varvec{\beta}}}-{\left(\boldsymbol{\alpha }{{\varvec{\tau}}}^{\boldsymbol{*}}\right)}^{{\varvec{\beta}}}}{1+{\left(\boldsymbol{\alpha }{\varvec{y}}\right)}^{{\varvec{\beta}}}}\), it is clear that \(Z\) has a Beta distribution \(B(p,n-r-d-p+1)\). It could be used as a pivot to obtain \((1-\gamma )100\%\) prediction interval of \(Y\) (Asgharzadeh et al. 2015). If \({B}_{\gamma }\) is the \({100}^{\gamma th}\) percentile of \(B(p,n-r-d-p+1)\) then \((1-\gamma )100\%\) PI of \(Y\) is \(({a}_{1},{b}_{1})\) where.

\({a}_{1}=\frac{1}{\alpha }{\left[\frac{{B}_{\frac{\gamma }{2}}+{\left(\alpha {\tau }^{*}\right)}^{{\varvec{\beta}}}}{1- {B}_{\frac{\gamma }{2}}}\right]}^{\frac{1}{\beta }}\) and \({a}_{2}=\frac{1}{\alpha }{\left[\frac{{B}_{1-\frac{\gamma }{2}}+{\left(\alpha {\tau }^{*}\right)}^{{\varvec{\beta}}}}{1- {B}_{1-\frac{\gamma }{2}}}\right]}^{\frac{1}{\beta }}\). (16).

The parameters \(\alpha\) and \(\beta\) are to be replaced by their MLEs. Another Prediction interval is based on the highest density interval, see Valiollahi et al. (2017). It is the interval consisting of all points with density function higher than that of other values. The HDI for unimodal distributions produces the shortest such interval. Since \(B\left(y\right)\) is distributed as \(B(p,n-r-d-p+1)\), the \((1-\gamma )100\%\) HDI for prediction of \(Y\) is \(({a}_{2},{b}_{2})\)

where \({a}_{2}=\frac{1}{\alpha }{\left[\frac{{w}_{1}+{\left(\alpha {\tau }^{*}\right)}^{{\varvec{\beta}}}}{1- {w}_{1}}\right]}^{\frac{1}{\beta }}\) and \({b}_{2}=\frac{1}{\alpha }\cdot {\left[\frac{{w}_{2}+{\left(\boldsymbol{\alpha }{{\varvec{\tau}}}^{\boldsymbol{*}}\right)}^{{\varvec{\beta}}}}{1- {w}_{2}}\right]}^{\frac{1}{\beta }}\), (17).where \({w}_{1}\), \({w}_{2}\) are defined as: \(\underset{{w}_{1}}{\overset{{w}_{2}}{\int }}g(z)dz=1-\gamma\) and \(g\left({w}_{1}\right)=g({w}_{2})\). Solving \(g\left({w}_{1}\right)=g\left({w}_{2}\right),\) we get

$${\left(\frac{{w}_{1}}{{w}_{2}}\right)}^{p-1}={\left(\frac{{1-w}_{2}}{1-{w}_{1}}\right)}^{n-r-d-1},$$
(18)

It is clear that if \(p=1\), we get \({(\frac{{1-w}_{2}}{1-{w}_{1}})}^{n-r-d-1}=1\), hence \({w}_{1}= {w}_{2}\) and no prediction interval can be obtained. For other values of \(p\), we obtain the solutions \({w}_{1}\) and \({w}_{2}\) of the above equation and then substitute MLEs of the parameters \(\alpha\) and \(\beta\).

5 Simulation study

We will design a simulation study to investigate the performance of the predictors. Hybrid censored samples of size \(n\) from log-logistic distribution will be generated. The parameters \((\alpha ,\beta )\) from which the samples are generated are taken as \((\mathrm{3,2})\), the sample size \(n\) is taken as 20,30,50 and 80.

Following Piegorsch (1987), we used 2000 replications, based on each sample we obtain the point and interval predictors for the future values of \(Y={T}_{p+(r+d)}\),\(p=\mathrm{1,2},\dots ,n-(r+d)\). We reported the bias and mean square prediction error (MSPE) for the point predictors MLP, BUP and CMP. The Bias and MSPE of each predictor value are calculated as follows: If \(\stackrel{\sim }{{y}_{i}}\) is the value of the predictor of \(Y={T}_{p+(r+d)}\) obtained from the \({i}^{th}\) iteration,\(i=1,\dots , 2000\), then Bias \(=\frac{1}{N}(\sum_{i=1}^{N}(\stackrel{\sim }{{y}_{i}} -Y))\) and MSPE \(=\frac{1}{N}(\sum_{i=1}^{N}{((\stackrel{\sim }{{y}_{i}} -Y)}^{2})\).

We also investigated the performance of the prediction intervals developed in this paper. We calculated their empirical coverage probabilities and simulated expected lengths. The results for the point and interval predictors are given in Tables 1, 2, 3.

Table 1 Performance of point and interval predictors for \(p=1\)
Full size table
Table 2 Performance of point and interval predictors for \(p=2\)
Full size table
Table 3 Performance of point and interval predictors for \(p=3\)
Full size table
Table 4 The values of point predictors and the \(95\mathrm{\%}\) prediction intervals
Full size table

6 A real data example

We will consider the real data set used by Schmee and Nelson (1977) and later discussed by Lawless (2003). It represents the number of miles to failure of 96 locomotive controls. The experiment was stopped after 135,000 miles and the 37 failure times were recorded (in thousands):

22.5, 37.5, 46.0, 48.5, 51.5, 53.0, 54.5, 57.5, 66.5, 68.0, 69.5, 76.5, 77.0, 78.5, 80.0,

81.5, 82.0, 83.0, 84.0, 91.5, 93.5, 102.5, 107.0, 108.5, 112.5, 113.5, 116.0, 117.0,

118.5, 119.0, 120.0, 122.5, 123.0, 127.5, 131.0, 132.5, 134.0.

Hybrid censored samples will be obtained from this data set. We will predict \({T}_{p}\) for \(p=1\), 2, 3, 4 and 5. We notice that the (MLEs) obtained are \(\widehat{\alpha }=0.00623\) and \(\widehat{\beta }=2.5941\). The following data were generated according to the scheme where \({t}_{0}=0\), \({t}_{1}=135\) and \({m}_{1}=25\):

Data values: 22.5, 37.5, 46.0, 48.5, 51.5, 53.0, 54.5, 57.5, 66.5, 68.0, 69.5, 76.5, 77.0, 78.5, 80.0, 81.5, 82.0, 83.0, 84.0, 91.5, 93.5, 102.5, 107.0, 108.5, 112.5

Using the formulas (10), (14), (15), (16) and (17) derived in this paper, we obtained the following prediction results.

We note that all Point Predictors produce accurate results. Moreover, both Prediction Intervals contain the true “future” failure. The HDI intervals are shorter than the corresponding pivotal intervals (Table 4).

7 Conclusions and suggestions for further research

In this paper, we studied prediction of future values of the log-logistic distribution under hybrid censored data with possible left censoring. We obtain the predictive likelihood function and use it to obtain the MLP. The conditional density of the future failure was used to obtain the BUP, and CMP. Prediction intervals based on pivotal quantities were constructed. Moreover, we obtained the HDI interval. We investigated and compared the performance of the point predictors in terms of their Biases and MSPE. The two prediction intervals were compared in terms of coverage probability and average width.

Based on the results of the simulation study, it appears that the BUP has the best performance in terms of Bias and MSPE, followed by the CMP. As for prediction intervals, it appears that the interval based on pivotal quantity when \(p=1\) has an observed coverage probability that is close to the nominal level for all combinations of \(n\), \({t}_{0}\), \({t}_{1}\), and \(m.\) \(n\ge 30\). As the value of \(p\) gets larger, the observed coverage probability of both intervals gets close to the nominal level for large values of \(n\). The expected length of the HDI interval is smaller than that of the interval based on pivotal quantity for \(p>1\).

Under the effect of left censoring, the expected length of both intervals get slightly larger while the coverage probabilities get closer to the nominal level. Left censoring does not appear to have clear fixed on the performance of point predictors.

As \(m\) and \({t}_{1}\) increase, the bias and MSPE ofthe point predictors are almost unchanged. However, it is slightly increasing for the CMP. On the other hand, the lengths of the pivotal and HDI intervals gets slightly larger and the coverage probability of both intervals gets closer to the nominal.

In conclusion, we recommend that the best point predictor is the BUP as it has the least bias and MSPE, and the best interval prediction method is the HDI method for \(p>1\).

The work in this paper can be extended in several ways. For example, it may be of interest to consider prediction under other types of censoring that occur frequently in life testing experiments. Another possibility is to consider Bayesian prediction techniques. Moreover, it is of interest to consider prediction and the performance of the prediction techniques developed in this paper under step-stress life testing models.