1 Introduction

Different methods are being implemented to improve the performance of an of ultrawide band (UWB) radar systems, based on the modification of the geometries of the antennas, the use of meta-materials, and the use of lenses (Jenssen et al. 2019; Choudhary et al. 2020). These methods have found applications in ground-based non-destructive testing. (Choudhary et al. 2020; Zhang et al. 2019).

Since several years researchers have shown interest in Vivaldi antennas for radar applications; the Vivaldi antenna was introduced for the first time in 1979, (Gibson 1979). To improve the antenna characteristics (such as wide operating frequency range, etc.) further a modified structure known as antipodal Vivaldi antenna was introduced in (Gazit 1988). To improve the limitations faced by this antenna (Langley et al. 1993) proposed another type of Vivaldi antenna known as the balanced antipodal Vivaldi antenna. Further different types of loads and slots of different length on the arms of the antenna (Bai et al. 2011) have been used to improve the band width, directivity, and characteristics of the radiation patterns.

An extended dielectric director or lens was used by researcher in the antenna’s aperture to improve the bandwidth and gain (Juan et al. 2013; Keskin et al. 2020) . The half circular shaped lens was used in an exponentially tapered corrugated slot edge on the radiator and ground plane for gain enhancement (Moosazadeh et al. 2017). Various other methods based on lenses and slots have been used to improve the bandwidth, directivity, front-to-back ratio, and reduction of co-polarization and cross-polarization of antennas (Avdushin et al. 2014).

In this work, a printed lens (which is printed in the antenna’s aperture on the same planar substrate) is proposed to improve the performance of UWB radar systems in ground-based applications. UWB radar has the ability to penetrate concrete structures and good resolution in time domain, making it suitable for non-destructive testing (Choudhary et al. 2019). One such example of a non-destructive testing is health monitoring of bridges. In the long term, bridges require maintenance that may include ground-based non-destructive testing methods. Moreover, due to thick lossy concrete, electrically small reinforced iron joists size, unwanted noise and measurement errors, and the measured radar echoes fail to provide sufficient object information. Therefore, to overcome this problem, the printed lens can be used to focus the electromagnetic (EM) radiation of the radar’s antenna, which allows the detection of electrically small objects and also compensating for phase distortion. Further, the printed lens causes suppression of the clutter from unwanted objects, in an application where the determination of complex refractive index was performed.

To our knowledge, this is the first time a printed board lens is proposed for an antipodal Vivaldi antenna. The electromagnetic simulations and analysis of the antipodal-antenna design and system simulations for radar performance, are carried out using time-domain method in ANSYS high frequency simulator for electronics.

The article is structured as follows: Sect. 2 describes the design and results of the antipodal-Vivaldi antenna with printed lens. The radar performance simulations are presented in Sect. 3; Sect. 4 presents the conclusions.

2 Design

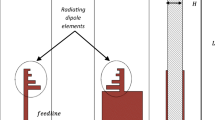
An antipodal-Vivaldi antenna with printed lens design is shown in Fig. 1(right). Figure 1(left) shows a zoomed view of the lens located in the antenna’s aperture. The lens was designed according to the design of the Antipodal-Vivaldi antenna, which has vertical symmetry (see Fig. 1). The design parameters are mentioned in Table 1 (see table 1). The structure consists of three layers: (1) a quarter elliptical design as a top metallic layer, (2) a low profile FR-4 epoxy substrate (\( \epsilon _{r}\) = 4.38, tan\( \delta \) = 0.003, with thickness t) as a dielectric substrate layer, and (3) a vertical mirror image of the top layer as a ground metallic layer. The top and bottom metallic layers are copper sheets with thickness (and conductivity of 5.8 \(\times \) 10\( ^{13} \) S/\( \mu \)m). All the three layers are sandwiched together in the z-plane.

Fig. 1
figure 1

An antipodal-Vivaldi antenna with the proposed printed lens (Left ) and, zoom view of lens (right)

Full size image
Table 1 Desgin parameters (in mm) of antipodal-Vivaldi antenna with printed lens in aperture
Full size table

On-board printed aperture lenses are insensitive to antenna rotation and misalignment, unlike bulky and separate metasurface microwave lenses as for example reported in (Azad et al. 2017), which may have misalignment issues. The Vivladi antenna (see Fig. 2) is used as the base-design to study the printed lens in the antenna’s aperture. The antenna is a tapered leaf shaped antipodal-designed structure. The antenna is feed along the height of the substrate in yz plane. The antenna is capable of operating in the frequency range 1–3 GHz. Initially, an aperture lens was reported in (Avdushin et al. 2014). It was tested and analysed, and the results were not as expected since the antipodal antenna device would require and antipodal-lens to achieve favorable results. Hence, we introduced the antipodal lens as shown in Fig. 1. We applied the optimization algorithm available in the electromagnetic simulator to optimize the printed lens’ parameters. The optimization aim is to maximize the gain and directivity without degrading the impedance matching to free space. Table 1 shows the optimized design paramters for the printed lens in aperture, (see zoomed view in Fig. 1). The frequency dependence of the S-parameters, i.e \( \mid S_{11} \mid \), of the antipodal-Vivaldi antenna with and without printed lens is shown in Fig. 2.

Fig. 2
figure 2

Magnitude of simulated \( S_{11} \) vs. frequency for the design shown in Fig. 1

Full size image

The proposed lens increases the gain of the antipodal-Vivaldi antenna (up to two decibel or more) as shown in Fig. 3. The figure also shows the dependence of gain versus frequency.

Fig. 3
figure 3

Simulated gain vs. frequency for the design shown in Fig. 1

Full size image

Further, Fig. 4 shows the 3D radiation pattern in xyz coordinates at a frequency of 1 GHz. As in the figure, the presence of the lens in the antenna’s aperture contributes to lowering the level of side lobes and focusing the EM radiation in the main beam lobe direction. The corresponding observation is made also for the increase in the antenna’s gain as shown in Fig. 3.

Fig. 4
figure 4

3D radiation pattern of the design shown in Fig.1, a without printed lens and b with printed lens in the antenna’s aperture

Full size image

Table 2 provides a comparison between the presented lenses with other different types of lenses proposed in the literature. We can compare lenses in terms of design, materials used, construction and performance as shown in the table (see Table 2). It can be seen that the design of the present lens is planar (see Fig. 1), which makes it cost-effective and simplifies the manufacturing process. Moreover, 3D lenses require a complex printing technology and complex artifical materials, which make fabrication difficult and expensive. Although the increase in gain is better observed in 3D lenses as compared to planar lenses, moreover problems like misalignment issues, design of complex artifical materials, bulky in size, costly manufaturing etc. make them challenging for researchers.

Table 2 Comparison between presented lens with other different type of lenses proposed in literature
Full size table

3 Radar performance simulation and analysis

The electromagnetic simulations of the antipodal Vivaldi antenna with printed lens and radar performance simulations were carried out using time domain methods in an electromagnetic simulator.

3.1 Object detection

The radar system contains two presented antipodal-Vivaldi antennas with print lenses, which are collocated as a transmitter and a receiver as shown in Fig. 5. The system operates in a wide frequency range as mentioned above (i.e. the wavelength is 0.3–0.1 m). Simulations of the radar performance were made for an electrically small object in a lossy dielectric medium, which corresponds to a bridge of concrete with reinforcement iron joists, as shown in Fig. 5.

Fig. 5
figure 5

The simulated radar system and setup

Full size image

In through-the-medium or through the wall non destructive testing, the medium’s high complex refractive index affects the radar echoes and results in high attenuation of received echoes (Juan et al. 2013). The electrically small metallic object (10 cm \(\times \) 5 cm ) is submerged in the dielectric medium (see Fig. 5). An electrically small object means that the size of the object is smaller than the operating wavelength. The distance between the air-concrete interface and the radar system is 30 cm to avoid near field effects as discussed in Juan et al. (2013). In our case, the dielectric properties of the medium (or concrete) is \( n= 4 \) and \( k=0.25 \), where n is the refractive index and k is the absorption of the medium. The simulated radar echoes without lens and with the lens are shown in Fig. 6a, b respectively. It is observed that the metallic object, replicating the radar cross section of a reinforced iron joist, is undetected in the radar echo without printed lens. In the case when the proposed lens is used, it is clearly detected. In addition, the noise level is reduced (see Fig. 6a, b).

Fig. 6
figure 6

Simulated radar echoes a the case without lens and b with the printed lens

Full size image

3.2 Radar imaging

Radar C-scan images are created by using frequency domain back projection imaging technique (Choudhary et al. 2019). To create the C-scan images the simulated radar echoes of different radar positions \( x_{i},y_{i} \) are processed together. For each \( x_{i},y_{i} \) positions of the antennas, the radar echo \( A(x_{i},y_{i}, \omega _{n}) \) is simulated. These received echoes are then combined in phase,

$$\begin{aligned} S(\overline{x},\overline{y}, \overline{z})=\sum _{n} \mid \sum _{i=0}^{N} A(x_{i},y_{i}, \omega _{n}) e^{(-j \omega _{n}\frac{d_{i}}{c_{0}})} \mid ^{2}, \end{aligned}$$
(1)

where \( d_{i} \) is the distance between radar position (\( x_{i},y_{i} \)) and image-pixel postion (\( \overline{x},\overline{y},\overline{z} \)).

The simulations were performed for different radar positions in a square pattern. The purpose of these simulations is to create the radar images (which are commonly used to visualize buried objects to a radar operator in industrial applications) and compare the results of radar images for the cases with and without lens. In Fig. 7a and b show the C-scan images of the metallic object. As expected, the metallic object is not clearly visible in the radar image, in which the printed lens was not used. However, in the case with the lens, the metallic object is clearly visible and easily distinguishable from the noise in the radar image.

Fig. 7
figure 7

Simulated C-scan radar images a the case without lens and b with the printed lens

Full size image

3.3 Clutter reduction in determination of complex refractive index

The two metallic objects and a dielectric object (with known dielectric properties) were used for simulations. One bigger metallic object (30 \( \times \) 30 cm\( ^{2} \)) used as a reference object (RO) whereas another metallic object (10 \( \times \) 10\( \hbox {cm}^{2} \)) used as a unintended object (UO). The geometry of the simulation is shown in Fig. 8, wherein the object under test is placed (at 40cm away from the radar) between the radar system and RO. RO and UO are positioned at distance of \( d_{1}= \) 1 m and \( d_{2} \) = 1.2 m from the radar system, respectively. UO is replicating the radar cross section of unintended objects such as metallic conveyor-belt housing, metallic joists, metallic small-structures, etc.(often present in industrial environments). We used a conventional method to determine the complex refractive index, \(\tilde{n}=n+jk\), as in (Choudhary and Rönnow 2020), in which the real part, n of the refractive index can determined from time delays of the reflected pulses from different interfaces. We do not consider multiple reflections; such pulses are small in amplitude and seen at longer times than three initial pulses from three interfaces (interfaces shown in Fig. 8). For the method to work properly, the reflected pulses from different interfaces must be separable in time domain. Reflected pulses are received in the recorded time series in the following steps:

  1. 1.

    Find the maximum peak value and the corresponding time instants of the time series. Define a time interval around this time instant; this is now one pulse.

  2. 2.

    Find the maximum value and the corresponding time instant of the time series, without the time interval from Step 1.

  3. 3.

    Continue until three maximum peak values from three pulses have been detected.

  4. 4.

    Sort the simulated pulses in adjacent order in time such that \( \tau _{1}, \tau _{2},\) and \( \tau _{3} \) are obtained.

  5. 5.

    Simiarly, \( \tau _{r} \) is obtained from the simulated reference pulse (without object under test).

Fig. 8
figure 8

The geometry of the simulation for determining the complex refractive index. Tx and Rx are the transmit and receive antenna. RO and UO are the reference object and unintended object, respectively

Full size image

Further, real part, n of the refractive index can determined as, (Choudhary and Rönnow 2020),

$$\begin{aligned} n= \frac{\tau _{2}-\tau _{1}}{\tau _{r}-\tau _{1}+\tau _{2}-\tau _{3}}, \end{aligned}$$
(2)

where \( \tau _{r} \) and \( \tau _{1} \) are the time delay of reference pulse (without object under test) and pulse from interface 1, etc., and the imagnary part, k, can be obtained from the slope of the ratio of the Fourier transforms of pulses, (Choudhary and Rönnow 2020),

$$\begin{aligned} k= M_{3r}\frac{c_{0}}{2(2\pi ) d} \end{aligned}$$
(3)

where \( M_{3r} \) is slope of the ratio of the Fourier transforms of pulse from interface 3 to reference pulse vs. frequency, \( c_{0} \) is the speed of light in vacuum, and d is the distance between radar and reflecting interface 2.

An example of slopes obtained from simulated data from setup (see Fig. 8) vs. frequency is shown in Fig. 9. It can be clearly seen in Fig. 9 that, in the presence of UO the ratio exhibits some frequency dependence, which results in a change in the slope (see black line and dashed line with \( \times \) marker). For the cases without and with lens, it can also be clearly seen in the figure that the slopes of the ratios in the different cases (i.e, UO is absent, wherein the lens is not used in the aperture of antenna and UO is present, wherein the lens is printed in the aperture of antenna) are in good agreement (see black line and \( \mathbf{o} \) markers), which means that focused EM radiation can avoid clutter from UO. Also, the slope of the ratio from the case, in which the UO is present (wherein lens is not used in the aperture of the antenna) shows relatively higher slope (see dashed line with \( \times \) marker) as discussed above. The effect may vary with the size of the UO as object, as experimentally investigated in (Choudhary and Rönnow 2020). Objects of different size results in different frequency dependence. We conclude omni- or wide EM radiation of the antenna may can introduce clutter from unintended objects.

Fig. 9
figure 9

Simulated values of the ratio of the amplitude of the reflected pulse from interface 3 to the reference pulse (in logarithm scale) vs. the frequency for the different cases

Full size image

Table 3 shows the true complex refractive index, \(\tilde{n}=n+jk\), of objects under test. Also, the real and imaginary parts of refractive index, which were determined for the two different cases (i.e, UO is present, wherein lens is not used and UO is present, wherein lens is printed in the aperture of the antenna). It also shows that the microwave lenses may can be used to reduce the clutter in determination of the complex refractive index of objects.

Table 3 Complex refractive index, \(\tilde{n}=n+jk\), of object under test
Full size table

4 Conclusions

We have presented the design of a printed lens for an antipodal-Vivaldi antenna, the purpose of which is to improve the performance of UWB radar systems at ground range. The presented lens works very well in the 1–3 GHz frequency band and furthermore an increase in gain can be seen up to 5.5 GHz (see Fig. 3). The lens is a modified micro-strips based structure printed in the antenna’s aperture. The antenna, intended for UWB radar applications is based on microstrip technology and is, hence, easy to fabricate. We can also conclude that the presented lens design contributes to lowering the level of side lobes and focusing EM radiation in the main beam lobe direction as well as ably compensate phase-distortion. Therefore, the gain is significantly increased for the antipodal-Vivaldi antenna. The lens design for the antenna is on the same substrate, so it is insensitive to rotation of the antenna. The 2-D printing technology can be used for lens fabrication, unlike 3-D lenses which require a complex printing technology. The results show that is suitable for non-destructive testing in ground-range (as shown in Sect. 3). The results also show that the microwave lens can be used to reduce the clutter in determination of the complex refractive index of objects in industrial applications.

The presented lens is limited to mentioned frequency range. It could be modified or improved for specific frequency range. Complex clutters could be measured and analysed. Other types of unintended-objects such as non-metallic objects (with differnet shapes) could be studied. The lens is also limited to antipodal antenna devices. The printed lens can be used for antipodal-antenna arrays and for beam-shaping applications.