The best single-observational and two-observational percentile estimations in the exponentiated Weibull-geometric distribution compared with maximum likelihood and percentile estimations

Abstract

In this research the best single-observation percentile estimation (BSPE) and best two-observation percentile estimation (BTPE), are introduced. Then theses estimators are obtained for probability density function and cumulative distribution function of the exponentiated Weibull-geometric (EWG) with increasing, decreasing, bathtub and unimodal shaped failure rate function. Finally, these estimators are compared with the maximum likelihood (ML) and percentile (PC) estimations using the Monte Carlo simulation and a real data set.

1 Introduction

The estimation of probability density function (PDF) and cumulative density function (CDF) of several lifetime distributions using the maximum likelihood (ML), uniformly minimum variance unbiased (UMVU), percentile (PC), least squares (LS) and weighted least squares (WLS) estimators have been obtained and compared by researchers. A number of papers have been attempted to estimate the lifetime distribution parameters, for instance the estimation of pdf and cdf of the Pareto distribution by Dixit and Jabbari Nooghabi (2010), exponentiated Pareto distribution by Jabbari Nooghabi and Jabbari Nooghabi (2010), exponentiated Gumbel distribution by Bagheri et al. (2013b), generalized Rayliegh distribution by Alizadeh et al. (2013) and generalized Poisson-exponential distribution by Bagheri et al. (2013a). Note that Menon (1963) and Zanakis and Mann (1982) estimated the parameters of Weibull distribution by best single-observation percentile estimation (BSPE) and best two-observation percentile estimation (BTPE), but in this research the PDF and CDF of the Exponentiated Weibull-Geometric (EWG) which is originally introduced by Mahmoudi and Shiran (2012) are obtained by BSPE and BTPE methods for One or Two known parameters and compared with the corresponding estimations found by PC and MLE procedures.

According to the structure in this paper, in Sects. 2 and 3, the BEPE, PCE, MLE and BTPE, PCE, MLE are obtained respectively. By using the Monte Carlo simulations, estimators were compared in Sect. 4, and the results for real data are provided in Sect. 5.

2 Calculating estimations when only one parameter is unknown

Let $X_{1} , \ldots ,X_{n}$ is a random sample with ordinal statistics of $Y_{1} , \ldots ,Y_{n}$, of a distribution with the following probability density and cumulative distribution functions:

$$ f\left( {x;\alpha ,\beta ,\gamma ,\theta } \right) = \frac{{\alpha \beta^{\gamma } \gamma \left( {1 - \theta } \right)x^{\gamma - 1} e^{{ - \left( {\beta x} \right)^{\gamma } }} \left( {1 - e^{{ - \left( {\beta x} \right)^{\gamma } }} } \right)^{\alpha - 1} }}{{\left[ {1 - \theta \left( {1 - e^{{ - \left( {\beta x} \right)^{\gamma } }} } \right)^{\alpha } } \right]^{2} }} $$

(1)

$$ F\left( {x;\alpha ,\beta ,\gamma ,\theta } \right) = \frac{{\left( {1 - \theta } \right)\left( {1 - e^{{ - \left( {\beta x} \right)^{\gamma } }} } \right)^{\alpha } }}{{1 - \theta \left( {1 - e^{{ - \left( {\beta x} \right)^{\gamma } }} } \right)^{\alpha } }} $$

(2)

Such that $x > 0, \alpha > 0, \beta > 0,\gamma > 0, 0 < \theta < 1$. In this section, assuming that parameters $\beta ,\gamma ,\theta$ are known and parameter $\alpha$ is unknown, the BSPE, PCE and MLE of $\alpha$ are obtained.

2.1 Estimation of the BSP

If $Y_{k}$ is the p-th percentile ($0 < p < 1$) of distribution (2), then

$$ p = F\left( {Y_{k} ;\alpha ,\beta ,\gamma ,\theta } \right) = \frac{{\left( {1 - \theta } \right)\left( {1 - e^{{ - \left( {\beta Y_{k} } \right)^{\gamma } }} } \right)^{\alpha } }}{{1 - \theta \left( {1 - e^{{ - \left( {\beta Y_{k} } \right)^{\gamma } }} } \right)^{\alpha } }} $$

where $k = \left[ {np} \right]$, if $np$ is an integer, otherwise, $k = \left[ {np} \right] + 1$ where $\left[ {np} \right]$ is the greatest integer smaller than $np$. Therefore, a single-observation percentile estimation of $\alpha$ which is shown by $\alpha^{*}$ is as follows:

$$ \alpha^{*} = \frac{{\log \frac{p}{{1 - \theta \left( {1 - p} \right)}}}}{{\log \left( {1 - e^{{\left( { - \beta Y_{k} } \right)^{\gamma } }} } \right)}} = \frac{{\log \left[ { - \log \left( {1 - p^{*} } \right)} \right]}}{{\log Z_{k} }} $$

(3)

Such that $p^{*} = 1 - e^{{ - \frac{p}{{1 - \theta \left( {1 - p} \right)}}}}$ and $Z_{k} = 1 - e^{{\left( { - \beta Y_{k} } \right)^{\gamma } }}$. According to Dubey (1967, p. 122), $\alpha^{*}$ has an asymptotic normal distribution with mean of $\alpha$ and variance of

$$ Var\left( {\alpha^{*} } \right) = \frac{{\alpha^{2} p^{*} }}{{n\left( {1 - p^{*} } \right)\log^{2} \left( {1 - p^{*} } \right)\log^{2} \left[ { - \log \left( {1 - p^{*} } \right)} \right]}} = \frac{{\alpha^{2} \left( {1 - e^{ - q} } \right)}}{{nq^{2} e^{ - q} \log^{2} q}} $$

where $q = \frac{p}{{1 - \theta \left( {1 - p} \right)}}$. Now $q$ is determined in a way that $Var\left( {\alpha^{*} } \right)$ is minimum, which in this case, solves the equation

$$ q\log q - 2\left( {1 + \log q} \right)\left( {1 + e^{ - q} } \right) = 0 $$

By an iterative method, $q = 0.1189$ and finally, the optimal $p$ is obtained by the following relation.

$$ p = \frac{{0.1189\left( {1 - \theta } \right)}}{1 - 0.1189\theta } $$

Therefore, the BSPE of $\alpha$ as shown by $\hat{\alpha }_{BSPE}$ is determined as follows:

$$ \hat{\alpha }_{BSPE} = \frac{{\log \left[ {0.1189\left( {1 - \theta } \right)/\left( {1 - 0.1189\theta } \right)} \right]}}{{\log \left( {1 - e^{{ - \left( {\beta Y_{k} } \right)^{\gamma } }} } \right)}} $$

Such that, $k = \left[ {n\frac{{0.1189\left( {1 - \theta } \right)}}{1 - 0.1189\theta }} \right]$ or $k = 1 + \left[ {n\frac{{0.1189\left( {1 - \theta } \right)}}{1 - 0.1189\theta }} \right]$.

Thus, the BSPE of functions (1) and (2) are obtained by the following relation, respectively.

$$ \hat{f}_{BSPE} \left( {x;\alpha ,\beta ,\gamma ,\theta } \right) = \frac{{\hat{\alpha }_{BSPE} \beta^{\gamma } \gamma \left( {1 - \theta } \right)x^{\gamma - 1} e^{{ - \left( {\beta x} \right)^{\gamma } }} \left( {1 - e^{{ - \left( {\beta x} \right)^{\gamma } }} } \right)^{{(\hat{\alpha }_{BSPE} ) - 1}} }}{{\left[ {1 - \theta \left( {1 - e^{{ - \left( {\beta x} \right)^{\gamma } }} } \right)^{{\hat{\alpha }_{BSPE} }} } \right]^{2} }} $$

$$ \hat{F}_{BSPE} \left( {x;\alpha ,\beta ,\gamma ,\theta } \right) = \frac{{\left( {1 - \theta } \right)\left( {1 - e^{{ - \left( {\beta x} \right)^{\gamma } }} } \right)^{{\hat{\alpha }_{BSPE} }} }}{{1 - \theta \left( {1 - e^{{ - \left( {\beta x} \right)^{\gamma } }} } \right)^{{\hat{\alpha }_{BSPE} }} }} $$

2.2 PCE

Let $X_{1} , \ldots ,X_{n}$ is a random sample distribution with CDF given in (2) with order statistics of $Y_{1} , \ldots ,Y_{n}$, and $p_{i}$ is the percentile of $Y_{i}$, then, $F\left( {Y_{i} ,\alpha ,\beta ,\gamma ,\theta } \right) = p_{i}$ or

$$ \log \frac{{p_{i} }}{{\left[ {1 - \theta \left( {1 - p_{i} } \right)} \right]}} = \alpha \log \left( {1 - e^{{ - \left( {\beta Y_{i} } \right)^{\gamma } }} } \right) $$

The PCE of $\alpha$ which is shown by $\hat{\alpha }_{PCE}$ is obtained by the minimization of

$$ \mathop \sum \limits_{i = 1}^{n} \left[ {\alpha \log \left( {1 - e^{{ - \left( {\beta Y_{i} } \right)^{\gamma } }} } \right) - \log \frac{{p_{i} }}{{\left[ {1 - \theta \left( {1 - p_{i} } \right)} \right]}}} \right]^{2} $$

with respect to $\alpha$. ($p_{i} = \frac{i}{n + 1}$), so

$$ \hat{\alpha }_{PCE} = \mathop \sum \limits_{i = 1}^{n} { \log }\frac{{p_{i} \left( {1 - e^{{ - \left( {\beta Y_{i} } \right)^{\gamma } }} } \right)}}{{\left[ {1 - \theta \left( {1 - p_{i} } \right)} \right]}} \left/\mathop \sum \limits_{i = 1}^{n} \left( {1 - e^{{ - \left( {\beta Y_{i} } \right)^{\gamma } }} } \right)^{2}\right. $$

Therefore, the PCEs of functions (1) and (2) are obtained as follows:

$$ \hat{f}_{PCE} \left( {x;\alpha ,\beta ,\gamma ,\theta } \right) = \frac{{\hat{\alpha }_{PCE} \beta^{\gamma } \gamma \left( {1 - \theta } \right)x^{\gamma - 1} e^{{ - \left( {\beta x} \right)^{\gamma } }} \left( {1 - e^{{ - \left( {\beta x} \right)^{\gamma } }} } \right)^{{(\hat{\alpha }_{PCE} ) - 1}} }}{{\left[ {1 - \theta \left( {1 - e^{{ - \left( {\beta x} \right)^{\gamma } }} } \right)^{{\hat{\alpha }_{PCE} }} } \right]^{2} }} $$

$$ \hat{F}_{PCE} \left( {x;\alpha ,\beta ,\gamma ,\theta } \right) = \frac{{\left( {1 - \theta } \right)\left( {1 - e^{{ - \left( {\beta x} \right)^{\gamma } }} } \right)^{{\hat{\alpha }_{PCE} }} }}{{1 - \theta \left( {1 - e^{{ - \left( {\beta x} \right)^{\gamma } }} } \right)^{{\hat{\alpha }_{PCE} }} }} $$

For more details about the PCE method, see Kao (1958, 1959) and Johnson et al. (1994). Mean square error (MSE) of percentile estimations of functions (1) and (2) is calculated by Monte Carlo simulation method of the sample mean.

2.3 MLE

According to a random sample of $X_{1} , \ldots ,X_{n}$ of distribution with the probability density function (1), the MLE of the parameter $\alpha$, i.e. $\hat{\alpha }_{MLE}$ is obtained by:

$$ \frac{n}{\alpha } + \mathop \sum \limits_{i = 1}^{n} \frac{{\left[ {1 + \theta \left( {1 - e^{{ - \left( {\beta x_{i} } \right)^{\gamma } }} } \right)^{\alpha } } \right]{ \log }\left( {1 - e^{{ - \left( {\beta x_{i} } \right)^{\gamma } }} } \right)}}{{1 - \theta \left( {1 - e^{{ - \left( {\beta x_{i} } \right)^{\gamma } }} } \right)^{\alpha } }} = 0 $$

where replacing $\hat{\alpha }_{MLE}$ by $\alpha$ in relations (1) and (2), The MLE of the probability density and cumulative distribution functions of EWG distribution can be obtained. Moreover, by Monte Carlo simulation method of the sample mean, the mean square error (MSE) of the MLE of functions (1) and (2) could be found.

3 Calculating estimators when two parameters are unknown

In this section, a random sample of size $n$ from the pdf given in (1) is considered. We assume that the parameters $\gamma$ and $\beta$ are unknown, and parameters α and $\theta$ are known,. Then the BTPE, PCE and MLE of $\gamma$ and $\beta$, for the pdf (1) and cdf (2) are obtained.

3.1 BTPE

Suppose $X_{1} , \ldots ,X_{n}$ is a random sample of distribution with cdf (2) with ordinal statistics of $Y_{1} , \ldots ,Y_{n}$, and $p_{i}$ is the percentile of $Y_{i}$, then, $F\left( {Y_{i} ,\alpha ,\beta ,\gamma ,\theta } \right) = p_{i}$ or

$$ \gamma \left( {{ \log }\beta + { \log }Y_{i} } \right) = { \log }\left\{ { - { \log }\left[ {1 - \left( {\frac{{p_{i} }}{{1 - \theta + \theta p_{i} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\} $$

(4)

such that for two real values of $p_{1}$ and $p_{2}$ ($0 < p_{1} < p_{2} < 1$) and with the help of relation (4), a two-observational percentile estimation of $\gamma$ which is shown by $\gamma^{*}$ can be obtained as follows:

$$ \gamma^{*} = \frac{{\log \left\{ { - \log \left[ {1 - \left( {\frac{{p_{1} }}{{1 - \theta + \theta p_{1} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\} - \log \left\{ { - \log \left[ {1 - \left( {\frac{{p_{2} }}{{1 - \theta + \theta p_{2} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\}}}{{\log Y_{{k_{1} }} - \log Y_{{k_{2} }} }} = \frac{{\log \left[ { - \log \left( {1 - p_{1}^{*} } \right)} \right] - \log \left[ { - \log \left( {1 - p_{2}^{*} } \right)} \right]}}{{\log Y_{{k_{1} }} - \log Y_{{k_{2} }} }} = \frac{k}{{\log Y_{{k_{1} }} - \log Y_{{k_{2} }} }} $$

where

$$ k = \log \left[ { - \log \left( {1 - p_{1}^{*} } \right)} \right] - \log \left[ { - \log \left( {1 - p_{2}^{*} } \right)} \right] $$

and for $i = 1,2$, $k_{i} = \left[ {np_{i} } \right]$ or $k_{i} = \left[ {np_{i} } \right] + 1$ and

$$ p_{i}^{*} = \left( {\frac{{p_{i} }}{{1 - \theta + \theta p_{i} }}} \right)^{{\frac{1}{\alpha }}} $$

(5)

According to Dubey (1967, p. 122), $\gamma^{*}$ has an asymptotic normal distribution with a mean of $\gamma$ and variance of

$$ Var\left( {\gamma^{*} } \right) = \frac{{\gamma^{2} }}{{nk^{2} }}\left[ {\frac{{p_{1}^{*} }}{{\left( {1 - p_{1}^{*} } \right)\log^{2} \left( {1 - p_{1}^{*} } \right)}} + \frac{{p_{2}^{*} }}{{\left( {1 - p_{2}^{*} } \right)\log^{2} \left( {1 - p_{2}^{*} } \right)}} - \frac{{2p_{1}^{*} p_{2}^{*} }}{{\left( {1 - p_{1}^{*} } \right)\left( {1 - p_{2}^{*} } \right)\log \left( {1 - p_{1}^{*} } \right)\log \left( {1 - p_{2}^{*} } \right)}}} \right] $$

Now, $p_{1}^{*}$ and $p_{2}^{*}$ should be determined in a way that $Var\left( {\gamma^{*} } \right)$ is minimized where, according to Dubey (1967, p. 122), $p_{1}^{*} = 0.16730679$ and $p_{2}^{*} = 0.97366352$. Therefore, calculating $p_{1}$ and $p_{2}$ with the help of (5), the BTPE of $\gamma$ which is shown by $\hat{\gamma }_{BTPE}$ is obtained as follows:

$$ \hat{\gamma }_{BTPE} = \frac{{\log \left\{ { - \log \left[ {1 - \left( {\frac{{q_{1} }}{{1 - \theta + \theta q_{1} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\} - \log \left\{ { - \log \left[ {1 - \left( {\frac{{q_{2} }}{{1 - \theta + \theta q_{2} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\}}}{{\log Y_{{k_{1} }} - \log Y_{{k_{2} }} }} $$

where

$$ q_{1} = \frac{{\left( {1 - \theta } \right)\left( {0.16730679} \right)^{\alpha } }}{{1 - \theta \left( {0.16730679} \right)^{\alpha } }},\quad q_{2} = \frac{{\left( {1 - \theta } \right)\left( {0.97366352} \right)^{\alpha } }}{{1 - \theta \left( {0.97366352} \right)^{\alpha } }} $$

In addition, for $p_{1}$ and $p_{2}$ ($0 < p_{1} < p_{2} < 1$), with the help of (3), a TPE of $\beta$ which is shown by $\beta^{*}$ is obtained as follows:

$$ \beta^{*} = \exp \left( {w_{1} \log Y_{k1} + w_{2} \log Y_{k2} } \right) $$

where $w_{1} = T_{2} /\left( {T_{1} - T_{2} } \right)$, $w_{1} + w_{2} = - 1$ and

$$ T_{i} = \log \left\{ { - \log \left[ {1 - \left( {\frac{{p_{i} }}{{1 - \theta + \theta p_{i} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\},\quad i = 1,2 $$

According to Dubey (1967, p. 122), $\beta^{ *}$ has an asymptotic normal distribution with a mean of $\beta$ and variance of

$$ Var\left( {\beta^{*} } \right) = \frac{{\beta^{2} }}{{n\gamma^{2} k^{2} }}\left\{ {r_{1}^{*} \left( {\frac{{k - \log k_{1} }}{{k_{1} }}} \right)\left[ {\frac{{k - \log k_{1} }}{{k_{1} }} + \frac{{2\log k_{1} }}{{k_{2} }}} \right] + \frac{{r_{2}^{*} \log^{2} k_{1} }}{{k_{2}^{2} }}} \right\} $$

where

$$ k = \log \left\{ { - \log \left[ {1 - \left( {\frac{{p_{1} }}{{1 - \theta + \theta p_{1} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\} - \log \left\{ { - \log \left[ {1 - \left( {\frac{{p_{2} }}{{1 - \theta + \theta p_{2} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\} $$

And for $i = 1,2$

$$ r_{i} = \left( {\frac{{p_{i} }}{{1 - \theta + \theta p_{i} }}} \right)^{{\frac{1}{\alpha }}} ,r_{i}^{*} = \frac{{r_{i} }}{{1 - r_{i} }},k_{i} = - \log \left( {1 - r_{i} } \right) $$

(6)

Now, $r_{1}$ and $r_{2}$ should be determined in a way that $Var\left( {\beta^{*} } \right)$ is minimized where, according to Dubey (1967, p. 122), $r_{1} = 0.39777$ and $r_{2} = 0.82111$. Therefore, calculating $p_{1}$ and $p_{2}$ with the help of (6), the BTPE of $\beta$ which is shown by $\hat{\beta }_{BTPE}$ is obtained as follows:

$$ \hat{\beta }_{BTPE} = \exp \left( {\hat{w}_{1} \log Y_{k1} + \hat{w}_{2} \log Y_{k2} } \right) $$

where

$$ \hat{w}_{1} = \frac{{\log \left\{ { - \log \left[ {1 - \left( {\frac{{r_{2}^{**} }}{{1 - \theta + \theta r_{2}^{**} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\}}}{{\log \left\{ { - \log \left[ {1 - \left( {\frac{{r_{1}^{**} }}{{1 - \theta + \theta r_{1}^{**} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\} - \log \left\{ { - \log \left[ {1 - \left( {\frac{{r_{2}^{**} }}{{1 - \theta + \theta r_{2}^{**} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\}}} $$

$$ \hat{w}_{2} = \frac{{\log \left\{ { - \log \left[ {1 - \left( {\frac{{r_{1}^{**} }}{{1 - \theta + \theta r_{1}^{**} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\}}}{{\log \left\{ { - \log \left[ {1 - \left( {\frac{{r_{1}^{**} }}{{1 - \theta + \theta r_{1}^{**} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\} - \log \left\{ { - \log \left[ {1 - \left( {\frac{{r_{2}^{**} }}{{1 - \theta + \theta r_{2}^{**} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\}}} $$

and $r_{1}^{**} = \frac{{\left( {1 - \theta } \right)\left( {0.39777 } \right)^{\alpha } }}{{1 - \theta \left( {0.39777 } \right)^{\alpha } }},\quad r_{2}^{**} = \frac{{\left( {1 - \theta } \right)\left( {0.82111 } \right)^{\alpha } }}{{1 - \theta \left( {0.82111 } \right)^{\alpha } }}$ where replacing $\hat{\gamma }_{BTPE}$ and $\hat{\beta }_{BTPE}$ in relations (1) and (2), the BTPE, for the pdf (1) and cdf (2), and MSE of these estimators can be achieved.

3.2 PCE

Let $X_{1} , \ldots ,X_{n}$ is a random sample of distribution with cdf (2) with ordinal statistics of $Y_{1} , \ldots ,Y_{n}$, and $p_{i}$ is the percentile of $Y_{i}$, then, $F\left( {Y_{i} ,\alpha ,\beta ,\gamma ,\theta } \right) = p_{i}$ or

$$ \gamma { \log }\left( {\beta Y_{i} } \right) = { \log }\left\{ { - { \log }\left[ {1 - \left( {\frac{{p_{i} }}{{1 - \theta + \theta p_{i} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\} $$

Percentile estimations of $\gamma$ and $\beta$ which are shown by $\hat{\gamma }_{PCE}$ and $\hat{\beta }_{PCE}$, respectively, are obtained by minimizing

$$\left[\kern-0.15em\left[ {\sum\limits_{{i = 1}}^{n} \gamma \log \left( {\beta Y_{i} } \right) - \log \left\{ { - \log \left[ {1 - \left( {\frac{{p_{i} }}{{1 - \theta + \theta p_{i} }}} \right)^{{\frac{1}{\alpha }}} } \right]} \right\}^{2} } \right]\kern-0.15em\right] $$

with respect to γ and β, i.e. by considering the following equations and the Newton–Raphson numerical method are obtained.

$$ \gamma \mathop \sum \limits_{i = 1}^{n} \left[ {\log \left( {\beta Y_{i} } \right)} \right]^{2} - \mathop \sum \limits_{i = 1}^{n} \log \left( {\beta Y_{i} } \right){ \log }\left\{ { - { \log }\left[ {1 - \left( {\frac{{p_{i} }}{{1 - \theta + \theta p_{i} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\} = 0 $$

$$ n\gamma \log \beta + \gamma \mathop \sum \limits_{i = 1}^{n} { \log }Y_{i} - \mathop \sum \limits_{i = 1}^{n} { \log }\left\{ { - { \log }\left[ {1 - \left( {\frac{{p_{i} }}{{1 - \theta + \theta p_{i} }}} \right)^{{\frac{1}{\alpha } }} } \right]} \right\} = 0 $$

Replacing $\hat{\gamma }_{MLE}$ and $\hat{\beta }_{BPTE}$ by $\gamma$ and $\beta$ in relations (1) and (2), the PCE of pdf and cdf of EWG distribution, and MSE of these estimators are obtained.

3.3 MLE

In this section, according to a random sample of $X_{1} , \ldots ,X_{n}$ from a distribution with pdf (1), the MLE of the parameters of $\gamma$ and $\beta$ which are shown by $\hat{\gamma }_{MLE}$ and $\hat{\beta }_{MLE}$, respectively, are obtained by the help of a set of equations

$$ \frac{n}{\gamma } + \mathop \sum \limits_{i = 1}^{n} \left[ {1 - \left( {\beta x_{i} } \right)^{\gamma } } \right]\log \left( {\beta x_{i} } \right) + \left( {\alpha - 1} \right)\mathop \sum \limits_{i = 1}^{n} \frac{{\left( {\beta x_{i} } \right)^{\gamma } \log \left( {\beta x_{i} } \right)e^{{ - \left( {\beta x_{i} } \right)^{\gamma } }} }}{{1 - e^{{ - \left( {\beta x_{i} } \right)^{\gamma } }} }} + 2\alpha \theta \mathop \sum \limits_{i = 1}^{n} \frac{{\left( {\beta x_{i} } \right)^{\gamma } \log \left( {\beta x_{i} } \right)e^{{ - \left( {\beta x_{i} } \right)^{\gamma } }} \left( {1 - e^{{ - \left( {\beta x_{i} } \right)^{\gamma } }} } \right)^{\alpha - 1} }}{{\left[ {1 - \theta \left( {1 - e^{{ - \left( {\beta x_{i} } \right)^{\gamma } }} } \right)^{\alpha } } \right]^{2} }} = 0 $$

$$ n + \beta^{\gamma } \left\{ {\mathop \sum \limits_{i = 1}^{n} x_{i}^{\gamma } + \left( {\alpha - 1} \right)\mathop \sum \limits_{i = 1}^{n} \frac{{x_{i}^{\gamma } e^{{ - \left( {\beta x_{i} } \right)^{\gamma } }} }}{{1 - e^{{ - \left( {\beta x_{i} } \right)^{\gamma } }} }} + 2\alpha \theta \mathop \sum \limits_{i = 1}^{n} \frac{{x_{i}^{\gamma } e^{{ - \left( {\beta x_{i} } \right)^{\gamma } }} \left( {1 - e^{{ - \left( {\beta x_{i} } \right)^{\gamma } }} } \right)^{\alpha - 1} }}{{\left[ {1 - \theta \left( {1 - e^{{ - \left( {\beta x_{i} } \right)^{\gamma } }} } \right)^{\alpha } } \right]^{2} }}} \right\} = 0 $$

and the Newton–Raphson numerical method. By replacing the $\gamma$ and $\beta$ by $\hat{\gamma }_{MLE}$ and $\hat{\beta }_{BPTE}$ in relations (1) and (2), the MLE of pdf and cdf of EWG distribution, and MSE of these estimators can be found.

4 Numerical experiments

In this section, a Monte Carlo simulation and a numerical example are presented to illustrate all the estimation methods described in the preceding sections.

4.1 Simulation studies

In this section, in the first step, using

$$ X = \frac{1}{\beta }\left\{ { - { \log }\left[ {1 - \left( {\frac{U}{{1 - \theta \left( {1 - U} \right)}}} \right)^{{\frac{1}{\alpha }}} } \right]} \right\}^{{\frac{1}{\gamma }}} $$

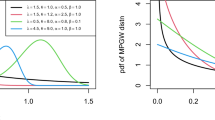
where $U$ has uniformly distribution in the interval (0,1), and for $\alpha = 1.5, 2, 4$, $\beta = 0.25,1.5, 3, 3.5$, $\gamma = 2, 3, 4, 4.5$ and $\theta = 0.2, 0.5, 0.6, 0.8$ random samples are generated as $n = 100, 200, \ldots ,500$. In the second step, the BSPE, PCE, and MLE of parameter α discussd in Sect. 2, and the BTPE, PCE, and MLE of parameters $\gamma$ and $\beta$ given in Sect. 3 are obtained. In the third step, the mean square error of estimations of functions (1) and (2) is calculated. Steps 1 to 3 were repeated 5000 times and the mean of MSE is obtained from 5000 times repetition was found. The optimal estimator is that one with a smallest Mean MSE. Comparing the results of simulations studies in Tables 1, 2, 3, 4 show that the BSPE and the BTPE are the best. On the other hand based on a 1000 random samples simulated from the EWG distribution, Fig. 1 show the graphs of estimations of the pdf (1) for the estimation methods of the third section which is given in Table 5, which represents the superiority of the BTPE toward other estimates.

Table 1 Α parameter $\alpha$ estimation and estimate the average mean square error (AM) of function (2) the second part of the estimation methods based on simulation results for different values $\left( {\alpha ,\beta ,\gamma ,\theta } \right)$ of EWG distribution

Table 2 Α parameter $\alpha$ estimation and estimate the average mean square error (AM) of function (1) the second part of the estimation methods based on simulation results for different values $\left( {\alpha ,\beta ,\gamma ,\theta } \right)$ of EWG distribution

Table 3 parameters $\gamma$ and $\beta$ estimation and estimate the average mean square error (AM) of function (2) the second part of the estimation methods based on simulation results for different values $\left( {\alpha ,\beta ,\gamma ,\theta } \right)$ of EWG distribution

Table 4 parameters $\alpha$ and $\beta$ estimation and estimate the average mean square error (AM) of function (1) the second part of the estimation methods based on simulation results for different values $\left( {\alpha ,\beta ,\gamma ,\theta } \right)$ of EWG distribution

Fig. 1

The graphs of estimations BTPE, PCE and MLE of the pdf (1)

Table 5 Estimate of parameters and corresponding log-liklihood

4.2 Application with real data set

In this section the BSPE, BTPE, PCE and MLE of pdf and cdf for the EWG distribution are computed and compared for a real data. The data is the waiting times (in minutes) of 100 bank customers collected by Ghitany et al. (2008) presented in the ‘Appendix’. For known parameters $\beta = 5.16$, $\gamma = 0.55$, $\theta = 0.95$ based on MLE method, Table 6 shows the average (AV) and corresponding mean square error (MSE) of the BSPE, PCE, MLE of pdf (1), cdf (2). Comparing theses results show that the BSPE provides better fit to waiting time data.

Table 6 Estimate the average (AV) estimation and corresponding mean square error of pdf (1) and cdf (2)

Also, For known parameters $\alpha = 2.11$, $\theta = 0.85$ based on MLE method, Table 7 shows the average (AV) and corresponding mean square error (MSE) of the BSPE, PCE, MLE of pdf (1), cdf (2). Comparing theses results show that the BTPE provides better fit to waiting time data.

Table 7 Estimate the average (AV) estimation and corresponding mean square error of pdf (1) and cdf (2)

5 Conclusion

In this research, the pdf and the cdf of the four-parameter EWG distribution were determined using several methods. To do this task, we first assume for an unknown parameter the BSPE, PCE and MLE of these functions are obtained. Then for two unknown parameters the BTPE, PCE and MLE of these functions are found. Then Using the Monte Carlo simulation and real data set, it was shown that the BSPE and BTPE are better than the other estimators.

Appendix

The waiting times (in minutes) of 100 bank customers

0.8, 0.8, 1.3, 1.5, 1.8, 1.9, 1.9, 2.1, 2.6, 2.7, 2.9, 3.1, 3.2, 3.3, 3.5, 3.6, 4.0, 4.1, 4.2, 4.2, 4.3, 4.3, 4.4, 4.4, 4.6, 4.7, 4.7, 4.8, 4.9, 4.9, 5.0, 5.3, 5.5, 5.7, 5.7, 6.1, 6.2, 6.2, 6.2, 6.3, 6.7, 6.9, 7.1, 7.1, 7.1, 7.1, 7.4, 7.6, 7.7, 8.0, 8.2, 8.6, 8.6, 8.6, 8.8, 8.8, 8.9, 8.9, 9.5, 9.6, 9.7, 9.8, 10.7, 10.9, 11.0, 11.0, 11.1, 11.2, 11.2, 11.5, 11.9, 12.4, 12.5, 12.9, 13.0, 13.1, 13.3, 13.6, 13.7, 13.9, 14.1, 15.4, 15.4, 17.3, 17.3, 18.1, 18.2, 18.4, 18.9, 19.0, 19.9, 20.6, 21.3, 21.4, 21.9, 23.0, 27.0, 31.6, 33.1, 38.5.