Application of non-decimated wavelet packet transfer function in web error prediction

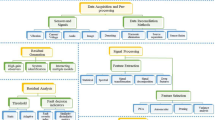
Abstract

This article shows how a non-decimated wavelet packet transform (NWPT) can be used to model and forecast a response time series $\left\{ {Y_{t} } \right\}_{t = 1}^{N} ,N \in {\mathbb{Z}}$ (Web software failure), in terms of several explanatory time series $\left\{ {X_{it} } \right\}\left( {i = 1,2,3,4} \right)$ (number of hits, amount of Bytes transferred, number of sessions created and number of users), decided by the well-known statistical procedure, Principal Component Analysis. In this paper we propose a new Web software fault prediction methodology that comprises simultaneous level-wise modeling in the wavelet domain. The proposed computational technique transforms the explanatory time series into a NWPT representation and then uses standard statistical modeling methods to identify which wavelet packets are useful for modeling the response time series, i.e., $\left\{ {Y_{t} } \right\}_{t = 1}^{N}$. The comprehensive empirical analysis of the proposed models is provided, as well as the illustration on the real life problem in forecasting the Web failures occurred during the execution of www.isical.ac.in/, the official Website for Indian Statistical Institute Kolkata, India and www.ismdhanbad.ac.in/, the official Website for Indian School of Mines Dhanbad, India.

Appendices

Appendix 1: descriptions of some frequently occurred error response codes

In this section some frequently occurred error response codes, having an influence on the reliability of the Web software, are discussed. The key words “MUST”, “MUST NOT”, “REQUIRED”, “SHALL”, “SHALL NOT”, “SHOULD”, “SHOULD NOT”, “RECOMMENDED”, “MAY”, and “OPTIONAL” in this document are to be interpreted as described in RFC 2119.

1.1 4XX class of HTTP error response codes (client side error)

4XX class of error response code is intended for cases in which the client seems to have erred. Except when responding to a HEAD request, the server SHOULD include an entity containing an explanation of the error situation, and whether it is a temporary or permanent condition. These status codes are applicable to any request method. User agents SHOULD display any included entity to the user.

1.1.1 403 (forbidden)

It comes under 4XX class. The server understood the request but refusing to fulfill it. The reason is same as that of the error corresponding to the error response code 401, i.e., authentication failure. If the server does not wish to make this information available to the client then it can issue 404 (not found). Huynh and Miller (2010) have classified this error code into two categories, viz., SCF and EF. Between those two categories, 403 occurred due to the SCF can be considered for the reliability analysis of the Web software.

1.1.2 404 (not found)

It comes under 4XX class. The server cannot find anything matching the request URI. Currently, it is the most dominating error code proposed by Arlitt and Williamson (1997), Popstojanova et al. (2006) and Tian et al. (2004). No indication is given on the condition, i.e., whether it is temporary or permanent. The 410 (Gone) status code should be used if the server knows, through some internally configurable mechanism that, an old resource is permanently unavailable and has no forwarding address. This status code is commonly used when the server does not wish to reveal exactly why the request has been refused or when no other response is applicable. Huynh and Miller (2010) have classified it into two categories, viz., SCF and EF. Between those two categories, 404 occurred due to the SCF (this matter has been discussed later) can be considered for the reliability analysis of the Web software.

1.1.3 410 (gone)

It comes under 4XX class. This will occur when the resource requested by the client is removed from the server. For example, suppose the client is requesting for a particular file which has been removed, the result is a 410 error. The nature of this error is same as 404 (not found). Therefore, in case of reliability analysis we will do the same as that of response code 404.

1.2 5XX class of HTTP error response codes (server error)

Response status codes beginning with the digit “5” indicate cases in which the server is aware that it has erred or is incapable of performing the request. Except when responding to a HEAD request, the server SHOULD include an entity containing an explanation of the error situation, and whether it is a temporary or permanent condition. User agents SHOULD display any included entity to the user. These response codes are applicable to any request method.

1.2.1 500 (internal error)

It comes under 5XX class. The server encountered an unexpected condition which prevented it from fulfilling the request. Therefore, it must be considered for reliability analysis.

1.2.2 501 (not implemented)

It comes under 5XX class. In this case the server does not understand the request of the client. It must be included in the reliability analysis of the Web software.

1.2.3 504 (gateway timeout)

It comes under 5XX class. In this case the server is acting as a gateway or a proxy server. This problem is entirely due to slow IP communication between back-end computers, possibly including the Web server. Hence, this error will not be considered for reliability analysis of the web software.

One point must be kept in mind that the log files contain requests from robots and other automated systems that should be removed as they are not actual requests from Web users. Automated systems are classified as systems that repeatedly request a resource from the Website after a predefined period of time. Several techniques to identify them can be used by Web administrators to remove automated requests. Most well known robots have a signature line that is included with every request as part of the USER AGENT field in the log file, especially HTTP error logs of the corresponding Web server.

Appendix 2: a review on wavelet and wavelet transforms

In this section, brief descriptions on wavelets and wavelet packets have been given.

2.1 Wavelet

A wavelet is a function $\psi \in L^{2} \left( {\mathbb{R}} \right)$ which satisfies the admissibility condition

$$ C_{\psi } = \int\limits_{ - \infty }^{\infty } {\frac{{\left| {\hat{\psi }\left( \omega \right)} \right|^{2} }}{\left| \omega \right|}d\omega } < \infty $$

(9)

where $\hat{\psi }\left( \omega \right)$ is the Fourier transform of $\psi \left( x \right)$, i.e.,

$$ \hat{\psi }\left( \omega \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{\infty } {e^{ - i\omega x} \psi \left( x \right)dx} . $$

2.2 Mother wavelet

Morlet first introduced the idea of wavelets as a family of function constructed from the translations and dilations of a single function called the “mother wavelet” or the “analyzing function” $\psi \left( t \right)$. They are defined as

$$ \psi_{a,b} \left( t \right) = \frac{1}{{\sqrt {\left| a \right|} }} \psi \left( {\frac{t - b}{a}} \right);a,b \in {\mathbb{R}};a \ne 0. $$

(10)

where, a is the scaling parameter which measures the degree of compression or scale and b is the translation parameter which determines the time location of the wavelet.

2.3 Mutliresolution analysis (MRA)

MRA provides the framework for examining signals at different resolutions. The MRA of $L^{2} \left( {\mathbb{R}} \right)$ is a chain of nested subspaces $\left\{ {V_{j} :j \in {\mathbb{Z}}} \right\}$ satisfying the following conditions

• (i) A succession of sub spaces: $V_{j} \subset V_{j + 1} \subset L^{2} \left( {\mathbb{R}} \right)$

• (ii) The union of all V _j ’s is $L^{2} \left( {\mathbb{R}} \right)$, i.e., $\overline{{\bigcup\nolimits_{n = - \infty }^{\infty } {V_{n} {\mathbb{R}}} }} = L^{2} \left( {\mathbb{R}} \right)$.

• (iii) The intersection of all of the spaces contains only the origin, i.e., $\bigcap\nolimits_{n = - \infty }^{\infty } {V_{n} } = \left\{ 0 \right\}$.

• (iv) $f\left( x \right) \in V_{j} \Leftrightarrow f\left( {2x} \right) \in V_{j + 1} .$

• (v) $f\left( x \right) \in V_{0} \Leftrightarrow f\left( {x - k} \right) \in V_{0} , k \in {\mathbb{Z}}$

• (vi) $\exists \phi \left( x \right) \in V_{0}$ such that the set $\phi_{0,n} = \left\{ {\phi \left( {x - n} \right),n \in {\mathbb{Z}}} \right\}$ constitutes an orthonormal basis for V ₀, i.e., $\left\| {f^{2} } \right\| = \mathop \smallint \limits_{ - \infty }^{\infty } \left| {f\left( x \right)} \right|^{2} dx = \mathop \sum \limits_{n = - \infty }^{\infty } \left| {\left\langle {f,\phi_{0,n} } \right\rangle } \right|^{2} dx\,\,\forall \,f \in V_{0}$

It follows that the set $\left\{ {\phi_{jk} \left( x \right) = 2^{ - j/2} \phi \left( {2^{ - j} x - k} \right),k \in {\mathbb{Z}}} \right\}$ is an orthonormal basis for $V_{j}$. Next, let $W_{j}$ be the orthogonal complement of $V_{j}$ in $V_{j + 1}$, i.e., $x \in V_{j} , y \in W_{j} \Leftrightarrow x,y = 0$ and $V_{j + 1} = V_{j} \oplus W_{j}$. Obviously, $V_{j} \subset V_{j + 1 }$ and $W_{j} \subset V_{j + 1}$, so that the basis functions of $V_{j}$ and $W_{j}$ (ϕ _jk (x) and $\psi_{jk} \left( x \right)$, respectively) can be written as a linear combination of the basis function of $V_{j + 1} \left( {\phi_{j + 1k} \left( x \right)} \right)$.

2.4 Father wavelet

Since,V ₀ ⊂ V ₋₁, the function ϕ(x) ∊ V ₀ can be represented as a linear combination of the functions from V ₁, i.e.,

$$ \phi \left( x \right) = \mathop \sum \limits_{{k \in {\mathbb{Z}}}} h_{k} \sqrt 2 \phi \left( {2x - k} \right), $$

(11)

for some coefficients $h_{k} ,k \in {\mathbb{Z}}$. We termed ϕ(x) the father wavelet or the scaling function and h _k the low pass filter.

For a suitable mother wavelet ψ, the set {ψ _jk } _jk provides a basis, which can be used to represent function

$$ f \in L^{2} \left( {\mathbb{R}} \right), f = \mathop \sum \limits_{k} c_{0k} \phi_{0k} + \mathop \sum \limits_{j = 1}^{J} \mathop \sum \limits_{k} d_{jk} \psi_{jk} \left( x \right). $$

(12)

where, c _0k is the father wavelet coefficient at the coarsest scale and d _jk are the mother wavelet coefficients or the detail (fine scale) coefficients, i.e. c _0k  = ∫ f(x)ϕ _0k (x)dx and $d_{jk} = \int {f\left( x \right)} \psi_{jk} \left( x \right)dx$. In short, the first term of the right hand side of the equation is the projection of f onto the coarse approximating space V ₀ while the second term represents the cumulated detail.

2.5 Discrete wavelet transform

Continuous wavelet transform is compared to the Fourier transform, which requires calculating the integral $\int_{ - \infty }^{\infty } {e^{ - i\omega x} } f\left( x \right)dx\; \forall \omega \in {\mathbb{R}}$, the discrete wavelet transform can be compared to the Fourier series, which requires calculating the integral $\int_{0}^{2\pi } {e^{ - inx} } f\left( x \right)dx \;\forall n \in {\mathbb{Z}}.$ Since the continuous wavelet transform is a two parameter representation of a function

$$ \left( {{\mathcal{W}}_{\psi } f} \right) = \frac{1}{{\sqrt {\left| a \right|} }}\mathop \smallint \limits_{ - \infty }^{\infty } f\left( t \right)\overline{{\psi \left( {\frac{x - b}{a}} \right)}} dt = f,\psi_{a,b} \left( t \right) $$

We can discretize it by assuming that a and b take only integer values.

There is an efficient algorithm for calculating the wavelet coefficients of a discrete sequence known as the discrete wavelet transform (DWT) or the pyramid algorithm, proposed by Mallat (1989). The algorithm is given below:

Given a function $f \in L^{2} \left( {\mathbb{R}} \right)$ which is observed at $N = 2^{J} ,j \in {\mathbb{Z}}$ equally spaced time points $\left\{ {t_{i} } \right\}_{{i = 0,1, \ldots 2^{J - 1} }}$, set $c_{J,i} = f\left( {t_{i} } \right)$ for $i = 0, \ldots ,2^{J - 1}$. The DWT of the sequence is obtained recursively using the relations:

$$ c_{J - 1,i} = \mathop \sum \limits_{n} h_{n - 2i} c_{j,n } $$

(13)

and

$$ d_{J - 1,i} = \mathop \sum \limits_{n} g_{n - 2i} c_{j,n } $$

(14)

to obtain $\left( {\widetilde{{c_{0} }},\widetilde{{d_{0} }}, \ldots ,\widetilde{{d_{j - 1} }}} \right)$, where, $\tilde{d}_{j} = \left( {d_{j,0} ,d_{j,1} , \ldots ,d_{{j,2^{j - 1} }} } \right),j = 0,1, \ldots ,J - 1$ and h and g are low and high pass quadrature mirror filters respectively for time series of length N. The computational complexity of the DWT is O(N)(Mallat 1989).

2.6 The non-decimated wavelet transform

The non-decimated wavelet transform (NWT) was developed to address certain deficiencies of the DWT in the area such as time series analysis and image analysis. A consequence of the decimation step in the DWT is that the DWT is not translation-equivariant, i.e., a shift in the time series is not characterized by an identical shift in the DWT coefficients. For a non-decimated transform, if a certain behavior occurs in X _t which is characterized by the NWT coefficients at time t then if the behavior is repeated again at time$\left( {t + \tau } \right),$ the NWT coefficients will be the same as those at time t. In addition, the number of coefficients in each wavelet scale is the same as the number of data points in the original data. This means that, the NWT coefficients of a time series can be represented as a (2N − 2)-dimensional multivariate time series, where each variable corresponds to a particular wavelet basis function.

Denote ${\mathcal{H}}$ and ${\mathcal{G}}$ as the low and the high pass filters defined by {h _n } and {g _n } respectively, i.e., ${\mathcal{H}}_{s} = \mathop \sum \nolimits_{n} h_{n - k} s_{n}$, whilst ${\mathcal{G}}_{s} = \mathop \sum \nolimits_{n} g_{n - k} s_{n}$, where s is a doubly infinite sequence. Let, ${\mathcal{Z}}$ denotes the operator which pads out x, a doubly infinite sequence, with zeros as follows:

$$ \left( {{\mathcal{Z}}x} \right)_{2j} = x_{j} \,\,{\text{and}}\,\,\left( {{\mathcal{Z}}x} \right)_{2j + 1} = 0. $$

Define the filters ${\mathcal{H}}^{\left[ r \right]}$ and ${\mathcal{G}}^{\left[ r \right]}$ to have weights ${\mathcal{Z}}^{r} h$ and ${\mathcal{Z}}^{r} g$ respectively. Thus the filter ${\mathcal{H}}^{\left[ r \right]}$ has weights $h_{{2^{r} j}}^{\left[ r \right]} = h_{j}$ and h ^[r] _k  = 0 if k is not a multiple of 2^r. The filter ${\mathcal{H}}^{\left[ r \right]}$ is obtained by inserting a zero between every adjacent pair of elements of the filter ${\mathcal{H}}^{{\left[ {r - 1} \right]}}$ and similarly for ${\mathcal{G}}^{\left[ r \right]}$. To define the stationary wavelet transform, set c ^J to be the original sequence. For j = J, J − 1, …, 1 we then recursively define $c^{j - 1} = {\mathcal{H}}^{{\left[ {J - j} \right]}} c^{j}$ and $d^{j - 1} = {\mathcal{G}}^{{\left[ {J - j} \right]}} c^{j}$. If the vector c ^J is of length 2 ^J, then the vectors c ^j and d ^j will be of the same length rather than getting shorter as j decreases, which is same as in the standard DWT. The computational complexity of NWT is O (NlogN).

2.7 The wavelet packet transform

The decomposition of a signal by DWT (or NWT) is rather restrictive in terms of frequency resolutions. For some time series, wavelet packets may be of more use as they provide a wider choice of decompositions of the frequency domain. They are particularly suited to represent signals which combine stationary and non-stationary characteristics, such as local and prolonged oscillations.

A time series is transformed to wavelet packets using the wavelet packet transform (WPT). The WPT is a generalization of DWT.

Given a function f which is observed at $N = 2^{J} ,j \in {\mathbb{Z}}$ equally spaced time points $\left\{ {t_{i} } \right\}_{{i = 0,1, \ldots 2^{J - 1} }}$, set ${\mathcal{W}}_{J,f = 0,i} = f\left( {t_{i} } \right)$ for $i = 0,1 \ldots 2^{J - 1}$, i.e., define the set of finest scale wavelet packet coefficients to be the original time series. At scale $J - 1$, the wavelet packet coefficients ${\mathcal{W}}_{J - 1,f,k} \left( {f = 0,1} \right)$ are obtained by applying the filters h and g to ${\mathcal{W}}_{J,0,k}$ followed by dyadic decimation. At each further scale in the analysis the filters h and g are recurresively applied (with dyadic decimation) to all the wavelet packet coefficients ${\mathcal{W}}_{j - 1,f,k} \left( {f = 0,1,2 \ldots } \right)$ from the previous scale. Each set of wavelet packet coefficients is indexed by an additional parameter f, which corresponds to the frequency index of the wavelet packet. Wavelet packet coefficients with frequency index 0 correspond to the father wavelet and the wavelet packet coefficients with frequency index 1 correspond to the mother wavelets.

The WPT is highly redundant, retaining (J + 1)N coefficients and its computational complexity is O(NlogN). In wavelet packet analysis, the details as well as the approximations can be split. This yields more than $2^{{2^{n - 1} }}$different ways to encode a signal.

2.8 The non-decimated wavelet packet transform

Its implementation follows the same procedure as the extension of the wavelet transform to the non-decimated wavelet transform. But extending the WPT, where the filters ${\mathcal{H}}$ (high-pass) and ${\mathcal{G}}$ (low-pass) are now applied to both the c ^j and d ^j recursively for both odd and even dyadic decimation (Debnath and Bhatta 2007). The computational complexity of NWPT is O(N ²).