Families of Discrete Circular Distributions with Some Novel Applications

Abstract

We give a unified treatment of constructing families of circular discrete distributions. Some of these families are deduced from established distributions such as von Mises and wrapped Cauchy. Some others are derived directly such as a flexible family based on trigonometric sums and the circular location family. Results interrelating these families are discussed. These distributions have been motivated by two examples of discrete circular data: casino roulette spins and smart health acrophase monitoring, and these data are analyzed using our proposed models. We discuss how using continuous circular models for circular discrete data can be misleading.

1 Introduction

The subject of Directional Statistics has grown tremendously, especially since the 1980’s, with advances in “Statistics on Manifolds” leading to new distributions on the hyper-sphere, torus, Stiefel manifold, Grassmann manifold and so on. The progress in this area can be seen through several books published since then: Fisher et al. (1987), Fisher (1993), Mardia and Jupp (2000), Jammalamadaka and Sengupta (2001), Ley and Verdebout (2017) and Ley and Verdebout (2018). There has been a recent special issue of Sankhya edited by Bharath and Dey (2019). Further, Pewsey and García-Portugués (2021) have given a comprehensive survey of directional statistics and in the discussion to the paper, Mardia (2021) has given a brief history of the subject. However, there is limited development of circular discrete models. There are good choices for continuous models for circular data, but there has been a dearth of models for discrete data. In this paper, we give the first unified treatment of constructing families of circular discrete distributions and present examples of circular data that are observed directly as discrete rather than created by grouping continuous data. The two data that motivated our paper are:

• (i) Roulette wheel data: A typical European roulette has 37 discrete outcomes, viz. {0,1,2,…,36}. If the outcome 0 is mapped to 0 radians, then the outcomes get mapped to a regular support of 37 points on the circle given by

  $$ \begin{array}{@{}rcl@{}} \left\{ \frac{2\pi r}{37}, ~r\in \{0,1,2,\ldots, 36\}\right\}. \end{array} $$

  (1)

  In Section 4.1, we consider data sequences obtained from spins of four different European roulette wheels, one from an online roulette simulator and three from two different casino industries. It should be pointed out that Karl Pearson, in the early 1890’s, acquired roulette spins data from Monte Carlo to examine the question of whether the roulette wheel was unbiased (see, Plackett, 1983, p.60), and indeed his paper of 1897 has the apt title “The scientific aspect of Monte Carlo roulette” (Pearson, 1897). Few authors have considered this problem but have used linearized methods, beginning with Karl Pearson and subsequently some others, e.g. Ethier (1982), Spencer (2009). Surprisingly, for this important application from the gaming industry, there has been little attention to inference that uses explicitly the circularity of the wheel.

• (ii) Acrophase data: In non-invasive smart health monitoring, parameters such as Systolic Blood Pressure (SBP) are recorded, by ambulatory devices, at predetermined discrete time points repeated each day. “Acrophase” is defined as the time point at which the maximum SBP reading is recorded on a given day. Typically, acrophase data is extracted from SBP measurements at each half hour during daytime (8 am to 8 pm) and each hour during nighttime (8 pm to 8 am). If we map 8 am to 0 radians and 8 pm to π radians, the acrophase times get mapped to an irregular support of 36 points on the circle given by

  $$ \begin{array}{@{}rcl@{}} \left\{\frac{2\pi r}{48}, r =0,1,2,\ldots,24\right\} \bigcup \left\{\frac{2\pi r}{48}, r =26, 28,\ldots, 44, 46\right\}, \end{array} $$

  (2)

  where the first set in the union corresponds to 25 half-hourly points during daytime and the second set corresponds to the 11 one-hourly points during nighttime.

In any application with discrete data in Linear Statistics, one usually takes into account the discrete nature of the underlying population. Our overall recommendation is the same here: “if one has discrete circular data then one should start with a discrete circular model”. Also, the “loss” due to use of a continuous model for circular discrete data can only be assessed after appropriate discrete modeling, which serves as a benchmark. Of course, this issue of discrete versus continuous distributions is a general problem, which is well known and has been dealt successfully in Linear Statistics and we treat this problem here as a model misspecification problem (see, Section 5).

In this paper, we give four methods to construct families of discrete distributions on the circle along with some basic results interrelating the methods. We apply these models to analyze the aforementioned examples of discrete data and also to provide insights based on comparisons among discrete as well as (approximate) continuous models for discrete data. Our methods to construct the probability distributions can be briefly described as follows:

• (i) Maximum entropy method: We start with a given set of moment conditions for the discrete distribution on the circle. We then determine the discrete probability distribution with the maximum Shannon entropy among those satisfying the moment constraints.

• (ii) Centered wrapping method: We start with a given discrete distribution on the line, and wrap it on the circle to obtain a discrete distribution on the circle.

• (iii) Marginalized method: We start with a continuous distribution on the circle, which we refer to as the “parent”, and then obtain a discrete distribution on the circle by integrating the probability density function (pdf) on pre-determined arcs on the circle.

• (iv) Conditionalized method: We start with a continuous distribution on the circle (parent), and then obtain the discrete distribution on the circle by restricting and normalizing the pdf to a pre-determined lattice on the circle.

In particular, we derive circular discrete distributions from general continuous location families and a family based on trigonometric sums. Key special cases include discrete families deduced from two established continuous distributions, viz. von Mises and wrapped Cauchy. These two distributions are commonly selected for circular data depending on whether the unimodal data has a long tail (wrapped Cauchy) or not (von Mises), which we now describe.

The direction of a unit random vector in two dimensions can be represented by an angle Θ. On the circle, the von Mises distribution for Θ (see, for example, Mardia and Jupp, 2000, p.36) plays the same role as the normal distribution on the line. It belongs to the exponential family with two analogous parameters. Its pdf is given by

$$ f_{v}(\theta\vert \kappa, \mu) = \frac{1}{2\pi I_{0}(\kappa)} e^{\kappa \cos(\theta-\mu)}, \theta\in [0, 2\pi), \mu\in [0, 2\pi), \kappa\geq 0, $$

(3)

where μ is the mean direction and κ is the concentration (precision) parameter. The normalization constant I₀(κ) is the modified Bessel function of order 0:

$$ I_{0}(\kappa)= \sum\limits_{r=0}^{\infty} \frac{\kappa^{2r}}{(r !)^{2}}.$$

For large κ, Θ is approximately normal with mean μ and variance 2/κ, and for κ = 0, Θ is uniformly distributed on the circle.

Given a distribution on the line, we can wrap it around the circumference of the circle with unit radius. If X is the random variable on the line, the random variable Θ of the wrapped distribution is given by

$$ {\Theta}=(X \text{ mod }2\pi ). $$

A popular example of wrapped distributions is the wrapped Cauchy distribution with its pdf (see, for example, Mardia and Jupp, 2000, p.51)

$$ f_{c}(\theta\vert \rho, \mu) = \frac{1}{2\pi}\frac{1-{\rho}^{2}}{1+{\rho}^{2}-2\rho\cos (\theta -\mu) }, \theta\in [0,2\pi), \mu\in[0,2\pi),\rho\in [0,1), $$

(4)

where μ is the mean direction parameter and ρ is the concentration parameter. It is one of the wrapped distributions whose density has a closed form and is heavy-tailed. When ρ = 0 it also reduces to the uniform distribution.

In what follows, Section 2 gives constructions of discrete circular families based on the four methods, along with some examples and results interrelating them. In particular, we deduce families from general continuous location families, and a flexible family based on trigonometric sums. Section 3 deduces some discrete families from established distributions such as von Mises and wrapped Cauchy. We apply some of the models to our discrete data in Section 4. In Section 5, we treat the problem of model misspecification for circular discrete distributions. We conclude the paper with a discussion in Section 6. Some supporting material is given in the supplement, including a table of abbreviations used in the paper.

2 Constructions of Families of Circular Discrete Distributions

In this section, we elaborate on the four different methods to construct families of circular discrete distributions that were mentioned in Section 1. Although our ideas naturally extend to constructing discrete distributions on an irregular support (such as in (2)), we will focus here on the regular lattice support (as in (1)) which lends itself to some mathematical simplifications.

We denote the set of real numbers by $\mathbb {R}$, non-negative real numbers by $\mathbb {R}^{+}$, the set of integers by $\mathbb {Z}$, non-negative integers by $\mathbb {Z}^{+}$ and the cyclic group of integers modulo a given positive integer m by $\mathbb {Z}_{m}$, i.e.

$$ \mathbb{Z}_{m}=\{0,1,\ldots, m-1\}. $$

(5)

The regular circular lattice domain is given by the vertices of a regular polygon on the circle, denoted by $\mathcal {D}_{m}$, i.e.

$$ \mathcal{D}_{m}= \{2\pi r/m, r\in \mathbb{Z}_{m} \}. $$

(6)

We generally use f(⋅) or g(⋅) to denote a probability density function (pdf) of a continuous distribution on the line or circle, and p(⋅) to denote a discrete probability function on $\mathbb {Z}_{m}$.

2.1 Maximum Entropy Discrete Circular Distributions

For a probability function $\{p(r), ~~r\in \mathbb {Z}_{m}\}$, with p(r) denoting the probability of the point $2\pi r/m \in \mathcal {D}_{m}$, Shannon’s entropy is defined as

$$ -\sum\limits_{r=0}^{m-1} p(r) \log p(r). $$

(7)

Let t₁,t₂,…,t_q be q real valued functions defined on $\mathbb {Z}_{m}$ and suppose we are interested in discrete distributions $\{p(r), ~~r\in \mathbb {Z}_{m}\}$ that satisfy a set of pre-selected moment conditions

$$ \begin{array}{@{}rcl@{}} \sum\limits_{r=0}^{m-1}p(r) t_{1}(r)=a_{1}, ~\sum\limits_{r=0}^{m-1}p(r) t_{2}(r)=a_{2}, \ldots, \sum\limits_{r=0}^{m-1}p(r) t_{q}(r)=a_{q}, \end{array} $$

(8)

with given constants a₁,a₂,…,a_q. Then, a useful method to construct discrete distributions is to maximize the entropy among all distributions on $\mathbb {Z}_{m}$ that satisfy the given conditions. As noted by Kemp (1997), the philosophy behind this construction is that “one should use all the given information and nothing else”. The following theorem gives this construction, which follows from Theorem 13.2.1 of Kagan et al. (1973, pp. 408–409) on the line and was adapted in Mardia (1975a) for directional distributions.

Theorem 1 (Maximum Entropy Distributions).

The probability function $\{p(r), ~~r\in \mathbb {Z}_{m}\}$ that maximizes the entropy (7) subject to the constraints (8) is of the form

$$ \begin{array}{@{}rcl@{}} p(r)&=& \frac{ e^{{\sum}_{j=1}^{q} b_{j} t_{j}(r)}}{{\sum}_{k=0}^{m-1}e^{{\sum}_{j=1}^{q} b_{j} t_{j}(k)}}, ~~r\in \mathbb{Z}_{m}, \end{array} $$

(9)

provided there exist constants b₁,b₂,…,b_q satisfying

$$ \begin{array}{@{}rcl@{}} \frac{{\sum}_{r=0}^{m-1} t_{j}(r) e^{{\sum}_{i=1}^{q} b_{i} t_{i}(r)}}{{\sum}_{k=0}^{m-1}e^{{\sum}_{i=1}^{q} b_{i} t_{i}(k)}} =a_{j}, ~~~j=1,2,\ldots, q. \end{array} $$

(10)

In that case, the distribution is unique.

We now give a few examples of maximum entropy discrete distributions.

Example 1.

von Mises distribution: Suppose q = 2 and $t_{1}(r)= \cos \limits (2\pi r/m)$ and $t_{2}(r)= \sin \limits (2\pi r/m)$, a discrete version of the von Mises distribution is of the form

$$ \begin{array}{@{}rcl@{}} p(r) &=& \frac{ e^{\kappa \cos(2\pi r/m - \mu) }}{{\sum}_{k=0}^{m-1}e^{\kappa \cos(2\pi r/m - \mu)}}, ~~r\in \mathbb{Z}_{m}, \end{array} $$

(11)

where $\kappa = \sqrt {{b_{1}^{2}}+{b_{2}^{2}}}$ and $\tan (\mu )= b_{2}/b_{1}$. We note that this also happens to be the conditionalized discrete von Mises distribution that is discussed in more detail later.

Example 2.

Beran distributions: A more general family than the previous example, a discrete version of the Beran family (Beran, 1979), is obtained by considering constraints on the expected values of $t_{j}(r)=\left (\cos \limits \left (2\pi r j/m\right ),\right .$ $\left .\sin \limits \left (2\pi r j/m\right ) \right )$, which leads to the probability function

$$ \begin{array}{@{}rcl@{}} p(r) \propto e^{{\sum}_{j=1}^{q} (a_{j} \cos\left( 2\pi r j/m\right) + b_{k} \sin\left( 2\pi r j/m\right))}, ~~r\in \mathbb{Z}_{m}. \end{array} $$

(12)

We will denote this distribution by ${\mathscr{B}}_{q}$, where q is the order of the distribution. So, ${\mathscr{B}}_{1}$ is von Mises discrete distribution as in the previous example. ${\mathscr{B}}_{2}$ is the discrete generalized von Mises distribution.

We note that this family can be traced back to Maksimov (1967), although his focus for this family is on a characterization for the unknown centering parameter (rather than the concentration parameter), so it is of limited practical importance.

Example 3.

Geometric distribution: Suppose q = 1 and t₁(r) = r the maximum entropy distribution is of the form

$$ \begin{array}{@{}rcl@{}} p(r) &= & \frac{ (1-p) p^{r} }{1-p^{m}}, ~~r\in \mathbb{Z}_{m}, \text{ where } p=e^{b_{1}}. \end{array} $$

(13)

Historically, Mardia (1972, p. 50) proposed the above distribution as a model for roulette outcomes (possibly biased).

The above three examples also arise out of the “conditionalized” construction of discrete circular distributions that we define below in Section 2.3. We note that (13) is also the “centered wrapped geometric distribution” discussed below in the next subsection.

2.2 Centered Wrapped Discrete Circular Distributions

A natural construction to obtain a circular discrete distribution is to start with a discrete distribution on the line and wrap it on the circle (see, for example, Mardia, 1972, p.50). Let Z be a random variable taking integer values (i.e. in $\mathbb {Z}$) with probability function p₀(⋅). For a given positive integer m, we define here the wrapped discrete random variable:

$$Z_{w}= \left( Z\text{ mod } m\right)\times (2\pi/m).$$

We note that $Z_{w}\in \mathcal {D}_{m}$ and its probability function is given by

$$ \begin{array}{@{}rcl@{}} p_{w0}(r)=P(Z_{w}=2\pi r/m)= \sum\limits_{k=-\infty}^{\infty} p_{0}(r+km), ~~ r\in \mathbb{Z}_{m}. \end{array} $$

(14)

It follows that the characteristic function of Z_w is given by

$$ \begin{array}{@{}rcl@{}} \psi_{p,m} = E\left( e^{i p Z_{w}}\right) = \phi (2\pi p/m), \end{array} $$

(15)

where ϕ(⋅) is the characteristic function of Z. In general, these distributions do not have a mean direction or centering parameter, and therefore we construct the “centered wrapped” probability function with a centering parameter t as follows,

$$ \begin{array}{@{}rcl@{}} p(r)= \begin{cases} p_{w0}(r-t+m), ~~ r<t \\ p_{w0}(r-t), ~~~~~~~~ r\ge t, \end{cases} ~~ r, t\in \mathbb{Z}_{m}. \end{array} $$

(16)

Choosing the domain of t as $\mathbb {Z}_{m}$ ensures probabilities are well defined without changing the domain of the distribution.

Example 4.

Centered wrapped Poisson distribution: For the Poisson distribution with mean λ, the wrapped Poisson distribution has the probability function

$$ \begin{array}{@{}rcl@{}} p_{w0}(r) = e^{-\lambda}\sum\limits_{k=0}^{\infty} \frac{\lambda^{r+km}}{(r+km)!}, ~r\in \mathbb{Z}_{m}. \end{array} $$

(17)

The centered wrapped probability function with centering parameter t is then given by

$$ \begin{array}{@{}rcl@{}} p(r) = \begin{cases} e^{-\lambda}{\sum}_{k=0}^{\infty} \frac{\lambda^{r-t+m+km}}{(r-t+m+km)!}, ~~r< t \\ e^{-\lambda}{\sum}_{k=0}^{\infty} \frac{\lambda^{r-t+km}}{(r-t+km)!}~~~, ~~r\geq t\end{cases} ~r,t \in \mathbb{Z}_{m}. \end{array} $$

(18)

The above expression is a special case of the distributions considered by Mastrantonio et al. (2019).

For practical applications with continuous circular data, it is well known that the selected probability density is continuous at 2π, i.e. the pdf value at 0 is same as its limiting value at 2π. Similarly, along the same lines, a desirable property for a circular discrete probability function p(⋅) on $\mathbb {Z}_{m}$ is to have p(0) = p(m). The maximum entropy and the centered wrapping methods do not necessarily ensure this property as is apparent from Examples 3 and 4. However, this property is ensured if we construct discrete distributions by applying the marginalized and conditionalized methods on continuous circular distributions, which we will discuss next.

2.3 Marginalized and Conditionalized Discrete Distributions

In this section, we focus on univariate circular constructions based on marginalized and conditionalized methods, whose brief descriptions were given in Section 1.

There has been literature on the marginalized and conditionalized discretization on the line. For example Kemp (1997) and Szabłowski (2001) discuss the conditionalized discrete normal, Inusaha and Kozubowski (2006) discuss the conditionalized discrete Laplace, and Papadatos (2018) derives the characteristic function of the conditionalized discrete Cauchy. The conditionalized approach can also be described as a “plug-in” approach, whereas the marginalized approach is in fact equivalent to the well known probit construction, usually used for univariate and multivariate normal distributions, see for example Joe (2014, p.20). Alzaatreh et al. (2012) and Chakraborty (2015) make references to both of these methods, while developing other methods of constructions. However, there have not been any insights relating these constructions.

Marginalized and conditionalized constructions of circular families of discrete distributions are very recent as proposed in Mardia and Sriram (2020). Besides, there has not been published in-depth analysis of truly discrete circular data. However, particular cases of the conditionalized approach, including von Mises and wrapped Cauchy distributions, have appeared, not only in Mardia and Sriram (2020) but also in Girija et al. (2019) and Imoto et al. (2020). We give a unified treatment of the different methods as a strategy to construct rich classes of discrete distributions on the circle. We derive new results (e.g. Theorems 1 to 4) that offer insights on the inter-relationships between the constructions.

We now define the marginalized and conditionalized discrete families for the circular case. There has been some very recent work on these approaches although not in a comprehensive and unified way, as we describe below. Let Θ be a random variable with pdf f(𝜃), 𝜃 ∈ [0,2π).

Definition 1.

The probability function of the marginalized discrete (MD) distribution on the circle is given by

$$ p(r)= {\int}_{\frac{2\pi r}{m}}^{\frac{2\pi (r+1)}{m}} f(\theta) d\theta= F\left( \frac{2\pi (r+1)}{m}\right) - F\left( \frac{2\pi r}{m}\right), ~r\in\mathbb{Z}_{m}, $$

(19)

where F(⋅) is the cumulative distribution function of the pdf f(⋅).

We note that this is also the probability function of the discrete random variable $\lfloor \frac {m {\Theta }} {2 \pi }\rfloor$, where ⌊⋅⌋ denotes the largest integer less than or equal to the given number.

Definition 2.

The probability function of the conditionalized discrete (CD) distribution on the circle is given by

$$ \mathrm{p} \left( r \right) = \frac{f (2\pi r/m)}{{\sum}_{k=0}^{m-1} f(2\pi k/m)}, r\in\mathbb{Z}_{m}. $$

(20)

For simplicity, we will denote both probability functions (19) and (20) by the same notation, but the choice will be obvious from the context. One question of interest is “can the marginalized and conditionalized methods lead to the same discrete distribution on the circle?” We show that under certain conditions, the two approaches will lead to diffent discrete distributions on the circle except for the trivial uniform case. This has implication when we come to selecting between the two approaches in practice and we give insights based on comparison of the two approaches for some particular cases in Section 5. Theorem 2 below gives one characterization. This theorem is inspired by a similar question for the linear case related to the exponential distribution (see supplement Section A7).

Theorem 2.

Suppose f(⋅) is a strictly positive and continuous circular pdf on [0,2π] with f(𝜃) = f(𝜃 + 2π). Then, the two discretization approaches (i.e. MD and CD) lead to the same discrete distribution, with

$$ \begin{array}{@{}rcl@{}} \frac{f(a+k\delta)}{{\sum}_{r=0}^{m-1} f(a+r\delta)}= \frac{{\int}_{a+k\delta}^{a+(k+1)\delta} f(\theta) d\theta}{{\int}_{a}^{a+m\delta} f(\theta) d\theta}, \forall , a, \delta\in[0, 2\pi), ~~\forall~k\in \mathbb{Z}_{m} \text{ with } m\delta\leq 2\pi,\\ \end{array} $$

(21)

iff f is the uniform density.

Proof.

Considering (21) for k = 1 and k = 0, and taking their ratio, we get

$$ \begin{array}{@{}rcl@{}} f(a+\delta){\int}_{a}^{a+\delta}f(\theta) d\theta =f(a){\int}_{a+\delta}^{a+2\delta}f(\theta) d\theta. \end{array} $$

(22)

Integrating both the left hand side (lhs) and right hand side (rhs) of (22) with respect to δ ∈ [0,2π), we get

$$ \begin{array}{@{}rcl@{}} {\int}_{0}^{2\pi}f(a+\delta){\int}_{a}^{a+\delta}f(\theta) d\theta d\delta =f(a) {\int}_{0}^{2\pi}{\int}_{a+\delta}^{a+2\delta}f(\theta) d\theta d\delta. \end{array} $$

(23)

Using continuity of f(⋅) including f(𝜃 + 2π) = f(𝜃), we have ${\int \limits }_{a}^{a+2\pi }f(\theta ) d\theta =1$ for any a, and the lhs of (23) can be simplified as

$$ \begin{array}{@{}rcl@{}} {\int}_{0}^{2\pi}f(a+\delta){\int}_{a}^{a+\delta}f(\theta) d\theta d\delta= \frac{1}{2} \left( {\int}_{a}^{a+\delta}f(\theta) d\theta\right)^{2} \vert_{\delta=0}^{2\pi}= 1/2. \end{array} $$

(24)

Now, the rhs of (23) can be shown to be

$$ \begin{array}{@{}rcl@{}} f(a) {\int}_{0}^{2\pi}{\int}_{a+\delta}^{a+2\delta}f(\theta) d\theta d\delta = f(a) (A- B) = f(a) \pi, \end{array} $$

(25)

Equation 25 follows because A and B can be simplified as below.

$$ \begin{array}{@{}rcl@{}} A&=& {\int}_{0}^{2\pi}{\int}_{a}^{a+2\delta}f(\theta) d\theta d\delta = \delta {\int}_{a}^{a+2\delta}f(\theta) d\theta \vert_{0}^{2\pi} - {\int}_{0}^{2\pi}2\delta f(a+2\delta) d\delta\\ &=& 2\pi {\int}_{a}^{a+4\pi}f(\theta) d\theta -\frac{1}{2}{\int}_{0}^{4\pi}\delta^{\prime} f(a+\delta^{\prime}) d\delta^{\prime}=4\pi - \left( \pi + {\int}_{0}^{2\pi}\delta^{\prime} f(a+\delta^{\prime}) d\delta^{\prime}\right), \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} B&=& {\int}_{0}^{2\pi}{\int}_{a}^{a+\delta}f(\theta) d\theta d\delta=\delta {\int}_{a}^{a+\delta}f(\theta) \vert_{0}^{2\pi} - {\int}_{0}^{2\pi} \delta f(a+\delta)d\delta = 2\pi - {\int}_{0}^{2\pi} \delta f(a+\delta)d\delta. \end{array} $$

Equating the lhs (24) and rhs (25), we get $f(a) = \frac {1}{2\pi }.$ Since a is arbitrary, this means that f(⋅) must be the uniform pdf on the circle. □

It is to be emphasized that the assumption on continuity of the pdf f(⋅) is crucial in the above theorem. For example, the marginalized and conditionalized methods applied to the wrapped exponential distribution on the circle lead to the same discrete distribution, i.e. geometric distribution. However, the wrapped exponential pdf is not continuous at 𝜃 = 2π.

A related question is whether the marginalized and conditionalized methods can belong to the same family of distributions. Indeed, it is easy to see that this property will hold for a generalized Cardioid-type family of distributions as given by the following theorem.

Theorem 3.

Consider the pdf of the parent family defined by

$$ \begin{array}{@{}rcl@{}} f(\theta) = \frac{1}{2\pi}\sum\limits_{k=1}^{\infty} \eta_{k}\left( 1+2\rho_{k} \cos(\theta - \mu_{k}) \right), ~~\theta\in[0, 2\pi), \end{array} $$

(26)

where ${\sum }_{k=1}^{\infty } \eta _{k}=1$, ∀ k, η_k ≥ 0, μ_k ∈ [0,2π), |ρ_k| < 1/2. Then the marginalized discrete distribution is also a member of the family of conditionalized discrete distributions.

An interesting connection between the constructions on the circle and line, is given by the following theorem.

Theorem 4 (Duality).

Consider the following dual approaches to constructing discrete circular distributions supported on $\mathbb {Z}_{m}$, starting with a real valued random variable X, with a pdf f(⋅) on $\mathbb {R}$, via either the marginalized or the conditionalized methods of discretization.

• Scale, discretize and wrap: Start with the pdf of the scaled random variable $\widetilde {X}= mX/(2\pi )$, obtain the marginalized [or conditionalized] discrete probability function on the line and denote the corresponding random variable by $\widetilde {X}_{d}$. Further, wrap $\tilde {X}_{d}$, i.e. let $\widetilde {X}_{dw}=(\widetilde {X}_{d}\text { mod }m)$.

• Wrap, scale and discretize: Let X_w = (X mod 2π) (i.e. X wrapped on the circle). Now, start with the pdf of the scaled random variable $\widetilde {X}_{w}= mX_{w}/(2\pi )$, obtain the marginalized [or conditionalized] discrete probability function on the circle and denote the corresponding random variable by $\widetilde {X}_{wd}$.

Then, $\widetilde {X}_{dw}$ and $\widetilde {X}_{wd}$ have the same distribution.

Proof.

For a given random variable Z with continuous support, recall that discretization by marginalized method means taking the random variable ⌊Z⌋, and discretization by conditionalized method means taking the random variable Z_d with its probability function defined by $P(Z_{d}=r)=\frac {f(r)}{{\sum }_{k}f(k)}$. First, we will prove the equivalence for the conditionalized discretization method. The probability function of the discrete distribution resulting from process (a) is given by

$$ P(\widetilde{X}_{dw}= r)= \sum\limits_{k\in \mathbb{Z}}P(\widetilde{X}_{d}= r+km) = \frac{{\sum}_{k\in \mathbb{Z}} f(2\pi(r+km)/m)}{{\sum}_{k\in \mathbb{Z}}f(2\pi k/m)} . $$

(27)

For the process in (b), let us denote the pdf of X_w by $f_{x_{w}}$. Then, the probability function of the discrete distribution resulting from process (b) will be

$$ \begin{array}{@{}rcl@{}} P(\widetilde{X}_{wd}= r)= \frac{f_{x_{w}}(2\pi r/m)}{{\sum}_{r=0}^{m-1}f_{x_{w}}(2\pi r/m)} = \frac{{\sum}_{k\in \mathbb{Z}} f(2\pi r/m + 2\pi k)}{{\sum}_{k\in \mathbb{Z}} f(2\pi k/m )}. \end{array} $$

(28)

Since (27) and (28) are the same, (a) and (b) yield the same discrete circular distribution. Now, to prove the equivalence under the marginalized method of discretization, we observe that process (a) leads to the probability function given by

$$ \begin{array}{@{}rcl@{}} P(\widetilde{X}_{dw}=r) &=& \sum\limits_{k\in \mathbb{Z}} P(\widetilde{X}_{d} = r +km ) = \sum\limits_{k \in \mathbb{Z}} \left( F\left( \frac{ 2\pi (r+1)}{m} + 2\pi k \right) - F\left( \frac{2\pi r}{m} + 2\pi k\right) \right), \end{array} $$

but process (b) also leads to the same probability function because

$$ \begin{array}{@{}rcl@{}} P(\widetilde{X}_{wd}=r) &=& P\left( X_{w} \in \left[\frac{2\pi r}{m}, \frac{2\pi (r+1)}{m}\right]\right)\\ &=&\sum\limits_{k \in \mathbb{Z}} \left( F\left( \frac{ 2\pi (r+1)}{m} + 2\pi k \right) - F\left( \frac{2\pi r}{m} + 2\pi k\right) \right). \end{array} $$

□

2.3.1 General Circular Discrete Location Family

Consider a general circular location family (see, for example, Mardia, 1975b) with probability density function given by

$$ f(\theta\vert\tau, \mu)= g_{\tau}(\theta - \mu), ~~\theta, \mu\in[0, 2\pi), ~\tau\geq 0 , $$

(29)

which we assume to be unimodal with mode at μ. For simplicity, we assume g_τ(𝜃) = g_τ(2π − 𝜃), g_τ(𝜃) > 0 for all 𝜃 ∈ [0,2π) and also that g_τ(2π) = g_τ(0). Note that the normalizing constant will depend only on τ and not on μ. Here, τ ≥ 0 is another parameter in addition to μ, such that τ = 0 corresponds to the case of uniform distribution and the dispersion around the mode decreases as τ increases. For example, τ = κ for the von Mises distribution (3), and τ = ρ for wrapped Cauchy distribution (4).

The probability function for the marginalized discrete distribution based on the circular location family (29) is given by

$$ \begin{array}{@{}rcl@{}} p(r\vert m, \tau, \mu)= {\int}_{2\pi r/m}^{2\pi (r+1)/m} g_{\tau}(\theta- \mu) d\theta, ~~ r\in \mathbb{Z}_{m}, ~\mu\in[0, 2\pi), \end{array} $$

(30)

and we will call this distribution the “marginalized discrete circular location family”.

Similarly, the probability function of the conditionalized discrete distribution based on the circular location family (29) is given by

$$ p(r\vert m, \tau ,\mu)= \frac{g_{\tau}(2\pi r/m-\mu )}{{\sum}_{r=0}^{m-1} g_{\tau}(2\pi r/m -\mu)}, ~r\in \mathbb{Z}_{m}, \mu\in[0,2\pi), $$

(31)

and we will call this distribution the “conditionalized discrete circular location family”.

The characteristic function for the probability function (30) or (31) is given by

$$ \psi_{p,m}= \sum\limits_{r=0}^{m-1}p(r\vert m, \tau ,\mu) e^{ip\frac{2\pi r}{m}}. $$

(32)

Since g_τ(𝜃) can be expressed in terms of its characteristic function ϕ_p (see Mardia and Jupp, 2000, p.27) as

$$ g_{\tau}(\theta)= \frac{1}{2\pi}\sum\limits_{q=-\infty}^{\infty} \phi_{q} e^{-iq\theta},$$

it can shown that the characteristic function of the marginalized discrete location family is

$$ \begin{array}{@{}rcl@{}} \psi_{p,m} &=& \begin{cases} 1, ~~~ p=0 \\ \frac{me^{ip(\mu-\frac{\pi}{m})}\sin(\pi p/m)}{\pi} {\sum}_{l=-\infty}^{\infty} \frac{\phi_{lm+p}}{lm+p}e^{i lm \mu}, p\in \mathbb{Z}_{m}\backslash \{0\},\end{cases} \end{array} $$

(33)

and the characteristic function of the conditionalized discrete location family is

$$ \begin{array}{@{}rcl@{}} \psi_{p,m} &=& e^{ip\mu}\frac{{\sum}_{l=-\infty}^{\infty} \phi_{lm+p}e^{i lm\mu}}{{\sum}_{l=-\infty}^{\infty} \phi_{lm}e^{ilm\mu}},~p\in\mathbb{Z}_{m}. \end{array} $$

(34)

2.3.2 Circular Discrete Family Based on Trigonometric Sums

In this section, we derive the marginalized and conditionalized discrete distributions starting from the flexible continuous distribution based on trigonometric sums introduced by Fernández-Durán (2004). For a set of complex numbers c = {c₀,c₁,…,c_J} such that

$$ \sum\limits_{k=0}^{J} |c_{k}|^{2}=\frac{1}{2\pi}, $$

(35)

the pdf defined by Fernández-Durán (2004) is

$$ \begin{array}{@{}rcl@{}} f(\theta)&= & \frac{1}{2\pi}+ \frac{1}{\pi}\sum\limits_{k=1}^{J} \left\{a_{k} \cos(k\theta) + b_{k} \sin(k\theta)\right\}, ~~\theta\in[0, 2\pi), \end{array} $$

(36)

where (a_k,b_k) are such that $a_{k}-i b_{k} = 2{\sum }_{\nu =0}^{J-k} c_{\nu +k} \bar {c}_{\nu }$. The specific choice of (a_k,b_k) is a necessary and sufficient condition to ensure positivity of the function f. The pdf (36) can also be written as

$$ \begin{array}{@{}rcl@{}} f(\theta)&= & \frac{1}{2\pi}+ \frac{1}{\pi}\sum\limits_{k=1}^{J} \rho_{k} \cos(k\theta-\phi_{k}), ~~\theta\in[0, 2\pi), \end{array} $$

(37)

where

$$ \rho_{k}=\sqrt{{a_{k}^{2}}+{b_{k}^{2}}} \text{ and } \phi_{k}=\arctan(b_{k}/a_{k}). $$

(38)

We will refer to the distributions obtained by applying Definitions 1 and 2 on the pdf (36) as the “marginalized discrete trigonometric sum” distribution (denoted MDTS(m,c)) and the “conditionalized discrete trigonometric sum” distribution (denoted CDTS(m,c)), respectively. It is easy to see from (36) and (37) that the probability function of MDTS(m,c) is given by

$$ p(r|m,\boldsymbol{c})= \frac{1}{m}+\frac{2}{\pi} \sum\limits_{k=1}^{J} \frac{\sin(\pi k/m)\rho_{k}}{k} \cos\left( \frac{2\pi k(r+1/2)}{m} - \phi_{k}\right) , ~r \in \mathbb{Z}_{m}, $$

(39)

and the probability function of CDTS(m,c) is given by

$$ \begin{array}{@{}rcl@{}} p(r|m,\boldsymbol{c})= \frac{1+2{\sum}_{k=1}^{J} \rho_{k} \cos\left( \frac{2\pi k r}{m}-\phi_{k}\right)}{m\left( 1+2\underset{k=0 (\text{mod m})}{{\sum}_{k=1}^{J} }a_{k}\right)}, ~r \in \mathbb{Z}_{m}, \end{array} $$

(40)

where ρ_k and ϕ_k are as in (38). Note that for J = 1, (39) and (40) give the marginalized and conditionalized discrete cardioid distributions, respectively. We see that the two distributional forms are identical although with different parametrization, which is consistent with Theorem 3.

As in the continuous case, the above constructed discrete families give flexibility in modeling multimodality and skewness in circular discrete data. See also Imoto et al. (2020). In this paper, we will give a particular application in Section 4.1.2.

3 Key Special Discrete Distributions and Their Properties

We now give the marginalized and conditionalized methods for the von Mises (3) and the wrapped Cauchy (4) as the parent distributions followed by some basic properties including characteristic function, estimation and hypothesis testing. We begin with the definitions of these distributions.

Definition 3.

Using (19), the probability function for the marginalized discrete von Mises distribution (MDVM) with mean parameter μ and concentration parameter κ, denoted by MDV M(m,κ,μ), is given by

$$ p(r\vert m, \kappa, \mu) = \frac{1}{2\pi I_{0}(\kappa)}{\int}_{2\pi r/m}^{2\pi(r+1)/m}e^{\kappa \cos\left( \theta-\mu\right)}d\theta, r\in\mathbb{Z}_{m},~~\mu\in[0, 2\pi), $$

(41)

Definition 4.

Using (20), the probability function for the conditionalized discrete von Mises (CDVM) distribution with mean parameter μ and concentration parameter κ, denoted by CDV M(m,κ,μ), is given by

$$ p(r\vert m, \kappa, \mu) = \frac{1}{L_{0}(\kappa,\mu)}e^{\kappa \cos\left( 2\pi r/m-\mu\right)}, r\in\mathbb{Z}_{m},~~\mu\in[0, 2\pi), $$

(42)

where the normalizing constant is the reciprocal of the function

$$ L_{0}(\kappa, \mu)= \sum\limits_{r=0}^{m-1} e^{\kappa \cos\left( 2\pi r/m-\mu\right)}. $$

(43)

Similarly, we have the following definitions for the wrapped Cauchy case.

Definition 5.

The probability function of the marginalized discrete wrapped Cauchy (MDWC) distribution with mean parameter μ and concentration parameter ρ, denoted by MDWC(m,ρ,μ), is given by

$$ \begin{array}{@{}rcl@{}} p(r\vert m, \rho, \mu)&=& \frac {1}{2\pi} \cos^{-1} \left\{ \frac {(1 + \rho^{2}) \cos (\frac{2\pi (r+1)}{m} - \mu ) - 2\rho} {1 + \rho^{2} - 2\rho \cos (\frac{2\pi (r+1)}{m} - \mu )} \right\} \\ &~& - \frac {1}{2\pi} \cos^{-1} \left\{ \frac {(1 + \rho^{2}) \cos (\frac{2\pi r}{m} - \mu ) - 2\rho} {1 + \rho^{2} - 2\rho \cos (\frac{2\pi r}{m} - \mu )} \right\} \\ && ~~~~~~r\in\mathbb{Z}_{m}, ~~\mu\in [0, 2\pi), ~~\rho\in[0,1). \end{array} $$

(44)

Alternatively, for computational purposes, the above expression can be written as

$$ \begin{array}{@{}rcl@{}} p(r\vert m, \rho, \mu)&=& \frac{1}{\pi} \arctan\left( \frac{ \frac{1+\rho}{1-\rho}\left\{\tan(\pi(r+1)/m- \mu/2)- \tan(\pi r/m-\mu/2)\right\}}{1+ \left( \frac{1+\rho}{1-\rho}\right)^{2}\tan(\pi(r+1)/m-\mu/2)\tan(\pi r/m -\mu/2) }\right),~ \\ && ~~r\in\mathbb{Z}_{m}, ~~\mu\in [0, 2\pi), ~~\rho\in[0,1). \end{array} $$

(45)

Further, we have

Definition 6.

The probability function of the conditionalized discrete wrapped Cauchy distribution with mean parameter μ and concentration parameter ρ, denoted by CDWC(m,ρ,μ), is given by

$$ \begin{array}{@{}rcl@{}} p(r\vert m, \rho, \mu)&= &\frac{1}{D_{0}(\rho, \mu)}\frac{1}{1-2\rho \cos\left( \frac{2\pi r}{m}-\mu\right) +\rho^{2}}, \\ &&~~ ~r\in \mathbb{Z}_{m},~ \mu\in[0, 2\pi),~ \rho\in[0,1). \end{array} $$

(46)

where the normalizing constant is the reciprocal of the function

$$ D_{0}(\rho, \mu)= \frac{m(1-\rho^{2m})}{(1-2\rho^{m} \cos(m\mu)+\rho^{2m})(1-\rho^{2})}. $$

(47)

The normalizing constant (47) is derived in the supplement Section A2, Corollary A1. For simplicity of notation, while writing the marginalized or conditionalized discrete probability functions, we will omit the subscripts such as v or c corresponding to von Mises or Cauchy, but they will be clear from the context and by the explicit mention of κ versus ρ as the concentration parameters. So, we will always denote the discrete probability functions by p(r|m,κ,μ) for von Mises or p(r|m,ρ,μ) for wrapped Cauchy. We now make some additional observations specific to CDVM and CDWC distributions.

Probability Functions

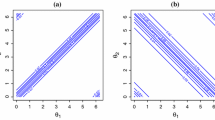
Figure 1 plots the probability functions of CDWC(m,ρ,μ) and CDV M(m,κ,μ), for (i) m = 10 and (ii) m = 37 with μ = 2π5/m and μ = 2π16/m respectively, for ρ = 0.5 and its mapped κ value. In order to compare the probability functions of CDWC(m,ρ,μ) and CDVM(m,κ,μ), we need to first map the parameters ρ to κ. We do so by matching their first trigonometric moments given by (50) and (52) below, i.e. B(κ) = ρ_w. We note that the CDWC is more spiked and heavy tailed compared to CDVM.

Figure 1

Probability functions of CDWC(m,ρ,μ)(triangles joined by solid line) and CDV M(m,κ,μ) (cross joined by dotted lines) plotted for (i) m = 10 and (ii) m = 37 with μ = 2π5/m and μ = 2π16/m respectively, for ρ = 0.5 and its mapped κ value by matching the first trigonometric moment

Characteristic Functions

We make some observations based on the characteristic functions of CDVM and CDWC distributions.

• (a) CDVM. For the CDVM distribution (with μ = 0), we can also obtain an alternative simplified form for the characteristic function. Let us write

  $$ L_{p}(\kappa)= \sum\limits_{r=0}^{m-1}\cos\left( p\frac{2\pi r}{m}\right)e^{\kappa \cos\left( \frac{2\pi r}{m}\right)}. $$

  (48)

  So, for ${\Theta } \sim CDVM(m, \kappa , \mu =0)$, we have

  $$ \begin{array}{@{}rcl@{}} \psi_{p,m}=E\left[e^{i p {\Theta}} \right]&=& B_{p}(\kappa) , \text{where }B_{p}(\kappa)= L_{p}(\kappa)/L_{0}(\kappa). \end{array} $$

  (49)

  It then follows by writing B₁(κ) = B(κ), that

  $$ B(\kappa)= E\left( \cos \frac{2\pi r}{m}\right) \text{ and } B^{\prime}(\kappa)= Var\left( \cos \frac{2\pi r}{m}\right) . $$

  (50)

  L_p(κ) is the discrete analogue of the Bessel function I_p(κ). It is to be noted that not all of the standard identities of I_p(κ) (see Mardia and Jupp (2000), Appendix 1) necessarily hold for its discrete analogue.

• (b) CDWC. For ${\Theta } \sim CDWC(m, \rho , \mu =0)$, the p th trigonometric moments ($p\in \mathbb {Z}_{m}$) are given by

  $$ \alpha_{p,m}=E\left[\sin \left( p{\Theta}\right)\right]=0, ~~\beta_{p,m}=E\left[\cos \left( p{\Theta}\right) \right]= \frac{\rho^{p}(1+\rho^{m-2p})}{1+\rho^{m}}. $$

  (51)

  For p = 1, this leads to the mean resultant length

  $$ \rho_{w} = \frac{\rho (1+\rho^{m-2})}{1+\rho^{m}}. $$

  (52)

  In general, 0 ≤ ρ_w ≤ 1 and as $m\rightarrow \infty$, $\rho _{w} \rightarrow \rho$. By property of characteristic functions, in general 0 ≤ β_p,m ≤ 1, and as $m\rightarrow \infty$, $\beta _{p,m} \rightarrow \rho ^{p}$, as can be seen from (51), which is known to be the characteristic function of the wrapped Cauchy distribution as expected. Further, this convergence happens at an exponential rate. To see this, note that

  $$ \begin{array}{@{}rcl@{}} \psi_{p,m}(\rho) - \rho^{p} &=& \frac{\rho^{p} \left( \rho^{m-2p}- \rho^{m}\right)}{1+\rho^{m}}= \frac{ \rho^{m-p} \left( 1-\rho^{2p}\right)}{1+\rho^{m}}. \end{array} $$

  For any fixed p, it follows that |ψ_p,m(ρ) − ρ^p|≤ ρ^m−p, and hence $|\psi _{p,m}(\rho ) - \rho ^{p}| = \mathcal {O}(\rho ^{m-p})$. In particular, since ψ_1,m = ρ_w, we have $|\rho _{w} - \rho | = \mathcal {O}(\rho ^{m-1})$.

Estimation

The maximum likelihood estimates (mle) of (μ,κ) for CDVM and (μ,ρ) for CDWC can be obtained by iteratively solving the maximum likelihood equations for the two parameters, the details of which are given in Section A5.1 of the supplement. Further, we give asymptotically equivalent estimates to mle which are simpler to compute:

• (a). Moment estimates: Characteristic functions for the marginalized discrete and conditionalized discrete location families with cardioid, von Mises and wrapped Cauchy as parent distributions, based on the general formulas (33) and (34), are given in the supplement (Section A3 Table S2). These can be used to estimate parameters based on matching of trigonometric moments from the data. For ${\Theta } \sim CDWC(m, \rho , \mu )$, the trigonometric moments have a closed form, given by

  $$ \begin{array}{@{}rcl@{}} E[\cos({\Theta})]&=& A\cos(\mu) + B\cos((m-1)\mu),\\ E[\sin({\Theta})]&=& A\sin(\mu) - B\sin((m-1)\mu), \end{array} $$

  where

  $$A=\frac{\rho(1-\rho^{2m-2})}{(1-\rho^{2m})}, B=\frac{\rho^{m-1}(1-\rho^{2})}{(1-\rho^{2m})}.$$

  For the constrained case when $\mu = 2\pi t/m, t\in \mathbb {Z}_{m}$, the above equations simplify to

  $$E[\cos({\Theta})]=\frac{\rho (1+\rho^{m-2})}{1+\rho^{m}}\cos(\mu) \text{ and }E[\sin({\Theta})]=\frac{\rho (1+\rho^{m-2})}{1+\rho^{m}}\sin(\mu). $$

• (b). Hybrid estimates: When n is large, plug-in the sample mean direction ($\bar {\theta }$) for μ, and obtain mle for only ρ or κ.

• (c) Constrained estimates: When m is large, constrain μ to $\{2\pi t/m, t\in \mathbb {Z}_{m}\}$. In this case, the normalizing constants (43) and (47) become free of μ, leading to some simplifications. For CDVM, this approach leads to following explicit equations for mle:

  $$B(\hat{\kappa}) = \bar{R} \cos\left( \bar{\theta} - \frac{2\pi \hat{t}}{m}\right) \text{ and }~~\hat{t}= \left[\frac{m\bar{\theta}}{2\pi}\right]_{m}, $$

  where $B(\kappa )= L_{1}(\kappa )/L_{0}(\kappa ), ~~L_{p}(\kappa )= {\sum }_{r=0}^{m-1}\cos \limits \left (p\frac {2\pi r}{m}\right )e^{\kappa \cos \limits \left (\frac {2\pi r}{m}\right )}$, $p\in \mathbb {Z}_{m},$ and [x]_m denotes the closest integer to x, modulo m.

  Asymptotic normality of these estimate follow using the results in Pewsey (2004) for the case (a) and Mardia et al. (2016) for the cases (b) and (c).

Testing of Hypothesis

We will give more details in the next section on testing of hypothesis as we apply the methodology as required in the next section but we outline some main points.

The Rayleigh Test is well known to test uniformity under the von Mises distribution, that is to test (see, for example, (Mardia and Jupp, 2000))

$$ H_{0} : \kappa =0,~~ H_{1}: \kappa >0, $$

where the mean μ is unknown. It is based on ${T_{1}^{2}}= 2n \bar {R}^{2}$, which under H₀, is approximately chi-squared with 2 degrees of freedom. Now, given the data vector w of iid observations under CDVM, the log-likelihood ratio test statistic (T) can be written as

$$ T(\boldsymbol{w},\hat{\kappa},\hat{\mu})= -2 LL(\boldsymbol{w}\vert m, \kappa=0) + 2 LL(\boldsymbol{w}\vert \hat{\kappa},\hat{\mu}), $$

where $(\hat {\kappa }, \hat {\mu })$ is the mle based on the data vector w and LL(⋅) is the log-likelihood. If we denote the computed value of T in the data sample by T_d, then

$$ \text{p-value}=P\left( T(\boldsymbol{w},\hat{\kappa},\hat{\mu} ) \geq T_{d}\right).$$

The test rule is then to reject H₀ for values of the p-value in comparison to a chosen significance level and use bootstrap for the mle and the p-values for the tests. For large m, the T-test = the Rayleigh test. We can extend it easily to the circular location family including CDWC which is easier to use as the normalizing constant is simpler.

4 Examples

We apply some of the models developed in the previous sections to analyze real data on roulette wheel outcomes and smart health monitoring readings on SBP acrophase. In both these situations, data are circular and discrete. Also, in both these situations, data are generated in abundance daily, although they may not usually be accessible in the public domain. Interestingly, the acrophase is an example where the data has an irregular discrete support. Our analysis and findings that are presented below are mainly illustrative of the kind of insights that are possible through the different circular discrete models.

4.1 Roulette Wheel Data: Online Gaming and Casino Spins

There has been ongoing search to find a plausible test for testing unbiasedness of a roulette wheel. The problem is now more pressing than ever before with the rise of many online gaming sites, e.g. An Online Gaming Site https://10bestcasinos.co.uk/en-en_d_rl.html. For example, the UK Gambling Commission requires statistical testing to ensure fairness, by an approved third party as per the guidelines provided in their “Testing strategy for compliance with remote gambling and software technical standards” at UK Government Compliance https://www.gamblingcommission.gov.uk/.

Indeed, Pearson (1894, 1897) was captivated by this problem and had acquired his data of n = 16,563 roulette spins from the Monte Carlo Casino as recorded in a journal “La Monaco”. He constructed three tests, but as the subject of Directional Statistics was still developing, it was usual to ignore the circular aspect of the data. A brief historical insight into his work, along with images of a typical European roulette wheel, are given in the supplement Section A4. Karl Pearson’s original sequence of roulette spin data is not available and we work with data from an online roulette simulator as well as some industrial casino data obtained from spins of different European roulette wheels. Note that here the number of outcomes is m = 37 (as against an American roulette m = 38). In some cases, the data is available as a streaming sequence of outcomes from successive spins of the roulette wheel, and in others we may just have the frequency distribution of the outcomes without knowledge of the sequence. Accordingly, we illustrate different types of analysis.

We look at the following four roulette data:- three different streaming sequence roulette data and one cumulative frequency data.

Roulette data 1 :

Our first data is of size n = 1000, a sequence of outcomes from successive spins of an online European roulette simulator available at http://datagenetics.com/blog/july12015/index.html

Roulette data 2 :

This data has outcomes from successive spins of a real European roulette recorded in a casino in Slovenia, n = 8299.

Roulette data 3 :

This data has outcomes from successive spins from the same casino as roulette data 2, but from a different roulette wheel, n = 8106.

Roulette data 4 :

This data is only of cumulative frequency of roulette wheel spins from an industrial consulting project at University of Leeds, n = 3094.

Rows (i)–(iv) of Table 1 give their respective frequency distributions. We will deal with sequential roulette Data 1, Data 2 and Data 3 in the next subsection (Section 4.1.1) and the cumulative roulette Data 4 in the subsequent subsection (Section 4.1.2).

Table 1 Frequency distributions for the roulette Data 1, 2, 3 and 4. The entries of angular positions (r) in the first row correspond to angles 2πr/m on the circle, the second row shows the corresponding label on the roulette wheel and the other rows show the frequencies of outcomes

4.1.1 Analysis of the Streaming Sequence Roulette Data 1–3

We consider here roulette Data 1, Data 2 and Data 3. The main challenge is to detect a possible bias in a roulette based on a streaming sequence of spin outcomes. We note here that since the roulette Data 1, 2 and 3 are available as a time series, we carried out a test for serial independence, in the lines of Watson and Beran (1967), but adapting to discrete data (more details are in Mardia and Sriram (2020)). The test indicates that overall there is no dependence. Our analyses and findings for these data are as follows. The main challenge is to detect a possible bias in a roulette based on a streaming sequence of spin outcomes.

Analysis 1

First, we carry out testing unbiased (of the wheels) using only cumulative frequencies for the roulette Data 1, 2, and 3 given in Table 1, which is equivalent to testing for uniformity, i.e. H₀ : τ = 0 (unbiased wheel) vs. H₁ : τ≠ 0 (biased wheel). For this purpose, we use a log-likelihood ratio test statistic (denoted T), which is computed as the difference in the log-likelihoods at the maximum likelihood estimates (mle) and at the null hypothesis τ = 0. Recall for the continuous circular location scale family, τ = 0 corresponds to the uniform distribution on the circle, so a specific value of μ is not required for H₀. We carry out this analysis using the CDWC model. Table 2 shows the mle, test statistic and the p-value for each the roulette Data 1,2 and 3. Comparing the p-value with a 5% significance level, we conclude that the evidence for bias does not exist for roulette data 1, is weak for roulette Data 2 and strong for roulette Data 3. The estimated mode for data 3 is $\hat {\mu }=5.34$ approximately corresponding to the angular position r ≈ 31. See Supplement Section A5 Figure S2 for the circular histogram of data 3. It turns out these conclusions happen to be the same if we had used the CDVM model, or if we had used some alternative tests known in the context of continuous data (see Supplement Section A5 for details).

Table 2 Based on CDWC model, results of Analysis 1 for roulette data 1-3

Analysis 2

Analysis 1 does not use the streaming nature of the outcomes, that is we have used only the cumulative frequency not the full time series. Here, we delve further into the sequence of outcomes. Let us denote the sequence of angular positions of the roulette outcomes by $\left \{w_{i} : i\in \{1,2,\ldots , n\}\right \}$. The mapping of angular positions to labels on the roulette wheel is given in Table 1. Our goal is to estimate a change-point in the data. The model with a changepoint at i = K can be constructed as follows:

$$ w_{i} \sim \begin{cases} p(\cdot \vert m, \tau_{1}, \mu_{1}) ~~~\text{ if } i\leq K \\ p(\cdot \vert m, \tau_{2}, \mu_{2}) ~~~\text{ if }i>K, \end{cases} $$

(53)

where p(⋅|m,τ,μ) is the probability function of the discrete circular distribution as in (30) and (31). Of particular interest is to detect a change from uniformity, i.e. τ₁ = 0, where μ₁ can be arbitrary but we take it as 0 without loss of generality. The likelihood for the data can then be written as

$$ L(\boldsymbol{w}\vert (\tau_{1}=0,\tau_{2}), (\mu_{1}=0, \mu_{2}), K) = \prod\limits_{i=1}^{K} p(w_{i} \vert m, \tau_{1}=0, \mu_{1}=0) \times \prod\limits_{i=K+1}^{n} p(w_{i} \vert m, \tau_{2}, \mu_{2}). $$

(54)

We can apply a Bayesian approach with standard Markov Chain Monte Carlo methods for estimation, using non-informative flat priors on the unknown parameters, viz τ₂,μ₂ and K. For our data, we carry out the changepoint analysis using the CDWC(m,ρ,μ) model, first based on the full data sequence and then based on partial data sequences. Specifically, we use a Gibbs sampling procedure to obtain the posterior distributions, by taking the support of (ρ₂, μ₂, K) to be a suitably fine grid of values, viz. ρ₂ ∈{0,0.001,0.002,…,0.999}, μ₂ ∈{0,0.001 × 2π,0.002 × 2π,…,0.999 × 2π} and K ∈{1,2,…,n}. The posterior distribution summaries obtained for each of the full sequences of roulette data 1,2, 3 are shown in Table 3. For any given roulette data sequence, we conclude that there is evidence for a changepoint if the 95% highest probability density (hpd) credible interval for ρ₂ is removed from 0. Accordingly, we conclude that there is no evidence for a change from uniformity in data sequences 1 and 2. For roulette data 1 and 2, we also see that the 95% hpd interval for K spans a very large range between 1 and n, as one would expect if the distribution of K is close to a discrete uniform on {1,2,…,n}. This further supports the absence of a changepoint in roulette data 1 and 2.

Table 3 Posterior distribution summaries from the CDWC changepoint model, for parameters (μ₂,ρ₂,K) based on full data ranges (i.e., 1 : n) for roulette data 1,2,3. The distribution before changepoint is assumed to be uniform, i.e. ρ₁ = 0,μ₁ = 0

However, there is evidence for a changepoint in roulette data 3 since the 95% hpd interval for ρ₂ is clearly removed from 0. We can also see that the estimated posterior mode for the changepoint in roulette data 3 is K = 1226. Therefore, subsequent to the changepoint, the distribution of outcomes in roulette data 3 has changed from uniform distribution to one that has a single mode (at μ₂ = 5.305 with angular position r ≈ 31). Such a bias might be resulting from a slight “tilt” in the roulette wheel downwards to favour such a mode. In Section 4.1.2, we also look at a different type of bias, possibly resulting from “wobble” of a roulette wheel.

Testing Streaming Consistency

Further, to see how early the changepoint would have been detected, we treat the spins as streaming data by increasing the number of spins sequentially by 500. So, we apply the same changepoint detection procedure on partial data sequences of roulette data 3, i.e. spins 1 : u for u ∈{500,1000,1500,…,8000,8106}. Figure 2 shows the plots of the 95% hpd intervals, posterior mean for ρ₂ and mode for K for different choices of the upper bound. We can see that starting from an upper bound of 4000 onwards, the 95% credible interval for ρ₂ appears to be removed from 0, and for 5500 onwards it is even more clearly removed from 0. Correspondingly the posterior mode for K is settled somewhere between 1000 and 2000. Also, the 95% hpd for K appears to be stabilize for the data range 1:5500 and after. So, while we start detecting the change weakly based on the first 4500 outcomes, the evidence becomes stronger as we start including outcomes 1:5500 and after.

Figure 2

Results of changepoint analysis based on different partial data ranges for Data 3. plot (i) shows posterior summaries for ρ₂ and (ii) for K plotted against data range upper bound. In each plot, solid lines mark the 95% credible intervals. The dotted line in plot (i) shows the posterior mean for ρ₂ and in plot (ii) shows the posterior mode for K

We now comment on how our work is basically different from some other work on circular change point detection. Pewsey and García-Portugués (2021) have given a survey of changepoint detection with continuous angular data, but our method is for discrete circular data. There has been other work in this area motivated by control charts, e.g. Lombard and Maxwell (2012), Laha and Gupta (2011) and Rao and Girija (2020). Compared to these approaches, our strategy is different as it is model-based with unknown parameters, whereas the method in Lombard and Maxwell (2012) is nonparametric. Further, control charts, e.g. Laha and Gupta (2011) and Rao and Girija (2020), are not suitable for testing uniformity for the following reasons. Broadly speaking, in their method, given a distribution, n samples of size n₁ are generated. For each sample, based on the n₁ observations, the circular mean is computed. Then two quantities are found after sorting the n values, viz. (a) CCR (clockwise control ray) by eliminating the first α percent values and (b) ACR (anti-clockwise control ray) by eliminating the last α percent values. Such an approach may not be suitable for checking deviation from uniformity because the ACR and CCR will be wide and symmetric around π and so it will not have any observations that fall in the rejection region if the data is actually coming from a distribution concentrated around π. Although their work is also based on some model assumptions, it requires a priori fixing of parameter values to determine the ACR and CCR.

4.1.2 Analysis of the Cumulative Frequency Data 4

Here, we consider Data 4 where only a cumulative frequency roulette outcomes is available, i.e. instead of a streaming sequence we only have the frequency distribution of outcomes. As part of an industrial consulting project at University of Leeds, Baines (1990) recommended a protocol for certifying a casino roulette wheel as “unbiased” using five different statistical tests, two based on chi-square statistic and the other three based on variations of the Rayleigh test (see Supplement Section A5.4 for detailed description of these tests which were given by K. V. Mardia in a personal correspondence). As per the protocol, if all five statistical tests resulted in the acceptance of the Null Hypothesis (H₀) (i.e. no evidence of bias), then the wheel would be certified as having passed the randomness test. However, if any of the five statistical tests resulted in the acceptance of the Alternative Hypothesis (H₁)(i.e. evidence of bias), a second series of at least 370 spins would be collected and the five statistical tests repeated on the new data as well as the combined data from the two series. The choice of the level for the tests would be contextual, i.e. chosen between 5% and 0.1% depending on the acceptable risk of wrongly concluding that the wheel is biased. The cost implications also influence the number of runs to be considered for such tests.

Based on an analysis of different sub-series of roulette spins as well as the combined series, Al Baines and Kanti Mardia reported evidence to suggest that the roulette had a quadri-modal bias with possible modes at the roulette slot positions 12,20,30 and 21, which correspond to angular positions r ∈{4,13,22,32}. However, his methodology is not based on a statistical model, so it does not systematically identify the nature of the specific alternative in H₁, in particular the positions of modes and their likelihood.

To allow some flexibility to capture the multimodal aspect of this data and to achieve the highest log pseudo marginal likelihood (see e.g. Carlin and Louis, 2009, p. 215), we chose J = 4 to fit the CDTS model as in (40) to the combined series of roulette outcomes used in Baines (1990). We refer to this as ‘Data 4’ and give its frequency distribution in row (iv) of Table 1. We find it convenient to estimate the model using a Bayesian approach with a standard MCMC approach based on a random walk Metropolis-Hastings algorithm. Figure 3 shows the fitted model along with the frequency distribution of the data. The fitted model suggests modes at angular positions r ∈{4,13,23,31}, which is somewhat consistent with Al Baines’ conclusion of 4 equi-spaced modes, although our finding suggests that the successive modes may not exactly be equi-spaced. As per our model, the angle subtended between successive modes (in degrees) are 87.6, 97.3, 77.8 and 97.3 respectively. The roulette slots corresponding to these angular positions are 12, 20, 11, 2, with estimated probabilities 0.0279, 0.0319, 0.0289 and 0.0305 respectively. So, our finding goes a bit beyond Baines (1990) to suggest that the roulette wheel possibly has an asymmetric wobble (i.e. modes that are not exactly equi-spaced and with unequal probabilities).

Figure 3

CDTS model fit to the combined series of roulette outcomes in Baines (1990)

4.2 Acrophase Data: Ambulatory BP Monitoring

Systolic blood pressure (SBP) has a circadian rhythm. To monitor it, patients wear ambulatory devices that regularly measure and record blood pressure. In non-invasive smart health monitoring, these readings are typically recorded at predetermined, possibly irregular, discrete time points during daytime and nighttime. Our objective is to analyze “acrophase”, the time at which maximum SBP is attained in a day. Monitoring the acrophase can provide an automated early warning of a possible medical condition before it becomes clinically obvious. Typically, the readings taken by industrial monitoring devices are more frequent during daytime (e.g. each half hour) than at nighttime (e.g. each hour). For more details, see Acrophase Times https://www.londoncardiovascularclinic.co.uk/cardiology-info/investigation/24-hr-ambulatory-blood-pressure.

Therefore, the resulting acrophase data is circular, discrete and supported on an irregular lattice on the circle.

We use acrophase data on SBP based on readings taken for an individual from 3-31-1998 to 7-7-2000, collected by the Halberg Chronobiology Center (University of Minnesota). We note that for a few days, there were multiple time points where maximum SBP was achieved. In such cases, we retained all such time points, thus resulting in a total of 880 data points. As mentioned in the introduction, typically, acrophase data is extracted from SBP measurements at each half hour during daytime (8 am to 8 pm) and each hour during nighttime (8 pm to 8 am). If we map 8 am to 0 radians and 8 pm to π radians, the acrophase times get mapped to an irregular support of m = 36 points on the circle given by

$$ \begin{array}{@{}rcl@{}} \left\{\frac{2\pi r}{48}, r =0,1,2,\ldots,24\right\} \bigcup \left\{\frac{2\pi r}{48}, r =26, 28,\ldots, 44, 46\right\}. \end{array} $$

(55)

Note that unlike the case of regular support where the points in the support are expressed in terms of $\mathbb {Z}_{m}$, here the points in the irregular support are expressed as 2πr/48 to accommodate the half-hour and one-hour time points. Table 4 shows the frequency distribution of this acrophase data. Our initial interest is to estimate the centering and concentration parameters for this data. While the centering parameter will be indicative of the most likely timing of acrophase, the concentration parameter will indicate the extent of variability around that timing. We adapt CD distributions to an irregular support as follows and prefix such distributions by ICD, that is, for example, ICDVM stands for the CDVM with irregular support. Let $\mathcal {S}=\{\theta _{0}, \theta _{2}, \ldots , \theta _{m-1}\}$ denote the irregular circular lattice support (55). The conditionalized discrete probability function for any given parent pdf f(⋅) on the irregular support $\mathcal {S}$, ICD, is given by

$$ \begin{array}{@{}rcl@{}} p(\theta_{l}) = \frac{f(\theta_{l})}{{\sum}_{k=0}^{m-1} f(\theta_{k})}, ~~~\theta_{l} \in \mathcal{S}. \end{array} $$

(56)

Table 4 Frequency distribution of the acrophase data. Also shown is r corresponding to each time point, which maps to the circle by 2πr/48

Table 5 shows the estimated centering (μ) and concentration (κ) for the ICDVM model. We found it computationally convenient to estimate the parameters using a Bayesian approach by assuming non-informative priors on the parameters, specifically we take uniform priors for μ ∈ [0,2π). Since the concentration parameter in CDVM is κ, a mapping is done to an equivalent value of ρ based on matching of first moment between von Mises and wrapped Cauchy distributions. To get a prior for κ, we first map it to ρ and use a uniform prior on ρ ∈ [0,1). From Table 5, we note that the estimates are

$$ \mu =2.462~(\approx 17:30~hrs), \kappa =1.114,~\rho= 0.48$$

so there is moderate concentration. Further, we note that the approximate 99% confidence interval for μ is 17 : 30 hours ± 33 minutes, slightly different from the mode of 19:00 hrs observed in the data in Table 4. This can be the effect of skewness in the data as seen in its histogram given in Fig. 4, which has led us to explore the analysis with the parent as a skew circular distribution since one of our objectives is a construction that allow flexible families of plausible discrete circular distributions.

Table 5 Parameter estimates for ICDVM on irregular support for the acrophase data

We have selected the circular distribution of Kato and Jones (2015), which has four parameters that control the first four trigonometric moments, leading to unimodal symmetrical as well as skew distributions as particular cases. This family also has an analytically tractable normalizing constant and its pdf is given by

$$ g_{KJ}(\theta)=\frac{1}{2\pi} \left( 1+ 2\gamma \frac{\cos(\theta-\mu)-\rho \cos\lambda}{1+\rho^{2} -2\rho\cos(\theta-\mu-\lambda)}\right),~-\pi<\theta \leq \pi, $$

(57)

where the parameters are constrained by

$$ 0\leq \rho <1, 0\leq \gamma \leq (1+\rho)/2, -\pi\leq \mu, \lambda \leq \pi, \text{ and } \rho\gamma \cos\lambda \geq (\rho^{2}+2\gamma-1)/2. $$

(58)

The conditionalized discrete distribution from (57), is given by the probability function

$$ p\left( r\vert m, \rho, \mu, \gamma, \lambda \right)= \frac{1}{D^{\star}} \left( 1+ 2\gamma \frac{\cos(\frac{2\pi r}{m}-\mu)-\rho \cos\lambda}{1+\rho^{2} -2\rho\cos(\frac{2\pi r}{m}-\mu-\lambda)}\right), r\in \mathbb{Z}_{m}, $$

(59)

where

$$ D^{\star}=m\left( 1+2\gamma \rho^{m-1}\frac{ \cos(m(\mu + \lambda)-\lambda)- \rho^{m}\cos\lambda }{1+\rho^{2m}-2\rho^{m}\cos(m(\mu+\lambda)) }\right), $$

(60)

with the same constraints on parameters as in (58). The normalizing constant D^⋆ is derived in the supplement (corollary A2). We will call this family, the conditionalized discrete Kato-Jones family, or briefly as CDKJ family. The CDWC is obtained as a special case when λ = 0 and γ = ρ. Note that the constraints ensure that the probability function in (57) is positive and hence also for the discretized version (59). We can now obtain from (56), the probability function for ICDKJ.

Adapting the method of moments approach in Kato and Jones (2015), we can obtain the estimates to use in the probability function of ICDKJ. The moment estimates are

$$\hat{\mu}=2.248, \hat{\lambda}=0.816, \hat{\rho}=0.495, \hat{\gamma}=0.584.$$

Figure 4 shows the histogram for the acrophase data along with the fitted ICDKJ probability function with these estimates. It can be seen that the mode of the fitted ICDKJ distribution is 18:30 hours approximately, which is roughly what is seen in the histogram. Also, visually, the fit captures the skew behaviour in the data adequately.

Figure 4

Histogram for the acrophase data along with the fitted ICDKJ probability function in solid line

5 Model Misspecification

In this section, we present some insights into the effect of model misspecification, specifically where a true model is a given discrete model but we apply statistical methodology developed for continuous circular distributions. As we have mentioned in Section 1, in any application with discrete data in Linear Statistics, one usually takes into account the discrete nature of the underlying population so the same principle applies here for Directional Statistics but due to lack of developments of Discrete Circular Statistics, Statistical Methodology for continuous circular statistics has been used in the literature and it is of some interest to learn where this use could lead to conflicting inference. The simulations experiments (where necessary) are given to provide some preliminary insight only and presenting elaborate simulation studies is far beyond the scope and the core of this methodology paper.

We will study three situations:

• Case 1. The effect on the basic summary statistics.

• Case 2. Behaviour of the maximum likelihood estimates. Case 2a Irregular case; Case 2b Regular case.

• Case 3. Power of the test of uniformity.

We give an overview of these three studies and our selection of n,m,κ. Case 1 is generic and a population based comparison so n is not relevant; m covers a wide range of values, μ = 0, and a fixed moderate concentration ρ = 0.5,κ = 1.159 (guided by the acrophase data with ρ = 0.485,κ = 1.114).

Case 2 has two parts Case 2a and Case 2b. Case 2a mimics the acrophase data so the support is irregular as it is for that Example, where the data is generated with n = 880, μ = 0.785 and ρ = 0.6 (κ = 1.516) from the ICDVM discrete distribution so the ground truth is known. Note that for simplicity, we have taken here μ = π/4 = 0.785 as the mean parameter can be arbitrary, and the concentration parameter κ = 1.516 computed for the acrophase data as $\bar R = 0.58$, so ρ = 0.6 which maps approximately to κ = 1.516.

Case 2b is for regular cases, n = 1000, m = 10,20 and varying values of the concentration parameter κ = 1,2.5,10 so n is nearly same as for the acrophase data and its concentration parameter is covered in this range but m is kept lower than the acrophase data of m = 36 as the case is here regular the effect would be more evident at the lower values of m. The choice of the distributions are given below in each case.

Case 3 is motivated by the roulette data sets where n is larger and the concentration parameter is low so we have taken κ = 0.05 (ρ = 0.03), for each of different choices of n = 1000,10000 and m = 10,37.

Case 1. The Effect on the Basic Summary Statistics

We carry out a study, where we sample from the marginalized and conditionalized wrapped Cauchy distributions with the parameters μ = 0,ρ = 0.5,κ = 1.159 and varying values of m. We study the first two trigonometric moments, since these are the basic moments to capture the behavior of the distribution (through $E\cos \limits (\theta )$) and its first order departure (through $E\cos \limits (2\theta )$). Table 6 shows these trigonometric moments computed for MDWC(m,ρ,μ) and CDWC(m,ρ,μ) for ρ = 0.5, μ = 0, for different values of m. As a reference, for wrapped Cauchy, $E\cos \limits (\theta )=0.5$ and $E\cos \limits (2\theta )=0.25$. Thus discretization matters for MDWC if m is less than 20, i.e. bin with angle 18 degrees. Surprisingly, the effect is a bit smaller for CDWC. Incidentally, the two moments for CDWC are obtained using the exact results given by (51) and these moments for MDWC were computed using simulated data of size 200000. Our study gives a specific flavor of the effect rather than the very broad Sheppard’s correction (Mardia, 1972), which is too generic. Our conclusion is that discretization matters for m ≤ 20.

Table 6 Trigonometric moments computed for MDWC(m,ρ,μ) and CDWC(m,ρ,μ) for ρ = 0.5, μ = 0, for different values of m. As reference, for WC, $\rho = E\cos \limits (\theta )=0.5$ and $E\cos \limits (2\theta )=0.25$

It should be noted that this study has broader implications as these moments indirectly would influence inference problems associated with the von Mises and the wrapped Cauchy distributions, and specific cases are examined below in Case 2 and Case 3

Case 2. Behaviour of the Maximum Likelihood Estimates

Case 2a The irregular case.

We first assess the effect of using VM vs ICDVM via a sampled drawn from ICDVM which mimics the acrophase data, that is the irregular support, and the same data size (n = 880) and call it “simulated acrophase data” where we take the true value of ICDVM to be μ = 0.785, κ = 1.516, and ρ = 0.6. Table 7 shows the estimation of centering parameter (μ) and concentration parameter (κ) for this simulated acrophase data. Parts (a) and (b) of Table 7 do not consider the discrete nature of the data. Part (a) uses sample statistics along with bootstrap (1000 resamples) standard errors, namely the circular mean of the data for μ and the mean resultant length $\bar {R}$ for ρ. Part (b) estimates the parameters by assuming a continuous model, namely von Mises. Both (a) and (b) are unable to closely estimate the true μ and κ (ρ) parameters unlike the discrete ICDVM model shown in part (c). Especially, the 95% interval for κ in parts (a) and (b) do not capture the true value. Thus the inappropriateness of applying techniques that are otherwise meant for continuous data become even more apparent when we are dealing with discrete circular data on an irregular support. In summary, this experiment clearly illustrates that using methods meant for continuous data on discrete data can be misleading.

Table 7 Estimated center and concentration parameters for data sampled from ICDVM with the same irregular support as acrophase data. The true values of parameters are μ = 0.785, ρ = 0.6, κ = 1.516

Case 2b The regular case.

We use CDVM (CDWC) as the true model so samples are drawn from this distribution and VM (WC) as the misspecified model and calculate the mle for m = 10,20 with different values of the concentration parameter using the VM model. We find that the mle using the misspecified model leads to biased estimates especially when there is a high concentration parameter in the true model.

The details are as follows. We simulate 1000 datasets, each of size n= 1000 for each choice of m∈{10,20} and κ∈{1,2.5,10} for CDV M(m,κ,μ= 0), and ρ ∈{0.5,0.6,0.8} for CDWC(m,ρ,μ = 0). We compute the mle from the conditionalized discrete model and compare it with that obtained from the continuous model. Table 8 shows the comparison of bias, standard deviation(sd) and mean squared error (mse)calculated based on the 1000 simulated datasets under different scenarios of m and the concentration parameter (κ or ρ). Part (a) of the table compares CDVM with VM, and part (b) compares CDWC with WC. We used the “CircStats” library in R to compute the mle under von Mises and wrapped Cauchy models.

Table 8 Bias, SD and MSE for the mle for the concentration parameter (κ in (a), ρ in (b)) computed based on 1000 datasets, each of size n = 1000 for each choice of m ∈{10,20} and κ ∈{1,2.5,10} for CDV M(m,κ,μ = 0), and ρ ∈{0.5,0.6,0.8} for CDWC(m,ρ,μ = 0)

In part (a) of Table 8 we can see that for m = 10, the bias, sd and mse for CDVM are comparable with that of VM for κ = 1,2.5, but much smaller than that of VM for κ = 10 (i.e larger concentration parameter). However, as m increases to 20, the differences between CDVM and VM decrease.

In part (b) of Table 8, the differences are more pronounced. For m = 10, we see that the bias, sd and mse for CDWC are comparable with that of WC for ρ = 0.5, but bias, sd and mse are much less than that of WC for ρ = 0.6 and 0.8. With increasing m to 20, the differences decrease at ρ = .6 decrease but remain at ρ = 0.8 which indicates that a larger m would be required for the two to match. So, using the continuous model for discrete data with possibly high concentration and moderate m can lead to highly biased and inaccurate estimation of parameters. Further, how large m needs to be for a continuous approximation to work depends on the concentration parameter. For example, in problems such as mixture estimation, where the underlying nature of concentration parameters are apriori unknown, it is more appropriate to work with the discrete distribution, as inferences from (the approximate) continuous model can be misleading.

Case 3. Power of the Test of Uniformity

Here we will concentrate on testing uniformity on highly dispersed data, as we have for our roulette data (Section 4.1.1). The test based on a discrete distribution, CDVM or CDWC, and the Rayleigh test based on a continuous distribution, will lead to similar conclusions (see the supplement, Section 5).

Recall that the test of uniformity for a discrete location family ((31) in the paper) is formulated as H₀ : τ = 0 vs. H₁ : τ≠ 0, where τ = κ for CDVM and τ = ρ for CDWC. This can be tested based on the discrete distribution using the test statistic T as discussed in Section A5. An alternative approach is to use the Rayleigh test based on test statistic $\bar {R}$. Table 9 shows the power computed for a 5% test based on either statistic at a specific alternative, viz. (κ = 0.05,μ = 0) for CDVM and (ρ = 0.03,μ = 0) for CDWC, for each of different choices of data-size n ∈{1000,10000} and m ∈{10,37}. The 5% critical values and the power for T are computed based 10000 simulated datasets under the null and alternative hypothesis respectively, from the conditionalized discrete distribution (CDVM in (a) and CDWC in (b) with a given value of m) of the given data-size n. The 5% critical values and the power for $\bar {R}$ are computed based 10000 simulated datasets under the null and alternative hypothesis respectively, from the continuous distribution (VM in (a) and WC in (b)) of the given data-size n. For both CDVM and CDWC, we find that the power of the test based on T is comparable to that based on $\bar {R}$ (i..e Rayleigh).

Table 9 shows the power computed for a 5% test based on the statistics T and $\bar {R}$ at a specific alternative, viz. (κ = 0.05,μ = 0) for CDVM and (ρ = 0.03,μ = 0) for CDWC, for each of different choices of data-size n ∈{1000,10000} and m ∈{10,37}. The 5% critical values and the power for T are computed based 10000 simulated datasets under the null and alternative hypothesis respectively

We now give some general remarks

Remark 1.

A key takeaway from these comparison studies is that discreteness of the data cannot be ignored in general and such data may need to be modeled using discrete circular distributions. At least, these discrete distributions provide a bench mark to assess any loss incurred in using continuous distribution.

Remark 2.

MD distributions are more relevant for the rounded circular data, whereas for any naturally circular discrete data, CD distributions are more appropriate.

Remark 3.

For $\lim m \to \infty$, the CD and MD distributions tend to their parent distribution as these are the Riemannian sums.

We have dealt here with the model misspecification problem between continuous and discrete distributions as this is the main focus of the paper; at the same time we have used both CDVM and CDWC in our comparison study wherever relevant. Incidentally, Mardia and Sriram (2020) show comparison among various different discrete circular models. For example, a comparison study of choices among conditionalized discrete distributions is based on divergence measures such as Kullback-Leibler, L₁ and L₂. It is found that CDVM and CDWC can be very different from each other but the CDVM and conditionalized discrete wrapped normal are very close to each other. These results are similar to the well known results for their respective continuous parent circular distribution: the von Mises, wrapped normal and wrapped Cauchy distributions.

6 Discussion

We have proposed flexible families of circular discrete distributions encompassing well established continuous circular distributions, such as von Mises and wrapped Cauchy. Our analysis of model misspecification (Section 5) highlights the importance of using discrete circular models for discrete data. We have selected the marginalized and conditionalized approaches for our analysis, but other constructions such as the centered wrapped families can be explored further. Also one can further explore the Beran family, in particular ${\mathscr{B}}_{2}$ and ${\mathscr{B}}_{3}$ given in Section 2.1. We have derived some insightful theorems interrelating the different methods of constructions. In particular, we have given an interesting characterization that under some regularity conditions, marginalized and conditionalized discrete distributions will be the same if and only if the parent circular distribution is uniform (leading to the discrete uniform). The marginalized and conditionalized families of distributions have a significant potential for further development beyond Directional Statistics. For example, we have also proved a characterization on the line that under some conditions, these two approaches lead to the same discrete distribution if and only if the parent is the exponential distribution (see supplement Section A7).

We note that some properties of the parent distributions such as unimodality and symmetry are inherited by the circular MD and CD. Also, maximum entropy characterization of the von Mises distribution is inherited by CDVM. However not everything carries over, namely, the normalizing constant for the CDVM depends on both the parameters, the Rayleigh test is no longer the likelihood ratio test for CDVM (supplement Section A5.1), and for CDWC the trigonometric moments are not as simple.

It is worth noting that Karl Pearson recognized that the roulette wheel data goes beyond coin tossing data experiments and raises some difficult inference problems in assessing unbiasedness (see Supplement A4 for more details). Perhaps due to the unavailability of adequate discrete circular models , it did not have much impact at the time. Also, bias in a roulette wheel can be due to a “tilt” or can due to “wobble” as we have seen in our examples. It could be said that wherever there is a wheel, there is inherently a natural circular discrete data, for example, a wheel used in some TV shows- Wheel of Fortune and other shows, in Industries (bicycle wheel, umbrella, and so on).

The field is full of new challenges in statistical methodology, for example, the marginalized and conditionalized approaches are amenable to extensions. We have outlined some extensions in Mardia and Sriram (2020), namely, alternative approaches to allow for an irregular lattice support, and extensions to higher manifolds such as the torus. However, it turns out that regular discretization on the sphere is not straightforward (see supplement, Section A6), and there can be multiple ways of constructing conditionalized discrete distributions.

Our overall recommendation from this paper is that “If you have circular discrete data, you should start with a discrete model”.