Appendix:
Claim 1
The process \(Z_{H}^{\alpha }(t)\) converges towards BH(t) in \(L^{p}\left ({{\varOmega }}\times [0,T] \right )\), p ≥ 1
Proof.
Let α ∈ (0,1) and fix ω ∈Ω. We know that there exists a nonnegative random variable Cε,T such that
$$ \left\vert B_{H}(u)-B_{H}(v)\right\vert \leq C_{\varepsilon,T} \left\vert u-v\right\vert^{H-\varepsilon},~\text{for all }u,v\in [0,T]\text{ and } \varepsilon\in (0,H). $$
(A.23)
The random variable Cε,T is due to Garsia et al. (1970) and satisfies
\(\mathbb {E} [ C_{\varepsilon ,T}^{p} ]<\infty \) for every p ≥ 1 (for more details see, Azmoodeh et al., 2014). Using the inequality: \(\left \vert {a+b}\right \vert ^{p}\leq 2^{p-1}\left (\left \vert {a}\right \vert ^{p}+\left \vert {b}\right \vert ^{p}\right )\) for all 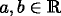 we obtain
we obtain
$$ \begin{array}{@{}rcl@{}} &&\mathbb{E} \left\Vert Z_{H}^{\alpha} - B_{H}\right\Vert_{L^{p}\left( {{\varOmega}}\times [0,T] \right)}^{p}\\ &=& {{\int}_{0}^{T}} \mathbb{E}\left\vert Z_{H}^{\alpha} (t) - B_{H}(t)\right\vert^{p} dt,\\ & \leq & 2^{p-1} \left\lbrace \frac{1}{{{\varGamma}}(\alpha)^{p}}{{\int}_{0}^{T}} \mathbb{E}\left\vert {{\int}_{0}^{t}} \frac{B_{H}(u)-B_{H}(t)}{(t-u)^{1-\alpha}} du\right\vert^{p} dt\right.\\ && \left.+ {{\int}_{0}^{T}} \mathbb{E}\left\vert B_{H}(t)\right\vert^{p}\left\vert \frac{t^{\alpha}}{{{\varGamma}}(\alpha+1)}-1\right\vert^{p} dt\right\rbrace,\\ & \leq & 2^{p-1} \left\lbrace \frac{1}{{{\varGamma}}(\alpha)^{p}}{{\int}_{0}^{T}} \left( {{\int}_{0}^{t}} \frac{\left[\mathbb{E}\left\vert {B_{H}(u)-B_{H}(t)}\right\vert^{p}\right]^{1/p}}{(t-u)^{1-\alpha}} du\right)^{p} dt\right.\\ &&\left. + {{\int}_{0}^{T}} \mathbb{E}\left\vert {B_{H}(t)}\right\vert^{p}\left\vert {\frac{t^{\alpha}}{{{\varGamma}}(\alpha+1)}-1}\right\vert^{p} dt\right\rbrace,\\ \end{array} $$
The last inequality is justified by generalized Minkowski inequality (e.g. §A.1 in Stein, 1970). Set \(\mathcal {C}_{p} :=\mathbb {E} [ C_{\varepsilon ,T}^{p} ]\). By virtue of Eq. A.23 and the last inequality above we have
$$ \begin{array}{@{}rcl@{}} &&\mathbb{E} \left\Vert Z_{H}^{\alpha} - B_{H}\right\Vert_{L^{p}\left( {{\varOmega}}\times [0,T] \right)}^{p}\\ \!\!\!& \leq &\!\!\! 2^{p-1}\mathcal{C}_{p} \left\lbrace \frac{\alpha^{p}}{{{\varGamma}}(\alpha+1)^{p}} {{\int}_{0}^{T}} \left( {{\int}_{0}^{t}} (t - u)^{\alpha-1}\times (t - u)^{H-\varepsilon} du\! \right)^{p} dt \right.\\ &~&~~~~~~~~~~~~~~~~\left. + {{\int}_{0}^{T}} t^{p(H-\varepsilon)} \left\vert \frac{t^{\alpha}}{{{\varGamma}}(\alpha+1)}-1\right\vert^{p} dt \right\rbrace,\\ & \leq &\!\!\! 2^{p-1}\mathcal{C}_{p} \left\lbrace \frac{\alpha^{p}}{{{\varGamma}}(\alpha+1)^{p}} {{\int}_{0}^{T}} \frac{t^{p\gamma}}{\gamma^{p}} dt + {{\int}_{0}^{T}} f_{\alpha} (t)dt \right\rbrace,\\ \text{ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!where }& ~&\!\!\! f_{\alpha} (t) := t^{p(H-\varepsilon)} \cdot\left\vert {\frac{t^{\alpha}}{{{\varGamma}}(\alpha+1)}-1}\right\vert^{p}\\&& \!\!\!\rightarrow 0,\text{ as } \alpha \rightarrow 0,\text{ for all }t\in (0,T], \end{array} $$
(A.24)
$$ \begin{array}{@{}rcl@{}} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\text{ and }&~&\!\!\! \left\vert f_{\alpha} (t)\right\vert \leq \left( \frac{(1\vee T)}{\inf_{s>0} {{\varGamma}}(s)}+1\right)^{p} t^{p(H-\varepsilon)},\text{ for all }t\in (0,T]. \end{array} $$
The first term in Eq. A.24 converges to 0 as \(\alpha \rightarrow 0 \). Now, apply Fatou’s lemma to the sequence fα(t) to conclude the convergence of the last integral in Eq. A.24 (\(\limsup _{\alpha \rightarrow 0} {{\int \limits }_{0}^{T}} f_{\alpha } (t)dt \leq {{\int \limits }_{0}^{T}} \limsup _{\alpha \rightarrow 0} f_{\alpha } (t)dt = 0\)). □
Proof of Proposition 2.3.
Let t > s > 0. We have
$$ \begin{array}{@{}rcl@{}} R_{H}^{\alpha}(t,s) &=& \mathbb{E} \left( Z_{H}^{\alpha}(t)Z_{H}^{\alpha}(s)\right),\\ &=& \frac{1}{{{\varGamma}} (\alpha)^{2}} {{\int}_{0}^{t}}{{\int}_{0}^{s}} (t-u)^{\alpha-1}(s-v)^{\alpha-1} R_{H}(u,v) du dv,\\ &=:&(I_{1}+I_{2}-I_{3})/(2{{\varGamma}} (\alpha)^{2}), \\ \text{where } ~~I_{1} &=& {{\int}_{0}^{t}}{{\int}_{0}^{s}} u^{2H}(t-u)^{\alpha-1}(s-v)^{\alpha-1} du dv,\\ I_{2} &=& {{\int}_{0}^{t}}{{\int}_{0}^{s}} v^{2H}(t-u)^{\alpha-1}(s-v)^{\alpha-1} du dv,\\ I_{3} &=& {{\int}_{0}^{t}}{{\int}_{0}^{s}} \left\vert {u-v}\right\vert^{2H}(t-u)^{\alpha-1}(s-v)^{\alpha-1} du dv.\\ \end{array} $$
Simple computations with change of variables lead to \(I_{1}+I_{2}=\frac {B_{H,\alpha }}{\alpha } (ts)^{\alpha }\) \(\left (t^{2H} + s^{2H}\right )\), where \(B_{H,\alpha } = {\mathscr{B}}(2H+1,\alpha )\). The last integral can be simplified as
$$ \begin{array}{@{}rcl@{}} I_{3} &=& {{\int}_{0}^{s}} dv (s-v)^{\alpha-1} {{\int}_{v}^{t}} du (t-u)^{\alpha-1}(u-v)^{2H}\\&& + {{\int}_{0}^{s}} du (t-u)^{\alpha-1} {{\int}_{u}^{s}} dv (s-v)^{\alpha-1}(v-u)^{2H},\\ &=& B_{H,\alpha} \left[ {{\int}_{0}^{s}} dv (s-v)^{\alpha-1} (t-v)^{2H+\alpha} + {{\int}_{0}^{s}} du (t-u)^{\alpha-1} (s-u)^{2H+\alpha}\right] ,\\ &=& B_{H,\alpha} (ts)^{\alpha} \left[ t^{2H} {{\int}_{0}^{1}} (1-v)^{\alpha-1} \left( 1-\frac{s}{t} v\right)^{2H+\alpha}dv \right.\\&&\left.+ s^{2H} \left( \frac{s}{t}\right){{\int}_{0}^{1}} \left( 1-\frac{s}{t} u\right)^{\alpha-1} (1-u)^{2H+\alpha}du\right], \end{array} $$
(25)
By (15.6.1) in Olver et al. (2010) the last equality is simplified as
$$ \begin{array}{@{}rcl@{}} I_{3} &=& B_{H,\alpha} (ts)^{\alpha} \left[ t^{2H}~\frac{{~}_{2} F_{1} \left( -2H-\alpha,1,\alpha+1,\frac{s}{t}\right) }{\alpha} \right.\\&&\left.+ s^{2H} \frac{ ~_{2} F_{1} \left( 1-\alpha,1,2H+\alpha+2,\frac{s}{t}\right)}{2H+\alpha+1} \left( \frac{s}{t}\right)\right], \end{array} $$
which completes the proof of Eq. 6. By virtue of self-similarity of the process \(Z_{H}^{\alpha }(t)\) we have \(\mathbb {E} Z_{H}^{\alpha }(t)^{2}=c_{H,\alpha } t^{2H+2\alpha }\) where \(c_{H,\alpha }=\mathbb {E} Z_{H}^{\alpha }(1)^{2} \). By letting t = s in Eq. 6. we derive the explicit form of cH,α. □
Proof Proof of Proposition 2.4.
In the sequel \(\mathcal {I}_{0^{+}}^{\alpha } f(t) \) and \(\mathcal {D}_{0^{+}}^{\alpha } f(t) \) will denote the fractional integral and the fractional derivative (of order α) of the function f(t), respectively.
$$ \mathcal{I}_{0^{+}}^{\alpha} f(t) = \frac{1}{{{\varGamma}}(\alpha)} {{\int}_{0}^{t}} \frac{f(u)}{(t-u)^{1-\alpha}}du,~~\alpha>0, $$
$$ \begin{array}{@{}rcl@{}} \mathcal{D}_{0^{+}}^{\alpha} f(t) &=& \frac{1}{{{\varGamma}}(1-\alpha)} \frac{d}{dt}{{\int}_{0}^{t}} \frac{f(u)}{(t-u)^{\alpha}}du,~~0\leq \alpha<1, \end{array} $$
(26)
$$ \begin{array}{@{}rcl@{}} \text{In particular } &~& \mathcal{D}_{0^{+}}^{0} f(t) = f(t),\\ \mathcal{D}_{0^{+}}^{\alpha} f(t) &=& \frac{d^{p}}{dt^{p}} \left( \mathcal{D}_{0^{+}}^{\alpha_{0}} f(t) \right),~~\text{if } \alpha\geq 1, \end{array} $$
(27)
where p is the integral part of the number α and α0 = α − p ∈ [0,1). Note that \(\mathcal {I}_{0^{+}}^{\alpha } f(t) \) exists if \(f(t)\in L^{1}\left ([0,T]\right )\) and \(\mathcal {D}_{0^{+}}^{\alpha } f(t) \) exists whenever \(f(t)=\mathcal {I}_{0^{+}}^{\alpha } \phi (t) \) with \(\phi (t) \in L^{1}\left ([0,T]\right )\). These conditions are satisfied by BH(t) and \(Z_{H}^{\alpha } (t)\), respectively.
Let us now start the proof of Proposition 2.4. The first statement (i) follows from the following general statement:
Claim 2 For every α > 0 and β ∈ (0,α] we have \(\mathcal {D}_{0^{+}}^{\beta } Z_{H}^{\alpha }(t) = Z_{H}^{\alpha -\beta }(t)\) almost surely. □
Proof.
Case 1. Assume β < 1, β ≤ α and fix ω ∈Ω. By definition of \(Z_{H}^{\alpha } (t)\) and Eq. 26 we have
$$ \begin{array}{@{}rcl@{}} \mathcal{D}_{0^{+}}^{\beta} Z_{H}^{\alpha}(t) &=& \frac{1}{{{\varGamma}}(1-\beta)} \frac{d}{dt} {{\int}_{0}^{t}} \frac{\left( \frac{1}{{{\varGamma}}(\alpha)}{{\int}_{0}^{u}} (u-\xi)^{\alpha-1}B_{H}(\xi) d\xi \right)}{(t-u)^{\beta}}du,\\ &=& \frac{1}{{{\varGamma}}(\alpha){{\varGamma}}(1-\beta)} \frac{d}{dt} {{\int}_{0}^{t}} B_{H}(\xi) \left( {\int}_{\xi}^{t} (t-u)^{-\beta} (u-\xi)^{\alpha-1} du \right)d\xi,\\ &=& \frac{\mathcal{B} (1-\beta,\alpha)}{{{\varGamma}}(\alpha){{\varGamma}}(1-\beta)} \frac{d}{dt} {{\int}_{0}^{t}} B_{H}(\xi) (t-\xi)^{\alpha-\beta} d\xi,\\ &=& \frac{1}{{{\varGamma}}(\alpha-\beta+1)} \frac{d}{dt} {{\int}_{0}^{t}} B_{H}(\xi) (t-\xi)^{\alpha-\beta} d\xi . \end{array} $$
If β = α, then by the last equality we have \(\mathcal {D}_{0^{+}}^{\beta } Z_{H}^{\alpha }(t) = B_{H}(t)\). Assume now that β < α. Thanks to 1.5.22 in Olver et al. (2010) we have
$$ \begin{array}{@{}rcl@{}} \mathcal{D}_{0^{+}}^{\beta} Z_{H}^{\alpha}(t) &=& \frac{d}{dt} \left( Z_{H}^{\alpha-\beta+1}(t) \right),\\ &=& \frac{1}{{{\varGamma}}(\alpha-\beta+1)} \frac{d}{dt} {{\int}_{0}^{t}} B_{H}(\xi) (t-\xi)^{\alpha-\beta} d\xi ,\\ &=& \frac{1}{{{\varGamma}}(\alpha-\beta+1)} \left\lbrace \frac{dt}{dt} \cdot B_{H}(\xi) (t-\xi)^{\alpha-\beta} |_{\xi=t}\right.\\&&\left.+{{\int}_{0}^{t}} B_{H}(\xi) \frac{d}{dt}(t-\xi)^{\alpha-\beta} d\xi \right\rbrace,\\ &=& \frac{1}{{{\varGamma}}(\alpha-\beta)} {{\int}_{0}^{t}} B_{H}(\xi) \frac{d}{dt}(t-\xi)^{\alpha-\beta-1} d\xi =Z_{H}^{\alpha-\beta}(t) \end{array} $$
□
Case 2
Assume β = p ≥ 1 (p is an integer), p < α and fix ω ∈Ω. Applying 1.5.22 in Olver et al. (2010) and by induction on p we get \(\mathcal {D}_{0^{+}}^{p} Z_{H}^{\alpha }(t) = Z_{H}^{\alpha -p}(t)\). The general case β = p + β0 with integral part p and β0 ∈ [0,1) follows immediately from the previous two cases and Eq. 27. Let us now return to the proof of Proposition 2.4. The second statement (ii) follows by induction on n. In fact one can use integration by parts to show that
$$ \begin{array}{@{}rcl@{}} {Z_{H}^{n}}(t) &=& \frac{1}{{{\varGamma}}(n)}{{\int}_{0}^{t}} (t-u)^{n-1} {B_{H}^{1}}(u) du,\\ &=& \frac{1}{{{\varGamma}}(n-1)}{{\int}_{0}^{t}} (t - u)^{n-2} B_{H+1}^{2}(u) du = {\cdots} = \frac{1}{{{\varGamma}}(1)}{{\int}_{0}^{t}} B_{H+n-1}^{n}(u) du,\\ &=& B_{H+n}^{n+1}(t), \end{array} $$
where \(B_{H+k}^{k+1}(t)\) denotes the k + 1th order-fBm (k is an integer).
The statement (iii) says that for every order α > 0 we can take the fractional derivative of order β < α and the outcome is still a process with more regularity than the fBm. The first part of (iii) follows from Claim 2. We shall only prove that for α > 0 such that α + H ≤ 1, the process \(Z_{H}^{\alpha }(t)\) is Hölderian with exponent γ = α + H − ε for any ε ∈ (0,H). In what follows the inequality (A.23) will be systematically used. Let t,s ∈ [0,T] with t > s, h = t − s and fix ω ∈Ω. By change of variables s − v = u
$$ \begin{array}{@{}rcl@{}} &&{{\varGamma}}(\alpha) \left( Z_{H}^{\alpha} (t) - Z_{H}^{\alpha} (s) \right) \\&=& {{\int}_{0}^{t}} (t-u)^{\alpha-1} B_{H}(u) du - {{\int}_{0}^{s}} (s-u)^{\alpha-1} B_{H}(u) du,\\ &=& {\int}_{-h}^{s} (h+v)^{\alpha-1} B_{H}(s-v) dv - {{\int}_{0}^{s}} v^{\alpha-1} B_{H}(s-v) dv,\\ &=& {\int}_{-h}^{0} (h+v)^{\alpha-1} B_{H}(s-v) dv + {{\int}_{0}^{s}} \left[ (h+v)^{\alpha-1} - v^{\alpha-1}\right] B_{H}(s-v) dv,\\ &=& {\int}_{-h}^{0} (h+v)^{\alpha-1} B_{H}(s-v) dv + {{\int}_{0}^{s}} \left[ (h+v)^{\alpha-1} - v^{\alpha-1}\right]\\&& \left( B_{H}(s-v) - B_{H}(s)\right) dv\\ &~&~~+B_{H}(s) {{\int}_{0}^{s}} \left[ (h+v)^{\alpha-1} - v^{\alpha-1}\right] dv,\\ &=& {\int}_{-h}^{0} (h+v)^{\alpha-1} \left[ B_{H}(s-v) - B_{H}(s)\right] dv + {{\int}_{0}^{s}} \left[ (h+v)^{\alpha-1} - v^{\alpha-1}\right]\\&& \left( B_{H}(s-v) - B_{H}(s)\right) dv\\ &~&~~+B_{H}(s) \left\lbrace {\int}_{-h}^{0} (h+v)^{\alpha-1} dv + {{\int}_{0}^{s}} \left[ (h+v)^{\alpha-1} - v^{\alpha-1}\right] dv \right\rbrace,\\ &= :& I_{1} + I_{2} +I_{3}~~\text{(Say)} \end{array} $$
We shall now examine the terms I1, I2 and I3. We have
$$ \begin{array}{@{}rcl@{}} \left\vert I_{1}\right\vert &=& \left\vert {\int}_{-h}^{0} (h+v)^{\alpha-1} \left[ B_{H}(s-v) - B_{H}(s)\right] dv \right\vert ,\\ &\leq & {\int}_{-h}^{0} (h+v)^{\alpha-1} \left\vert B_{H}(s-v) - B_{H}(s)\right\vert dv ,\\ &\leq & C_{\varepsilon,T}{\int}_{-h}^{0} (h+v)^{\alpha-1} \left\vert v\right\vert^{H-\varepsilon} dv, ~~\text{(By Eq.~A.23)}\\ &\leq & C_{\varepsilon,T}h^{H-\varepsilon}{\int}_{-h}^{0} (h+v)^{\alpha-1}dv ~=~\frac{C_{\varepsilon,T}h^{\gamma}}{\alpha},~~ \text{(}\gamma=\alpha+H-\varepsilon\text{)}. \end{array} $$
For the second term I2 we have
$$ \begin{array}{@{}rcl@{}} \left\vert I_{2}\right\vert &=& \left\vert {{\int}_{0}^{s}} \left[ (h+v)^{\alpha-1} - v^{\alpha-1}\right] \left( B_{H}(s-v) - B_{H}(s)\right) dv\right\vert ,\\ &\leq & {{\int}_{0}^{s}} \left[ v^{\alpha-1} - (h+v)^{\alpha-1}\right] \left\vert B_{H}(s-v) - B_{H}(s)\right\vert dv,~~(\alpha <1)\\ &\leq & C_{\varepsilon,T} {{\int}_{0}^{s}} \left[ v^{\alpha-1} - (h+v)^{\alpha-1}\right] v^{H-\varepsilon} dv,~~\text{(By Eq.~A.23)}\\ &\leq & C_{\varepsilon,T} h^{\gamma} {\int}_{0}^{s/h} u^{\alpha-1} \left[ 1 - \left( 1+\frac{1}{u}\right)^{\alpha-1}\right] u^{H-\varepsilon} du,\\&&\text{(By change of variables } u=v/h) \end{array} $$
On the other hand we know that 1 − (1 + x)−δ ≤ 1 ∧ (δx), for all x > 0 and δ > 0. Thereby
$$ \begin{array}{@{}rcl@{}} \left\vert I_{2}\right\vert &\leq & (1-\alpha) C_{\varepsilon,T} h^{\gamma} {\int}_{0}^{s/h} u^{\gamma-1} \left[1\wedge\left( \frac{1}{u}\right)\right] du,\\ &\leq & (1-\alpha) C_{\varepsilon,T} h^{\gamma} \left\lbrace {{\int}_{0}^{1}} u^{\gamma-1} du + {\int}_{1}^{1\vee (s/h)} u^{\gamma-1} \cdot\left( \frac{1}{u}\right) du \right\rbrace,\\ &\leq & (1-\alpha) C_{\varepsilon,T} h^{\gamma} \left\lbrace {{\int}_{0}^{1}} u^{\gamma-1} du + {\int}_{1}^{\infty} u^{\gamma-2} du \right\rbrace <\infty. \end{array} $$
The last two integrals are convergent (because 0 < γ < 1). For the last term I3, we have
$$ \begin{array}{@{}rcl@{}} \left\vert I_{3}\right\vert &=& \left\vert B_{H}(s) \left\lbrace {\int}_{-h}^{0} (h+v)^{\alpha-1} dv + {{\int}_{0}^{s}} \left[ (h+v)^{\alpha-1} - v^{\alpha-1}\right] dv \right\rbrace\right\vert ,\\ &=& \left\vert \frac{B_{H}(s)}{\alpha} \right\vert \left( (h+s)^{\alpha}-s^{\alpha} \right),\\ &\leq & \frac{C_{\varepsilon,T}}{\alpha} s^{H-\varepsilon}\left( (h+s)^{\alpha}-s^{\alpha} \right), ~~\text{(By Eq.~A.23)}\\ &\leq & \frac{C_{\varepsilon,T}}{\alpha} s^{H-\varepsilon } h^{\alpha} \leq \frac{C_{\varepsilon,T}}{\alpha} h^{\gamma},~~~\text{ If } s\leq h,~(\gamma=\alpha+H-\varepsilon ). \end{array} $$
If s > h, then by using the fact that (1 + x)δ − 1 ≤ δx, for all x > 0 and 0 < δ < 1 we obtain
$$ \begin{array}{@{}rcl@{}} \left\vert I_{3}\right\vert &\leq & \frac{C_{\varepsilon,T}}{\alpha} s^{H-\varepsilon}\left( (h+s)^{\alpha}-s^{\alpha} \right),\\ &\leq & \frac{C_{\varepsilon,T}}{\alpha} s^{\gamma}\left( \left( 1+\frac{h}{s}\right)^{\alpha}-1 \right),\\ &\leq & \frac{C_{\varepsilon,T}}{\alpha} s^{\gamma}\left( \alpha \frac{h}{s}\right)= C_{\varepsilon,T} h s^{\gamma-1},\\ &\leq & C_{\varepsilon,T} h^{\gamma},~~\text{(because } \gamma -1 <0 \text{ and }s >h \text{)}. \end{array} $$
Combining the previous results we conclude that \(\left \vert Z_{H}^{\alpha } (t) - Z_{H}^{\alpha } (s) \right \vert \leq A C_{\varepsilon ,T} \left \vert t-s\right \vert ^{\gamma }\), for every t,s ∈ [0,T], where γ = α + H − ε and A is some nonnegative constant; while Cε,T is a nonnegative random variable appearing (A.23).
(iv) Let \(\alpha ,\alpha ^{\prime }\in [\underline {\alpha },\overline {\alpha }]\subset (0,\infty )\) and \(H,H^{\prime }\in [\underline {H},\overline {H}]\subset (0,1)\). For a fixed ω ∈Ω we have
$$ \begin{array}{@{}rcl@{}} \left\vert Z_{H}^{\alpha} (t) - Z_{H^{\prime}}^{\alpha^{\prime}} (t)\right\vert \!\!\!&\leq &\!\!\! \frac{1}{{{\varGamma}}(\alpha)}{{\int}_{0}^{t}} (t-u)^{\alpha-1}\left\vert {B_{H}(u)-B_{H^{\prime}}(u)}\right\vert du\\ &~& + {{\int}_{0}^{t}} \left\vert \frac{(t-u)^{\alpha-1}}{{{\varGamma}}(\alpha)} - \frac{(t-u)^{\alpha^{\prime}-1}}{{{\varGamma}}(\alpha^{\prime})} \right\vert \cdot \left\vert B_{H^{\prime}}(u)\right\vert du,\\ &\leq &\!\!\! \frac{T^{\alpha}}{{{\varGamma}}(\alpha+1)}\sup_{s\leq T}\left\vert B_{H}(s)-B_{H^{\prime}}(s)\right\vert + \sup_{s\leq T}\left\vert B_{}(s)\right\vert J_{t} (\alpha,\alpha^{\prime}),\\ && \\ \text{where} &~& J_{t} (\alpha,\alpha^{\prime}):= {{\int}_{0}^{t}} \left\vert \frac{(t-u)^{\alpha-1}}{{{\varGamma}}(\alpha)} - \frac{(t-u)^{\alpha^{\prime}-1}}{{{\varGamma}}(\alpha^{\prime})} \right\vert du. \end{array} $$
(A.28)
We shall evaluate the integral \(J_{t} (\alpha ,\alpha ^{\prime })\).
$$ \begin{array}{@{}rcl@{}} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! J_{t} (\alpha,\alpha^{\prime}) \!\!\!\!&\leq &\!\!\!\! {{\int}_{0}^{t}} (t-u)^{\alpha-1} du \left\vert \frac{1}{{{\varGamma}}(\alpha)}-\frac{1}{{{\varGamma}}(\alpha^{\prime})}\right\vert +\frac{1}{{{\varGamma}}(\alpha^{\prime})}{{\int}_{0}^{t}}\\ && \left\vert (t-u)^{\alpha-1} - (t-u)^{\alpha^{\prime}-1}\right\vert du,\\ \!\!\!\!&\leq &\!\!\!\! \frac{T^{\alpha}}{\alpha} \left\vert \frac{1}{{{\varGamma}}(\alpha)} - \frac{1}{{{\varGamma}}(\alpha^{\prime})}\right\vert + \frac{1}{{{\varGamma}}(\alpha^{\prime})}{{\int}_{0}^{t}} \left\vert (t - u)^{\alpha-1} - (t - u)^{\alpha^{\prime}-1}\right\vert du. \end{array} $$
(A.29)
By the mean value theorem, one can show that
$$ \left\vert \frac{1}{{{\varGamma}}(\alpha)}-\frac{1}{{{\varGamma}}(\alpha^{\prime})}\right\vert \leq A_{1} \left\vert \alpha-\alpha^{\prime}\right\vert \text{ for all } \alpha,\alpha^{\prime}\in [\underline{\alpha},\overline{\alpha}], $$
(A.30)
where A1 is some nonnegative constant. Once again, by the mean value theorem we have
$$ \begin{array}{@{}rcl@{}} &&{{\int}_{0}^{t}} \left\vert (t-u)^{\alpha-1} - (t-u)^{\alpha^{\prime}-1}\right\vert du\\ &=& \left\vert \alpha-\alpha^{\prime}\right\vert {{\int}_{0}^{t}} (t-u)^{\alpha^{*}-1} \left\vert \log(t-u)\right\vert du,\\ &~& \text{(where }\alpha^{*} \text{ is a linear combination of }\alpha\text{ and }\alpha^{\prime} \text{)}\\ &=& \left\vert \alpha-\alpha^{\prime}\right\vert {{\int}_{0}^{t}} v^{\alpha^{*}-1} \left\vert \log(v)\right\vert dv,~~\text{(By change of variables }v=t-u\text{)}\\ &\leq & \left\vert \alpha-\alpha^{\prime}\right\vert \left\lbrace {{\int}_{0}^{1}} v^{\underline{\alpha}-1} \left\vert \log(v)\right\vert dv + {\int}_{1}^{1\vee T} v^{\overline{\alpha}-1} \left\vert \log(v)\right\vert dv \right\rbrace,\\ &\leq & A_{2} \left\vert \alpha-\alpha^{\prime}\right\vert ~~\text{(Say)}. \end{array} $$
(A.31)
Using Eq. A.23 and the fact x↦1/Γ(x) is bounded on \((0,\infty )\) (say by some constant M > 0), Eq. A.28 yields
$$ \begin{array}{@{}rcl@{}} \sup_{0\leq t\leq T} \left\vert Z_{H}^{\alpha} (t) - Z_{H^{\prime}}^{\alpha^{\prime}} (t)\right\vert &\leq & M \left( 1\vee T^{\overline{\alpha}}\right) \sup_{t\leq T}\left\vert {B_{H}(t)-B_{H^{\prime}}(t)}\right\vert\\ &&+ C_{\varepsilon,T} \left( 1\vee T^{\overline{H}-\varepsilon}\right) \sup_{t\leq T} J_{t} (\alpha,\alpha^{\prime}). \end{array} $$
(A.32)
Combining Eqs. A.29–A.31 with Eq. A.32 and using Theorem 4 in Peltier and Vehel (1995), we obtain (iv), and the proof of Proposition 2.4 is complete.
Proof of Proposition 2.5.
Set \(d_{H,\alpha }^{(k)}=\begin {pmatrix}2H+\alpha \\ k \end {pmatrix} (-1)^{k} {\mathscr{B}}(\alpha ,k+1) \), \({{\varPhi }}_{H,\alpha ,s}(t):={{\int \limits }_{0}^{1}} \left (1-\frac {s}{t}u \right )^{\alpha -1} (1-u)^{2H+\alpha } du\) and \(B_{H,\alpha }={\mathscr{B}}(2H+1,\alpha )\). Clearly \( d_{H,\alpha }^{(0)} = 1/\alpha \) and \({{\varPhi }}_{H,\alpha ,s}(t)\rightarrow 1/(2H+\alpha +1)\) as \(t\rightarrow \infty \). Using previous notations and expanding \(\left (1-\frac {s}{t}v \right )^{2H+\alpha }\) in Eq. 25 as a series we get
$$ \begin{array}{@{}rcl@{}} R_{H}^{\alpha}(t,s) &=& \frac{1}{2{{\varGamma}} (\alpha)^{2}} \left[ \frac{B_{H,\alpha}}{\alpha} t^{2H+\alpha}s^{\alpha} + \frac{B_{H,\alpha}}{\alpha} s^{2H+\alpha}t^{\alpha} \right. \\ &~& ~~~-\left. B_{H,\alpha} s^{\alpha} t^{2H+\alpha} \sum\limits_{k=0}^{\infty} d_{H,\alpha}^{(k)} \left( \frac{s}{t}\right)^{k} - t^{\alpha-1} s^{2H+\alpha+1} {{\varPhi}}_{H,\alpha,s}(t)\right]. \end{array} $$
Hence the correlation function has the following form
$$ \begin{array}{@{}rcl@{}} &&Corr \left( Z_{H}^{\alpha}(t) Z_{H}^{\alpha}(s)\right) \\&=& \frac{B_{H,\alpha}c_{H,\alpha}^{-1}}{2{{\varGamma}} (\alpha)^{2}}\left[\frac{s^{H} t^{-H}}{\alpha} - \sum\limits_{k=1}^{\infty} d_{H,\alpha}^{(k)} s^{k-H } t^{H-k} - s^{H } t^{-H-1} {{\varPhi}}_{H,\alpha,s}(t) \right]\\ &=& \begin{cases} \mathcal{O}(t^{-H}),~~\text{if }H\in (0,1/2],\\ \mathcal{O}(t^{H-1}),~~\text{if }H\in (1/2,1).\end{cases} \end{array} $$
□
Proof of Propositions 2.6 & 2.7.
Set zj := zj,T(f), j = 1,2. Considering the random variable ST(f) with decomposition (10) and using the fact that \(e^{-\lambda z^{2}} = \frac {1}{2\sqrt {\pi }}{\int \limits } e^{i\sqrt {\lambda } x z -x^{2}/4} dx\), for all 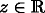 and λ > 0, we obtain
and λ > 0, we obtain
$$ \begin{array}{@{}rcl@{}} {{\varPhi}}_{\lambda} &:=& \mathbb{E} \left( e^{-\lambda S_{T}(f)} \right)= \mathbb{E} \left[ e^{-\lambda ({z_{1}^{2}} +{z_{2}^{2}})} \right],\\ &=& \frac{1}{4\pi} \int\int e^{-(x^{2}+y^{2})/4}\mathbb{E}\left[e^{i\sqrt{\lambda}(x z_{1} + y z_{2} )} \right] dxdy. \end{array} $$
But we know that the vector \(z=\left (z_{1},z_{2} \right )^{\prime }\) is Gaussian with zero mean and the covariance matrix M with entries mkl, k,l ∈{1,2}. Thus
$$ {{\varPhi}}_{\lambda} = \frac{1}{4\pi} \int\int e^{-\frac{1}{2} \mathrm{u}^{\prime} V_{z} \mathrm{u}} d\mathrm{u} = 1/2 \left\vert {V_{z}}\right\vert^{-1/2},$$
where \(\mathrm {u}:=\sqrt {\lambda } (x,y)^{\prime }\), Vz := (1/2)I + λM and I stands for the identity matrix. Note that the matrix Vz is invertible with determinant \(\left \vert {V_{z}}\right \vert =\left \vert {M}\right \vert \lambda ^{2}+(m_{11}+m_{22})+1/4\), \(\left \vert {M}\right \vert =m_{11}m_{22}-m_{12}^{2}\).
We shall now find explicit forms of the entries of the matrix M. Set \(d_{H,\alpha }={\mathscr{B}}(2H+1,\alpha )/(2{{\varGamma }}(\alpha )^{2})\) and β = 2H + 2α + 1. We have
$$ \begin{array}{@{}rcl@{}} m_{11} &=& \mathbb{E} ({z_{1}^{2}}) = \frac{1}{T} {{\int}_{0}^{T}}{{\int}_{0}^{T}} \cos(ft)\cos(fs) R_{H}^{\alpha} (t,s) ds dt\\ &=& \frac{2}{T} {{\int}_{0}^{T}} \left( {{\int}_{0}^{t}} \cos(fs) R_{H}^{\alpha} (t,s) ds \right) \cos(ft)dt\\ &=& \frac{2d_{H,\alpha}}{T} {{\int}_{0}^{T}} \left( {{\int}_{0}^{1}} \cos(ft\xi) g(\xi) d\xi \right) t^{\beta} \cos(ft)dt,\\ &~& ~~~~\text{(By change of variables } s=t\xi,~\xi \in (0,1) \text{ and }g(\xi)\\&& \text{ is defined in Eq.~2.15),}\\ &=& 2d_{H,\alpha} T^{\beta} {{\int}_{0}^{1}}{{\int}_{0}^{1}} t^{\beta} \cos(\omega t)\cos(\omega t\xi)g(\xi) d\xi dt,~\omega=fT, \end{array} $$
Applying standard trigonometric formulas we get \(m_{11} = d_{H,\alpha }T^{\beta }\left (I_{\beta ,\omega }^{-} + I_{\beta ,\omega }^{+} \right )\), where
$$ \begin{array}{@{}rcl@{}} I_{\beta,\omega}^{\pm} &:=& {{\int}_{0}^{1}}{{\int}_{0}^{1}} t^{\beta} \cos\left( \omega t (1\pm\xi)\right) g(\xi) d\xi dt,\\ &=& -\frac{{{\varGamma}}(\beta+1)\sin \left( \frac{\pi}{2}\beta \right)}{\omega^{\beta+1}} \boldsymbol{C}_{\beta}^{\pm}-\frac{i}{2\omega^{\beta+1}}{{\int}_{0}^{1}} g(\xi) (1\pm\xi)^{-\beta-1}F_{\omega}(1\pm\xi) d\xi,\\ \boldsymbol{C}_{\beta}^{\pm} &=& {{\int}_{0}^{1}} g(\xi) (1\pm\xi)^{-\beta-1} d\xi, \end{array} $$
and \(F_{\omega }(x) = e^{i \frac {\pi }{2}\beta } {{\varGamma }} (\beta +1, -i\omega x)-e^{-i \frac {\pi }{2}\beta } {{\varGamma }} (\beta +1, i\omega x)\). Similarly, we show that \(m_{22}=d_{H,\alpha }T^{\beta }\left (I_{\beta ,\omega }^{-}-I_{\beta ,\omega }^{+} \right )\) and \( m_{12} = d_{H,\alpha }T^{\beta } J_{\beta ,\omega }^{+} \), where
$$ \begin{array}{@{}rcl@{}} J_{\beta,\omega}^{+} &:=& {{\int}_{0}^{1}}{{\int}_{0}^{1}} t^{\beta} \sin\left( \omega t (1+\xi)\right) g(\xi) d\xi dt,\\ &=& \frac{{{\varGamma}}(\beta+1)\cos \left( \frac{\pi}{2}\beta \right)}{\omega^{\beta+1}} \boldsymbol{C}_{\beta}^{+}-\frac{1}{2\omega^{\beta+1}}{{\int}_{0}^{1}} g(\xi) (1+\xi)^{-\beta-1}G_{\omega}(1+\xi) d\xi, \end{array} $$
with \(G_{\omega }(x) = e^{i \frac {\pi }{2}\beta } {{\varGamma }} (\beta +1, -i\omega x)+e^{-i \frac {\pi }{2}\beta } {{\varGamma }} (\beta +1, i\omega x)\).
Straightforward computations yield μ = m11 + m22 and \(\mu \left (T,\omega = 0\right ) = \frac {2d_{H,\alpha }T^{\beta }}{\beta +1}{{\int \limits }_{0}^{1}} g(\xi ) d\xi \). Since the vector \(z=(z_{1},z_{2})^{\prime }\) is Gaussian with \(z_{j}\sim \mathcal {N}(0,m_{jj})\), j = 1,2 we have
$$ \begin{array}{@{}rcl@{}} \mu^{2}+\sigma^{2} &=& \mathbb{E} \left( S_{T}(f)^{2} \right) = \mathbb{E} \left( {z_{1}^{2}} +{z_{2}^{2}}\right)^{2},\\ &=& \mathbb{E}({z_{1}^{4}})+\mathbb{E}({z_{2}^{4}})+2 \mathbb{E}({z_{1}^{2}} {z_{2}^{2}})= 3\left( m_{11}^{2}+m_{22}^{2}\right)+2 \mathbb{E}({z_{1}^{2}} {z_{2}^{2}}). \end{array} $$
As the process \(Z_{H}^{\alpha } (t)\) is Gaussian, we use Wick’s lemma to get \(\mathbb {E}({z_{1}^{2}} {z_{2}^{2}})=m_{11}m_{22}+2m_{12}^{2}\). In fact, we have
$$ \begin{array}{@{}rcl@{}} \mathbb{E} \left( {z_{1}^{2}} {z_{2}^{2}}\right) &=& \frac{1}{T^{2}} {\int}_{[0,T]^{4}} \cos(ft)\cos(fs)\sin(fu)\sin(fv) \mathbb{E}\left[ Z_{H}^{\alpha}(t)Z_{H}^{\alpha}(s)\right.\\&&\left. Z_{H}^{\alpha}(u)Z_{H}^{\alpha}(v) \right] dv du ds dt\\ &=& \frac{1}{T^{2}} \left\lbrace{\int}_{[0,T]^{2}} dtds \cos(ft)\cos(fs) \mathbb{E}(Z_{H}^{\alpha}(t)Z_{H}^{\alpha}(s)){\int}_{[0,T]^{2}}\right.\\&&\left.dudv\sin(fu)\sin(fv)\mathbb{E} (Z_{H}^{\alpha}(u)Z_{H}^{\alpha}(v)) \right.\\ && \left. +2{\int}_{[0,T]^{2}} dtdu \cos(ft)\sin(fu) \mathbb{E}(Z_{H}^{\alpha}(t)Z_{H}^{\alpha}(u)){\int}_{[0,T]^{2}}\right.\\&&\left.dsdv\cos(fs)\sin(fv)\mathbb{E} (Z_{H}^{\alpha}(u)Z_{H}^{\alpha}(v) \right\rbrace\\ &=& m_{11}\times m_{22} + 2 m_{12}\times m_{12}. \end{array} $$
Hence \(\sigma ^{2}= 2(m_{11}^{2}+m_{22}^{2}+2m_{12}^{2})\) and Eq. 17 follows immediately. It is not also hard to check that \(\gamma \sim \sqrt {2}\) when ω becomes small enough. □
Proof of Proposition 2.8 & Proposition 2.9.
Let us first state an asymptotic result of the incomplete Gamma function ((8.11.1)-(8.11.3) in Olver et al., 2010), which will be systematically used to prove Eqs. 18–20.
$$ \begin{array}{@{}rcl@{}} {{\varGamma}} (a,z) &=& z^{a-1}e^{-z} \left( \sum\limits_{k=0}^{N-1} \frac{u_{k}(a)}{z^{k}}+R_{N}(a,z) \right),~N=1,2,\cdots,\text{ as } z\rightarrow \infty,\\ u_{0}(a) &=& 1,~u_{1}(a)=(a-1),\cdots, u_{k}(a) = (a-1)(a-2){\cdots} (a-k),\\ \end{array} $$
(A.33)
with \(R_{N}(a,z)=\mathcal {O}\left (z^{-N}\right )\) whenever \(\left \vert \arg (z)\right \vert < \frac {3\pi }{2}\). Applying Eq. A.33, we get for large ω the following expansion of Fω(x)
$$ \begin{array}{@{}rcl@{}} F_{\omega} (x) &=& 2i (\omega x)^{\beta} \left\lbrace \sum\limits_{k=0}^{N-1} u_{k}(\beta) \sin \left( \omega x+\frac{\pi}{2}k\right) (\omega x)^{-k} +\mathcal{O}\left( (\omega x)^{-N}\right)\right\rbrace,\\~N&=&1,2,\cdots, \end{array} $$
which in turn implies
$$ \begin{array}{@{}rcl@{}} I_{\beta,\omega}^{\pm} &=& -\frac{{{\varGamma}}(\beta+1)\sin \left( \frac{\pi}{2}\beta \right)}{\omega^{\beta+1}} \boldsymbol{C}_{\beta}^{\pm}\\ &~& -\frac{1}{\omega}\left\lbrace \sum\limits_{k=0}^{N-1} u_{k}(\beta) \omega^{-k}{{\int}_{0}^{1}} g(\xi)(1\pm\xi)^{-k-1}\sin \left( \omega (1\pm\xi)+\frac{\pi}{2}k\right)d\xi \right.\\&&\left.+\mathcal{O}\left( (\omega x)^{-N}\right)\vphantom{\sum\limits_{k=0}^{N-1}}\right\rbrace. \end{array} $$
Hence Eq. 19 holds true. Similarly we use expansions of \(I_{\beta ,\omega }^{\pm }\) and \(J_{\beta ,\omega }^{+}\) at order N = 1 to get Eq. 20. Finally Eq. 18 follows from Eqs. 19 and 20 by taking the ratio of σ, μ and get rid of negligeable terms. □
Proof Proof of the statement (
21
).
Substituting x by its value 𝜃u + z in the expression of \(\widehat {\theta }_{MLE}(h)\) gives
$$ \begin{array}{@{}rcl@{}} \widehat{\theta}_{MLE}(h) &=& \frac{u^{\prime}M_{H,\alpha}^{-1}\mathrm{x}}{u^{\prime}M_{H,\alpha}^{-1}u},\\ &=& \theta + \frac{u^{\prime}M_{H,\alpha}^{-1}\mathrm{z}}{u^{\prime}M_{H,\alpha}^{-1}u}. \end{array} $$
The last term in the equality above is a linear combination of centered Gaussian variables. Thus, \(\mathbb {E} [\widehat {\theta }_{MLE}(h)]=\theta \). Let \(w:=u^{\prime }M_{H,\alpha }^{-1}=(w_{1},\cdots ,w_{n})\). We have
$$ \begin{array}{@{}rcl@{}} &&\left( u^{\prime}M_{H,\alpha}^{-1}u\right)^{2} Var [\widehat{\theta}_{MLE}(h)]\\ &=& \mathbb{E} \left[ u^{\prime}M_{H,\alpha}^{-1}\mathrm{z}\right]^{2} = \sum\limits_{k,j}^{n} w_{j} w_{k} \mathbb{E} (\mathrm{z}_{k}\mathrm{z}_{j}),\\ &=& \sum\limits_{k,j}^{n} w_{j} w_{k} (M_{H,\alpha} )_{k,j}= w M_{H,\alpha} w^{\prime},\\ &=& (u^{\prime}M_{H,\alpha}^{-1}) M_{H,\alpha} (u^{\prime}M_{H,\alpha}^{-1})^{\prime} = u^{\prime} \left( M_{H,\alpha}^{-1} M_{H,\alpha} \right) M_{H,\alpha}^{-1} u,\\ &=& u^{\prime} M_{H,\alpha}^{-1} u . \end{array} $$
(A.34)
By change of variables, one can show that
$$ M_{H,\alpha} = h^{2(\alpha+H)}{{\varPhi}},~~\text{where }{{\varPhi}}\text{ is given by Eq.~2.22}, $$
which in turn combined with Eq. A.34 implies Eq. 21. □
 (hereafter \(Z_{H}^{\alpha } (t),~t\geq 0\)), as extension of the n th fBm where n is a nonnegative integer and H ∈ (n − 1,n) (e.g. Perrin et al. IEEE Trans. Signal Process., 49, 1049–1059, 2001). We show that the process \(Z_{H}^{\alpha } (t)\) is (H + α)-self-similar and satisfies the long-range dependence property. The covariance function and single-trajectory power spectral density (PSD) are also examined. Finally, via an illustrative example we discuss the impact of the order α on procedures of estimation.
(hereafter \(Z_{H}^{\alpha } (t),~t\geq 0\)), as extension of the n th fBm where n is a nonnegative integer and H ∈ (n − 1,n) (e.g. Perrin et al. IEEE Trans. Signal Process., 49, 1049–1059, 2001). We show that the process \(Z_{H}^{\alpha } (t)\) is (H + α)-self-similar and satisfies the long-range dependence property. The covariance function and single-trajectory power spectral density (PSD) are also examined. Finally, via an illustrative example we discuss the impact of the order α on procedures of estimation.



 we obtain
we obtain
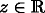 and λ > 0, we obtain
and λ > 0, we obtain



