Optimal Designs for Model Averaging in non-nested Models

Abstract

In this paper we construct optimal designs for frequentist model averaging estimation. We derive the asymptotic distribution of the model averaging estimate with fixed weights in the case where the competing models are non-nested. A Bayesian optimal design minimizes an expectation of the asymptotic mean squared error of the model averaging estimate calculated with respect to a suitable prior distribution. We derive a necessary condition for the optimality of a given design with respect to this new criterion. We demonstrate that Bayesian optimal designs can improve the accuracy of model averaging substantially. Moreover, the derived designs also improve the accuracy of estimation in a model selected by model selection and model averaging estimates with random weights.

1 Introduction

There exists an enormous amount of literature on selecting an adequate model from a set of candidate models for statistical analysis. Numerous model selection criteria have been developed for this purpose. These procedures are widely used in practice and have the advantage of delivering a single model from a class of competing models, which makes them very attractive for practitioners. Exemplarily, we mention Akaike’s information criterion (AIC), the Bayesian information criterion (BIC) and its extensions, Mallow’s C_p, the generalized cross-validation and the minimum description length (see the monographs of Burnham and Anderson (2002) and Konishi and Kitagawa (2008) and Claeskens and Hjort (2008) for more details). Different criteria have different properties, such as consistency, efficiency, minimax-rate optimality, and parsimony (used in the sense of Claeskens and Hjort, (2008, Chapter 4).

Yang (2005) proves that the different properties cannot be combined and that there is no universally optimal model selection criterion in sense of consistency and minimax-optimality. Consequently, different criteria might be preferable in different situations depending on the particular application.

On the other hand, there exists a well known post-selection problem in this approach because model selection introduces an additional variance that is often ignored in statistical inference after model selection (see Pötscher (1991) for one of the first contributions discussing this issue). This post-selection problem is inter alia attributable to the fact, that estimates after model selection behave like mixtures of potential estimates. For example, ignoring the model selection step (and thus the additional variability) may lead to confidence intervals with coverage probability smaller than the nominal value, see for example Chapter 7 in Claeskens and Hjort (2008) for a mathematical treatment of this phenomenon.

An alternative to model selection is model averaging, where estimates of a target parameter are smoothed across several models, rather than restricting inference on a single selected model.

This approach has been widely discussed in the Bayesian literature, where it is known as “Bayesian model averaginn (see the tutorial of Hoeting et al. (1999) among many others). For Bayesian model averaging prior probabilities have to be specified. This might not always be possible and therefore Buckland et al. (1997) proposed a “frequentist model averaging”, where smoothing across several models is commonly based on information criteria. Kapetanios et al. (2008) demonstrated that the frequentist approach is a worthwhile alternative to Bayesian model averaging. Stock and Watson (2003) observed that averaging predictions usually performs better than forecasting in a single model. Hong and Preston (2012) substantiate these observations with theoretical findings for Bayesian model averaging if the competing models are “sufficiently close”. Further results pointing in this direction can be found in Raftery and Zheng (2003) and Schorning et al. (2016) and Buatois et al. (2018).

Independently of this discussion there exists a large amount of research how to optimally design experiments under model uncertainty (see Box and Hill (1967) and Atkinson and Fedorov (1975) for early contributions). This work is motivated by the fact that an optimal design can improve the efficiency of the statistical analysis substantially if the postulated model assumptions are correct, but may be inefficient if the model is misspecified. Many authors suggested to choose the design for model discrimination such that the power of a test between competing regression models is maximized (see Ucinski and Bogacka (2005), López-Fidalgo et al. (2007), and Tommasi and López-Fidalgo (2010) or Dette et al. (2015) for some more recent references). Other authors proposed to minimize an average of optimality criteria from different models to obtain an efficient design for all models under consideration (see Dette (1990), Zen and Tsai (2002), and Tommasi (2009) among many others).

Although model selection or averaging are commonly used tools for statistical inference under model uncertainty most of the literature on designing experiments under model uncertainty does not address the specific aspects of these methods directly. Optimal designs are usually constructed to maximize the power of a test for discriminating between competing models or to minimize a functional of the asymptotic variance of estimates in the different models. To the best of our knowledge (Alhorn et al. 2019) is the first contribution, which addresses the specific challenges of designing experiments for model selection or model averaging. These authors constructed optimal designs minimizing the asymptotic mean squared error of the model averaging estimate and showed that optimal designs can yield a reduction of the mean squared error up to 45%. Moreover, they also showed that these designs improve the performance of estimates in models chosen by model selection criteria. However, their theory relies heavily on the assumption of nested models embedded in a framework of local alternatives as developed by Hjort and Claeskens (2003).

The goal of the present contribution is the construction of optimal designs for model averaging in cases where the competing models are not nested (note that in this case local alternatives cannot be formulated).

In order to derive an optimality criterion, which can be used for the determination of optimal designs in this context, we further develop the approach of Hjort and Claeskens (2003) and derive an asymptotic theory for model averaging estimates for classes of competing models which are non-nested. Optimal designs are then constructed minimizing the asymptotic mean squared error of the model averaging estimate and it is demonstrated that these designs yield substantially more precise model averaging estimates. Moreover, these designs also improve the performance of estimates after model selection. Our work also contributes to the discussion of the superiority of model averaging over model selection. Most of the results presented in literature indicate that model averaging has some advantages over model selection in general. We demonstrate that conclusions of this type depend sensitively on the class of models under consideration. In particular, we observe some advantages of estimation after model selection if the competing models are of rather different shape for small sample sizes. Nevertheless, the optimal designs developed in this paper improve both estimation methods, where the improvement can be substantial in many cases.

The remaining part of this paper is organized as follows. The pros and cons of model averaging and model selection are briefly discussed in Section 2 where we introduce the basic methodology and investigate the impact of similarity of the candidate models on the performance of the different estimates. In Section 3 we develop asymptotic theory for model averaging estimation in the case where the models are non-nested. Based on these results we derive a criterion for the determination of optimal designs and establish a necessary condition for optimality. In Section 4 we study the performance of these designs by means of a simulation study. In Section 5 we discuss some robustness properties of the optimal designs if either the true data generating model is not contained in the set of competing models or if they are used to estimate other parameters. Finally, technical assumptions and proofs are given Appendix.

2 Model Averaging Versus Model Selection

In this section we introduce the basic terminology and also illustrate in a regression framework that the superiority of model averaging about estimation in a model chosen by model selection depends sensitively on the class of competing models.

2.1 Basic Terminology

We consider data obtained at k different experimental conditions, say x₁,…,x_k chosen in a design space $\mathcal {X}$. At each experimental condition x_i one observes n_i responses, say $y_{i1},\ldots ,y_{in_{i}}$ (i = 1,…,k), and the total sample size is $n={\sum }_{i=1}^{k} n_{i}$. We also assume that the responses $y_{i1},\ldots ,y_{in_{i}}$ are realizations of random variables of the form

$$ \begin{array}{@{}rcl@{}} Y_{ij} = \eta_{s}(x_{i},\vartheta_{s}) + \varepsilon_{ij}, i=1,\ldots,k, j=1,\ldots,n_{i}, s=1,\ldots,r, \end{array} $$

(2.1)

where the regression function η_s is a differentiable function with respect to the parameter 𝜗_s and the random errors ε_ij are independent normally distributed with mean 0 and common variance σ². Furthermore, the index s in η_s corresponds to different models (with parameters 𝜗_s) and we assume that there are r competing regression functions η₁,…,η_r under consideration.

Having r different candidate models (differing by the regression functions η_s) a classical approach for estimating a parameter of interest, say μ, is to calculate an information criterion for each model under consideration and estimate this parameter in the model optimizing this criterion. For this purpose, we denote the density of the normal distribution corresponding to a regression model (2.1) by f_s(⋅∣ x_i, 𝜃s) with parameter 𝜃_s = (σ², 𝜗_s)^⊤ and identify the different models by their densities f₁,…,f_r (note that in the situation considered in this sections these only differ in the mean). Using the observations $y_{n}=(y_{11},\ldots ,y_{1n_{1}},y_{21},\ldots ,y_{kn_{k}})^{\top }$ we calculate in each model the maximum likelihood estimate

$$ \begin{array}{@{}rcl@{}} \hat{\theta}_{n,s} = \arg \max\limits_{\theta_{s} \in {\Theta}_{s}} \ell_{n,s}(\theta_{s} \mid y_{n}) \end{array} $$

(2.2)

of the parameter 𝜃_s, where

$$ \begin{array}{@{}rcl@{}} \ell_{n,s}(\theta_{s} \mid y_{n}) = \sum\limits_{i=1}^{k} \sum\limits_{j=1}^{n_{i}} \log f_{s}(y_{ij} \mid x_{i},\theta_{s}) \end{array} $$

(2.3)

is the log-likelihood in candidate model f_s (s = 1,…r). Each estimate $\hat {\theta }_{n,s}$ of the parameter 𝜃_s yields an estimate $\hat {\mu }_{s} = \mu _{s}(\hat {\theta }_{n,s})$ for the quantity of interest, where μ_s is the target parameter in model s.

For example, regression models of the type (2.1) are frequently used in dose finding studies (see MacDougall (2006) or Bretz et al., 2008). In this case a typical target function μ_s of interest is the “quantile” defined by

$$ \mu_{s}(\theta_{s}) = \inf \left\{ x \in \mathcal{X }~ \Big |~\frac{ \eta_{s} (x, \vartheta_{s}) - \eta_{s} (a, \vartheta_{s}) }{\eta_{s} (b, \vartheta_{s}) - \eta_{s} (a, \vartheta_{s})} \geq \alpha \right\}. $$

(2.4)

The value defined in Eq. 2.4 is well-known as ED_α, that is, the effective dose at which 100 × α% of the maximum effect in the design space $\mathcal { X }= [a,b]$ is achieved.

We now briefly discuss the principle of model selection and averaging to estimate the target parameter μ. For model selection we choose the model $f_{s^{*}}$ from f₁,…,f_s, which maximizes Akaike’s information criterion (AIC)

$$ \begin{array}{@{}rcl@{}} \text{AIC}(f_{s} \mid y_{n}) = \frac{2}{n} \ell_{n,s}(\hat{\theta}_{n,s} \mid y_{n}) - 2 p_{s} , \end{array} $$

(2.5)

where p_s is the number of parameters in model f_s (see Claeskens and Hjort, 2008, Chapter 2). The target parameter is finally estimated by $\hat \mu = \mu _{s^{*}}(\hat {\theta }_{n,{s^{*}}})$. Obviously, other model selection schemes, such as the Bayesian or focussed information criterion can be used here as well, but we restrict ourselves to the AIC for the sake of a transparent presentation.

Roughly speaking, model averaging is a weighted average of the individual estimates in the competing models. It might be viewed from a Bayesian (see for example Wassermann, 2000) or a frequentist point of view (see for example Claeskens and Hjort, 2008) resulting in different choices of model averaging weights. We will focus here on non-Bayesian methods. More explicitly, assigning nonnegative weights w₁,…,w_r to the candidate models f₁,…,f_r, with ${\sum }_{i=1}^{r}w_{i}=1$, the model averaging estimate for μ is given by

$$ \begin{array}{@{}rcl@{}} \hat{\mu}_{\text{mav}} = \sum\limits_{s=1}^{r} w_{s} \mu_{s}(\hat{\theta}_{n,s}). \end{array} $$

(2.6)

Frequently used weights are uniform weights (see, for example Stock and Watson (2004) and Kapetanios et al. (2008)). More elaborate model averaging weights can be chosen depending on the data. For example, Buckland et al. (1997) define smooth AIC-weights as

$$ w^{{ \text{smAIC}}}_{s} (y_{n}) = \frac{\exp\{\frac{1}{2} \text{AIC}(f_{s} \mid y_{n})\}}{\sum\limits_{s=1}^{r} \exp\{\frac{1}{2} \text{AIC}(f_{s} \mid y_{n})\}}. $$

(2.7)

Alternative data dependent weights can be constructed using other information criteria or model selection criteria. There also exists a vast amount of literature on determining optimal data dependent weights such that the resulting mean squared error of the model averaging estimate is minimal (see Hjort and Claeskens (2003), Hansen (2007), and Zhang et al. (2016) and Liang et al. (2011) among many others). For the sake of brevity, we will concentrate on smooth AIC-weights, which are frequently used in the context of dose-finding studies (see Sébastien et al. (2016) and Verrier et al. (2014), among others). Nevertheless, similar observations as presented in this paper could be made for other data dependent weights which are constructed using information criteria like the Bayesian information criterion.

2.2 The Class of Competing Models Matters

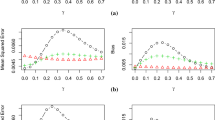
In this section we illustrate the influence of the candidate set on the properties of model averaging estimation and estimation after model selection by means of a brief simulation study. For this purpose we consider four regression models of the form (2.1), which are commonly used in dose-response modeling and specified in Table 1 with corresponding parameters.

Table 1 Models and parameters used for the simulation study

Here we adapt the setting of Pinheiro et al. (2006) who model the dose-response relationship of an anti-anxiety drug, where the dose of the drug may vary in the interval $\mathcal {X} = [0,150]$. In particular, we have k = 6 different dose levels x_i ∈{0,10,25,50,100,150} and patients are allocated to each dose level most equally, where the total sample size is n ∈{50,100,250}. Additionally, we present results for a larger sample size (n = 1000) in order to investigate the asymptotic properties of the different estimation methods.

We consider the problem of estimating the ED_0.4, as defined in Eq. 2.4.

To investigate the particular differences between both estimation methods we choose two different sets of competing models from Table 1. The first set

$$ \mathcal{S}_{1}= \{ f_{1} , f_{2}, f_{4} \} $$

(2.8)

contains the log-linear, the Emax and the quadratic model, while the second set

$$ \mathcal{S}_{2}= \{ f_{1} , f_{2}, f_{3} \} $$

(2.9)

contains the log-linear, the Emax and the exponential model. The set $\mathcal {S}_{1}$ serves as a prototype set of “similar” models while the set $\mathcal {S}_{2}$ contains models of more “different” shape. This is illustrated in Fig. 1. In the left panel we show the quadratic model f₄ (for the parameters specified in Table 1) and the best approximations of this function by a log-linear model (f₁) and an Emax model (f₂) with respect to the Kullback-Leibler divergence

$$ \frac{1}{6 } \sum\limits_{i=1}^{6} \int f_{4}(y \mid x_{i}, \theta_{4}) \log \left( \frac{f_{4}(y \mid x_{i},\theta_{4})}{f_{s}(y \mid x_{i} ,\theta_{s})} \right) dy,~s=1,2. $$

(2.10)

In this case, all models have a very similar shape and we obtain for the ED_0.4 the values 32.581, 32.261 and 33.810 for the log-linear (f₁), Emax (f₂) and quadratic model (f₄). Similarly the right panel shows the exponential model (f₃, solid line) and its corresponding best approximations by the log-linear model (f₁) and the Emax model (f₂). Here we observe larger differences between the models in the candidate set and we obtain for the ED_0.4 the values 58.116, 42.857 and 91.547 for the models f₁, f₂ and f₃, respectively.

Figure 1

Left panel: quadratic model (solid line) and its best approximations by the log-linear (dashed line) and the Emax model (dotted line) with respect to the Kullback-Leibler divergence (2.10). Right panel: exponential model (solid line) and its best approximations by the log-linear (dashed line) and the Emax model (dotted line)

All results presented in this paper are based on 1000 simulation runs generating in each run n observations of the form

$$ y_{ij}^{(l)} = \eta_{s}(x_{i},{\vartheta}_{s}) + {\varepsilon}_{ij}^{(l)} ,i=1,\ldots,k,j=1,\ldots,n_{i}, $$

(2.11)

where the errors ${\varepsilon }_{ij}^{(l)}$ are independent centered normal distributed random variables with σ² = 0.1 and η_s is one of the models η₁,…,η₄ (with parameters specified in Table 1). The parameter μ = ED_0.4 is estimated by model averaging with uniform weights, smooth AIC-weights given in Eq. 2.7 and estimation after model selection by the AIC.

In Tables 2 and 3 we show the simulated mean squared errors of the model averaging estimates with uniform weights (left column), smooth AIC-weights (middle column) and estimation after model selection (right column). Here, different rows correspond to different models. The numbers printed in bold face indicate the estimation method with the smallest mean squared error.

Table 2 Simulated mean squared error of different estimates of the ED_0.4

Table 3 Simulated mean squared error of different estimates of the ED_0.4

2.2.1 Models of similar shape

We will first discuss the results for the set of similar models in Eq. 2.8 (see Table 2). If the sample size is small, model averaging with uniform weights performs very well. Model averaging with smooth AIC-weights yields an about 10% -25% larger mean squared error (except for two cases, where it performs better than model averaging with uniform weights). On the other hand the mean squared error of estimation after model selection is substantially larger than that of model averaging, if the sample size is small. This is a consequence of the additional variability associated with data-dependent weights. For example, if the sample size is n = 50 and the data generating model is given by f₁, the mean squared errors of the model averaging estimates with uniform and smooth AIC-weights and the estimate after model selection are given by 437.0, 498.3 and 759.0, respectively. The corresponding variances are given by 235.2, 337.6 and 599.7, respectively. For the squared bias the order is exactly the opposite, that is 201.9, 160.7, 159.3, but the differences are not so large. This means that the bias can be reduced by using random weights, because these put more weight on the “correct” model.

If the sample size is n = 1000, the mean squared error of the model averaging estimates with uniform weights is larger than the mean squared errors obtained by smooth AIC-weights and the estimate after model selection. Exemplarily, if the data generating model is given by f₁, the model averaging estimator with uniform weights yields an about five times larger mean squared error than the model averaging estimator with smooth AIC-weights and the estimate after model selection. Thus, both AIC-based methods outperform the model averaging estimate with uniform weights if the sample size is large. This behaviour can be explained by the fact that the AIC is weakly consistent, i.e. in the setting under consideration, it selects the best (true) model with probability converging to one with increasing sample size. Consequently, for large sample size the model averaging estimator and the estimator after model selection do not differ much and either often select or put a high weight to the true data generating model.

Summarizing, for small sample sizes model averaging performs better than estimation after model selection. These observations coincide with the findings of Schorning et al. (2016) and Buatois et al. (2018) who compared model averaging and model selection in the context of dose finding studies (see also Chen et al. (2018) for similar results for the AIC in the context of ordered probit and nested logit models). In particular, model averaging with (fixed) uniform weights yields very reasonable results in our case. Note that the phenomenon that model averaging with uniform weights can improve the estimation accuracy in comparison to the estimation after model selection and even outperforms other averaging methods can also be observed in other situations (see, for example, Bates and Granger (1969) and Smith and Wallis (2009) or Qian et al. (2019) and the references in these papers). Exemplarily, Claeskens et al. (2016) proved for the situation of forecasting one value of a time series that there is no guarentee that model averaging with random weights (not only smooth AIC-weights, but also other random weights) will be better than the model averaging estimator with fixed uniform weights. However, we observe that for large sample sizes the estimator after model selection and the model averaging estimator with smooth AIC-weights behave similar and outperform the model averaging estimator with uniform weights due to their asymptotic properties.

2.2.2 Models of more different shape

We will now consider the candidate set $\mathcal {S}_{2}$ in Eq. 2.9, which serves as an example of more different models and includes the log-linear, the Emax and the exponential model. The simulated mean squared errors of the three estimates of the ED_0.4 are given in Table 3.

In contrast to Section 2.2.1 we observe only one scenario, where model averaging with uniform weights gives the smallest mean squared error (but in this case model averaging with smooth AIC-weights yields very similar results). If the sample size increases model averaging with smooth AIC-weights and estimation after model selection yield a substantially smaller mean squared error. An explanation of this observation consists in the fact that for a candidate set containing models with a rather different shape model averaging with uniform weights produces a large bias. On the other hand model averaging with smooth AIC-weights and estimation after model selection adapt to the data and put more weight on the “true” model, in particular if the sample size is large. As estimation after model selection has a larger variance and the variance is decreasing with increasing sample size, the bias is dominating the mean squared error for large sample sizes and thus estimation in the model selected by the AIC is more efficient for large sample sizes.

The numerical study in Sections 2.2.1 and 2.2.2 can be summarized as follows. The results observed in the literature have to be partially relativized. If the candidate set is a subset of commonly used dose-response curves as in Table 1, the superiority of model averaging with uniform weights can only be observed for classes of “similar” competing models and a not too large signal to noise ratio. On the other hand if the dose-response models in the candidate set are of rather different structure or the sample size is large (leading to a small signal to noise ratio), model averaging with data dependent weights (such as smooth AIC-weights) or estimation after model selection may show a better performance. For these reasons we will investigate optimal/efficient designs for all three estimation methods in the following sections. We will demonstrate that a careful design of experiments can improve the accuracy of all three estimates substantially.

3 Asymptotic Properties and Optimal Design

In this section we will derive the asymptotic properties of model averaging estimates with fixed weights in the case where the competing models are not nested. The results can be used for (at least) two purposes. On the one hand they provide some understanding of the empirical findings in Section 2, where we observed, that for increasing sample size the mean squared error of model averaging estimates is dominated by its bias. On the other hand, we will use these results to develop an asymptotic representation of the mean squared error of the model averaging estimate, which can be used for the construction of optimal designs.

3.1 Model Averaging for Non-Nested Models

Hjort and Claeskens, (2003) provide an asymptotic distribution of frequentist model averaging estimates making use of local alternatives which require the true data generating process to lie inside a wide parametric model. All candidate models are sub-models of this wide model and the deviations in the parameters are restricted to be of order n^− 1/2. Using this assumption results in convenient approximations for the mean squared error as variance and bias are both of order O(1/n). However, in the discussion of this paper Raftery and Zheng (2003) pose the question if the framework of local alternatives is realistic. More importantly, frequentist model averaging is also often used for non-nested models (see for example Verrier et al., 2014). In this section we will develop asymptotic theory for model averaging estimation in non-nested models. In particular, we do not assume that the “true” model is among the candidate models used in the model averaging estimate.

As we will apply our results for the construction of efficient designs for model averaging estimation we use the common notation of this field. To be precise, let Y denote a response variable and let x denote a vector of explanatory variables defined on a given compact design space $\mathcal {X}$. Suppose that Y has a density g(y∣x) with respect to a dominating measure. For estimating a quantity of interest, say μ, from the distribution g we use r different parametric candidate models with densities

$$ f_{1}(y \mid x,\theta_{1}),\ldots,f_{r}(y \mid x ,\theta_{r}) $$

(3.1)

where 𝜃_s denotes the parameter in the s th model, which varies in a compact parameter space, say ${\Theta }_{s} \subset \mathbb {R}^{p_{s}}$(s = 1,...,r). Note, that in general we do not assume that the density g is contained in the set of candidate models in Eq. 3.1 and that the regression model (2.1) investigated in Section 2 is a special case of this general notation.

We assume that k different experimental conditions, say x₁,…,x_k, can be chosen in a design space $\mathcal {X}$ and that at each experimental condition x_i one can observe n_i responses, say $y_{i1},\ldots ,y_{in_{i}}$ (thus the total sample size is $n={\sum }_{i=1}^{k} n_{i}$), which are realizations of independent identically distributed random variables $y_{i1},\ldots ,y_{in_{i}}$ with density g(⋅∣x_i). For example, if g coincides with f_s then the density of the random variables $y_{i1},\ldots ,y_{in_{i}}$ is given by f_s(⋅∣x_i, 𝜃_s) (i = 1,…,k). To measure efficiency and to compare different experimental designs we will use asymptotic arguments and consider the case $\lim _{n \to \infty } \frac {n_{i}}{n}=\xi _{i} \in (0,1)$ for i = 1,…,k. As common in optimal design theory we collect this information in the form

$$ \xi= \left \{ x_{1} , {\ldots} , x_{k} ; \xi_{1} , {\dots} , \xi_{k} \right\}, $$

(3.2)

which is called approximate design in the following discussion (see, for example, Kiefer, 1974). For an approximate design ξ of the form Eq. 3.2 and total sample size n a rounding procedure is applied to obtain integers n_i taken at each x_i (i = 1,…,k) from the not necessarily integer valued quantities ξ_in (see, for example Pukelsheim (2006), Chapter 12).

The asymptotic properties of the maximum likelihood estimate (calculated under the assumption that f_s is the correct density) is derived under certain assumptions of regularity (see the Assumptions (A1)-(A6) in Appendix). In particular, we assume that the functions f_s are twice continuously differentiable with respect to 𝜃_s and that several expectations of derivatives of the log-densities exist. For a given approximate design ξ and a candidate density f_s we denote by

$$ \begin{array}{@{}rcl@{}} \text{KL}(g:f_{s} \mid \theta_{s},\xi) = \int g(y \mid x) \log \left( \frac{g(y \mid x)}{f_{s}(y \mid x ,\theta_{s})} \right) dy d\xi(x), \end{array} $$

(3.3)

the Kullback-Leibler divergence between the models g and f_s and assume that

$$ \begin{array}{@{}rcl@{}} \theta_{s,g}^{*}(\xi) = \arg\min\limits_{\theta_{s} \in {\Theta}_{s}} \text{KL}(g:f_{s} \mid \theta_{s},\xi) \end{array} $$

(3.4)

is unique for each s ∈{1,…,r}. For notational simplicity we will omit the dependency of the minimum on the density g, whenever it is clear from the context and denote the minimizer by $\theta _{s}^{*}(\xi )$. We also assume that the matrices

$$ \begin{array}{@{}rcl@{}} A_{s}(\theta_{s},\xi) &=& \sum\limits_{i=1}^{k }\xi_{i} \ \mathbb{E}_{g(\cdot \mid x_{i} )} \Big (\frac{\partial^{2} \log f_{s}(Y_{ij} \mid x_{i},\theta_{s})}{\partial \theta_{s} \partial \theta_{s}^{\top}} \Big ) , \end{array} $$

(3.5)

$$ \begin{array}{@{}rcl@{}} B_{st}(\theta_{s},\theta_{t},\xi) &=& \sum\limits_{i=1}^{k }\xi_{i} \ \mathbb{E}_{g(\cdot \mid x_{i} )} \Big (\frac{\partial \log f_{s}(Y_{ij} \mid x_{i},\theta_{s})}{\partial \theta_{s}} \Big (\frac{\partial \log f_{t}(Y_{ij} \mid x_{i},\theta_{t})}{\partial \theta_{t}} \Big )^{\top} \Big ) , \end{array} $$

(3.6)

exist, where expectations are taken with respect to the true distribution g(⋅∣x_i).

Under standard assumptions White (1982) shows the existence of a measurable maximum likelihood estimate $\hat {\theta }_{n,s}$ for all candidate models which is strongly consistent for the (unique) minimizer $\theta _{s}^{*}(\xi )$ in Eq. 3.4. Moreover, the estimate is also asymptotically normal distributed, that is

$$ \begin{array}{@{}rcl@{}} \sqrt{n}(\hat{\theta}_{n,s} - \theta_{s}^{*}(\xi)) \overset{\mathcal{D}}{\longrightarrow} \mathcal{N}\left( 0,A_{s}^{-1}(\theta_{s}^{*}(\xi))B_{ss}(\theta_{s}^{*}(\xi),\theta_{s}^{*}(\xi))A_{s}^{-1}(\theta_{s}^{*}(\xi))\right), \end{array} $$

(3.7)

where we assume the existence of the inverse matrices, $\overset {\mathcal {D}}{\longrightarrow }$ denotes convergence in distribution and we use the notations

$$ A_{s}(\theta_{s}^{*}(\xi)) = A_{s}(\theta_{s}^{*}(\xi), \xi ) ~ , ~~B_{st}(\theta_{s}^{*}(\xi),\theta_{t}^{*}(\xi)) = B_{st}(\theta_{s}^{*}(\xi),\theta_{t}^{*}(\xi), \xi) $$

(3.8)

(s, t = 1,…r). The following result gives the asymptotic distribution of model averaging estimates of the form Eq. 2.6.

Theorem 3.1.

If Assumptions (A1) - (A7) in Appendix are satisfied, then the model averaging estimate (2.6) satisfies

$$ \begin{array}{@{}rcl@{}} \sqrt{n} \Big (\hat{\mu}_{\text{mav}} - \sum\limits_{s=1}^{r} w_{s} \mu_{s}(\theta_{s}^{*}(\xi))\Big ) \overset{\mathcal{D}}{\longrightarrow} \mathcal{N} \left( 0, {\sigma_{w}^{2}}(\theta^{*}(\xi)) \right), \end{array} $$

(3.9)

where the asymptotic variance is given by

$$ \begin{array}{@{}rcl@{}} {\sigma_{w}^{2}}(\theta^{*}(\xi)) = \sum\limits_{s,t=1}^{r} w_{s} w_{t} \Big (\frac{\partial \mu_{s} (\theta_{s}^{*}(\xi))}{\partial \theta_{s}} \Big )^{\top} A_{s}^{-1} (\theta_{s}^{*}(\xi)) B_{st} \left( \theta_{s}^{*}(\xi),\theta_{t}^{*}(\xi)\right) A_{t}^{-1} \left( \theta_{t}^{*}(\xi)\right) \frac{\partial \mu_{t} (\theta_{t}^{*}(\xi))}{\partial \theta_{t}}. \end{array} $$

(3.10)

Theorem 3.1 shows, that the model averaging estimate is biased for the true target parameter μ_true, unless we have ${\sum }_{s=1}^{r} w_{s} \mu _{s}(\theta _{s}^{*}(\xi )) = \mu _{\text {true}}$. Hence we aim to minimize the asymptotic mean squared error of the model averaging estimate. Note, that the bias does not depend on the sample size, while the variance is of order O(1/n).

3.2 Optimal Designs for Model Averaging of Non-Nested Models

Alhorn et al. (2019) determined optimal designs for model averaging minimizing the asymptotic mean squared error of the estimate calculated in a class of nested models under local alternatives and demonstrated that optimal designs lead to substantially more precise model averaging estimates than commonly used designs in dose finding studies. With the results of Section 3.1 we can develop a more general concept of design of experiments for model averaging estimation, which is applicable for non-nested models.

To be precise, we consider the criterion

$$ \begin{array}{@{}rcl@{}} {\Phi}_{\text{mav}}(\xi, g, \mu_{\text{true}}) = \frac{1}{n} {\sigma_{w}^{2}}(\theta^{*}(\xi)) + \Big (\sum\limits_{s=1}^{r} w_{s} \mu_{s}(\theta_{s}^{*}(\xi)) - \mu_{\text{true}} \Big )^{2} \!\approx\! \text{MSE} (\hat\mu_{\text{mav}}) ,\!\!\!\!\!\\ \end{array} $$

(3.11)

where μ_true is the target parameter in the “true” model with density g and ${\sigma _{w}^{2}}(\theta ^{*}(\xi ))$ and $\theta _{s}^{*}(\xi )$ are defined in Eqs. 3.10 and 3.4, respectively. Note that this criterion depends on the “true” distribution via μ_true and the best approximating parameters $\theta _{s}^{*}(\xi ) = \theta _{s,g}^{*}(\xi )$.

For estimating the target parameter μ via a model averaging estimate of the form (2.6) most precisely a “good” design ξ yields small values of the criterion function Φ_mav(ξ, g, μ_true). Therefore, for a given finite set of candidate models f₁,…,f_r and weights w_s, s = 1,…,r, a design ξ^∗ is called locally optimal design for model averaging estimation of the parameter μ, if it minimizes the function Φ_mav(ξ, g, μ_true) in Eq. 3.11 in the class of all approximate designs on $\mathcal {X}$. Here the term “locally” refers to the seminal paper of Chernoff (1953) on optimal designs for nonlinear regression models, because the optimality criterion still depends the unkown density g(y∣x).

A general approach to address this uncertainty problem is a Bayesian approach based on a class of models for the density g. To be precise, let $\mathcal {G}$ denote a finite set of potential densities and let π denote a probability distribution on $\mathcal {G}$, then we call a design Bayesian optimal design for model averaging estimation of the parameterμ if it minimizes the function

$$ \begin{array}{@{}rcl@{}} {\Phi}_{\text{mav}}^{\pi} (\xi, \mu_{true}) = {\int}_\mathcal{G} {\Phi}_{\text{mav}} (\xi,g, \mu_{true} ) d \pi (g). \end{array} $$

(3.12)

In general, the set $\mathcal {G}$ can be constructed independently of the set of candidate models. However, in the context of model averaging it is reasonable to construct a class of potential models $\mathcal {G}$ from the candidate set as follows. We denote the candidate set of models in Eq. 3.1 by $\mathcal {S}$. Each of these models depends on a unknown parameter 𝜃_s and we denote by $\mathcal {F}_{f_{s}} \subset {\Theta }_{s}$ a set of possible parameter values for the model f_s. Now let π₂ denote a prior distribution on $\mathcal {S}$ and for each $f_{s} \in \mathcal {S}$ let π₁(⋅∣f_s) denote a prior distribution on $\mathcal {F}_{f_{s}}$. Finally, we define $\mathcal {G} = \{(g,\theta ): g \in \mathcal {S}, \theta \in \mathcal {F}_{g} \}$ and a prior

$$ d \pi (g , \theta )= d\pi_{1} (\theta \mid g ) ~d\pi_{2} (g), $$

(3.13)

then the criterion (3.12) can be rewritten as

$$ \begin{array}{@{}rcl@{}} {\Phi}_{\text{mav}}^{\pi} (\xi,\mu_{\text{true}}) = {\int}_\mathcal{S} {\int}_{\mathcal{F}_{g}} {\Phi}_{\text{mav}} (\xi,g, \mu_{true}) d\pi_{1}(\theta \mid g) ~d \pi_{2}(g), \end{array} $$

(3.14)

In the finite sample study of the following section the set $\mathcal {S}$ and the set $\mathcal {F}_{g}$ (for any $g \in \mathcal {S}$) are finite, which results in a finite set $\mathcal {G}$.

Locally and Bayesian optimal designs for model averaging estimation have to be calculated numerically in all cases of practical interest. We will state now a necessary condition for the optimality of a given design with respect to the criterion $\phi _{\text {mav}}^{\pi }$. Note, that this criterion is not convex and therefore a sufficient condition cannot be derived. In the following discussion we denote by $A_{s}^{*} = A_{s}(\theta _{s,g}^{*}(\xi ^{*}),\xi ^{*})$ and $B_{st}^{*} = B_{st}(\theta _{s,g}^{*}(\xi ^{*}),\theta _{t,g}^{*}(\xi ^{*}),\xi ^{*})$ the matrices defined in Eqs. 3.5 and 3.6, respectively, evaluated in ξ^∗ and 𝜃_{s, g}(ξ^∗).

Theorem 3.2.

If a design ξ^∗ is Bayesian optimal for model averaging estimation of the parameter μ with respect to the prior π, then

$$ \begin{array}{@{}rcl@{}} &&d_{\pi} (x , \xi^{*}) =\\ &&{\int}_{\mathcal{G}} \frac{1}{n} \sigma_{g}^{\prime}(\xi^{*},x) + 2 \Big (\sum\limits_{s=1}^{r} w_{s} \mu_{s}(\theta_{s,g}^{*}(\xi^{*})) - \mu_{\text{true}} \Big) \sum\limits_{s=1}^{r} w_{s} \Big (\frac{\partial \mu_{s}(\theta_{s,g}^{*}(\xi^{*}))}{\partial \theta_{s}} \Big)^{\top} \theta_{s,g}^{\prime}(\xi^{*},x) d\pi(g) \leq 0 \end{array} $$

(3.15)

holds for all $x \in \mathcal {X}$, where the derivatives $\theta _{s,g}^{\prime }(\xi ^{*},x)$ and $\sigma _{g}^{\prime }(\xi ^{*},x)$ are given by

$$ \begin{array}{@{}rcl@{}} \theta_{s,g}^{\prime}(\xi^{*},x) &=& - \Big (\int \int g(y\mid t) \frac{\partial^{2}}{\partial \theta_{s} \partial \theta_{s}^{\top}} \log f_{s} (y\mid t,\theta_{s,g}^{*}(\xi^{*})) dy d\xi^{*}(t) \Big )^{-1} \cdot\\ && ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \int g(y\mid x) \frac{\partial}{\partial \theta_{s}} \log f_{s} (y\mid x,\theta_{s,g}^{*}(\xi^{*})) dy \end{array} $$

(3.16)

$$ \begin{array}{@{}rcl@{}} \sigma_{g}^{\prime}(\xi^{*},x) & =& \sum\limits_{s,t} w_{s} w_{t} \cdot\! \Big [ \Big (\frac{\partial^{2} \mu_{s}(\theta_{s,g}^{*}(\xi^{*}))}{\partial \theta_{s} \partial \theta_{s}^{\top}} \theta_{s,g}^{\prime}(\xi^{*},x) \Big)^{\top} (A_{s}^{*})^{-\!1} B_{st}^{*} (A_{t}^{*})^{-\!1} \frac{\partial \mu_{t}(\theta_{t,g}^{*}(\xi^{*}))}{\partial \theta_{t}} \end{array} $$

(3.17)

$$ \begin{array}{@{}rcl@{}} & &- \Big (\frac{\partial \mu_{s}(\theta_{s,g}^{*}(\xi^{*}))}{\partial \theta_{s}} \Big )^{\top} \big ((A_{s}^{*})^{-1} h_{s,g}^{\prime}(\xi^{*},x) (A_{s}^{*})^{-1} \big ) B_{st}^{*} (A_{t}^{*})^{-1} \frac{\partial \mu_{t}(\theta_{t,g}^{*}(\xi^{*}))}{\partial \theta_{t}} \\ & &+ \Big (\frac{\partial \mu_{s}(\theta_{s,g}^{*}(\xi^{*}))}{\partial \theta_{s}} \Big)^{\top} (A_{s}^{*})^{-1} h_{st,g}^{\prime}(\xi^{*},x) (A_{t}^{*})^{-1} \frac{\partial \mu_{t}(\theta_{t,g}^{*}(\xi^{*}))}{\partial \theta_{t}} \\ &&- \Big (\frac{\partial \mu_{s}(\theta_{s,g}^{*}(\xi^{*}))}{\partial \theta_{s}} \Big )^{\top} (A_{s}^{*})^{-1}B_{st}^{*} \left( (A_{t}^{*})^{-1} h_{t,g}^{\prime}(\xi^{*},x) (A_{t}^{*})^{-1} \right) \frac{\partial \mu_{t}(\theta_{t,g}^{*}(\xi^{*}))}{\partial \theta_{t}} \\ & &+ \Big (\frac{\partial \mu_{s}(\theta_{s,g}^{*}(\xi^{*}))}{\partial \theta_{s}} \Big )^{\top} (A_{s}^{*})^{-1} B_{st}^{*}(A_{t}^{*})^{-1} \frac{\partial^{2} \mu_{t}(\theta_{t,g}^{*}(\xi^{*}))}{\partial \theta_{t} \partial \theta_{t}^{\top}} \theta_{t,g}^{\prime}(\xi^{*},x) \Big ], \end{array} $$

respectively. Here the matrices $h_{st,g}^{\prime }(\xi ^{*},x)$ and $h_{s,g}^{\prime }(\xi ^{*},x)$ are given by

$$ \begin{array}{@{}rcl@{}} h_{st,g}^{\prime}(\xi^{*},x) & =& \int \int g(y\mid u) \left[ \frac{\partial^{2} \log f_{s}(y \mid u,\theta_{s,g}^{*}(\xi^{*}))}{\partial \theta_{s} \partial \theta_{s}^{\top}} \theta_{s,g}^{\prime}(\xi^{*},x) \left( \frac{\partial \log f_{t}(y\mid u,\theta_{t,g}^{*}(\xi^{*}))}{\partial \theta_{t}} \right)^{\top} \right. \\ && \left. + \frac{\partial \log f_{s}(y \mid u,\theta_{s,g}^{*}(\xi^{*}))}{\partial \theta_{s}} \left( \theta_{t,g}^{\prime}(\xi^{*},x)\right)^{\top} \left( \frac{\partial^{2} \log f_{t}(y\mid u,\theta_{t,g}^{*}(\xi^{*}))}{\partial \theta_{t} \partial \theta_{t}^{\top}} \right)^{\top} \right] dy d\xi^{*}(u) \\ & +& B_{st}(\theta_{s,g}^{*}(\xi^{*}),\theta_{t,g}^{*}(\xi^{*}),\xi_{x}) - B_{st}(\theta_{s,g}^{*}(\xi^{*}),\theta_{t,g}^{*}(\xi^{*}),\xi^{*}) \end{array} $$

(3.18)

$$ \begin{array}{@{}rcl@{}} h_{s,g}^{\prime}(\xi^{*},x) & =& \int \int g(y \mid u) D_{s}(\theta_{s,g}^{*}(\xi^{*})) (I_{p_{s}} \otimes \theta_{s,g}^{\prime}(\xi^{*},x)) dy d\xi^{*}(u) \end{array} $$

$$ \begin{array}{@{}rcl@{}} & +& A_{s}(\theta_{s,g}^{*}(\xi^{*}),\xi_{x}) - A_{s}(\theta_{s,g}^{*}(\xi^{*}),\xi^{*}) \end{array} $$

(3.19)

where the matrix

$$ \begin{array}{@{}rcl@{}} &&{}D_{s}(\theta_{s})\\ &&{} = \left( \!\!\begin{array}{cccccccc} \frac{\partial^{3} \log f_{s}(y \mid x , \theta_{s})}{\partial \theta_{s,1} \partial\theta_{s,1} \partial \theta_{s,1}} & {\cdots} & \frac{\partial^{3} \log f_{s}(y \mid x , \theta_{s})}{\partial \theta_{s,1} \partial \theta_{s,1} \partial \theta_{s,p_{s}}} & {\cdots} & \frac{\partial^{3} \log f_{s}(y \mid x , \theta_{s})}{\partial \theta_{s,1} \partial \theta_{s,p_{s}} \partial \theta_{s,1}} & {\cdots} & \frac{\partial^{3} \log f_{s}(y \mid x , \theta_{s})}{\partial \theta_{s,1} \partial \theta_{s,p_{s}} \partial\theta_{s,p_{s}}} \\ \frac{\partial^{3} \log f_{s}(y \mid x , \theta_{s})}{\partial \theta_{s,2} \partial \theta_{s,1} \partial \theta_{s,1}} & {\cdots} & \frac{\partial^{3} \log f_{s}(y \mid x , \theta_{s})}{\partial \theta_{s,2}\partial\theta_{s,1}\partial\theta_{s,p_{s}}} & {\cdots} & \frac{\partial^{3} \log f_{s}(y \mid x , \theta_{s})}{\partial \theta_{s,2} \partial\theta_{s,p_{s}} \partial\theta_{s,1}} & {\cdots} & \frac{\partial^{3} \log f_{s}(y \mid x , \theta_{s})}{\partial \theta_{s,2} \partial \theta_{s,p_{s}} \partial \theta_{s,p_{s}}} \\ {\vdots} & & \vdots & & {\vdots} & & {\vdots} \\ \frac{\partial^{3} \log f_{s}(y \mid x , \theta_{s})}{\partial \theta_{s,p_{s}}\partial\theta_{s,1}\partial\theta_{s,1}} & {\cdots} & \frac{\partial^{3} \log f_{s}(y \mid x , \theta_{s})}{\partial \theta_{s,p_{s}}\partial\theta_{s,1}\partial\theta_{s,p_{s}}} & {\cdots} & \frac{\partial^{3} \log f_{s}(y \mid x , \theta_{s})}{\partial \theta_{s,p_{s}}\partial\theta_{s,p_{s}}\partial \theta_{s,1}} & {\cdots} & \frac{\partial^{3} \log f_{s}(y \mid x , \theta_{s})}{\partial \theta_{s,p_{s}}\partial\theta_{s,p_{s}}\partial\theta_{s,p_{s}}} \end{array} \!\!\right) \end{array} $$

contains the third derivatives of the log-likelihood with respect to the parameters $\theta _{s} = (\theta _{s,1},\ldots ,\theta _{s,p_{s}})^{\top }$. Moreover, there is equality in Eq. 3.15 for all support points of the optimal design.

Example 3.1.

We illustrate the application of Theorem 3.2 for regression models of the from Eq. 2.1 with centred normal distributed errors. As regression functions we use the log-linear and the Emax model and their parameter specifications given in Table 1. Then, the locally optimal designs for estimation of the ED_0.4 in the log-linear model f₁ and in the Emax model f₂ are given by

$$ \begin{array}{@{}rcl@{}} \xi_{2} = \left\{ 0 , 4.051 , 150 ;~ 0.339 , 0.5 , 0.161 \right\}, \end{array} $$

(3.20)

and $\left \{ 0 , 18.75 , 150 ;~ 0.25 , 0.5 , 0.25 \right \},$ respectively see Dette et al. (2010). For sample size n = 100 we determine a Bayesian optimal design for model averaging estimation of the ED_0.4 (with uniform weights) with respect to the criterion (3.12). The set of possible models is given by $\mathcal {G} = \{f_{1},f_{2}\}$ with parameters specified in Table 1, and we choose a uniform prior on this set. The optimal design has been calculated numerically using the COBYLA algorithm (see (Powell, 1994)) and is given by

$$ \begin{array}{@{}rcl@{}} \xi_{12}^{*} = \left\{ 0 , 13.026 , 150 ;~ 0.281, 0.498, 0.220 \right\}. \end{array} $$

(3.21)

The necessary condition of Theorem 3.2 is satisfied as illustrated in Fig. 2. Note that the design $\xi _{12}^{*}$ can be considered as a compromise between the locally optimal designs for the individual models and that $\xi _{12}^{*}$ would not be optimal if the inequality was not satisfied.

Figure 2

Necessary condition of Theorem 3.2 for the optimal design (3.21)

We conclude noting that the optimality criteria proposed in this section have been derived for model averaging estimates with fixed weights. The asymptotic theory presented here cannot be easily adapted to estimates using data-dependent (random) weights (as considered in Section 2), because it is difficult to get an explicit expression for the asymptotic distribution, which is not normal in general. Nevertheless, we will demonstrate in the following section that designs minimizing the mean squared error of model averaging estimates with fixed weights will also yield a substantial improvement in model averaging estimation with smooth AIC-weights and in estimation after model selection.

4 Bayesian Optimal Designs For Model Averaging

We will demonstrate by means of a simulation study that the performance of all considered estimates can be improved substantially by the choice of an appropriate design. For this purpose we consider the same situation as in Section 2, that is regression models of the form (2.1) with centred normal distributed errors. We also consider the two different candidate sets $\mathcal {S}_{1}$ and $\mathcal {S}_{2}$ defined in Eq. 2.8 (log-linear, Emax and quadratic model) and Eq. 2.9 (log-linear, Emax and exponential model), respectively.

Using the criterion introduced in Section 3 we now determine a Bayesian optimal design for model averaging estimation of the ED_0.4 with uniform weights from n = 100 observations. Note that we use the sample size n = 100 since this is a common available sample size in the context of dose finding studies. We require a prior distribution for the unknown density g, and we use a distribution of the form Eq. 3.13 for this purpose. To be precise, let f_s(y∣x, 𝜃_s) denote the density of a normal distribution with mean η_s(x, 𝜗_s) and variance ${\sigma ^{2}_{s}} =0.1$ (s = 1,…,r), where the mean functions are given in Table 1. As the criterion (3.14) does not depend on the intercept 𝜗_s1, these are not varied and taken from Table 1. For each of the other parameters we use three different values: the values specified in Table 1 and a 10% larger and smaller value of this parameter.

$$ \begin{array}{@{}rcl@{}} \mathcal{F}_{f_{1}} &=& \{ (0, \vartheta_{12}, \vartheta_{13}) : \vartheta_{12} = 0.0797 \pm 10\% , \vartheta_{13} = 1 \pm 10\% \}, \\ \mathcal{F}_{f_{2}} &=& \{(0,\vartheta_{22}, \vartheta_{23}) : \vartheta_{22} = 0.467 \pm 10\%, \vartheta_{23} = 25 \pm 10\% \} , \\ \mathcal{F}_{f_{3}} &=& \{(-0.08265, \vartheta_{32}, \vartheta_{33}) : \vartheta_{32} = 0.08265 \pm 10 \%, \vartheta_{33} = 85 \pm 10\% \} , \\ \mathcal{F}_{f_{4}} &=& \{(0, \vartheta_{42}, \vartheta_{43}) : \vartheta_{42} = 0.00533 \pm 10\%, \vartheta_{43} = -0.00002 \pm 10\% \}. \end{array} $$

(4.1)

4.1 Models of similar shape

We will first consider the candidate set $\mathcal {S}_{1} =\{ f_{1},f_{2},f_{4} \}$ consisting of the log-linear, the Emax and the quadratic model. For the definition of the prior distribution (3.13) in the criterion (3.14) we consider a uniform distribution π₂ on the set $\mathcal {S}_{1}$ and a uniform prior π₁(⋅∣f_s) on each set $\mathcal {F}_{f_{s}}$ in Eq. 4.1 (s = 1,2,4). The Bayesian optimal design for model averaging estimation of the ED_0.4 minimizing the criterion (3.14) is given by

$$ \begin{array}{@{}rcl@{}} \xi_{\mathcal{S}_{1}}^{*} = \left\{ 0 , 18.310, 67.102, 150;~ 0.205, 0.290, 0.281, 0.224 \right\}. \end{array} $$

(4.2)

We will compare this design with the design

$$ \begin{array}{@{}rcl@{}} \xi_{1} = \left\{ 0 , 10 , 25 , 50 , 100 , 150 ;~ 1/6 , 1/6 , 1/6 , 1/6 , 1/6 , 1/6 \right\}, \end{array} $$

(4.3)

proposed in Pinheiro et al. (2006) for a a similar setting (this design has also been used in Section 2) and the locally optimal design for the estimation of the ED_0.4 in the log-linear model given by Eq. 3.20.

Results for the locally optimal designs for estimation of the ED_0.4 in the Emax and exponential model are similar and omitted for the sake of brevity. We use the same setup as in Section 2.

The corresponding results are given in Table 4, where we use the models f₁, f₂ and f₄ from Table 1 to generate the data. The different columns represent the different estimation methods (left column: model averaging with uniform weights; middle column: smooth AIC-weights, right column: model selection). The numbers printed in boldface indicate the minimal mean squared error for each estimation method obtained from the different experimental designs. Compared to the designs ξ₁ and ξ₂ the Bayesian optimal design $\xi _{\mathcal {S}_{1}}^{*}$ for model averaging with uniform weights improves the efficiency of all estimation techniques. For example, when data is generated using the log-linear model f₁ the mean squared error of the model averaging estimate with uniform weights is reduced by 20.5% and 4.2%, when the optimal design is used instead of the designs ξ₁ or ξ₂, respectively. This improvement is remarkable as the design ξ₂ is locally optimal for estimating the ED_0.4 in the model f₁ and data is generated from this model. In other cases the improvement is even more visible. For example, if data is generated by the model f₂ the improvement in model averaging estimation with uniform weights is 25.1% and 71.7% compared to the designs ξ₁ and ξ₂ defined in Eqs. 4.3 and 3.20. Moreover, although the designs are constructed for model averaging with uniform weights they also yield substantially more accurate model averaging estimates with smooth AIC-weights and a more precise estimate after model selection. For example, if the data is generated from model f₁ the mean squared error is reduced by 24.2% and by 10.2% for estimation with smooth AIC-weights and by 39.1% and 49.1% for estimation after model selection, respectively. Similar results can be observed for the models f₂ and f₄.

Table 4 Simulated mean squared errors of different estimates of the ED_0.4 for different experimental designs

Summarizing, our numerical results show that the Bayesian optimal design for model averaging estimation of the ED_0.4 yields a substantial improvement of the mean squared error of the model averaging estimate with uniform weights (4.2%-71.7%), smooth AIC-weights (10.2%-69.3%) and the estimate after model selection (23.5%-85.4%) for all three models under consideration.

4.2 Models of Different Shape

We will now consider the second candidate set $\mathcal {S}_{2}$ consisting of the log-linear (f₁) the Emax (f₂) and the exponential model (f₃). For the definition of the prior distribution (3.13) in the criterion (3.14) we use a uniform distribution π₂ on the set $\mathcal {S}_{2}$ and a uniform prior π₁(⋅∣f_s) on each set $\mathcal {F}_{f_{s}}$ (s = 1,2,3) in Eq. 4.1. For this choice the Bayesian optimal design for model averaging estimation of the ED_0.4 is given by

$$ \begin{array}{@{}rcl@{}} \xi^{*}_{\mathcal{S}_{2}}= \left\{ 0 , 10.025, 77.746, 84.556, 150 ; ~ 0.192, 0.212, 0.198, 0.189, 0.208 \right\}, \end{array} $$

(4.4)

and has (in comparison to the design $\xi _{\mathcal {S}_{1}}^{*}$ in Section 4.1) five instead of four support points.

The simulated mean squared errors of the three estimates under different designs are given in Table 5. We observe again that compared to the designs ξ₁ and ξ₂ in Eqs. 4.3 and 3.20 the Bayesian optimal design $\xi ^{*}_{\mathcal {S}_{2}}$ improves most estimation techniques substantially. However, if model averaging with uniform weights is used and data is generated by model f₂ or f₃, the mean squared error of the model averaging estimate from the optimal design is 5.4% and 4.5% larger than the mean squared error obtained by the design ξ₁, respectively. For model averaging with smooth AIC-weights and data being generated from model f₂ this difference is 5.9%. Overall, the reported results demonstrate a substantial improvement in efficiency by usage of the Bayesian optimal design independently of the estimation method. If the Bayesian optimal design is used, estimation after model selection yields the smallest mean squared error if the data is generated from a model of the candidate set $\mathcal {S}_{2}$.

Table 5 Simulated mean squared errors of different estimates of the ED_0.4 for different experimental designs

Summarizing, our numerical results show that compared to the designs ξ₁ and ξ₂ the design $\xi ^{*}_{\mathcal {S}_{2}}$ reduces the mean squared error of model averaging estimates with uniform weights up to 50.3%. Furthermore, for smooth AIC-weights and estimation after model selection the reduction can be even larger and is up to 70.5% and 85.3%, respectively.

5 Robustness of the Designs

The designs determined in Sections 4.1 and 4.2 are Bayesian optimal for estimating the ED_0.4 under the assumption that the true data generating model is part of the set of candidate models $\mathcal {S}_{1}$ and $\mathcal {S}_{2}$, respectively.

In the following we will analyse the behavior of these designs if these assumptions are not completely satisfied. More precisely, in Section 5.1 we investigate the performance of the different estimators using the designs (4.2) and (4.4) if the underlying true model is not part of the candidate sets. In Section 5.2 we consider the performance of these designs if they are used to estimate not only the ED_0.4, but also the ED_0.5 and ED_0.8. In this context, we also derive multi-objective designs which are recommended if more than one parameter of interest has to be estimated.

5.1 Robustness with Respect to Data Generating Model

In this section we analyse the performance of the designs determined in Sections 4.1 and 4.2, if the true data generating model is not among the candidate models. More precisely, we consider the same setup as in Section 4.1 with candidate set $\mathcal {S}_{1} = \{f_{1}, f_{2}, f_{4}\}$ and the corresponding design in Eq. 4.2 where we use the model f₃ to generate the data, and the setup as in Section 4.2 with candidate set $\mathcal {S}_{2}=\{f_{1}, f_{2}, f_{3}\}$ and the corresponding design in Eq. 4.4 where we use the model f₄ to generate the data, respectively.

The corresponding results are presented in Tables 6 and 7, respectively. Compared to the designs ξ₁ (see Eq. 4.3) and ξ₂ (see Eq. 3.20) the Bayesian optimal designs still improve substantially the efficiency of all estimation techniques, although the true data generating models are not contained the candidate sets used in the definition of the corresponding optimality criterion.

Table 6 Simulated mean squared errors of different estimates of the ED_0.4 for different experimental designs

Table 7 Simulated mean squared errors of different estimates of the ED_0.4 for different experimental designs

In the setup of Section 4.1 where the candidate set $\mathcal {S}_{1}$ with corresponding optimal design is used (see Table 6), the improvement is less pronounced for model averaging with uniform weights (4.6% and 66.8% compared to the designs ξ₁ and ξ₂ in Eqs. 4.3 and 3.20, respectively) than for smooth AIC-weights (10.5% and 77.5%) and estimation after model selection (16.9% and 85.2%). Considering the setup of Section 4.2 where the candidate set $\mathcal {S}_{2}$ with corresponding optimal design is used (see Table 7), the improvement of the model averaging methods with uniform weights (23.4% and 69.4% compared to the designs ξ₁ and ξ₂ in Eqs. 4.3 and 3.20, respectively) and estimation after model selection (17.3% and 81.2%) are most obvious.

Moreover, we observe that the model averaging estimator with uniform weights is outperformed by the model averaging estimator with smooth AIC weights and the estimate after model selection in the setup of Section 4.1 (see Table 6), whereas it is the other way around in the setup of Section 4.2 (see Table 7), where the model averaging estimator with uniform weights performs best. The good performance of model averaging estimates with uniform weights can also be observed in other settings where all candidate models misspecify the true data generating model. As stated in Section 2.2.1, several theoretical and heuristical results about this phenomenon were deduced especially in the context of forecasting of time series and we again refer to Qian et al. (2019) for a good review on that issue.

Summarizing, the Bayesian optimal designs still improve the accurarcy of all estimation techniques even if the true data generating model is not among the candidate models.

5.2 Robustness with respect to parameter of interest

In the previous sections we assumed that there is one target parameter μ and the considered Bayesian optimal designs were supposed to improve the performance of the three estimation methods for μ. In the following, we briefly indicate how this methodology can be further extended to adress the problem of estimating several target parameters, say μ⁽¹⁾,…,μ^(L). For this purpose we follow the idea of Kao et al. (2009) and define a multi-objective criterion by an average of the criteria resulting from the individual target parameters.

More precisely, we consider a similar setup as in Section 3.2, that is, $\mathcal {G}$ is a finite set of potential densities and π is a probability distribution on $\mathcal { G}$. We call a design multi-objective Bayesian optimal design for model averaging estimation of the parameters μ⁽¹⁾,…,μ^(L) if it minimizes the function

$$ \begin{array}{@{}rcl@{}} \bar{\Phi}_{\text{mav}}^{\pi} (\xi ) =\frac{1}{L}\sum\limits_{\ell=1}^{L} {\int}_\mathcal{G} {\Phi}_{\text{mav}} (\xi,g, \mu^{(\ell)}) d \pi (g), \end{array} $$

(5.1)

where Φ_mav(ξ, g, μ^(ℓ)) denotes the Bayesian optimality criterion defined in Eq. 3.12 depending on the individual target parameter μ^(ℓ) (ℓ = 1,…,L).

We now demonstrate by means of a simulation study that the designs based on the extended criterion defined in Eq. 5.1 can be useful to improve the performance of all considered estimation methods if several parameters are of interest. For the sake of brevity, we concentrate on the situation of Section 4.1, where the candidate set is given by $\mathcal {S}_{1}=\{f_{1}, f_{2}, f_{4}\}$ (log-linear, Emax and quadratic model, cf. Table 1) with the corresponding uniform prior distribution given by a uniform distribution π₂ on the set $\mathcal {S}_{1}$ and by a uniform prior π₁(⋅∣f_s) on each set $\mathcal {F}_{f_{s}}$ in Eq. 4.1 (s = 1,2,4). Results for the setup used in Section 4.2 are similar and omitted for the sake of brevity. We will consider the problem of estimating the three target parameters $\mu ^{(1)}= \text {ED}_{0.4}$, $\mu ^{(2)} =\text {ED}_{0.5}$ and $\mu ^{(3)} =\text {ED}_{0.8}$ as defined in Eq. 2.4 using the designs given in Eqs. 4.2, 4.3, and 3.20 on the one hand. On the other hand we will use the multi-objective Bayesian optimal design for model averaging estimation of the ED_0.4, ED_0.5 and ED_0.8 minimizing the criterion (5.1) which is given by

$$ \begin{array}{@{}rcl@{}} \bar{\xi}_{\mathcal{S}_{1}}^{*} = \left\{ 0 , 15.437, 60.887, 150;~ 0.214, 0.301, 0.242, 0.242 \right\}. \end{array} $$

(5.2)

The simulated averages of the mean squared errors

$$ {1 \over 3} \sum\limits_{\ell=1}^{3} \mathbb{E} \big [ (\hat \mu^{(\ell )}- \mu^{(\ell )} )^{2} \big ] $$

of the estimates for the three target parameters ED_0.4, ED_0.5 and ED_0.8 under the different designs and different estimation methods are given in Table 8. Again, we use the same simulation setup as in Section 4.1. We observe that compared to the designs ξ₁ and ξ₂ in Eqs. 4.3 and 3.20 the multi-objective Bayesian optimal design $\bar {\xi }^{*}_{\mathcal {S}_{1}}$ improves most estimation techniques. However, if model averaging with smooth AIC weights is used and data is generated by the log-linear model f₁, the average of the mean squared errors is 7.09% larger than the average of the mean squared errors obtained by design ξ₂ which is locally optimal for estimation of the ED_0.4 in the log-linear model. Moreover, we observe that the Bayesian optimal design for model averaging estimation of ED_0.4 in Eq. 4.2 yields similar results as the multi-objective Bayesian design in Eq. 5.1. In the case where data is generated by the quadratic model f₄ the design $\xi ^{*}_{\mathcal {S}_{1}}$ even improves the mean squared error of all three estimation techniques compared to the design $\bar {\xi }^{*}_{\mathcal {S}_{1}}$. Consequently, the design $\xi ^{*}_{\mathcal {S}_{1}}$, which is supposed to result in a precise estimation of the ED_0.4, is robust with respect to variations of the target parameter and can also be used for efficient estimation of other ED_p values.

Table 8 The average of the simulated mean squared errors of the different estimates of the ED_0.4, ED_0.5, ED_0.8 for different experimental designs

Nevertheless, the criterion defined in Eq. 5.1 can be useful if the focus is widened to the estimation of more different parameters, for instance the estimation of the ED_0.4 and the prediction of an effect at a prespecified dose level.

6 Conclusions

In this paper we derived the asymptotic distribution of the frequentist model averaging estimate with fixed weights from a class of not necessarily nested models.

We use these results to determine Bayesian optimal designs for model averaging, which can improve the estimation accuracy of the estimate substantially. Although these designs are constructed for model averaging with fixed weights, they also yield a substantial improvement of accuracy for model averaging with data dependent weights and for estimation after model selection.

We also demonstrate that the superiority of model averaging against estimation after model selection in the context of dose finding studies depends sensitively on the class of competing models, which is used in the model averaging procedure. If the competing models are similar (which means that a given model from the class can be well approximated by all other models) and the signal to noise ratio is large, then model averaging should be preferred. Otherwise, we observe advantages for estimation after model selection, in particular, if the signal to noise ratio is small.

Although, the new designs show a very good performance for estimation after model selection and for model averaging with data dependent weights, it is of interest to develop optimal designs, which address the specific issues of data dependent weights in the estimates. This is a very challenging problem for future research as there is no simple expression of the asymptotic mean squared error of these estimates. A first approach to solve this problem is an adaptive one and a further interesting and very challenging question of future research is to improve the accuracy of adaptive designs.

Moreover, in the present paper we only briefly discuss the situation where the true data generating model is not among the candidate models. In this situation different estimation strategies might be suitable, such as the use of data-dependent weights for model combining which directly take the minimization of the mean squared error into account (see Qian et al. (2019) and Zhang et al. (2016) and Wang et al. (2009) among many others) or adaptive approaches, which work both for the parametric candidate and for nonparametric models (see Yang 2001, 2003). Consequently, another interesting problem for future research will be the construction of optimal designs for these estimators.

A further extremely challenging topic of future research is the construction of designs for different estimation techniques in big data analysis (such as convolutional neural networks or random forests). In such applications the focus is on (sub-)sampling and the construction of design strategies for a fixed model and a given estimation technique is just at the beginning of its development (see Ma et al. (2015) and Wang et al. (2019b) or Wang 2019a). An extension of these (sub-)sampling techniques to the case of multiple models and different estimation techniques is of particular practical importance.

Appendix A: Technical Assumptions and Proofs

1.1 Assumptions

Following White (1982) we assume:

• (A1) The random variables Y_ij, i = 1,…,k, j = 1,…,n_i are independent. Furthermore, $Y_{i1},{\ldots } ,Y_{in_{i}}$ have a common distribution function with a measurable density g(⋅∣x_i) with respect to a dominating measure ν.

• (A2) The distribution function of each candidate model s ∈{1,…,r} has a measurable density f_s(⋅∣x, 𝜃_s) with respect to ν (for all 𝜃_s ∈Θ_s) that is continuous in 𝜃_s.

• (A3) For all $x \in \mathcal {X}$ the expectation $\mathbb {E}(\log (g(Y\mid x)))$ exists (where expectation is taken with respect to g(⋅∣x)) and for each candidate model the function $y \mapsto |\log f_{s}(y \mid x,\theta _{s})|$ is dominated by a function that is integrable with respect to g(⋅∣x) and does not depend on 𝜃_s. Furthermore the Kullback-Leibler divergence (3.3) has a unique minimum $\theta _{s,g}^{*}(\xi )$ defined in Eq. 3.4 and $\theta _{s,g}^{*}(\xi )$ is an interior point of Θ_s.

• (A4) For all $x \in \mathcal {X}$ the function $y \mapsto \frac {\partial \log f_{s}(y \mid x,\theta _{s})}{\partial \theta _{s}}$ is a measurable function for all 𝜃_s ∈Θ_s and continuously differentiable with respect to 𝜃_s for all $y\in \mathbb {R}$.

• (A5) The entries of the (matrix valued) functions $\frac {\partial ^{2} \log f_{s}(y \mid x,\theta _{s})}{\partial \theta _{s} \partial \theta _{s}^{\top }}$, $\frac {\partial \log f_{s}(y \mid x,\theta _{s})}{\partial \theta _{s}}$ $\big (\frac {\partial \log f_{t}(y \mid x,\theta _{t})}{\partial \theta _{t}} \big )^{\top }$ are dominated by integrable functions with respect to g(⋅∣x) for all $x\in \mathcal {X}$ and 𝜃_s ∈Θ_s.

• (A6) The matrices $B_{ss}(\theta _{s}^{*}(\xi ),\theta _{s}^{*}(\xi ), \xi )$ and $A_{s}(\theta _{s}^{*}(\xi ), \xi )$ in Eqs. 3.5 and 3.6 are nonsingular.

• (A7) The functions 𝜃_s↦μ_s(𝜃_s) are once continuously differentiable.

Proof of Theorem 3.1..

By equation (A.2) in White (1982) we have

$$ \sqrt{n} (\hat{\theta}_{n,s} - \theta_{s}^{*}(\xi)) + A_{s}^{-1}(\theta_{s}^{*}(\xi)) \frac{1}{\sqrt{n}} \sum\limits_{i=1}^{k} \sum\limits_{j=1}^{n_{i}} \frac{\partial \log f_{s}(Y_{ij} \mid x_{i},\theta_{s}^{*}(\xi))}{\partial \theta_{s}} \overset{p}{\longrightarrow} 0, $$

(A.1)

where $\overset {p}{\longrightarrow }$ denotes convergence in probability (note that the matrix $A_{s}(\theta _{s}^{*})= A_{s}(\theta _{s}^{*},\xi )$ is nonsingular by assumption). An application of the multivariate central limit theorem now leads to

$$ \frac{1}{\sqrt{n}} \left( \begin{array}{c} {\sum}_{i=1}^{k} {\sum}_{j=1}^{n_{i}} \frac{\partial \log f_{1}(Y_{ij}\mid x_{i},\theta_{1}^{*}(\xi))}{\partial \theta_{1}} \\ {\vdots} \\ {\sum}_{i=1}^{k} {\sum}_{j=1}^{n_{i}} \frac{\partial \log f_{r}(Y_{ij}\mid x_{i},\theta_{r}^{*}(\xi))}{\partial \theta_{r}} \end{array} \right) \overset{\mathcal{D}}{\longrightarrow} \mathcal{N}\left( 0, \left( \begin{array}{cccc} B_{11} & \hdots & B_{1r} \\ {\vdots} & {\ddots} & {\vdots} \\ B_{r1} & \hdots & B_{rr} \end{array} \right) \right), $$

(A.2)

where $B_{{st}} = B_{{st}} (\theta _{s}^{*}(\xi ), \theta _{t}^{*}(\xi ), \xi )$ is defined in Eq. 3.6. Combining (A.1) and (A.2) we obtain the weak convergence of the vector $\hat {\theta }_{n} = (\hat {\theta }_{n,1}^{\top },\ldots ,\hat {\theta }_{n,r}^{\top })^{\top }$, that is $\sqrt {n} (\hat {\theta }_{n} - \theta ^{*}(\xi )) \overset {\mathcal {D}}{\longrightarrow } \mathcal {N}(0,{\Sigma }),$ where Σ = (Σ_st)_{s, t= 1,…,r} is a block matrix with entries ${\Sigma }_{{st}} = A_{s}^{-1}(\theta _{s}^{*}(\xi )) B_{st} (\theta _{s}^{*}(\xi ),\theta _{t}^{*}(\xi )) A_{t}^{-1}(\theta _{t}^{*}(\xi ))$ (s, t = 1,…,r) and the vector $\theta _{s}^{*}(\xi )$ is given by $\theta _{s}^{*}(\xi ) = (\theta _{1}^{*}(\xi )^{\top },\ldots ,\theta _{r}^{*}(\xi )^{\top })^{\top }$.

Next, we define for the parameter vector $\theta ^{\top } = (\theta _{1}^{\top },...,\theta _{r}^{\top }) \in \mathbb {R}^{{\sum }_{s=1}^{r} p_{s}}$ the projection π_s by π_s𝜃 := 𝜃_s and the vector

$\tilde {\mu }(\theta ) = \big (\mu _{1}(\pi _{1} \theta ) , {\ldots } , \mu _{r}(\pi _{r} \theta ) \big )^{T}$ with derivative

$$ \begin{array}{@{}rcl@{}} \mu_{\theta}^{\prime} = \left( \begin{array}{ccccc} \left( \frac{\partial \mu_{1}(\theta_{1})}{\partial \theta_{1}} \right)^{\top} & 0 & \hdots & & 0 \\ 0 & \left( \frac{\partial \mu_{2}(\theta_{2})}{\partial \theta_{2}} \right)^{\top} & 0 & \hdots & 0 \\ 0 & \hdots & & 0 & \left( \frac{\partial \mu_{r}(\theta_{r})}{\partial \theta_{r}} \right)^{\top} \end{array} \right). \end{array} $$

(A.3)

An application of the Delta method shows that $\sqrt {n} (\tilde {\mu }(\hat {\theta }_{n}) - \tilde {\mu }(\theta ^{*}(\xi ))) \overset {\mathcal {D}}{\longrightarrow } \mathcal {N} \big (0, \mu _{\theta ^{*}(\xi )}^{\prime } {\Sigma }(\mu _{\theta ^{*}(\xi )}^{\prime } )^{\top } \big ).$ The assertion finally follows from the continuous mapping theorem observing the representation $\hat {\mu }_{\text {mav}} = \left (w_{1}, \hdots , w_{r} \right ) \tilde {\mu }(\hat {\theta }_{n}).$□

Proof of Theorem 3.2..

Throughout this proof we assume that integration and differentiation are interchangeable. Following the arguments in Pukelsheim (2006), Chapter 11, a Bayesian optimal design ξ^∗ for model averaging estimation of the parameter μ satisfies the inequality

$$ -{\int}_{\mathcal{G} } D {\Phi}_{\text{mav}}^{\pi}(\xi,\mu_{\text{true}})(\xi_{x} - \xi^{*}) d\pi(g) \leq 0 $$

(A.4)

for all $x \in \mathcal {X}$, where $D {\Phi }_{\text {mav}}^{\pi }(\xi ,\mu _{\text {true}})(\xi _{x} - \xi ^{*})$ denotes the directional derivative of the function Φ_mav evaluated in the optimal design ξ^∗ in direction ξ_x − ξ^∗ and ξ_x denotes the Dirac measure at the point $x \in \mathcal {X}$.

To calculate the derivative we start with the derivative of the parameter $\theta _{s,g}^{*}(\xi )$ defined in Eq. 3.4 and define $\theta _{s,g}(\alpha ) := \theta _{s,g}^{*}(\xi _{\alpha })$ for ξ_α = αξ_x + (1 − α)ξ^∗. Note that 𝜃_{s, g}(α) is the solution of the equation

$$ \begin{array}{@{}rcl@{}} F_{s,g}(\alpha,\theta_{s}) = - \int \int g(y\mid t) \frac{\partial}{\partial \theta_{s}} \log f_{s} (y\mid t,\theta_{s}) dy d\xi_{\alpha}(t) = 0, \end{array} $$

(A.5)

and that the derivatives of the left hand side are given by

$$ \begin{array}{@{}rcl@{}} \frac{\partial F_{s,g}}{\partial \alpha} &=& - \int \int g(y\mid t) \frac{\partial}{\partial \theta_{s}} \log f_{s} (y\mid t,\theta_{s}) dy d(\xi_{x}-\xi^{*})(t), \end{array} $$

(A.6)

$$ \begin{array}{@{}rcl@{}} \frac{\partial F_{s,g}}{\partial \theta_{s}} &=& - \int \int g(y\mid t) \frac{\partial^{2}}{\partial \theta_{s} \partial \theta_{s}^{\top}} \log f_{s} (y\mid t,\theta_{s}) dy d\xi_{\alpha}(t). \end{array} $$

(A.7)

By the implicit function theorem we get $\frac {\partial \theta _{s,g}(\alpha )}{\partial \alpha } = - \big (\frac {\partial F_{s,g}}{\partial \theta _{s}} \big )^{-1} \frac {\partial F_{s,g}}{\partial \alpha }$ and hence

$$ \begin{array}{@{}rcl@{}} \left. \frac{\partial}{\partial \alpha} \theta_{s,g}(\alpha) \right\vert_{\alpha=0} &=& - \Big (\int \int g(y\mid t) \frac{\partial^{2}}{\partial \theta_{s} \partial \theta_{s}^{\top}} \log f_{s} (y\mid t,\theta_{s,g}^{*}(\xi^{*})) dy d\xi^{*}(t) \Big )^{-1} \cdot \\ && \int \int g(y\mid t) \frac{\partial}{\partial \theta_{s}} \log f_{s} (y\mid t,\theta_{s,g}^{*}(\xi^{*})) dy d(\xi_{x}-\xi^{*})(t) =\theta_{s,g}^{\prime}(\xi^{*},x), \end{array} $$

where $\theta _{s,g}^{\prime }(\xi ^{*},x)$ is defined in Eq. 3.16. Consider now the directional derivative of the matrix B_st defined in Eq. 3.6. An application of chain and product rule gives

$$ \begin{array}{@{}rcl@{}} && \frac{\partial B_{st}(\theta_{s,g}^{*}(\xi_{\alpha}),\theta_{t,g}^{*}(\xi_{\alpha}),\xi_{\alpha})}{\partial \alpha} \Big \vert_{\alpha=0} \\ &&= \Big (\int \int g(y\mid u) \frac{\partial}{\partial \alpha} \Big (\frac{\partial \log f_{s}(y\mid u,\theta_{s,g}^{*}(\xi_{\alpha}))}{\partial \theta_{s}} \Big (\frac{\partial \log f_{t}(y\mid u,\theta_{t,g}^{*}(\xi_{\alpha}))}{\partial \theta_{t}} \Big )^{\top} \Big ) dy d\xi_{\alpha}(u) \\ && + \int \int g(y \mid u) \frac{\partial \log f_{s}(y\mid u,\theta_{s,g}^{*}(\xi_{\alpha}))}{\partial \theta_{s}} \Big (\frac{\partial \log f_{t}(y\mid u,\theta_{t,g}^{*}(\xi_{\alpha}))}{\partial \theta_{t}} \Big )^{\top} dy d(\xi_{x} - \xi^{*})(u) \Big ) \Big \vert_{\alpha=0} \\ &=&h_{st,g}^{\prime}(\xi^{*},x), \end{array} $$

where $h_{st,g}^{\prime }(\xi ^{*},x)$ is defined in Eq. 3.18. In a similar way the derivative of the matrix A_s defined in Eq. 3.5 can be determined. First, using the chain rule, we observe that with $\theta _{s,g}^{\prime }(\xi ^{*},x) = (\theta _{s,g,1}^{\prime }(\xi ^{*},x),\cdots ,\theta _{s,g,p_{s}}^{\prime }(\xi ^{*},x))^{\top }$

$$ \begin{array}{@{}rcl@{}} \frac{\partial}{\partial \alpha} \left. \left( \frac{\partial^{2} \log f_{s}(y \mid x,\theta_{s,g}^{*}(\xi_{\alpha}))}{\partial \theta_{s} \partial {\theta_{s}^{T}}} \right) \right\vert_{\alpha=0} = D_{s}(\theta_{s,g}^{*}(\xi^{*})) (I_{p_{s}} \otimes \theta_{s,g}^{\prime}(\xi^{*},x)) , \end{array} $$

where D_s is defined in Theorem 3.2.

We now observe, that $\frac {\partial A_{s}(\theta _{s,g}^{*}(\xi _{\alpha }),\xi _{\alpha })}{\partial \alpha } \big \vert _{\alpha =0} = h_{s,g}^{\prime }(\xi ^{*},x)$, where $h_{s,g}^{\prime }(\xi ^{*},x)$ is defined in Eq. 3.19.

Noting, that

$$ \begin{array}{@{}rcl@{}} \left. \frac{\partial}{\partial \alpha} \frac{\partial \mu_{s}(\theta_{s,g}^{*}(\xi_{\alpha}))}{\partial \theta_{s}} \right\vert_{\alpha=0} = \frac{\partial^{2} \mu_{s}(\theta_{s,g}^{*}(\xi^{*}))}{\partial \theta_{s} \partial \theta_{s}^{\top}} \theta_{s,g}^{\prime}(\xi^{*},x). \end{array} $$

(A.8)

Equation 3.16 results by an application of the product rule and combination of the derivatives given above. Finally, we have

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial }{\partial\alpha} \Big (\sum\limits_{s=1}^{r} w_{s} \mu_{s}(\theta_{s,g}^{*}(\xi)) - \mu_{\text{true}} \Big )^{2} \Big \vert_{\alpha=0} \\ &&\qquad= 2 \Big (\sum\limits_{s=1}^{r} w_{s} \mu_{s}(\theta_{s,g}^{*}(\xi^{*})) - \mu_{\text{true}} \Big ) \sum\limits_{s=1}^{r} w_{s} \Big (\frac{\partial \mu_{s}(\theta_{s,g}^{*}(\xi^{*}))}{\partial \theta_{s}} \Big )^{\top} \theta_{s,g}^{\prime}(\xi^{*},x), \end{array} $$

and Eq. 3.15 follows.

The proof that there is equality in Eq. 3.15 for all support points of the optimal design ξ^∗ follows by a standard argument and the details are omitted for the sake of brevity. □