1 Introduction

Susan Carey’s general account of conceptual development, as developed in her The Origin of Concepts (henceforth TOOC), is centered around a mechanism of concept learning that she calls ‘Quinean Bootstrapping’. Despite the popularity of Carey’s account, it remains largely unclear what exactly Quinean Bootstrapping is, how it works, and whether it can account for genuine concept learning (Rey 2014, Rips 2013, Fodor 2008; 2010). In this paper, we will offer an improved model of bootstrapping that will contribute to explicating the cognitive mechanism behind Quinean Bootstrapping. Our refined model of bootstrapping, which we will call hybrid bootstrapping, will build upon Nancy Nersessian’s (2010) hybrid-models-based account of conceptual creativity in science. We will show how we can model the acquisition of a new concept through Quinean Bootstrapping as involving the iterated hybridization of different representational domains, in analogy with how, according to Nersessian, scientists create new concepts. We demonstrate the adequacy of our model by reconstructing within it Carey’s main example, the acquisition of number concepts. Thanks to hybrid bootstrapping, we will be able to defend Carey’s theory against two major challenges that have been placed against it in the literature: the circularity challenge and the specification challenge.

In Section 2, we present (Carey’s 2009) bootstrapping-based account of conceptual development, together with some refinements of it, and we discuss the main critiques leveled against it in the related literature. In Section 3, we present Nersessian’s fine-grained account of conceptual creativity in science. In Section 4, we offer our refined model of bootstrapping, i.e., hybrid bootstrapping. Our refined model understands bootstrapping as centered around the iterated hybridization of different representational domains. We show the adequacy of our refined model of bootstrapping by reconstructing within it an example of concept acquisition from Carey, i.e., the case of natural numbers. In Section 5, we show how our refined model of bootstrapping answers to the circularity challenge and the specification challenge. Finally, we conclude with some considerations on what our proposal achieves.

2 Bootstrapping in Conceptual Development

2.1 Carey’s Theory of Bootstrapping

Carey’s (2009) theory of conceptual development starts with the assumption that learners are equipped from birth with mechanisms that turn sensory inputs into proto-conceptual representations. These innate systems are called core cognition systems. The proto-conceptual representations produced by core cognition systems have an iconic format, they act continuously throughout life, they are inferentially rich, and they are specific to certain cognitive domains (e.g., numbers, action, cause).

These initial proto-conceptual representations are, in Carey’s picture, just the first step of our conceptual development. Learners very soon build proper conceptual representations that are different in several respects from the ones produced by core cognition system. Carey (2009, p. 22) stresses how these mature conceptual representations are structured in intuitive theories, they are not identifiable by innate mechanisms, they usually have a symbolic format, and they do not act continuously throughout the life of an individual. For mature concepts, then, Carey upholds the so-called theory-theory view of conceptual structure, according to which concepts are structured into semantic networks (i.e., the intuitive theories) of inferential connections, from which they get their semantic content.Footnote 1

Differently from core cognition systems, which are innate and act continuously throughout life, mature concepts are in Carey’s picture learned and they (often) get replaced with time. That is, conceptual development is, according to Carey, discontinuous, i.e., children and adults change multiple times the concepts that they possess. Carey conceptualizes the nature of these conceptual discontinuities in the life of an individual with the concept of incommensurability from philosophy of science (see, inter alia, Kuhn 1962). According to Carey (2009, p. 364), an individual, at different times of her life, enjoys concepts that are incommensurable to each other, in the sense that certain beliefs and inferences connected to one concept cannot be formulated within the resources of the other concept. More exactly, Carey stresses that incommensurability in conceptual development is always local, i.e., it affects only some parts of the semantic networks related to the relevant concepts. Nevertheless, this local incommensurability between incompatible subsets of two semantic networks often results in the relevant concepts having incompatible meanings and references. Just like in the history of science, where a new scientific theory does not often grow cumulatively from an old one, but it replaces instead the old conceptual system with an incompatible one, analogously, Carey argues, children’s ‘intuitive theories’ do not develop cumulatively with the addition of new information to existing concepts, but they often replace old concepts with new, incompatible ones.Footnote 2

Because of these conceptual discontinuities, Carey stresses how the phenomenon of conceptual change must be distinguished from knowledge enrichment and belief revision (Carey 2009, pp. 364-365) since “[in] cases of conceptual change, new primitives are created, whereas belief revision always involves testing hypothesis that are stated in terms of already available concepts” (Carey 2009, p. 520). This brings us to a major contribution of TOOC, namely, its attempt to tackle Fodor’s (1998) circularity challenge to concept learning. Fodor thinks about concept learning as a mere process of hypothesis testing. He argues that formulating the hypotheses to be tested requires having the relevant concepts. As a consequence, he argues that any concept that derives from this learning method is not truly learned because it must be available in the learner’s mind before learning. According to Fodor, this makes the whole idea of concept learning (as a matter of hypothesis formation and testing) circular. TOOC provides a promising response to the challenge that Fodor’s problem poses, i.e., a general learning mechanism by which children and adults learn new concepts from old ones. This learning mechanism is called by Carey Quinean Bootstrapping.

Quinean Bootstrapping, as described by Carey, involves three steps. In the initial step, children start out with a developmentally prior, uninterpreted and purely syntactically structured conceptual system. Let us call this initial conceptual system, which is the input of an episode of bootstrapping, CS1, while, instead, we will refer to the new conceptual system, i.e., the output of an episode of bootstrapping, as CS2. In the first step of bootstrapping, the ‘concepts’ involved in CS2 are initially learned as placeholder symbolic representations without content. For example, when learning to count, each of the symbols “1”, “2”, ... is not associated with a representation of a particular number of objects, but these symbols take the form of empty labels. Nevertheless, at this first stage of the bootstrapping process, children do establish internal (syntactic) relations between the placeholders. In the second step of Quinean Bootstrapping, children acquire a gradual or partial semantic interpretation of CS2 via CS1. According to Carey, children acquire such interpretations by performing repeated mappings between component substructures of the two systems. The mappings may include analogies, abduction, thought experiments and limiting case analysis. Finally, in the third step of Quinean Bootstrapping, children are able to fully interpret CS2 and integrate the newly acquired concept with other concepts in domain-general and coherent ways. Together, the three steps can be summarized as follows:

Summary of the steps involved in Quinean Bootstrapping

  1. Step 1:

    Constructing a syntactic placeholder structure. The learner starts by constructing CS1, which contains uninterpreted and purely syntactically connected placeholder symbolic representations without content.

  2. Step 2:

    Establishing partial mappings between substructures. The learner establishes a partial semantic interpretation of CS2 by repeatedly mapping component substructures between CS1 and CS2.

  3. Step 3:

    Completing and choosing the best interpretation. The learner establishes a full semantic interpretation of CS2, the representations of which are inferentially inter-connected (embedded in intuitive theories).

2.2 Critiques and Refinements

Several critiques have thrown doubts about the theoretical rigor and success of Carey’s account and, especially, on the viability of Quinean Bootstrapping as a general learning mechanism. We will discuss three different critiques that have been raised against Carey’s account, i.e., the circularity challenge, the deviant interpretation challenge, and the specification challenge. Together with these critiques, we are going to present also some refinements of bootstrapping that have been proposed as solutions to (some of) these critiques. We will then critically assess these critiques and the proposed solutions and we will conclude that there remain some important obstacles to a successful account of bootstrapping.

The first critique to Carey’s Quinean Bootstrapping that we are going to discuss is Fodor’s (1980; 1998; 2010) circularity challenge. We have briefly outlined this challenge in Section 2.1. The key insight of Fodor’s circularity challenge is that insofar as concept learning is a problem of rational inductive inference involving hypothesis testing, the formation of those hypotheses to be tested presupposes the existence of the relevant concepts to be learned. We think that the major issue justifying the popularity of the circularity challenge in cognitive science is the following unanswered question. How can an information-processing system come up with genuinely novel representations, without somehow already having the information that is transferred by manipulating those representations already be encoded, if only implicitly, in the system? This is the version of the circularity challenge that is most pressing for Carey’s account of conceptual development.

Beck (2017) takes Quinean Bootstrapping to be able to meet the circularity challenge thanks to the notion of a computational constraint. This notion, argues Beck, albeit only implicitly used by Carey, is pivotal to the success of her account of conceptual development. Computational constraints are, for Beck (2017, pp. 115-117), implicit or explicit rules for the use of a concept that we acquire in the process of learning a new concept. Beck divides these computational constraints into two categories, internal and external constraints. External constraints are rules governing conceptual use that learners acquire from the external world, such as, for instance, the law \( f= m \times a \), which acts as a computational constraint in our learning of high-school physical concepts. They typically refer to immediate and direct physical, social, and situational influences from the environment that shape cognitive processes in a situation-specific manner (e.g., ambient noise can affect attentional mechanisms and problem-solving) (Gibson 1979; Clark 1997). Internal constraints are, instead, innate rules that govern conceptual learning and inference capabilities of the learners, such as, for instance, the essentialist tendency that, according to some theorists, children exhibit in their conceptual development. These constraints, argues Beck (2017, pp. 118-120), guide children’s interpretation of the symbolic placeholders in an episode of bootstrapping by constraining the possible interpretations of the symbols. By guiding the learners’ acquisition of new conceptual roles, the notion of computational constraint is what allows Quinean Bootstrapping to meet Fodor’s challenge. Carey’s account does not need to presuppose that the concepts that children learn are already somehow stored in their cognition. All that needs to be presupposed is core cognition together with some general rules governing concept learning (i.e., the internal computational constraints, in Beck’s terminology), from which learners, thanks to the outside stimuli and the pivotal action of externally learned rules governing conceptual use (i.e., Beck’s external computational constraints), can learn new conceptual systems.

Although we agree that more attention should be shifted towards the pivotal role of computational constraints in Quinean Bootstrapping, we remain not entirely convinced by Beck’s explanation. Firstly, it remains unclear what exactly a computational constraint amounts to. Furthermore, it remains unclear how appealing to internal and external computational constraints solves the circularity challenge. Beck’s discussion convincingly argues that computational constraints are indeed used by the bootstrapping learners for partially interpreting the placeholders from which, according to the bootstrapping procedure, the new concepts will arise. Yet, how exactly is a learner able to assign a new (meta)semantic role to a given representation? What is the cognitive mechanism through which the learner, guided by the computational constraints, learns a new concept? To solve the circularity challenge, one must answer these two questions.

The second critique we are going to discuss is the deviant interpretation challenge. This challenge concerns the question why we learn natural concepts (e.g., green and blue), as opposed to strange or unnatural concepts (e.g., grue and bleen). If, according to Carey, children learn many concepts via bootstrapping them from innate core cognition, which part of this process makes children learn the natural concepts that they actually learn (and not some other alternative)? This challenge is not specific to bootstrapping, but, as Beck (2017, p. 113) and Pantsar (2021, p. 5796) stress, can be leveled against any inductive theory of concept learning. Yet, some refinements of bootstrapping pointed to a possible solution to this challenge. Recently, Pantsar (2021) proposed a refined account of our bootstrapping of integers number concepts that tackles the deviant interpretation challenge for this important case of concept construction.

Pantsar’s refinement of bootstrapping adds two components to Carey’s and Beck’s accounts. First, he stresses that a plurality of numerical core cognition systems is arguably active in this episode of bootstrapping (cf. Pantsar 2021, pp. 5803-5805). That is, in order to construct integer concepts, learners need to construct a hybrid model of two different core cognition systems (i.e., what we will call in Section 4 the analog magnitude representation system and the parallel individuation system). Secondly, such a bootstrapping process is pivotally fostered and thus constrained in its interpretation, by external cultural factors (cf. Pantsar 2021, pp. 5806-5808). It is thus a process of enculturation of our number cognition, i.e., the interaction with external cultural factors, that influences the development of our number cognition. More specifically, enculturation is a gradual process of cultural learning that shapes cognitive processes over time, involving the internalization of external constraints, cultural and societal norms, values, beliefs, and practices through socialization processes and participation in institutions and traditions, e.g., education, family upbringing or media exposure (Vygotsky 1978; Bruner 1990). In particular, for the case of numbers, socio-cultural factors support children’s engagement in counting routines, allowing them to associate a sequence of meaningless words with new conceptual roles, e.g., to notice that “three” is regularly expressed in light of observations of three objects. According to Pantsar, such an enculturation process, together with the aforementioned construction of a hybrid model of numerical core cognition, makes children learn the natural integers concepts and not some non-standard version of them. We agree with Pantsar that external factors, such as socio-cultural ones, are crucial for explaining why we learn certain concepts and not some others. Enriched with such enculturation-driven considerations, then, the process of bootstrapping can answer the deviant interpretation challenge, at least as well as other inductive theories of conceptual learning.

Finally, the third critique that we are going to focus on is what we call the specification challenge. This amounts to establishing a precise model of how Quinean Bootstrapping works and, thus, to specify all the steps involved in Carey’s outline of this procedure. One notable attempt at explicating Quinean Bootstrapping was presented by Piantadosi et al. (2012), who modeled bootstrapping as governed by Bayesian hypothesis testing: learning a concept means inferring the hypothesis that best maps a label onto the correct concept. For example, according to the authors, the process of learning the concept two can be modeled as the process of learning which hypothesis best maps the label ‘two’ onto a subset representation with cardinality two. The formal framework of Piantadosi et al. involves two ingredients: the first ingredient is a symbolic representational system, i.e., lambda calculus (a formal language for compositional semantics). The second ingredient is a formalization of the learning task in terms of Bayesian inference, used to “determine which compositions of primitives are likely to be correct, given the observed data” (ibid.). Piantadosi et al. claim that their model ‘bootstraps’ number concepts with these ingredients. However, as Carey herself stressed (Carey 2015), Piantadosi et al.’s attempt at modeling Quinean bootstrapping fails to be a genuine model of conceptual learning because it equates learning with mere hypothesis testing, thereby making bootstrapping fall prey to Fodor’s circularity challenge. And indeed this failure of Bayesian models to account for genuine conceptual change traces back to long-standing issues in Bayesian confirmation theory (see, inter alia, Earman 1992). Bayesian models, in fact, typically focus on modest discontinuities that explain only a change in the available expressive power associated with a given conceptual system, while, as we saw in Section 2.1, Carey’s theory focuses on identifying and explaining radical discontinuities, i.e., those involved when altering the total expressive power of a given conceptual system beyond possible combinations of its primitives. This focus on radical discontinuities is not captured in the model of Piantadosi et al., since the model assumes a latent hypothesis space that already determines before learning which hypotheses are possible to infer. In the model, the aspects that do change during learning are not the representational capacities but only how much probability is assigned to a hypothesis mapping an existing candidate concept onto a given label. It hence remains unclear how radical bootstrapping could proceed via Bayesian hypothesis testing.

We saw three critiques to Carey’s bootstrapping account of conceptual development and three proposed refinements of the bootstrapping process. Our assessment is that bootstrapping, when adequately refined and complemented, will be able to meet all the aforementioned challenges in a satisfactory way. In fact, Beck’s insistence on the pivotal role of computational constraints points to a way out of Fodor’s circularity challenge. Moreover, the importance of external cultural factors in constraining the learning of new concepts, highlighted by Pantsar, equips bootstrapping with a viable response to the deviant interpretation challenge. Finally, the idea of modeling bootstrapping within a broadly Bayesian framework championed by Piantadosi et al. (2012) opens a wide array of possible ways of formalizing the bootstrapping process for trying to tackle the specification challenge.

However, despite the virtues of these refinements, we saw that there remain serious doubts concerning the circularity and the specification challenges. In particular, the common stumbling block for a satisfactory solution of these two challenges seems to be the vagueness of the cognitive processes involved in the partial interpretation of a new conceptual system by a given learner and in the related pivotal step of creating new metasemantic roles with the help of computational constraints. The specific steps of the cognitive processes involved in bootstrapping need to be properly explicated before we can explain why bootstrapping offers genuine concept learning and before we can formalize this process.

3 Nersessian’s Theory of Scientific Conceptual Change

In the next section, we will present an explication of the specific steps involved in the cognitive mechanism behind bootstrapping. Before doing that, we present here the theory of scientific conceptual change upon which our explication of the steps involved in bootstrapping is built, that is, Nersessian’s (2010) hybrid-models-based theory of conceptual creativity. This is the focus of the present section.

Nersessian (2010) presents in detail her model of scientific conceptual change in her book Creating Scientific Concepts. In this book, she gives a general cognitive account of how novel scientific concepts are created. New scientific concepts, argues Nersessian, arise from the step-wise modification of the reasoning practices of scientists, in response to specific problems. More specifically, scientific reasoning is understood by Nersessian as primarily model-based, i.e., as centered around the iterated construction and manipulation of idealized representations of phenomena. The nature of these models is understood pluralistically as realizable in different formats combining internal and external representations (i.e., diagrams, formulas, etc.). The construction and manipulation of these models involve a vast array of techniques such as visual modeling, thought experiments, imagination, limiting case analysis, abductive reasoning, and analogical reasoning.

A central role in Nersessian’s model is played by (what she calls) hybrid models. Hybrid models are scientific models that represent, at the same time, phenomena from multiple domains. More exactly, hybrid models merge together information from multiple source (i.e., the domains of phenomena from which we draw concepts and tools for representing something) and target (i.e., the domain of phenomena that we want to represent) domains. The construction and manipulation of these hybrid models are heavily directed by multiple kinds of constraints arising from all the source and target domains involved, as well as from the related scientific practice, the specific problems under focus, and the nature of the mathematical tools chosen to construct the model itself. Thanks to the construction and manipulation of hybrid models, information belonging to different representational domains gets merged in unexpected ways, creating conceptual and inferential possibilities that were not afforded before the construction of the hybrid model.

3.1 Nersessian Bootstrapping

Nersessian (2010, pp. 184-185) structures the process of constructing and manipulating hybrid models as a cyclic process of four steps. We will refer to this specific four-step way of constructing and manipulating hybrid idealized representations of phenomena as hybridization or Nersessian bootstrapping:Footnote 3

  1. 1.

    Model construction: the first step of Nersessian bootstrapping amounts to the initial construction of a hybrid model that combines the relevant components of the target phenomenon and of one or more source domains.

  2. 2.

    Simulation: the second step of Nersessian bootstrapping amounts to the manipulation of the hybrid model to produce new states, new inferences, and (possibly) the emergence of new constraints.

  3. 3.

    Evaluation: the third step of Nersessian bootstrapping amounts to the evaluation of the adequacy of the hybrid model via the analogical comparison of the salient features of the model with the ones of the target phenomenon.

  4. 4.

    Adaptation: the fourth, possible, step of Nersessian bootstrapping amounts to the recombination of the hybrid model to solve the (possible) problems of fit between the model and the target that arose in the third step. When an adaptation of the model is needed, the components and the salient features of the hybrid model are re-combined, together with the possible addition of new source domains. A new hybrid model is constructed, thus leading to a new cycle of the bootstrapping process.

Nersessian bootstrapping starts with the construction of a hybrid idealized model of the target phenomenon, based upon a crude understanding of the problem under focus and the related choice of a source domain that seems an adequate basis for modeling the salient features of the target. Then, scientists start using the hybrid model, drawing inferences from it via thought experiments and simulations, and realizing its constraints. After this exploratory work, scientists evaluate the adequacy of the model by comparing its salient features with the ones of the target phenomenon. This step involves, as Nersessian stresses, traditional processes of analogical mapping and transfer from the hybrid model to the target phenomenon. If, as it is indeed in most cases of scientific theorizing, the fit between the model and the target is not perfect, scientists have to change the model. This re-combination of the hybrid model often involves re-thinking its basic components and the most salient features that get abstracted from the source domain(s), as well as, sometimes, the introduction of additional source domains. The product of this re-combination is a different, more adequate, hybrid model of the target phenomenon. With the construction of this second model, the cycle of hybridization continues until, hopefully, a fully satisfying fit between the hybrid model and the target phenomenon is achieved.

In order to see how Nersessian bootstrapping can genuinely explain novel concept learning, it is helpful to take a look at Nersessian’s (2010, ch. 2) most-detailed case study, i.e., Maxwell’s invention of the field concept.

3.2 Maxwell’s Invention of the Field Concept

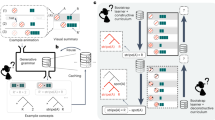
Maxwell introduced the field concept in physics in the context of deriving his field equations for electromagnetic phenomena.Footnote 4 As Nersessian (2010, pp. 22-27) recalls, Maxwell’s creation of the field concept started with a specific problem situation, namely, the need to expand Faraday and Lord Kelvin’s work using the kind of mathematics that Maxwell was trained in. Through a detailed historical analysis of Maxwell’s diary and original sketches, Nersessian reconstructs the development of Maxwell’s reasoning practices as an iterated process of hybridization, i.e., as the iterated cycle of construction, simulation, evaluation, and adaptation of hybrid models illustrated in Fig. 1 from Nersessian (2010, p. 57).

Fig. 1
figure 1

Maxwell’s invention of the field concept analyzed via cycles of conceptual bootstrapping. From Nersessian (2010, p. 57)

Full size image

The first hybrid model around which Maxwell’s reasoning centered is the vortex fluid model (Nersessian 2010, pp. 29-35) (Model 1 in Fig. 1). Maxwell wanted to provide with this model a unified account of electric and magnetic forces, understood as transmitting continuously in a mechanical medium (i.e., the aether). This continuous-transmission assumption constrains Maxwell’s construction of the vortex-fluid model, by pushing him to choose continuum mechanics as the source domain of the model. Then, Maxwell’s vortex-fluid model construction was further constrained by both the target and the source domains. From the target domain, i.e., electro-magnetic phenomena, Maxwell’s model inherited the constraint that tension and repulsion actions had to work along the lines of the forces, the constraint that the angle between the action of electric and magnetic forces ought to measure ninety degrees, and the connection between magnetism and polarized light. From the source domain of continuum mechanics, instead, Maxwell’s model inherited the constraint that tensions should act across the forces line, while pressure should be greater in the equatorial than in the axial direction. As Nersessian recalls, Maxwell’s simulation activity with the vortex fluid model allowed him to derive several new constraints for the target phenomena, including the so-called “stress-tensor", i.e., a representation of the force on an element of the magnetic medium due to its internal stress. The target constraints derived by Maxwell from his first hybrid model were also consistent with both Ampere’s and Coulomb’s laws, two mathematical results already well-established in Maxwell’s time. Yet, despite these initial successes, Maxwell’s evaluation of his first model was not optimal, because this initial model could not account for the dynamic aspects of electromagnetic phenomena. In particular, the vortex fluid model does not say anything about the relations between the magnetic vortices and the electric currents and it does not explain how different vortices interact together (cf. Nersessian 2010, p. 35).

These difficulties pushed Maxwell to radically adapt his first hybrid model into what Nersessian considers Maxwell’s second hybrid model, i.e., the vortex-idle wheel model (Nersessian 2010, pp. 36-43) (Model 2 in Fig. 1). This new hybrid model conceptualized the interactions between different vortices as mediated by layers of particles, acting as idle wheels. The introduction of idle wheels in Maxwell’s second hybrid model radically modifies the analogies and the constraints central to Maxwell’s reasoning, adding another source domain to his reasoning, i.e., machine mechanics. From this new source domain, Maxwell derives, via simulations with the model, several constraints on how these idle wheels-like layers of particles should behave, including the permanence of force lines around a constant magnetic source and the connection between resistance to motion and energy loss (cf. Nersessian 2010, pp. 37-39). Thanks to these new inferences and constraints afforded by his new hybrid model, Maxwell was finally able to approach the questions of the dynamic forces that could determine electrodynamical phenomena. With the vortex-idle wheel model, Maxwell achieved a significant description of many static and dynamic electromagnetic phenomena in terms of forces. Yet, as Nersessian (2010, pp. 43-44) recalls, Maxwell’s evaluation of the vortex-idle wheel model is also not optimal, in that the model could not account for static electricity phenomena and for the necessity of continuous action in a medium for transmitting electromagnetic forces.

Pushed by these two problems, Maxwell had to adapt once again his hybrid model, ending up constructing a third hybrid model, i.e., the elastic vortex-idle wheel model (Nersessian 2010, pp. 44-48) (Model 3 in Fig. 1). This new hybrid model changes completely the nature of the vortices. If, in fact, in the two hybrid models before, Maxwell assumed that the vortices approximate rigid spheres, he now felt the need to construct them as elastic blobs. Only vertices made of elastic material, reasoned Maxwell, could make sense of the transmission of rotation from the vortex exterior to its interior and of the electrically induced distortions in the vortices. Also this third hybrid model, then, radically modifies the inferences and the constraints in Maxwell’s reasoning, thanks to the addition of yet another source domain, i.e., elastic mechanics. It is only via the addition of this new source domain that Maxwell can finally give an adequate, unified, account of the full dynamics of electric and magnetic phenomena in terms of forces that are transmitted continuously in a medium. Via this elastic vortex-idle wheel account of electric magnetic phenomena, successfully refined in Maxwell’s famous equations for electromagnetic phenomena, the modern field concept makes its implicit appearance as a non-mechanical dynamical system.

As the example of Maxwell shows, Nersessian understands concept creation as the result of the iterated construction and manipulation of hybrid models. This process of hybridization allows the learner to acquire a genuinely novel concept thanks to the creative recombination of representations and constraints originating from multiple domains of phenomena.

4 Quinean Bootstrapping Refined

We now use Nersessian bootstrapping to refine Carey’s model of Quinean Bootstrapping. Specifically, we will see how the iterated process of hybridization described by Nersessian can be seen as a plausible blueprint for the cognitive mechanisms behind the second step of Carey’s bootstrapping, i.e., the partial interpretation of a new conceptual system through the existing conceptual resources of the learner. We will call our refined model of bootstrapping hybrid bootstrapping. We will first present our model in the next subsection (Section 4.1). Subsequently, in Section 4.2, we will show the adequacy of our model by applying it to a paradigmatic case study from Carey, i.e., the acquisition of the concept of natural number (TOOC, Ch. 8).

4.1 Hybrid Bootstrapping

Hybrid Bootstrapping is meant as an extension and a complement to existing ones in the literature, being compatible both with Carey’s outline of this procedure in TOOC and with the aforementioned refinements of it (cf. Beck 2017; Pantsar 2021). Specifically, our refined model explicates the pivotal second step of Carey’s Quinean bootstrapping (cf. Section 2.1), i.e., the partial interpretation of a new conceptual system by the conceptual resources available to the learner. We claim that this fundamental step of the bootstrapping procedure involves a sequence of steps structurally similar to the ones involved in Nersessian bootstrapping. That is, the second step of Quinean bootstrapping can be considered an instance of Nersessian bootstrapping, involving the construction, simulation, evaluation, and adaptation of hybrid models. Thus, hybrid bootstrapping refines the second step of Quinean bootstrapping into four, possibly cyclic, sub-steps:

  1. Step 1:

    Constructing a syntactic placeholder structure: Parts of a new conceptual system get learned only syntactically, i.e., without interpretation.

  2. Step 2:

    Establishing partial mappings between substructures: Parts of a new conceptual system get interpreted via the construction, simulation, evaluation, and adaptation of hybrid models merging information from the new conceptual system and the conceptual resources available to the learner.

    1. Step 2.1:

      Hybrid model construction. The first sub-step of this step-wise interpretation of the new conceptual system amounts to the creation of hybrid models, constructed through the pragmatic choice of suitable conceptual resources in the learner’s mind related to the newly learned placeholder structure.

    2. Step 2.2:

      Hybrid model simulation. The learner actively manipulates the hybrid model so-constructed, enriching it with states, inferences, and (possibly) new constraints, thus expanding the partial interpretation of the new conceptual system.

    3. Step 2.3:

      Hybrid model evaluation. The learner compares analogically the salient features of the hybrid model with the entities related to the new conceptual system, implicitly evaluating the adequacy of her interpretation of the new conceptual system.Footnote 5.

    4. Step 2.4:

      Hybrid model adaptation. If the adequacy of the interpretation is not enough, the components and the features of the hybrid model get re-combined into a new hybrid model, restarting the step-wise interpretation of the new conceptual system.

  3. Step 3:

    Completing and choosing the best interpretation: When the fit between the hybrid model and the entities related to the new conceptual system is adequate enough, the new conceptual system is fully interpreted and thus learned by the learner.

According to hybrid bootstrapping, children perform the second step of the bootstrapping process via a process of hybridization, i.e., via the construction, simulation, evaluation, and adaptation of hybrid models. Specifically, via the construction and further manipulation of hybrid models learners encode increasingly more semantic content into the placeholders that they have learned, merging external constraints from different domains with internal constraints. Our refined bootstrapping model makes this important implicit cognitive mechanism of bootstrapping explicit, conceptualizing it as a cyclic sub-process contained in the second step of Quinean bootstrapping (Fig. 2).

Fig. 2
figure 2

Steps involved in our refined model of Quinean Bootstrapping

Full size image

4.2 Hybrid Bootstrapping at Work: The Case of Number Concepts

Let us substantiate our refined model of bootstrapping by applying it to an example of bootstrapping described by Carey, i.e., the construction of the natural concept. A major task in applying our refined bootstrapping model to Carey’s example consists in identifying a set of hybrid models during the bootstrapping process. We can identify several such hybrid models in children’s learning of natural number. In this case, the relevant source domain consists of children’s core cognition systems with numerical content, while the target domain is the integer list.Footnote 6

According to Carey’s reconstruction (Carey 2009, Ch. 4,8,9), children are initially (Step 1 of the bootstrapping process) equipped with five ingredients from core number cognition when they interpret the count list (i.e., the initial placeholder structure “one”, “two”, ‘three”). Specifically, they are equipped with three different types of representational capacities: (1) analog magnitude representations, (2) a parallel individuation system that creates working-memory models of sets in which symbols represent specific individuals like {this box}, and (3) an ability for set-based quantification that allows the child to draw a distinction between singular and plural in terms of the abstract concepts individual vs. set (whereby they can grasp the difference between ‘one’ and ‘some’). Additionally, children are equipped with two computational constraints: (4) the stable-order principle, according to which a list of symbols that is to be memorized must be arranged in a stable order, and (5) the 1-1 correspondence principle, according to which the symbols used in the counting routine must be applied in 1-1 correspondence to the individuals in the set being listed.

The empirical evidence suggests that when learning to count, already 1-2 year old children develop an understanding of numerosities. They start by understanding what ‘one’ means – for instance, they can give a puppet one item from a pile when asked (Wynn 1990, p. 181), and they can correctly distinguish pictures representing one versus three fish (Wynn 1992, p. 230) – and successively expand their knowledge with increasing age, such that children who understand larger numerosities are older than children who grasp smaller numerosities.

Children then start to interpret the placeholders (Step 2 of bootstrapping). The first sub-step of this development is the construction of a hybrid model (Step 2.1) of core-cognition ingredients (1) and (2), i.e., what Carey calls a system of “enriched parallel individuation” (see also Le Corre and Carey 2007). Enriched parallel individuation transcends core cognition because it is a hybrid combination of ingredients (1) and (2). We thus find it appropriate to identify the outcome of this process as a hybrid mental model (corresponding to Model 1 in Fig. 3). In this initial phase, children additionally rely on (4) to interpret relations between the symbols in the count list, and specifically, to notice that “one” quantifies individuals in the same cases as “a” does.

Children then engage in simulation with this hybrid model (Step 2.2). They manipulate their representations of individuals to produce new inferences and constraints on future mappings of natural number. In particular, while relying on (2), the learner builds a mental model of a particular subset of objects in working memory that they want to quantify (e.g., {cookie}). The child may then engage in evaluation of the hybrid model (Step 2.3) by introducing (5) as a novel computational constraint. Specifically, the child may use analogical comparisons to map the working-memory subset-model (e.g., of {cookie}) onto a model that is already stored in long-term memory and that satisfies a 1-1 correspondence (e.g., {block}). They can then retrieve the corresponding sequence from the placeholder structure (i.e., “one”) to understand that “one” refers to a thing (e.g., a discrete object such as a cookie or a block). 1-1 correspondence is important in this phase as it prohibits pairing “three”, which is associated with three individual object-file representations such as {cookie cookie cookie}, with two individual object-file representations of the form {cookie cookie}. The result of the application of 1-1 correspondence is yet another hybrid model that adapts (Step 2.4) the previous interpretation of “one” with its generalization to single discrete objects of any kind. Thus, children rely on hybrid model construction to become a one knower: someone who has learned the meaning of the symbol “one” on the count list (corresponding to Model 2 in Fig. 3), and the hybridization process repeats itself.

Also the next learning stage described by Carey, i.e., the stage at which children interpret “two” (typically at 30-39 months of age, see Carey 2009, p. 298), can be modeled as a process of hybridization. While relying on (3), the singular/plural distinction, the learner can recombine models of individuals to combine to pairs (e.g., they can recombine {cookie} and {cookie} to {cookie cookie}). While simulating and evaluating as before, the learner maps their working-memory model {cookie cookie} to {block block} and retrieves “two”. A two-knower has learned that “two” refers only to that subset of plural representations that correspond to a set containing two individual object files (Carey 2009, p. 326).Footnote 7 By repeatedly mapping parts of the placeholder structure that is associated with models in long-term memory in 1-1 correspondence onto models from working memory, children progress towards three- and four-knowers. Carey (2009, p. 299) therefore calls them “subset-knowers” (corresponding to Model 3 in Fig. 3).

At the final stage of bootstrapping natural numbers, subset-knowers expand their existing representational capacities by considering a novel principle: (6) the cardinality principle, according to which the cardinal value of a set is determined by the ordinal position of the last symbol reached in the count list. With this additional ingredient, children (at around 40 months of age, Carey 2009, pp. 298-299) become fully capable of representing natural number by virtue of applying a successor function that returns for any symbol in the count list, with cardinal value n, the next symbol, with cardinal value \(n+1\). They become “cardinal-principle knowers” (corresponding to Model 4 in Fig. 3). The division between these stages maps onto Carey’s developmental distinction between cardinal principle knowers and subset-knowers based on how well they can identify numerals on a card: while cardinal principle knowers produce cardinal responses for all cards in a given test set up to sets of 8. subset knowers only produce responses for sets of 1-3 or 4, depending on their subset-knowledge level, i.e., whether they are one- , two-, three-, or four-knowers (Gelman 1993; Le Corre et al. 2006).

Fig. 3
figure 3

Iterative transition from core cognition to the natural number system (NN)

Full size image

Let us compare Carey’s analysis of children’s interpretation of the count list with Nersessian’s case study of Maxwell’s construction of the vortex-fluid model. We think that this comparison is helpful insofar as it highlights that what is important to concept learning in both cases is the use of computational constraints for the construction of hybrid representations (for the moment we ignore the many differences that may be invoked between scientific and mental representations). Nersessian highlights that Maxwell adapted this hybrid model in light of inconsistencies with observations of electromagnetism, whereby he recombined the vortex model (i.e., his first hybrid model) with the idea of idle wheels, into a new hybrid model, i.e., the vortex-idle wheel model. Crucially, the vortex idle-wheel model assumes new constraints from the domain of machine mechanics (i.e., the new source domain added in the step from the first hybrid model to the second one). Analogously, it is constitutive of children’s learning of new concepts that they hybridize their available constraints and existing representational capacities. The importance of hybridization becomes evident when at the final stage of learning natural number concepts, children go through an inductive leap that is motivated by the crucial observation that the last word in a count sequence refers to the cardinal value of the whole set (e.g., they notice that “one, two, three” refers to three objects). To accommodate this observation, children must evaluate their hybrid subset representation by drawing a creative analogy between ‘next in the numeral list’ and ‘next in the series of mental models ({i}, {j k}, {m n o}, {x x y z})’. Following Carey (2009, p. 328), the analogy between next on the numeral list and next state after the addition of an item in a set requires “that the child recognize, one way or another, that successive numerals among ‘one,’ ‘two,’ ‘three,’ and ‘four’ refer to sets that are related by +1, and induce that all successive numerals in the count list are so related”. As a result of the mapping, they adapt their initial, enriched parallel individuation, system by adding ingredient (6) from the integer domain and this establishes a precursor to the successor function.

In summary, we have explained how Carey’s case study of bootstrapping natural numbers crucially involves the construction and manipulation of hybrid models. Of course, the constraints and the hybrid models involved in children’s construction of concepts appear much simpler than those involved in Maxwell’s reasoning practice. Nevertheless, they function in a similar way in fostering genuine conceptual creativity. They allow the child to make further distinctions between individual object files and sets of object files (captured in the distinction between “one” and “two”) and to separate further among subsets of different sizes (i.e., distinguishing between “two”, “three” and “four”). Without this progression of hybrid model-construction, children would not come to notice the crucial analogy between the property of ‘being next in numeral list’ and ‘being next in the series of models’. They would then neither be able to establish the successor function, which is central to the ability to represent natural number.

Moreover, it is important to stress that the aforementioned differences in complexity and explicitness of representations between Maxwell’s case and children’s bootstrapping of number concepts do not conflict with our bootstrapping model. These differences illustrate, in fact, a difference in degree, not in kind, as there seems to be a fundamental continuity between these processes of conceptual change. Recent insights into the role of cultural factors in childhood learning support the idea that bootstrapping in this context involves combining innate cognitive capacities and cultural influences already at the early stages of children’s development (Núñez 2017; Pantsar 2021), e.g., as in the case where children transition from core cognition to natural number concepts. It is thus not in principle implausible to assume that children, like adults, draw on capacities of the same kind to combine different representational domains, adapting their hybrid models accordingly. Thus, we can view Maxwell’s case and children’s bootstrapping of numbers as being positioned at the two extremes of a continuum of bootstrapping episodes, with various cases of bootstrapping varying in their complexity in between these. Indeed, many concepts that we learn in school are arguably only possible because of external constraints and capacities similar to the ones involved in Maxwell’s case. For this reason, we maintain that differences between Maxwell’s case and children’s learning do not necessarily reflect a difference in the cognitive capacities involved but rather in the degree of sophistication and deliberation used in conceptual change.

5 New Perspectives on Known Challenges

After having presented our refined bootstrapping model, i.e., hybrid bootstrapping, we can now show how this model can answer two major challenges to Carey’s TOOC, i.e., the circularity challenge and the specification challenge (cf. Sec. 2.2).

The first challenge is the circularity challenge, i.e., the Fodor-inspired impossibility argument against any non-circular way of learning new concepts. Our model answers this challenge by pointing to the fundamental role of hybrid models in conceptual creativity. By abstracting and idealizing information from different domains, hybrid models allow learners to construct genuinely new representations and constraints. That is, hybridization allows the construction of representations and constraints that were previously impossible to create within single domains. As Nersessian stressed in her account of conceptual creativity in science, in fact, mixing different source and target domains affords scientists conceptual and inferential resources not already available to them, as Maxwell’s invention of the field concept shows:

“On my interpretation of Maxwell’s reasoning, we have a plausible answer to the puzzle of creativity in conceptual change posed earlier. In this case, the puzzle is: If Maxwell really did derive the mathematical representation of the electromagnetic field through the modeling processes described, how is it possible that by making analogies from Newtonian mechanical domains he constructed the laws of a non-Newtonian dynamical system? The answer lies in seeing that Maxwell did not make direct analogies between the domains. Rather, he constructed intermediary, hybrid models that embodied constraints from both Newtonian sources and the electromagnetic target domain. Abstractive processes, especially generic modeling, enabled integrating selective constraints from the different domains because they were considered at a level of generality that eliminated the domain-specific differences. Thus a fundamentally new kind of representational structure emerged-one that abstracted the notion of “mechanism” from the analysis, creating a representation of a non-mechanical, dynamical system." (Nersessian 2010, pp. 59-60, emphasis added)

This novelty-conductive mixture of domains is also the reason why hybrid bootstrapping provides an answer to the circularity challenge. Hybridizing information from different domains, a representational system is able to come up with genuinely novel representations, without requiring the information encoded in the concept already being encoded in the system. This is why, in contrast to previous accounts of bootstrapping, our model does not fall prey to previous rejoinders to Fodor’s challenge (such as Rey’s 2014). Before the bootstrapping process, representational domains are separated and so inferences remain domain-specific. Hybridization of domains makes it, then, possible to draw substantially new connections that range over a wider set of domains. That is, the construction, simulation, evaluation, and adaptation of hybrid models allows the formation of new inferential roles. Such bootstrapped inferential-semantic content is genuinely novel because it cannot be logically constructed from the inferential-semantic content available at earlier developmental stages.

We saw an example of this non-circular conceptual learning in our reconstruction of Carey’s example of natural numbers (Section 4.2), where the newly learned conceptual system cannot be expressed in terms of the old concepts. While children initially cannot express information about a successor relationship based on parallel individuation alone, by hybridizing principles pertaining to different domains such as 1-1 correspondence and cardinality they become able to fully interpret the count list as integers. It is only after this crucial hybridization that numerals can allow new inferences across the count list and, in this way, obtain new semantic roles. It is from this perspective, then, that hybrid bootstrapping avoids the circularity challenge, by assuming that a new conceptual role can be created by the iterative hybridization of different representational domains governed by pragmatic constraints and criteria.

The second challenge is what we called the specification challenge. Our model addresses this challenge by identifying all the steps that radical bootstrapping involves. Specifically, we saw how hybrid bootstrapping explicates Carey’s second step via four additional steps, i.e., the construction, simulation, evaluation, and adaptation of hybrid models. By specifying these further steps, our model paves the way for establishing in future work a formal model of bootstrapping. Such a model would require a good formalization of the construction (2.1) and the adaptation (2.4) steps, that is, a good formalization of how learners merge different representational domains into a hybrid one and how they modify it in the learning process.

Our refined model of bootstrapping offers a first step towards a formalization of the specific steps involved in Carey’s informal account of Quinean Bootstrapping, and specifically the substeps involved in the second step. Hybrid bootstrapping does this by providing a clearer theoretical demarcation between these specific sub-steps. Previous distinctions between aspects of the process were rather vague but our fine-grained recipe shows how they can obtain sharper boundaries. Specifically, according to our model, the process by virtue of which a new conceptual system is being partially interpreted by the conceptual resources already available to the learners corresponds to step 2.2 in the process. The model furthermore provides a more refined place for the influence of external constraints that may take the role of teacher’s instructions in step 2.3 of the process to guide the evaluation of the fit between a hybrid model and the target domain. In this way, hybrid bootstrapping makes significant progress in this debate by clarifying the exact ways in which the steps of bootstrapping are supposed to work.

6 Conclusion

Let us recall the main steps of the present work. We started with analyzing Carey’s account of conceptual development, together with two major critiques of it, i.e., the circularity challenge and the lack of formal models challenge. We then presented a refined model of bootstrapping that is able to meet these challenges. Our refined model of bootstrapping, i.e., hybrid bootstrapping, builds upon Nersessian’s account of scientific conceptual creativity and it is centered around the cyclic construction, simulation, evaluation, and adaptation of hybrid models. Thanks to this iterated creation and modification of hybrid representations, hybrid bootstrapping gives a non-circular picture of concept learning, escaping the standard Fodorian worries by recombining information from different representational domains governed by pragmatic constraints.

Hybrid Bootstrapping advances the debate over Carey’s TOOC by clarifying what is exactly at work in the process of bootstrapping concepts. It does so by drawing analogies between conceptual change in childhood and in science, where the process of constructing hybrid models from various representational domains is key to the creation of new concepts, promoting the interactions between theories of conceptual development and contemporary account of scientific change. The present proposal is open to several extensions, such as an already mentioned formalization of the model or a possible integration with other general accounts of learning.