Abstract
This paper offers a novel account of practical factor effects on knowledge attributions that is consistent with the denial of contextualism, relativism and pragmatic encroachemt. The account goes as follows. Knowledge depends on factors like safety, reliability or probability. In many cases, it is uncertain just how safe, how reliably formed or how probable the target proposition is. This means that we have to estimate these quantities in order to form knowledge judgements. Such estimates of uncertain quantities are independently known to be affected by pragmatic factors. When overestimation is costlier than underestimation, for instance, we tend to underestimate the relevant quantity to avoid greater losses. On the suggested account, high stakes and other pragmatic factors induce such “asymmetric loss functions” on quantities like safety, reliability and probability. This skews our estimates of these quantities and thereby our judgements about knowledge. The resulting theory is an error-theory, but one that rationlizes the error in question.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Intuitions and experimental studies suggest that our knowledge ascribing practice is sensitive to pragmatic factors such as what is at stake. This seems puzzling given familiar analyses of knowledge. These analyses refer to parameters such as justification, evidence, probability, safety, sensitivity, etc. On the face of it, none of these parameters has anything to do with stakes. So why are knowledge ascriptions sensitive to this factor?
Extant accounts include revisionary accounts based on contextualism (e.g. Cohen 2008; DeRose 2009), relativism (e.g. MacFarlane 2014) or pragmatic encroachment on belief or knowledge (e.g. Hawthorne 2004; Stanley 2005; Weatherson 2005; Fantl and McGrath 2009) and conservative accounts that trade instead on phenomena like conversational implicatures (e.g. Rysiew 2001; Brown 2006), psychological effects of stakes on belief (e.g. Nagel 2008; Gao 2019; Dinges 2020) or heuristic shortcuts we use in ascribing knowledge (e.g. Gerken 2017).
The primary goal of this paper is to add a novel, superior account to the mix. On this account, knowledge judgements are sensitive to stakes because high stakes induce asymmetric loss functions on our estimates of evidential probability and related epistemic quantities; where an asymmetric loss function is a function that assigns asymmetric costs to over- and underestimation. This distorts these estimates and, consequently, our judgements about knowledge. The resulting view is an error-theory in the sense that some knowledge judgements come out as false. As I will argue though, the error can be rationalized and thus it is no cause for concern.Footnote 1
My proposed view has many advantages. First, neither contextualism, nor relativism nor pragmatic encroachment are required to get the account going. I take this to be an advantage because these views are highly controversial. Second, my account accommodates many data points that can seem troublesome for other, similarly conservative accounts, as I will argue below. Finally, my account, unlike many others, predicts that not just knowledge judgements but judgements about evidential probability vary with stakes. I confirm this prediction in a new experimental study.
The structure of the paper is as follows. Section 1 presents some basic data on stakes effects on knowledge ascriptions. Section 2 presents theoretical background and, in particular, an account of the data based on pragmatic encroachment. This account serves as a contrast to my own account, which I present in section 3. Section 4 confirms a crucial prediction of this account, before I conclude in section 4.2.
A preliminary dialectical remark. This paper is not, or not primarily, about pragmatic encroachment, epistemic contextualism or relativism. It bears on these views because if I am right, pragmatic factor effects on knowledge attributions do not motivate these views, for as I argue, these effects can be explained more conservatively. However, there are many other familiar arguments for these positions, and I will not touch on those (see e.g. Weatherson 2017 and Wright 2017 for overviews). The central goal of this paper rather is to explain a puzzling pattern of data—pragmatic factor effects on knowledge ascriptions—and thereby to contribute to a deeper understanding of our overall practice of ascribing knowledge. Given the importance of knowledge ascriptions to both philosophy and everyday life, I take this to be a worthwhile project in its own right, even though this project was initially pursued only in the service of deciding between e.g. invariantism and contextualism.
2 Data
Some authors have voiced intuitions to the effect that knowledge is sensitive to stakes (e.g. Fantl and McGrath 2002; Stanley 2005). When the stakes are high, they hold, we become intuitively less inclined to ascribe knowledge. These intuitions have been challenged with experimental data (e.g. Buckwalter 2010; Buckwalter and Schaffer 2015; Rose et al. 2019). Recent experimental studies, however, confirm them, and I will present the key findings in this section. These findings will be the primary explananda for the discussion to follow. I will discuss some more specific findings below.
In studies using the so-called evidence-seeking paradigm (e.g. Pinillos 2012; Pinillos and Simpson 2014; Buckwalter and Schaffer 2015; Francis et al. 2019), participants answer how much evidence a protagonist needs to collect before she gains knowledge. Buckwalter and Schaffer (2015: 208–209), for instance, presented participants with the following vignettes. (These vignettes are roughly length-matched versions of vignettes due to Pinillos (2012). I present these specific vignettes because I will use them myself in the study below.)
Typo low: Peter, a good college student, has just finished writing a two-page paper for an English class. The paper is due tomorrow. Even though Peter is a pretty good speller, he has a dictionary with him that he can use to check and make sure there are no typos. But very little is at stake. The teacher is just asking for a rough draft and it won’t matter if there are a few typos. Nonetheless Peter would like to have no typos at all.
Typo high short: Peter, a good college student, has just finished writing a two-page paper for an English class. The paper is due tomorrow. Even though Peter is a pretty good speller, he has a dictionary with him that he can use to check and make sure there are no typos. There is a lot at stake. The teacher is a stickler and guarantees that no one will get an A for the paper if there is a typo. Peter needs an A on the paper to get an A for the class, and he needs an A for the class to keep his scholarship. If he loses the scholarship he will have to leave school, which would be devastating for him. So it is extremely important for Peter that there are no typos in the paper.
Participants were asked, “How many times do you think Peter has to proofread his paper before he knows that there are no typos?” They required substantially more rounds of proofreading for knowledge when the stakes were high.Footnote 2
Studies using the retraction paradigm further support these findings. In this paradigm, participants imagine themselves in a situation where they have made a knowledge ascription. Later they assess whether they want to stand by this knowledge ascription or retract it. It turns out that if the stakes change in the meantime, people become more inclined to retract. Dinges and Zakkou (2020) use e.g. the following versions of the familiar bank cases (due to DeRose (1995)).
You are driving home from work on a Friday afternoon with a colleague, Peter. You plan to stop at the bank to deposit your paychecks. As you drive past the bank, you notice that the lines inside are very long, as they often are on Friday. Peter asks whether you know whether the bank will be open tomorrow, on Saturday. If it is open tomorrow, you can come back tomorrow, when the lines are shorter. You remember having been at the bank three weeks before on a Saturday. Based on this, you respond:
“I know the bank will be open tomorrow.”
At this point, …
NEUTRAL … you receive a phone call from your partner. S/he tells you that one of your children has gotten sick and that they are still waiting at the doctor’s office to get an appointment. S/he asks whether you can water the plants if you come home and prepare dinner. There’s enough food at home so you don’t have to buy anything extra. You agree. As you hang up, Peter asks whether you stand by your previous claim that you know the bank will be open tomorrow. You respond:
STAKES … you receive a phone call from your partner. S/he tells you that it is extremely important that your paycheck is deposited by Saturday at the latest. A very important bill is coming due, and there is too little in the account. You realize that it would be a disaster if you drove home today and found the bank closed tomorrow. As you hang up, Peter asks whether you stand by your previous claim that you know the bank will be open tomorrow. You respond:
EVIDENCE … you receive a phone call from your partner. S/he tells you that s/he was at a different branch of your bank earlier today. A sign said that the branch no longer opens on Saturdays. You see a similar sign in the branch you were about to visit. You can’t properly read the sign from the distance, but it seems to concern the opening hours. As you hang up, Peter asks whether you stand by your previous claim that you know the bank will be open tomorrow. You respond:
Each participant read the initial case-setup together with one of the three continuations. Then they reported whether they would be more likely to respond with “Yes” or “No.” Retractions rates were much higher in STAKES (48%) than in NEUTRAL (9.8%) and even higher in EVIDENCE (96.1%). Participants also rated how confident they were in their response. The indicated trend remained when the initial “Yes/No” responses were weighted by this factor.
One may wonder why stakes effects appear in the reported evidence-seeking and retraction studies while being difficult to detect in traditional studies, where participants directly judge whether a protagonist of the story has knowledge (e.g. Buckwalter 2010; Buckwalter and Schaffer 2015; Rose et al. 2019). Sripada and Stanley (2012), Pinillos and Simpson (2014: 23–25) and Francis et al. (2019: 454–455) confirm stakes effects even in this paradigm, and they discuss many possible explanations for why other traditional studies failed to detect similar effects. I will not go into this. Instead, I will run with the robust data from the studies above. These data need to be explained.
3 Pragmatic Encroachment
One way to explain the data appeals to pragmatic encroachment on knowledge (e.g. Hawthorne 2004; Stanley 2005; Fantl and McGrath 2009). Pragmatic encroachment on knowledge is roughly the view that differences in pragmatic factors such as what is at stake can ground differences in knowledge. Here is one way to spell this out. Knowledge requires a high level of evidential probability i.e. you can know that p only if the probability of p on your evidence is high. How high? Pragmatic factors set the threshold. When the stakes are high, for instance, you need better evidence than when the stakes are low.
Pragmatic encroachment directly explains the findings above. Consider evidence-seeking studies. According to pragmatic encroachment, the evidential threshold for knowledge rises when the stakes rise. For this reason, Peter with high stakes needs to proofread his paper more frequently than Peter with low stakes before he comes to know there are no typos in the paper anymore. Consider retraction studies. Again, a shift in stakes supposedly shifts the evidential requirements for knowledge. Hence, even if the protagonist initially knew that the bank would be open, they may fail to know this once the stakes are high. Their unchanged body of evidence no longer suffices to surpass the shifted threshold for knowledge.
Much more could be said here about the merits and demerits of pragmatic encroachment, and the various ways in which this view can be spelled out (see e.g. Weatherson 2017 for an overview). I will not go into this. I present this view only to be able to contrast it with my own position, to which I will turn now.
4 The Loss Function Account
4.1 Basic Structure
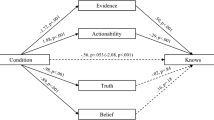
Let me begin by presenting the basic structure of the account I am going to propose. According to the indicated version of pragmatic encroachment, knowledge ascriptions are sensitive to stakes because the evidential threshold for knowledge varies between the low and the high stakes condition. Thus, a fixed body of evidence can suffice to surpass this threshold in one condition but not the other (Fig. 1). Meanwhile, on my account, knowledge ascriptions are sensitive to stakes because our estimates of evidential probability vary between the low and the high stakes condition. Thus, even if the threshold for knowledge remains fixed, we may estimate that it is surpassed in one condition but not the other (Fig. 2).Footnote 3 The evidential probability in question here is the evidential probability of the target proposition on the subject’s evidence, e.g., the evidential probability on Peter’s evidence of the proposition that there are no typos in his paper anymore. This evidential probability is relevant for knowledge and our estimates of it vary on my view. (I will later suggest that the low stakes estimates is more likely to be correct.)
As stated, one central assumption in the suggested account is that knowledge entails a high, yet non-maximal evidential probability. I will stick with this assumption in what follows (see e.g. Brown 2018 for sympathetic discussion), but it should be unproblematic to replace the notion of evidential probability with other notions familiar from the debate on the analysis of knowledge such as safety, reliability or justification. Each of these factors comes in degrees (e.g. Sosa 2000: 6), and a knowledge-level threshold needs to be specified. Pragmatic encroachers can say that this threshold varies with stakes. I say that our estimates of the relevant quantity vary, while the threshold may remain fixed.
Another central assumption is that estimates of evidential probability, and other relevant epistemic quantities, vary between the low and the high stakes condition. The remainder of this section aims to establish this key assumption by appeal to the notion of an asymmetric loss function. I begin by explaining the general idea of an asymmetric loss function, and the effects that loss functions have on estimates of uncertain quantities. Then I show how to explain stakes effects on knowledge ascriptions on this basis. Again, I focus on evidential probability, but it should be unproblematic to couch the subsequent discussion in terms of e.g. safety or reliability.
4.2 Loss Functions and their Effects
Suppose I force you to estimate an uncertain quantity such as Brad Pitt’s age (assume that you do not know Pitt’s exact age), and that I will punish you for mistakes. In one situation, the punishment is symmetric: I take $1 from you for each year by which you underestimate Pitt’s age and $1 for each year by which you overestimate Pitt’s age. In the other situation, the punishment is asymmetric: I take $1 per year for underestimation but $10 per year for overestimation. The former type of situation features a symmetric loss function. Misestimates are equally costly, independently of the direction in which you err. Situations of the latter type, meanwhile, feature an asymmetric loss function, in that losses for underestimation and overestimation are asymmetric.
The estimate you give in the latter situation will presumably be lower than the estimate you give in the former situation. In the former situation, you will presumably offer the age that is most likely correct from your perspective. In the latter situation, you will presumably pick a lower age to reduce the chance of overestimation, which is costlier than underestimation. Numerous studies suggest that our estimates of uncertain quantities are affected by whether the loss function is symmetric or asymmetric, and that asymmetric loss functions bias us towards the safer bet in the indicated way (e.g. Weber 1994).
This sensitivity to loss functions seems practically rational at least in the sense that it tends to maximize expected utility. Suppose overestimations are costlier than underestimations. Then the expected utility of a higher estimate may be lower even if it is more probably correct. This is because higher estimates increase the chance of costly overestimation. The exact magnitude of this bias will depend on the exact loss function involved (e.g. whether it is linear, as in the Pitt example above, or how steep it is), but for my purposes, these details do not matter. All I need is that people are rationally biased in the direction of the loss function.Footnote 4
Some clarifying remarks are in order. First, even if sensitivity to loss functions is rational, this does not mean that we are consciously aware of adjusting our estimates when we do. The available evidence seems to suggest that we are not (e.g. Harris et al. 2009: 61). Second, the making of an estimate need not involve an utterance. You can estimate Pitt’s age in solitary thought. And when you aim to make use of this estimate later, say, in a situation where I force you to voice an estimate under asymmetric loss, you may face an asymmetric loss function already from the start, and thus it may be wise to adjust the internal estimate accordingly. Third, the internal or external estimate you make need not align with the response to which you assign the highest credence or with the response that is most probable on your evidence. As indicated, asymmetric loss functions make it practically rational to diverge from this response.Footnote 5
Harris et al. (2009) confirm sensitivity to loss functions in a way that is particularly relevant for my purposes. They specifically looked at estimates of uncertain probabilities (rather than e.g. Pitt’s age) and loss functions induced by subsequent decisions (rather than e.g. monetary rewards). It is worthwhile to consider their studies in some detail, and I will do so in what follows.
In one of their studies, one group of participants read the following story:
The RAF are in need of a new training site for their pilots. The location currently favoured would involve flying over the area pictured below, in which the white area represents a densely populated town and the blue area represents the river that flows through that town. Crashes and falling plane debris are not uncommon occurrences in RAF training sites, and if falling debris were to land on a populous area, it would kill anybody beneath it. Any debris falling from the sky during training could land in any of the grid squares in the picture below.
The RAF have asked you to use the picture below to estimate the chance that any falling debris would land on the densely populated dry land.
After reading the story, participants saw a simple, two-colored visual representation of the river (blue) running through the densely populated town (white) as seen from above. Participants could use the relative sizes of the white and the blue areas to estimate the requested probability on a scale from 0% to 100%. Another group of participants was confronted with the very same task except that this time the white area in the picture was described as “uninhabitable wasteland.” Falling debris was said to “litter that area” rather than “kill anybody beneath it.” Since participants saw exactly the same picture in both conditions, one would expect same responses. In fact, however, estimates were higher in the populous-town condition (59).Footnote 6
Why? Sensitivity to loss functions explains the data. Following Harris et al. (2009: 56), participants face loss functions due to a consequent decision on the part of the RAF. The RAF presumably has to make a decision on whether to use the training site. It is natural for participants to picture the situation such that the RAF will base this decision on their probability estimate. As Harris et al. put it, participants have “an implicit sense of controllability” (57) over the decisions of the RAF. Over- and underestimations of the relevant probabilities will thus be associated with costs to the extent that they lead to bad decisions on the part of the RAF.Footnote 7
The resulting loss functions differ between the scenarios. Consider the first scenario, where the white area stands for a densely populated town. Here the loss function is asymmetric. Underestimating the probability that debris will land in the densely populated area potentially leads the RAF to decide to use the training site when it is actually unsafe. This is extremely costly because falling debris might kill people. Overestimating the probability may lead the RAF to decide to abandon the training site when it is actually safe enough. This would presumably be somewhat costly too, but not as costly as death from falling debris. Consider the second scenario, where the white area stands for wasteland. Here the loss function is roughly symmetric, or at least it is less asymmetric than before. Underestimation may lead to littered wasteland, which is approximately as bad as the unnecessary search for a new training site in the case of overestimation.
If asymmetric loss functions shift estimates of uncertain quantities towards the safer bet, as indicated before, we would now expect higher estimates for the first situation (densely populated town) compared to the second (wasteland). This is because underestimation is extremely costly in the first but not the second situation, while overestimation is equally unproblematic. As indicated, this is exactly what was found.
To support the idea that the results are driven by the loss functions described, Harris et al. manipulated their story in such a way that the loss functions became symmetric. In particular, they added the sentence “This is the only air space available to the RAF and hence must be used, as the training of new pilots is essential.” (58) Over- and underestimations are no longer tied to relevant decisions because the RAF will use the training site anyway. This eliminates the difference in loss functions between the scenarios. In line with the previous account, estimates of probability no longer differed between the scenarios (59).
In sum, there is good evidence that, in cases of asymmetric loss, estimates of uncertain quantities are skewed towards the less costly error and, more specifically, that probability estimates are so affected. When underestimation is costlier, for instance, estimates of probability are “inflated which acts as a preventive measure against the negative effects associated with an underestimate.” (60) Moreover, subsequent decisions can induce loss functions when the decision depends on the respective estimate.
Notice that even though sensitivity to loss functions is practically rational as indicated before, this does not change the fact that, in the RAF study, for instance, at least one probability estimate must be mistaken. After all, the relevant probabilities do not shift with the loss function we face. This makes the loss function account an error-theory, but one that rationalizes the error in question. Notice also that when I say that the indicated estimates of probability are practically rational, I am not saying anything about credences and their rationality. An estimate of a probability is not a credence. It is the answer to a question about probabilities that you settle on when you have to while being uncertain about what the true probability is. You do not even need a precise credence for this.Footnote 8
4.3 Explaining Stakes Effects
In this section, I explain stakes effects on knowledge ascriptions based on the indicated effects of loss functions on probability estimates. The basic idea is that high stakes induce an asymmetric loss function. People rationally adjust their estimates as a result and end up with different knowledge judgements.
4.3.1 Retraction Studies
Consider stakes effects in retraction studies i.e. the finding that people tend to become more inclined to retract previous knowledge ascriptions when the stakes rise. I will focus on the bank cases, NEUTRAL and STAKES, from above for concreteness. Loss functions bear on these cases in the following way.
As indicated, I adopt the working assumption that knowledge is governed by some threshold principle to the effect that S knows that p only if the evidential probability of p on S’s evidence surpasses a given threshold. Given this threshold principle, participants implicitly assess the evidential probability of the target proposition when they assess whether they want to retract their previous knowledge ascription. In the bank cases, for instance, they assess the probability of the proposition that the bank will be open given their memory of their previous visit at the bank.
This evidential probability is an uncertain quantity. It depends on how exactly we construe the cases. For instance, one may wonder just how strong one’s memory is supposed to be. The evidential probability will also depend on background knowledge people lack, say, about how frequently banks change their hours.Footnote 9
Moreover, under- and overestimation of the relevant probability are associated with losses. Participants picture themselves in a situation where they have to make a decision on whether to wait in line or come back another day. This decision is going to depend on their estimate of how probable it is that the bank will be open, and under- and overestimation will be associated with the losses that mistaken estimates entail for this decision.Footnote 10
Crucially, the loss functions differ between NEUTRAL and STAKES. Take NEUTRAL, where the stakes are low. Here the loss function is more or less symmetric. Underestimating the probability of the bank being open increases the risk of waiting in line when one could have come back another day. Meanwhile, overestimation potentially leads one to drive home and find the bank closed on the next day. Neither cost is particularly severe. Take STAKES, where the stakes are high. Here the loss function is strongly asymmetric. As before, underestimation increases the risk of waiting in line unnecessarily. Overestimation will potentially lead one to return on the next day and find the bank closed, which would be a disaster.
Given the previous results, participants should end up with lower probability estimates for the proposition that the bank will be open in STAKES than in NEUTRAL. In this way, they can avoid costly overestimation. They will thus become less inclined to stand by their previous knowledge claim given the threshold principle, and this explains the reported findings.
Notice here that participants do not actually face an asymmetric loss function, for they do not actually have to make a decision about the bank. However, they imagine themselves in such a situation, and they offer verdicts on how they would respond in this imagined situation. In fact, they would face an asymmetric loss function, which would skew their estimates. Participants are presumably sensitive to these facts, and so their responses are skewed accordingly. A similar assumption is required in the RAF study above, where participants also only imagine the situation with the RAF.
Let me briefly respond to two questions that may naturally arise at this point. First, whose probability estimate is correct, the one by participants in NEUTRAL, which warrants standing by, or the one by participants in STAKES, which tends to warrant retraction? I am not committed to a specific view here. All that counts is that estimates differ between conditions and that retraction behavior differs as a result. If we want to endorse either the estimates in NEUTRAL or the estimates in STAKES, the loss function account suggests that we go with NEUTRAL. Asymmetric loss functions lead to biased estimates, and hence the estimates in NEUTRAL are less biased than the estimates in STAKES in at least one regard. This might help to vindicate the anti-skeptical commitments many philosophers seem to have, whereby judgements about high stakes cases are often overly skeptical.
Second, why do only some people retract in STAKES while others stand by? There are going to be individual differences in whether participants perceive the estimated evidential probability as approximating the threshold for knowledge or dropping below the threshold. This depends on how exactly they construe the case, say, in terms of how reliable the bank is. It also depends on how they perceive the reliability of their own memory (recall that they imagine themselves in the situation in question). A participant with a very good memory, for instance, may decide to stand by her previous knowledge claim in STAKES even after she reduces her probability estimate. The initial probability estimate may have been high enough so that even the lowered estimate remains above the threshold for knowledge.
4.3.2 Evidence-Seeking Studies
So much for stakes effects on retraction. Let us turn to stakes effects in evidence seeking studies, this time focusing on the typo cases. The basic account here is the same as before in the case of retraction studies, but some crucial differences remain.
In the typo studies, participants estimate the number of rounds of proofreading required before Peter knows that there are no typos in the paper anymore. Given the indicated threshold principle for knowledge, this means that they thereby estimate how many reads are required to surpass the probability threshold for knowledge.
The number of reads required to surpass the probability threshold for knowledge is an uncertain quantity. Participants presumably do not know exactly how many times a paper has to be proofread before a given probability level is reached. The number of required reads will depend e.g. on how good a proofreader Peter happens to be and on how likely we are in general to miss a typo on any given round.
As before, under- and overestimations of the number of required reads are associated with losses due to the decision that has to be made about when to submit the paper. Peter has to make a decision on when to submit the paper. Participants plausibly picture themselves as advisers whose estimate is going to be used as a basis for this decision. Potential losses for under- and overestimation result from potentially bad decisions on Peter’s part.Footnote 11
Notice the difference to the loss function account as applied to retraction studies. In retraction studies, participants imagine a situation where they have to make a decision themselves. This decision induces loss functions because it depends on the relevant estimate. In evidence-seeking studies, participants imagine a situation in which somebody else (Peter) has to make a decision. The loss function exists because this other person is expected (or at least suspected) to act on their estimate and because participants thus feel responsible if this third party makes an unwise decision. The situation here is similar to the RAF study above, where the subsequent decision of the RAF induced the relevant loss functions.
As in the case of retraction studies, there are differences in loss functions between conditions. Consider the low stakes typo case. As in the low stakes version of the bank cases, losses seem roughly symmetric. If participants underestimate the number of reads required for reaching a given level of probability, Peter potentially becomes overconfident as a result and reads the paper less frequently than he has to. Meanwhile, overestimation potentially leads to under-confidence and unnecessary rounds of proofreading. Neither outcome is particularly problematic. Consider the high stakes typo case. Here the loss function is strongly asymmetric, as in the high stakes version of the bank cases. Underestimation increases the risk of premature submission with all the horrible consequences this is supposed to have. Overestimation only leads to unnecessary rounds of proofreading, as before.
Given the sensitivity to loss functions, participants should choose higher estimates for the number of reads required for knowledge-level probability in the high stakes rather than the low stakes condition. After all, they will want to avoid the high costs of underestimation. This should lead to higher estimates for the number of reads required for knowledge via the threshold principle i.e. it should lead to the stakes effects we observe.
Again, we can ask whether the low stakes or the high stakes estimate is correct. As before, my account does not entail commitments here. If we want to endorse one or the other estimate, we should presumably endorse the estimate from the low stakes case featuring roughly symmetric loss. As indicated, asymmetric loss functions tend to lead people to offer estimates that do not correspond to the estimate that is most likely to be correct from their perspective. Judgements are skewed in accordance with the loss function. Such skewed judgements presumably are a poor guide to what knowledge actually requires.
4.4 Advantages of the Loss Function Account
A number of additional findings support the suggested loss function account, while putting pressure on alternative views.
First, stakes effects remain in evidence-seeking studies when it is stipulated that Peter believes that the paper is free of typos (Pinillos 2012: 203). The loss function account easily explains this. People no longer want to ascribe knowledge when the stakes are high because they no longer estimate that the target proposition is probable enough on Peter’s evidence. This may entail that Peter should be less confident. But even if he retains his confidence, he will be taken to lack knowledge because the probability threshold for knowledge is not perceived to be surpassed.
Second, stakes effects remain when it is stipulated that Peter is unaware of what is at stake (Pinillos 2012: 202–203). The loss function account explains that too. Estimates of probability are skewed when the stakes are high because participants perceive underestimations as very costly. And they do so because they know about the high stakes. Whether Peter knows about the stakes is irrelevant.
On both of these counts, the loss function account is better off than familiar accounts that trade on the belief condition on knowledge (e.g. Weatherson 2005; Nagel 2008; Gao 2019). On these views, Peter’s confidence is shaken when the stakes rise, and he supposedly loses knowledge because knowledge entails confidence (or belief or some other relevant psychological state). Special pleading is required to explain why stakes effects remain when it is stipulated that Peter is confident enough or that he is unaware of what is at stake (though see e.g. Nagel 2008 for ways to go; but see also Dinges 2018).
Third, stakes effects remain when the familiar knowledge prompt is presented next to a question about what Peter should do in order to highlight the distinction between questions about knowledge and questions about actionability (Pinillos 2012: 203–204). Again, the loss function account explains this. For it does not say that participants in evidence-seeking studies implicitly answer any other question than the question they are being asked. On the loss function account, shifted judgements result from the fact that participants face different loss functions when it comes to the very question of when Peter has knowledge.
Here, the loss function account is superior to views whereby knowledge judgements are heuristically processed as actionability judgements (Gerken 2017), or where they are pragmatically reinterpreted along these lines (e.g. Rysiew 2001; Brown 2006). Special pleading is required on these views to explain why stakes effects remain when we focus participants on knowledge rather than action (see Pinillos 2012: 203–204 for this point).
Finally, the loss function account straightforwardly predicts time constraint effects, i.e. the finding that we become more inclined to ascribe knowledge when time is running low (Shin 2014). When time is running low, it becomes costly to underestimate your epistemic standing because if you underestimate your epistemic standing, you will waste your precious time collecting unnecessary evidence. This leads to higher estimates, via loss function sensitivity, and thus to an increased willingness to ascribe knowledge, in line with the data (see Shin 2014: 166–177 for how time constraint effects may put pressure on some alternative views).
To be sure, the loss function account is not the only account that makes straightforward sense of this data. Standard versions of pragmatic encroachment, for instance, make relevantly similar predictions, and the same goes for contextualism and relativism. These revisionary views, however, face familiar, independent concerns. Contextualists, for instance, have trouble explaining intuitions about when speakers disagree (see e.g. Khoo 2017 for an overview of this debate) and pragmatic encroachment validates awkward counterfactuals such as “Peter knows there are no typos, but he wouldn’t know this if the stakes were higher” (e.g. Dimmock 2018). Relativism will be too radical for many people anyway, but it also faces direct concerns (e.g. Dinges 2020). The loss function account faces none of these problems because it is compatible with the denial of contextualism, relativism and pragmatic encroachment. The subsequently reported study strengthens the case for the loss function account even further.
5 Study
This study aims to confirm stakes effects on estimates of evidential probability in an evidence-seeking design.Footnote 12 It thereby aims to confirm a key prediction of the loss function account while challenging alternative positions. The loss function account crucially predicts stakes effects on estimates of evidential probability. For on this account, knowledge judgements vary with stakes because participants’ estimates of probability vary. Meanwhile, such effects would be unexpected on many alternative accounts of stakes effects. On the standard version of pragmatic encroachment from above, for instance, knowledge judgements shift because the evidential threshold for knowledge shifts. The estimated probability remains constant throughout.
Gerken’s (2017) heuristic proxy account is exceptional in that it naturally predicts stakes effects on estimates of evidential probability. On Gerken’s view, knowledge judgements serve as “heuristic proxies” for actionability judgements because knowledge and actionability normally align (143). As a consequence, the story goes, participants in e.g. evidence-seeking studies assess the question of when Peter knows his paper is free of typos by assessing the question of when he should submit it. Stakes effects supposedly arise because actionability is sensitive to stakes. This account naturally extends to probability judgements. One could hold that e.g. 90 percent evidential probability normally tracks actionability too and hence that actionability judgements continue to serve as heuristic proxies.
To derive a testable prediction, notice that it seems implausible that both 90 percent probability and, say, 70 percent probability equally serve as heuristic proxies for actionability. Indeed, 70 percent probability presumably does not normally suffice for actionability. Hence, it should not serve as a heuristic proxy for actionability at all. We should thus expect no stakes effects for 70 percent probability, or at least the percentage level should affect the strength of the stakes effects we observe. Statistically, the heuristic proxy account predicts an interaction between variations in stakes and probability levels. The study below tests this interaction hypothesis in addition to the already indicated prediction about stakes effects on estimates of evidential probability. The loss function account predicts no such interaction, for participants face asymmetric loss functions at each level of probability in that e.g. underestimations may lead to premature submission, which is very costly only when the stakes are high.Footnote 13
5.1 Method
120 participants were recruited through Prolific Academic (73 % female, mean age 35). Each participant was randomly assigned to one of four conditions in a 2x2 design. The first variable was whether participants read the low stakes or the high stakes version of the typo cases cited above. The second variable was whether participant received the 90 percent version or the 70 percent version of the following question. “How many times does Peter have to proofread his paper before you would be [90/70] percent certain that no typos remain? ¶ Please fill in a number.” A number could be entered into a text-box below. After filling in a number, participants moved on to a control question on a new screen. They had to select whether Peter was writing the paper for an English, French or History class. They specified their age and gender and entered their Prolific-ID, before concluding the study.Footnote 14
Notice that the study aimed to test participants’ estimates of the probability of typos on Peter’s evidence. For, variations in these estimates lead to variations in knowledge ascriptions on my account. One strategy to test these estimates would have been to ask about Peter’s confidence after he has read the paper so-and-so many times. I did not choose this strategy, as seen in the prompt above. Responses would have tracked participants’ estimates of Peter’s actual confidence rather than the confidence he should have given his evidence, i.e., the respective evidential probability. These may come apart (see e.g. Gao 2019). Instead, I asked participants about their confidence. This presumably tracks participants’ estimates of evidential probability on their evidence rather than Peter’s. This seemed unproblematic though because these bodies of evidence seem to align in relevant respects. The part of Peter’s evidence that bears on the probability of remaining typos presumably is that he has read the paper so-and-so many times and eliminated all typos he found. Study participants presumably take themselves to share this evidence when they respond to the prompt above.
5.2 Results
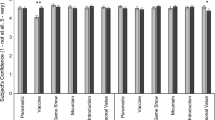
8 participants failed the attention check, and they were thus excluded from the subsequent analysis. I further excluded three extreme outliers: one participant in the low-stakes-90-percent condition who had answered 65, and two participants in high-stakes-70-percent condition who had respectively answered 50 and 70 (Fig. 3). These responses just did not make sense assuming that participants understood the task at hand, for recall that Peter’s paper only has two pages, that he is a pretty good speller and has a dictionary with him.Footnote 15 Admittedly, the responses are understandable if we think of the respondents as extreme skeptics, who think that you can never be certain of anything to any degree. Even so, we should exclude their responses because the specified number would be an arbitrary placeholder for their actual response, which is that the relevant level of certainty is unreachable (Francis et al. 2019: 444 independently confirm such “never” responses and analyze them separately).
Mean responses for the remaining participants are shown in Table 1 and Fig. 4.
A two-way ANOVA was used to determine the effect of stakes and probability levels on rounds of proofreading. A significant main effect of stakes was observed, F(1, 105) = 21.569, p < .001, ηp2 = .17, such that high stakes participants required more rounds of proofreading (M = 4.13, SD = 2.96) than low stakes participants (M = 2.19, SD = 1.03). There was also a significant main effect of probability level, F(1, 105) = 5.94, p = .017, ηp2 = .054, such that participants in the 90-percent condition required more rounds of proofreading (M = 3.7, SD = 2.83) than participants in the 70-percent condition (M = 2.64, SD = 1.82). There was no significant interaction, F(1, 105) = 2.84, p = .10.Footnote 16
5.3 Discussion
When the stakes are high, people require more rounds of proofreading before judging that a given probability threshold is reached. This was the prediction of the loss function account, and it is borne out by the data. We saw that the heuristic proxy account can be spelled out such that it makes similar predictions. On this view, however, we would expect an interaction between stakes and probability level because lower probabilities have a weaker connection to actionability. No such interaction was observed. Finally, the number of required reads was lower in the 70-percent condition than in the 90-percent condition. This result is unsurprising on any account, but it confirms the proper function of my study design.
Admittedly, the results go somewhat in the direction of the heuristic proxy account in that the means in the 70-percent condition look closer together than the means in the 90-percent condition (Fig. 4). This warrants replication with more statistical power. One should keep in mind though that it is unclear why, at the 70 percent level, the heuristic proxy account should predict any stakes effect at all. A stakes effect at this level is already evidence against this view. One should also heed the possibility of a floor effect, whereby participants cannot go lower than 0 (or maybe 1, if they accommodate a pertinent presupposition). To support the heuristic proxy account, one will have to show that any interaction observed is not just due to this lower bound of the scale.
6 Conclusion
I have offered a novel account of stakes effects on knowledge ascriptions. On this view, stakes effects arise because participants in high stakes conditions face asymmetric loss functions, which makes it rational for them to adjust their responses, thus becoming less inclined to ascribe knowledge. If the account goes through, revisionary views like contextualism, relativism and pragmatic encroachment are not required to make sense of the data. Moreover, we can straightforwardly accommodate a wide range of otherwise recalcitrant findings about e.g. ignorant stakes cases, cases stipulating belief and time constraints. I have also confirmed one major prediction of the loss function account, namely, that estimates of evidential probability are stakes-sensitive in the relevant cases. This result puts further pressure on many alternative views, where such an effect is unexpected.
Notes
My notion of an estimate is closely linked to the notion of a guess as discussed e.g. in Horowitz 2019, Builes et al. 2020 and Dorst and Mandelkern forthcoming. Dorst and Mandelkern (forthcoming) also use this notion to explain recalcitrant findings from cognitive psychology, and my proposal can be seen as a continuation of their general project to identify guesses as a central explanatory notion. See also Kukla 2015 for ideas that are similar in spirit to mine, in particular, the idea of connecting stakes effects with broader debates about risk in the philosophy of science.
Buckwalter and Schaffer (2015: 214) and Rose et al. (2019: 240) worry that the above prompt is unsuited to detect stakes effects on knowledge ascriptions. Instead, they hold, we are seeing stakes effects on the modal “has to,” which allegedly receives a deontic interpretation. Pinillos and Simpson (2014: 19), Francis et al. (2019: 449) and Dinges (2020: 4) rebut this concern by confirming stakes effects with various prompts that do not contain relevant modals.
I am not wedded to the idea that the threshold always stays fixed. Maybe it can vary. The point here is that, on my account, this assumption is not required to make sense of stakes effects.
For details on how various types of loss functions affect the most rational estimate, see e.g. Granger 1969; Christoffersen and Diebold 1997 and Patton and Timmermann 2007. These considerations are consistent with the considerations on rational guessing in e.g. Horowitz 2019, Builes et al. 2020 and Dorst and Mandelkern forthcoming, where sensitivity to loss functions does not figure. The latter authors focus on epistemic rationality, while I focus on practical rationality.
Dorst and Mandelkern (forthcoming) argue that even an epistemically rational guess need not align with the answer to which you assign the highest credence.
Dorst and Mandelkern (forthcoming) emphasize the ubiquitous role guesses/estimates play in probabilistic reasoning, which aligns with the idea that they can form the input to decision-making as well.
See also the closely related discussion of guesses in e.g. Horowitz 2019, Builes et al. 2020 and Dorst and Mandelkern forthcoming.
One may worry that even if the evidential probability is uncertain in the bank cases as described, we could easily modify these cases such that the evidential probability is known and stakes effects would remain. I doubt that this is so. It will not do, for instance, to stipulate that the evidential probability of the target proposition is, say, .9, in those terms. Study participants presumably cannot make sense of the semi-technical notion of an evidential probability. It will not do either to fix evidential probabilities by introducing statistical evidence from, for example, a lottery. Such statistical evidence is generally perceived as insufficient for knowledge (e.g. Turri and Friedman 2014), thus participants would presumably deny knowledge in both the low stakes and the high stakes condition, and we would not observe stakes effects anymore.
This holds similarly for other epistemic qualities like safety or reliability if, as seems plausible, estimates of these qualities also bear on the decisions we make. I may even be able to jettison the entire appeal to evidential probability and related epistemic quantities if decision-making depends directly on what we know (see e.g. Weisberg 2013 for discussion). In that case, subsequent decisions may directly induce loss functions on our estimates about knowledge with “overestimation,” i.e. estimating that you know when you don’t, bearing different costs than “underestimation,” i.e. estimating that you don’t know when you do. Thanks to Patricia Rich.
The remarks from footnote 10 apply mutatis mutandis.
So-called “total pragmatic encroachment” seems to be the only view in the literature that shares all predictions with the loss function account here. But, first, this view faces all the problems that any form of pragmatic encroachment faces (see above) and more (e.g. Ichikawa et al. 2012: 333–336; Rubin 2015). Second, an account of the data below in terms of total pragmatic encroachment would leave the parallels to the general effects of loss functions unexplained. Loss functions affect our estimates of any uncertain quantity, including e.g. Pitt’s age. But surely there is no pragmatic encroachment on this latter quantity.
One could have chosen an even lower threshold of, say, 50 percent rather than 70 percent. But, first, and as indicated, 70 percent should be low enough for my purposes because 70 percent probability does not generally suffice for actionability (even if it sometimes does) and only such a general connection would warrant Gerken’s heuristic proxy account. Second, a lower threshold might create unwanted floor effects. We might fail to see a stakes effects in a 50 percent condition only because participants in the high stakes condition think that 0 rounds of proofreading suffice, and participants in the low stakes condition cannot go lower than that. I still grant that it would be worthwhile to try out lower thresholds in future studies.
Notice also that the participant who had answered 50 in the 70-percent condition was the only participant who had entered an incomplete Prolific-ID, which was independently suspicious. The other answer in the 70-percent condition was exactly 70, which seems like a curious coincidence too.
A complete data set is available at https://osf.io/qknmh/?view_only=6001afa3de4e44baa438ed936d9b38d0.
References
Brown, Jessica. 2006. Contextualism and warranted assertibility manoeuvres. Philosophical Studies 130 (3): 407–435.
Brown, Jessica. 2018. Fallibilism: Evidence and Knowledge. Oxford: Oxford University Press.
Buckwalter, Wesley. 2010. Knowledge isn’t closed on Saturday. A study in ordinary language. Review of Philosophy and Psychology 1 (3): 395–406.
Brown, Jessica. 2014. The mystery of stakes and error in ascriber intuitions. In Advances in Experimental Epistemology, ed. J.R. Beebe, 145–173. New York, NY: Bloomsbury Publishing.
Buckwalter, Wesley, and Jonathan Schaffer. 2015. Knowledge, stakes, and mistakes. Noûs 49 (2): 201–234.
Builes, David; Sophie Horowitz and Miriam Schoenfield (2020), “Dilating and contracting arbitrarily”, Noûs, Early View.
Christoffersen, Peter F., and Francis X. Diebold. 1997. Optimal prediction under asymmetric loss. Econometric Theory 13 (6): 808–817.
Cohen, Stewart. 2008. Ascriber contextualism. In The Oxford Handbook of Skepticism, ed. J. Greco, 415–436. Oxford: Oxford University Press.
DeRose, Keith. 1995. Solving the skeptical problem. The Philosophical Review 104 (1): 1–52.
DeRose, Keith (2009), The Case for Contextualism (Knowledge, Skepticism, and Context, 1, Oxford: Oxford University Press).
Dimmock, Paul. 2018. Strange-but-true. A (quick) new argument for contextualism about ‘know’. Philosophical Studies 175 (8): 2005–2015.
Dinges, A. 2020. Relativism and conservatism. Erkenntnis 85 (4): 757–772.
Dinges, Alexander. 2018. Anti-intellectualism, egocentrism and bank case intuitions. Philosophical Studies 175 (11): 2841–2857.
Dinges, Alexander (2020), “Knowledge and non-traditional factors. Prospects for doxastic accounts”, Synthese.
Dinges, Alexander and Julia Zakkou (2020), “Much at stake in knowledge”, Mind & Language, Early View: 1–21.
Dorst, Kevin and Matthew Mandelkern (forthcoming), “Good guesses”, Philosophy and Phenomenological Research.
Fantl, Jeremy and Matthew McGrath (2002), “Evidence, pragmatics, and justification”, The Philosophical Review, 111/1: 67–94.
Fantl, Jeremy, and Matthew McGrath. 2009. Knowledge in an Uncertain World. Oxford: Oxford University Press.
Francis, Kathryn B., Philip Beaman, and Nat Hansen. 2019. Stakes, scales, and skepticism. Ergo 6 (16): 427–487.
Gao, Jie. 2019. Credal pragmatism. Philosophical Studies 176 (6): 1595–1617.
Gerken, Mikkel. 2017. On Folk Epistemology: How We Think and Talk about Knowledge. Oxford: Oxford University Press.
Granger, C. W. J. (1969), “Prediction with a generalized cost of error function”, OR, 20/2: 199.
Harris, Adam J. L. and Adam Corner (2011), “Communicating environmental risks. Clarifying the severity effect in interpretations of verbal probability expressions”, Journal of Experimental Psychology: Learning, Memory, and Cognition, 37/6: 1571–1578.
Harris, Adam J.L., Adam Corner, and Ulrike Hahn. 2009. Estimating the probability of negative events. Cognition 110 (1): 51–64.
Harris, Adam J.L., Laura de Molière, Melinda Soh, et al. 2017. Unrealistic comparative optimism. An unsuccessful search for evidence of a genuinely motivational bias. PloS one 12 (3): 1–35.
Hawthorne, John. 2004. Knowledge and Lotteries. Oxford: Oxford University Press.
Horowitz, Sophie. 2019. Accuracy and educated guesses. In Oxford Studies in Epistemology, volume 6, ed. T. Szabó Gendler and J. Hawthorne, 85–113. Oxford: Oxford University Press.
Ichikawa, Jonathan Jenkins, Benjamin Jarvis, and Katherine Rubin. 2012. Pragmatic encroachment and belief-desire psychology. Analytic Philosophy 53 (4): 327–343.
Khoo, Justin (2017), “The disagreement challenge to contextualism”, in J. J. Ichikawa (ed.), The Routledge Handbook of Epistemic Contextualism (New York, NY: Routledge).
Kukla, Rebecca. 2015. Delimiting the proper scope of epistemology. Philosophical Perspectives 29 (1): 202–216.
MacFarlane, John. 2014. Assessment Sensitivity: Relative Truth and its Applications. Oxford: Oxford University Press.
Nagel, Jennifer. 2008. Knowledge ascriptions and the psychological consequences of changing stakes. Australasian Journal of Philosophy 86 (2): 279–294.
Patton, Andrew J., and Allan Timmermann. 2007. Properties of optimal forecasts under asymmetric loss and nonlinearity. Journal of Econometrics 140 (2): 884–918.
Pinillos, Nestor Ángel. 2012. Knowledge, experiments and practical interests. In Knowledge Ascriptions, ed. J. Brown and M. Gerken, 192–219. Oxford: Oxford University Press.
Pinillos, Nestor Ángel, and Shawn Simpson. 2014. Experimental evidence supporting anti-intellectualism about knowledge. In Advances in Experimental Epistemology, ed. J.R. Beebe, 9–44. New York, NY: Bloomsbury Publishing.
Rose, David, Edouard Machery, Stephen Stich, et al. 2019. Nothing at stake in knowledge. Noûs 53 (1): 224–247.
Rubin, Katherine. 2015. Total pragmatic encroachment and epistemic permissiveness. Pacific Philosophical Quarterly 96 (1): 12–38.
Rysiew, Patrick. 2001. The context-sensitivity of knowledge attributions. Noûs 35 (4): 477–514.
Shin, Joseph. 2014. Time constraints and pragmatic encroachment on knowledge. Episteme 11 (2): 157–180.
Sosa, Ernest. 2000. Skepticism and contextualism. Philosophical Issues 10 (1): 1–18.
Sripada, Chandra Sekhar, and Jason Stanley. 2012. Empirical tests of interest-relative invariantism. Episteme 9 (1): 3–26.
Stanley, Jason (2005), Knowledge and Practical Interests (Short Philosophical Books, Oxford: Oxford University Press).
Turri, John. 2017. Epistemic contextualism. An idle hypothesis. Australasian Journal of Philosophy 95 (1): 141–156.
Turri, John, and Wesley Buckwalter. 2017. Descartes’s schism, Locke’s reunion. Completing the pragmatic turn in epistemology. American Philosophical Quarterly 54 (1): 25–46.
Turri, John, Wesley Buckwalter, and David Rose. 2016. Actionability judgments cause knowledge judgments. Thought: A Journal of Philosophy 5 (3): 212–222.
Turri, John, and Ori Friedman. 2014. Winners and loosers in the folk epistemology of lotteries. In Advances in Experimental Epistemology, ed. J.R. Beebe, 45–69. New York, NY: Bloomsbury Publishing.
Weatherson, Brian. 2005. Can we do without pragmatic encroachment? Philosophical Perspectives 19 (1): 417–443.
Weatherson, Brian. 2017. Interest-relative invariantism. In The Routledge Handbook of Epistemic Contextualism, ed. J.J. Ichikawa, 240–254. New York, NY: Routledge.
Weber, Elke U. 1994. From subjective probabilities to decision weights. The effect of asymmetric loss functions on the evaluation of uncertain outcomes and events. Psychological Bulletin 115 (2): 228–242.
Weisberg, Jonathan. 2013. Knowledge in action. Philosophers’ Imprint 22: 1–23.
Wright, Crispin. 2017. The variability of ‘knows’. An opinionated overview. In The Routledge Handbook of Epistemic Contextualism, ed. J.J. Ichikawa, 13–31. New York, NY: Routledge.
Acknowledgements
I am grateful to Adam Harris, Julia Zakkou, two anonymous reviewers and an editor for helpful comments on the paper and to audiences in Bochum, Frankfurt a.M., Berlin, Hamburg, Odense, Peking and Regensburg for illuminating Q&As. This project was funded by the German Research Foundation (DI 2172/1-1).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dinges, A. Knowledge and Asymmetric Loss. Rev.Phil.Psych. 14, 1055–1076 (2023). https://doi.org/10.1007/s13164-021-00596-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13164-021-00596-9