Numerical computation of blood flow for a patient-specific hemodialysis shunt model

Abstract

Hemodialysis procedure is usually advisable for end-stage renal disease patients. This study is aimed at computational investigation of hemodynamical characteristics in three-dimensional arteriovenous shunt for hemodialysis, for which computed tomography scanning and phase-contrast magnetic resonance imaging are used. Several hemodynamical characteristics are presented and discussed depending on the patient-specific morphology and flow conditions including regurgitating flow from the distal artery caused by the construction of the arteriovenous shunt. A simple backflow prevention technique at an outflow boundary is presented, with stabilized finite element approaches for incompressible Navier–Stokes equations.

1 Introduction

Over the last decades, end-stage renal disease (ESRD) has emerged as a severe clinical difficulty leading to high rates of morbidity [1, 2]. The condition of ESRD is associated with impaired kidney function for which hemodialysis procedures are strongly advisable [3]. Such procedures require well-functioning vascular access placed between an artery and a vein, which is known as arteriovenous shunt. Brescia et al. [4] surgically introduced the use of arteriovenous shunt for hemodialysis in 1966. Morphologies of anastomotic sites play a vital role in efficient shunt operation. They are also responsible for altering hemodynamic forces, as discussed in the literature [5,6,7]. Indeed, with these clinical advancements, some underlying issues remain, such as the existence of intimal hyperplasia to the artery, stenosis development, and insufficient flow occurrence after remodeling, which are related to high longevity of vascular access, as described in clinical studies [8,9,10,11]. These phenomena occur because strong arterial blood flow dynamics affect vein flow directly, which alters the vein hemodynamics dramatically. To maintain arteriovenous shunt functions, elucidation of blood flow fields through them and fluid dynamical forces exerted on the vessel walls are strongly required.

Numerous experimental and computational studies have elucidated the flow dynamics within shunt models [12,13,14,15]. However, because of the large variety of actual shunt morphologies among individual patients, physical experiments using phantoms have presented some difficulties. Patient-specific computational simulation is expected to play an important role in assessment and planning for surgical shunt placements by elucidating complex flow dynamics and wall shear stress (WSS) distributions using medical imaging technologies such as magnetic resonance imaging (MRI) and computed tomography (CT). Browne et al. [16] presented a comparative study designed to observe the mean pressure drop across arteriovenous shunts in physical experiments and computational simulations. Other studies [17,18,19] have presented extensive information about arteriovenous shunt related blood flows.

This study was conducted to investigate a physiological flow in an arteriovenous shunt using patient-specific CT scan data for vessel morphology and corresponding phase-contrast MRI (PC-MRI) data for velocity boundary conditions. The patient case targeted in this study has two characteristics from physiological points of view. The first is that regurgitation occurs in a certain time period from the distal artery, which strongly affects flow behavior near the anastomotic site. Second is that the anastomotic site has three-dimensionally complex morphology because of constraints in surgery. These characteristics engender several difficulties for computation, but provide new insights into medical practices. Although several studies [12,13,14,15,16,17,18,19] have presented extensive information about blood flows for arteriovenous shunts, a class of patient cases with complex morphologies and flow conditions has apparently been only insufficiently investigated. Therefore, the novelty of this paper is presentation of detailed flow behaviors, especially for three-dimensionally complex morphology of anastomotic site and a flow condition with direction change caused by physiological regurgitation.

In simulating blood flows in complicated vessel geometries, unphysical backflows frequently occur numerically, as reported from several studies [20, 21]. These phenomena arise in several situations such as occurrences of vortical structures, local flow separations, and widening of the cross-sectional area near outlets. Bazilevs et al. [22] and Moghadam et al. [23] presented outflow boundary conditions to prevent backflows and performed a comparative study of various types of outflow boundary conditions. Because such outflow boundary conditions require consideration from mathematical analysis perspectives, Saito et al. [24], and Zhou and Saito [25] have explained well-posedness and energy inequality of the outflow boundary conditions of Signorini’s type for incompressible Navier–Stokes equations. They also proved the existence of a unique solution for Galerkin method with outflow boundary conditions. As described in this paper, we present another type of backflow prevention technique by giving an external force near the outflow boundary without affecting the inner region. It is noteworthy that the unphysical backflow from the outflow boundary is attributable to numerical instability, whereas the regurgitating flow from the distal artery represents a physiological phenomenon.

The remainder of the paper is presented as follows. Section 2 presents governing equations, model construction using medical imaging data, stabilized finite element formulation and backflow prevention technique. Section 3 explains the results and presents some discussion. Section 4 concludes this study.

2 Materials and methods

2.1 Patient data

This study, which was conducted in accordance with the Declaration of Helsinki, was approved by the institutional review boards (IRBs) at Akashi Medical Center Hospital (#2020-12) and Tohoku University School of Medicine (#2020-1-511). The solid surface of shunt geometry is extracted from CT scan data of a hemodialysis patient in digital imaging and communications in medicine (DICOM) format.

Fig. 1

Extracted shunt model with an anastomotic site

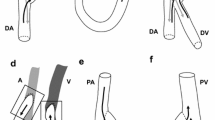
Figure 1 portrays the configuration of an arteriovenous shunt: the target of this study. During the surgery conducted for this patient case, artery-side-to-end-vein anastomosis [26] was performed between the side of the radial artery and the end of the cephalic vein in the wrist area. This configuration consists of three parts connected at the anastomotic site presented in Fig. 1: the proximal artery (PA), distal artery (DA), and distal vein (DV). Therefore, three boundaries, $\varGamma _{\mathrm{PA}}$, $\varGamma _{\mathrm{DA}}$, and $\varGamma _{\mathrm{DV}}$, are included in our configuration in addition to the vessel wall boundary $\varGamma _{\mathrm{wall}}$. Here, the direction vectors of centerlines of three vessels PA, DA, and DV cannot be laid on one flat plane, reflecting the special three-dimensional feature of the morphology of this patient’s case.

2.2 Governing equations and model configurations

Let $\varOmega \times \left( 0,T\right) \subset {{\mathbf{R}}}^{n_{\mathrm{sd}}}\times \left( 0,T\right)$ be the space-time domain, where $\varGamma$ = $\varGamma _{\mathrm{PA}} \cup \varGamma _{\mathrm{DA}} \cup \varGamma _{\mathrm{DV}} \cup \varGamma _{\mathrm{wall}}$ denotes the domain boundary, and $n_{\mathrm{sd}}=3$ represents the number of space dimensions, we assume that blood behaves as a Newtonian fluid, which is governed by unsteady, incompressible Navier–Stokes equations.

$$\begin{aligned} { \rho \, \left( {{\mathbf{u}}}_{,t} + {{\mathbf{u}}} \cdot \nabla {{\mathbf{u}}} \right) - \nabla \cdot {\boldsymbol{\sigma}} } = 0 \quad \text{in} \ \varOmega \times \left( 0,T\right) , \end{aligned}$$

(1)

$$\begin{aligned} \nabla \cdot {{\mathbf{u}}} = 0 \quad \text{in} \ \varOmega \times \left( 0,T\right) , \end{aligned}$$

(2)

$$\begin{aligned} {{\mathbf{u}}} = {\mathbf{g}} \quad \text{on} \ \varGamma _{g}\times \left( 0,T\right) , \end{aligned}$$

(3)

$$\begin{aligned} {{\boldsymbol{\sigma}} \cdot {\mathbf{n}} = {\mathbf{h}} } \quad \text{on} \ \varGamma _{h}\times \left( 0,T\right) , \end{aligned}$$

(4)

$$\begin{aligned} {{\mathbf{u}}}\left( {\mathbf{x}}, 0\right) = {{\mathbf{u}}}_0 \quad \text{on} \ \varOmega \times \{0\}, \end{aligned}$$

(5)

where $\rho$, ${{\mathbf{u}}}$, and ${\mathbf{n}}$ respectively denote the density, velocity vector, and the unit outward normal vector on the boundary $\varGamma$, and ${\boldsymbol{\sigma}\left( \mathbf{u}, p \right)} = \big ( - p\,{\mathbf{I}} + 2\,\mu \,{\boldsymbol{\epsilon}} \left( {{\mathbf{u}}}\right) \big )$ is the stress tensor. Here p, ${\mathbf{I}}$, and $\mu$ are the pressure, identity tensor, and blood viscosity respectively. Also, ${\boldsymbol{\epsilon}} \left( {{\mathbf{u}}} \right) = \frac{1}{2} \left( \nabla \,{{\mathbf{u}}} + \left( \nabla \,{{\mathbf{u}}}\right) ^{T} \right)$ is the strain-rate tensor. Stress ${\boldsymbol{\sigma}}$ in the matrix form is expressed as $\sigma _{ij} = \left( -p\,\delta _{ij} + \mu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \right)$ for $i,j = 1, 2, 3$ with the Kronecker delta $\delta _{ij}$. Here, $\sigma _{ij}$ is symmetric, which implies that $\sigma _{ij} = \sigma _{ji}$. Boundary conditions (3) and (4) respectively represent the typical form of the essential and natural boundary conditions defined on $\varGamma _g$ and $\varGamma _h$ with the given functions g and h. Divergence free velocity vector ${\mathbf{u}} _0$ is given as an initial condition. In this study, $\varGamma _g$ = $\varGamma _{\mathrm{wall}} \cup \varGamma _{\mathrm{PA}} \cup \varGamma _{\mathrm{DA}}$ is a disjoint union of the vessel wall and the inlet or outlet boundaries. Also, $\varGamma _{\mathrm{DV}}$ is set as $\varGamma _h$ defined in (4). The vessel wall is assumed to be rigid. Therefore, a no-slip condition ${\mathbf{g}} = {\mathbf{0}}$ is applied on $\varGamma _{\mathrm{wall}}$ in (3).

2.3 Stabilized finite element formulation

Numerical solutions of (1)–(5) with complex geometries are obtainable using Galerkin finite element methods. However, such formulations are often associated with potential numerical instabilities [27]. Tezduyar et al. [28, 29] proposed stabilized finite element formulations for incompressible fluid flows. This formulation also allows for equal-order polynomial approximation for velocity–pressure variables.

For discretizing (1)–(5), we used the streamline upwind Petrov–Galerkin (SUPG) and pressure stabilizing Petrov–Galerkin (PSPG) methods [28, 29]. Spatial domain $\varOmega$ is discretized into the elements $\varOmega _e,\,e=1,2,\ldots ,n_{\mathrm{el}}$, where $n_{\mathrm{el}}$ represents the number of elements. Let $S_u^h$, $V_u^h$ be trial and test function spaces for velocity and $S_p^h$, $V_p^h$ for pressure, expressed as

$$\begin{aligned} S_u^h= \{{{\mathbf{u}}}^h \mid {{\mathbf{u}}}^h \in (X^h)^{n_{\mathrm{sd}}}, \quad {{\mathbf{u}}}^h = {\mathbf{g}}^h \text{ on } \varGamma _g \}, \end{aligned}$$

(6)

$$\begin{aligned} V_u^h= \{ {\mathbf{w}}^h \mid {\mathbf{w}}^h \in (X^h)^{n_{\mathrm{sd}}},\quad {\mathbf{w}}^h = 0 \text{ on } \varGamma _g \}, \end{aligned}$$

(7)

$$\begin{aligned} S_p^h= V_p^h = \{ {q}^h \mid {q}^h \in (X^h)^{n_{\mathrm{sd}}} \}, \end{aligned}$$

(8)

$$\begin{aligned} X^h= \{ \phi \mid \phi \in C^0\left( {\overline{\varOmega }}\right) ,\, \phi |_{\varOmega _e} \in P^1, \, \forall \, e \}, \end{aligned}$$

(9)

where $P^1$ stands for the set of first-order polynomials in space. The stabilized finite element formulation of (1)–(5) with the stabilization parameter $\tau$ is given below.

Find ${{\mathbf{u}}}^h \in S_u^h$ and $p^h \in S_p^h$ such that $\forall \,\, {\mathbf{w}}^h \in V_u^h \,\, \text{ and } \,\, \forall q^h \in V_p^h$:

$$\begin{aligned}&{\int _{\varOmega }{{\mathbf{w}}^h \cdot \rho \,\left(\partial _t {{\mathbf{u}}}^h + \overline{{{\mathbf{u}}}}^h \cdot \nabla {{\mathbf{u}}}^h \right) }d\varOmega + \int _{\varOmega }{\boldsymbol{\epsilon}\left({\mathbf{w}}^h \right) : \boldsymbol{\sigma}{\left({\mathbf{u}}^h, p^h\right)}} d\varOmega - \int_{\varGamma_h}{{\mathbf{w}}^h \cdot \mathbf{{h}}^h} d\varGamma } \\&\quad {+ \sum _{e=1}^{n_{\mathrm{el}}}{\int _{\varOmega _e}{ \tau \left( \overline{{{\mathbf{u}}}}^h \cdot \nabla {\mathbf{w}}^h \right) \left(\rho \left(\partial _t {{\mathbf{u}}}^h + \overline{{{\mathbf{u}}}}^h\cdot \nabla {{\mathbf{u}}}^h \right) - \nabla \cdot {\boldsymbol{{\sigma}}{\left({\mathbf{{u}}^h}, p^h \right)} } \right)} d\varOmega }} = 0, \end{aligned}$$

(10)

$$\begin{aligned}&\int _{\varOmega }{q^h \nabla \cdot {{\mathbf{u}}}^h}d\varOmega + { \sum _{e=1}^{n_{\mathrm{el}}}{\int _{\varOmega _e}{ \tau \,\left( \frac{\nabla q^h}{\rho }\right) \left(\rho \left(\partial _t {{\mathbf{u}}}^h + \overline{{{\mathbf{u}}}}^h\cdot \nabla {{\mathbf{u}}}^h \right) - \nabla \cdot {\boldsymbol{\sigma}{\left( {\mathbf{u}^h, p^h}\right)}} \right)} d\varOmega }} = 0. \end{aligned}$$

(11)

The advection velocity is represented by $\overline{{{\mathbf{u}}}}$ in (10) and (11). These equations are rewritten in the form of

$$\begin{aligned}A({\mathbf{w}}^{h}, {{\mathbf{u}}}^{h}) + B({\mathbf{w}}^{h}, p^h) + S_{\tau }({\mathbf{w}}^h, {{\mathbf{u}}}^h, p^h) = 0, \end{aligned}$$

(12)

$$\begin{aligned} B({{\mathbf{u}}}^h, q^h) + P_{\tau }({{\mathbf{u}}}^h, q^h, p^h) = 0. \end{aligned}$$

(13)

The space discretization of (12) and (13) leads to the following system of ordinary differential equations.

$$\begin{aligned} \left( M + M_S \right) \frac{ d{{\mathbf{u}}}^h}{ dt} + { \left( C(\overline{{{\mathbf{u}}}}^h) + C_S(\overline{{{\mathbf{u}}}}^h) \right) {{\mathbf{u}}}^h} + \left( D + D_S \right) {{\mathbf{u}}}^h - \left( G - G_S \right) p^h = F + F_S, \end{aligned}$$

(14)

$$\begin{aligned} G^T {{\mathbf{u}}}^h + M_P\frac{ d{{\mathbf{u}}}^h}{ dt} + { C_P \left( \overline{{{\mathbf{u}}}}^h\right) {{\mathbf{u}}}^h + D_P\, {{\mathbf{u}}}^h + G_P \,p^h} = E + E_P. \end{aligned}$$

(15)

Therein, matrices M, C, D, and G respectively correspond to acceleration, convection, diffusion, and pressure gradient terms. Vectors F and E are related to the boundary conditions. Subscripts S and P respectively stand for the SUPG and PSPG contributions. Crank–Nicolson method is used for time-discretization of differential equations (14) and (15). Then the advection velocity $\overline{{{\mathbf{u}}}}$ is approximated by the Adams–Bashforth method, which leads to the system of linear equations.

The stabilization parameter $\tau$ for each element is given as [28]

$$\begin{aligned} \tau = \left[ \left( \frac{2}{\varDelta t}\right) ^2 + \left( \frac{2 || \overline{{{\mathbf{u}}}}_e ||}{h_e}\right) ^2 + \left( \frac{4 \,\mu }{\rho \,h_e^2}\right) ^2 \right] ^{-1/2}, \end{aligned}$$

(16)

where $\varDelta t$ and $||\overline{{{\mathbf{u}}}}_e||$ respectively represent the time-step and norm of the advection velocity. The element length $h_e$ of $\varOmega _e$ computed as

$$\begin{aligned} h_e = 2 \left( \sum _{a=1}^{n_{\mathrm {en}}} |{\mathbf{r}}\cdot \nabla N_a |\right) ^{-1}, \end{aligned}$$

(17)

where ${\mathbf{r}}$ is the unit vector in the direction of flow, $n_{\mathrm{en}}$ denotes the number of nodes in an element, and $N_a$ is the basis function corresponds to the node a.

2.4 Method for preventing backflows

In this section, we examine a backflow presence at the outflow boundary and a prevention technique for it. Computational blood flow simulation for complex vessel geometries extracted from realistic medical data mostly yield undesirable instabilities at outflow boundaries. This situation might occur because of a lack of accurate velocity profiles or necessity for setting relevant boundary conditions for these boundaries. We consider a stabilized weak formulation of the governing equation given in Sect. 2.3 with an artificial external force term as shown below.

$$\begin{aligned} A({\mathbf{w}}^h, {{\mathbf{u}}}^h)+B({\mathbf{w}}^h, p^h)+S_{\tau }({\mathbf{w}}^h, {{\mathbf{u}}}^h, p^h)+\varTheta ({{\mathbf{u}}}^h; {\tilde{\varGamma }}_h({{\mathbf{u}}}^h)) = 0, \end{aligned}$$

(18)

$$\begin{aligned} B({{\mathbf{u}}}^h, q^h) + P_{\tau }({{\mathbf{u}}}^h, q^h, p^h) = 0, \end{aligned}$$

(19)

where $\varTheta$ denotes the artificial external force term to account the backflow instability at the outflow boundary ${\varGamma }_h$. For this study, we express this term as a function of the velocity vector,

$$\begin{aligned} \varTheta ({{\mathbf{u}}}^h; {\tilde{\varGamma }}_h({{\mathbf{u}}}^h)) = \beta {\mathbf{1}}_{{\tilde{\varGamma }}_h({{\mathbf{u}}}^h)} {{\mathbf{u}}}^h. \end{aligned}$$

(20)

Here $\beta$ is a positive constant, ${\tilde{\varGamma }}_h\left( {{\mathbf{u}}}^h\right)$ represents a region of backflow near $\varGamma _h$, and ${{\mathbf{1}}}_{{\tilde{\varGamma }}_h\left( {{\mathbf{u}}}^h\right) }$ denotes the indicator function,

$$\begin{aligned} {{\mathbf{1}}}_{{\tilde{\varGamma }}_h\left( {{\mathbf{u}}}^h\right) } = {\left\{ \begin{array}{ll} 1, &{} \text{on }{\tilde{\varGamma }}_h\left( {{\mathbf{u}}}^h\right) ; \\ 0, &{} \text{elsewhere.} \end{array}\right. } \end{aligned}$$

(21)

We choose a union of elements in which the backflow occurs at some boundary node to be ${\tilde{\varGamma }}_h\left( {{\mathbf{u}}}^h\right)$;

$$\begin{aligned} {\tilde{\varGamma }}_h({{\mathbf{u}}}^h) = \bigcup \{ \varOmega _e \mid 1 \le e \le n_{el},\ \exists {\mathbf{x}} \in \varOmega _e \cap \varGamma _h;\quad {{{\mathbf{u}}}^h\left( {\mathbf{x}}\right) \cdot {\mathbf{n}} < 0} \}. \end{aligned}$$

(22)

Consequently, $\varTheta ({{\mathbf{u}}}^h; {\tilde{\varGamma }}_h^{'})$ is linear in the velocity vector ${{\mathbf{u}}}^h$ if the region of backflow, ${\tilde{\varGamma }}_h^{'}$, is fixed. The last term of (18) is expected to be applicable in the situation of flow reversal. After implementation of this external force, the system of equations becomes the following.

$$\begin{aligned} \left( M + M_S\right) \frac{ d{{\mathbf{u}}}^h}{ dt} + {( C(\overline{{{\mathbf{u}}}}^h) + C_S(\overline{{{\mathbf{u}}}}^h) ){{\mathbf{u}}}^h} + M \varTheta ({{\mathbf{u}}}^h; {\tilde{\varGamma }}_h({{\mathbf{u}}}^h)) + (D + D_S) {{\mathbf{u}}}^h \\&\quad - (G - G_S)p^h = F + F_S, \end{aligned}$$

(23)

$$\begin{aligned} G^T {{\mathbf{u}}}^h + M_P \frac{ d{{\mathbf{u}}}^h}{ dt} + {C_P (\overline{{{\mathbf{u}}}}^h){{\mathbf{u}}}^h + D_P \,{{\mathbf{u}}}^h + G_P \,p^h} = E + E_P, \end{aligned}$$

(24)

for ${{\mathbf{u}}}^h \in \left( X^h\right) ^{n_{\mathrm{sd}}}$ and ${p}^h \in (X^h)^{n_{\mathrm{sd}}}$. We discretize acceleration and artificial external force terms $\left( M + M_S\right) \frac{ d{{\mathbf{u}}}^h}{ dt} + M \varTheta \left( {{\mathbf{u}}}^h; {\tilde{\varGamma }}_h\left( {{\mathbf{u}}}^h\right) \right)$ in (23) with a time-step length $\varDelta t$ as

$$\begin{aligned} \left( \left( 1 + \beta \varDelta t {{\mathbf{1}}}_{{\tilde{\varGamma }}_h\left( {{\mathbf{u}}}^h\right) }\right) M + M_S\right) \frac{{{\mathbf{u}}}^{h}\left( \left( k+1\right) \,\varDelta t\right) }{\varDelta t} - \left( M + M_S\right) \frac{{{\mathbf{u}}}^{h}\left( k\,\varDelta t\right) }{\varDelta t}, \end{aligned}$$

(25)

where the artificial force part is discretized separately as

$$\begin{aligned} M\varTheta ({{\mathbf{u}}}^h((k + 1)\,\varDelta t); {\tilde{\varGamma }}_h({{\mathbf{u}}}^h(k \varDelta t))) = \beta M {{\mathbf{1}}}_{{\tilde{\varGamma }}_h({{\mathbf{u}}}^h(k\,\varDelta t))} {{\mathbf{u}}}^h((k+1)\,\varDelta t). \end{aligned}$$

In other words, we judge whether the backflow occurs or not in the current time step and put the artificial force there in the next time step. The implementation is realized easily by adding the piecewise constant $\beta \varDelta t {{\mathbf{1}}}_{{\tilde{\varGamma }}_h}$ to the coefficient of stiffness matrix M.

Zhou and Saito [25] proved that boundary conditions of Signorini’s type satisfy the energy inequality, by which backflows are prevented by introducing a conditional vector, similarly to our technique. The energy inequality is not assured, in general, because of a possibly negative boundary integral term in the weak formulation when we use the do-nothing boundary condition. Although our prevention technique is combined with the do-nothing boundary condition, we might expect that the possibly negative term corresponding to the backflow is canceled by adding artificial force $\varTheta$.

2.5 Boundary conditions using PC-MRI

For this study, boundary conditions are constructed using PC-MRI measurements. As presented in Fig. 1, our target configuration has three inlet or outlet boundaries: $\varGamma _{\mathrm{PA}}$, $\varGamma _{\mathrm{DA}}$, and $\varGamma _{\mathrm{DV}}$. Flow rates $Q_{\varGamma _{\mathrm{PA}}} = \int _{\varGamma _{\mathrm{PA}}}{{{\mathbf{u}}} \cdot {\mathbf{n}}}\,ds$ and $Q_{\varGamma _{\mathrm{DV}}} = \int _{\varGamma _{\mathrm{DV}}}{{{\mathbf{u}}} \cdot {\mathbf{n}}}\,ds$ at 36 discrete time-steps during one heart period are obtained by PC-MRI. Cubic spline interpolation is used to obtain flow rate profiles with sufficient time resolutions. Because we assume incompressible fluid flow, total incoming and outgoing flow rates must be conserved, i.e., $Q_{\varGamma _{\mathrm{PA}}} + Q_{\varGamma _{\mathrm{DA}}} + Q_{\varGamma _{\mathrm{DV}}} = 0$, where flow directions are taken in outward normal directions. Therefore, we calculate $Q_{\varGamma _{\mathrm{DA}}}$ = $-\left( Q_{\varGamma _{\mathrm{PA}}} + Q_{\varGamma _{\mathrm{DV}}}\right)$. We set $\varGamma_\mathrm{DV}\mbox{ as }\varGamma_{h}\mbox{ with }{\mathbf{h}} = 0,\mbox{ and } \varGamma _{\mathrm{DA}}$ as $\varGamma _g$ because this boundary plays an important role in reproducing the flow dynamics for this patient’s case with regurgitation. Actually, the velocity direction at this boundary changes from outlet to inlet and vice-versa during one heartbeat. Another choice for boundary conditions is to set $\varGamma _{\mathrm{DV}}$ as $\varGamma _g$ and $\varGamma _{\mathrm{DA}}$ as $\varGamma _h$. However, this setting is too restrictive because we only have integrated flow rate data on DV boundary but do not know the velocity profile there, and our target is the complex flow near the anastomosis site, especially in the vein part.

Fig. 2

Flow rates for the proximal artery (PA), the distal artery (DA), and the distal vein (DV)

According to the special feature of this patient case with flow direction change at $\varGamma _{\mathrm{DA}}$ because of regurgitation from DA, we define splitting and merging phases. In the splitting phase, incoming flow from PA splits into DA and DV from $t=0$ to $t=0.18$ and $t=0.49$ to $t=1.1,$ as presented in Fig. 2. In the merging phase, $\varGamma _{\mathrm{DA}}$ acts as an inflow boundary, which means that two incoming flows from PA and DA merge at the anastomotic site. The merging phase lasts from $t=0.18$ to $t=0.49$ as presented in Fig. 2. The flow rate at DA becomes 0 at $t=0.18$ and $t=0.49,$ at which flow behaviors at DA change respectively from outlet to inlet and vice-versa. Detailed characteristics of flow behaviors in these phases are discussed in Sect. 3.

2.6 Mesh generation and numerical computation

Vascular modeling toolkit (VMTK) [30] was used for drawing the centerline in the extracted solid model. Then, a tetrahedral finite element mesh was generated using Gmsh [31] with a thin layered mesh near the vessel wall to resolve a large velocity gradient in boundary layers. The finite element mesh is depicted in Fig. 3, where the total numbers of nodes $n_{\mathrm{nd}}$ and elements $n_{\mathrm{el}}$ are, respectively, 26292 and 140052.

Fig. 3

Cross-sections of finite element mesh

A sparse non-symmetric system of linear equations is solved using GPBi-CG method, as discussed in [32, 33]. Density $\rho$ and blood viscosity $\mu$ are set respectively as 1060.0 kg/$\text{m}^3$ and $2.66 \times 10^{-3}$ N s/$\text{m}^2$. Time step length of $\varDelta t = 2 \times 10^{-4}$ s is adopted for a cardiac cycle T = 1.1 s. We have heuristically taken $\beta = 0.5$ in this study for efficient prevention of backflow from outflow boundary $\varGamma _{\mathrm{DV}}$.

3 Results and discussion

3.1 Effect of backflow prevention technique

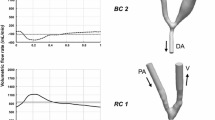
Figures 4 and 5 portray velocity vectors on the outflow boundary $\varGamma _{\mathrm{DV}}$ with outward normal vectors ${\mathbf{n}}_{\varGamma _{\mathrm {DV}}}$ in black color. In Fig. 4a at t=0.09, backflow appears in the central part of $\varGamma _{\mathrm{DV}}$. Subsequently, it grows, as portrayed in Fig. 4b at t=0.14 and immediately diverges. Figure 4c shows the magnitude of velocity on the plane perpendicular to $\varGamma _{\mathrm{DV}}$. When applying the external force presented in Sect. 2.4, the instability is well suppressed. Figure 5 portrays velocity vectors and their magnitude for the same time steps as those shown in Fig. 4. This comparison portrays that our backflow prevention technique works well in the region near the outflow boundary without exerting too strong an effect on upstream regions.

Fig. 4

Velocities without backflow prevention technique

Fig. 5

Velocities with backflow prevention technique

3.2 Periodicity check

We have no appropriate initial conditions. Therefore, we performed a periodicity check by computing flow fields for five cardiac cycles starting from an initial condition ${{\mathbf{u}}}_0 = {\mathbf{0}}$. Spatially-averaged WSS magnitudes are depicted in Fig. 6 for different cardiac cycles.

Fig. 6

Specially averaged WSS for the five cardiac cycles

Based on the periodicity check, we adopted the computational results from third to fourth periods (from $t=2.8$ to $t=3.9$) as portrayed in Fig. 7 for discussing blood flow characteristics in the following subsections. The four yellow lines of (a), (b), (c), and (d) in Fig. 7 respectively correspond to time-instants $t=2.88, 3.48, 3.63,$ and 3.78. The period of (b)–(d) is a merging phase, whereas the other is a splitting phase. Lines (a) and (c) respectively correspond to the instants at which maximum flow comes from PA and DA in the splitting and merging phases. Lines (b) and (d) respectively correspond to time instants at which phase changes from splitting to merging, and from merging to splitting.

Fig. 7

Splitting and merging phases from third to fourth heart periods

3.3 Characteristics of flow fields in the arteriovenous shunt model

As described in Sect. 2.5, blood enters from PA and exits from both DA and DV during the splitting phase, whereas blood enters from both PA and DA, and exits from DV during the merging phase. Therefore, DA plays two roles in the present patient case. Figures 8 and 9 show instantaneous streamlines in different phases and in the intervening transitions. Figure 8a shows the splitting phase in which the flow from PA splits into DA and DV in a complex way affected by the three-dimensional morphology of anastomotic site. Then, flow rate in DA begins to decrease and change directions, which causes strong circulation in DA, as presented in Fig. 8b. In the merging phase presented in Fig 8c, flows coming in from both PA and DA are comparable. Then, because of the morphology around the anastomotic site, it merges to form strong spirals in DV. Figure 9 presents the same timings with Fig. 8 from a different viewing angle. In Fig. 9c, because of the patient-specific morphology of this patient case, formation of spiral flow in DV driven by two incoming flows from PA and DA is readily apparent, which implies that the flow in merging phase is much smoother than that in the splitting phase. It is noteworthy that if an arteriovenous shunt is not surgically constructed, then no direct connection exists between the radial artery and cephalic vein. Blood coming in from PA simply passes out of DA. Therefore, the patient case analyzed in this paper represents a specific problem in blood flows with arteriovenous shunt.

Fig. 8

Streamlines in different phases (front view)

Fig. 9

Streamlines in different phases (back view)

3.4 Characteristics of this morphology from physiological viewpoints

Wall shear stress (WSS) exerted on the endothelial surface of blood vessels is defined as

$$\begin{aligned} { {\boldsymbol{\tau}}_w = {\mathbf{t}} - \left( {\mathbf{t}} \cdot {\mathbf{n}} \right) {\mathbf{n}},} \end{aligned}$$

(26)

where ${\mathbf{t}}$ is a traction vector computed from the stress tensor and surface normal vector, as ${\mathbf{t}} = {\boldsymbol{\sigma}}{\mathbf{n}}$. We first compute the elementwise WSS distribution. Then, we get the nodal approximated distribution as the local arithmetic mean of elementwise one. Figures 10 and 11 respectively present the WSS distribution for splitting and merging phases from two viewing angles. At t=2.88 during the splitting phase in Fig. 10, maximum flow coming in from PA, colliding to the anastomotic site wall, and splitting into DA and DV causes high WSS around the anastomotic site. At t=3.63 during the merging phase in Fig. 11, two incoming flows from PA and DA merge smoothly and generate swirling flow in DV, causing the slightly high WSS near the anastomotic site. Other high-WSS regions are apparently because of the local bumps in this patient’s morphology.

Fig. 10

WSS distributions at splitting phase $(t=2.88)$

Fig. 11

WSS distributions at merging phase $(t=3.63)$

Then, we compute the Oscillatory Shear Index (OSI) for one cardiac cycle $[T_0, T_1] = [2.8, 3.9]$ defined as shown below.

$$\begin{aligned} \text{OSI} = {0.5\,\left( 1 - \frac{\left| \int _{T_0}^{T_1} \,{\boldsymbol{\tau}}_w \,dt\, \right| }{\int _{T_0}^{T_1}\,\left| \,{\boldsymbol{\tau}}_w \,\right| \,dt}\right) }. \end{aligned}$$

(27)

Fig. 12

Circulations at the anastomotic site and OSI distribution

High OSI denotes areas with frequent changes in WSS vectors directions. Figure 12 portrays the streamlines in splitting and merging phases and the OSI distribution. Around the root of DV near the anastomotic site, circulations rotating in opposite directions in splitting and merging phases are apparent, which brings about high OSI there. OSI is known to be related strongly to atherosclerosis [34]. Therefore, this information can be important for planning surgical procedures considering shunt morphologies.

4 Concluding remarks

This study was conducted to investigate details of blood flow dynamics in an arteriovenous shunt model extracted from patient-specific CT scan and PC-MRI data. We have presented a simple backflow prevention technique to avoid computational instability. Characteristics of hemodynamics within the arteriovenous shunt model depend greatly on patient-specific morphologies and flow conditions, which differ widely among individual patients. In the patient case examined for this study, complex three-dimensional morphology around the anastomotic site and the existence of regurgitating flow from the distal artery (DA) bring about characteristic flow structures and WSS/OSI distributions in different phases and in transitions between them, which provides useful information for clinical practice.