1 Introduction

Large numbers of independent individuals sometimes cooperate as a collection. Examples where the collection develops a function can be observed in biological systems such as flocks of birds [1], schools of fish swim [49], insect swarms, bacterial colonies [50] and cell group motions [35]. Vicsek [48] has shown the appearance of collective motions by using a particle model and, subsequently to his pioneering work, theoretical research has been conducted in terms of nonlinear physics for understanding the mechanism of collective motions performed by living organisms [36, 48, 49].

On the other hand, to study collective motions from the viewpoint of experimental systems, many researchers have utilized self-propelled materials as non-biological systems. Examples of a simple experimental system for self-propelled materials include surfactants on particles or droplets driven by the difference of the surrounding surface tension [2, 4, 6, 10, 19, 24, 27,28,29, 32, 33, 41, 44, 47]. In addition, experiments to control the motions of self-propelled materials by a chemical reaction have also been reported [30, 31, 45]. For the theoretical understanding of these experimental results of self-propelled materials, a mathematical model for the experimental system was introduced and its mathematical analysis was carried out. In particular, one-dimensional motions of self-propelled materials, such as motions on the water surface of elongated channels, are described by a particle reaction-diffusion systems. For instance, let \(x_c(t)\) and u(x, t) be the center of the surfactant material disk and the surface concentration of the surfactant, respectively. Then, a mathematical model for self-propelled motions is described as follows:

$$\begin{aligned} \begin{aligned} \rho \dfrac{d^2 x_c}{dt^2}&= G(u) - \mu \dfrac{d x_c}{dt} , \\ \dfrac{\partial u}{\partial t}&= d_u \dfrac{\partial ^2 u}{\partial x^2} - k u + F(x - x_c(t)), \end{aligned} \end{aligned}$$
(1)

where \(\rho\), \(\mu\), \(d_u\) and k denote an area density of the surfactant disk, a viscosity coefficient, a diffusion coefficient and a combined rate of sublimation and dissolution of the surfactant, respectively. The function F(x) represents the supply of the surfactant molecules and a simple example of it is the supply from solid surfactant, which is described by

$$\begin{aligned} F(x) = \left\{ \begin{array}{ll} k_u u_0, &{} \ |x| \le r, \\ 0, &{} \ |x| > r, \end{array} \right. \quad \mathrm {or} \quad F(x) = k_u u_0 \delta (x) , \end{aligned}$$

where \(k_u\) and \(u_0\) are the supply rate and the density of the solid surfactant, respectively, and \(\delta (x)\) is the Dirac delta function. The function G(u) is a driving force to the self-propelled particle, which is given by, for example,

$$\begin{aligned} G(u) = \dfrac{1}{2r} \left( \gamma (u(t, x_c(t) + r) ) - \gamma (u(t, x_c(t) - r)) \right) , \end{aligned}$$

or

$$\begin{aligned} G(u) = \left. \frac{d \gamma (u(t, x))}{dx} \right| _{x = x_c(t)}. \end{aligned}$$

Here, the function \(\gamma (u)\), which is a strictly decreasing function of the surface concentration of the surfactant, represents the surface tension of the water surface and, for instance, it is given by

$$\begin{aligned} \gamma (u) = \frac{a^m}{a^m + u^m} (\gamma _0 - \gamma _1) + \gamma _1, \end{aligned}$$
(2)

where \(a > 0\), \(m \in \mathbb {N}\), and \(\gamma _0\), \(\gamma _1 > 0\) represent the surface tension of pure water and that of the critical micelle concentration of the surfactant, respectively. Although it is difficult to determine the surface tension function \(\gamma (u)\) from experimental measurements, mathematical models phenomenologically assume that \(\gamma (u)\) is strictly deceasing. Indeed, this assumption has been employed in preceding studies and the following functions have been proposed as candidates for \(\gamma (u)\) [20, 42]:

$$\begin{aligned} \gamma (u) = \frac{1}{2}\left( \gamma _0 - \gamma _1\right) \left( \tanh ( - (u - u_0) ) +1 \right) + \gamma _1, \end{aligned}$$
(3)

in which \(u_0\) is a positive constant, and

$$\begin{aligned} \gamma (u) = \gamma _0 - a u. \end{aligned}$$
(4)

To understand the mechanism of self-propelled motions theoretically, the mathematical model (1) with a strictly decreasing function \(\gamma\) has been studied by use of computer-aided analysis [3, 10, 19, 20, 23, 25, 38]. Moreover, a mathematical model for two-dimensional problems, such as motions on water surfaces, have been constructed [5, 16, 18, 33] and the model has been studied theoretically [14, 17, 21, 22]. In addition, the experiments to control motions of self-propelled materials by a chemical reaction have been reported [30, 31, 45], and their theoretical studies have been conducted by using the mathematical model (1) coupled with a chemical reaction model [13, 26, 37]. From these studies, the particle reaction-diffusion system (1) is considered as a physically relevant model for describing self-propelled motions in nonlinear physics and physical chemistry.

One of the remarkable phenomena observed in self-propelled motions is the appearance of collective motions. Indeed, several patterns of collective motions have been reported in the preceding studies [11, 39, 40, 42, 43, 46]. For example, Suematsu et al. have observed that camphor boats cause a phenomena like traffic jams [42], and oscillatory motions of camphor disks appear depending on the number of disks and their surface areas [43]. Nakata et al. have also reported collective motions of camphor disks such as billiard motions and traffic jam phenomena in an annular water channel [15]. Our concern is whether these collective motions appear in the mathematical model (1) as well. Since camphor disks used in the experiments are very light, Nishi et al. have analyzed motions of two camphor disks by using the following dimensionless mathematical model without the inertia term [34]:

$$\begin{aligned} \begin{aligned} \mu \dfrac{d x^i_c}{dt}&= \dfrac{\gamma (u(t, \pi _L(x^i_c + r))) - \gamma (u(t, \pi _L(x^i_c - r)))}{2r}, \\ \dfrac{\partial u}{\partial t}&= \dfrac{\partial ^2 u}{\partial x^2} - u + F(x - x^1_c) + F(x - x^2_c), \\ \end{aligned} \end{aligned}$$
(5)

for \(i = 1, 2\), and \(x \in [0, L) {\setminus }\{\pi _L(x^1_c + r), \pi _L(x^1_c - r), \pi _L(x^2_c + r), \pi _L(x^2_c - r)\}\), where \(\mu > 0\) and \(L> 4r > 0\). The function \(\gamma (u) > 0\) is strictly decreasing for \(u>0\) and the function F(x) is given by

$$\begin{aligned} F(x) = \left\{ \begin{array}{ll} 1, &{} \ |x|_L \le r, \\ 0, &{} \ |x|_L > r, \end{array} \right. \qquad |x|_L = \min _{n \in \mathbb {Z}} |x + nL|. \end{aligned}$$

Meanwhile, \(\pi _L\) denotes the map from \(\mathbb R\) to [0, L), that is, for any \(x \in \mathbb {R}\), there exists \(n \in \mathbb Z\) such that \(x = \pi _L(x) + nL\). The periodic boundary condition is imposed by \(u(t, L) = u(t, 0)\) and \(\partial u(t, L)/\partial x = \partial u(t, 0) /\partial x\). Note that a solution of (5) satisfies \(u \in C([0, T] \times [0, L])\) and \(u(t, \cdot )\in C[0, L]\) for any \(t > 0\).

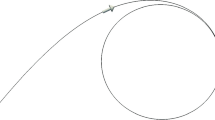
The preceding study [34] has clarified the mechanism of the emergence of billiard and traffic jam motions in the model (5) by computer aided analysis. In addition, they have also reported notable motions: a symmetrically and an asymmetrically oscillating motions, a symmetrically and an asymmetrically rotating motions (see Fig. 1), an oscillating and rotating motion. Furthermore, both the experimental measurement and the numerical computation have shown that the asymmetrically rotating motion of two camphor disks is stable as shown in Fig. 1b.

Fig. 1
figure 1

The trajectory of a a symmetrically rotating motion of two camphor disks for \(\mu = 0.004\) and b an asymmetrically rotating motion of two camphor disks for \(\mu = 0.001\). Both solutions are obtained by the numerical computation for (5) with \(r = 0.5\), \(L = 70.665\) and \(\gamma (u) = a^2 /(a^2 + u^2)\), where \(a = 0.05\). The solid line and dashed line show the trajectory of two camphor disks

Full size image

On the other hand, the density of camphor molecules just behind camphor disks is higher than that in other area in general, since camphor molecules remain behind for a while after the passing of a camphor disk. Then, the driving force for the disk behind, which is generated by the difference in the surface tensions, seems to be weaker than that for the previous disk, and consequently the disk behind moves slower than the previous one. Hence, it seems reasonable that the distance between the two camphor disks increases gradually and their motions become symmetric in the end. In fact, reduced equations for camphor motions are derived based on the weak interaction theory, suggesting that repulsive forces act on the camphor particles through the reaction diffusion field [7,8,9]. From the above considerations, the appearance of asymmetrically rotating motions suggested numerically in [34] seems to be curious and implies that an attractive force between camphor disks exists. Moreover, the computer aided analysis in [34] has shown that the asymmetrically rotating solution appears via a pitch-fork bifurcation of the symmetrically rotating solution. Our motivation in this study is, through the analysis of the model (5), making it clear what kind of effect is essential for the existence of asymmetrically rotating motions for a strictly decreasing function \(\gamma\) with mathematical rigor. For convenience in the mathematical analysis, we introduce the uniform rotation velocity, \(c \ge 0\), and consider the steady state problem of (5) via the moving coordinate \(z = x - c t\). Then, rotating solutions of (5) on the moving coordinate are defined as follows:

Definition 1

The quadruple \((U(z), c, z^1_c, z^2_c)\) is called a rotating solution to (5) if it satisfies the following equations:

$$\begin{aligned} \begin{aligned} 0&= \gamma (U(\pi _L(z^i_c + r))) - \gamma (U(\pi _L(z^i_c - r))) - 2r \mu c, \\ 0&= \dfrac{\partial ^2 U}{\partial z^2} + c\dfrac{\partial U}{\partial z} - U + F(z - z^1_c) + F(z - z^2_c), \end{aligned} \end{aligned}$$
(6)

for \(i = 1, 2\), and \(z \in [0, L) {\setminus }\{\pi _L(z^1_c + r), \pi _L(z^1_c - r), \pi _L(z^2 + r), \pi _L(z^2_c - r)\}\), where U is a \(C^1\)-periodic function on [0, L]. In particular, the rotating solution \(( U(z), c, z^1_c, z^2_c )\) satisfying \(|z^1_c - z^2_c| = L/2\) is called a symmetrically rotating solution, and otherwise the solution is called an asymmetrically rotating solution.

On the basis of the above definition, we state the following theorem about the existence of symmetrically and asymmetrically rotating solutions.

Theorem 1

Assume \(|z^1_c - z^2_c|_L > 2r\) and that \(\gamma \in C^1[0,\infty )\) satisfies \(\gamma (u) > 0\) and \(\gamma '(u) < 0\) for \(u>0\). Then the following statements hold.

  1. (a)

    For any \(c > 0\), there exists a unique \(\mu > 0\) such that (6) has a symmetrically rotating solution. In the case of \(c = 0\), there always exists a symmetrically rotating solution for any value of \(\mu > 0\).

  2. (b)

    For any \(\mu > 0\), (6) has no asymmetrically rotating solution with \(c = 0\).

  3. (c)

    Suppose \(\gamma \in C^2(0, \infty )\) and \(\gamma '' \ge 0\). Then, for any \(c > 0\) and \(\mu > 0\), (6) has no asymmetrically rotating solution.

  4. (d)

    Suppose that \(\gamma \in C^2(0, 1)\) satisfies

    $$\begin{aligned} \dfrac{1}{2}\left( 1 + \dfrac{1}{4r^2(1 - \rho )}\right) \gamma '(\rho )< (1 - \rho )\gamma ''(\rho ) < \gamma '(\rho ), \end{aligned}$$
    (7)

    where \(\rho = 4r/L\). Then, (6) has an asymmetrically rotating solution for sufficiently large c.

Here, we impose the assumption \(|z^1_c - z^2_c|_L > 2r\) since the effect of contact between two disks are not considered in the model (6). According to Theorem 1, the existence of asymmetrically rotating solutions depends on the shape of the function \(\gamma (u)\), which corresponds to the surface tension. We remark that it can be confirmed that there exists a function \(\gamma (u)\) in (2) satisfying the condition (7), and \(\gamma (u)\) in (3) satisfies the condition (7) with some suitable parameters. For the linear function \(\gamma (u)\) in (4), Theorem 1 claims that there is no asymmetrically rotating solution. For motions of a single camphor, we can obtain a similar result to Theorem 1, which is discussed in Appendix A. In the next section, we give the proof of Theorem 1.

2 Proof of the Main Theorem

2.1 Reformulation

Since solutions of (5) are recovered from those of (6), it is sufficient to show the existence and non-existence of stationary solutions of (6). That is to say, we consider the following equations:

$$\begin{aligned} 0&= \gamma (U(\pi _L({{Z^{i}} } + r))) - \gamma (U(\pi _L({{Z^{i}} } - r))) - {2r \mu c}, \end{aligned}$$
(8)
$$\begin{aligned} 0&= U'' + c U' - U + F(z - {{Z^{1}} }) + F(z - {{Z^{2}} }), \end{aligned}$$
(9)

for \(i = 1, 2\), and

$$\begin{aligned} z \in [0, L) {\setminus }\{\pi _L({{Z^{1}} } + r), \pi _L({{Z^{1}} } - r), \pi _L({{Z^{2}} } + r), \pi _L({{Z^{2}} } - r)\}, \end{aligned}$$

where \(U \in C^1[0, L]\) with \(U(L) = U(0)\) and \(U'(L) = U'(0)\). To see the translational symmetry of (8) and (9), we introduce the following periodically extended equations:

$$\begin{aligned} \left\{ \begin{gathered} 0 = \gamma (U^p(Z^{i, n} + r)) - \gamma (U^p(Z^{i, n} - r)) - 2r \mu c, \\ Z^{i, n + 1} - Z^{i, n} = L, \\ Z^{2, n} - Z^{1, n}> 2r, \quad Z^{1, n + 1} - Z^{2, n} > 2r, \end{gathered}\right. \end{aligned}$$
(10)

for \(i = 1, 2\), \(n \in \mathbb {Z}\), and

$$\begin{aligned} \left\{ \begin{gathered} 0 = {U^p}'' + c{U^p}' - U + \sum _{\begin{array}{c} i \in \{ 1, 2\}, \ n \in \mathbb Z \end{array}}F(z - Z^{i, n}), \\ U^p(z + L) = U^p(z), \\ \end{gathered}\right. \end{aligned}$$
(11)

for \(z \in \mathbb R {\setminus } \bigcup _{\begin{array}{c} i \in \{1, 2\}, \ n \in \mathbb Z \end{array}}\{Z^{i, n} + r, Z^{i, n} - r\}\), where \(U^p \in C^1(\mathbb R)\). It is easily confirmed that if \((Z^{1*}, Z^{2*}, U^*)\) is a solution to (8) and (9), then \((Z^{1*} + nL, Z^{2*} + nL, U^{*p})\) is a solution to (10) and (11), where \(U^{*p}\) is a periodically extended function of \(U^*\). Conversely, if \((Z^{{1, n}*}, Z^{{2, n}*}, U^{p*})\) is a solution to (10) and (11), then \((Z^{1, 0}, Z^{2, 0}, \left. U^{p*} \right| _{[0, L)})\) satisfies (8) and (9). In this sense, the system (8) and (9) is equivalent to (10) and (11). Since the system (10) and (11) has the translational symmetry, it is sufficient to consider the system (8) and (9) with \(Z^1 = r\). Then, (9) is rewritten by

$$\begin{aligned} \begin{aligned}&0 = U'' + c U' - U + 1,&z \in (0, l_1), \\&0 = U'' + c U' - U,&z \in (l_1, l_2), \\&0 = U'' + c U' - U + 1,&z \in (l_2, l_3), \\&0 = U'' + c U' - U,&z \in (l_3, L), \end{aligned} \end{aligned}$$
(12)

where \(l_1 = 2r\), \(l_2 = 2r + d\), \(l_3 = 4r + d\) and \(d = Z^2 - r - (Z^1 + r)\). We assume that \(U \in C^1[0, L]\) satisfies the periodic boundary condition given by \(U(L) = U(0)\) and \(U'(L) = U'(0)\). Note that, in the above formulation, symmetrically and asymmetrically rotating solutions correspond with \(d = L/2 -2r\) and \(d \ne L/2 -2r\), respectively.

For the sake of simplicity, we define the following functions:

$$\begin{aligned} \begin{aligned} \phi (c)&= \frac{-c}{2}, \quad \theta (c) = \frac{\sqrt{c^2 + 4}}{2}, \quad \lambda _+(c) = \phi (c) + \theta (c), \quad \lambda _-(c) = \phi (c) - \theta (c), \\ E_+(c, z)&= \exp (-\lambda _+(c) z), \quad E_-(c, z) = \exp (\lambda _-(c) z), \\ U_+(c)&= \frac{1}{2\theta (c)\lambda _+(c)}\frac{1 - E_+(c, 2r)}{1 - E_+(c, L)}, \quad U_-(c) = \frac{-1}{2\theta (c)\lambda _-(c)}\frac{1 - E_-(c, 2r)}{1 - E_-(c, L)}. \end{aligned} \end{aligned}$$
(13)

Throughout this paper, we will omit the discussion on c when it is fixed. We first show that the system (12) has a unique solution.

Lemma 1

Let the constants \(l_1< l_2< l_3 < L\) be \(l_1 = 2r\), \(l_2 = 2r + d\) and \(l_3 = 4r + d\) with \(d, r > 0\). For any given \(c \in \mathbb R\), there exists a unique solution of (12). Moreover, U(0), \(U(l_1)\), \(U(l_2)\) and \(U(l_3)\) are expressed by

$$\begin{aligned} U(0)&= U_+(1 + E_+(l_2)) + U_-(E_-(L - l_3) + E_-(L - l_1)), \\ U(l_1)&= U_+(E_+(L - l_1) + E_+(d)) + U_-(E_-(L - l_2) + 1), \\ U(l_2)&= U_+(1 + E_+(L - l_2)) + U_-(E_-(L - l_1) + E_-(d)), \\ U(l_3)&= U_+(E_+(L - l_3) + E_+(L - l_1)) + U_-(1 + E_-(l_2)). \end{aligned}$$

Proof

Let us fix \(c\in \mathbb R\). By a classical theory, we can represent a solution of (12) by

$$\begin{aligned} \begin{aligned} U(z)&= a^1_+E_+(-z) + a^1_-E_-(z) + 1,&z \in (0, l_1), \\ U(z)&= b^1_+E_+(-(z - l_1)) + b^1_-E_-(z - l_1),&z \in (l_1, l_2), \\ U(z)&= a^2_+E_+(-(z - l_2)) + a^2_-E_-(z - l_2) + 1,&z \in (l_2, l_3), \\ U(z)&= b^2_+E_+(-(z - l_3)) + b^2_-E_-(z - l_3),&z \in (l_3, L). \end{aligned} \end{aligned}$$
(14)

Thus, it is sufficient to show the unique existence of constants \(a^1_\pm\), \(a^2_\pm\), \(b^1_\pm\) and \(b^2_\pm\). The periodic boundary condition, \(U(L) = U(0)\) and \(U'(L) = U'(0)\), requires that

$$\begin{aligned} \lim _{z\rightarrow +0} U(z) = \lim _{z\rightarrow L - 0} U(z), \quad \lim _{z\rightarrow +0} U'(z) = \lim _{z\rightarrow L - 0} U'(z), \end{aligned}$$

which is equivalent to

$$\begin{aligned} a^1_+ + a^1_- + 1&= b^2_+E_+(-(L - l_3)) + b^2_-E_-(L - l_3), \\ a^1_+\lambda _+ + a^1_-\lambda _-&= b^2_+\lambda _+E_+(-(L - l_3)) + b^2_-\lambda _-E_-(L - l_3). \end{aligned}$$

These relations are rewritten by

$$\begin{aligned} \varLambda \varvec{a}^1 + \varvec{e}&= \varLambda E(L - l_3) \varvec{b}^2, \end{aligned}$$
(15)

where

$$\begin{aligned} \varvec{a}^i= & {} \begin{pmatrix} a^i_+ \\ a^i_- \end{pmatrix}, \quad \varvec{b}^i = \begin{pmatrix} b^i_+ \\ b^i_- \end{pmatrix}, \quad \varvec{e} = \begin{pmatrix} 1 \\ 0 \end{pmatrix},\\ \varLambda= & {} \begin{pmatrix} 1 &{} 1 \\ \lambda _+ &{} \lambda _- \end{pmatrix}, \quad E(z) = \begin{pmatrix} E_+(-z) &{} 0 \\ 0 &{} E_-(z) \end{pmatrix}. \end{aligned}$$

Similarly, since U is continuously differentiable at \(l_1\), \(l_2\) and \(l_3\), we have

$$\begin{aligned} \begin{aligned} \varLambda E(l_1) \varvec{a}^1 + \varvec{e}&= \varLambda \varvec{b}^1, \\ \varLambda \varvec{a}^2 + \varvec{e}&= \varLambda E(l_2 - l_1) \varvec{b}^1, \\ \varLambda E(l_3 - l_2) \varvec{a}^2 + \varvec{e}&= \varLambda \varvec{b}^2. \end{aligned} \end{aligned}$$
(16)

Note that it follows from \(\det \varLambda = \lambda _- - \lambda _+ = -2\theta < 0\) that \(\varLambda\) is a regular matrix. We find that (15) and (16) are equivalent to

$$\begin{aligned} \begin{aligned} \varvec{a}^1&= E(L - l_3)\varvec{b}^2 - \varLambda ^{-1}\varvec{e}, \\ \varvec{b}^1&= E(l_1) \varvec{a}^1 + \varLambda ^{-1}\varvec{e}, \\ \varvec{a}^2&= E(l_2 - l_1) \varvec{b}^1 - \varLambda ^{-1}\varvec{e} , \\ \varvec{b}^2&= E(l_3 - l_2) \varvec{a}^2 + \varLambda ^{-1}\varvec{e}. \end{aligned} \end{aligned}$$
(17)

Substituting these equalities in order, we obtain

$$\begin{aligned} \varvec{a}^1&= - \varLambda ^{-1}\varvec{e} + E(L - l_3)(E(l_3 - l_2)(E(l_2 - l_1)(E(l_1) \varvec{a}^1 + \varLambda ^{-1}\varvec{e}) - \varLambda ^{-1}\varvec{e}) + \varLambda ^{-1}\varvec{e}) , \\&= E(L)\varvec{a}^1 + (E(L - l_1) - E(L - l_2) + E(L - l_3) - I)\varLambda ^{-1}\varvec{e}. \end{aligned}$$

Here, we used \(E(z_1)E(z_2) = E(z_1 + z_2)\). Note that \(\det \left( I - E(z)\right) = (1 - E_+(-z))(1 - E_-(z)) \ne 0\) for any \(z \ne 0\). Then, we have

$$\begin{aligned} \varvec{a}^1&= (I - E(L))^{-1}(E(L - l_1) -E(L - l_2) + E(L - l_3) - I)\varLambda ^{-1}\varvec{e}, \end{aligned}$$

which indicates that constants \(a^1_\pm\) are uniquely determined. Using (17), we obtain the other constants \(a^2_\pm\), \(b^1_\pm\) and \(b^2_\pm\) that are uniquely expressed by

$$\begin{aligned} \varvec{b}^1&= (I - E(L))^{-1}(-E(L - l_2 + l_1) + E(L - l_3 + l_1) - E(l_1) + I)\varLambda ^{-1}\varvec{e}, \\ \varvec{a}^2&= (I - E(L))^{-1}( E(L - l_3 + l_2) - E(l_2) + E(l_2 - l_1) - I)\varLambda ^{-1}\varvec{e}, \\ \varvec{b}^2&= (I - E(L))^{-1}(-E(l_3) + E(l_3 - l_1) - E(l_3 - l_2) + I)\varLambda ^{-1}\varvec{e}. \end{aligned}$$

Thus, we conclude that (12) has a unique solution \(U \in C^1[0, L)\) satisfying the periodic boundary condition.

On the other hand, considering

$$\begin{aligned} (I - E(L))^{-1} = \begin{pmatrix} \dfrac{1}{1 - E_+(-L)} &{} 0 \\ 0 &{} \dfrac{1}{1 - E_-(L)} \end{pmatrix}, \quad \varLambda ^{-1} = -\frac{1}{2\theta }\begin{pmatrix} \lambda _- &{} -1 \\ -\lambda _+ &{} 1 \end{pmatrix}, \end{aligned}$$

we find

$$\begin{aligned} \begin{pmatrix} a^1_+ \\ a^1_- \end{pmatrix}&= \begin{pmatrix} \dfrac{-\lambda _-}{2\theta }\dfrac{E_+(-(L - l_1)) - E_+(-(L - l_2)) + E_+(-(L - l_3)) - 1}{1 - E_+(-L)} \\ \dfrac{\lambda _+}{2\theta }\dfrac{E_-(L - l_1) - E_-(L - l_2) + E_-(L - l_3) - 1}{1 - E_-(L)} \end{pmatrix}. \end{aligned}$$

Substituting \(a^1_\pm\) into the first line in (14), we obtain

$$\begin{aligned} U(z)&= 1 - \dfrac{\lambda _- E_+(-z)}{2\theta }\dfrac{E_+(-(L - l_1)) - E_+(-(L - l_2)) + E_+(-(L - l_3)) - 1}{1 - E_+(-L)} \\&\quad + \dfrac{\lambda _+ E_-(z)}{2\theta }\dfrac{E_-(L - l_1) - E_-(L - l_2) + E_-(L - l_3) - 1}{1 - E_-(L)}, \end{aligned}$$

for \(z \in (0, l_1)\). Since the constants \(\varvec{a}^1\), \(\varvec{a}^2\), \(\varvec{b}^1\) and \(\varvec{b}^2\) are determined so that \(U\in C^1[0, L]\), we have

$$\begin{aligned} U(0)&= \lim _{z \rightarrow + 0}U(z) \\&= 1 - \dfrac{\lambda _-}{2\theta }\dfrac{E_+(-(L - l_1)) - E_+(-(L - l_2)) + E_+(-(L - l_3)) - 1}{1 - E_+(-L)} \\&\quad + \dfrac{\lambda _+}{2\theta }\dfrac{E_-(L - l_1) - E_-(L - l_2) + E_-(L - l_3) - 1}{1 - E_-(L)}. \end{aligned}$$

It follows from \(\lambda _+ - \lambda _- = 2\theta\) and \(\lambda _+\lambda _- = -1\) that

$$\begin{aligned}&1 - \dfrac{-\lambda _-}{2\theta }\dfrac{1}{1 - E_+(-L)} - \dfrac{\lambda _+}{2\theta }\dfrac{1}{1 - E_-(L)} \\&\quad = -\dfrac{-\lambda _-}{2\theta }\dfrac{E_+(-L)}{1 - E_+(-L)} - \dfrac{\lambda _+}{2\theta }\dfrac{E_-(L)}{1 - E_-(L)}, \\&\quad = -\dfrac{1}{2\theta \lambda _+}\dfrac{E_+(-L)}{1 - E_+(-L)} - \dfrac{1}{-2\theta \lambda _-}\dfrac{E_-(L)}{1 - E_-(L)}. \end{aligned}$$

Thus, we obtain

$$\begin{aligned} U(0)&= \dfrac{1}{2\theta \lambda _+}\dfrac{E_+(-(L - l_1)) - E_+(-(L - l_2)) + E_+(-(L - l_3)) - E_+(L)}{1 - E_+(-L)} \\&\quad - \dfrac{1}{2\theta \lambda _-}\dfrac{E_-(L - l_1) - E_-(L - l_2) + E_-(L - l_3) - E_-(L)}{1 - E_-(L)} \\&= \dfrac{1}{2\theta \lambda _+}\dfrac{E_+(-L)}{1 - E_+(-L)}(E_+(l_1) - E_+(l_2) + E_+(l_3) - 1) \\&\quad - \dfrac{1}{2\theta \lambda _-}\dfrac{E_-(L - l_1) - E_-(L - l_2) + E_-(L - l_3) - E_-(L)}{1 - E_-(L)} \\&= \dfrac{1}{2\theta \lambda _+}\dfrac{1 - E_+(2r) + E_+(2r + d) - E_+(4r + d)}{1 - E_+(L)} \\&\quad - \dfrac{1}{2\theta \lambda _-}\dfrac{E_-(L - 2r) - E_-(L - 2r - d) + E_-(L - 4r - d) - E_-(L)}{1 - E_-(L)} \\&= \dfrac{1}{2\theta \lambda _+}\dfrac{1 - E_+(2r)}{1 - E_+(L)}(1 + E_+(2r + d)) \\&\quad - \dfrac{1}{2\theta \lambda _-}\dfrac{1 - E_-(2r)}{1 - E_-(L)}E_-(L - 4r - d)(1 + E_-(2r + d)). \end{aligned}$$

The definitions of \(U_+\) and \(U_-\) yield

$$\begin{aligned} U(0) = (1 + E_+(2r + d))U_+ + (E_-(L - 4r - d) + E_-(L - 2r))U_-. \end{aligned}$$

Similarly, it is confirmed that

$$\begin{aligned} U(2r)&= (E_+(L - 2r) + E_+(d))U_+ + (E_-(L - 2r - d) + 1)U_-, \\ U(2r + d)&= (1 + E_+(L - 2r - d))U_+ + (E_-(L - 2r) + E_-(d))U_-, \\ U(4r + d)&= (E_+(L - 4r - d) + E_+(L - 2r))U_+ + (1 + E_-(2r + d))U_-. \end{aligned}$$

\(\square\)

For later use, we introduce the following notations:

$$\begin{aligned} U_{1f}(c, d)\equiv & {} U(2r), \quad U_{1r}(c, d) \equiv U(0), \\ U_{2f}(c, d)\equiv & {} U(4r + d), \quad U_{2r}(c, d) \equiv U(2r + d),\\ \varDelta U_1(c, d)\equiv & {} U_{1f}(c, d) - U_{1r}(c, d), \quad \varDelta U_2(c, d) \equiv U_{2f}(c, d) - U_{2r}(c, d). \end{aligned}$$

We will omit the discussion on c and d when they are fixed. Before stating the proof of Theorem 1, we show some properties of \(U_{1f}\), \(U_{1r}\), \(U_{2f}\) and \(U_{2r}\).

Lemma 2

Let \(c > 0\) be a fixed constant. Then, we have

  1. (a)

    \(\varDelta U_1(c, L/2 - 2r) = \varDelta U_2(c, L/2 - 2r) < 0\).

  2. (b)

    \(\varDelta U_1(c, d) - \varDelta U_2(c, d) = 0\) if and only if \(L/2 - 2r -d = 0\). If \(L/2 - 2r - d \ne 0\), then the sign of \(\varDelta U_1(c, d) - \varDelta U_2(c, d)\) is equal to that of \(L/2 - 2r - d\).

  3. (c)

    \(U_{1f}(c, d) - U_{2f}(c, d) = 0\) if and only if \(L/2 - 2r -d = 0\). If \(L/2 - 2r - d \ne 0\), then the sign of \(U_{1f}(c, d) - U_{2f}(c, d)\) is equal to that of \(L/2 - 2r - d\).

Proof

We consider \(\varDelta U_i\), \(U_{if}\), and \(U_{ir}\) as functions of d, that is, \(\varDelta U_i(d)\), \(U_{if}(d)\), and \(U_{ir}(d)\) for \(i = 1, 2\).

  1. (a)

    It is straightforward to check that \(U_{1f}(c,L/2 - 2r) = U_{2f}(c,L/2 - 2r)\) and \(U_{1r}(c,L/2 - 2r) = U_{2r}(c,L/2 - 2r)\) so that \(\varDelta U_1(c, L/2 - 2r) = \varDelta U_2(c, L/2 - 2r)\). We have

    $$\begin{aligned} \varDelta U_1(L/2 - 2r)&= (E_+(L - 2r) + E_+(L/2 - 2r) - 1 - E_+(L/2))U_+ \\&\quad + (E_-(L/2) + 1 - E_-(L/2 - 2r) - E_-(L - 2r))U_- \\&= - (1 + E_+(L/2))(1 - E_+(L/2 - 2r))U_+ \\&\quad + (1 + E_-(L/2))(1 - E_-(L/2 - 2r))U_-. \end{aligned}$$

    Note that

    $$\begin{aligned}&\theta (1 + E_+(L/2))(1 - E_+(L/2 - 2r))U_+\\&\quad = \frac{(1 + \exp (-(L/2)\lambda _+))(1 - \exp (-(L/2 - 2r)\lambda _+))}{2\lambda _+}\frac{1 - \exp (-2r\lambda _+)}{1 - \exp (-L\lambda _+)} \\&\quad = \frac{1}{\lambda _+}\frac{\sinh (r\lambda _+)}{\sinh ((L/4)\lambda _+)}\sinh ((L/4 - r)\lambda _+) \\&\quad = \xi _2(\lambda _+; r, L/4), \end{aligned}$$

    and \(\theta U_-(1 + E_-(L/2))(1 - E_+(L/2 - 2r)) = \xi _2(-\lambda _-; r, L/4)\). Since it follows from \(0< 4r < L\) that \(\xi _2(x; r, L/4)\) is strictly decreasing for \(x>0\) (see Appendix A.2), we find that \(\xi _2(\lambda _+; r, L/4) < \xi _2(\lambda _-; r, L/4)\), that is, \(U_+(1 + E_+(L/2))(1 - E_+(L/2 - 2r)) > U_-(1 + E_-(L/2))(1 - E_-(L/2 - 2r))\). Hence, we obtain \(\varDelta U_1(L/2 - 2r) < 0\).

  2. (b)

    It follows that

    $$\begin{aligned} \varDelta U_1(d) - \varDelta U_2(d)&= U_+E_+(d)(1 - E_+(2r))(1 - E_+(L - 4r - 2d)) \\&\quad + U_-E_-(d)(1 - E_-(2r))(1 - E_-(L - 4r - 2d)). \end{aligned}$$

    Since we have \(U_\pm E_\pm (d)(1 - E_\pm (2r)) > 0\) and \(1 - E_\pm (z)\) has the same sign as that of z, we obtain the desired result.

  3. (c)

    Note that

    $$\begin{aligned} \begin{aligned} U_{1f}(d) - U_{2f}(d)&= E_+(d)(1 - E_+(L - 4r - 2d))U_+ \\&\quad - E_-(2r + d)(1 - E_-(L - 4r - 2d))U_-. \end{aligned} \end{aligned}$$
    (18)

    Since we have

    $$\begin{aligned}&\theta E_+(r + d)(1 - E_+(L - 4r - 2d))U_+\\&\quad = \frac{\exp (-(r + d)\lambda _+)}{2\lambda _+}\frac{1 - \exp (-2r\lambda _+)}{1 - \exp (-L\lambda _+)}(1 - \exp (-(L - 4r - 2d)\lambda _+)) \\&\quad = \frac{\sinh ((L/2 - 2r - d)\lambda _+)}{\lambda _+}\frac{\sinh (r\lambda _+)}{\sinh ((L/2)\lambda _+)} \\&\quad = \xi _3(\lambda _+; r, L/2, d/2), \end{aligned}$$

    and, similarly, \(\theta E_-(r + d)(1 - E_-(L - 4r - 2d))U_- = \xi _3(-\lambda _-; r, L/2, d/2)\), we find that (18) is rewritten by

    $$\begin{aligned} U_{1f}(d) - U_{2f}(d) = \frac{E_+(-r)}{\theta }\xi _3(\lambda _+; r, L/2, d/2) - \frac{E_-(r)}{\theta }\xi _3(-\lambda _-; r, L/2, d/2). \end{aligned}$$

    For the case of \(L - 4r - 2d > 0\), owing to \(0< 4r < L\)and \(0< d < L - 4r\), \(\xi _3(x; r, L/2, d/2)\) is strictly decreasing for \(x>0\) (see Appendix A.3). Thus, considering \(E_+(-r)> 1 > E_-(r)\), we find

    $$\begin{aligned} U_{1f}(d) - U_{2f}(d) = \frac{1}{\theta }(E_+(-r)\xi _3(\lambda _+; r, L/2, d/2) - E_-(r)\xi _3(-\lambda _-; r, L/2, d/2)) > 0. \end{aligned}$$

    For the case of \(L - 4r - 2d < 0\), we have

    $$\begin{aligned} \xi _3(\lambda _+; r, L/2, d/2)< \xi _3(-\lambda _-; r, L/2, d/2) < 0, \end{aligned}$$

    and thus

    $$\begin{aligned} U_{1f}(d) - U_{2f}(d) = \frac{1}{\theta }(E_+(-r)\xi _3(\lambda _+; r, L/2, d/2) - E_-(r)\xi _3(-\lambda _-; r, L/2, d/2)) < 0. \end{aligned}$$

    Finally, we easily confirm that \(L - 4r - 2d = 0\) is equivalent to \(U_{1f}(c) - U_{2f}(c) = 0\). \(\square\)

2.2 Proofs of Theorem 1(a), (b)

We first prove Theorem 1(a) for the case of \(c > 0\). Note that (8) are rewritten by

$$\begin{aligned} 2r \mu c&= \gamma (U_{1f}(c, d)) - \gamma (U_{1r}(c, d)), \end{aligned}$$
(19)
$$\begin{aligned} 0&= \gamma (U_{1f}(c, d)) - \gamma (U_{1r}(c, d)) - (\gamma (U_{2f}(c, d)) - \gamma (U_{2r}(c, d))). \end{aligned}$$
(20)

Since, for symmetric solutions satisfying \(d = L/2 - 2r\), Lemma 2(a) gives \(U_{1f}(c, L/2 - 2r) < U_{1r}(c, L/2 - 2r)\) and \(\gamma (u)\) is strictly decreasing for \(u>0\), there exists a unique \(\mu > 0\) satisfying (19). Thus, it is sufficient to show that \(U_{1f}(c, L/2 - 2r)\), \(U_{1r}(c, L/2 - 2r)\), \(U_{2f}(c, L/2 - 2r)\) and \(U_{2r}(c, L/2 - 2r)\) satisfy (20). It follows from Lemma 2(b), (c) that

$$\begin{aligned} U_{1f}(c, L/2 - 2r) = U_{2f}(c, L/2 - 2r), \end{aligned}$$
(21)

and

$$\begin{aligned} U_{1f}(c, L/2 - 2r) - U_{1r}(c, L/2 - 2r) = U_{2f}(c, L/2 - 2r) - U_{2r}(c, L/2 - 2r), \end{aligned}$$

respectively. Thus, we find

$$\begin{aligned} U_{1r}(c, L/2 - 2r) = U_{2r}(c, L/2 - 2r). \end{aligned}$$
(22)

Combining (21) with (22), we obtain (20).

Next, we consider the case of \(c = 0\). Note that (8) are equivalent to

$$\begin{aligned} \gamma (U_{1f}(0, d)) = \gamma (U_{1r}(0, d)), \quad \gamma (U_{2r}(0, d)) = \gamma (U_{2r}(0, d)). \end{aligned}$$
(23)

Since \(\gamma (u)\) is strictly decreasing for \(u>0\), (23) is satisfied if and only if \(\varDelta U_1(0, d) = \varDelta U_2(0, d) = 0\) holds. Considering \(\lambda _-(0) = -\lambda _+(0) = -1\) and \(U_+(0, d) = U_-(0, d) = U_0\), where

$$\begin{aligned} U_0 = \frac{1}{2}\frac{1 - E_0(2r)}{1 - E_0(L)},\quad E_0(z) = \exp (-z), \end{aligned}$$

we obtain

$$\begin{aligned} U_{1f}(0, d)&= U_0(1 + E_0(L - 2r) + E_0(d) + E_0(L - 2r - d)), \\ U_{1r}(0, d)&= U_0(1 + E_0(L - 2r) + E_0(2r + d) + E_0(L - 4r - d)), \\ U_{2f}(0, d)&= U_0(1 + E_0(L - 2r) + E_0(2r + d) + E_0(L - 4r - d)), \\ U_{2r}(0, d)&= U_0(1 + E_0(L - 2r) + E_0(d) + E_0(L - 2r - d)), \end{aligned}$$

which implies

$$\begin{aligned} \varDelta U_1(0, d) = -\varDelta U_2(0, d) = U_0E_0(d)(1 - E_0(2r))(1 - E_0(L - 4r - 2d)). \end{aligned}$$

Hence, (23) holds if and only if \(d = L/2 - 2r\), which concludes Theorem 1(a) with \(c=0\) and Theorem 1(b).

2.3 Proof of Theorem 1(c)

We prove Theorem 1(c) by contradiction. Let \(c > 0\) be a fixed constant. If there exists a rotating solution, then (20) is satisfied with \(\varDelta U_1 < 0\) and \(\varDelta U_2 < 0\). Thus, it is sufficient to prove that (20) is not satisfied provided that \(\varDelta U_1 < 0\) and \(\varDelta U_2 < 0\). For asymmetric solutions, that is, \(d \ne L/2 - 2r\), we should consider the following three cases.

  1. 1.

    \(U_{1f} > U_{2r}\).

  2. 2.

    \(U_{1f} \le U_{2r} \text{ and } L/2 - 2r - d < 0\).

  3. 3.

    \(U_{1f} \le U_{2r} \text{ and } L/2 - 2r - d > 0\).

For the case 1, (20) is equivalent to

$$\begin{aligned} \int ^{U_{1r}}_{U_{1f}}-\gamma '(U)dU = \int ^{U_{2r}}_{U_{2f}}-\gamma '(U)dU. \end{aligned}$$
(24)

It follows from \(\varDelta U_1 < 0\), \(\varDelta U_2 < 0\) and \(U_{1f} > U_{2r}\) that

$$\begin{aligned} U_{1r}> U_{1f}> U_{2r} > U_{2f}. \end{aligned}$$
(25)

Since we have \(\gamma '(u) < 0\) and \(\gamma ''(u) \ge 0\) for \(u > 0\), (25) yields

$$\begin{aligned} 0 < -\gamma '(U_{1r}) \le -\gamma '(U_{1f}) \le -\gamma '(U_{2r}) \le -\gamma '(U_{2f}). \end{aligned}$$
(26)

Owing to Lemma 2(c), \(U_{1f} > U_{2f}\) in (25) implies \(L/2 - 2r - d > 0\). Thus, Lemma 2(b) yields \(0> U_{1f} - U_{1r} > U_{2f} - U_{2r}\). Hence, we obtain

$$\begin{aligned} 0< U_{1r} - U_{1f} < U_{2r} - U_{2f}. \end{aligned}$$
(27)

It follows from (26) and (27) that

$$\begin{aligned} \int ^{U_{1r}}_{U_{1f}}-\gamma '(U)dU&\le -\gamma '(U_{1f}) (U_{1r} - U_{1f}) \\&< -\gamma '(U_{2r}) (U_{2r} - U_{2f}) \le \int ^{U_{2r}}_{U_{2f}}-\gamma '(U)dU, \end{aligned}$$

which contradicts (24).

For the case 2, (20) is equivalent to

$$\begin{aligned} \int ^{U_{2f}}_{U_{1f}}-\gamma '(U)dU = \int ^{U_{2r}}_{U_{1r}}-\gamma '(U)dU. \end{aligned}$$
(28)

Owing to \(L/2 - 2r - d < 0\), it follows from Lemma 2(c) that \(U_{1f} < U_{2f}\). Thus, (28) and \(\gamma ' < 0\) yield \(U_{1r} < U_{2r}\). In addition, the assumption \(\varDelta U_2 < 0\) gives

$$\begin{aligned} U_{1f}< U_{2f} < U_{2r}. \end{aligned}$$

If \(U_{2f} \le U_{1r}\), then we have \(U_{1f}< U_{2f} \le U_{1r} < U_{2r}\) and it follows from \(L/2 - 2r - d < 0\) and Lemma 2(b) that \(\varDelta U_1 < \varDelta U_2\), that is, \(U_{2r} - U_{1r} < U_{2f} - U_{1f}\). Thus,

$$\begin{aligned} \int ^{U_{2r}}_{U_{1r}}-\gamma '(U)dU&\le -\gamma '(U_{1r}) (U_{2r} - U_{1r}) \\&< -\gamma '(U_{2f})(U_{2f} - U_{1f}) \le \int ^{U_{2f}}_{U_{1f}}-\gamma '(U)dU, \end{aligned}$$

which contradicts (28). As for \(U_{2f} > U_{1r}\), we obtain \(U_{1f}< U_{1r}< U_{2f} < U_{2r}\) and following inequality:

$$\begin{aligned} \int ^{U_{2r}}_{U_{2f}}-\gamma '(U)dU&\le -\gamma '(U_{2f}) (U_{2r} - U_{2f}) \\&< -\gamma '(U_{1r})(U_{1r} - U_{1f}) \le \int ^{U_{1r}}_{U_{1f}}-\gamma '(U)dU, \end{aligned}$$

owing to \(0< -\varDelta U_2 < -\varDelta U_1\), which contradicts (28). Thus, (20) is not satisfied in the case 2.

For the case 3, it follows from \(L/2 - 2r - d > 0\) and Lemma 2(c) that \(U_{2f} < U_{1f}\). Hence, we have \(U_{2f} < U_{1f} \le U_{2r}\). In the same manner as that for the case 2, we assume that \(U_{2r} < U_{1r}\). By \(L/2 - 2r - d > 0\), Lemma 2(b) gives \(\varDelta U_1 > \varDelta U_2\), that is, \(U_{1f} - U_{2f} > U_{1r} - U_{2r}\). Hence, we find

$$\begin{aligned} \int ^{U_{1r}}_{U_{2r}}-\gamma '(U)dU&\le -\gamma '(U_{2r}) (U_{1r} - U_{2r}) \\&< -\gamma '(U_{1f}) (U_{1f} - U_{2f}) \le \int ^{U_{1f}}_{U_{2f}}-\gamma '(U)dU, \end{aligned}$$

which contradicts (20).

2.4 Proof of Theorem 1(d)

Let \(\varGamma (c, d) \equiv \gamma (U_{1f}(c,d)) - \gamma (U_{1r}(c,d)) - \left[ \gamma (U_{2f}(c,d)) - \gamma (U_{2r}(c,d)) \right]\). We show that there exists a constant \(d_0 \in (0,L/2 - 2r)\) such that \(\varGamma (c, d_0) = 0\). Our strategy is to investigate the asymptotic behavior of \(\varGamma (c, d)\) as \(d\rightarrow +0\) and \(d \rightarrow L/2 - 2r - 0\) for sufficiently large c. We first consider the limit of \(\varGamma (c, d)\) as \(d\rightarrow +0\). It follows that

$$\begin{aligned} \varGamma (c, 0)&= \lim _{d\rightarrow 0} \varGamma (c, d) \\&= \gamma (U_{1f}(c, 0)) - \gamma (U_{1r}(c, 0)) - \left[ \gamma (U_{2f}(c, 0)) - \gamma (U_{2r}(c, 0)) \right] , \end{aligned}$$

and

$$\begin{aligned} U_{1f}(c, 0)&= U_+(c)(1 + E_+(c, L - 2r)) + U_-(c)(E_-(c, L - 2r) + 1), \\ U_{1r}(c, 0)&= U_+(c)(1 + E_+(c, 2r)) + U_-(c)(E_-(c, L - 4r) + E_-(c, L - 2r)), \\ U_{2f}(c, 0)&= U_+(c)(E_+(c, L - 4r) + E_+(c, L - 2r)) + U_-(c)(1 + E_-(c, 2r)), \\ U_{2r}(c, 0)&= U_+(c)(1 + E_+(c, L - 2r)) + U_-(c)(E_-(c, L - 2r) + 1), \end{aligned}$$

in the same limit. Note that

$$\begin{aligned}&U_{1f}(c, 0) - U_{1r}(c, 0) \\&\quad = -E_+(c, 2r)U_+(c)(1 - E_+(c, L - 4r)) + U_-(c)(1 - E_-(c, L - 4r)), \\ & U_{2f}(c, 0) - U_{2r}(c, 0) \\&\quad = -U_+(c)(1 - E_+(c, L - 4r)) + E_-(c, 2r)U_-(c)(1 - E_-(c, L - 4r)). \end{aligned}$$

Then, we have \(U_{1f}(c, 0) - U_{1r}(c, 0) < 0\) and \(U_{2f}(c, 0) - U_{2r}(c, 0) < 0\) for sufficiently large c. Indeed, since it follows that

$$\begin{aligned}&U_{1f}(c, 0) - U_{1r}(c, 0) \\&\quad = (1 - E_+(c, L - 4r)) \left[ -E_+(c, 2r)U_+(c) + U_-(c)\dfrac{1 - E_-(c, L - 4r)}{1 - E_+(c, L - 4r)} \right] , \end{aligned}$$

and Lemma 3 in Appendix C gives

$$\begin{aligned} \lim _{c\rightarrow \infty } \left[ -E_+(2r)U_+(c) + U_-(c)\frac{1 - E_-(c, L - 4r)}{1 - E_+(c, L - 4r)} \right] = -\frac{2r}{L} < 0, \end{aligned}$$

we obtain \(U_{1f}(c, 0) - U_{1r}(c, 0) < 0\) for sufficiently large c. On the other hand, we have

$$\begin{aligned} \theta U_+ (1 - E_+(L - 4r))&= \frac{1}{2\lambda _+}\frac{1 - E_+(2r)}{1 - E_+(L)}(1 - E_+(L - 4r)) \\&= \frac{1}{\lambda _+}\frac{\sinh (r\lambda _+)}{\sinh (L/2\lambda _+)}\sinh ((L/2 - 2r)\lambda _+)E_+(-r) \\&= \xi _3(\lambda _+;r, L/2, 0)E_+(-r), \end{aligned}$$

and, similarly,

$$\begin{aligned} \theta U_-(1 - E_-(L - 4r))&= \xi _3(-\lambda _-;r, L/2, 0)E_-(r). \end{aligned}$$

Since \(\xi _3(x; r, L/2, 0)\) is strictly decreasing for \(x>0\) (see Appendix B), we find

$$\begin{aligned}&U_+(1 - E_+(L - 4r))> \frac{\xi _3(\lambda _+;r, L/2, 0)}{\theta }\\&\quad> \frac{\xi _3(\lambda _-;r, L/2, 0)}{\theta } > E_-(2r) U_- (1 - E_-(L - 4r)), \end{aligned}$$

in which we used \(E_+(-r) > 1\) and \(E_-(r) < 1\). Thus, \(U_{2f}(c, 0) - U_{2r}(c, 0) < 0\) holds for sufficiently large c.

From the above estimates, we have \(U_{2f}(c, 0)< U_{2r}(c, 0) = U_{1f}(c, 0) < U_{1r}(c, 0)\). Hence, the mean value theorem implies that there exist \(U^*\) and \(U^{**}\) such that

$$\begin{aligned} \begin{aligned} \gamma (U_{1r}(c, 0)) - \gamma (U_{1f}(c, 0)) =&( U_{1r}(c, 0) - U_{1f}(c, 0) ) \gamma '(U^*), \\ \gamma (U_{2r}(c, 0)) - \gamma (U_{2f}(c, 0)) =&( U_{2r}(c, 0) - U_{2f}(c, 0) ) \gamma '(U^{**}), \end{aligned} \end{aligned}$$
(29)

where \(U^*\) and \(U^{**}\) satisfy

$$\begin{aligned} \begin{aligned} U_{2f}(c, 0)< U^{**}< U_{2r}(c, 0) = U_{1f}(c, 0)< U^{*} < U_{1r}(c, 0). \end{aligned} \end{aligned}$$
(30)

Similarly, it follows from \(U^{**} < U^{*}\) that there exists \(U^{***}\) satisfying \(U^{**}< U^{***} < U^*\) such that

$$\begin{aligned} \gamma '(U^*) - \gamma '(U^{**}) = (U^* - U^{**})\gamma ''(U^{***}). \end{aligned}$$
(31)

Using (29) and (31), we find

$$\begin{aligned} \varGamma (c,0)&= ( U_{1r}(c, 0) - U_{1f}(c, 0) ) \gamma '(U^*) - ( U_{2r}(c, 0) - U_{2f}(c, 0) ) \gamma '(U^{**}) \\&= ( U_{1r}(c, 0) - U_{2f}(c, 0) ) \gamma '(U^{**}) \\&\quad + ( U_{1r}(c, 0) - U_{1f}(c, 0) ) (U^* - U^{**})\gamma ''(U^{***})\\&= \left[ U_+ (1 - E_+(2r))(1 - E_+(L - 4r)) \right. \\&\quad \left. + U_- (1 - E_-(2r))(1 - E_-(L - 4r)) \right] \gamma '(U^{**})\\&\quad - \left[ E_+(2r)U_+(1 - E_+(L - 4r)) \right. \\&\quad \left. - U_-(1 - E_-(L - 4r)) \right] (U^* - U^{**})\gamma ''(U^{***}). \end{aligned}$$

Here, we introduce the function \(\varGamma _0(c)\) defined by

$$\begin{aligned} \varGamma _{0}(c)&\equiv \dfrac{1}{(U^* - U^{**})(1 - E_+(2r))}\varGamma (c,0) \\&= \left[ \dfrac{U_+ (1 - E_+(L - 4r))}{U^* - U^{**}} + \dfrac{U_- (1 - E_-(2r)) (1 - E_-(L - 4r)) }{(U^* - U^{**})(1 - E_+(2r))} \right] \gamma '(U^{**})\\&\quad - \left[ E_+(2r)U_+\dfrac{1 - E_+(L - 4r)}{1 - E_+(2r)} - U_- \dfrac{1 - E_-(L - 4r)}{1 - E_+(2r)}\right] \gamma ''(U^{***}). \end{aligned}$$

Then, owing to \((U^* - U^{**})(1 - E_+(2r)) > 0\), the sign of \(\varGamma (c,0)\) coincides with that of \(\varGamma _{0}(c)\). Since it follows from (30) that

$$\begin{aligned} 0&< U^* - U^{**} \\&< U_+(1 - E_+(L - 4r))(1 + E_+(2r)) - U_-(1 - E_-(L - 4r))(1 + E_-(2r)), \end{aligned}$$

defining the function \(\widetilde{\varGamma }_{0}(c)\) by

$$\begin{aligned} \widetilde{\varGamma }_{0}&= \dfrac{U_+(1 - E_+(L - 4r)) \gamma '(U^{**})}{U_+(1 - E_+(L - 4r))(1 + E_+(2r)) - U_-(1 - E_-(L - 4r))(1 + E_-(2r))} \\&\quad + \dfrac{U_- (1 - E_+(2r))^{-1}(1 - E_-(2r))(1 - E_-(L - 4r)) \gamma '(U^{**})}{U_+(1 - E_+(L - 4r))(1 + E_+(2r)) - U_-(1 - E_-(L - 4r))(1 + E_-(2r))}\\&\quad - \left[ E_+(2r)U_+\dfrac{1 - E_+(L - 4r)}{1 - E_+(2r)} - \dfrac{U_- (1 - E_-(L - 4r))}{1 - E_+(2r)} \right] \gamma ''(U^{***})\\&\equiv \widetilde{\varGamma }_1 + \widetilde{\varGamma }_2 - \widetilde{\varGamma }_3, \end{aligned}$$

we find \(\varGamma _{0} < \widetilde{\varGamma }_{0}\), owing to \(\gamma ' < 0\). We remark that if the limit of \(\widetilde{\varGamma }_{0}\) as \(c\rightarrow \infty\) is negative, then \(\widetilde{\varGamma }_{0}(c) < 0\) holds for sufficiently large c by the continuity of \(\widetilde{\varGamma }_{0}\), which implies that \(\varGamma _{0}(c)\) and \(\varGamma (c,0)\) are also negative. Thus, it is enough to investigate the limit of \(\widetilde{\varGamma }_{0}(c)\) as \(c\rightarrow \infty\) to determine the condition on which \(\varGamma (c,0)\) is negative for sufficiently large c. For simplicity of notation, we set \(\rho \equiv 4r/L\). Then, we have

$$\begin{aligned} \lim _{c\rightarrow \infty }U^{**}(c) = \lim _{c\rightarrow \infty }U^{***}(c) = \lim _{c\rightarrow \infty }U^{*}(c) = \rho . \end{aligned}$$

Indeed, it follows from (30) and \(U^{**}< U^{***} < U^*\) that

$$\begin{aligned}&U_+(E_+(L - 4r) + E_+(L - 2r)) + U_-(1 + E_-(2r)) \\&\quad< U^{**}< U^{***}< U^{*} \\&\quad < U_+(1 + E_+(2r)) + U_-(E_-(L - 4r) + E_-(L - 2r)), \end{aligned}$$

and Lemma 3 in Appendix C gives

$$\begin{aligned} \lim _{c\rightarrow \infty }U_+(c)(E_+(c, L - 4r) + E_+(c, L - 2r)) + U_-(c)(1 + E_-(c, 2r)) =&\rho , \\ \lim _{c\rightarrow \infty }U_+(c)(1 + E_+(c, 2r)) + U_-(c)(E_-(c, L - 4r) + E_-(c, L - 2r)) =&\rho . \end{aligned}$$

As for the limit of \(\widetilde{\varGamma }_1(c)\) as \(c\rightarrow \infty\), since we have

$$\begin{aligned}&\dfrac{U_+(1 - E_+(L - 4r))}{U_+(1 - E_+(L - 4r))(1 + E_+(2r)) - U_-(1 - E_-(L - 4r))(1 + E_-(2r))} \\&\quad = \left[ 1 + E_+(2r) - \dfrac{U_-}{1 - E_+(L - 4r)}\dfrac{(1 - E_-(L - 4r))(1 + E_-(2r))}{U_+} \right] ^{-1}, \end{aligned}$$

Lemma 3 in Appendix C yields \(\widetilde{\varGamma }_1(c) \rightarrow \frac{1}{2}\gamma '(\rho )\) as \(c \rightarrow \infty\). In the same manner as that for \(\widetilde{\varGamma }_1\), we confirm that \(\widetilde{\varGamma }_2(c) \rightarrow \frac{1}{8r^2(1 - \rho )}\gamma '(\rho )\) as \(c \rightarrow \infty\). Owing to the estimate

$$\begin{aligned} \lim _{c\rightarrow \infty } \left[ E_+(c, 2r)U_+(c)\dfrac{1 - E_+(c, L - 4r)}{1 - E_+(c, 2r)} - U_-(c) \dfrac{1 - E_-(c, L - 4r)}{1 - E_+(c, 2r)} \right] = 1 - \rho , \end{aligned}$$

we obtain \(\widetilde{\varGamma }_3(c) \rightarrow (1 - \rho )\gamma ''(\rho )\) as \(c \rightarrow \infty\). Summarizing the above estimates for \(\widetilde{\varGamma }_1\), \(\widetilde{\varGamma }_2\) and \(\widetilde{\varGamma }_3\), we find

$$\begin{aligned} \lim _{c\rightarrow \infty } \widetilde{\varGamma }_{0}(c) = \dfrac{1}{2}\left( 1 + \dfrac{1}{4r^2(1 - \rho )}\right) \gamma '(\rho ) - (1 - \rho )\gamma ''(\rho ). \end{aligned}$$

Thus, we conclude that \(\varGamma (c,0) < 0\) holds for sufficiently large c provided that

$$\begin{aligned} \dfrac{1}{2}\left( 1 + \dfrac{1}{4r^2(1 - \rho )}\right) \gamma '(\rho ) - (1 - \rho )\gamma ''(\rho ) < 0. \end{aligned}$$
(32)

Next, we estimate the limit of \(\partial \varGamma (c, d)/\partial d\) as \(d \rightarrow L/2 - 2r - 0\), where

$$\begin{aligned} \frac{\partial \varGamma }{\partial d}(c, d)&= \frac{\partial U_{1f}}{\partial d}(c, d) \gamma '(U_{1f}(c,d)) - \frac{\partial U_{1r}}{\partial d}(c, d) \gamma '(U_{1r}(c,d)) \\&\quad - \left[ \frac{\partial U_{2f}}{\partial d}(c, d) \gamma '(U_{2f}(c,d)) - \frac{\partial U_{2r}}{\partial d}(c, d) \gamma '(U_{2r}(c,d)) \right] . \end{aligned}$$

From Lemma 2(a), we have \(U_{1f}(c, L/2 - 2r) = U_{2f}(c, L/2 - 2r) \equiv U_f(c)\) and \(U_{1r}(c, L/2 - 2r) = U_{2r}(c, L/2 - 2r) \equiv U_r(c)\) with

$$\begin{aligned} U_f(c)&= U_+(c)(E_+(c, L - 2r) + E_+(c, L/2 - 2r)) + U_-(c)(E_-(c, L/2) + 1), \\ U_r(c)&= U_+(c)(E_+(c, L/2) + 1) + U_-(c)(E_-(c, L/2 - 2r) + E_-(c, L - 2r)), \end{aligned}$$

which yields \(\varGamma (c, L/2 - 2r) = 0\) and \(U_f(c) < U_r(c)\). Since it follows that

$$\begin{aligned} \begin{aligned} \frac{\partial U_{1f}}{\partial d}(c, d)&= -\lambda _+(c)U_+(c)E_+(c, d) - \lambda _-(c)U_-(c)E_-(c, L - 2r - d), \\ \frac{\partial U_{1r}}{\partial d}(c, d)&= -\lambda _+(c)U_+(c)E_+(c, 2r + d) - \lambda _-(c)U_-(c)E_-(c, L - 4r - d), \\ \frac{\partial U_{2f}}{\partial d}(c, d)&= \lambda _+(c)U_+(c)E_+(c, L - 4r - d) + \lambda _-(c)U_-(c)E_-(c, 2r + d), \\ \frac{\partial U_{2r}}{\partial d}(c, d)&= \lambda _+(c)U_+(c)E_+(c, L - 2r - d) + \lambda _-(c)U_-(c)E_-(c, d), \end{aligned} \end{aligned}$$
(33)

substituting \(d = L/2 - 2r\) into (33), we obtain

$$\begin{aligned} \frac{\partial U_{1f}}{\partial d}(c, L/2 - 2r)&= -\frac{\partial U_{2f}}{\partial d}(c, L/2 - 2r) = u_f(c), \\ \frac{\partial U_{1r}}{\partial d}(c, L/2 - 2r)&= -\frac{\partial U_{2r}}{\partial d}(c, L/2 - 2r) = u_r(c), \end{aligned}$$

where

$$\begin{aligned} u_f(c)&= -\lambda _+(c)U_+(c)E_+(c, L/2 - 2r) - \lambda _-(c)U_-(c)E_-(c, L/2), \\ u_r(c)&= -\lambda _+(c)U_+(c)E_+(c, L/2) - \lambda _-(c)U_-(c)E_-(c, L/2 - 2r). \end{aligned}$$

Thus, we find

$$\begin{aligned} \frac{\partial \varGamma }{\partial d}(c, L/2 - 2r) = 2 \left[ u_f(c)\gamma '(U_f(c)) - u_r(c)\gamma '(U_r(c)) \right] . \end{aligned}$$

Owing to \(U_f(c) < U_r(c)\), the mean value theorem gives \(U^*\) satisfying

$$\begin{aligned} \gamma '(U_r(c)) - \gamma '(U_f(c)) = (U_r(c) - U_f(c))\gamma ''(U^*), \end{aligned}$$

and \(U_f(c)< U^* < U_r(c)\). Hence, we obtain

$$\begin{aligned}&\frac{1}{2}\frac{\partial \varGamma }{\partial d}(c, L/2 - 2r) \\&\quad = (u_f(c) - u_r(c))\gamma '(U_r(c)) - u_f(c)(U_r(c) - U_f(c))\gamma ''(U^*) \\&\quad = u_f(c)(U_r(c) - U_f(c))\left[ \frac{u_f(c) - u_r(c)}{u_f(c)(U_r(c) - U_f(c))}\gamma '(U_r(c)) - \gamma ''(U^*) \right] \\&\quad \equiv u_f(c)(U_r(c) - U_f(c)) \widetilde{\varGamma }_d(c). \end{aligned}$$

Note that \(u_f(c) < 0\). Indeed, it follows that

$$\begin{aligned} 2\theta u_f&= -\frac{1 - \exp (-2r\lambda _+)}{1 - \exp (-L\lambda _+)}\exp (-(L/2 - 2r)\lambda _+) \\&\quad + \frac{1 - \exp (2r\lambda _-)}{1 - \exp (L\lambda _-)}\exp (L/2\lambda _-) \\&= -\frac{\sinh (r\lambda _+)}{\sinh (L/2\lambda _+)}\exp (r\lambda _+) + \frac{\sinh (-r\lambda _-)}{\sinh (-L/2\lambda _-)}\exp (r\lambda _-) \\&= -\xi _1(\lambda _+; r, L/2)\exp (r\lambda _+) + \xi _1(-\lambda _-; r, L/2)\exp (r\lambda _-). \end{aligned}$$

Since \(\xi _1(x, r, L/2)\) is strictly decreasing for \(x > 0\), it follows from \(0< \exp (r\lambda _-)< 1 < \exp (r\lambda _+)\) that

$$\begin{aligned} \xi _1(\lambda _+; r, L/2)\exp (r\lambda _+) > \xi _1(-\lambda _-; r, L/2)\exp (r\lambda _-), \end{aligned}$$

which concludes \(u_f(c) < 0\). We now investigate the limit of \(\widetilde{\varGamma }_d(c)\) as \(c\rightarrow \infty\). Since Lemma 3 in Appendix C gives \(U_f(c)\), \(U_r(c) \rightarrow \rho\) so that \(U^*(c) \rightarrow \rho\) as \(c\rightarrow \infty\), we have \(\gamma '(U_r(c)) \rightarrow \gamma '(\rho )\) and \(\gamma ''(U^*(c)) \rightarrow \gamma ''(\rho )\). Then,

$$\begin{aligned}&\frac{u_f - u_r}{u_f} \\&\quad = \frac{-\lambda _+ U_+ E_+(L/2 - 2r)(1 - E_+(2r)) + \lambda _- U_- E_-(L/2 - 2r)(1 - E_-(2r))}{-\lambda _+ U_+ E_+(L/2 - 2r) - \lambda _- U_- E_-(L/2)} \\&\quad = \frac{U_+ E_+(L/2 - 2r)(1 - E_+(2r)) + \lambda _-^2 U_- E_-(L/2 - 2r)(1 - E_-(2r))}{U_+ E_+(L/2 - 2r) - \lambda _-^2 U_- E_-(L/2)} \\&\quad = \left[ 1 - \frac{\lambda _-^2 U_- E_-(L/2)}{U_+ E_+(L/2 - 2r)} \right] ^{-1} \\&\qquad \times \left[ (1 - E_+(2r)) + \frac{\lambda _-^2 U_- (1 - E_-(2r))}{U_+ E_+(L/2 - 2r)}E_-(L/2 - 2r) \right] . \end{aligned}$$

It follows from Lemma 3 in Appendix C that

$$\begin{aligned} \lim _{c\rightarrow \infty } \frac{\lambda _-(c)^2U_-(c) (1 - E_-(2r))}{U_+(c)E_+(c, L/2 - 2r)}&= \frac{2}{L - 4r}, \\ \lim _{c\rightarrow \infty } \left[ 1 - \frac{\lambda _-(c)^2 U_-(c)E_-(c, L/2)}{U_+(c)E_+(c, L/2 - 2r)} \right]&= 1. \end{aligned}$$

To estimate the limit of \((u_f(c) - u_r(c))\left[ u_f(c)(U_r(c) - U_f(c))\right] ^{-1}\), it remains to see the limits of \((1 - E_+(c, 2r))(U_r(c) - U_f(c))^{-1}\) and \(E_-(c, L/2)(U_r(c) - U_f(c))^{-1}\) as \(c\rightarrow \infty\). It follows that

$$\begin{aligned} \frac{1 - E_+(c,2r)}{U_r(c) - U_f(c)}&= \frac{1 - E_+(c,2r)}{1 - E_+(c,L/2 - 2r)} h(c), \\ \frac{E_-(c,L/2)}{U_r(c) - U_f(c)}&= \frac{E_-(c,L/2)}{1 - E_+(c,L/2 - 2r)} h(c), \end{aligned}$$

where

$$\begin{aligned} h(c) \equiv \left[ U_+(E_+(L/2) + 1) + \frac{U_- (E_-(L/2) + 1)(1 - E_-(L/2 - 2r))}{1 - E_+(L/2 - 2r)}\right] ^{-1}. \end{aligned}$$

Thus, we find from Lemma 3 in Appendix C that

$$\begin{aligned} \lim _{c\rightarrow \infty } \frac{1 - E_+(c, 2r)}{U_r(c) - U_f(c)}= \frac{1}{1 - \rho }, \quad \lim _{c\rightarrow \infty } \frac{E_-(c, L/2)}{U_r(c) - U_f(c)} = 0, \end{aligned}$$

which leads to

$$\begin{aligned} \lim _{c\rightarrow \infty } \frac{u_f(c) - u_r(c)}{u_f(c)(U_r(c) - U_f(c))} = \frac{1}{1 - \rho }. \end{aligned}$$

As a consequence, we obtain

$$\begin{aligned} \lim _{c\rightarrow \infty } \widetilde{\varGamma }_d(c) = \frac{1}{1- \rho }\gamma '\left( \rho \right) - \gamma ''\left( \rho \right) , \end{aligned}$$
(34)

and conclude that \(\partial \varGamma /\partial d(c, L/2 - 2r) < 0\) holds for sufficiently large c provided that \(\frac{1}{1 - \rho }\gamma '(\rho ) - \gamma ''(\rho ) < 0\). Then, owing to \(\varGamma (c, L/2 - 2r) = 0\), there exists a constant \(0< d^*(c) < L/2 - 2r\) such that \(\varGamma (c, d)\) is positive for any \(d \in (d^*, L/2 - 2r)\) for sufficiently large c.

Summarizing the estimates (32) and (34), we find that, under the condition \(\frac{1}{2} \left( 1 + \frac{1}{4r^2(1 - \rho )}\right) \gamma '(\rho )< (1 - \rho )\gamma ''(\rho ) < \gamma '(\rho )\), it follows that \(\varGamma (c, 0) < 0\) and \(\varGamma (c, d) > 0\) with \(d \in (d^*, L/2 - 2r)\) for sufficiently large c. Therefore, it follows from the continuity of \(\varGamma (c,d)\) that there exists \(d_0\) such that \(0< d_0 < L/2 - 2r\) and \(\varGamma (c, d_0) = 0\).

3 Concluding remarks

In this paper, we have shown the existence of symmetrically rotating solutions and have given necessary conditions for the existence and non-existence of asymmetrically rotating solutions for the two camphor model (5). In particular, it has been shown that a concave part of the function \(\gamma\), which describes the surface tension, is necessary for the existence of asymmetrically rotating solutions. Our result clarifies an essential condition for the existence of solutions and provides a clue for the dependence between the surfactant concentration and the surface tension in the mathematical model, which is difficult to measure in experiments. Moreover, it is suggested that the characteristic motion varies depending on the form of the surface tension function \(\gamma\) and, thus, the change of the qualitative motion is caused by \(\gamma\) in other mathematical models. Although this study treats the mathematical model without the inertial force, we note that our proof of the existence theorem for symmetrically or asymmetrically rotating solutions is still valid for the following model including the inertial term \(d^2 x^i_c / d t^2\):

$$\begin{aligned} \begin{aligned} \rho \dfrac{d^2 x^i}{dt^2}&= \frac{\gamma (u(t, \pi _L(x^i + r))) - \gamma (u(t, \pi _L(x^i - r)))}{2r} - \mu \dfrac{dx^i}{dt}, \\ \dfrac{\partial u}{\partial t}&= \dfrac{\partial ^2 u}{\partial x^2} - u + F(x - x^1) + F(x - x^2), \end{aligned} \end{aligned}$$
(35)

for \(i = 1, \ldots , N\), and \(x \in [0, L) \setminus \{\pi _L(x^1 + r), \pi _L(x^1 - r), \ldots , \pi _L(x^N + r), \pi _L(x^N - r)\}\), where \(\rho\) is the area density of a camphor disk. Our analysis shows that there exists an asymmetrically rotating solution for \(N=2\). For the model (35) with \(N \ge 2\), the preceding study [12] has reported the appearance of collective motions of camphor disks. As the future work of the present study, it is worthwhile to investigate the stability of asymmetrically or symmetrically rotating solutions mathematically. Indeed, it has been shown numerically in [34] that an asymmetrically rotating solution is stable as far as it exists and moreover, an oscillating and rotating motion appears via a Hopf bifurcation from a symmetrically rotating solution branch.