Abstract
Empty houses, Akiya, are of substantial concern to the ageing society of Japan; the ratio of Akiya is projected to worsen to 30.5% in 2033. Such a high ratio of Akiya will influence the social system and the Japanese economy overall in the near future. Nonetheless, Akiya continues to increase unabated because there are no specific government measures to address the problem. In this study, we develop a simple mathematical model based on Markovian transition whereby we anticipate the future tendency of empty houses based on real data. Using the model, we demonstrate three tax policies and estimate the effectiveness of the policies considering the extent of Akiya and local government financing. We also consider the spatial distribution of Akiya and suggest both a spatially and quantitaviely effective policy that could reduce Akiya. Our study suggests that to solve the Akiya problem, tax policies and spatial policies should be initiated together, and the policies should be conducted strategically based on the regional characteristics of cities such as economic scale and the population age distribution.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Population ageing is a worldwide issue. According to the report of the Department of Economic and Social Affairs of the United Nations Secretariat, the number of persons aged 60 years or over in the world reached 962 million in 2017 and is expected to increase to 2080 million by 2050 [1]. Additionally, older people are projected to account for one in five of the global population in 2050. In 2050, older people are expected to account for 35% of the population in Europe, 28% in North America, and 24% in Asia. Japan has the most aged population in the world. The population aged 60 or over in Japan was 33% in 2017 and is projected to reach 42% by 2050.
The fundamental cause of an aging society is a decreasing total population, which heightens various problems such as economic market contraction and a shrinking labor pool. An aging society also accentuates problems associated with the provision of pensions, housing, transportation, and more [2]. The problem of vacant homes, called Akiya in Japanese, is a representative phenomenon of the aging society of Japan. Changes in the economic structure have increased the number of nuclear families, and houses that belonged to older generations remain as Akiya after the householder has died. The percentage of Akiya in Japan was 13.5% in 2013 (statistically measured data), and the percentage is expected to increase to 30.5% in 2033 implying that one in three houses will become Akiya (Fig. 1a, [3, 4]).
Akiya houses create various problems unless they are managed consistently. Akiya quickly degrades with age and spoils a town’s appearance and landscape. In addition, Akiya often becomes a hotbed for pests and stray animals. Empty houses also attract crime such as arson and trespassing. Such criminal activity creates financial problems for the owners of Akiya and causes house prices to fall. Thus, an increase in Akiya affects the residential environment of the surrounding area. Moreover, when the rate of empty houses exceeds 30%, the local government may risk fiscal collapse because new residents will not move in, and tax revenue will be lost. The rate of Akiya in Yubari city of Japan, which collapsed fiscally in 2007, was 33% [5], and the rate of empty houses in Detroit, United States, where a fiscal collapse occurred in 2013, was 29.3% [6].
The problem of Akiya is a local issue but also a dilemma that Japan faces as a country [7]. Recently, the Japanese government established a law allowing the demolition of empty houses without owners’ permission for severely affected states. The government also instructed local governments to consider such measures because Akiya that is ignored exacerbate the aforementioned problems. At this stage, specific policies are entrusted to local governments, and various measures have been devised [8]. On representative case is the reuse of land after Akiya have collapsed. Reuse of Akiya is considered one of the most effective measures for decreasing the number of Akiya. For example, small car parks and guest houses are the most common examples of Akiya reuse in Japan. In particular, car parks are the most popular example of reuse because they represent low risk business that requires minimal management.
Although the Japanese government has begun to take action to mitigate the Akiya problem in 2015, it is local governments that must manage the problem in the absence of prescribed measures. That is, local government measures are not yet integrated and are executed without predicted outcomes. Thus, in this study, we suggest a simple probability mathematical model based on Markovian transition that can anticipate the future extent of Akiya. Using this model and real data on the Japanese population, taxes, land prices, and current Akiya rates, we suggest tax policies that can reduce the extent of Akiya. We also discuss the optimal policies by including the effects of the financial aspects and spatial condition of the model. Our study suggests that policies to decrease Akiya should be chosen based on regional characteristics such as economic scale and population age distribution.
Statistical prediction of Akiya and model assumptions. a Statistical data for Japanese Akiya (blue squares) and numerical prediction of Akiya by the mathematical model (red dots). b Schematic diagram of mathematical model. c Transition probability functions from one state to another. In \(r_{ij}\), the dots are real data of 1-[survival rate]. The survival rate is defined by the ratio of those who survive to the specified age on the life table including annual change. Survival is based on the real data for Japanese women [10] (Table 1). \(Y_c=87.14\) is the average lifespan of Japanese women [10]. The detailed parameter values are shown in Table 2
2 The Akiya model
We develop a mathematical model that has three transition states: residential dwelling, empty house (Akiya) state, and Akiya reuse. In what follows, we construct a minimal model based on the Markovian transition [9].
2.1 Modeling for resident house—Akiya–Reuse dynamics
We assume that there are \(N^2\) land parcels \(\{(i, j)|1\le i \le N, 1\le j\le N\}\), each of which represents one of the three states. Let \(S_{ij}(t)\) be the state variable at the land parcel (i, j) in year t. Then, for a single parcel, we have
We also define the ratio of lands at each state by
We assume that the state of each parcel transits to the other state every year as shown in Fig. 1 with a probability \(p_{ij}(t)\)
Note that each parcel keeps a state with a probability of \(1-p_{ij}(t)\). In what follows, we construct the transition probability functions.
2.1.1 Transition from \(H\rightarrow E\)
The state of empty house occurs when the last resident in the house has died and the house is empty. Thus, we assume that \(r_{ij}(t)\) is determined by the probability that the resident is going to die in the next year and is given by
where \(Y_{ij}(t)\) is the age of the last resident living at parcel (i, j) in t year, and \(Y_c\) is the average lifespan. \(\alpha \) is a positive constant that controls the degree of stochasticity in the transition. We determine \(\alpha \) using the data for the survival rate of the house that survives in the next year (Table S1). That is, we calculate the death rate (\(1-\)[survive rate]) from the real data of the survival rate of Japanese women [10] fitted \(r_{ij}(t)\) to the death rate data and estimated \(\alpha \) as shown in Fig. 1c (Left panel). Since the lifespan of women is longer than men, we use the data for women.
2.1.2 Transition from \(E\rightarrow R\)
We assume that whether the owner of an empty house retains it as Akiya or reuses the property is determined by the economic gain or loss, which is given by the following probability function.
where \(\beta \) is a positive constant that controls the degree of stochasticity in the transition, \(V_{ij}^{\text {gain}}(t)\) is the function describing the gains expected by the owner when the Akiya state changes to the reuse state each year, and \(V_{ij}^{\text {out}}(t)\) is the function describing the presumed loss for the owner when the Akiya state changes to reuse each year.
In more detail, we assume the following:
The direct income on reuse management is dependent on the economic location; namely, whether the street is busy or not. Thus we assume that profit from reuse is proportional to the land price.
Reuse competition exists, and reuse income decreases depending on the amount of similar reuse in the area.
Then, the detailed form of \(V_{ij}^{\text {gain}}(t)\) and \(V_{ij}^{\text {out}}(t)\) are given as
where \(\omega _{ij}\) is the land price of each single land parcel, \(\varphi \) is the property tax rate on the land, \(\rho \) is the special discount rate for reduced property tax on the land, which is the current policy in Japan. \(v_h\) is the minimum utility charge for Akiya, \(v_p\) is the initial investment for reuse, and \(T_p\) is the expected period within which owners want to recover the initial investment in reuse, and we use random value in [1, 20](years). \(c_1\) and \(c_2\) are the estimation constants for the reuse profit and land tax, respectively, and these values are chosen by model fitting using real data. \(F_{ij}^{nc}\) is the decreasing function describing the influence of reuse competition, and we simply assume that the competition effect is determined globally by the reuse ratio for the total area such that
where \(c_3\) is a positive constant determining the effect of the degree of competition.
2.1.3 Transition from \(R\rightarrow H\)
We suppose that the transition from the reuse state to the house state is determined by the net income of reuse management. If net income is a deficit, the owner wants to sell the land. For simplicity, we assume that the land is sold only for residential purposes. Then, the probability of the transition from \(R\rightarrow H\) can be written as
where \(V_{ij}^{\text {in}}(t)\) is net income and given as
2.1.4 Spatial dependence/independence in the model
When we consider the change of Akiya from a global perspective and in a broad area, we assume that land price is homogeneous and averaged. In this case, we consider a spatially independent Markov transition model for Akiya with
This assumption is applicable to the case where we seek a predicted number of Akiya on a global scale.
On the other hand, when we change our perspective to a local area, the land price varies. Typically, the city center has higher land prices, and suburbs have lower land prices. In this case, we assume a spatially dependent land price, such as
In the representative results, we estimate the function \(\omega (i, j)\) using real land price data for Hiroshima city in Japan. The detailed function is provided in the results section.
Policy diagram and the income of local government. a Schematic diagram for each policy. The red arrow implies an activation effect on the transition from E to R from either a subsidy policy or abolition policy. The blue symbol implies an inhibition effect on the transition both from E to R and from R to H by a land tax mitigation policy. b Schematic diagram for local government income. \(N_{X} (X, Y\in \{ H, E, R \})\) implies the total number at X state. \(N_{X\rightarrow Y}\) indicates the number of transited lands from X state to Y state. \(G_{sub}\) is the subsidy from the central government. The details of \(I_{tax}^{H},~P_{tax}^{H},~P_{tax}^{E},~I_{tax}^{R}\), and \(L_{tax}\) are given in (6)
2.2 Policy and cost evaluation function
2.2.1 Policy for reducing Akiya
We consider the following three policies executable by local or central government (Fig. 2a).
(i) Subsidy policy: A policy whereby the local or central government supports the dismantling cost of Akiya or a subsidy for the initial cost of reuse investment.
(ii) Mitigation policy for land property tax: A policy that decreases the land property tax.
(iii) Special tax abolition policy applied to house property: A policy that abolishes the special tax rate (discount rate) applied to the land where the house is built.
The subsidy policy is given in (1) of the model with
Thus, this policy promotes the transition of \(E \rightarrow R\). On the other hand, the mitigation policy is given by a decrease in \(\varphi \) in the model, and this policy inhibits the transitions of both \(E \rightarrow R\) and \(R \rightarrow H\). The abolition policy is given by an increase in \(\rho \) in (1) of the model, and \(\rho =1\) is the state with no special discount rate. This policy promotes the transition of \(E \rightarrow R\) (Fig. 2a).
2.2.2 Cost evaluation function
The policies above affect the financial situation of local governments directly. Thus, we introduce a cost evaluation function whereby the gain or loss for local government from policy implementation can be evaluated. The local government earns income from tax, and we evaluate the optimal policy by measuring how much the income changes before and after policy implementation. We consider the tax income that the local government obtains at each state, such as
We define the tax incomes above as
In addition, we consider the subsidy from the central government (\(G_{sub}\)). The diagram for the local government incomes are shown in Fig. 2b.
Then, defining the number of states (H, E, R) and transited states (\(H\rightarrow E,~E\rightarrow R, ~R\rightarrow H\)) by \(N_H,~N_E,~N_R,\)\(N_{H\rightarrow E},~N_{E\rightarrow R},~N_{R\rightarrow H}\), respectively, the expected income of local government at t year is given as
On the other hand, the subsidy from the central government depends on the size (population) of the prefecture or city, and we assume that the subsidy is determined by the number of resident houses and is decreased by the number of Akiya because people do not live in Akiya. Then, the expected subsidy from central government at t year is given as
where \(\delta \) is a positive constant reflecting the weight of the decreasing degree of subsidy by the ratio of Akiya to the resident houses.
Now, we define an estimation function whereby we can anticipate the future cost of the three policies: subsidy policy, mitigation policy, and abolition policy. We call this function cost estimation function and define it as the following.
Finally, since we do not have an absolute cost value for local government, we compare whether the policy is effective by measuring the value of the increase or decrease in the cost estimation before and after the policy implementation each year. We call this measure cost evaluation function and define it as the following.
where \(L_0\) and \(P_0\) represent the local government incomes from the land property tax and Akiya before the policy, respectively, and they are given as \(L_0=1.4 \%\times \omega \) and \(P_0=(1/6)\times 1.4\%\times \omega \) (1/6 is the special discount rate of property tax, which is currently underway in Japan). \(EV_{policy}(t^*)>0\) implies that local government income at \(t^*\) year increases after policy implementation is effective. In contrast, \(EV_{policy}(t^*)\le 0\) implies that nothing happens, or the income decreases after policy implementation implying that the policy is ineffective and that no policy is optimal.
2.3 Reflection of regionality using parameter choice of real data
To reflect regionality, we chose the real land price and the initial ratio of each state in that region based on data provided by the ministry of land, infrastructure, transport and tourism (MLIT) of Japan. We also chose the age of the householder using data provided by the Ministry of Internal Affairs and Communications (MIC) of Japan. The detailed data are shown in Table 1. We chose other parameters based on the real data given in Table 2.
To choose the constants that control the degree of stochasticity in each transition, we estimated the model with the Akiya data measured and anticipated by the Ministry of Internal Affairs and Communications (MIC) of Japan and the Nomura Research Institute (Fig. 1a). For this parameter fitting, we used the real data for the Japanese national average land value for each year during [1983, 2013] and compared the value \(x(t)+y(t)\) of the model with the given data [11,12,13, 15]. The real data and detailed parameter values are shown in Table 2 and Supporting informations (Table S1 and Table S2).
3 Result
3.1 Future tendency of Akiya: countryside areas versus urban areas
We simulated the model for countryside and urban cases for 100 years using the initial data for 2016 (Fig. 3a, b). Both results show that the rate of residences will decrease, and both Akiya and reuse will increase. In the case of countryside areas, the ratio of Akiya is always smaller than that of reuse. In contrast, urban cases show that the ratios of reuse and Akiya switch for several years, and the ratio of reuse will dramatically increase. If we compare only the Akiya rate between the countryside and urban cases, the countryside case has a higher rate. However, the increasing tendency of the urban case with respect to the number of Akiya and reuse ratios exceeds that of the countryside case because of a significant increase in reuse in urban areas indicates that the transited total number of Akiya from the state of residence will decrease more significantly in urban areas than countryside areas (Fig. 3c). This implies that Akiya is a problem afflicting both countryside and urban areas, and urban areas may be more of a future concern.
Results after carrying out policies. a Subsidy policy for the initial cost of reuse investment. b Mitigation policy for land property tax. c Abolition policy for special taxes applied to house property. Green and red dots indicate the case for countryside areas and urban areas, respectively. The detailed parameter values are given in Tables 1 and 2
3.2 Optima policies for reducing Akiya
As shown in Fig. 3, the ratio for each state tends to converge over several decades. Thus, we explored the effectiveness of the three policies under the condition that each policy is in existence during the 100 years. To compare the effectiveness of the policy, we investigated the relative variation in Akiya and resident houses using the ratios before/after policy execution, respectively. The results are shown in Fig. 4.
First, we found that the results varied among countryside and urban areas depending on the policies. For the subsidy policy, both countryside and urban areas show a notable decrease in Akiya (Fig. 4a). Additionally, the rate of residences showed a tendency to increase and a constant tendency in countryside and urban areas, respectively, indicating that the subsidy policy is effective for both countryside and urban areas. Next, we investigated the effect of the mitigation policy of the land property tax (Fig. 4b). The results showed that countryside areas are affected to a small extend, and there is a substantial decrease in Akiya in urban areas as the rate of property tax decreases. However, the rate of resident houses in urban areas also showed a significant decrease implying that the mitigation policy increases the ratio of the reuse state and substantially decreases the resident population. Thus, we conclude that the mitigation policy is not effective in urban areas but somewhat effective in countryside areas. Finally, we investigated the effect of an abolition policy for the special tax applied to houses (Fig. 4c). The results showed that countryside areas are not as effective as urban areas in decreasing the ratio of Akiya because the ratio of resident houses is constant as the special tax rate (\(\rho \)) increases. This result indicates that the special tax abolition policy is more effective in urban areas than countryside areas.
3.3 Optimal policies with respect to the cost evaluation function
We consider the effectiveness of the policy from the perspective of the cost to local governments. We first investigated how the local government income changes every year with the absence of policy implementation (Fig. 5a). We found that local government income in countryside areas substantially decreases with no policy implementation. On the other hand, urban areas show an increase in income for the initial 25 years even without a policy although urban areas show a negative value after that. This result indicates that local government income will decrease with future Akiya transition, and the effect of a decrease in local government income will be greater in countryside area than urban areas.
We explored how each policy affects the future income of local governments. Since income without policy varies each year as shown in Fig. 5a, we calculated the difference in income without/with policy. We found that the subsidy policy is effective in countryside areas but not in urban areas (Fig. 5b). Similarly, the mitigation policy also showed an increase in income in most regions except for the first two years; however, this was not the case for almost all parameter regions in urban areas (Fig. 5c). For the abolishment policy, we found that both countryside and urban areas showed a positive effect in most of the parameter regions (Fig. 5d).
We summarize the policy results for effectiveness with respect to the number of Akiya and cost evaluation in Fig. 5e (the black and red characters are the results for the number of Akiya, Fig. 4, and the cost evaluation, Fig. 5b–d, respectively). The results showed that the subsidy policy is most effective in countryside areas. In contrast, the abolishment policy is most effective in urban areas. The mitigation policy is least effective in urban areas. Overall, we consider it important to include the cost evaluation perspective when we consider the optimal policy, and the policy selected should be different for countryside and urban areas.
Cost evaluation on each policy. a Tendency of cost evaluation for 100 years for urban areas (red) and countryside areas (green) when policies are not enacted. b–d Tendency of cost evaluation for 100 years for each policy. White circles or dots show the regions where the cost evaluation function has a negative value implying that policy implementation results in a worse situation than no policy implementation. e Summary table for the effectiveness of policies. The black characters indicate the case for each policy shown in Fig. 4, and the red characters indicate the case for each policy with respect to cost evaluations. The detailed parameter values are given in Tables 1 and 2
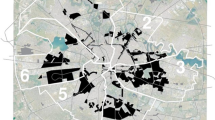
Spatial distribution of each state by spatially heterogeneous land price. a The upper panel shows a map of Hiroshima city. The lower panel shows land prices for subregions in Hiroshima city (real data, green dots) given in Table 3 and the estimated graph. The estimated graph was obtained by exponential regression calculated by \(\omega _{ij}(x)=5\times 10^{7}\exp {(-0.16x)}\). b Spatio-temporal dynamics for 100 years. c The rate of each state for case (b)
3.4 Spatial policy for reuse decentralization
We consider the case whereby the considered region is small in scale and the land tax has spatial dependence. We investigated the land price of districts in Hiroshima city (Table S3, [17]) and plotted the data with the distance from the Hiroshima station, which is located in the center (the busiest area) of Hiroshima city (Fig. 6a). Next, we estimated the data using exponential regression and approximated the graph to calculate the land price function \(\omega _{ij}\). The approximated function is given by \(\omega (i, j)=5\times 10^{7}\exp {(-0.16\sqrt{(i-N/2)^2+(j-N/2)^2})}\).
Using these data, we explored how the three states are spatially distributed (Fig. 6a). If the resident area is concentrated in the center of the city, the local government can cut the budget for infrastructure maintenance because the area required for maintenance is reduced. However, we found that reuse is concentrated in the center of the region and both Akiya and house states are distributed in the suburbs. This is because land prices are high in the city center and reuse income is expected to be higher in the city center than the suburbs. This implies that local government should conduct infrastructure maintenance in all areas because the residence area density is high even in the suburbs.
Thus, we considered a measure by which we can decentralize reuse and increase the possible resident area as a spatial policy. We focused on how the degree of competition effects reuse decentralization. In local areas, income from reuse management is likely to be affected by the number of similar reuse in the surrounding area. Thus, we extend the function \(F_{ij}^{nc}\) of (2) to
where
That is, \(z_{ij}^{ar}\) indicates the ratio of the neighboring reuse around land in (i, j). The parameters \(c_i (i=3,\dots ,5)\) are positive constants determining the degree of the competition effect. The function \(G_{ij}\) implies the global competition effect, and \(L_{ij}\) implies the local competition effect. A detailed example is given in Fig. 7a.
Spatial policy for reuse decentralization. a Revenue reduction by competition dynamics. The bold black line is the case for the absence of competition, the green line is the case for mid-level competition, and red line is the case for high-level competition in reuse (\(z_{ij}^{ar}\)). b The spatial distribution of each state with the competition effect. c The rate of each state for the area (left panels) and the half-radius area (right panels). The detailed parameter values are given in Tables 1 and 2
By changing the parameters \(c_4\) and \(c_5\), we tested the effect of the degree of local competition. We found that the phenomenon of reuse centralization is reduced as the local competition level increases, and the distribution of reuse is almost homogeneous when the level of local competition is high (Fig. 7b). Next, we compared the ratio of reuse for the whole area and the half-radius area from the center (Fig. 7c). The results show that the ratios of the three states for the whole area are not sensitive to local competition levels. In contrast, the reuse ratio decreases notably, and the summation ratios of resident houses and Akiya increase in the half-radius area. This implies that a spatial policy using local competition levels can decentralize reuse and limit the area for residence to the central part of the city without changing the total number of Akiya.
4 Discussion
The empty house is a significant area of concern for Japan and its ageing society. This area of concern is anticipated to influence the social system and economy of Japan in the near future. However, no specific measures have been implemented to address the empty house problem. In this study, we developed a simple mathematical model that anticipates the future tendency of the empty house phenomenon based on real data. Using the model, we first found that the Akiya problem might be more serious in urban areas than countryside areas in the future (Fig. 3c). In the case of urban areas, the ratio of Akiya and reuse states approached 50% implying that one in two houses will be empty. Since the total number of houses is significantly higher in urban areas than countryside areas, the whole city is in danger of hollowing out.
We demonstrated three policies using the model and found that the efficiency of the policy to decrease the number of Akiya is sensitive with respect to age distribution and city land prices. For the representative parameter sets, we found that the subsidy policy is effective in both countryside and urban areas, but the special tax abolition policy applied to house property is only effective in urban areas. We also found that the mitigation policy for land property tax is not effective in countryside areas and is even less effective in urban areas. Since the mitigation policy creates substantial inhibition effects on the transition from Akiya to reuse and from reuse to resident houses, it may retain the Akiya state. Consequently, the mitigation policy would not lead to a decrease in the number of Akiya. On the other hand, both the subsidy policy and abolition policy create a substantial activation effect on the transition from Akiya to reuse, and these policies may result in a positive effect in reducing Akiya. However, in contrast to the subsidy policy, the abolition policy was less effective in countryside areas. The reason for the abolition policy’s low level of effectiveness is low initial land prices in countryside areas. These low initial prices render the abolition policy for special tax negligible in terms of results. On the one hand, when we consider cost evaluation, the results differed from the result where we merely considered the effectiveness of policy as the number of Akiya. For urban areas, both subsidy and mitigation policy resulted in a highly negative effect on local government finances. This implies that although the rate of Akiya can be reduced, the policy related to tax can influence the financial state of local government significantly, and the policy should be chosen carefully.
In this study, we also considered the spatial distribution of reuse states and found that the city center is likely to be dominated by reuse. This situation may result in wasteful use of land. Since the Japanese population is decreasing, local government income will decrease in the future. Thus, concentrated cities will help the financial situation of local governments who can, at least, allocate resources for infrastructure maintenance. We found that when the competition among reuse agents is increased, reuse centralization is ameliorated and resident space increases. Local government control of the level of reuse competition may not be feasible. However, if the local government subsidizes reuse depending on reuse types, this might prevent extensive centralization.
Our study suggests that to solve the Akiya problem, tax policies and spatial policy should be considered together, and any policy must be implemented carefully based on the regional characteristics of the city. In this study, we suggested a simple mathematical model, and it may not be appropriate to use our model to predict the accuracy of quantity data of Akiya. However, it is important to identify a measure by which the future can be approximated, particularly for social or economic issues related to budget and policy where failure cannot be permitted. Our model is the first to suggest that these real societal problems at the national level could be solved with an interdisciplinary mathematical approach.
In the current study, we did not consider the effect of population dynamics in our model such as a trend in population structure for the future. However, changing to aging society and declining population of Japan must be important factors affecting Akiya dynamics. The factor of population dynamics may be involved in the transition probability from resident dwelling state to Akiya state, and the transition probability from reuse state to resident dwelling state. It also could be a challenging work to combine an age structure model with current stochastic model.
Finally, Akiya may not only be the problem in aging society of Japan but also is the important issue in Europe, although the cause of the increase of empty house is slightly different. There are 11 million empty houses across Europe; 3.4 million homes lying vacant in Spain, over 2 million empty in France, and the same in Italy, 1.8 million in Germany and more than 700,000 in the UK [18]. It is emerging as a significant social problem. In this study, we only focused on the empty house problem of Japan but our mathematical approaches to solve Akiya problem could be generalized and applicable to the empty house problems based on different causes by defining the transition probability functions properly according to the situation.
References
World Population Ageing, United Nations. https://www.un.org/en/development/desa/population/publications/pdf/ageing/WPA2017_Highlights.pdf. Accessed 7 Jan 2019
Problems of rapid population decline and super-aging, Cabinet Office, Japan. https://www5.cao.go.jp/keizai-shimon/kaigi/special/future/sentaku/s2_3.html. Accessed 7 Jan 2019
Japan has so many vacant homes it’s giving them away, CNN. https://edition.cnn.com/2018/12/05/asia/japan-vacant-akiya-ghost-homes/index.html. Accessed 7 Jan 2019
News Release: Nomura Research Institute (2016). https://www.nippon.com. https://www.nri.com/-/media/Corporate/jp/Files/PDF/news/newsrelease/cc/2016/160607_1.pdf. Accessed 14 Aug 2018
Yubari, Japan: a city learns how to die. https://www.theguardian.com/cities/2014/aug/15/yubari-japan-city-learns-die-lost-population-detroit. Accessed 29 Aug 2018
Detroit: From Motor City to Housing Incubator. https://www.nytimes.com/2017/11/04/business/detroit-housing.html. Accessed 11 June 2018
Empty Homes: A Growing Problem for a Shrinking Nation (2014). https://www.nippon.com/en/currents/d00140/empty-homes-a-growing-problem-for-a-shrinking-nation.html. Accessed 9 Mar 2018
Hidetaka Yoneyama, Vacant Housing Rate Forecast and Effects of Vacant Homes Special Measures Act: Fujitsu Research Institute (2015). https://www.fujitsu.com/jp/group/fri/en/column/message/2015/2015-06-30.html. Accessed 9 Mar 2018
Satake, A., Rudel, T.K.: Modeling the forest transition: forest scarcity and ecosystem service hypotheses. Ecol. Appl. 17(7), 2024–2036 (2007)
Ministry of Health, Labour and Welfare (Japan), Year life table (2016). http://www.mhlw.go.jp/toukei/saikin/hw/life/life16/index.html. Accessed 20 June 2018
Minisstry of Land, Infrastructure, Transport and Tourism (Japan), Land price. http://www.mlit.go.jp/totikensangyo/totikensangyo_fr4_000043.html. Accessed 20 June 2018
Ministry of Internal Affairs and Communications (Japan), Statistical data for empty house. https://www.pref.kagoshima.jp/ah14/documents/61643_20170915194851-1.pdf. Accessed 11 July 2018
National Institute of Population and Social Security Research (Japan), Statistical data for number of households. http://www.ipss.go.jp/pp-ajsetai/j/HPRJ2018/t-page.asp. Accessed 11 July 2018
Ministry of Internal Affairs and Communications (Japan), Tax. http://www.soumu.go.jp/main_sosiki/jichi_zeisei/czaisei/czaisei_seido/ichiran01.html. Accessed 2 Dec 2018
Ministry of Internal Affairs and Communications (Japan), Population of Japan. https://www.stat.go.jp/data/jinsui/2.html. Accessed 2 Dec 2018
Ministry of Health, Labour and Welfare (Japan), Overview of basic statistical survey on wage structure (2017). https://www.mhlw.go.jp/toukei/itiran/roudou/chingin/kouzou/z2017/dl/13.pdf. Accessed 25 Dec 2018
Hiroshima prefecture office (Japan), Hiroshima land price survey 2018. https://www.pref.hiroshima.lg.jp/soshiki/39/30chikachosa.html. Accessed 2 Feb 2019
Scandal of Europe’s 11m empty homes, The Guardian (2015). https://www.theguardian.com/society/2014/feb/23/europe-11m-empty-properties-enough-house-homeless-continent-twice. Accessed 28 Jan 2019
Acknowledgements
This work was partially supported by Grants-in-Aid for Scientific Research from the Ministry of Education, Culture, Sports, Science and Technology, Japan (19H01805 and 17KK0094 to S.S.L), the JST PRESTO program, Japan to S.S.L. (JPMJPR16E2), and A3 Foresight Program. The authors would like to express thanks to Prof. A. Satake (Kyushu University, Japan) and Prof. M. Nagayama (Hokkaido University, Japan) for their valuable comments for this study.
Author information
Authors and Affiliations
Contributions
SSL designed the study and developed the mathematical model, simulated and analyzed the data, and wrote the paper. MN and MM constructed the programming code and discussed the study.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Seirin-Lee, S., Nomata, M. & Mukunoki, M. Mathematical modeling and regionality-based optimal policy to reduce empty houses, Akiya, in Japan. Japan J. Indust. Appl. Math. 37, 365–382 (2020). https://doi.org/10.1007/s13160-019-00400-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13160-019-00400-3