Abstract
The acquisition of diagnostic competences is an essential goal of teacher education. Thus, evidence on how learning environments facilitate pre-service teachers’ acquisition of corresponding competences is important. In teacher education, approximations of practice (such as simulations) are discussed as being learning environments that can support learners in activating acquired knowledge in authentic situations. Simulated diagnostic interviews are recommended to foster teachers’ diagnostic competences.
The conceptualization of diagnostic competences highlights the importance of cognitive and motivational characteristics. Motivational learning theories predict that the activation of acquired knowledge in learning situations may be influenced by motivational characteristics such as individual interest. Although teachers’ diagnostic competences constitute an increasing research focus, how cognitive and motivational characteristics interact when shaping the diagnostic process and accuracy in authentic learning situations remains an open question.
To address this question, we report on data from 126 simulated diagnostic one-on-one interviews conducted by 63 pre-service secondary school mathematics teachers (students simulated by research assistants), studying the combined effects of interest and professional knowledge on the diagnostic process and accuracy. In addition to the main effect of content knowledge, interaction effects indicate that participants’ interest plays the role of a “door-opener” for the activation of knowledge during simulation-based learning. Thus, the results highlight the importance of both, cognitive and motivational characteristics. This implies that simulation-based learning environments should be designed to arouse participants’ interest to support their learning or to support less interested learners in activating relevant knowledge.
Zusammenfassung
Ein wesentliches Ziel der Lehramtsausbildung ist es, den Erwerb diagnostischer Kompetenzen zu fördern. Um diesen Erwerb bestmöglich zu unterstützen, sind Implikationen hinsichtlich der Gestaltung entsprechender Lernumgebungen von zentraler Bedeutsamkeit. In der Lehrerbildung wird insbesondere der Einsatz sogenannter „approximations of practice“, wie beispielsweise Simulationen, diskutiert, um die praktische Anwendung gelernter Inhalte zu trainieren. Simulationen diagnostischer Interviews werden für die Förderung diagnostischer Kompetenzen empfohlen.
Konzeptualisierungen diagnostischer Kompetenz betonen dabei die Rolle kognitiver und motivationaler Lernvoraussetzungen. Motivationale Lerntheorien legen nahe, dass die Wissensaktivierung in solchen Lernumgebungen möglicherweise durch motivationale Merkmale, wie beispielsweise dem Interesse, beeinflusst wird. Wie das Zusammenspiel kognitiver und motivationaler Personenmerkmale mit dem Verlauf diagnostischer Prozesse und der Akkuratheit der Diagnose in simulationsbasierten Lernumgebungen zusammenhängt, ist bisher jedoch unklar.
Um derartige (Interaktions-)effekte zwischen professionellem Wissen und Interesse auf den Prozess und die Akkuratheit der Diagnose zu untersuchen, wurden 126 simulierte diagnostische Einzelinterviews von 63 Mathematiklehramtsstudierenden (Lehramt an weiterführenden Schulen; Schülerrolle gespielt von Projektmitarbeiterinnen) analysiert. Neben einem Haupteffekt von Fachwissen, implizieren die Interaktionseffekte, dass das Interesse der Teilnehmenden die Rolle eines „Türöffners“ für die Aktivierung von Wissen zu übernehmen scheint. Die Ergebnisse bestätigen damit die Relevanz beider Personenmerkmale, motivationaler und kognitiver Art. Eine Implikation ist daher, dass simulierte Lernumgebungen darauf abzielen sollten, das Interesse der Lernenden zu wecken, oder über entsprechende Unterstützungsmaßnahmen verfügen sollten, um Lernende mit fehlendem Interesse bei der Wissensaktivierung zu unterstützen, um Lernprozesse optimal zu unterstützen.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The importance of diagnostic competences for adaptive teaching is mostly undisputed (Behrmann and Souvignier 2013). The process of diagnosing can be defined as the goal-directed accumulation and integration of information to reduce uncertainty regarding educational decisions (Heitzmann et al. 2019). The situations, in which teachers can gather such diagnostic information vary substantially (Karst et al. 2017; Philipp 2018). In such situations, teachers must elicit, interpret, and use verbal and written answers during whole-group classroom discussions or individual work.
As effective teacher decisions rely on the accurate assessment of students’ current learning (van de Pol et al. 2010), the acquisition of diagnostic competences is considered an essential part of pre-service teacher education (Kultusministerkonferenz 2019). Diagnostic competences are often conceptualized as judgment accuracy, which is the match between a teacher’s estimation of a student’s test performance and its actual test performance. Following a holistic approach, conceptualizations of diagnostic competences go beyond this (Südkamp et al. 2012), and include the processes of evidence generation during diagnosis (Praetorius et al. 2012; von Aufschnaiter et al. 2015). This broader conceptualization of diagnostic competences allows for a differentiated perspective on teachers’ diagnoses, as well as learning opportunities to shape and foster diagnostic competences. This contribution focuses on both the diagnostic processes and accuracy.
Weinert (2001) defines “competence” as an individual’s disposition to solve a specified type of problems, as well as the motivational, volitional, and social dispositions required to successfully use these skills in various situations. The term “disposition” indicates that the individual coherently shows successful performance according to predefined criteria when engaging in such situations. These dispositions are assumed to be specific to certain problem types, and learnable (Herppich et al. 2018). According to Heitzmann et al. (2019), diagnostic competences require the activation of professional knowledge in the diagnostic process to arrive at an accurate diagnosis, which is one of the central criteria for judging performance in diagnostic situations. Definitions of diagnostic competences highlight the role of both cognitive and motivational characteristics in explaining teachers’ performance in diagnostic situations. Whereas the role of professional knowledge (e.g., pedagogical content knowledge about students’ misconceptions) in diagnostic competences is explicitly emphasized (Tröbst et al. 2018), motivational characteristics are mostly assumed to have a moderating influence (Herppich et al. 2017) on the effects of knowledge. The features of diagnostic processes are usually considered an additional intermediate indicator for mastering a specific diagnostic situation. Corresponding features, such as the extent to which the teacher engages in actions to elicit students’ understanding in a diagnostic interview (e.g., posing questions; see van den Kieboom et al. 2014), are usually assumed to be based on similar individual characteristics.
Prior findings highlight the need to foster the diagnostic competences of pre-service teachers (Kron et al. 2021; Praetorius et al. 2012), as the acquisition of initial conceptual knowledge (so-called personal knowledge, pPCK; e.g. Carlson et al. 2019), often in a declarative form during teacher education, does not automatically lead to a successful application of knowledge. Grossman et al. (2009) propose approximations of later professional practices as a specific type of learning environment, that (given suitable scaffolds) allows learners to apply, elaborate upon and extend their initially acquired conceptual knowledge within authentic settings. Simulation-based learning environments, which model “a natural or artificial system with certain features which can be manipulated” (Heitzmann et al. 2019), can be regarded as such approximations (Fischer and Opitz 2022). Simulated diagnostic interviews, in which pre-service teachers interview students played by trained actors, are examples of such simulations. Engaging in these environments is assumed to complement acquired conceptual knowledge with strategic and procedural knowledge, which are considered crucial for the successful activation and application of knowledge (Förtsch et al. 2019). This type of applicable knowledge resonates with the concept of enacted pedagogical content knowledge (ePCK) in the refined consensus model of PCK (Carlson et al. 2019). To support the process of establishing applicable knowledge, it is important to understand the conditions under which pre-service teachers activate and apply their knowledge during approximations of practice (Carlson et al. 2019; Grossman and McDonald 2008). Furthermore, it is an open question which knowledge component in terms of knowledge content is actually activated (and potentially developed toward ePCK) during approximations of practice.
In analogy to real diagnostic situations (Herppich et al. 2018), it is plausible that also during approximations of practice motivational dispositions play the role of a “door-opener” and trigger the activation of specific knowledge components. Owing to the complexity of authentic situations (even if approximated), this can be of particular importance to ensure that pre-service teachers approach the presented situations with the intended knowledge components (e.g., PCK, see Sect. 1.2.) instead of merely focusing on general pedagogical knowledge during the diagnosis of mathematical understanding. More specifically, research indicates that individual interest in a topic shapes situational interest, which in turn has been found to trigger deeper processing and sustained attention during learning (Ainley et al. 2002; Hidi and Renninger 2006). However, it remains an open question how different facets of interest moderate the effects of different components of professional knowledge regarding diagnostic competences.
Heitzmann et al. (2019) note that research should investigate diagnostic competences by considering individual dispositions holistically, focusing on diagnostic judgement accuracy and the diagnostic process that leads to that respective judgment. This contribution focuses on the main and interaction effects of interest and professional knowledge on the diagnostic process and diagnostic accuracy in roleplay-based simulations, which approximate an authentic setting from later teaching practice. The relationship between the measure of a knowledge component and pre-service teachers’ performance during the simulation of diagnostic practice is considered as evidence of activation of the respective knowledge component. We lay out the theoretical foundations of our study in more detail in the following subsections.
1.1 Diagnosing Students’ Mathematical Understanding
Assessing students’ mathematical understanding requires teachers to acquire diagnostic competences. Judgment or diagnostic accuracy is commonly used as a measure of the diagnostic competences of teachers. It refers to the match between teachers’ assessment of students’ understanding and their actual understanding as measured by an independent test (Südkamp et al. 2012) or as presented in a crafted vignette or simulation (Chernikova et al. 2019). Behrmann and Souvignier (2013) established a relationship between teachers’ judgment accuracy and their students’ learning. From this perspective, diagnostic competences are observable in the accuracy of teachers’ diagnoses. In this sense, individual characteristics such as cognitive and motivational characteristics are assumed to form the central basis of diagnostic competences. However, competences go beyond these individual characteristics because accurate diagnoses require the activation of applicable knowledge in authentic situations under specific motivational conditions (Herppich et al. 2018).
The sole focus on diagnostic accuracy has been criticized in the past because the diagnostic process often remains unexplained and is usually not investigated (Herppich et al. 2018). Addressing this, different models of diagnostic processes were developed, moving from generic models (Klug et al. 2013) that focus on process regulation, to more detailed models that focus on how diagnostic information is gathered and processed (NeDiKo: Herppich et al. 2018; DiaCoM: Loibl et al. 2020; COSIMA: Heitzmann et al. 2019).
Tasks play an indisputable role in mathematics instruction (Bromme 1981) and in eliciting evidence of student understanding (Black and Wiliam 2009). More specifically, assigning students meaningful tasks is central to the generation of diagnostic information. This is also mirrored in the NeDiKo and COSIMA models, which explicitly note the role of teacher actions in eliciting diagnostic information. Mathematical tasks vary in their diagnostic potential that is, their ability to unveil diagnostically relevant information (Maier et al. 2010). When solving diagnostic tasks, students may rely strongly on deep understanding of the targeted mathematical concepts, or they may solve them correctly using deficient or superficial strategies, or strategies that do not use the targeted concepts. Thus, selecting high-potential tasks in diagnostic processes is crucial, but teachers’ diagnostic task selection has rarely been investigated. Kron et al. (2021) introduce the concept of sensitivity to the diagnostic potential of tasks as a facet of diagnostic competences, defining the diagnostic potential of a task as “its ability to stimulate student responses, allowing for the generation of reliable evidence about students’ mathematical understanding”. This sensitivity is reflected in the tendency to prefer tasks with high diagnostic potential during diagnostic processes. Sensitivity to the diagnostic potential of tasks digs into teachers’ competences to elicit reliable information about student understanding, comparable to asking probing questions, as previously studied by van den Kieboom et al. (2014). As Takker and Subramaniam (2019) note, “Rich knowledge and anticipation of student thinking”—in correct and incorrect aspects—is a central basis of “interpretative listening” when diagnosing decimal understanding. We assumed that this is similarly to selecting tasks that elicit students’ understanding. Thus, beyond the accuracy of the diagnosis, teachers’ sensitivity to the diagnostic potential of a task is an additional measure of diagnostic competences that reflects the quality of the diagnostic process. Current models of diagnostic competences assume that the quality of diagnostic processes depends on individual knowledge and motivational characteristics. The quality of the diagnostic process is key to generating accurate diagnoses, which reveals the importance of individual characteristics.
1.2 The Role of Professional Knowledge
Models of diagnostic competences highlight the role of teachers’ professional knowledge (NeDiKo: Herppich et al. 2018; DiaCoM: Loibl et al. 2020; COSIMA: Heitzmann et al. 2019). These models assume an influence of professional knowledge on the diagnosis, which is mediated by the characteristics of the diagnostic process (Leuders et al. 2017). In the context of teacher education, Shulman’s (1987) categorization of professional knowledge is commonly used to separate different knowledge components (for a recent overview in the context of diagnosis see Förtsch et al. 2019). In mathematics education research, content knowledge (CK) is often described as knowledge of school mathematics and its mathematical background (COACTIV: Baumert and Kunter 2013; TEDS-M: Blömeke et al. 2011; KiL: Kleickmann et al. 2014). Subject-specific knowledge about teaching, student cognition, diagnostic tasks, and instructional strategies for a specific subject is subsumed under pedagogical content knowledge (PCK) (Baumert and Kunter 2013), whereas general knowledge about teaching and, for example, diagnosis without connection to a specific subject refers to pedagogical knowledge (PK) (Kleickmann et al. 2014). How these different components of knowledge influence the diagnostic process remains unclear (Tröbst et al. 2018). Analyzing pre-service teachers’ questioning in diagnostic interviews that focused on investigating students’ algebraic thinking, van den Kieboom et al. (2014) found that participants with high CK on algebra asked more probing questions than did participants with lower CK. An intervention study of Ostermann et al. (2018) indicates that content-specific PCK influences pre-service teachers’ estimates of the difficulty of tasks in the area of functions and graphs. Investigating pre-service teachers’ task selection during diagnostic interviews on decimal fractions, Kron et al. (2021) report a relationship between participants’ CK on decimals and their sensitivity to the diagnostic potential of tasks on decimals. Regarding the accuracy of diagnosis, research has emphasized the influence of CK as well as PCK (Binder et al. 2018).
The specific and relative roles of different knowledge components have not yet been analyzed systematically. From a theoretical perspective, a prominent role of PCK related to the content at hand for diagnostic performance is plausible, since knowledge about potential misconceptions and the diagnostic potential of tasks are usually subsumed under PCK. Some results also highlight the important role of content-related CK in diagnostic task selection and questioning. One reason may be that judging the diagnostic potential of a task or question requires the generation of multiple possible solutions to the task, which are based on more or less correct and efficient strategies. Finally, definite conclusions about the different components of professional knowledge that play a role during the diagnostic process cannot be drawn (Herppich et al. 2018). In particular, it is an open question as to which knowledge components are actually used by (pre-service) teachers to diagnose efficiently and accurately, as well as under which conditions beginning teachers activate, use, and deepen different subject-specific knowledge components in authentic (learning) situations (Jeschke et al. 2021).
1.3 Approximations of Practice (AoPs)
Despite the role of professional knowledge for diagnosing, novice teachers who have acquired some professional knowledge also struggle to activate and apply this knowledge in authentic situations (Correa et al. 2015; Dicke et al. 2015; Levin et al. 2009). This activation and application requires knowledge structures that link conceptual knowledge about central terms and principles with procedural components on how to approach specific problems, and strategic components on which approaches are more or less efficient in which situations. Moreover, it is assumed that these components must be tied to practical applications (cf. Förtsch et al. 2019). In teacher education, the so-called approximations of practice, or AoP (Grossman et al. 2009), have been proposed as efficient means to build such knowledge structures.
AoPs, which can be used as learning or assessment situation, reconstruct real-life situations, control disruptive factors, and limit the complexity of presented situations. This limitation is necessary because complex and authentic situations, as they occur in real classrooms, are often considered overwhelming by novice pre-service teachers (Seidel and Stürmer 2014). In AoPs, pre-service teachers are expected to develop their (diagnostic) competences by applying their professional knowledge in authentic situations, which are not as cognitive demanding as traditional practical studies in real classrooms (Codreanu et al. 2020; Marczynski et al. 2022). While AoPs in teacher education have strongly focused on the use of video cases (e.g., Seidel et al. 2011; van Es and Sherin 2008), the field of medical education has a long tradition of investigating the use of simulations and simulated patients (Lane and Rollnick 2007). In particular, the use of roleplay-based simulations with actors as patients has been investigated (e.g., Lane et al. 2008; Stegmann et al. 2012), as these simulations allow for interpersonal interaction, portray the natural behavior of participants and allow them to make their own decisions. Paralleling this development, research in teacher education has started to investigate roleplay-based live simulations, such as teacher-parent communication (Gartmeier et al. 2011) or diagnostic one-on-one interviews with students (Marczynski et al. 2022). In the context of diagnosing students’ understanding, Wollring (2004) highlights the use of diagnostic interviews with real students as diagnostic situations that allow for the application of professional knowledge and ultimately further develop diagnostic competences (cf. van den Kieboom et al. 2014; Schack et al. 2013). Interviews with real students, however, may provide varying and unpredictable challenges for pre-service teachers, so using simulations with standardized student profiles as AoPs would be helpful.
A key point in the effectiveness of AoPs is that the learner activates and applies relevant knowledge when working in an authentic (approximated) situation. For example, Seidel et al. (2011) argue and provide some evidence that analyzing one’s own classroom videos leads to a stronger activation of relevant knowledge than analyzing others’ classroom videos. In diagnostic situations, pre-service teachers who have little experience in applying pedagogical content knowledge might thus primarily activate their content knowledge to check the mathematical correctness of students’ final solutions (CK) rather than explicitly considering students’ specific strategies or potential misconceptions (PCK). This is supported by prior evidence (van den Kieboom et al. 2014). Likewise, participants may also focus on general principles of diagnosis, such as observer bias (PK), without considering subject-specific knowledge components, which would be of additional value in a specific situation. Whether and how pre-service teachers differ in the knowledge they activate during AoPs is an open question.
To measure knowledge activation, some studies (e.g., Seidel et al. 2011) have analyzed participants’ responses to prompts embedded in an AoP. Alternatively, the relationship between performance in an AoP (e.g., task selection or accuracy of the diagnosis) and individual knowledge measures (e.g., based on CK, PCK, or PK tests) may be analyzed, and varying correlations between individual knowledge scores and measures of performance in the presented authentic situation may be taken as evidence of differences in knowledge activation. This perspective is part of the NeDiKo model (Herppich et al. 2018). Both approaches also allow to study whether interindividual differences in knowledge activation can be explained by other individual characteristics such as motivational characteristics.
1.4 Individual Interest as a “Door-Opener” for Knowledge Activation
As described above, the activation of knowledge in an AoP requires not only that this knowledge is available but also that it is identified as relevant in the corresponding situation. Individuals’ interest is expected to trigger knowledge activation (Hidi 1990).
In the sense of person-object theories of interest (Krapp 2002), individual interest as a motivational trait is usually understood as a relatively stable person-object relationship which is reflected in a “tendency to occupy oneself with an object of interest” (intrinsic component, Krapp 2002), a positive emotional relationship to the object (emotional component), and ascribing the object of interest a certain value (value component, cf. Schiefele et al. 1992). Sometimes, the “intrinsic component” is considered under the perspective of knowledge construction, indicating the desire to learn more about the “object” (epistemic component, Krapp and Prenzel 2011). The “object of interest” may be any cognitively represented entity from the individuals’ “life-space” (Lebensraum; Krapp 2002). Understanding interest as a relationship between a person and a specific object (e.g., a certain knowledge domain or a certain type of activity, such as educational diagnosis) implies that facets of interest may be distinguished by different objects. This leads to the question of which facet of interest serves as a trigger for the activation of which knowledge component.
From this perspective, an individual’s interest in a certain knowledge domain should increase the tendency to activate this knowledge in situations where it can be applied. According to theories of interest as a motivational state, individual interest is an important antecedent of situational interest. Hidi and Renninger (2006) argue that situational interest positively influences learning processes and gains by establishing a positive mood for the learner. Furthermore, situational interest is assumed to generally contribute to sustained attention (Ainley et al. 2002; Hidi and Renninger 2006), self-regulative processes (Lee et al. 2014), and deep levels of learning (Hidi and Renninger 2006). Again, these processes can be assumed to stimulate a stronger focus on the object of interest, leading to a deeper analysis of the situation at hand when working on an AoP, and thus, a more goal-directed activation of knowledge components that are connected to the respective object of interest. This is in line with Kosiol et al. (2019) who argue—based on Holland’s (1973) congruence hypothesis—that for interest to be relevant for learning, the object of interest must align with the contents of the learning situation. However, it is unclear whether interest in the general type of situation (interest in diagnosis) is sufficient to ensure this alignment, or if a specific interest in the specific knowledge component to be applied (interest in mathematics education, in this case) is required.
These mechanisms suggest that individual interest supports the activation of relevant knowledge in approximations of practice, such as simulated diagnostic interviews, and subsequently leads to improved diagnostic processes and more accurate diagnoses. Thus, interest is expected to moderate the relationship between professional knowledge and performance in the diagnostic situation, as hypothesized in Sect. 1.3. and the NeDiKo model (Herppich et al. 2018). In this sense, individual interest can be expected to act as a “door-opener” for the activation of professional knowledge during an AoP in pre-service teacher education if the object of interest corresponds to the contents of the AoP. For example, it is reasonable to expect that activating PCK especially depends on interest in mathematics education and that this leads to more efficient diagnostic processes and higher diagnostic accuracy. A more general interest in educational diagnosis could support the activation of PK, pointing participants towards general judgment errors, which could also influence the diagnostic process and the accuracy of diagnoses, whereas we did not expect that CK activation would be affected by an interest in mathematics education or an interest in diagnosis.
2 The Present Study
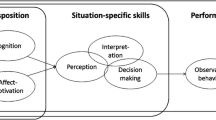
We have argued that the productive use of AoPs, such as simulated diagnostic interviews, depends on the activation of already acquired knowledge components such as CK, PCK, or PK. Moreover, we have proposed the hypothesis that, in such AoPs, individual interest facets, such as interest in mathematics education or interest in diagnosis, might function as a relevant moderator (the aforementioned “door-opener”) that stimulates the activation of specific knowledge components (Fig. 1).
This study strives to contribute to this topic not only by analyzing whether such moderation effects can be observed, but also by exploring which knowledge component pre-service teachers (the participants of our study) activate in simulated diagnostic interviews and which facets of interest play a role in this knowledge activation. It can be considered a theoretically plausible hypothesis that some facets of interest affect the activation of relevant knowledge components (see Sect. 1.4.). Which interest facets moderate the activation of which knowledge components is a more exploratory question. In particular, we focused on the following questions.
RQ 1
How are the different components of pre-service teachers’ professional knowledge (CK, PCK, PK) related to pre-service teachers’ sensitivity to diagnostic task potential and diagnostic accuracy?
As described above, the main effects of the knowledge components would only be expected if the respective component is activated, irrespective of the interest level. This might be because of sufficiently high interest levels, or because the knowledge component is obviously highly relevant for the situation at hand (e.g., CK on decimal fractions in a diagnostic interview dealing with decimal fraction tasks). Based on prior research findings and assuming that participants were sufficiently interested, we expected that the participants’ CK and PCK would be linked to their sensitivity to diagnostic task potential and diagnostic accuracy. We expected that higher CK would positively influence the evaluation of the diagnostic potential of tasks and the selection of tasks with high diagnostic potential (e.g., relying on an evaluation of possible solution strategies) and would also be related to diagnostic accuracy by influencing the evaluation of the student’s responses to the selected tasks. For PCK, we expected a relationship to diagnostic accuracy, as the interpretation of the diagnostic information gathered about the student’s understanding with respect to typical student misconceptions would be primarily related to knowledge about student cognition. Based on prior findings, we did not expect a relationship between PCK and task selection (Kron et al. 2021). Since the diagnostic interview had a strongly subject-related focus, we did not expect PK to have a strong influence.
RQ 2
How are different facets of pre-service teachers’ interest (interest in diagnosis, interest in mathematics education) related to pre-service teachers’ sensitivity to diagnostic task potential and diagnostic accuracy?
Again, the main effects of interest facets would only be expected if all participants had sufficient knowledge to accomplish the diagnostic task. As studies have shown that interest facilitates deep processing, we assumed that higher levels of interest would be reflected in stronger sensitivity to diagnostic task potential in the diagnostic process, and higher scores of diagnostic accuracy.
RQ 3a
Does the interaction of professional knowledge and interest affect pre-service teachers’ sensitivity to diagnostic task potential and their diagnostic accuracy?
Assuming that individuals’ interest influences the activation of knowledge, as reflected in the relationship between acquired professional knowledge and performance in AoPs, we expected to find moderating effects of interest in the relationship between professional knowledge and participants’ diagnostic performance. In particular, we expected that the interplay of high interest and professional knowledge would be reflected in a higher ratio of high-potential tasks, as well as a more accurate diagnosis.
Since prior studies do not provide a sufficient basis to predict which interest facets would interact with which knowledge components, the following, more detailed question is treated in an exploratory way:
RQ 3b
Which knowledge components and interest facets interact in their effects on pre-service teachers’ sensitivity to diagnostic task potential and diagnostic accuracy?
To provide first, exploratory insights into the interplay between interest and professional knowledge while performing in authentic situations, we investigated the interaction of CK, PCK, and PK with interest in diagnosis and interest in mathematics education in detail.
2.1 Method
Simulated diagnostic one-on-one interviews on decimal fractions were designed to answer these research questions (Marczynski et al. 2022). Reliable assessments of student understanding may be particularly important for decimal arithmetic with (positive) rational numbers (Padberg and Wartha 2017), as a range of student problems has been reported in the past (Lortie-Forgues et al. 2015). For example, how quantities are structured into decimal bundles with sizes larger than or equal to one (1, 10, 100, …) and smaller than one (0.1, 0.01, …; i.e., the bundling principle), and how the number of these bundles relates to the digits in different positions (the place value principle). This knowledge is assumed to underlie specific individual strategies to compare decimals and perform calculations. However, less optimal strategies, such as treating the parts before and after the decimal point as separate natural numbers, have been frequently observed in the past (i.e., a natural number bias; Alibali and Sidney 2015; cf. Steinle and Pierce 2006). Decimal comparison and calculation tasks that cannot be solved correctly using these strategies (e.g., comparing, or adding 1.25 and 1.4) can be considered to have higher diagnostic potential than tasks for which these strategies lead to a correct solution (comparing or adding 1.25 and 1.51). Moreover, how students adaptively select efficient calculation strategies depending on the numerical structure of the task has been proposed as an important measure of arithmetic skill (Heinze et al. 2009). Finally, the transition to rational numbers leads to new phenomena with arithmetic operations, e.g., that multiplication can have a result that is smaller than one of the two factors (Fischbein et al. 1985; Siegler and Lortie-Forgues 2015).
In the employed roleplay-based live simulated interviews, participants took the role of a teacher who diagnoses a student’s understanding of decimal fractions. Research assistants were well-trained to enact four different student case profiles that were used as scenarios in the simulations (for a description of the constructed student case profiles, see Kron et al. 2021). Before the two half-hour interviews, participants had time to familiarize themselves with the computer-based system and had 15 minutes to review the given set of tasks and prepare notes for the interviews. Each participant participated in two diagnostic interviews in a row with different student case profiles (enacted by different research assistants). Immediately before the first interview, the participants’ interest in diagnosis and mathematics education was measured. During the interviews, participants selected tasks from the given task set, which consisted of 45 mathematical tasks with varying diagnostic potential. The diagnostic tasks refer to the understanding of the decimal place value system, including the comparison of decimals, performing calculations, and solving word problems. Apart from the time limit, there were no restrictions on task selection. Participants were encouraged to ask verbal follow-up questions to elicit further diagnostic information after the simulated student answered. After each interview, the participants were asked to rate the simulated student’s mathematical understanding using a closed-answer format. Finally, the participants’ professional knowledge was assessed using a paper-and-pencil test (duration: 60 min). Experts rated the implementation and design of the simulation positively (Stürmer et al. 2021).
2.1.1 Instruments
Professional knowledge. Participants’ professional knowledge was assessed separately for each component as described by Shulman (1987). CK was measured using 12 items to assess mathematical knowledge of decimal fractions. These items required substantial reflection on school mathematics. For example, participants had to justify (without using the usual calculation rules for decimal fractions), that \(0.3\cdot 0.4=0.12\) (see Sect. 6.2. in the Supplementary Materials). The participants’ PCK regarding the teaching and learning of decimal fractions was measured using eight items. For example, participants were asked to analyze an incorrect student solution and select two of the four given potential student misconceptions, which might have led to this incorrect solution (Sect. 6.2. in Supplementary Materials). The PK scale was adopted from the KiL project (Kleickmann et al. 2014). From this scale only 11 items covering knowledge of diagnosis were used. These are related to assessments from a psychological standpoint, for example, focusing on general judgment errors and observer biases. While all PK items had a multiple-choice format, also single-choice and open-ended items were used for the CK and PCK scales. The answers to all items were coded dichotomously.
Data for all tests were gathered from the participants of this study and from an additional scaling sample of 292 pre-service mathematics secondary school teachers studying at the same university. For CK and PCK, the scaling sample covered a larger pool of items (24 CK items and 16 PCK items) that were employed in a multi-matrix design with four booklets. Individual knowledge scores (person-parameters)Footnote 1 for each of the three components as well as scale characteristics (e.g., item-parameters) were calculated for both samples together (see Table 1; for detailed information see Table 1.1 in the Supplementary Materials) using the one-dimensional one-parameter logistic Rasch model (Rasch 1960). The person-parameters are presented separately for each sample. All the items covered the knowledge required in the diagnostic interviews. The mean person-parameters for CK and PCK in the present study were comparable to or larger than the mean item-parameters, indicating that participants had acquired relevant knowledge to a substantial extent (see Table 1). Standard deviations of person-parameters in the present study indicate that the tasks in our test were harder for some of our participants, but that there were also participants who could master a substantial number of tasks.
Interest
We adopted the scales of Rotgans and Schmidt (2011) to assess participants’ interest and distinguish between two objects of interest: interest in diagnosis (example item: “I want to learn more about diagnosis”) and interest in mathematics education (example item: “I want to learn more about mathematics education”). Each of the two interest scales contained three items (listed in the Supplementary Materials, see Sect. 6.3.). Five-point Likert scales were used (0 = not true at all; 4 = very true for me). Cronbach’s alpha was calculated to measure reliability (Table 2). It should be noted that, on average, interest ratings were above the midpoint of the scale and had substantial variability among participants.Footnote 2
Diagnostic Process
We focused on the sensitive selection of tasks, considering their varying diagnostic potential during the interviews (Kron et al. 2021) to investigate the diagnostic process. The diagnostic potential of each task was coded a priori as low or high based on prior research on students’ understanding of decimal fractions (e.g., Steinle 2004). The coding of diagnostic potential relied only on the characteristics of the task itself. It was independent of the student case profiles and thus independent of the students’ responses and solutions to the tasks. Of the 45 tasks, 20 were coded as high-potential tasks. Based on this, we were primarily interested in the relative amount (ratio) of high-potential tasks among all selected tasks, reflecting participants’ sensitivity to diagnostic task potential (Kron et al. 2021). However, to ensure that the observed effects were specific to this ratio, we also considered the absolute number of selected tasks and the absolute number of selected high-potential tasks.
Diagnostic Accuracy
Participants rated the interviewed student’s understanding in nine subareas of decimal fractions, which were analyzed to measure diagnostic accuracy. Participants were asked to rate the interviewed student in terms of (1) the place value principle, (2) the bundling principle, (3) the comparison of decimals, (4) the basic concept of addition and subtraction, (5) arithmetic abilities in addition and subtraction, (6) flexible use of strategies regarding addition and subtraction, (7) the basic concept of multiplication and division, (8) arithmetic abilities in multiplication and division, and (9) flexible use of strategies regarding multiplication and division, all in the context of decimal fractions. There were three response options: “student mastered”, “student did not master”, and “diagnosis not possible”. Correct responses were coded as 1 and incorrect with 0. Abstaining answers (“diagnosis not possible”) were coded with 0.5 as a partial credit, since we considered abstaining more helpful than a wrong diagnosis. For example, participants were asked to rate the student’s understanding of the place value principle. One of the four designed student case profiles showed no reliable understanding of the place value principle but compared some pairs of decimals correctly using superficial strategies. In this case, the correct evaluation would have been “student did not master” as the student did not show a basic understanding of the place value principle. As the designed student case profiles differ in their composition of understanding and misconceptions in the field of decimal fractions, the correct rating of the nine subareas of knowledge differed among the student case profiles. Student case profiles 1 and 3 were capable in two of the nine subareas and student case profiles 2 and 4 in five, while those subareas differed between the two profiles. An accuracy score was built by averaging the participants’ performance on the nine items.
Diagnostic accuracy values around 0.5 may either reflect a similar number of correct and false evaluations or abstaining answers (or a mixture of both). Guessing or systematically selecting abstaining answers would lead to a score of approximately 0.5. In this vein, an accuracy score of 0.66 may for example reflect six abstentions and three correct assessments, or three wrong and six correct assessments.
2.1.2 Sample
The simulation was embedded in regular courses in pre-service mathematics secondary school teacher education in a large university in Germany. N = 63 participants participated in the simulation.Footnote 3 Participation in the study, including the provision of data for analysis, was voluntary and remunerated, and informed consent was obtained. Participation in the simulation had no influence on course grades. The local ethics committee and data protection officer approved the study.Footnote 4
On average, the participants were 23.7 years old \((SD=5.3)\) and mostly female (37 female, 25 male, 1 diverse). Most participants were in their fifth or lower semester \((M=4.8,SD=2.2)\) and almost all had finished at least four university courses (amounting to 12 European credit transfer system credits out 12 to 21, depending on the program) focusing on mathematics education in previous semesters \(\left(M=3.9,SD=1.2\right).\) Based on these degree program curricula, each participant should have completed one course focusing on the topic of decimal fractions before participating in the study. Two-thirds of the participants explicitly reported that they had taken at least one course, specifically covering PCK in decimal fractions. Regular mathematics education courses do not include diagnostic interviews. Most participants had at least some teaching experience from their practical studies; on average, they had conducted 9.3 school lessons on their own \((SD=6.5)\) and reported 2.1 years of experience in private tutoring (\(SD=1.6\); for details see Table 10 in Supplementary Materials).
2.1.3 Dataset and Analysis Strategy
The dataset contains knowledge scores for cognitive (person-parameters of CK, PCK, and PK) and motivational (interest in diagnosis, interest in mathematics education) characteristics. For each interview, the dependent performance measures were the number of all selected tasks, number of selected high-potential tasks, ratio of high-potential tasks among all selected tasks, and diagnostic accuracy score. As every participant worked on two simulations, the data for single interviews (first or second interview, student case profile, task selection data, and accuracy) were nested within the participants. Except for professional knowledge, all data were collected in log files using a web-based interview system.
Data were analyzed using linear mixed models (Bates et al. 2014), taking the nested structure of the data into account. The interview position (first vs. second) and the student case profile (1, 2, 3, or 4) were included as fixed factors in all models. For each research question, the effects on the ratio of high-potential tasks as a measure of the diagnostic process and effects on the diagnostic accuracy as a characteristic of the diagnostic outcome were investigated. Analyses of the number of all selected tasks and the number of selected high-potential tasks were conducted to exclude the possibility that results would be more pronounced for these two measures than for their quotient, the ratio of high-potential tasks.
To investigate the effects of professional knowledge (RQ 1), the person-parameters of CK, PCK, and PK were included as sole predictors. For RQ 2, both interest facets were included as well. As every participant conducted two interviews with different student case profiles, the interaction effects between interview position, respectively student case profile and the individual characteristic (knowledge respectively interest) were analyzed, as well. The interaction of professional knowledge components and interest facets was investigated using chi-square omnibus tests (RQ 3a) and further explored with separate models, each including one interaction term between one knowledge component and one interest facet (RQ 3b). Before presenting the results from each model, we explain why this model with certain fixed effects and interactions was selected.Footnote 5
In the case of interactions between knowledge components and interest facets, we illustrate the overall relationship between knowledge and performance measures with scatterplots visualizing the regression lines predicted by the respective model for different levels of the interest measure.
3 Results
3.1 Preliminary Analyses
3.1.1 Diagnostic Process
Focusing first on participants’ task selection, the results reveal that significantly more tasks were selected in the second interview (M = 16.57; see Table 3) than in the first (M = 13.75, \(F\left(1,59.19\right)=24.53,p< 0.001\)). Significantly more high-potential tasks were selected in the second interview (M = 7.86) than in the first (M = 6.35, \(F\left(1,59.25\right)=15.00,p< 0.001\)). There was no significant difference in the ratio of high-potential tasks between the first \((M=0.47)\) and the second interview (\(M=0.48,F\left(1,59.74\right)=0.43,p=0.516\)). This is consistent with the findings reported by Kron et al. (2021).
No significant differences in the number of selected tasks \((F\left(3,68.75\right)=1.47,p=0.231)\), the number of selected high potential tasks \((F\left(3,76.33\right)=0.46,p=0.708)\) and the ratio of high-potential tasks \((F\left(3,86.06\right)=1.07,p=0.367)\) by student case profiles were observed.
3.1.2 Diagnostic Accuracy
The participants reached an average diagnostic accuracy of 0.67 (\(SD=0.15,\mathit{\min }=0.22,\mathit{\max }=1.00)\). Regarding the position of the interview, no significant differences occurred \((F\left(1,59.62\right)=2.51,p=0.118)\). Contrasting the student case profiles, results revealed that student case profile 4 was significantly more difficult to diagnose than student case profile 2 and 3 \((p< 0.0001)\). Whereas the accuracy on student case profiles 1, 2, and 3 were significantly higher than 0.5 (profile 1: \(M=0.66,95\mathrm{\% }\mathrm{CI}]0.61,0.70[\); profile 2: \(M=0.72,\) 95% CI ]0.68,0.77[; profile 3: \(M=0.74,\) 95% CI ]0.69,0.78[), the solution rate of student case profile 4 exceeds this threshold only descriptively (\(M=0.55,95\% \mathrm{CI}\) ]0.50,0.60[).Footnote 6
Overall, only a small number of abstaining answers occurred, mainly in the area of the bundling principle and the flexible use of strategies (see Table 4). A comparison of the mean values of the nine accuracy items indicates that the diagnoses regarding the place value number representation system are descriptively more accurate than those regarding arithmetic operations.
3.2 RQ1: Effects of Professional Knowledge
To investigate the effects of professional knowledge, person-parameters for CK, PCK and PK were added as fixed factors to the models from the preliminary analyses (see Sect. 6.5. in Supplementary Materials). None of the two-way interactions between a knowledge component and interview position or student case profile was significant, neither for accuracy nor for measures of the diagnostic process. Thus, these interaction terms were removed from the subsequent models regarding this research question.
3.2.1 Diagnostic Process
Analyses indicated no significant relationships between any knowledge component and the number of selected tasks and the number of selected high-potential tasks (\(p> 0.148\); see Table 5).
For the ratio of high-potential tasks, a significant effect of CK occurred \((B=0.030,F\left(1,59.46\right)=5.13,p=0.027)\), indicating that higher CK scores went along with a higher ratio of high-potential tasks.
3.2.2 Diagnostic Accuracy
A significant effect of CK also occurred regarding the diagnostic accuracy (\(B=0.031,F\left(1,59.10\right)=5.30,p=0.025\); see Table 6), indicating that participants with higher CK scores also had higher accuracy scores. The main effects of PCK and PK were not significant (\(p> 0.278\); see Table 6).
3.3 RQ2: Effects of Interest
To investigate the effects of interest, scores for interest in diagnosis and interest in mathematics education were added as fixed factors in the models of preliminary analyses. None of the two-way interactions of interest facets with student case profile were significant for the accuracy or measures of the diagnostic process. Thus, these interaction terms were removed from the subsequent models regarding this question.
3.3.1 Diagnostic Process
Analyses indicated no significant relationships between interest measures and the number of selected tasks, number of high-potential tasks, and ratio of high-potential tasks (\(p> 0.104\); see Table 7).
3.3.2 Diagnostic Accuracy
No main effect of one of the two facets of interest on the accuracy could be identified. A significant interaction effect between interest in diagnosis and interview position indicated that the relationship between interest in diagnosis and accuracy was stronger in the second interview than in the first interview (B1st = −0.038, B2nd = 0.049, \(F\left(1,60.43\right)=5.79,p=0.019\)). However, for both interview positions the influence of interest in diagnosis was not significantly different from zero (first interview: 95% CI ]−0.09,0.02[; second interview: 95% CI ]−0.01,0.10[).
3.4 RQ3a: Omnibus Tests of Interactions Between Professional Knowledge and Interest
First, we analyzed whether the interaction of interest facets with knowledge components would significantly improve the prediction of the different performance measures. To this end, we compared a baseline model, containing the main effects of interview position, profile, knowledge components, and interest facets without any interactions, to two increasingly more complex models. The omnibus model, which additionally contains all two-way interactions of knowledge components and interest facets, allowed us to test the hypothesis if there are any interactions between knowledge components and interest facets. The extended model, containing all two- and three-way interactions between knowledge components, interest facets, and interview position, allowed us to investigate whether such interaction effects might differ by interview position (as some effects seemed to vary by interview position in previous analyses). Table 8 summarizes the fit indices and chi-square difference tests between these models for performance measures.
As expected, the corresponding interaction (omnibus) models showed a significantly better fit to the data for the ratio of high-potential tasks and for accuracy. However, the interactions between knowledge and interest for diagnostic accuracy as the dependent variable seem to differ between the first and second interviews (significantly improved fit for the extended model).
3.5 RQ3b: Exploring Interactions Between Professional Knowledge and Interest
Based on these results, we explored the two cases with significant omnibus tests in greater detail. Due to limitations in power, and to arrive at interpretable regression slope values, we only included one facet of interest, one knowledge component, and the corresponding interaction per model.
Significant interactions occurred between CK and interest in diagnosis, PCK and interest in mathematics education, whereas PK significantly interacted with both interest facets (see Table 9). Each significant interaction effect is reported in detail in the following sections.
In post-hoc analyses of the identified interactions, the relationships between knowledge components and performance measures were calculated for five levels of interest around the sample mean (\(M\pm 0\,SD,M\pm 0.75\,SD,M\pm 1.5\,SD\)) based on the estimated model.
3.5.1 Interaction of CK and Interest in Diagnosis
CK showed a significant three-way interaction with interest in diagnosis and interview position \((F\left(1,58.00\right)=6.12,p=0.016)\) on diagnostic accuracy. Follow-up analyses indicated that higher CK significantly went along with higher diagnostic accuracy for participants with average and above-average interest in diagnosis in the first interview (\(B_{1st,M\pm 0\,SD}=0.051,95\% \mathrm{CI}]0.02,0.08\left[;B_{1st,M+0.75SD}=0.074,95\% \mathrm{CI}\right]0.03,0.11[;B_{1st,M+1.5\,SD}=0.097,95\% \mathrm{CI}]0.04,0.15[\); see left side of Fig. 2). For the second interview, however, a different effect pattern occurred, as higher CK significantly went along with higher diagnostic accuracy for participants with below-average interest in diagnosis (\(B_{2nd,M-0.75\,SD}=0.042,95\% \mathrm{CI}]0.00,0.08[;B_{2nd,M-1.5\,SD}=0.056,95\% \mathrm{CI}]0.00,0.11[\)).
3.5.2 Interaction of PCK and Interest in Mathematics Education
For the ratio of high-potential tasks, a significant two-way interaction of PCK and interest in mathematics education occurred \((F\left(1,59.40\right)=5.34,p=0.024)\). Follow-up analyses indicated that higher PCK significantly went along with a higher ratio of high-potential tasks for participants with high interest in mathematics education (\(B_{M+1.5SD}=0.057,95\% \mathrm{CI}]0.00,0.11[\); see Fig. 3). This interaction was not qualified by a significant three-way interaction with the interview position.
Moreover, PCK and interest in mathematics education showed a significant three-way interaction with the interview position for diagnostic accuracy \((F\left(1,56.80\right)=6.12,p=0.016)\). Follow-up analyses revealed that higher PCK significantly went along with higher accuracy for participants with above-average interest in mathematics education in the first interview (\(B_{1st,M+0.75\,SD}=0.055,95\% \mathrm{CI}]0.00,0.11[\); \(B_{1st,M+1.5\,SD}=0.089,95\% \mathrm{CI}]0.02,0.16[\); see left side of Fig. 4). In the second interview, no significant relationship between PCK and diagnostic accuracy for the different levels of interest could be identified. However, the relationship between accuracy and PCK appeared to be slightly stronger for participants with lower interest.
3.5.3 Interaction of PK and Interest
A significant two-way interaction of PK with interest in mathematics education \((F\left(1,59.46\right)=4.60,p=0.036)\) occurred for the ratio of high-potential tasks. Follow-up analyses indicated that higher PK significantly went along with higher ratios of high-potential tasks for participants with an above-average interest in mathematics education (BM + 0.75 SD = 0.042, 95% CI]0.00,0.08[; BM + 1.5 SD = 0.067, 95% CI ]0.01,0.12[; see Fig. 5). This interaction was not qualified by a significant three-way interaction with the interview position.
Interest in diagnosis and PK showed a significant two-way interaction with diagnostic accuracy \((F\left(1,58.76\right)=6.10,p=0.016)\), but the three-way interaction did not reach significance \((F\left(1,57.07\right)=2.4,p=0.127)\). Follow-up analyses indicated that a higher PK significantly went along with higher accuracy for participants with a below-average interest in diagnosis (\(B_{M-0.75\,SD}=0.065,95\% \mathrm{CI}]0.02,0.11[\); \(B_{M-1.5\,SD}=0.100,95\% \mathrm{CI}]0.04,0.16[\); see Fig. 6).
4 Discussion
The main goal of this study was to obtain first insights into the role of interest in pre-service teachers’ knowledge activation in a simulation-based learning environment for diagnosing students’ understanding of decimal fractions. To this end, the ratio of high-potential tasks and diagnostic accuracy were considered as performance measures, following calls for a wider conceptualization of diagnostic competences (Herppich et al. 2018; Südkamp and Praetorius 2017). Overall, the results only partially reflect our assumptions regarding the main effects of interest and knowledge on diagnostic performance and provide first empirical evidence about the specific interactions of different interest facets and knowledge components.
4.1 Explaining Diagnostic Performance by Individual Knowledge and by Interest, Separately
Among the measures of the diagnostic process, only the ratio of selected high-potential tasks went along with the participants’ prerequisites, in particular their CK. That judging the diagnostic potential of tasks requires a close analysis of the task’s content, might explain the effects. As reported in a prior publication focusing on pre-service teachers’ sensitivity to and adaptive use of diagnostic task potential (Kron et al. 2021), higher CK could allow pre-service teachers to identify and eliminate low-potential tasks, primarily relying on a mathematical analysis of possible strategies to solve that task.
A connection between performance and participants’ PCK would have been expected, as knowledge about the diagnostic potential of tasks is considered as a central part of PCK (Baumert and Kunter 2013). However, it must be acknowledged that the activation of decimal-related CK is most clearly triggered by the simulation setting, given that tasks on decimal fractions are the central topic. Furthermore, the time for the evaluation of the tasks was limited, which might have led to a superficial analysis of the tasks considering only CK, without a deeper evaluation on the basis of PCK. Later analyses were used to investigate whether this applies equally to all participants, or whether an effect of PCK can be observed for participants with a higher interest in mathematics education that may have delved into a deeper analysis. In particular, the effects of knowledge would only become visible if participants were sufficiently interested in engaging in the diagnostic situation. In our study, participants’ interest was above the scale mean on average, but substantial variation in interest was observable.
Interest alone, without including interactions with knowledge components, did not predict accuracy. While this might be unexpected at first sight, an effect of interest would only be plausible if a sufficient number of interested participants had sufficient knowledge to approach the task successfully. One explanation for the lack of a significant main effect of interest might be that, even among the highly interested participants, a substantial number did not have sufficient knowledge that they could have activated during the simulation (according to our professional knowledge test), even if they would have been sufficiently engaged by their interest to try it. Moderate to low correlations between interest measures and knowledge components (r < 0.24 for all combinations, see Table 1.2 in the Supplementary Materials) support the assumption that at least some participants with high interest had low professional knowledge.
In summary, our results indicate that interest and professional knowledge alone explain only few differences in individual performance during the simulation. This must be seen in the context of the study: most of our participants had acquired initial mathematics education knowledge but had not completed their study program and had restricted practical experience. Exactly this situation of less experienced pre-service teachers, however, is of high interest when developing AoPs as learning environments for university-based teacher education programs.
4.2 Interest as a “Door-Opener” for Knowledge Activation?
Based on predictions from interest theories (Ainley et al. 2002; Hidi and Renninger 2006; Krapp 2002; Lee et al. 2014; Schiefele et al. 1992), we expected that individual interest would trigger the activation of the relevant knowledge components in the simulation. Indeed, the results of omnibus tests indicate that including the moderation effects of interest facets on the relationship between knowledge and performance significantly improves the explanation of individual differences in performance measures. Without more detailed exploratory analysis, this indicates that, at least under certain conditions, the interaction of motivational variables and knowledge is relevant for learning in AoPs.
In the context of our analysis, it must be considered that corresponding moderation effects can only be expected if (a) participating pre-service teachers vary in the amount of relevant professional knowledge they have acquired and (b) not all but a substantial number of the participants are sufficiently interested to activate the respective knowledge components in the AoP. The results of the omnibus tests indicate that this situation arises during the initial teacher education. The main idea of AoPs is knowledge application. Our findings indicate that two prerequisites are necessary to achieve this: participants must have acquired sufficient and relevant professional knowledge to engage with the task, and they must activate this knowledge, for example because they are specifically interested in the task or in applying this knowledge. This leaves at least two options: (1) implementing measures to raise pre-service teachers’ interest before engaging them in AoPs (e.g., value interventions, such as emphasizing the importance of accurate diagnosis; Priniski et al. 2019) or (2) finding other measures to trigger knowledge activation during AoPs (e.g., prompts, such as information about typical misconceptions of students; Chernikova et al. 2019). Both options are commonly used as scaffolds in the context of AoPs and in similar environments to enhance learning effects.
4.3 Differences Between the First and the Second Interview
Unexpectedly, some effect patterns differed between the first and second interviews conducted by each participant. This effect was less pronounced for the main effects of knowledge. Only the influence of interest in diagnosis on accuracy was stronger in the second interview than in the first. However, some of the interactions of knowledge and interest measures with accuracy showed interactions with the interview position. This was unexpected, and without further investigation, the reasons for this can only be hypothesized after the present study. One explanation may be that the experiences made during the first interview affected participants’ approach to the second interview (which was conducted directly after the first interview). Similarly, participants’ initially reported (situational) interest could have been affected by the first interview, leading to a reduced validity of the interest measure for the second interview. A related explanation may be that pre-service teachers with little interest needed a certain amount of time to gather experience in the simulation setting before they started focusing and activating their knowledge in the second interview. The effects of repeated encounters with AoPs (with or without longer time spans in between) have received little attention in research so far. These unexpected findings raise the question of whether some pre-service teachers might need time to become acquainted with such authentic settings, but also whether subsequent encounters might overstrain them and impede their knowledge activation. If this pattern of results is sustained in further studies, the risk of overstraining learners must be considered. This holds, in particular, when engaging pre-service teachers in more than one longer and complex simulation without a longer break, as in this study.
4.4 Which Interest Facet Triggers the Activation of Which Knowledge Component?
Based on the promising findings from the omnibus tests, the interactions between interest facets and knowledge components were explored in more detail. The clearest pattern of findings, in our perception, arose for PCK, as its relationship to the selection of high-potential tasks and diagnostic accuracy was moderated by participants’ interest in mathematics education. For task selection and accuracy (first interview), above-average interest in mathematics education went along with a positive relation of PCK to both performance measures. This is in line with assumptions derived from interest theories (Ainley et al. 2002; Hidi and Renninger 2006; Krapp 2002; Lee et al. 2014; Schiefele et al. 1992). That interest in mathematics education significantly moderated the effect of PCK, but not interest in diagnosis, is also in line with the assumption based on the congruence hypothesis (Kosiol et al. 2019), that an overlap between the object of interest and the content of the relevant knowledge would be relevant for successful learning.
Regarding CK, we found that the already established relationship with the selection of high-potential tasks was not moderated by interest facets. In contrast, the relationship with accuracy was moderated by interest. It was interest in diagnosis, not interest in mathematics education, which was involved in this moderation, which is also in line with the congruence hypothesis (Kosiol et al. 2019). However, we found a significant relationship between CK and accuracy for both, participants with high and low interest. Whereas this relationship was significantly positive for participants with average and above-average interest in diagnosis in the first interview, it was significantly positive for participants with below-average interest in diagnosis in the second interview.
In summary, the positive relationships of CK with accuracy and the selection of high-potential tasks parallels the results of prior studies that CK seems to play an important role in diagnostic practice (e.g., van den Kieboom et al. 2014). The relationship between CK and task selection was not significantly related to interest, indicating that the activation of CK for task selection might be more obviously triggered by the simulation itself, whereas the activation for diagnosing is dependent on interest in diagnosis. The pattern of effects is in line with expectations from motivational theories (Hidi and Renninger 2006) in the first interview, but alternative explanations will be required for the reverse pattern in the second interview. Participants’ situational interest might be considered when studying if participants with low individual interest require time and experience in the simulation setting before developing sufficient situational interest to trigger knowledge activation.
The pattern of relations was most diverse for PK: while participants with above-average interest in mathematics education showed a significant positive relationship between PK and a tendency to select high-potential tasks, participants with below-average interest in diagnosis showed a significantly positive relationship between PK and accuracy. The positive relationship for above-average interest in mathematics education is in line with our assumptions on the role of interest in knowledge activation in general, indicating that PK can also be productively used for focused task selection. However, a similar effect was observed for PCK. From a theoretical perspective, the relationship between PCK and task selection would be more plausible because PCK explicitly includes knowledge about the diagnostic potential of tasks, whereas PK comprises general knowledge about diagnosis (Baumert and Kunter 2013). A congruence hypothesis would rather let us assume, but without certainty, that PCK activation is influenced more by interest in mathematics education than PK activation (Kosiol et al. 2019). The real reasons behind these findings cannot be conclusively identified here, since the limited power of our study does not allow the disentanglement of the two similar effects in a joint analysis, which underlines the need for further research.
Finally, the positive relationship between PK and accuracy for participants with below-average interest in diagnosis contradicts our assumptions based on motivational theories. In addition, only first hypothesis can be put forward to explain this finding and gain ideas for further analyses of this relationship. One possible explanation may be that low interest in diagnosis could lead to superficial task processing (Hidi and Renninger 2006), which, in turn, could favor the activation of generic knowledge components, such as PK, since it is not tied to a specific domain or subject. Even though such an argument could explain the observed finding, it must be seen as a speculative post-hoc explanation at this point. Explicit or implicit measures of deep task processing could be used to investigate whether low-interest pre-service teachers are indeed at danger of superficial task processing and whether this affects the activation of specific knowledge components.
4.5 Summary
As argued above, we draw the following conclusions. For some of them, evidence was specifically generated in the described study, while others have the status of hypotheses, since they are based on the more exploratory part of our analyses:
-
1.
Our study provides evidence for the assumption that, at certain early stages of the acquisition of diagnostic competences, knowledge measures (alone) and interest measures (alone) have some, but limited, explanatory power for their performance in AoPs, such as the simulation studied in this contribution.
-
2.
Instead, knowledge activation during such AoPs depends on the interaction of motivational characteristics, such as interest and available knowledge. Including interaction terms leads to a significantly better fit of the regression models, as the omnibus tests indicated.
-
3.
Moreover, the exploratory results support the assumption that interest in mathematics education plays a central role in PCK activation in the investigated simulations.
-
4.
The exploratory findings lead to the question, of whether repeated participation in AoPs, such as this simulation, with or without temporal spacing, leads to specific effects in terms of knowledge activation. For repetitions without temporal spacing, some results might be explained by overstraining participants. On the other hand, other results would be in line with the assumption that low-interest pre-service teachers might require some time and experience with the simulation setting before they engage deeply and activate relevant knowledge components. Here, our results merely cast a first light into a less-researched area.
-
5.
Finally, some results might be explained by the assumption that low interest might accompany the activation of more generic knowledge components such as PK in subject-related AoPs. This is theoretically plausible, but the evidence from our study is weak. Therefore, this relationship requires further investigation in future research.
4.6 Limitations
Some limitations of this study must be considered when drawing final conclusions. Most centrally, the exploratory nature of parts of our study implies that some conclusions should not be taken as established facts, but as working hypotheses guiding further research. This is particularly relevant for possible explanations of the detailed results of the observed interactions.
Different performance criteria were used to measure the diagnostic competences of pre-service secondary school mathematics teachers. In particular, the selection of tasks to investigate the participants’ sensitivity to diagnostic task potential, and diagnostic accuracy. These criteria reflect only selected aspects of pre-service teachers’ diagnostic competences. Additionally, the accuracy measure during the final rating may be prone to guessing. However, even though there was the option to abstain (“diagnosis not possible”), the accuracy was significantly above 50% for almost all student case profiles, speaking against a systematic guessing strategy. However, a more detailed analysis for example, of participants’ questioning during the interviews or their written diagnostic reports may provide additional insights about their diagnostic competences in the longer run.
Moreover, the professional knowledge tests used to measure CK, PCK, and PK had somewhat low reliability scores. When collecting data for this study (winter term 2019/2020), we did not know of an existing, validated test for measuring CK and PCK in the area of decimal fractions. Therefore, we designed this test from scratch and further research is required to increase its internal consistency without reducing its validity. In addition, the test was designed to measure the specific knowledge needed to complete the diagnostic interviews. Comparing item- and person-parameters raises the question of whether the CK and PCK tests differentiate well between persons with high CK and PCK person-parameters. The PK test also had low reliability scores. Finally, the number of participants may have also influenced the fit of the underlying Rasch model and contributed to the low reliabilities.
Regarding the applied simulation as an AoP, allocating 30 min to diagnose a student’s understanding may not be a part of teachers’ everyday practice. However, in our context, this setting provides a controlled assessment situation representing professional diagnostic demands (e.g., selection of tasks, observation of student responses, asking probing questions, and evaluation of student responses to diagnose its understanding) authentically without increasing complexity by digging into pedagogical decisions (cf. Kaiser et al. 2017). As students were simulated by trained research assistants, it was quite obvious that students were not “real”. However, in contrast to using videotaped “real” students, this allowed us to implement live interviews in which participants were able to ask their own questions. Nevertheless, future research should consider how many long and complex simulations can be applied in a row without overstraining pre-service teachers when using such simulations as learning opportunities.
Finally, the sample of 126 interviews performed by 63 pre-service teachers limited the statistical power of our study. As mentioned above, the main effects of professional knowledge or interest may only be expected if all participants were sufficiently interested, respectively had acquired the relevant knowledge for the diagnostic situation beforehand. Thus, similar investigations with a larger sample size, including more advanced participants or in-service teachers, could provide more nuanced interactions. With higher statistical power, motivational state variables or cognitive demand (Codreanu et al. 2020) could be included in the analyses, helping explain the moderation effects in more detail. In this regard, the heterogeneity of our sample is vital to identifying the interaction effects between knowledge and interest variables. However, it must be kept in mind that not all variables that constitute the sample’s heterogeneity could be considered. For example, we did not include more distal measures of performance, such as prior tutoring experience, because we assumed that their effects would be at least partially mediated by the included variables. Finally, transferability to other AoPs, varying in their design or area of content, is of special interest. Different simulations developed in the COSIMA research unit (Fischer and Opitz 2022) are currently being studied from a similar perspective.
4.7 Conclusion and Implications
The current study addresses the question of under what conditions pre-service teachers, who have acquired initial professional knowledge, activate different components of this knowledge when participating in authentic AoPs such as simulated diagnostic interviews. This seems particularly important for transforming personal knowledge into applicable or enacted knowledge in teacher education (Carlson et al. 2019; Grossman and McDonald 2008). To this end, we studied a complex, authentic AoP in the valid field setting of a university-based teacher education program, to provide insights into pre-service teachers’ knowledge activation in such authentic situations. This seems of particular interest, when using AoPs as learning environments efficiently. As a first result, we found evidence that at least some pre-service teachers activate and apply components of their personal knowledge in simulated situations. This suggests that AoPs, especially when including appropriate scaffolds to increase learning effects, can play a role in the transformation of personal knowledge to applicable or enacted knowledge and that further research in this area is warranted.
Second, in our less-experienced sample of pre-service teachers, not all knowledge components seem to be activated systematically. Paralleling the results of prior studies (van den Kieboom et al. 2014), a main effect on task selection indicates that pre-service teachers might systematically activate their CK during simulated diagnostic interviews. Given the obvious need to evaluate students’ responses, it seems plausible at first sight that interest might play a minor role in CK activation. Follow-up analyses, however, indicated that interest in diagnosis moderated its effect on accuracy differently in the first and second interviews. As argued above, the robust effect of CK over different studies indicates that beginning teachers might approach diagnostic interviews from a very content-related perspective, without much consideration of pedagogical content knowledge, since this kind of knowledge is mostly newer to them. This underlines the importance of performing theory-based moderator analyses to investigate whether the observed correlations are valid for all participants, or only for a subset of them.
Third, we find evidence that individual interest can function as a “door-opener” toward the activation of relevant knowledge components. The corresponding effect patterns were particularly pronounced for interest in mathematics education and the activation of personal PCK, pointing to a potential effect of interest congruence (Holland 1973; Kosiol et al. 2019). It is, of course, problematic that some pre-service teachers do not activate and deepen certain knowledge components during AoPs due to lower interest. Apart from supporting interest development (e.g., by allowing for fulfillment of basic needs, Schukajlow et al. 2017; value interventions, Priniski et al. 2019), university students’ expectations have been found to influence learning (Rach et al. 2014), therefore it might be helpful to sensitize university students to what is expected from them in a certain learning situation and which knowledge is considered relevant. Moreover, university students who still have limited professional knowledge will most likely benefit from support that allows them to acquire this missing knowledge.
Finally, unexpected results from our study trigger a set of open questions because the reasons for these findings could only be hypothesized. One such hypothesis is that low interest may lead to a superficial approach towards subject-specific AoPs, instead of using deep learning strategies involving the intended knowledge components (Hidi and Renninger 2006). Investigating deep and surface learning strategies, which have been discussed in connection to interest for secondary mathematics pre-service teachers in the past (Murayama et al. 2013), could be one step towards this issue. A second area for further study is the role of repeated participation in similar AoPs.
This study’s findings indicate that the activation and application of knowledge in authentic situations depends not only on the availability of relevant knowledge. Rather, other factors may influence whether individuals activate this knowledge, including their interest in the topic, which reflects personal significance. Based on our results, which relate to an approximation without specific learning support, we assume that the effectiveness of AoPs, in particular regarding the activation and application of knowledge, requires careful attention when designing such authentic situations, especially when using it as a learning environment by embedding scaffolds. Here, it might be helpful to arouse participants’ interest supporting the activation of specific knowledge components or to support less-interested learners in their activation of knowledge.
Notes
The IRT knowledge scores can be interpreted in the following way: a person with knowledge score (person parameter) θ will, according to the underlying Rasch model, solve an item with item-parameter δ with a probability of \(p=\frac{1}{\left(1+exp\left(\delta -\theta \right)\right)}\).
For correlations of knowledge components and interest facets please see Table 1.2 in the Supplementary Materials.
The sample of this study initially consisted of 65 participants. Due to extremely low PCK scores, two of the 65 participants were excluded from the analysis. Evaluation of all test booklets indicated that these participants did not work seriously on the test.
Some data from the current study have already been reported by the Kron et al. (2021). In this contribution, the focus was on a fine-grained analysis of the selection of tasks during the interview. The previous article focused on the construct of sensitivity to and adaptive use of diagnostic task potential, and the role of professional knowledge in task selection. The current contribution goes beyond this prior analysis in considering the moderating role of interest and focusing on diagnostic performance more broadly, also incorporating diagnostic accuracy. Thus, the main effect of knowledge components for task selection is reported in both manuscripts, but in the present study, it merely has the role of a preliminary analysis.
For an overview of the syntax of the separate linear mixed models please see Table 11 in the Supplementary Materials. Additional information about the instruments, the dataset, and the analysis of the data are available from the authors on request.
For a description of the constructed student case profiles see Kron et al. (2021).
References
Ainley, M., Hidi, S., & Berndorff, D. (2002). Interest, learning and the psychological processes that mediate their relationship. Journal of Educational Psychology, 94(3), 545–561.
Alibali, M. W., & Sidney, P. G. (2015). Variability in the natural number bias: Who, when, how, and why. Learning and Instruction, 37, 56–61.
von Aufschnaiter, C., Cappell, J., Dübbelde, G., Ennemoser, M., Mayer, J., Stiensmeier-Pelster, J., Sträßer, R., & Wolgast, A. (2015). Diagnostische Kompetenz. Theoretische Überlegungen zu einem zentralen Konstrukt der Lehrerbildung. Zeitschrift für Pädagogik, 61(5), 738–758.
Bates, D., Mächler, M., Bolker, B., & Walker, S. (2014). Package Lme4: linear mixed-effects models using Eigen and S4. Journal of statistical software, 67, 1–103.
Baumert, J., & Kunter, M. (2013). The COACTIV model of teachers’ professional competence. In M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss & M. Neubrand (Eds.), Cognitive activation in the mathematics classroom and professional competence of teachers: results from the COACTIV project (pp. 25–48). Springer.
Behrmann, L., & Souvignier, E. (2013). The relation between teachers’ diagnostic sensitivity, their instructional activities, and their students’ achievement gains in reading. Journal of Educational Psychology, 27(4), 283–293.
Binder, K., Krauss, S., Hilbert, S., Brunner, M., Anders, Y., & Kunter, M. (2018). Diagnostic skills of mathematics teachers in the COACTIV study. In T. Leuders, K. Philipp & J. Leuders (Eds.), Diagnostic competence of mathematics teachers—Unpacking a complex construct in teacher education and teacher practice (pp. 33–53). Springer.
Black, P., & Wiliam, D. (2009). Developing the theory of formative assessment. Educational Assessment, Evaluation and Accountability, 21(1), 5.
Blömeke, S., Kaiser, G., & Lehmann, R. (2011). Messung professioneller Kompetenz angehender Lehrkräfte: „Mathematics Teaching in the 21st Century“ und die IEA-Studie TEDS‑M. In H. Bayrhuber, U. Harms, B. Muszynski, B. Ralle, M. Rothgangel, L.-H. Schön, H. J. Vollmer & H.-G. Weigand (Eds.), Empirische Fundierung in den Fachdidaktiken (pp. 9–26). Waxmann.
Bromme, R. (1981). Das Denken von Lehrern bei der Unterrichtsvorbereitung: Eine empirische Untersuchung zu kognitiven Prozessen von Mathematiklehrern. Beltz.
Carlson, J., Daehler, K. R., Alonzo, A. C., Barendsen, E., Berry, A., Borowski, A., Carpendale, J., Kam Ho Chan, K., Cooper, R., Friedrichsen, P., Gess-Newsome, J., Henze-Rietveld, I., Hume, A., Kirschner, S., Liepertz, S., Loughran, J., Mavhunga, E., Neumann, K., & Nilsson, P. (2019). The refined consensus model of pedagogical content knowledge in science education. In A. Hume, R. Cooper & A. Borowski (Eds.), Repositioning pedagogical content knowledge in teachers’ knowledge for teaching science (pp. 77–94). Springer Singapore.
Chernikova, O., Heitzmann, N., Fink, M. C., Timothy, V., Seidel, T., & Fischer, F. (2019). Facilitating diagnostic Competences in higher education—A meta-analysis in medical and teacher education. Educational Psychology Review, 32(1), 157–196.
Codreanu, E., Sommerhoff, D., Huber, S., Ufer, S., & Seidel, T. (2020). Between authenticity and cognitive demand: Finding a balance in designing a video-based simulation in the context of mathematics teacher education. Teaching and Teacher Education, 95, 103146.
Correa, J. M., Martínez-Arbelaiz, A., & Aberasturi-Apraiz, E. (2015). Post-modern reality shock: Beginning teachers as sojourners in communities of practice. Teaching and Teacher Education, 48, 66–74.
Dicke, T., Elling, J., Schmeck, A., & Leutner, D. (2015). Reducing reality shock: The effects of classroom management skills training on beginning teachers. Teaching and Teacher Education, 48, 1–12.
van Es, E., & Sherin, M. G. (2008). Mathematics teachers’ “learning to notice” in the context of a video club. Teaching and Teacher Education, 24, 244–276.
Fischbein, E., Deri, M., Nello, M. S., & Marino, M. S. (1985). The role of implicit models in solving verbal problems in multiplication and division. Journal for research in mathematics education, 16, 3–17.
Fischer, F., & Opitz, A. (2022). Learning to diagnose with simulations—Examples from teacher education and medical education. Springer Briefs in Education. Springer.
Förtsch, C., Sommerhoff, D., Fischer, F., Fischer, M., Girwidz, R., Obersteiner, A., Reiss, K., Stürmer, K., Siebeck, M., Schmidmaier, R., Seidel, T., Ufer, S., Wecker, C., & Neuhaus, B. (2019). Systematizing professional knowledge of medical doctors and teachers: development of an interdisciplinary framework in the context of diagnostic competences. Education Sciences, 8(4), 207.
Gartmeier, M., Bauer, J., Fischer, M. R., Karsten, G., & Prenzel, M. (2011). Modellierung und Assessment professioneller Gesprächsführungskompetenz von Lehrpersonen im Lehrer-Elterngespräch [Modeling and assessment of teachers’ professional competence for parent-teacher conversations]. In O. Zlatikin-Troitschanskaia (Ed.), Stationen Empirischer Bildungsforschung. Traditionslinien und Perspektiven (pp. 412–426). VS.
Grossman, P., & McDonald, M. (2008). Back to the future: Directions for research in teaching and teacher education. American Educational Research Journal, 45(1), 184–205.
Grossman, P., Compton, C., Igra, D., Ronfeldt, M., Shahan, E., & Williamson, P. (2009). Teaching practice: a cross-professional perspective. Teachers College Record, 111(9), 2055–2100.
Heinze, A., Star, J. R., & Verschaffel, L. (2009). Flexible and adaptive use of strategies and representations in mathematics education. ZDM—International Journal on Mathematics Education, 41, 535–540.
Heitzmann, N., Seidel, T., Opitz, A., Hetmanek, A., Wecker, C., Fischer, M., Ufer, S., Schmidmaier, R., Neuhaus, B., Siebeck, M., Stürmer, K., Obersteiner, A., Reiss, K., Girwidz, R., & Fischer, F. (2019). Facilitating diagnostic competences in simulations: A conceptual framework and a research agenda for medical and teacher education. Frontline Learning Research, 7, 1–24.
Herppich, S., Praetorius, A.-K., Förster, N., Glogger-Frey, I., Karst, K., Leutner, D., Behrmann, L., Böhmer, M., Ufer, S., Klug, J., Hetmanek, A., Ohle-Peters, A., Böhmer, I., Karing, C., Kaiser, J., & Südkamp, A. (2018). Teachers’ assessment competence: Integrating knowledge-, process-, and product-oriented approaches into a competence-oriented conceptual model. Teaching and Teacher Education, 76, 181–193.
Herppich, S., Praetorius, A.-K., Hetmanek, A., Glogger-Frey, I., Ufer, S., Leutner, D., Behrmann, L., Böhmer, I., Böhmer, M., Förster, N., Kaiser, J., Karing, C., Karst, K., Klug, J., Ohle, A., & Südkamp, A. (2017). Ein Arbeitsmodell für die empirische Erforschung der diagnostischen Kompetenz von Lehrkräften. In A. Südkamp & A.-K. Praetorius (Eds.), Diagnostische Kompetenz von Lehrkräften: Theoretische und methodische Weiterentwicklungen. Waxmann.
Hidi, S. (1990). Interest and its contribution as a mental resource for learning. Review of Educational Research, 60(4), 549–571.
Hidi, S., & Renninger, K. A. (2006). The four-phase model of interest development. Educational Psychologist, 41(2), 111–127.
Holland, J. L. (1973). Making vocational choices: A theory of careers. Prentice Hall.
Jeschke, C., Kuhn, C., Heinze, A., Zlatkin-Troitschanskaia, O., Saas, H., & Lindmeier, A. M. (2021). Teachers’ ability to apply their subject-specific knowledge in instructional settings—A qualitative comparative study in the subjects mathematics and economics. Frontiers in Education, 6(256), . Original Research.
Kaiser, J., Praetorius, A.-K., Südkamp, A., & Ufer, S. (2017). Die enge Verwobenheit von diagnostischem und pädagogischem Handeln als Herausforderung bei der Erfassung diagnostischer Kompetenz. In A. Südkamp & A.-K. Praetorius (Eds.), Diagnostische Kompetenz von Lehrkräften. Theoretische und methodische Weiterentwicklungen (pp. 114–123). Waxmann.
Karst, K., Klug, J., & Ufer, S. (2017). Strukturierung diagnostischer Situationen im inner- und außerunterrichtlichen Handeln von Lehrkräften. In A. Südkamp & A.-K. Praetorius (Eds.), Diagnostische Kompetenz von Lehrkräften: Theoretische und methodische Weiterentwicklungen (pp. 95–113). Waxmann.
van den Kieboom, L. A., Magiera, M. T., & Moyer, J. C. (2014). Exploring the relationship between K‑8 prospective teachers’ algebraic thinking proficiency and the questions they pose during diagnostic algebraic thinking interviews. Journal of Mathematics Teacher Education, 17, 429–461.
Kleickmann, T., Großschedl, J., Harms, U., Heinze, A., Herzog, S., Hohenstein, F., Köller, O., Kröger, J., Lindmeier, A., & Loch, C. (2014). Professionswissen von Lehramtsstudierenden der mathematisch-naturwissenschaftlichen Fächer – Testentwicklung im Rahmen des Projekts KiL. Unterrichtswissenschaft – Zeitschrift für Lernforschung, 42(3), 280–288.
Klug, J., Bruder, S., Kelava, A., Spiel, C., & Schmitz, B. (2013). Diagnostic competence of teachers: A process model that accounts for diagnosing learning behavior tested by means of a case scenario. Teaching and Teacher Education, 30, 38–46.
Kosiol, T., Rach, S., & Ufer, S. (2019). (Which) mathematics interest is important for a successful transition to a university study program? International Journal of Science and Mathematics Education, 17(7), 1359–1380.
Krapp, A. (2002). Structural and dynamic aspects of interest development: Theoretical considerations from an ontogenetic perspective. Learning and Instruction, 12(4), 383–409.
Krapp, A., & Prenzel, M. (2011). Research on interest in science: Theories, methods, and findings. International Journal of Science Education, 33(1), 27–50.
Kron, S., Sommerhoff, D., Achtner, M., & Ufer, S. (2021). Selecting mathematical tasks for assessing student’s understanding: pre-service teachers’ sensitivity to and adaptive use of diagnostic task potential in simulated diagnostic one-to-one interviews. Frontiers in Education, 6, 604568. Original Research.
Kultusministerkonferenz (2019). Ländergemeinsame inhaltliche Anforderungen für die Fachwissenschaften und Fachdidaktiken in der Lehrerbildung. Beschluss der Kultusministerkonferenz vom 16.10.2008 i. d. F. vom 16.05.2019: KMK
Lane, C., & Rollnick, S. (2007). The use of simulated patients and role-play in communication skills training: a review of the literature to August 2005. Patient education and counseling, 67(1), 13–20.
Lane, C., Hood, K., & Rollnick, S. (2008). Teaching motivational interviewing: using role play is as effective as using simulated patients. Medical Education, 42(6), 637–644.
Lee, W., Lee, M.-J., & Bing, M. (2014). Testing interest and self-efficacy as predictors of academic self-regulation and achievement. Contemporary Educational Psychology, 39, 86–99.
Leuders, T., Dörfler, T., Leuders, J., & Philipp, K. (2017). Diagnostic competence of mathematics teachers: unpacking a complex construct. In T. Leuders, T. Dörfler, J. Leuders & K. Philipp (Eds.), Diagnostic competence of mathematics teachers. Unpacking a complex construct in teacher education and teacher practice (pp. 3–32). Springer.
Levin, D. M., Hammer, D., & Coffey, J. E. (2009). Novice teachers’ attention to student thinking. Journal of Teacher Education, 60(2), 142–154.
Loibl, K., Leuders, T., & Dörfler, T. (2020). A framework for explaining teachers’ diagnostic judgements by cognitive modeling (DiacoM). Teaching and Teacher Education, 91, 103059.
Lortie-Forgues, H., Tian, J., & Siegler, R. S. (2015). Why is learning fraction and decimal arithmetic so difficult? Developmental Review, 38, 201–221.
Maier, U., Kleinknecht, M., & Metz, K. (2010). Ein fächerübergreifendes Kategoriensystem zur Analyse und Konstruktion von Aufgaben. In H. Kiper, W. Meints, S. Peters, S. Schlump & S. Schmit (Eds.), Lernaufgaben und Lernmaterialien im kompetenzorientierten Unterricht (pp. 28–43). Kohlhammer.
Marczynski, B., Kaltefleiter, L. J., Siebeck, M., Wecker, C., Stürmer, K., & Ufer, S. (2022). Diagnosing 6th graders’ understanding of decimal fractions. Fostering mathematics pre-service teachers’ diagnostic competences with simulated one-to-one interviews. In F. Fischer & A. Opitz (Eds.), Learning to diagnose with simulations—Examples from teacher education and medical education. Springer.
Murayama, K., Pekrun, R., Lichtenfeld, S., & Vom Hofe, R. (2013). Predicting long-term growth in students’ mathematics achievement: the unique contributions of motivation and cognitive strategies. Child Development, 84(4), 1475–1490.
Ostermann, A., Leuders, T., & Nückles, M. (2018). Improving the judgment of task difficulties: prospective teachers’ diagnostic competence in the area of functions and graphs. Journal of Mathematics Teacher Education, 21(6), 579–605. https://doi.org/10.1007/s10857-017-9369-z.
Padberg, F., & Wartha, S. (2017). Didaktik der Bruchrechnung. Springer Spektrum.
Philipp, K. (2018). Diagnostic competences of mathematics teachers with a view to processes and knowledge resources. In T. Leuders, J. Leuders & K. Philipp (Eds.), Diagnostic competence of mathematics teachers: Unpacking a complex construct in teacher education and teacher practice (pp. 109–127). Springer.
van de Pol, J., Volman, M., & Beishuizen, J. (2010). Scaffolding in teacher–student interaction: a decade of research. Educational Psychology Review, 22(3), 271–296.
Praetorius, A.-K., Lipowsky, F., & Karst, K. (2012). Diagnostische Kompetenz von Lehrkräften. Aktueller Forschungsstand, unterrichtspraktische Umsetzbarkeit und Bedeutung für den Unterricht. In R. Lazarides & A. Ittel (Eds.), Differenzierung im mathematisch-naturwissenschaftlichen Unterricht. Implikationen für Theorie und Praxis (pp. 115–146). Klinkhardt.
Priniski, S., Rosenzweig, E., Canning, E., Hecht, C., Tibbetts, Y., Hyde, J., & Harackiewicz, J. (2019). The benefits of combining value for the self and others in utility-value interventions. Journal of Educational Psychology, 111, 1478–1497.
Rach, S., Heinze, A., & Ufer, S. (2014). Welche mathematischen Anforderungen erwarten Studierende im ersten Semester des Mathematikstudiums? Journal für Mathematik-Didaktik, 35(2), 205–228.
Rasch, G. (1960). Studies in mathematical psychology: I. Probabilistic models for some intelligence and attainment tests. Nielsen & Lydiche.
Rotgans, J. I., & Schmidt, H. G. (2011). Situational interest in academic achievement in the active-learning classroom. Learning and Instruction, 21(1), 58–67.
Schack, E., Fisher, M., Thomas, J., Eisenhardt, S., Tassell, J., & Yoder, M. (2013). Prospective elementary school teachers’ professional noticing of children’s early numeracy. Journal of Mathematics Teacher Education, 16(5), 379–397.
Schiefele, U., Krapp, A., & Winteler, A. (1992). Interest as a predictor of academic achievement: A meta-analysis of research. In K. A. Renninger, S. Hidi & A. Krapp (Eds.), The role of interest in learning and development (pp. 183–212). Lawrence Erlbaum.
Schukajlow, S., Rakoczy, K., & Pekrun, R. (2017). Emotions and motivation in mathematics education: theoretical considerations and empirical contributions. ZDM—International Journal on Mathematics Education, 49(3), 307–322.
Seidel, T., & Stürmer, K. (2014). Modeling and measuring the structure of professional vision in preservice teachers. American Educational Research Journal, 51, 739–771.
Seidel, T., Stürmer, K., Blomberg, G., Kobarg, M., & Schwindt, K. (2011). Teacher learning from analysis of videotaped classroom situations: Does it make a difference whether teachers observe their own teaching or that of others? Teaching and Teacher Education, 27, 259–267.
Shulman, L. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57(1), 1–23.
Siegler, R. S., & Lortie-Forgues, H. (2015). Conceptual knowledge of fraction arithmetic. Journal of Educational Psychology, 107(3), 909.
Stegmann, K., Pilz, F., Siebeck, M., & Fischer, F. (2012). Vicarious learning during simulations: is it more effective than hands-on training? Medical Education, 46(10), 1001–1008.
Steinle, V. (2004). Changes with age in students’ misconceptions of decimal numbers, Dissertation, University of Melbourne. http://hdl.handle.net/11343/39024. Accessed 17 June 2020.
Steinle, V., & Pierce, R. (2006). Incomplete or incorrect understanding of decimals: an important deficit for studnet nurses. PME.
Stürmer, K., Marczynski, B., Wecker, C., Siebeck, M., & Ufer, S. (2021). Praxisnahe Lerngelegenheiten in der Lehrerausbildung – Validierung der simulationsbasierten Lernumgebung DiMaL zur Förderung diagnostischer Kompetenz von angehenden Mathematiklehrpersonen. In N. Beck, T. Bohl & S. Meissner (Eds.), Vielfältig herausgefordert. Forschungs- und Entwicklungsfelder der Lehrerbildung auf dem Prüfstand. Tübingen University Press.
Südkamp, A., & Praetorius, A.-K. (2017). Eine Einführung in das Thema der diagnostischen Kompetenz von Lehrkräften. In A. Südkamp & A.-K. Praetorius (Eds.), Diagnostische Kompetenz von Lehrkräften: Theoretische und methodische Weiterentwicklungen (pp. 13–18). Waxmann.
Südkamp, A., Kaiser, J., & Möller, J. (2012). Accuracy of teachers’ judgments of students’ academic achievement: A meta-analysis. Journal of Educational Psychology, 104(3), 743–762.
Takker, S., & Subramaniam, K. (2019). Knowledge demands in teaching decimal numbers. Journal of Mathematics Teacher Education, 22(3), 257–280.
Tröbst, S., Kleickmann, T., Heinze, A., Bernholt, A., Rink, R., & Kunter, M. (2018). Teacher knowledge experiment: testing mechanisms underlying the formation of preservice elementary school teachers’ pedagogical content knowledge concerning fractions and fractional arithmetic. Journal of Educational Psychology, 110(8), 1049–1065.
Weinert, F. E. (2001). Vergleichende Leistungsmessung in Schulen. In Leistungsmessungen in Schulen (pp. 17–32). Beltz.
Wollring, B. (2004). Individualdiagnostik im Mathematikunterricht der Grundschule als Impulsgeber für Fördern, Unterrichten und Ausbildung. Teil 2: Handlungsleitende Diagnostik. Schulverwaltung HRS, 8(11), 297–298.
Acknowledgements
The research presented in this contribution was funded by a DFG (Deutsche Forschungsgemeinschaft) grant to Stefan Ufer, Kathleen Stürmer, Christof Wecker, and Matthias Siebeck (Grant numbers UF59/5‑1 and UF59/5‑2 as part of COSIMA, FOR2385).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
SU, KS, CW and MS conceived the study. SK participated in the design of the simulation, creation of the employed scales, collected the data, performed the main analyses, and wrote the manuscript. DS supported during the design of the simulation, the creation of the scales for professional knowledge, data analysis and revised the analysis scripts and the manuscript. MA supported during data collection. SU supported the design of the simulation, during data collection, and during data analysis. He revised the analyses and the manuscript. KS, CW and MS supported the design of the simulation and the creation of the employed scales.
Corresponding author
Ethics declarations
Conflict of interest
S. Kron, D. Sommerhoff, M. Achtner, K. Stürmer, C. Wecker, M. Siebeck and S. Ufer declare that they have no competing interests.
Ethical standards
The studies involving human participants were reviewed and approved by the ethics committee of the Faculty of Mathematics, Computer Science and Statistics, LMU Munich.
Supplementary Information
13138_2022_200_MOESM1_ESM.docx
Detailed item statistics of professional knowledge test, correlations of knowledge components and interest facets, item examples of professional knowledge test (CK and PCK), items of interest scale, detailed sample statistics and syntax of the used linear mixed models can be found in the Supplementary Materials.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kron, S., Sommerhoff, D., Achtner, M. et al. Cognitive and Motivational Person Characteristics as Predictors of Diagnostic Performance: Combined Effects on Pre-Service Teachers’ Diagnostic Task Selection and Accuracy. J Math Didakt 43, 135–172 (2022). https://doi.org/10.1007/s13138-022-00200-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13138-022-00200-2
Keywords
- Diagnostic competences
- Teachers’ professional knowledge
- Interest
- Approximations of practice
- Diagnostic task potential
- Simulation-based learning