1 Introduction

The transition from school to the mathematics studies at university often comes with high dropout rates ranging from 38% (Germany, Dieter 2012) up to 70% (U.S.A., Chen 2009). This dropout is often explained by the academic demands freshmen have to face during the first year of the mathematics studies (e.g., Clark and Lovric 2009; Kosiol et al. 2019). As such, studying mathematics at university usually demands freshmen to adapt to the characteristics of scientific mathematics, which focuses deductive reasoning and proving mathematical statements, and requires more autonomous, self-regulated learning (Hoyles et al. 2001; Rach and Heinze 2017). The challenges may cause frustration and other negative emotions against the study of mathematics. As a consequence, freshmen often drop out from the mathematics studies due to such excessive demands they do not feel able to cope with (e.g., Gausch and Seemann 2012).

Mathematical resilience describes “a positive affective stance towards mathematics” to overcome any affective barriers presented when learning mathematics (Johnston-Wilder and Lee 2010, Introduction; also Lee and Johnston-Wilder 2017). The concept of mathematical resilience could thus be important for investigating first year mathematics students’ coping with challenges at university (Lawson 2015). However, research focusing mathematical resilience of university mathematics students is still scarce (Duah 2017; Kooken et al. 2016; Schulmeister 2014).

In this article, we therefore propose to adapt the concept of mathematical resilience to the context of the mathematics studies at university and introduce a novel measure of mathematical resilience that considers specific educational challenges for the mathematics studies. First, we provide a short overview on current research on dropout from university and explore the contribution of mathematical resilience to this research. Second, we analyse the challenges that are specific to the study of mathematics and that have to be mastered by mathematics freshmen to avoid dropout. Third, we introduce an instrument assessing mathematical resilience of first year university mathematics students. Finally, we report about a study investigating the instrument’s empirical quality.

2 Theoretical Background

2.1 Research On Dropout from University

Dropout from university has been subject of many studies over the last decades which leads to an extensive body of research (e.g., Bean 1985; Pascarella and Terenzini 1980; Spady 1971; Tinto 1975). Many studies examined different cognitive and non-cognitive factors that possibly influence academic performance and thus affect students’ decision to change their major subject or drop out from higher education.

2.1.1 Cognitive Factors

Cognitive abilities enable students to acquire knowledge and skills more quickly and thus may reduce the extent to which academic demands overcharge them (e.g., Deary 2012). Accordingly, early research considered general cognitive abilities (i.e. intelligence) as the main predictor for dropout (Furnham et al. 2002; Sewell and Shah 1967; Spady 1971). However, much of this research found both, general cognitive abilities to explain only small amounts of variance in university academic success or dropout or, even worse, to have no significant relation to academic success at all (Furnham and Chamorro-Premuzic 2004; McLaurin and Farrar 1973; Morgan et al. 1990). Students’ school achievement, mostly assessed with average final school grades such as the Grade Point Average, showed far better predictive validity for university students’ academic success (Brandstätter et al. 2006; DeBerard et al. 2004; Pascarella and Terenzini 1980; Sarcletti and Müller 2011). For example, the meta-analysis by Trapmann et al. (2007) found averaged school grade to explain 21% of the variance in academic success at university. Though this is a considerable amount, much of the variance still remains unexplained. In addition, averaged school grades are usually considered to be a merged measure of not only cognitive abilities, but also affect-motivational factors, self-regulative skills and the like (e.g., Rach and Heinze 2017).

2.1.2 Motivation and Interest

Research on motivational measures and college success resulted in ambiguous insights. For example, some researchers reported on relevant relations between achievement motivation and college grades (Covington and Omelich 1979; Dunham 1973; Harackiewicz et al. 2002), whereas others found only weak relationships between achievement motivation and postsecondary academic performance (Cantor et al. 1990; Entwisle 1972; Weinberger and McClelland 1990; Harackiewicz et al. 2002). And although situation-specific measures of motivational orientation such as achievement goals were often found significant predictors of college achievement (Church et al. 2001; Elliot and Church 1997; Finney et al. 2004; Skaalvik 1997; Tanaka and Yamauchi 2000; Urdan 2004), null results or only weak relations have also been reported (Elliot et al. 1999; Harackiewicz et al. 2000; F. K. Lee et al. 2003; Pekrun et al. 2009; Sideridis 2005). Similarly, research on interest revealed ambiguous results. Although students’ interest in mathematics is generally known to be related to and to predict students’ achievement in mathematics (Halverscheid et al. 2014; W. Lee et al. 2014; Schiefele et al. 1992), this relation is questioned for students transitioning from high school to a mathematics study at university (Rach and Heinze 2017). This might be due to the operationalization of “interest” being too unspecific, given the change in the nature of mathematics and in the learning of mathematics from high school to university (Ufer et al. 2017). There are also findings that students’ interest in mathematics is quite stable during the first year at university in case of mathematics courses without research-orientation (Liebendörfer and Schukajlow 2017). Hence, the mathematical demands in the first year of study might play a role.

2.1.3 Self-beliefs

Academic self-concept was found significantly and positively related to students’ course grades and Grade Point Average (e.g., Choi 2005; Gerardi 1990; Lent et al. 1997; Reynolds 1988). In contrast, academic self-efficacy was sometimes found significantly related (e.g., Robbins et al. 2004; Wood and Locke 1987), and sometimes not related at all (e.g., Choi 2005; Lent et al. 1997). Interestingly, studies employing contextualized operationalization of students’ academic self-concept and self-efficacy reported about stronger correlations to academic performance than those employing more general operationalisations. Such contextualized operationalisations would ask for students’ beliefs with respect to specific situations the students are confronted with. For example, Pajares and David (1994) and Hackett and Betz (1989) assessed mathematics freshmen’s domain specific mathematics self-efficacy and mathematics performance, and revealed moderate significant relations. Measuring in a task-specific manner thus seems crucial for accurate predictions of individuals’ future task performances (Choi 2005).

2.1.4 Personality Traits

Research on personality traits and students’ academic success provided more consistent insights. Typically personality traits are conceptualized by the so-called OCEAN model, including five central traits Openness, Conscientiousness, Extraversion, Agreeableness, and Neuroticism (McCrae and Costa 1989). A meta-analysis by O’Connor and Paunonen (2007) showed conscientiousness consistently positively, openness sometimes positively and extraversion sometimes negatively related to academic success. Chamorro-Premuzic and Furnham (2003) also found academic performance correlated with conscientiousness (positively) and extraversion (negatively). In this study, neuroticism was also negatively associated with academic performance and, overall, personality traits explained almost 30% of the variance in university examination grades (Furnham et al. 2002; Chamorro-Premuzic and Furnham 2003). Hakimi et al. (2011) reported about even higher percentages (48%) of explained variance in senior students’ academic achievement due to personality traits. Here, conscientiousness, extraversion and neuroticism were again the personality factors with the most significant predictive power towards academic achievement. Similar results have been reported by Alcock et al. (2014), who also found conscientiousness and neuroticism to predict mathematics students grades after the first year of their studies. Despite these quite promising results, researchers criticized the OCEAN model to be too global and less situation-specific to predict specific behaviour of students in an academic context (Jers 2012; Schulmeister 2014). Some research even suggested specific conceptualizations of personality traits to maximize its use for predicting university dropout (e.g., Schulmeister 2014).

2.2 Mathematical Resilience

Another non-cognitive factor that specifically addresses students’ attitude to cope with affective academic challenges, but which has hardly been considered in higher education research, is resilience. Resilience refers to the “successful adaptation despite challenging or threatening circumstances” (Masten et al. 1990, p. 425). Whilst general resilience was investigated extensively in the past (Luthar 2006; Masten et al. 1990; Wagnild and Young 1993), only few studies examined resilience in academic settings and specifically resilience in the mathematics studies (Johnston-Wilder and Lee 2010; Kooken et al. 2016; Ricketts et al. 2017). The concept of mathematical resilience refers to learners’ stance to approach mathematics with confidence and persistence (Johnston-Wilder and Lee 2010). Mathematical resilience thus enables a student to be persistent particularly in absence of intrinsic motivation. Prior research found that school students with high mathematical resilience are more likely to persevere and succeed in mathematics than students with low levels of mathematical resilience (Duah 2017; Johnston-Wilder and Lee 2010). Johnston-Wilder and Lee (2010) also showed that school students’ mathematical resilience can be fostered through coaching.

Following this description, mathematical resilience can be theoretically distinguished from constructs such as general resilience, conscientiousness, mathematics interest, academic self-concept and self-regulated learning competencies. First, mathematical resilience differs from general resilience and conscientiousness by means of domain and context specificity. As researchers often pointed out that a person’s self-perception may strongly depend on the context (Jers 2012; Luthar 2006; Sarcletti and Müller 2011; Schulmeister 2014), it can be assumed that mathematical resilience is separable from context-unspecific constructs. In addition, although conscientiousness is often considered to support resilience (Ercan 2017; Friborg et al. 2005; Oshio et al. 2018), it has been argued that resilience should not be identified with one particular personality trait but can be considered to be an interplay of different traits (possibly including conscientiousness, openness and low levels of neuroticism; Ercan 2017). Second, mathematical resilience differs from interest in mathematics as resilience enables students to “function” (e.g., learn, work) despite amotivation, which can be seen as a hassle in the learning process (Johnston-Wilder and Lee 2010; Martin and Marsh 2008). Third, mathematical resilience differs from academic self-concept as self-concept particularly encompasses the self-perception of the own academic performance, whereas mathematical resilience addresses one’s stance in certain stressful situations. Finally, we assume that mathematical resilience may help learners to self-regulate their learning. However, in contrast to self-regulated learning, which rather addresses (meta)cognitive competencies such as knowledge about the domain, setting goals or strategies to evaluate the learning process (e.g., Wirth and Leutner 2008), mathematical resilience rather describes a learner’s attitude. It does not provide the core self-regulated learning competence “to make solid comparisons between an actual state and a desired state” (Wirth and Leutner 2008, p. 104), but it likely helps the learner to persist in a challenging learning process, when actual and desired state often differ.

In summary, mathematical resilience may provide informative insights in the mechanisms of learning mathematics at university. Unfortunately, only little research has been conducted on mathematical resilience with mathematics students in higher education so far (see Duah 2017). Also, current conceptualizations of mathematical resilience focus mainly the context of learning mathematics at school and do not address specific situations that mathematics students encounter in their university studies. As such, those approaches to mathematical resilience often included aspects like self-perceived usefulness of mathematics for the future which are of little use in a sample of mathematics freshmen (see Johnston-Wilder and Lee 2010; Kooken et al. 2016). To be useful for investigating university dropout, the concept of mathematical resilience thus has to be revised and adapted to the specific demands of university mathematics students.

2.3 Challenges of Mathematics Freshmen

To investigate the role of mathematical resilience for academic success and failure in university mathematics education in a contextualized, task-specific manner, the first step is to identify the particular everyday difficulties and challenges mathematics freshmen have to cope with. The literature of dropout in the mathematics studies provides a rich resource of typical difficulties and challenges and typically traces back the difficulties to the transition from school to university (Brandell et al. 2008; Rach and Heinze 2017). The transition is characterized by a change in (a) the nature of mathematics itself and (b) the culture of learning (Andrà et al. 2011; Gueudet 2008; Liebendörfer 2018; Rach and Heinze 2017).

School mathematics education aims at promoting general mathematical literacy. Students typically learn routines of calculation, modeling or problem solving which shall enable them to successfully apply mathematics to everyday problems. As such, school mathematics matches well with the requirements for general study readiness (Rüede et al. 2019). In the university study of mathematics, however, mathematics is introduced as a scientific discipline, that is, the focus is on successively establishing the axiomatic body of mathematical knowledge rather than learning to apply the knowledge. College students are thus required to develop skills of proving and deductive logic which are common practices to generate new mathematical knowledge (Hoyles et al. 2001; Rach et al. 2014). As a consequence, typical exercises in university mathematics education include the development of own proofs (Liebendörfer 2018). Students typically encounter manifold challenges with such university mathematics exercises, such as a missing understanding of the exact problem to be solved or a missing understanding of possible options how to handle the problem (Ableitinger 2012). As developing own proofs is not the focus of school mathematics education, mathematics freshmen usually are poorly skilled in proving and thus feel overtaxed by such exercises (Brandell et al. 2008; Ko and Knuth 2009; Rach and Heinze 2011; Schwarz et al. 2008).

In addition to this change in the nature of mathematics, the culture of learning mathematics changes as well (Gueudet 2008; Gueudet and Pepin 2018; Rach and Heinze 2017). In school, mathematics learning processes are designed and monitored by a teacher, who, for example, selects exercises appropriate for the students’ current zone of proximal development (Vygotsky 1978); at university, learning processes are much more self-regulated as college students mostly have to learn on their own (e.g., Crawford et al. 1994; Wood 2001). University education is structured by lectures, seminars and (weekly) assignments, which typically need to be passed for passing a class (Alsina 2006; Kirchgraber 2006; Liebendörfer 2018). The weekly mathematics assignment may be particularly challenging and stressful for mathematics freshmen (for qualitative evidence see Göller 2019; Liebendörfer 2018). As a consequence of the changed nature in mathematics and the changed culture of learning, the assignments typically includes delicate proving tasks that the students have to solve more or less on their own. Given the above reported difficulties students have with proving tasks, this might put mathematics freshmen in distress of thinking that they are not able to meet the standards of the mathematics studies (Brandell et al. 2008; Rach et al. 2014). For instance, Martínez-Sierra and García-González (2016) interviewed undergraduate mathematics students about the emotions they perceived linear algebra courses. Solving mathematics problems was associated with a variety of negative emotions from disappointment and distress right up to fear. Failing to solve the homework assignments was perceived as particularly distressful, as students felt this would lead to failing the course (i.e., the exam).

2.4 Operationalizing Resilience Towards Mathematics Exercises

Given that mathematical resilience has hardly been investigated in higher mathematics education, and given that working on mathematics assignments/exercises seems to be a major source for students’ to experience difficulties, challenges and setbacks especially in the first year of the mathematics studies, we suggest to investigate a specific part of university mathematics students’ mathematical resilience: their resilience towards mathematics exercises. In order to conceptualize this part of mathematical resilience, we considered five key aspects that characterize persistent working on challenging mathematics exercise and, thus, through which resilience towards mathematics exercises can be defined:

  1. 1.

    Short-term persistence: Resilient students keep working on a mathematics exercise even when there is no perceptible progress in learning or solving the task (e.g., for several hours).

  2. 2.

    Medium-term persistence (assignments): Resilient students restart working on a mathematics exercise even if they recently failed on this task multiple times.

  3. 3.

    Medium-term persistence (study): Resilient students keep studying mathematics in the first semester despite of reoccurring difficulties in solving mathematics exercises.

  4. 4.

    Persistence despite low motivation regarding the current content: Resilient students work on mathematics exercises even if they are not interested in the content of the particular tasks.

  5. 5.

    Persistence despite low motivation regarding the current learning process: Resilient students work on mathematics exercises even if the learning goals associated with the particular tasks is unclear for them.

Aspects 1 and 2 are relevant because students are required to apply advanced mathematical skills like proving skills instead of performing raw calculation schemes or arithmetic problems they are familiar with from school mathematics education. Since in most freshmen proving skills are poorly developed (e.g., Brandell et al. 2008) and students at university learn more autonomous and receive less assistance from teachers than at school, they likely have difficulties with the assignment tasks and need more time and several attempts for solving. Beyond that, aspect 3 also addresses how the constant emotional burden that mathematics assignments exert on students may affect their choices to drop out of the studies during the first semester. Since each semester of the mathematics studies includes the working on (weekly) assignments, it is possible that students perceive themselves not only as incapable of passing single assignments or courses but as incapable of studying mathematics at all. This assumption is in line with the finding from dropout studies, that students often explain their decision to quit by the excessive demands they encountered and not felt able to cope with (e.g., Gausch and Seemann 2012). Aspect 4 takes into account that, as a consequence of the changed nature of mathematics, students’ interest in mathematics may change as well (although the literature is ambiguous here, too: compare Liebendörfer and Schukajlow 2017 vs. Rach and Heinze 2011). Finally, aspect 5 takes into account the changing culture of learning, and students thus struggling to easily see the learning goals of single tasks. Since mathematical concepts are taught in a specific axiomatic and rigorous manner, which is common practice in academic mathematics, the content or the intended learning goals is often hard to understand for students (Gueudet 2008).

Those five aspects of resilience towards mathematics exercises are not to be seen as different subdimensions of mathematical resilience, but as different types of behaviour that can be expected from students with high resilience towards mathematics exercises. Based on those five key aspects, we designed a self-evaluation questionnaire, the “Inventory of Resilience towards Mathematics Exercises (IRME)”. The IRME consists of 11 items addressing university students’ stance when handling assignment related challenges and setbacks (Table 1). Each item contains a statement and a 7-point rating scale to indicate agreement or disagreement to each statement (1 = “strongly disagree”, 7 = “strongly agree”). The questionnaire covers all of the five identified key aspects by each item addressing one aspect: Items 1, 2, 3—aspect 1; items 4, 5—aspect 2; items 10, 11—aspect 3; items 6, 7—aspect 4; and items 8, 9—aspect 5. In order to avoid systematic ticking, we used negative wording in six items. The instrument is available in English (Table 1) and in German (Table 6 in the appendix).

Table 1 The Inventory of Resilience towards Mathematics Exercises (IRME) (English version)
Full size table

3 Research Questions and Hypotheses

In the above presented theoretical background we argued, that mathematical resilience has not been considered in the research on academic success and dropout of mathematics freshmen, so far. Nevertheless, it is well known that the changing nature of mathematics and the changing learning of mathematics provide mathematics freshmen with particular challenges when transitioning from high school to university. It is also known that persistence is regarded an important prerequisite for mathematics freshmen (Deeken et al. 2019). Mathematical resilience, if tailored to the specific situation of mathematics freshmen, may thus help to generate new and fruitful insights in the processes of students’ academic success and failure.

To promote such research, we developed an instrument (the IRME) specifically designed for investigating university mathematics students’ resilience to successfully cope with setbacks caused by the challenging mathematics assignments. The assumption that mathematics exercises are a major challenge for mathematics freshmen is well established in the literature, yet empirical evidence is missing so far. Also, the IRME has not been empirically examined with respect to reliability and validity (AERA, APA and NCME 2014) so far. To address these issues, we conducted a study guided by the following research questions (RQ):

RQ1

To what extent does the IRME address typical challenges perceived by mathematics freshmen?

Hypothesis 1

We assume that compulsory mathematics assignments (i.e. exercises) are perceived as the most pressing everyday challenge of the mathematics studies.

RQ2

To what extent …

2.1. … do IRME scores allow interpretations that are valid from a structural perspective?

Hypothesis 2.1

We assume that the data collected with the IRME can be described using a unidimensional model.

2.2. … does the IRME provide scores that are psychometrically reliable?

Hypothesis 2.2

We assume the IRME to show an at least acceptable internal consistency (>0.70 according to George and Mallery 2006).

2.3. … do IRME scores allow interpretations that are valid from a convergent and discriminant validity perspective?

Hypothesis 2.3

As described in Sect. 2.2, mathematical resilience may be related to general resilience, conscientiousness, openness, mathematics interest, and mathematics-specific academic self-concept, as those constructs have been assumed to positively influence persistence in an academic context. We therefore assume the IRME scores to be at least weakly correlatedFootnote 1to those constructs as well (|r| > 0.20). We also assume that mathematical resilience is distinguishable from the above constructs and, thus, the IRME should not show more than strong correlations (|r| < 0.70).

2.4. … do IRME scores allow interpretations that are valid from a predictive perspective?

Hypothesis 2.4

We assume that mathematically resilient freshmen are more likely to persevere the first semester of the mathematics studies. Thus, we assume that students who show larger IRME scores at the beginning of the first semester are less likely to drop out of the mathematics studies in the first semester.

4 Methods

In order to evaluate this new instrument’s quality, we conducted an empirical study investigating the above validity aspects and reliability of the instrument. To this end, we gathered data from three subsamples employing the IRME and other instruments (for an overview see Table 2). In all subsamples, we collected data twice (pre- and post-measurement). The decision to include subsamples from different universities (two from Germany, one from another country) was based on the idea to have a broad range of students in the sample when collecting data for the validity study.

Table 2 Overview of the sample and the employed instruments
Full size table

Subsample 1 consisted of mathematics freshmen who started their studies in fall 2014 at Kiel University, a mid-sized university in Northern Germany. Pre-data were collected at the end of a mathematics preparatory course shortly before the first semester officially started (N = 83; 64% females). Since in this preparatory course basic mathematical skills, such as working on mathematical problems and writing proofs, are practiced, we may assume that the participating freshmen had gained sufficient experience in working on university-like mathematics problems and thus would respond to the IRME appropriately. In addition to the IRME, we employed a questionnaire assessing general resilience (RS-13; e.g., “When I make plans I follow through with them”; Leppert et al. 2008). This questionnaire is a shortened version (13 items, Cronbach’s α = 0.82) of the well-established “Resilience Scale” (RS; Wagnild and Young 1993). We also employed a questionnaire on the Big Five personality traits (BFI-SOEP; Gerlitz and Schupp 2005; 3 items per Trait; Cronbach’s α from 0.48 to 0.72), which is a shortened version of the Big Five Inventory (BFI; John et al. 1991). Post-data were collected during calculus tutorials at the beginning of the second semester, which were obligatory for students who aimed to pass the first year (N = 91; 31% females; n = 47 students, 23% females, participated in both measurements). Here, we gathered data about the presence in the tutorials, and administered a self-designed questionnaire on the activities of the first semester mathematics studies perceived as most stressing by the students (Table 7 in the appendix). This questionnaire included key activities that mathematics freshmen have to face in their studies (e.g., preparing for the examinations, working on homework assignments, visiting the lectures). Students were asked to indicate on a 10-point Likert-scale to what extent they were stressed by the respective activity.

Subsample 2 consisted of freshmen at Stockholm University in Sweden, who started their studies in fall 2015. These students started a five-year program aiming at both a teaching diploma (for mathematics, physics, chemistry and technology) and a master of engineering. Pre-data were collected during a mathematics lecture in the first few weeks of the first semester (N = 50; 56% females). Post-data were collected with N = 45 students (60% females) during a mathematics lecture in the first few weeks of the second semester. Those 45 students participated in both, the pre- and the post-data collection. The remaining 5 students dropped out from the studies. This rather low drop-out rate is likely due to a specific measure supporting students’ learning (that is, a mathematics help desk, students received advice on a nearly daily base). In this subsample, we employed the IRME, the RS-13, and the BFI-SOEP.

Subsample 3 consisted of mathematics freshmen who started their studies in fall 2015 at LMU Munich, a large university in southern Germany. Pre-data were collected during the calculus tutorials in the first few weeks of the first semester (N = 291, 31% females). As in subsamples 1 and 2, we employed the IRME as well as the questionnaire on general resilience. Additionally, we employed a Big Five personality questionnaire containing five items per subscale, that is, the three items per subscale as used in subsamples 1 and 2 together with two additional items each (Benet-Martínez and John 1998; Cronbach’s α from 0.65 to 0.80). Moreover, we assessed students’ mathematics-specific self-concept (4 items; e.g., “I am good at mathematics”; Cronbach’s α = 0.81; Kauper et al. 2012), and a measure on students’ interest in mathematics (6 items; e.g., “I enjoy working on mathematical problems”; Cronbach’s α = 0.76; adapted from Köller et al. 2001). Post-data were collected from N = 163 students (30% females) based on their course examinations at the end of the first semester. We assessed if they participated in the examinations and how they were graded on the examinations. Again, those 163 students participated in both, the pre- and the post-data collection.

5 Results

5.1 Typical Challenges Perceived by Mathematics Freshmen (RQ1)

The IRME’s items were designed addressing the (weekly) assignments assuming that these assignments are one of the most pressing challenges freshmen are faced with. Prior research already provided qualitative evidence on this assumption. In order to quantitatively substantiate it, we assessed the opinion of mathematics freshmen who just had finished their first and just had begun their second semester (post-data in subsample 1). In particular, we assessed to what extent the weekly exercises are in fact viewed a main factor of pressure and burden from a mathematics freshman’s perspective. With respect to the key activities that mathematics freshmen have to process in their mathematics studies (see Table 7 in the appendix), the participants were asked to rate the perceived degree of stress that was caused by each activity (1: “no stress”; 10: “massive stress”). Particularly, students were asked to consider not only the workload of the activities, but the emotional burden given by those activities.

The results show that, mathematics students view the preparation for examinations at the end of the semester (M = 8.5) and working on assignments (M = 8.3) as the most stressing activities (Fig. 1). The rating on both activities significantly differed from the rating on the other six activities. Also, compared to the other activities (M ≤ 5.5), the ratings on assignments and examinations were rather high. Considering that preparing for an examination is typically increased when the exams are imminent at the end of the semester, this activity may be viewed not a daily stressor throughout the whole semester. The finding thus substantiates the IRME item design based on assignments and provides evidence that the IRME items are related to the construct to be measured, that is, mathematical resilience.

Fig. 1
figure 1

Means (standard errors) for students’ perceived stress that is caused by key activities of the mathematics studies (rating scale: 1 = “no stress” to 10 = “massive stress”)

Full size image

5.2 Investigating the IRME’s Empirical Quality (RQ2)

In order to get insight in the IRME’s quality, we analysed the gathered data with respect to validity and reliability (see AERA, APA and NCME 2014). In particular, we investigated evidence for structural validity (RQ2.1), reliability (RQ2.2), convergent and discriminant evidence (RQ2.3), and evidence for predictive validity (RQ2.4).

5.2.1 Evidence for Structural Validity

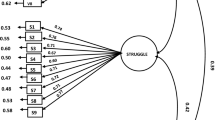
The questionnaire was designed to provide a unidimensional measure of mathematics freshmen’s mathematical resilience. We therefore performed confirmatory factor analyses (CFA) to investigate the factorial structure of the data collected with the IRME. In particular, we compared a unidimensional model with a three-dimensional modelFootnote 2 that corresponds to the types of key aspects of short-term persistence in the mathematics studies, medium-term-persistence in the mathematics studies and persistence despite low motivation in the mathematics studies as described in Sect. 2.4. For both models, we then evaluated model fit based on the χ2-, RMSEA-, CFI-, and BIC-statistics (see Jackson et al. 2009) and compared it with the following cut-off recommendations: 1) CFI should be close to 0.95 (Hu and Bentler 1999) but at least 0.90 (Bentler 1992), 2) RMSEA should be lower than 0.08 (Browne and Cudeck 1992), 3) SRMR should be lower than 0.08 (Hu and Bentler 1999), and 4) comparing models, the model with a lower BIC should be preferred if the difference is larger than 2 (Raftery 1995). Table 3 provides an overview of fit indices for different factor solutions within CFA.

Table 3 Goodness-of-Fit Indicators of two competing models for the data collected with the IRME (n = 403)
Full size table

The indices show that neither model describes the collected data substantially better than the other. In both models, factor loadings were larger than 0.40 (with the only exception of Item 9 which loaded in both models with 0.39). In the three-factor model, the factor correlations were at least 0.88 (p < 0.001). In sum, both models show an acceptable fit to the data in terms of the CFI, RMSEA, and SRMR. The unidimensional model showed a slightly lower BIC than the three-factor model, but the difference is neglectable (≤2). Given the similarity in the goodness of fit and the high factor correlations in the three-factor model, we cannot reject our hypothesis (H2.1), and we use the more parsimonious unidimensional model for the following analyses.

5.2.2 Reliability

As a next step, we investigated the IRME’s internal consistency as a measure for reliability. We found Cronbach’s Alpha to be good (α = 0.85). Also, we did not find Cronbach’s Alpha to increase if an item was excluded from the scale. Overall, this provides evidence for reliability of the unidimensional IRME measures and confirms hypothesis H2.2.

5.2.3 Convergent and Discriminant Evidence

Employing the data we gathered on general resilience, personality traits, mathematical self-concept, and interest in mathematics, we also investigated relationships of the IRME’s measures to these constructs in order to gain convergent and discriminant evidence (see Hypothesis 2.3). To this end, we computed bivariate (Pearson) correlations.

In the overall sample (N = 424), the IRME correlated moderately with the measure of general resilience (r = 0.37, p < 0.001). If corrected for the reliability of the two scalesFootnote 3, we still find a moderate correlation (rcorr = 0.44), indicating the IRME does in fact measure something different than general resilience.

With respect to the Big Five personality traits, the results of subsample 3 are reported separately from subsample 1 and 2 as an extended scale was administered in subsample 3 as a consequence of poor scale reliabilities for conscientiousness (α = 0.50) and agreeableness (α = 0.45) in subsample 1 and 2. Table 4 shows that, nevertheless, the IRME scores correlated moderately with conscientiousness in subsample 1/2 (r = 0.27, p < 0.01) and strongly in subsample 3 (r = 0.45, p < 0.01). Similar to general resilience, the corrected correlation coefficients to conscientiousness were nowhere near 1 (subsample 1/2: rcorr = 0.41; subsample 3: rcorr = 0.58). The other personality traits showed rather weak correlations to the IRME scores, with only openness showing a tendency to a moderate correlation in subsample 3 (r = 0.23, p < 0.001).

Table 4 Correlations of the IRME measures and external variables. Results are reported separately for subsample 3 as expanded measures have been used to assess the Big Five personality traits in this subsample
Full size table

Mathematics-specific academic self-concept and interest both showed significant positive correlations to the IRME scores in subsample 3 (the only subsample where those measures were administered). Whereas the correlation to self-concept appears to be rather weak (r = 0.25, p < 0.001), the correlation to mathematics interest can be considered strong (r = 0.51, p < 0.001). However, the corrected correlation between interest and the IRME scores (rcorr = 0.65) again suggests that the IRME is not measuring interest in mathematics.

Overall, these findings underpin hypothesis H2.3 and indicate that the IRME assesses a trait that is related to but not the same as general resilience, conscientiousness, openness, mathematics interest, and mathematics-specific academic self-concept.

5.2.4 Evidence for Predictive Validity

Finally, we would expect students with a high IRME score more likely to persist the first semester of the mathematics studies, given that they are more successful in withstanding everyday challenges and setbacks of the mathematics studies. This would be considered as predictive validity. In order to investigate this assumption, we compared data from the pre- and post-measurements. Subsample 2 students received extensive additional supporting learning opportunities (see sample description), and thus studied under other conditions than subsamples 1 and 3 which resulted in a very low drop-out. We therefore excluded subsample 2 for the analyses of students’ persistence. For the N = 374 students from subsamples 1 and 3, we related the students’ IRME score with their participation in the post-data collection (yes/no). Students who intended to complete their first semester were required to participate in either the tutorials (subsample 1) or exams (subsample 3) we had chosen for the data collection. Participating in the tutorials or exams therefore was a good indicator for persistence.

Results from a logistic regression show that students with a high score in the IRME were more likely to participate in the post-data collection (β = 0.41, exp(β) = 1.51, SE = 0.11, p < 0.001). This result corresponds to a biserial correlation of r = 0.24 (p < 0.001). Given the correlations of the IRME measures with general resilience, conscientiousness, openness, neuroticism, agreeableness, mathematics specific self-concept and interest in mathematics (see Table 3), we investigated the role of the IRME measures in combination with these variables in predicting persistence, as well. Given that self-concept and interest was only assessed in subsample 3, we investigated two logistic regressions models (Table 5). A logistic regression analysis based on subsamples 1 and 3, including all but self-concept and interest and using the reduced 3‑item personality scales in subsample 3, indicated that only students’ IRME scores had a significant effect on persistence (β = 0.47, p < 0.001). A logistic regression analysis based on only subsample 3, now including self-concept and interest as well and using the full 5‑item personality scales, indicated an additional significant effect of self-concept on persistence (β = 0.39, p < 0.01). Nevertheless, students’ IRME scores were still found as significant predictors for persistence (β = 0.41, p < 0.05).

Table 5 Logistic regression coefficients β (unstandardized) and corresponding odds ratios exp(β) predicting students’ persistence of the first semester of the mathematics studies
Full size table

It would be interesting to see how mathematical resilience develops after the first semester, and which role it takes for students’ achievement over the duration of their studies. Unfortunately, the current data cannot provide insights into these questions. We would expect mathematical resilience to influence rather students’ persisting in the mathematics studies but not necessarily achieving good exam grades. Nevertheless, future studies should investigate a possible predictive use of mathematical resilience for achievement as well.

6 Discussion

The present paper aimed at investigating resilience towards mathematical exercises and introduces the IRME questionnaire. Based on a survey with mathematics freshmen, we found evidence that weekly assignments are experienced as the most pressing everyday hassle of mathematics students in the first semester. Thus, the IRME does in fact address typical challenges perceived by mathematics freshmen, supporting Hypothesis 1. With respect to the IRME’s empirical quality, we found evidence for validity and reliability: Confirmatory factor analyses showed that a unidimensional model fits the data collected by our instrument in a similar fashion than a 3-dimensional model (that corresponds to the aspects of the construct that were developed theoretically). The more parsimonious unidimensional model reflecting mathematical resilience as a latent attitudinal trait can therefore be preferred, which supports Hypothesis 2.1 (structural validity). For this scale, we also found good internal consistency, indicating psychometrical reliability and thus supporting Hypothesis 2.2. Regarding convergent validity, we found the IRME scores to correlate positively with a measure of general resilience, which is in line with our assumptions as mathematically resilient individuals should, at least tendentially, show resilient behaviour in general. However the correlation was no more than moderate, indicating that situation- and task-specificity seems to be important, as suggested by the literature (Jers 2012; Luthar 2006; Schulmeister 2014). We also found the IRME scores to correlate positively to conscientiousness, which is also in line with our assumptions as it is considered a source of resilience (Ercan 2017; Oshio et al. 2018). Openness as well as low levels of neuroticism were also reported to positively influence (mathematical) resilience, but this only was only tentatively reflected through our data as corresponding correlations were weak and only visible in one of the subsamples. None of the constructs showed correlations beyond 0.70 (which might be considered as evidence for empirical separability), not even if the correlations were corrected for scale reliability. This provides empirical evidence that the IRME does not measure general resilience, conscientiousness, interest or self-concept regarding mathematics and can be considered as discriminant validity. Overall, this supports Hypothesis 2.3. Finally, we found the IRME scores to predict if students persisted the first semester of the mathematics studies, which is interpreted to support Hypothesis 2.4 (predictive validity).

When interpreting these results, we should also account for limitations of our study. First, insights in students’ most pressing everyday demands were based on only a sample of N = 83 freshmen. Thus, our results should be considered tentative and corroborated based on a larger sample. Second, we did not investigate convergent validity by comparing the IRME’s measures with measures of other instruments measuring mathematical resilience. By the time of the data collection (2014–2016), there had been no instruments available, to our knowledge. Instead, we used constructs that were assumed to be a source of resilience (e.g., conscientiousness). Recently, Kooken et al. (2016) suggested another instrument measuring mathematical resilience, including three “protective factors that contribute to resilience” (p. 220): 1) value, which addresses students finding mathematics valuable; 2) struggle, which addresses students recognizing that doing mathematics comes with challenges beyond personal (in)competence; and 3) growth, which refers to students being confident that mathematics knowledge can be increased. From a theoretical point of view, the IRME presented here does not measure one of these factors but rather students’ attitude when handling challenges and setbacks related to mathematics assignments. Nevertheless, a comparison of both instruments might provide further fruitful insights, in particular on the relation between students’ resilient attitude and their views regarding value, struggle and growth. Third, we aimed to measure mathematical resilience as an attitudinal trait, yet it is unclear how such trait relates to students’ behaviour. A comparison of students’ IRME scores with their actual behaviour when working on mathematics assignments as well as their stability over time would thus help to elucidate this question. Fourth, we only employed data from mathematics freshmen at the beginning of their studies and after completing their first semester. The presented prediction-related validity evidence should thus be substantiated by investigating the predictive power with respect to students’ persistence in the studies over a longer period (e.g., their persisting in the whole first year of the studies). In that case it might be worth to examine possible differences in the impact of mathematical resilience. Fifth, some of the short scales used to assess personality traits in subsample 1 and 2 showed rather weak scale reliability (particularly, conscientiousness and agreeableness). Corresponding analyses should therefore be interpreted with caution and compared with the findings in subsample 3, for which extended personality scales were used. Finally, our investigations were based on only three subsamples from two German universities and one Swedish university. As such our findings and validity and reliability evidence is not restricted to one single cohort from one single university, but cannot be considered representative for German or Swedish students either. Our results should therefore be corroborated with further samples of other universities for the sake of generalizability.

Nevertheless, our study provides promising evidence that the IRME allows valid interpretations about mathematics freshmen’s mathematical resilience. Given the extraordinarily high dropout rates in the mathematics studies, mathematical resilience may be a relevant factor to be considered in modelling university dropout in future studies. Moreover, mathematical resilience could not only be relevant for the mathematics studies, but also for other university courses in which mathematics plays a major role (e.g., physics, engineering). Future studies could investigate how stressful mathematics exercises are perceived even if the courses do not primarily focus mathematical proving (which is distinctive for research-oriented mathematics courses). Further research should also substantiate our results and investigate if mathematical resilience is related not only to persistence in the mathematics study, but also if it might affect students’ academic achievement. Mathematically resilient students may not only be persisting longer in the mathematics studies despite setbacks, but may also be spending more learning time trying to comprehend mathematics; high quality learning time may in turn relate to student retention and success (e.g., Schulmeister 2014). Moreover, future research may investigate whether and by what means mathematical resilience can be trained in freshmen. Present research on this question is (again) limited to school students only (Johnston-Wilder and Lee 2010), but insights may be adapted to university students as well. Finally, our study also contributes implications from the more practical perspective. For example, if mathematical resilience is confirmed relevant for student dropout and can be fostered in students, respective courses and tutorials could help to reduce the dropout rates. Another strategy could be to rethink and adapt the way of college teaching to decrease the need for mathematical resilience. In summary, when we know more about the mechanisms of how mathematical resilience is related to mathematics freshmen’s academic learning and success, and how they can better be supported, we may help them to master the crucial first phase of the mathematics studies and exploit their full potential as future mathematicians and mathematics teachers.