1 Introduction

Mathematical models involving jump conditions at phase or material interfaces are widespread in many CFD, environmental, and biomedical applications. Examples include coupled subsurface/free-surfaces flow systems (Sochala et al. 2009), incompressible two-phase flows with different densities (Abels et al. 2012,) interfaces between cells or cell parts (Jäger et al. 2009), simulations of different phases within concrete (Muntean and Böhm 2009), and many more. For Darcy flows considered in the current work, the position of the interface is often fixed and known in advance, and the diffusion coefficient is a symmetric tensor with a uniformly symmetric positive definite inverse. This is precisely the setup investigated and analyzed in this paper for a numerical scheme based on a hybridizable discontinuous Galerkin (HDG) method.

The HDG methods first proposed by Cockburn and co-workers in Cockburn et al. (2008b, 2009) inherit many benefits of discontinuous Galerkin (DG) methods such as natural support for non-conforming meshes and hanging nodes, hp-adaptivity, local mass conservation, etc. Moreover, due to the hybrid nature of these methods, they intrinsically support static condensation, which allows decreasing the size of the system of linear equations while keeping this linear system sparse and symmetric positive definite. Static condensation can be interpreted both in an algebraic sense or as an alternative interpretation of the numerical scheme in terms of skeleton unknowns and numerical fluxes. The latter interpretation suggests more general numerical fluxes (that can otherwise only be achieved at higher computational costs) and thus can be utilized to build HDG schemes with an increased accuracy, i.e. optimally convergent and even superconvergent methods, which can be exploited by post-processing techniques (see Nguyen et al. 2009 for an overview of the early developments of the HDG methods).

The aforementioned advantages of the HDG methodology gave rise to a large number of applications for different problems. To name just a few: incompressible Stokes (Nguyen et al. 2010) and Navier–Stokes (Nguyen et al. 2011a) equations, Maxwell equations (Nguyen et al. 2011b), linear elasticity (Di Pietro and Ern 2015), linearized shallow-water equations (Bui-Thanh 2016). Furthermore, comparisons of accuracy, robustness, and computational efficiency between HDG and DG (Woopen et al. 2014; Jaust et al. 2018), HDG and classical Finite Elements (Kirby et al. 2012), HDG and Finite Volumes (Ahnert and Bärwolff 2014) also received some attention. Notably, some recent studies (Vila-Pérez et al. 2022; Kronbichler and Wall 2018) suggest that HDG schemes are not necessarily faster than the corresponding DG discretizations—this aspect must be rather evaluated on a case-by-case basis. However, in a decade of development, only a few studies focusing on porous media problems appeared in the HDG literature: For example, Samii et al. (2016) investigates an adaptive HDG method to deal with anisotropic diffusion in an elliptic setting, Costa-Solè et al. (2019), Fabien et al. (2018) apply hybrid methods to two-phase flows in porous media, Gatica and Sequeira (2018) analyzes the Brinkman problem, and Moon et al. (2019) investigates multiscale approaches that are related to HDG. However, discontinuities in the solution (arising from physics) are disregarded in their respective models.

Our main interest in connection with HDG schemes concerns the flow and transport in porous media, where their DG counterparts proved to be very useful with their affinity to unstructured meshes and adaptivity combined with low regularity requirements on the solution and coefficients—making the DG method well-suited for complex geometries encountered in real-world problems (Ray et al. 2017). Another feature distinguishing the HDG schemes from their DG counterparts is the convergence for approximation spaces of order zero. This capability is often desirable for porous media applications, where many numerical models utilize lowest order spaces (cf. Samii et al. 2016).

In the current work, we investigate an LDG-H method—a particular type of HDG scheme (Cockburn et al. 2009) related to the local DG (LDG) discretizations. We analyze stability and convergence when applied to instationary equations with (mildly) non-linear tensor-valued diffusion coefficients exemplified by Darcy flows. Numerically, we confirm our analytical findings for linear, optionally anisotropic diffusion tensors on polytopically bounded domains with flat interfaces. Of particular interest are approximation spaces of different orders for different unknowns such as in Cockburn et al. (2009), Rupp et al. (2018). Our formulation in principal allows for non-linear diffusion tensors and enforces jumps in the primary unknown described by Henry’s law. Similar problems have already been analyzed for LDG (Rupp et al. 2018) and enriched Galerkin (Rupp and Lee 2020) schemes. The analysis relies in part on techniques employed for an LDG formulation in Aizinger et al. (2018), Rupp and Knabner (2017), Rupp et al. (2018), Reuter et al. (2019) and extends them to the LDG-H method.

The first analysis for a HDG-type method was given by Cockburn et al. (2008b) for a special LDG-H variant called the single face hybridizable (SFH) method; its distinctive feature is the penalty coefficient \(\tau \) chosen as a positive constant on one face of each simplex and zero everywhere else. A more general result for elliptic problems followed in Cockburn et al. (2010) that relied on a special projection (exclusively for simplex-meshes) tailored to fit the characteristics of HDG methods. These results were generalized to non-conforming simplicial meshes in Chen and Cockburn (2012) and squares, cubes, and prisms in Cockburn et al. (2012). An analysis for a Poisson equation involving additive jumps in the primary and the flux unknowns (as opposed to multiplicative jumps considered here) was presented in Dong et al. (2017), and parabolic problems with non-linear diffusion tensors were considered in Moon et al. (2017).

The current paper (based, in part, on results presented in Rupp 2019) is structured as follows. The next section introduces the model problem followed by its semi-discrete LDG-H formulation in Sect. 3. Section 4 contains the energy stability and convergence estimates for the semi-discrete formulation. Numerical convergence studies and a realistic problem with discontinuous diffusion coefficients are presented in Sect. 5.

2 Problem formulation

Similarly to Rupp et al. (2018), we consider a bounded Lipschitz domain \( \varOmega \subset {\mathbb {R}}^d\) subdivided into two open, disjoint, non-degenerated, Lipschitz polytopes \(\varOmega ^l\), \(\varOmega ^g\) such that \({{\bar{\varOmega }}} = {{\bar{\varOmega }}}^l \cup {\bar{\varOmega }}^g\). We assume \(\partial \varOmega \) to be disjointly subdivided into \(\varGamma _D \) and \(\varGamma _N \) denoting the Dirichlet and Neumann boundaries, respectively. Moreover, \(\varGamma _LG := \partial \varOmega ^l \cap \partial \varOmega ^g\) is the boundary between \(\varOmega ^l\) and \(\varOmega ^g\) where the Henry jump condition is imposed. The problem can be formulated as follows:

$$\begin{aligned} \partial _t u + \nabla \cdot {\textbf{q}}&= f&\textrm{in }\,&\left( 0,T\right) \times \left( \varOmega ^l \cup \varOmega ^g\right) , \end{aligned}$$
(1a)
$$\begin{aligned} D^{-1}\left( u\right) {\textbf{q}} + \nabla u&= 0&\textrm{in }\,&\left( 0,T\right) \times \left( \varOmega ^l \cup \varOmega ^g\right) ,\end{aligned}$$
(1b)
$$\begin{aligned} u_l / u_g&= H^LG&\textrm{on }\,&\left( 0,T\right) \times {\varGamma _{LG }},\end{aligned}$$
(1c)
$$\begin{aligned} {\textbf{q}}_l \cdot \varvec{\nu }_l + {\textbf{q}}_g \cdot \varvec{\nu }_g&= 0&\textrm{on }\,&\left( 0,T\right) \times {\varGamma _{LG }}, \end{aligned}$$
(1d)
$$\begin{aligned} {\textbf{q}} \cdot \varvec{\nu }&= g_N&\textrm{on }\,&\left( 0,T\right) \times \varGamma _N , \end{aligned}$$
(1e)
$$\begin{aligned} u&= u_D&\textrm{on}\,&\left( 0,T\right) \times \varGamma _D , \end{aligned}$$
(1f)
$$\begin{aligned} u\left( 0,\textbf{x}\right)&= u_0\left( \textbf{x}\right)&\textrm{in }\,&\varOmega ^l \cup \varOmega ^g, \end{aligned}$$
(1g)

for \(H^LG \in {\mathbb {R}}^+\), \(f \in L^2\left( 0,T;L^2\left( \varOmega \right) \right) \), and \(u_D , g_N \in L^2\left( 0,T;H^1\left( \varOmega ^l \cup \varOmega ^g\right) \right) \). The inverse of the diffusion tensor \(D^{-1}\left( \cdot \right) \in L^\infty \left( 0,T;W^{1,\infty }\left( \varOmega ^l \cup \varOmega ^g\right) ^{d,d}\right) \) is assumed to be strongly Lipschitz and uniformly symmetric positive definite with constants \(L_D\) and \(C_D\), respectively (see Remark 2.1). Here and in the following, \(\varvec{\nu }_\alpha \) denotes the outward unit normal with respect to \(\varOmega ^\alpha \) (\(\alpha = l,g\)), and \(\varvec{\nu }\) is the outward unit normal with respect to \(\varOmega \).

Remark 2.1

  1. 1.

    In this work, \(D^{-1}\left( \cdot \right) \) being Lipschitz means that there is a constant \(L_D > 0\) such that for all \(v, w \in L^2\left( \varOmega \right) \)

    $$\begin{aligned} \Vert D^{-1}\left( v\right) - D^{-1}\left( w\right) \Vert _{L^2\left( \varOmega \right) ^{d,d}} \le L_D \Vert v - w \Vert _{L^2\left( \varOmega \right) }. \end{aligned}$$
  2. 2.

    \(D^{-1}\left( \cdot \right) \) being uniformly symmetric positive definite is equivalent to the existence of a constant \(C_D \ge 1\) (independent of \(u \in L^2\left( \left( 0,T\right) \times \varOmega \right) \), \(t \in \left( 0,T\right) \), and \(\textbf{x} \in \varOmega ^l \cup \varOmega ^g\)) such that for all \(\varvec{\xi }\in {\mathbb {R}}^d\)

    $$\begin{aligned} C_D^{-1} \Vert \varvec{\xi }\Vert ^2_2 \le \varvec{\xi }\cdot D^{-1}\left( u\right) \varvec{\xi }\le C_D \Vert \varvec{\xi }\Vert ^2_2. \end{aligned}$$
    (2)

    This implies \(\Vert D^{-1}\left( u\left( t,\cdot \right) \right) \Vert _{L^\infty (\varOmega )} \le C_D\).

  3. 3.

    In the setting of the Darcy equation, the flux unknown \({\textbf{q}} = - D\left( u\right) \nabla u\) can be interpreted as Darcy flux, and its “continuity” (1d) across \({\varGamma _{LG }}\) ensures the conservation of mass, while the primary unknown u can be interpreted as the hydraulic head.

Having defined our problem, we now specify the requirements for a weak solution to the above problem.

Problem 2.2

(Weak problem) A weak solution of (1) on domain \(\varOmega \) is defined as \(\left( u, {\textbf{q}}\right) \in L^2 \left( \left( 0,T\right) \times \varOmega \right) \times L^2 \left( \left( 0,T\right) \times \varOmega \right) ^d\) satisfying the following conditions:

  1. 1.

    For \(\alpha = l, g\), the restriction of u to \(\varOmega ^\alpha \) fulfills \(u_\alpha \in H^1\left( (0,T) \times \varOmega ^\alpha \right) \).

  2. 2.

    The restriction of \({\textbf{q}}\) to \(\varOmega ^\alpha \) fulfills \({\textbf{q}}_\alpha \in L^2\left( 0,T;H^1\left( \varOmega ^\alpha \right) ^d\right) \) for \(\alpha = l,g\).

  3. 3.

    System (3) holds for any smooth test functions \(\varphi _u\), \(\varvec{\varphi }_{\textbf{q}}\), any Lipschitz subdomain \(\varOmega _e \subset \varOmega \), and for a.e. \(t \in \left( 0,T\right) \):

    $$\begin{aligned} \int _{\varOmega _e}&\partial _t u\, \varphi _u \, d\textbf{x}- \int _{\varOmega _e} {\textbf{q}} \cdot \nabla \varphi _u \, d\textbf{x}+ \int _{\partial \varOmega _e \setminus \varGamma _N } \!\!\!\!\!\!\!\! {\textbf{q}} \cdot \varvec{\nu }\varphi _u \, d\sigma + \int _{\partial \varOmega _e \cap \varGamma _N } g_N \, \varphi _u \, d\sigma = \int _{\varOmega _e} f \varphi _u \, d\textbf{x}, \end{aligned}$$
    (3a)
    $$\begin{aligned} \int _{\varOmega _e}&D^{-1} \left( u\right) {\textbf{q}} \cdot \varvec{\varphi }_{\textbf{q}} \, d\textbf{x}- \int _{\varOmega _e} u \left( \nabla \cdot \varvec{\varphi }_{\textbf{q}} \right) \, d\textbf{x}+ \int _{\varOmega _e \cap {\varGamma _{LG }}} \left( u_l-u_g\right) \varvec{\varphi }_{\textbf{q}} \cdot \varvec{\nu }_l {\, d\sigma } \nonumber \\&\quad + \int _{\partial \varOmega _e \setminus \varGamma _D } u\, \varvec{\varphi }_{\textbf{q}} \cdot \varvec{\nu }\, d\sigma + \int _{\partial \varOmega _e \cap \varGamma _D } u_D \, \varvec{\varphi }_{\textbf{q}} \cdot \varvec{\nu }\, d\sigma = 0. \end{aligned}$$
    (3b)

Note that this problem can be formulated under quite general conditions concerning the non-linearity. Our analysis covers the case of mildly non-linear problems. At the same time, our numerical studies in Sect. 5 are limited to linear problems and explore the effects of different approximation polynomial orders, discontinuity size, and diffusion coefficient anisotropy.

3 An LDG-H method capable of dealing with jump conditions

3.1 Basic definitions and some auxiliary results

The notation will be, as far as possible, kept analogous to the notation in Rupp et al. (2018) with some parts taken from Samii et al. (2016). This means that in the following, \({\mathcal {T}}_h = \lbrace {\mathcal {K}}_i: i = 1, \dots , N_{el}\rbrace \) denotes a d-dimensional non-overlapping polytopic partition of \(\varOmega \) (see Di Pietro and Ern 2012, Def. 1.12) such that, for each element \({\mathcal {K}}_i\), either \({\mathcal {K}}_i \subset \varOmega _l\) or \({\mathcal {K}}_i \subset \varOmega _g\) is fulfilled. For simplicity, all partitions of \(\varOmega \) are assumed to be geometrically conformal (in the sense of Ern and Guermond 2004, Def 1.55). We denote by \({\mathcal {F}}= {\mathcal {F}}\left( {\mathcal {T}}_h\right) \) the set of faces, by \({\mathcal {F}}_I \) the set of interior faces (that do not intersect with \({\varGamma _{LG }}\)), by \({\mathcal {F}}_D \) Dirichlet, and by \({\mathcal {F}}_N \) Neumann boundary faces, and by \({\mathcal {F}}_LG \) the set of faces that belong to \({\varGamma _{LG }}\). Note that every face of the mesh is an element of one and only one of the following sets: \({\mathcal {F}}_I , {\mathcal {F}}_LG , {\mathcal {F}}_D , {\mathcal {F}}_N \).

The test- and ansatz-spaces are defined as the broken polynomial spaces of order at most k:

$$\begin{aligned} {\mathbb {P}}_k^d\left( {\mathcal {T}}_h \right) := \lbrace \textbf{v} \in L^2\left( \varOmega \right) ^d: \textbf{v} |_{\mathcal {K}} \text{ is } \text{ a } \text{ polynomial } \text{ of } \text{ degree } \text{ at } \text{ most } k,\ \forall {\mathcal {K}}\in {\mathcal {T}}_h \rbrace . \end{aligned}$$

For hybridization purposes, another ansatz space—the so-called skeleton space on the element faces (excluding those with the Dirichlet boundary conditions)—needs to be defined:

$$\begin{aligned} {\mathbb {P}}_k\left( {\mathcal {F}}\setminus {\mathcal {F}}_D \right) := \left\{ \mu \in L^2\left( \bigcup _{F \in {\mathcal {F}}\setminus {\mathcal {F}}_D } F \right) : \mu |_F \in {\mathbb {P}}_k(F),\, \forall F \in {\mathcal {F}}\setminus {\mathcal {F}}_D \right\} . \end{aligned}$$

For an element-wise defined scalar function w and an element-wise vector function \(\textbf{v}\), we define the jump \(\llbracket \cdot \rrbracket \) on \(\partial {\mathcal {K}}_i \cap \partial {\mathcal {K}}_j\) for neighboring mesh elements \({\mathcal {K}}_i, {\mathcal {K}}_j \in {\mathcal {T}}_h,\, {\mathcal {K}}_i \ne {\mathcal {K}}_j\) in the following way:

$$\begin{aligned} \llbracket w \rrbracket&= w_{\mid {\mathcal {K}}_i}\varvec{\nu }_{{\mathcal {K}}_i} + w_{\mid {\mathcal {K}}_j}\varvec{\nu }_{{\mathcal {K}}_j},&\llbracket \textbf{v} \rrbracket = \textbf{v}_{\mid {\mathcal {K}}_i} \cdot \varvec{\nu }_{{\mathcal {K}}_i} + \textbf{v}_{\mid {\mathcal {K}}_j} \cdot \varvec{\nu }_{{\mathcal {K}}_j}, \end{aligned}$$

where \(\varvec{\nu }_{\mathcal {K}}\) is the outward unit normal with respect to \({\mathcal {K}}\). Note that a jump in a scalar variable is a vector, whereas a jump in a vector is a scalar. For \(F \in {\mathcal {F}}_I \), an interior face shared by cells \({\mathcal {K}}^-\) and \({\mathcal {K}}^+\), and for \(x \in F\), we define the one-sided values of a scalar quantity \(w = w(x)\) by

$$\begin{aligned} w^-(x):= \lim _{\varepsilon \rightarrow 0^+} w(x - \varepsilon \varvec{\nu }_{{\mathcal {K}}^-}) \quad \textrm{ and }\, \quad w^+(x):= \lim _{\varepsilon \rightarrow 0^+} w(x - \varepsilon \varvec{\nu }_{{\mathcal {K}}^+}) \end{aligned}$$

and for \(F \in {\mathcal {F}}_LG \), a face on \({\varGamma _{LG }}\) shared by cells \({\mathcal {K}}^l \subset \varOmega ^l\) and \({\mathcal {K}}^g \subset \varOmega ^g\), and for \(x \in F\), we define the one-sided values of a scalar quantity \(w = w(x)\) by

$$\begin{aligned} w^l(x):= \lim _{\varepsilon \rightarrow 0^+} w(x - \varepsilon \varvec{\nu }_{{\mathcal {K}}^l}) \quad \textrm{ and }\, \quad w^g(x):= \lim _{\varepsilon \rightarrow 0^+} w(x - \varepsilon \varvec{\nu }_{{\mathcal {K}}^g}). \end{aligned}$$

Definition 3.1

(Shape and contact regularity) A family of meshes \({\mathcal {T}}_h\) is said to be shape and contact regular (short regular) if, for all \(h > 0\), \({\mathcal {T}}_h\) admits a geometrically conformal, matching simplicial submesh \(\bar{\mathcal {T}}_h\) (Di Pietro and Ern 2012, Definition 1.37) such that

  1. 1.

    \(\left( {{\bar{{\mathcal {T}}}}}_h\right) _{h>0}\) is shape-regular in the usual sense of Ciarlet (1990), meaning that there is a parameter \(\lambda _1 > 0\), independent of h, such that for all \({{\bar{{\mathcal {K}}}}} \in {{\bar{{\mathcal {T}}}}}_h\),

    $$\begin{aligned} \lambda _1 h_{{{\bar{{\mathcal {K}}}}}} \le \rho _{{{\bar{{\mathcal {K}}}}}}, \end{aligned}$$

    where \(\rho _{{{\bar{{\mathcal {K}}}}}}\) is the diameter of the largest ball that can be inscribed in \({{\bar{{\mathcal {K}}}}}\).

  2. 2.

    there is a constant \(\lambda _2 > 0\), independent of h, such that for all \({\mathcal {K}}\in {\mathcal {T}}_h\) and for all \({{\bar{{\mathcal {K}}}}} \in {{\bar{{\mathcal {T}}}}}_h\) with \({{\bar{{\mathcal {K}}}}} \subset {\mathcal {K}}\),

    $$\begin{aligned} \lambda _2 h_{\mathcal {K}}\le h_{{{\bar{{\mathcal {K}}}}}}, \end{aligned}$$

Lemma 3.2

(Discrete trace inequality) Let \(({\mathcal {T}}_h)_{h>0}\) be a regular mesh family with parameters \(\lambda _1, \lambda _2, \lambda _3\). Then, for all \(h > 0\) and all \(\textbf{p} \in {\mathbb {P}}^d_k({\mathcal {T}}_h)\), the following holds with \(C_\textrm{tr}\) only depending on \(\lambda _1, \lambda _2\), d, and k:

$$\begin{aligned} \sum _{F \in {\mathcal {F}}} h_F^{1/2} \Vert \textbf{p} \Vert _{L^2(F)}&\le \; C_\textrm{tr} \sum _{{\mathcal {K}}\in {\mathcal {T}}_h} \Vert \textbf{p} \Vert _{L^2({\mathcal {K}})} \;=\; C_\textrm{tr} \Vert \textbf{p} \Vert _{L^2(\varOmega )},\\ \sum _{F \in {\mathcal {F}}} h_F^{1/2} \Vert \textbf{p} \cdot \varvec{\nu }\Vert _{L^2(F)}&\le \; \sqrt{d}\, C_\textrm{tr} \sum _{{\mathcal {K}}\in {\mathcal {T}}_h} \Vert \textbf{p} \Vert _{L^2({\mathcal {K}})} \;=\; \sqrt{d}\, C_\textrm{tr} \Vert \textbf{p} \Vert _{L^2(\varOmega )}. \end{aligned}$$

For an interior face, \(\Vert \textbf{p} \Vert _{L^2(F)}\) is assumed to contain traces from both elements

$$\begin{aligned} \Vert \textbf{p} \Vert _{L^2(F)} \;=\; \Vert \textbf{p}_{\mid {\mathcal {K}}_i} \Vert _{L^2(F)} + \Vert \textbf{p}_{\mid {\mathcal {K}}_j} \Vert _{L^2(F)}. \end{aligned}$$

Proof

The first inequality follows from Lemma 1.46 in Di Pietro and Ern (2012) and the fact that \(h_F \le h_T\) for all faces F of element T. The second inequality follows from the first one and the fact that \(\varvec{\nu }\) is a constant vector on each face. \(\square \)

To simplify notation, we denote in the following \(\Vert \cdot \Vert _{L^2(A)}\) as \(\Vert \cdot \Vert _A\) and use explicit norm notation for all other norms.

3.2 Spatial discretization

For hybridization, a new variable on the skeleton space \({\mathbb {P}}_k\left( {\mathcal {F}}\setminus {\mathcal {F}}_D \right) \) is introduced and denoted by \(\lambda _h\). In the following, we propose a modification of the LDG-H method described in Samii et al. (2016) capable of dealing with jump conditions across a submanifold \({\varGamma _{LG }}\) (i.e., Henry’s Law) using instationary Darcy flow as an example application. An investigation of the same model problem using a classical LDG method was conducted in Rupp et al. (2018).

To deal with Henry’s law, the numerical trace \({\hat{u}}_h\) is defined as

$$\begin{aligned} {\hat{u}}_{h\mid \partial {\mathcal {K}}}:= \left\{ \begin{array}{rll} &{} u_D &{} \partial {\mathcal {K}}\cap \partial \varOmega _D \\ &{} \lambda _h &{} \partial {\mathcal {K}}\setminus \left( \partial \varOmega _D \cup \varGamma _LG \right) \\ &{} \lambda _h &{} \left( \partial {\mathcal {K}}\cap \varGamma _LG \right) \wedge \left( {\mathcal {K}}\subset \varOmega ^g\right) \\ &{} H^LG \lambda _h &{} \left( \partial {\mathcal {K}}\cap \varGamma _LG \right) \wedge \left( {\mathcal {K}}\subset \varOmega ^l\right) \end{array}\right. \end{aligned}$$
(4)

whereas the numerical flux \(\hat{{\textbf{q}}}_h\) is chosen as

$$\begin{aligned} \hat{{\textbf{q}}}_{h\mid \partial {\mathcal {K}}}:= {\textbf{q}}_h + \tau \left( u_h - \hat{u}_h\right) \varvec{\nu }_{\mathcal {K}}, \end{aligned}$$

where \(\tau \ge 0\) is a stabilization parameter (possibly depending on h). For more information on the stabilization parameter \(\tau \), the reader is referred to Cockburn et al. (2008a), Cockburn et al. (2008b).

The (semi-discrete) LDG-H formulation of the model problem (1) reads:

Problem 3.3

(Semi-discrete LDG-H problem for Henry’s law) Find \(\left( u_h, {\textbf{q}}_h, \lambda _h\right) \in {\mathbb {P}}_k\left( {\mathcal {T}}_h\right) \times {\mathbb {P}}_{{\hat{k}}}^d\left( {\mathcal {T}}_h\right) \times {\mathbb {P}}_{\bar{k}}\left( {\mathcal {F}}{\setminus } {\mathcal {F}}_D \right) \) such that (5) holds for all \(\left( \varphi _u, \varvec{\varphi }_{\textbf{q}}, \varphi _\lambda \right) \in {\mathbb {P}}_k\left( {\mathcal {T}}_h\right) \times {\mathbb {P}}_{{\hat{k}}}^d\left( {\mathcal {T}}_h\right) \times {\mathbb {P}}_{\bar{k}}\left( {\mathcal {F}}{\setminus } {\mathcal {F}}_D \right) \), all \({\mathcal {K}}\in {\mathcal {T}}_h\), and a.e. \(t \in (0,T)\)

$$\begin{aligned}&\int _{{\mathcal {K}}} \partial _t u_h \varphi _u \, d\textbf{x}- \int _{{\mathcal {K}}} {\textbf{q}}_h \cdot \nabla \varphi _u \, d\textbf{x}+ \int _{\partial {\mathcal {K}}\setminus \left( \varGamma _D \cup {\varGamma _{LG }}\right) } \left( {\textbf{q}}_h \cdot \varvec{\nu }_{\mathcal {K}}+ \tau \left( u_h - \lambda _h \right) \right) \varphi _u \, d\sigma \nonumber \\&\quad + \int _{\partial {\mathcal {K}}\cap {\varGamma _{LG }}} \left( {\textbf{q}}_h \cdot \varvec{\nu }_{\mathcal {K}}+ \left\{ \begin{array}{ll} \tau \left( u_h^l - H^LG \lambda _h \right) &{}\textrm{ if }\, {\mathcal {K}}\subset \varOmega ^l\\ \tau \left( u_h^g - \lambda _h \right) &{}\textrm{ if }\, {\mathcal {K}}\subset \varOmega ^g \end{array} \right. \right) \varphi _u \, d\sigma \nonumber \\&\quad + \int _{\partial {\mathcal {K}}\cap \varGamma _D } \left( {\textbf{q}}_h \cdot \varvec{\nu }+ \tau \left( u_h - u_D \right) \right) \varphi _u \, d\sigma = \int _{{\mathcal {K}}} f \varphi _u \, d\textbf{x}, \end{aligned}$$
(5a)
$$\begin{aligned}&\int _{{\mathcal {K}}} D^{-1} \left( u_h \right) {\textbf{q}}_h \cdot \varvec{\varphi }_{\textbf{q}} \, d\textbf{x}- \int _{{\mathcal {K}}} u_h \left( \nabla \cdot \varvec{\varphi }_{\textbf{q}} \right) \, d\textbf{x}+ \int _{\partial {\mathcal {K}}\setminus \left( \varGamma _D \cup {\varGamma _{LG }}\right) } \lambda _h \varvec{\varphi }_{\textbf{q}} \cdot \varvec{\nu }_{\mathcal {K}}\, d\sigma \nonumber \\&\quad + \int _{\partial {\mathcal {K}}\cap {\varGamma _{LG }}} \left( \left\{ \begin{array}{ll} H^LG \lambda _h &{}\textrm{ if }\, {\mathcal {K}}\subset \varOmega ^l\\ \lambda _h &{}\textrm{ if }\, {\mathcal {K}}\subset \varOmega ^g \end{array} \right. \right) \varvec{\varphi }_{\textbf{q}} \cdot \varvec{\nu }_{\mathcal {K}}\, d\sigma + \int _{\partial {\mathcal {K}}\cap \varGamma _D } u_D \, \varvec{\varphi }_{\textbf{q}} \cdot \varvec{\nu }\, d\sigma =0, \end{aligned}$$
(5b)
$$\begin{aligned}&\sum _{F \in {\mathcal {F}}_I } \int _F \left( \llbracket {\textbf{q}}_h\rrbracket + \tau \left( u_h^- + u_h^+ - 2 \lambda _h \right) \right) \varphi _\lambda \, d\sigma + \sum _{F \in {\mathcal {F}}_N } \int _F \left( {\textbf{q}}_h \cdot \varvec{\nu }+ \tau \left( u_h - \lambda _h \right) \right) \varphi _\lambda \, d\sigma \nonumber \\&\quad + \sum _{F \in {\mathcal {F}}_LG } \int _F \left( \llbracket {\textbf{q}}_h\rrbracket + \tau \left( u_h^l + u_h^g - (1+ H^LG ) \lambda _h \right) \right) \varphi _\lambda \, d\sigma = \sum _{F \in {\mathcal {F}}_N } \int _F g_N \varphi _\lambda \, d\sigma . \end{aligned}$$
(5c)

Here, \(k, {\hat{k}}, {\bar{k}}\) denote orders of polynomial ansatz spaces for different unknowns.

Remark 3.4

(5c) is a globally coupled system that ensures the local mass conservation, whereas (5a), (5b) are element-local and can be solved elementwise.

4 Stability and error analysis

Our analysis heavily relies on techniques presented in Aizinger et al. (2018), Rupp and Knabner (2017), Rupp et al. (2018), Reuter et al. (2019), additional results used in the proofs are introduced in the corresponding sections.

4.1 Stability estimate

First, we introduce a new function \({{\widetilde{H}}^LG }(\textbf{x})\) that generalizes the Henry coefficient to the whole domain \(\varOmega \) (note that argument \(\textbf{x}\) is omitted later on):

$$\begin{aligned} {{\widetilde{H}}^LG }(\textbf{x}):= {\left\{ \begin{array}{ll} 1 &{} \textbf{x} \in \bar{\varOmega }^l \setminus \varGamma _LG , \\ H^LG &{} \textbf{x} \in \bar{\varOmega }^g. \end{array}\right. } \end{aligned}$$

Theorem 4.1

(Energy stability of the semi-discrete problem) Assume that \(\left( u_h, {\textbf{q}}_h, \lambda _h\right) \) is a solution of Problem 3.3. For every regular, geometrically conformal family of meshes \(\left( {\mathcal {T}}_h\right) _{h > 0}\) and for all \(\tau , h>0\) in (5), there exists a function \(C\left( s\right) \) such that for a.e. \(s \in \left( 0,T\right) \)

$$\begin{aligned}&\left\| \sqrt{{{\widetilde{H}}^LG }} u_h \left( s,\cdot \right) \right\| _{\varOmega }^2 + \int _0^s \bigg [ \left\| \sqrt{{{\widetilde{H}}^LG }D^{-1}\left( u_h\right) } {\textbf{q}}_h \right\| _{\varOmega }^2 \nonumber \\&\quad + \sum _{F \in {\mathcal {F}}\setminus {\mathcal {F}}_{D }} \tau {{\widetilde{H}}^LG }\left\| \lambda _h \right\| _{F}^2 + \sum _{F \in {\mathcal {F}}_D } \tau {{\widetilde{H}}^LG }\Vert u_h \Vert _{F}^2 \bigg ] \, dt\le C\left( s\right) . \end{aligned}$$

Here, the second term is interpreted as

$$\begin{aligned} \left\| \sqrt{{{\widetilde{H}}^LG }D^{-1}\left( u_h\right) } {\textbf{q}}_h \right\| _{\varOmega }^2 = \int _\varOmega {{\widetilde{H}}^LG }{\textbf{q}}_h^T D^{-1}\left( u_h\right) {\textbf{q}}_h \, d\textbf{x}. \end{aligned}$$

We highlight that C(s) depends on h and becomes larger as h goes to 0. Nonetheless, for each fixed value of h, we obtain temporal stability and therefore globally unique existence of semi-discrete solutions.

Proof

The proof uses ideas from the proof of Rupp et al. (2018, Theorem 4.9). Special care must be taken of the boundary with the specified jump condition \({\varGamma _{LG }}\).

We test Eq. (5) with \({{\widetilde{H}}^LG }u_h\), \({{\widetilde{H}}^LG }{{\textbf{q}}}_h\), and \(-{{\widetilde{H}}^LG }\lambda _h\), integrate the second equation by parts, and sum the first two over all \({\mathcal {K}}\in {\mathcal {T}}_h\). This yields

$$\begin{aligned} \int _\varOmega&\left( \partial _t u_h\right) {{\widetilde{H}}^LG }u_h \, d\textbf{x}- \sum _{{\mathcal {K}}\in {\mathcal {T}}_h}\int _{\mathcal {K}}{{\widetilde{H}}^LG }{\textbf{q}}_h \cdot \nabla u_h \, d\textbf{x}\\&+ \sum _{F \in {\mathcal {F}}_D } \int _F \left( {\textbf{q}}_h \cdot \varvec{\nu }+ \tau \left( u_h - u_D \right) \right) {{\widetilde{H}}^LG }u_h \, d\sigma \\&+ \sum _{F \in {\mathcal {F}}_I } \int _F \left( {{\widetilde{H}}^LG }\llbracket {\textbf{q}}_h u_h\rrbracket + \tau \left( u_h^- - \lambda _h \right) {{\widetilde{H}}^LG }u_h^- + \tau \left( u_h^+ - \lambda _h \right) {{\widetilde{H}}^LG }u_h^+ \right) \, d\sigma \\&+ \sum _{F \in {\mathcal {F}}_LG } \int _F \left( \llbracket {\textbf{q}}_h {{\widetilde{H}}^LG }u_h\rrbracket + \tau \left( u_h^l - H^LG \lambda _h \right) u_h^l + \tau \left( u_h^g - \lambda _h\right) H^LG u_h^g \right) \, d\sigma \\&+ \sum _{F \in {\mathcal {F}}_N } \int _F \left( {\textbf{q}}_h \cdot \varvec{\nu }+ \tau \left( u_h - \lambda _h \right) \right) {{\widetilde{H}}^LG }u_h \, d\sigma = \int _\varOmega f {{\widetilde{H}}^LG }u_h \, d\textbf{x},\\ \int _\varOmega&D^{-1}\left( u_h\right) {{\widetilde{H}}^LG }{\textbf{q}}_h \cdot {{\textbf{q}}}_h \, d\textbf{x}+ \sum _{{\mathcal {K}}\in {\mathcal {T}}_h}\int _{\mathcal {K}}{{\widetilde{H}}^LG }\nabla u_h \cdot {{\textbf{q}}}_h \, d\textbf{x}- \sum _{F \in \left( {\mathcal {F}}_I \cup {\mathcal {F}}_LG \right) } \int _F \llbracket u_h {{\widetilde{H}}^LG }{{\textbf{q}}}_h\rrbracket \, d\sigma \\&- \sum _{F \in \left( {\mathcal {F}}_D \cup {\mathcal {F}}_N \right) } \int _F u_h {{\widetilde{H}}^LG }{{\textbf{q}}}_h \cdot \varvec{\nu }\, d\sigma + \sum _{F \in {\mathcal {F}}_I } \int _F \lambda _h {{\widetilde{H}}^LG }\llbracket {{\textbf{q}}}_h\rrbracket \, d\sigma + \sum _{F \in {\mathcal {F}}_N } \int _F \lambda _h {{\widetilde{H}}^LG }{{\textbf{q}}}_h \cdot \varvec{\nu }\, d\sigma \\&+ \sum _{F \in {\mathcal {F}}_D } \int _F u_D {{\widetilde{H}}^LG }{{\textbf{q}}}_h \cdot \varvec{\nu }\, d\sigma + \sum _{F \in {\mathcal {F}}_LG } \int _F \lambda _h H^LG \llbracket {\textbf{q}}_h\rrbracket \, d\sigma = 0,\\ \sum _{F \in {\mathcal {F}}_I }&\int _F \left( \llbracket {\textbf{q}}_h\rrbracket + \tau \left( u_h^- - \lambda _h + u_h^+ - \lambda _h\right) \right) \left( -{{\widetilde{H}}^LG }\lambda _h\right) \, d\sigma \\&+ \sum _{F \in {\mathcal {F}}_LG } \int _F \left( \llbracket {\textbf{q}}_h\rrbracket + \tau \left( u_h^l - H^LG \lambda _h + u_h^g - \lambda _h\right) \right) \left( -H^LG \lambda _h\right) \, d\sigma \\&+ \sum _{F \in {\mathcal {F}}_N } \int _F \left( {\textbf{q}}_h \cdot \varvec{\nu }+ \tau \left( u_h - \lambda _h\right) \right) \left( -{{\widetilde{H}}^LG }\lambda _h\right) \, d\sigma = \sum _{F \in {\mathcal {F}}_N } \int _F g_N \left( -{{\widetilde{H}}^LG }\lambda _h\right) \, d\sigma . \end{aligned}$$

Adding the above equations together and using algebraic simplifications gives

$$\begin{aligned} \frac{1}{2}&\partial _t \Vert \sqrt{{{\widetilde{H}}^LG }}\, u_h \Vert _{\varOmega }^2 +\left\| \sqrt{{{\widetilde{H}}^LG }D^{-1}\left( u_h\right) }\, {\textbf{q}}_h \right\| _{\varOmega }^2 + \sum _{F \in {\mathcal {F}}_N }\tau {{\widetilde{H}}^LG }\left( \Vert u_h \Vert _{F}^2 + \Vert \lambda _h \Vert _{F}^2 \right) \nonumber \\&+ \sum _{F \in {\mathcal {F}}_I } \tau {{\widetilde{H}}^LG }\left( \Vert u_h^- \Vert _{F}^2 + \Vert u_h^+ \Vert _{F}^2 + 2 \Vert \lambda _h \Vert _{F}^2 \right) + \sum _{F \in {\mathcal {F}}_D } \tau {{\widetilde{H}}^LG }\Vert u_h \Vert _{F}^2 \nonumber \\&+ \sum _{F \in {\mathcal {F}}_LG } \tau \left( \Vert u_h^l \Vert _{F}^2 + H^LG \Vert u_h^g \Vert _{F}^2 + H^LG \left( H^LG + 1 \right) \Vert \lambda _h \Vert _{F}^2 \right) \nonumber \\ =&\underbrace{ \int _{\varOmega } {{\widetilde{H}}^LG }f u_h \, d\textbf{x}}_{ \varXi _1 } - \underbrace{ \sum _{F \in {\mathcal {F}}_N } {{\widetilde{H}}^LG }\int _F g_N \lambda _h \, d\sigma }_{\varXi _2} + \underbrace{ \sum _{F \in {\mathcal {F}}_I } \tau {{\widetilde{H}}^LG }\int _F 2 \lambda _h \left( u_h^- + u_h^+ \right) \, d\sigma }_{\varXi _3} \nonumber \nonumber \\&+ \underbrace{ \sum _{F \in {\mathcal {F}}_LG } \tau H^LG \int _F 2 \lambda _h (u_h^l + u_h^g) \, d\sigma }_{\varXi _4} + \underbrace{ \sum _{F \in {\mathcal {F}}_N } \tau {{\widetilde{H}}^LG }\int _F 2 \lambda _h u_h \, d\sigma }_{\varXi _5}\nonumber \\&+ \underbrace{ \sum _{F \in {\mathcal {F}}_D } \tau {{\widetilde{H}}^LG }\int _F u_D u_h \, d\sigma }_{\varXi _6} - \underbrace{ \sum _{F \in {\mathcal {F}}_D } {{\widetilde{H}}^LG }\int _F u_D {\textbf{q}}_h \cdot \varvec{\nu }\, d\sigma . }_{\varXi _7} \end{aligned}$$
(6)

Using Young’s and Cauchy-Schwarz’ inequalities, \(\varXi _i\) terms can be estimated as follows:

$$\begin{aligned} |\varXi _1|&\le \frac{1}{2} \Vert \sqrt{{{\widetilde{H}}^LG }}\, f \Vert _{\varOmega }^2 + \frac{1}{2} \Vert \sqrt{{{\widetilde{H}}^LG }}\, u_h \Vert _{\varOmega }^2 \\ |\varXi _2|&\le \sum _{F \in {\mathcal {F}}_N } {{\widetilde{H}}^LG }\left( \frac{1}{\tau }\Vert g_N \Vert _{F}^2 + \frac{\tau }{4} \Vert \lambda _h \Vert _{F}^2 \right) \\ | \varXi _3 |&\le \sum _{F \in {\mathcal {F}}_I } \tau {{\widetilde{H}}^LG }\left( \Vert \lambda _h \Vert _{F}^2 + \Vert u_h^- \Vert _{F}^2 + \frac{1}{2} \Vert \lambda _h \Vert _{F}^2 + 2 \Vert u_h^+ \Vert _{F}^2 \right) \\ | \varXi _4 |&\le \sum _{F \in {\mathcal {F}}_LG } \tau \left( \left( H^LG \right) ^2 \Vert \lambda _h \Vert _{F}^2 + \Vert u_h^l \Vert _{F}^2 + H^LG \left( \frac{1}{2} \Vert \lambda _h \Vert _{F}^2 + 2 \Vert u_h^g \Vert _{F}^2 \right) \right) \\ | \varXi _5 |&\le \sum _{F \in {\mathcal {F}}_N } \tau {{\widetilde{H}}^LG }\left( \frac{1}{4} \Vert \lambda _h \Vert _{F}^2 + 4 \Vert u_h \Vert _{F}^2 \right) \\ |\varXi _6|&\le \sum _{F \in {\mathcal {F}}_D } \tau {{\widetilde{H}}^LG }\left( \frac{1}{2} \Vert u_D \Vert _{F}^2 + \frac{1}{2} \Vert u_h \Vert _{F}^2 \right) \\ |\varXi _7|&\le \sum _{F \in {\mathcal {F}}_D } \frac{{{\widetilde{H}}^LG }d\, C_D C_\textrm{tr}}{2 h_F } \Vert u_D \Vert _{F}^2 + \sum _{F \in {\mathcal {F}}_D } \frac{{{\widetilde{H}}^LG }}{2} C^{-1}_D \frac{h_F}{d\, C_\textrm{tr}} \Vert {\textbf{q}}_h \cdot \varvec{\nu }\Vert _{F}^2 \\&\le \sum _{F \in {\mathcal {F}}_D } \frac{{{\widetilde{H}}^LG }d\, C_D C_\textrm{tr}}{2 h_{F} } \Vert u_D \Vert _{F}^2 + \frac{1}{2} \int _{\varOmega } {{\widetilde{H}}^LG }D^{-1}\left( u_h\right) {\textbf{q}}_h \cdot {\textbf{q}}_h \, d\textbf{x}\end{aligned}$$

The last inequality is obtained by first invoking Lemma 3.2 and then using (2) pointwise. Substituting the above estimates into (6) and collecting similar terms gives us the following expression:

$$\begin{aligned} \partial _t&\Vert \sqrt{{{\widetilde{H}}^LG }}\, u_h \Vert _{\varOmega }^2 + \left\| \sqrt{{{\widetilde{H}}^LG }D^{-1}\left( u_h\right) }\, {\textbf{q}}_h \right\| _{\varOmega }^2 + \sum _{F \in {\mathcal {F}}\setminus {\mathcal {F}}_D } \tau {{\widetilde{H}}^LG }\Vert \lambda _h \Vert _{F}^2 + \sum _{F \in {\mathcal {F}}_D } \tau {{\widetilde{H}}^LG }\Vert u_h \Vert _{F}^2 \\ \le&\Vert \sqrt{{{\widetilde{H}}^LG }}\, f \Vert _{\varOmega }^2 + \Vert \sqrt{{{\widetilde{H}}^LG }}\, u_h \Vert _{\varOmega }^2 + \sum _{F \in {\mathcal {F}}_N } \frac{2 {{\widetilde{H}}^LG }}{\tau }\Vert g_N \Vert _{F}^2 + \sum _{F \in {\mathcal {F}}_I } 2\, \tau {{\widetilde{H}}^LG }\Vert u_h^+ \Vert _{F}^2 \\&+ \sum _{F \in {\mathcal {F}}_LG } 2\, \tau H^LG \Vert u_h^g \Vert _{F}^2 + \sum _{F \in {\mathcal {F}}_N } 6\, \tau {{\widetilde{H}}^LG }\Vert u_h \Vert _{F}^2 + \sum _{F \in {\mathcal {F}}_D } \left( \tau + \frac{d\, C_D C_\textrm{tr}}{h_{F}} \right) {{\widetilde{H}}^LG }\Vert u_D \Vert _{F}^2\,. \end{aligned}$$

The stability result follows from, first, using the discrete trace inequality given in Lemma 3.2 on boundary integral terms involving unknown solution and then applying Grönwall’s inequality. Notably, this might create a factor \(h_{F,min }^{-1}\) (with \(h_{F,min }\) denoting the minimum face diameter) on the right-hand side of the stability estimate. \(\square \)

Remark 4.2

Although the factor \(h_{F,min }^{-1}\) enters the right-hand side of the stability estimate, this estimate can still be used to ensure that for any fixed \(h > 0\) the discrete solution is stable and therefore exists globally for any time. Our estimate should be understood in that sense. However, this result does not imply the existence of a weak solution by letting \(h \searrow 0\). In order to show that the weak solution of (1) exists uniquely, one can, for example, use the results of Rupp and Lee (2020) and plug them into the general existence and uniqueness theory presented in Evans (2010, §7.1.2).

4.2 Convergence order estimate

The convergence analysis of the semi-discrete scheme given in Problem 3.3 relies on a special type of Projection \((\varPi _w, \varvec{\varPi }_v)\) introduced in Cockburn et al. (2010) and also used in Chabaud and Cockburn (2012). It is defined on each simplex \({\mathcal {K}}\) as

$$\begin{aligned}&\int _{\mathcal {K}}\varvec{\varPi }_v {\textbf{q}} \cdot \textbf{v} \, d\textbf{x}= \int _{\mathcal {K}}{\textbf{q}} \cdot \textbf{v} \, d\textbf{x}\quad \forall \textbf{v} \in {\mathbb {P}}_{k-1}^d\left( {\mathcal {K}}\right) , \nonumber \\&\int _{\mathcal {K}}\varPi _w u w \, d\textbf{x}= \int _{\mathcal {K}}u w \, d\textbf{x}\quad \forall w \in {\mathbb {P}}_{k-1}\left( {\mathcal {K}}\right) ,\nonumber \\&\int _F \left( \varvec{\varPi }_v {\textbf{q}} \cdot \varvec{\nu }+ \tau \varPi _w u \right) \mu \, d\sigma = \int _F \left( {\textbf{q}} \cdot \varvec{\nu }+ \tau u\right) \mu \, d\sigma \quad \forall F \subset \partial {\mathcal {K}},\, \forall \mu \in {\mathbb {P}}_k\left( F\right) . \end{aligned}$$
(7)

The approximation properties of this projection are given in the following

Lemma 4.3

(Corollary of Theorem 2.1 from Cockburn et al. 2010) Let \(\tau |_{\partial {\mathcal {K}}}\) be non-negative, and let \(\tau _{\mathcal {K}}^{\max }:= \max \tau |_{\partial {\mathcal {K}}} > 0\). Then for \(k \ge 0\) and for given \(u \in H^{k+1}\left( {\mathcal {K}}\right) \) and \({\textbf{q}}\in H^{k+1}\left( {\mathcal {K}}\right) ^d\), system (7) is uniquely solvable for \(\varvec{\varPi }_v {\textbf{q}}\) and \(\varPi _w u\). Furthermore, there exists a constant \(C_\varPi \) independent of \({\mathcal {K}}\) and \(\tau \) such that

$$\begin{aligned} \Vert \varvec{\varPi }_v {\textbf{q}} - {\textbf{q}} \Vert _{{\mathcal {K}}}&\le C_\varPi h^{k + 1} \left( |{\textbf{q}}|_{H^{k+ 1}\left( {\mathcal {K}}\right) ^d} + \tau _{\mathcal {K}}^{\max } |u|_{H^{k+1}\left( {\mathcal {K}}\right) } \right) , \\ \Vert \varPi _w u - u \Vert _{{\mathcal {K}}}&\le C_\varPi h^{k + 1} \left( |u|_{H^{k+1}\left( {\mathcal {K}}\right) } + \frac{1}{\tau _{\mathcal {K}}^{\max }} |{\textbf{q}}|_{H^{k+1}\left( {\mathcal {K}}\right) ^d} \right) , \end{aligned}$$

where \(|\cdot |_{H^{k+1}\left( {\mathcal {K}}\right) }\) denotes the standard semi-norm on \(H^{k+1}\left( {\mathcal {K}}\right) \).

Proof

This corollary trivially follows from Cockburn et al. (2010, Theorem 2.1) proved in the appendix of Cockburn et al. (2010). For \(k=0\), only the third equation of (7) makes sense and is sufficient to compute the projection. \(\square \)

Remark 4.4

The fact that this analysis technique only works for simplex-shaped elements certainly constitutes a limitation of our methodology; however, our convergence results shown in Sect. 5 indicate that our scheme also converges with the same order for rectangular elements.

For the analytical solution \(\left( u, {\textbf{q}}\right) \) and the discrete solution \(\left( u_h, {\textbf{q}}_h\right) \) of our problem, we denote

$$\begin{aligned} \begin{array}{ll} e_u:= u_h - \varPi _w u, &{} \theta _u:= \varPi _w u - u,\\ e_q:= {\textbf{q}}_h - \varvec{\varPi }_v {\textbf{q}}, &{} \theta _q:= \varvec{\varPi }_v {\textbf{q}} - {\textbf{q}},\\ e_{\lambda }:= \lambda _h - \varPi u, &{} \theta _{\lambda }:= \varPi u - u, \\ e_{\lambda }^g:= \lambda _h - \varPi u^g, &{} \theta _{\lambda }^g:= \varPi u^g - u^g, \\ e_{\lambda }^l:= H^LG \lambda _h - \varPi u^l,\; &{} \theta _{\lambda }^l:= \varPi u^l - u^l, \end{array} \end{aligned}$$
(8)

Here, \(\varPi \) denotes an \(L^2\)-projection acting on a given \(\zeta \in L^2({\mathcal {F}}{\setminus } {\mathcal {F}}_D )\). Note that the restriction of \(\varPi \zeta \) to \(F \in {\mathcal {F}}{\setminus } {\mathcal {F}}_D \) is in \({\mathbb {P}}_k\left( F\right) \) and satisfies:

$$\begin{aligned} \varPi : F \rightarrow {\mathbb {P}}_k(F), \qquad \langle \varPi \zeta - \zeta , \mu \rangle _{F} = 0, \quad \forall \mu \in {\mathbb {P}}_k\left( F\right) . \end{aligned}$$

Note that \(H^LG e_{\lambda }^g = e_{\lambda }^l\) on \({\varGamma _{LG }}\) since \(u^l = H^LG u^g\) and \(\varPi \) is linear.

To deal with non-linear diffusion coefficients we state

Lemma 4.5

The following inequality holds for \(u \in H^{k+1}(\varOmega ^\alpha )\), \(u_h \in {\mathbb {P}}_k\left( {\mathcal {T}}_h\right) \), \({\textbf{q}} \in L^\infty \left( \varOmega ^\alpha \right) ^d \cap H^{k+1}(\varOmega ^\alpha )^d\), \(\alpha = l,g\), and \(e_{\textbf{q}}\) defined in (8):

$$\begin{aligned} \int _{\varOmega }&\left( D^{-1}\left( u_h\right) - D^{-1} \left( u\right) \right) {\textbf{q}} \cdot e_{\textbf{q}}\, d\textbf{x}\; \le \; \varepsilon \Vert e_{\textbf{q}}\Vert _{\varOmega }^2 \\&+ \frac{L_D^2}{4 \varepsilon } \Vert {\textbf{q}} \Vert _{L^\infty \left( \varOmega \right) ^d}^2 \left( \Vert e_u\Vert _{\varOmega }^2 + C_\varPi ^2 h^{2k + 2} \sum _{{\mathcal {K}}\in {\mathcal {T}}_h} \left( |u|_{H^{k+1}\left( {\mathcal {K}}\right) } + \frac{1}{\tau _{\mathcal {K}}^{\max }} |{\textbf{q}}|_{H^{k+1}\left( {\mathcal {K}}\right) ^d} \right) ^2 \right) \end{aligned}$$

for some arbitrary \(\varepsilon >0\).

Proof

Using Hölder’s, Young’s inequalities and properties of \(D^{-1}(\cdot )\) we obtain

$$\begin{aligned} \int _{\varOmega }&\left( D^{-1}\left( u_h\right) - D^{-1} \left( u\right) \right) {\textbf{q}} \cdot e_{\textbf{q}}\, d\textbf{x}\le \Vert {\textbf{q}} \Vert _{L^\infty \left( \varOmega \right) ^{d}} \Vert \left( D^{-1}\left( u_h\right) - D^{-1} \left( u\right) \right) \Vert _{\varOmega } \Vert e_{\textbf{q}}\Vert _{\varOmega } \\&\le L_D \Vert u_h - u \Vert _{\varOmega } \Vert {\textbf{q}} \Vert _{L^\infty \left( \varOmega \right) ^d} \Vert e_{\textbf{q}}\Vert _{\varOmega } \le \varepsilon \Vert e_{\textbf{q}}\Vert _{\varOmega }^2 + \frac{L_D^2}{4 \varepsilon } \Vert {\textbf{q}} \Vert _{L^\infty \left( \varOmega \right) ^d}^2 \left( \Vert e_u\Vert _{\varOmega }^2 + \Vert \theta _u\Vert _{\varOmega }^2 \right) , \end{aligned}$$

and the result then follows by Lemma 4.3. \(\square \)

Remark 4.6

A result related to Lemma 4.5 is mentioned in Rupp et al. (2018, Rem. 4.8) without proof. In our analysis, the projection defined in Lemma 4.3 is used instead of the standard \(L^2\)-projection utilized in Rupp et al. (2018).

Next, we prove our main convergence result.

Theorem 4.7

(Convergence order estimate for the LDG-H method) Let \((u, {\textbf{q}}) \in H^1\left( 0,T;H^{k+1}(\varOmega ^l \cup \varOmega ^g )\right) \times H^1\left( 0,T;H^{k+1}(\varOmega ^l \cup \varOmega ^g)^d\right) \) be a solution to Problem 2.2. Then for every regular, geometrically conformal family of simplicial meshes \({\mathcal {T}}_h\) and a uniformly bounded for all \(h>0\) parameter \(\tau =\textrm{const}>0\), the solution of Problem 3.3\((u_h, {\textbf{q}}_h, \lambda _h) \in {\mathbb {P}}_k\left( {\mathcal {T}}_h\right) \times {\mathbb {P}}_{k}^d\left( {\mathcal {T}}_h\right) \times {\mathbb {P}}_{k}\left( {\mathcal {F}}{\setminus } {\mathcal {F}}_D \right) \) converges for almost every \(s \in (0,T)\) with order \(k+1\) to the solution of Problem 2.2\((u, {\textbf{q}})\) in the following sense:

$$\begin{aligned}&\Vert \sqrt{{{\widetilde{H}}^LG }}\, e_u\left( s, \cdot \right) \Vert _{\varOmega }^2 + \int _0^s \Big [ \Vert \sqrt{{{\widetilde{H}}^LG }}\, e_{\textbf{q}}\Vert _{\varOmega }^2 + \sum _{F \in {\mathcal {F}}_{N }} \tau {{\widetilde{H}}^LG }\Vert e_u- e_{\lambda }\Vert _{F}^2 \\&\quad + \sum _{F \in {\mathcal {F}}_I } \tau {{\widetilde{H}}^LG }\left( \Vert e_u^- - e_{\lambda }\Vert _{F}^2 + \Vert e_u^+ - e_{\lambda }\Vert _{F}^2 \right) + \sum _{F \in {\mathcal {F}}_D } \tau {{\widetilde{H}}^LG }\Vert e_u\Vert _{F}^2 \\&\quad + \sum _{F \in {\mathcal {F}}_LG } \tau \left( \Vert e_u^l - e_{\lambda }^l \Vert _{F}^2 + H^LG \Vert e_u^g - e_{\lambda }^g \Vert _{F}^2 \right) \Big ] \, dt\le \; C h^{2k+2}, \end{aligned}$$

where C is independent of h.

Proof

We subtract Eqs. (3a)–(3b) from Eqs. (5a) to (5b), respectively, introduce \(\pm \varPi _w u, \pm \varvec{\varPi }_v {\textbf{q}}\) terms into corresponding integrals in (5c), test the equations with \({{\widetilde{H}}^LG }e_u\), \({{\widetilde{H}}^LG }e_{\textbf{q}}\), and \(-{{\widetilde{H}}^LG }e_{\lambda }\), respectively, integrate the second equation by parts, and sum over all \({\mathcal {K}}\in {\mathcal {T}}_h\). This yields

$$\begin{aligned} \int _\varOmega&\partial _t e_u{{\widetilde{H}}^LG }e_u\, d\textbf{x}- \sum _{{\mathcal {K}}\in {\mathcal {T}}_h} \int _{\mathcal {K}}{{\widetilde{H}}^LG }e_{\textbf{q}}\cdot \nabla e_u\, d\textbf{x}+ \sum _{F \in {\mathcal {F}}_D } \int _F \left( e_{\textbf{q}}\cdot \varvec{\nu }+ \tau e_u \right) {{\widetilde{H}}^LG }e_u\, d\sigma \\&+ \sum _{F \in {\mathcal {F}}_I } \int _F \left( {{\widetilde{H}}^LG }\llbracket e_{\textbf{q}}e_u\rrbracket + \tau \left( e_u^- - e_{\lambda }\right) {{\widetilde{H}}^LG }e_u^- + \tau \left( e_u^+ - e_{\lambda }\right) {{\widetilde{H}}^LG }e_u^+ \right) \, d\sigma \\&+ \sum _{F \in {\mathcal {F}}_LG } \int _F \left( \llbracket e_{\textbf{q}}{{\widetilde{H}}^LG }e_u\rrbracket + \tau \left( e_u^l - e_{\lambda }^l \right) e_u^l + \tau \left( e_u^g - e_{\lambda }^g \right) H^LG e_u^g \right) \, d\sigma \\&+ \sum _{F \in {\mathcal {F}}_N } \int _F \left( e_{\textbf{q}}\cdot \varvec{\nu }+ \tau \left( e_u- e_{\lambda }\right) \right) {{\widetilde{H}}^LG }e_u\, d\sigma = - \int _{\varOmega } \partial _t \theta _u {{\widetilde{H}}^LG }e_u\, d\textbf{x},\\ \int _\varOmega&D^{-1} \left( u_h\right) e_{\textbf{q}}\cdot {{\widetilde{H}}^LG }e_{\textbf{q}}\, d\textbf{x}+ \sum _{{\mathcal {K}}\in {\mathcal {T}}_h} \int _{\mathcal {K}}{{\widetilde{H}}^LG }\nabla e_u\cdot e_{\textbf{q}}\, d\textbf{x}- \sum _{F \in {\mathcal {F}}_I } \int _F {{\widetilde{H}}^LG }\llbracket e_ue_{\textbf{q}}\rrbracket \, d\sigma \\&- \sum _{F \in \left( {\mathcal {F}}_D \cup {\mathcal {F}}_N \right) } \int _F e_u{{\widetilde{H}}^LG }e_{\textbf{q}}\cdot \varvec{\nu }\, d\sigma - \sum _{F \in {\mathcal {F}}_LG } \int _F \llbracket e_u{{\widetilde{H}}^LG }e_{\textbf{q}}\rrbracket \, d\sigma + \sum _{F \in {\mathcal {F}}_I } \int _F {{\widetilde{H}}^LG }\llbracket e_{\textbf{q}}\rrbracket e_{\lambda }\, d\sigma \\&+ \sum _{F \in {\mathcal {F}}_LG } \int _F \left( e_{\lambda }^l e_{\textbf{q}}^l \cdot \varvec{\nu }_{{\mathcal {K}}^l} + e_{\lambda }^g H^LG e_{\textbf{q}}^g \cdot \varvec{\nu }_{{\mathcal {K}}^g} \right) \, d\sigma + \sum _{F \in {\mathcal {F}}_N } \int _F e_{\lambda }{{\widetilde{H}}^LG }e_{\textbf{q}}\cdot \varvec{\nu }\, d\sigma \\ =&- \int _{\varOmega } {{\widetilde{H}}^LG }\left( D^{-1}\left( u_h\right) \theta _{\textbf{q}}+ \left( D^{-1}\left( u_h\right) - D^{-1} \left( u\right) \right) {\textbf{q}} \right) \cdot e_{\textbf{q}}\, d\textbf{x},\\ -&\sum _{F \in {\mathcal {F}}_I } \int _F \left( \llbracket \textbf{e}_q\rrbracket + \tau \left( e_u^- + e_u^+ - 2 e_{\lambda }\right) \right) {{\widetilde{H}}^LG }e_{\lambda }\, d\sigma - \sum _{F \in {\mathcal {F}}_N } \int _F \left( \textbf{e}_q \cdot \varvec{\nu }+ \tau \left( e_u - e_{\lambda }\right) \right) {{\widetilde{H}}^LG }e_{\lambda }\, d\sigma \\&- \sum _{F \in {\mathcal {F}}_LG } \int _F \left( \llbracket \textbf{e}_q\rrbracket + \tau \left( e_u^l - e_{\lambda }^l + e_u^g - e_{\lambda }^g\right) \right) H^LG e_{\lambda }^g \, d\sigma = 0. \end{aligned}$$

Most of the projection error terms vanish due to the orthogonality properties of the chosen projection specified in Lemma 4.3. Adding up the equations, simple algebraic manipulations give us

$$\begin{aligned}&\frac{1}{2} \partial _t \Vert \sqrt{{{\widetilde{H}}^LG }}\, e_u\Vert _{\varOmega }^2 + \Vert \sqrt{{{\widetilde{H}}^LG }\, D^{-1}\left( u_h\right) }\, e_{\textbf{q}}\Vert _{\varOmega }^2\\&\qquad + \sum _{F \in {\mathcal {F}}_{D }} \tau {{\widetilde{H}}^LG }\Vert e_u \Vert _{F}^2 + \sum _{F \in {\mathcal {F}}_{N }} \tau {{\widetilde{H}}^LG }\Vert e_u- e_{\lambda }\Vert _{F}^2 \\&\qquad + \sum _{F \in {\mathcal {F}}_I } \tau {{\widetilde{H}}^LG }\left( \Vert e_u^- - e_{\lambda }\Vert _{F}^2 + \Vert e_u^+ - e_{\lambda }\Vert _{F}^2 \right) \\&\qquad + \sum _{F \in {\mathcal {F}}_LG } \tau \left( \Vert e_u^l - e_{\lambda }^l \Vert _{F}^2 + H^LG \Vert e_u^g - e_{\lambda }^g \Vert _{F}^2 \right) \\&\quad = - \underbrace{ \int _{\varOmega } {{\widetilde{H}}^LG }\partial _t \theta _u e_u\, d\textbf{x}}_{\varLambda _1} - \underbrace{ \int _{\varOmega } {{\widetilde{H}}^LG }D^{-1}\left( u_h\right) \theta _{\textbf{q}}\cdot e_{\textbf{q}}\, d\textbf{x}}_{\varLambda _2} \\&\qquad - \underbrace{ \int _{\varOmega } {{\widetilde{H}}^LG }\left( D^{-1} \left( u_h\right) - D^{-1}\left( u\right) \right) {\textbf{q}} \cdot e_{\textbf{q}}\, d\textbf{x}}_{\varLambda _3} \end{aligned}$$

Using Young’s and Cauchy-Schwarz’ inequalities as well as Lemma 4.5 we get

$$\begin{aligned} |\varLambda _1|&\le \frac{1}{2} \Vert \sqrt{{{\widetilde{H}}^LG }}\, e_u\Vert _{\varOmega }^2 + \frac{1}{2} C_\varPi ^2 {{\widetilde{H}}^LG }h^{2k + 2} \sum _{{\mathcal {K}}\in {\mathcal {T}}_h} \left( |\partial _t u|_{H^{k+1}\left( {\mathcal {K}}\right) } + \frac{1}{\tau _{\mathcal {K}}^{\max }} |\partial _t {\textbf{q}}|_{H^{k+1}\left( {\mathcal {K}}\right) ^d} \right) ^2 \\ |\varLambda _2|&\le \frac{1}{4} \Vert \sqrt{{{\widetilde{H}}^LG }\, D^{-1}\left( u_h\right) }\, e_{\textbf{q}}\Vert _{\varOmega }^2 + C_D C_\varPi ^2 {{\widetilde{H}}^LG }h^{2k + 2} \sum _{{\mathcal {K}}\in {\mathcal {T}}_h} \left( |{\textbf{q}}|_{\textbf{H}^{k + 1}\left( {\mathcal {K}}\right) ^d} + \tau _{\mathcal {K}}^{\max } |u|_{H^{k+1}\left( {\mathcal {K}}\right) } \right) ^2 \\ |\varLambda _3|&\le \frac{1}{4 C_D} \Vert \sqrt{{{\widetilde{H}}^LG }}\, e_{\textbf{q}}\Vert _{\varOmega }^2 \\&\; + C_D L_D^2 {{\widetilde{H}}^LG }\Vert {\textbf{q}} \Vert _{L^\infty \left( \varOmega \right) }^2 \left( \Vert e_u\Vert _{\varOmega }^2 + C_\varPi ^2 h^{2k + 2} \sum _{{\mathcal {K}}\in {\mathcal {T}}_h} \left( |u|_{H^{k+1}\left( {\mathcal {K}}\right) } + \frac{1}{\tau _{\mathcal {K}}^{\max }} |{\textbf{q}}|_{H^{k+1}\left( {\mathcal {K}}\right) ^d} \right) ^2 \right) \end{aligned}$$

The remainder of the proof boils down to some simple algebraic manipulations, omitting some non-negative left-hand-side terms, and using Grönwall’s inequality. \(\square \)

Remark 4.8

The fact that the above estimates contain \(\tau \) in both numerator and denominator indicates that choosing \(\tau \) as a constant (per face \(F \in {\mathcal {F}}\setminus {\mathcal {F}}_D \)) is optimal in contrast to \(\tau = 1/h\), or \(\tau = h\), or any other h-dependent choice.

5 Numerical results

In Secs. 5.1, 5.3, the discretization in time is performed via the implicit Euler scheme, and the implementation has been carried out in the C++ based Finite Element toolbox M++ (Wieners 2005). The numerical results in Sec 5.2 were obtained using the programming framework introduced in Rupp et al. (2022), Rupp and Kanschat (2021) and rely on the Crank-Nicolson time stepping method.

5.1 Numerical convergence study for piecewise constant diffusion coefficients

First, we verify the convergence estimates by using a smooth test problem with known solution. Our smooth test problem is

$$\begin{aligned}&T = 1,{} & {} \varDelta t = 10^{-4},\\&\varOmega ^l = \left( 0,10\right) \times \left( 0,5\right) ,{} & {} \varOmega ^g = \left( 0,10\right) \times \left( 5,10\right) ,\\&H^LG = 10,{} & {} \tau \in \{1, 1/h\},\\&D = \left\{ \begin{array}{cl} 0.1 &{} if x_2< 5, \\ {1} &{} otherwise, \end{array}\right. \\&u = \left\{ \begin{array}{cl} 10 \cos \left( x_1+t\right) \cos \left( x_2+t\right) &{} if x_2 < 5, \\ \cos \left( x_1+t\right) \cos \left( x_2+t\right) &{} otherwise. \end{array}\right. \end{aligned}$$

We choose \(\varOmega \) as a square of side length ten and set Neumann boundary conditions at the top and bottom boundaries while letting the left and right boundaries be of Dirichlet type. The right-hand side function, initial-, and boundary conditions are chosen appropriately. The spatial domain is discretized by \(2^i \times 2^i\) squares (where i denotes the number of refinement steps). As the mesh skeleton space associated with the edges grows with each mesh refinement, the error on the skeleton space is scaled with respect to the measure of the skeleton space. sadov Choosing the penalty parameter \(\tau = 1\) and using equal order approximations for all unknowns, the LDG-H-discretization shows an optimal order of convergence of \(k+1\) in both variables for ansatz spaces of order k (see Tables 1, 2 and 3 uppermost block). Notably, this means an improved order of convergence in the flux variable compared to the LDG discretization of the same order. For \(\tau = 1/h\) the order of convergence in the flux variable decreases by one. This is consistent with analytical results and also with numerical studies for elliptic problems given in Cockburn et al. (2008a).

Table 1 Errors (E) and estimated orders of convergence (eoc) for constant approximations
Full size table
Table 2 Errors (E) and estimated orders of convergence (eoc) for linear approximations
Full size table
Table 3 Errors (E) and estimated orders of convergence (eoc) for quadratic approximations
Full size table

In Rupp et al. (2018), different orders of approximation spaces for the scalar and the flux variable were investigated for an LDG method. There it was shown analytically that if the order was reduced for the flux variable by one to \(k-1\) while the order for the scalar variable was still k, both variables would converge at least with order k. In numerical experiments presented in Rupp et al. (2018), the order of convergence for the scalar variable appeared to be higher than the analytical result indicates whereas the estimate for the flux variable was sharp. Next, we consider similar scenarios for our LDG-H scheme with penalty parameters \(\tau = 1\) and \(\tau = 1/h\), respectively. Since there is yet another ansatz space to approximate the solution on element boundaries, there arises one additional possibility to vary the order of approximation. For \(\tau = 1\), the experimental order of convergence for all variables decreased as soon as we reduced the order of one of the approximation spaces. In the case of \(\tau = 1/h\) though, the order of convergence decreased when we reduced the order of approximation for the primary \(u_h\) or the hybrid variable \(\lambda _h\), and no convergence was detected if the order of one of the corresponding spaces was 0. However, if the order of the approximation space for the flux variable is reduced by one, the same effect as for the LDG method can be seen: The experimental order of convergence turns out to be the same as for the approximations using equal orders for all variables (Tables 2 and 3 third block). Thus one may be able to substantially reduce the total number of the degrees of freedom (the flux unknown is a d-dimensional vector!) without sacrificing the convergence order. Usually, this is not considered to be significant since classical HDG literature assumes the local solutions to be computationally cheap and the total performance to be dominated by the global solve. However, hybrid methods are often implemented in a matrix-free fashion (see e.g. Rupp et al. 2022). In this case, the base assumption that solving a local system of equations is cheap still holds, but since local systems have to be solved in every mesh cell per iteration of an iterative solver per time step the local solution time dominates the overall runtime of the code. The authors experienced this bottleneck when implementing their own code (Rupp and Kanschat 2021). In this specific situation, a significant speedup is obtained by our approach.

5.2 Numerical convergence study for piecewise continuous, spatially varying diffusion coefficients

The convergence study presented in Sect. 5.1 focused on a simple example in two spatial dimensions. There we observed that one sees the convergence orders of \(k+1\) for all unknowns if one chooses all polynomial spaces order k and \(\tau = 1\). Next, we demonstrate that a variable diffusion coefficient or the number of spatial dimensions does not affect the convergence rates. To this end, we consider

$$\begin{aligned}&T = 1,{} & {} \varDelta t = 10^{-4},\\&\varOmega ^l = \left( 0.5,1\right) \times \left( 0,1\right) ^{d-1},{} & {} \varOmega ^g = \left( 0,0.5\right) \times \left( 0,1\right) ^{d-1},\\&H^LG = 10,{} & {} \tau = 1,\\&D = e^{\sum _{i=1}^d x_i} \times \left\{ \begin{array}{cl} 1 &{} if x_1< 0.5, \\ \tfrac{1}{H^LG } &{} otherwise, \end{array}\right.{} & {} u = \left[ \prod _{i=1}^d \sin (x_i + t)\right] \times {\left\{ \begin{array}{ll} 1 &{} \text { if } x_1 < 0.5, \\ H^LG &{} \text { otherwise.} \end{array}\right. } \end{aligned}$$

The numerical results shown in Table 4 indicate that the expected orders of convergence are obtained for the primary unknown (for conciseness, we omit the errors for the flux and skeleton unknowns). The first two columns (\(d=1\), \(d=2\)) consider the aforementioned setting. The third column (\(H^LG = 1000\)) describes the two-dimensional example in which the factor \(H^LG \) has been increased to 1000. Finally, the last column (\({\tilde{D}}\)) corresponds to the anisotropic tensor-valued coefficient

$$\begin{aligned} {\tilde{D}} = D \begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad 100 \end{pmatrix} \end{aligned}$$

used instead of the scalar D for the two-dimensional experiments.

In all cases, we can see similar convergence rates. This showcases that Henry’s constant does not influence the convergence rate but does influence the constant, since the solution’s semi-norm scales with it. Moreover, the results validate our claim that our method is suitable for anisotropic diffusion.

Remark 5.1

(Sharp convergence rates) None of the aforementioned numerical experiments indicate that the observed rates of convergence exceed those obtained in our error analysis. Thus, we deduce that our analytical findings are sharp with respect to the observed rate.

Table 4 Errors (E) and estimated orders of convergence (eoc)
Full size table
Fig. 1
figure 1

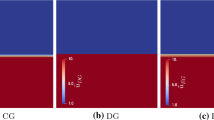
Solution for the nested rectangle problem (left panel): initial condition (top), final states at \(T=1\) for \({\mathbb {P}}_1 \times {\mathbb {P}}_1^d \times {\mathbb {P}}_1\) (middle) and \({\mathbb {P}}_2 \times {\mathbb {P}}_2^d \times {\mathbb {P}}_2\) (bottom). Difference plots (right panel): \({u_h}_{\mid {\mathbb {P}}_2 \times {\mathbb {P}}_2^d \times {\mathbb {P}}_2} - {u_h}_{\mid {\mathbb {P}}_1 \times {\mathbb {P}}_1^d \times {\mathbb {P}}_1}\), \({u_h}_{\mid {\mathbb {P}}_1 \times {\mathbb {P}}_1^d \times {\mathbb {P}}_1} - {u_h}_{\mid {\mathbb {P}}_1 \times {\mathbb {P}}_0^d \times {\mathbb {P}}_1}\) (middle), \({u_h}_{\mid {\mathbb {P}}_2 \times {\mathbb {P}}_2^d \times {\mathbb {P}}_2} - {u_h}_{\mid {\mathbb {P}}_2 \times {\mathbb {P}}_1^d \times {\mathbb {P}}_2}\) (bottom)

Full size image

5.3 Nested rectangle problem

To demonstrate the robustness of our method we show results for a more involved non-smooth test problem given by

$$\begin{aligned}&T = 1,{} & {} \varDelta t = 10^{-4},\\&\varOmega ^l = \left( 0,10\right) \times \left( 0,5\right) ,{} & {} \varOmega ^g = \left( 0,10\right) \times \left( 5,10\right) ,\\&H^LG = 0.5 ,{} & {} \tau = 1/h,\\&D = \left\{ \begin{array}{cl} 0.1 &{} if x_2< 5, \\ 4 &{} otherwise, \end{array}\right. \\&u_0 = \left\{ \begin{array}{cl} 5 &{} if \left( \left( 2.5<= y<= 5\right) \wedge \left( 2.5<= x<= 7.5\right) \right) \\ &{} \vee \left( \left( 3.75<= y<= 5\right) \wedge \left( 0<= x<= 10\right) \right) , \\ 10 &{} if \left( \left( 5<= y<= 7.5\right) \wedge \left( 2.5<= x<= 7.5\right) \right) \\ &{} \vee \left( \left( 5<= y<= 6.25\right) \wedge \left( 0<= x <= 10\right) \right) , \\ 0 &{} otherwise. \end{array}\right. \end{aligned}$$

On a square of side length ten, we set homogeneous Neumann boundary conditions on all boundaries and set the right-hand-side function to zero.

The initial condition for the nested rectangle problem is plotted in Fig. 1 (top left), the solutions at time \(T=1\) for piecewise linear and piecewise quadratic (equal order) approximation are shown in Fig. 1 (middle left) and Fig. 1 (bottom left), respectively, and the difference plot between these two is displayed in Fig. 1 (top right). In order to illustrate the effect of reducing by one the approximation order for the flux unknown \({\textbf{q}}_h\), we also display the difference plots between equal and reduced (for \({\textbf{q}}_h\)) order solutions for linear in Fig. 1 (middle right) and quadratic in Fig. 1 (bottom right) approximations. Especially for the piecewise quadratic approximation the difference between the solutions appears to be very small.

6 Conclusions

The current work introduced and investigated a hybridizable DG formulation for parabolic equations with non-linear tensor-valued coefficients and jump conditions described by Henry’s law. Optimal convergence estimates were proved for mildly non-linear problems on simplex meshes, and numerical studies demonstrated the same convergence on rectangular meshes. Our numerical studies of mixed-order approximations indicate the same behavior as in the case of LDG discretizations, namely the possibility of reducing the approximation order for flux unknowns by one polynomial order without any loss of convergence or accuracy. Extending the analysis techniques to more general element shapes appears to be very desirable though challenging.

An important future step that needs to be undertaken in order to apply our method to real-world scenarios is the implementation and analysis of the presented approach for cases, in which the interface is curved and evolving in time. In such scenarios, it is particularly important to accurately track the interface and update the quadrature rules on the interface and in the elements. In these cases, hybrid versions of CutFEM or extended FEM might be useful. Another possible research direction concerns more involved non-itineraries and numerical treatment of highly anisotropic diffusion tensors.