How did the meter acquire its definitive length?

Abstract

The French Academy of Science decided in 1791 that the new unit of length, the meter, is to be as one ten millionth part of the meridian quarter from the north pole to the equator. In order to find out the numerical value for this length, the Academy equipped two expeditions for measuring the meridian arc between Dunkirk and Barcelona. Then by mathematical calculations one could derive the length of the meridian quarter. After the expeditions had returned to Paris and their data had become available, Pierre-Simon Laplace (1749–1827) estimated the flattening of the earth. He obtained the value 1/150.6, which cannot stand as regards known facts. This is a story about how Laplace managed to save the meter project. Combining the new French arc measurements with the older measurements made in Peru 1730–40 he estimated the flattening anew and found the plausible value 1/334. With the help of this new flattening he calculated the definitive length of the meter to be 443.296 Parisian lines. The final section of the article tells the refinements of the meter’s definitions from the year 1799 to the present.

1 Introduction

On March 19, in 1791 The French Academy of Science decided to establish a new unit of length (Borda et al. 1791, p. 1)¹:

“The idea of relating all measurements to a unit of length taken from Nature presented itself to mathematicians as soon as they knew of the existence of such a unit, and the possibility of determining it. They saw it was the only way of excluding all arbitrariness from the system of measurements. [...] They felt that such a system not belonging exclusively to any nation, could not flatter anyone at being adopted by all.”

The Academy considered three options:

• 1. The length of the simple pendulum at the $45^\circ$ latitude.

• 2. The ten millionth part of the quarter of the equatorial circle.

• 3. The ten millionth part of the meridian quarter.

All three alternatives were carefully examined (Borda et al. 1791, pp. 4–5). The pendulum length had many good qualities, but finally it was rejected, mainly because it depended on the time unit, the second, that was an arbitrary division of a day. A better choice would have been ten billionth ($10^{10}$) part of the hypothetical pendulum that makes one oscillation in one day. This length is equal to the length of the pendulum making hundred thousand oscillations in a day. However, further considerations led the academicians to conclude that it is more natural to base the new unit of length on the measurements of the earth itself, which had also the advantage being perfectly analogous to all current measurements taken in the daily life.

The quarter of the equatorial circle was rejected, because the measuring operations ought to be performed in remote countries and therefore being too tedious and expensive without compensating any benefits. Thus, the Academy finally decided to base the new unit of measure on the meridian quarter. Additionally, the new invention of physicist Jean-Charles Borda (1733–99) and instrument maker Étienne Lenoir (1744–1832), the repeating circle, could be adapted to measure both terrestrial and celestial angles. It promised to reduce errors nearly to zero (Alder 2002, pp. 13, 40, 45). Accurate angle measurements were an important part in the method of triangulation used in measuring the meridian arc as well as in determining the latitude.

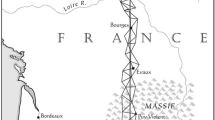
In order to find the value of the meridian quarter, two expeditions were sent to measure the meridian arc between Dunkirk and Barcelona. The main reasons for the chosen arc were (Borda et al. 1791, p. 8):

• 1. It covered more than nine and a half degrees and was the longest meridian arc measured until then.

• 2. The mid-latitude $45^\circ$ of the meridian quarter was between the end points of the measured arc.

• 3. The end points were at the sea level, which helped to extend the length of the measured arc in a comparable manner.

The measuring expeditions were led by two astronomers, Jean-Baptist Delambre (1749–1822) and Pierre-François-André Méchain (1744–1804). The northern part of the arc from Dunkirk to Rodez, led by Delambre, was much longer (ca. 741 km) than the southern one, led by Méchain, from Rodez to Barcelona (ca. 331 km), but the northern part had already been measured twice (Delambre 1806 p. 22). This alleviated Delambre in his task. In the southern part Méchain had to start from the scratch and to overcome the problems with crossing the Pyrenees. In June 1792 both expeditions left for their journey. After many difficulties and obstacles the measuring process was finished in November 1798. A vivid account of all this is told by Alder (2002).

In September 1798 a number of men of science assembled in Paris for establishing the metric system (Crosland 1969 p. 229). In addition to French participants a group of foreign scientists from Western Europe had been invited by Charles-Maurice de Talleyrand-Périgord (1754–1838), the Minister of Foreign Affairs. The invitation was reported in the official French newspaper, Le Moniteur, as follows²:

“Letter of the Minister of Foreign Affairs, Talleyrand, to all diplomatic agents, transmitting to them a decree of the National Institute, of which the purpose is to invite the governments of the allied and neutral powers to send to Paris scholars, who would meet with the commissioners of the Institute for the definitive fixing of the fundamental unit of new weights and measures.”

The list of all participants is given in Sect. 8. The representatives outside France came from Denmark, Italy, the Netherlands, Spain and Switzerland.

The first meeting of the International Commission for Weights and Measures was held on November 28, 1798 (Crosland 1969 p. 229), but not until about half a year later on May 25 1799, the Commission was given the report of the new standards of the meter and the kilogram (Van Swinden 1799). The meter was defined to be 443.296 Parisian lines. This length, given in six figures, was defined by the copper standard called Toise du Pérou. On June 22 1799 the platinum bar, as the definitive meter made by the aforementioned Étienne Lenoir (Alder 2002, p. 266), was presented to the French legislative assemblies (Crosland 1969, p. 230). But before this important event took place, there was a substantial problem to be solved.

As soon as Delambre and Méchain had published their data, Laplace estimated the flattening of the earth. His estimate turned out to be 1/150.6 (Laplace 1799, p. 142), which is absolutely too great. The flattening of the earth cannot be greater than 1/230, the flattening of the homogeneous earth. Since Laplace had been the most eminent proponent for the new metric system, he apparently felt responsible to find a way out from this trouble. After some preliminary trials he decided to take advantage of the older measurements carried out by Pierre Bouguer (1698–1758) and Charles-Marie de La Condamine (1701–74) in Peru 1730–40. Combining these two data sets Laplace succeeded to estimate the flattening anew and was happy to find the suitable value 1/334. It also fitted well with his estimate 1/335.78 based on 15 pendulum measurements (Laplace 1799, p. 150).

However, Laplace does not give any details on how he has combined the new French arc measurements with those measured in Peru and obtained the flattening 1/334. In order to find an answer to this question we need to take a look at the mathematical description of earth’s size and shape.

2 Meridian arc length

Let us assume that the earth is an ellipsoid of revolution around the polar axis. The length of the equatorial radius is denoted by a and the polar radius by b. The flattening is defined as $\rho = (a-b)/a$ and the first eccentricity as $e = \sqrt{a^2 - b^2}/a$. Because $\rho$ is small

$$\begin{aligned} e^2 = \frac{a^2 - b^2}{a^2} = \frac{(a-b)(a+b)}{a^2} = \rho (2 - \rho ) \approx 2\rho . \end{aligned}$$

In the following we repeatedly use this approximation.

The meridian arc length from the equator to the latitude $\phi$, given in radians and denoted by $A(0,\phi )$, is expressible as the elliptic integral (Torge 2001, p. 97)

$$\begin{aligned} A(0, \phi ) = a(1 - e^2) \int _{0}^{\phi } (1 - e^2 \sin ^2 t)^{-\frac{3}{2}}\textrm{d}t. \end{aligned}$$

(1)

The formula is perhaps first derived by Leonhard Euler (1707–83) (Euler 1755, p. 261). As $e^2$ is small, we have for all t

$$\begin{aligned} (1 - e^2 \sin ^2 t)^{-3/2} \approx 1 + \frac{3}{2} e^2 \sin ^2 t. \end{aligned}$$

Then with this approximation the arc length (1) is found by integration as

$$\begin{aligned} A(0, \phi ) = a(1 - e^2) \left[ \left( 1 + \frac{3}{4} e^2 \right) \phi - \frac{3}{8} e^2 \sin 2\phi \right] , \end{aligned}$$

(2)

where the equal sign is used for simplicity. If it is not otherwise stated we follow this convention in the following. The arc length between latitudes $\phi _1 < \phi _2$ is

$$\begin{aligned} A(\phi _1, \phi _2) = a(1 - e^2) \left[ \left( 1 + \frac{3}{4} e^2 \right) (\phi _2-\phi _1) - \frac{3}{8} e^2 (\sin 2\phi _2 - \sin 2\phi _1) \right] . \end{aligned}$$

Write $\sin 2\phi _2 - \sin 2\phi _1 = 2\sin (\phi _2-\phi _1)\cos (\phi _2+\phi _1)$. Assuming that $\phi _2-\phi _1$ is small we have $\sin (\phi _2-\phi _1) \approx \phi _2 - \phi _1$. Using this approximation and denoting $(\phi _2 + \phi _1)/2 = \bar{\phi }$ and $\cos (\phi _2+\phi _1) = \cos (2\bar{\phi }) = 1 - 2\sin ^2(\bar{\phi })$, then we can write the average length of the short arc between $\phi _1 < \phi _2$ as

$$\begin{aligned} \frac{A(\phi _1,\phi _2)}{\phi _2 - \phi _1}\approx & {} a(1 - e^2) \left[ 1 + \frac{3}{2} e^2 \sin ^2(\bar{\phi })\right] \nonumber \\\approx & {} a(1 - e^2) \left[ 1 + 3\rho \sin ^2(\bar{\phi })\right] . \end{aligned}$$

(3)

3 More accurate arc lengths

It is possible to compute the arc length from (1) as accurately as we wish. Start with the convergent power series

$$\begin{aligned} (1 - x)^{-3/2} = c_0 + c_1 x + c_2 x^2 + c_3 x^3 + \cdots , |x| < 1. \end{aligned}$$

As we have already seen $c_0 = 1$ and $c_1 = 3/2$. All coefficients are obtainable by the recursion

$$\begin{aligned} c_0 = 1, \ c_k = \frac{2k+1}{2k} c_{k-1}, \ k = 1,2, \ldots ~. \end{aligned}$$

(4)

Because $e^2 < 1$, we have the convergent series expansion also for the arc length (1),

$$\begin{aligned} A(0, \phi ) = a(1 - e^2) \left( \phi + \sum _{k=1}^\infty c_k e^{2k} \int _{0}^{\phi } \sin ^{2k} t \, \textrm{d}t \right) , \end{aligned}$$

(5)

where the integrals obey the recursions, verified by differentiating on both sides, as

$$\begin{aligned} \int _{0}^{\phi } \sin ^{2k} t \, \textrm{d}t = - \frac{1}{2k} \cos \phi \, \sin ^{2k-1} \phi + \frac{2k-1}{2k} \int _{0}^{\phi } \sin ^{2k-2} t \, \textrm{d}t, \ k=1,2,\ldots . \nonumber \\ \end{aligned}$$

(6)

4 Meridian arc length—another parametrization

Laplace uses centesimal degrees, i.e. the common $90^\circ$ at the poles corresponds to his $100^\circ$. Using Laplace’s convention the mean length of the one degree arc is by (2)

$$\begin{aligned} s = \frac{A(0,\pi /2)}{100} = a(1 - e^2) \left( 1 + \frac{3}{4} e^2 \right) \frac{\pi }{200}. \end{aligned}$$

With the parameters $e^2$ and s we can write

$$\begin{aligned} A(0, \phi ) = s \frac{A(0, \phi )}{s} = s\left[ \frac{200 \phi }{\pi } - \frac{200}{\pi } \frac{\frac{3}{8} e^2}{1 + \frac{3}{4} e^2} \sin 2\phi \right] . \end{aligned}$$

(7)

This formula yields additionally the (approximate) result that the mean arc length between latitudes $\pi /4 \pm \phi$ is also equal to s. This is seen as $\sin (2(\pi /4 + \phi )) = \sin (2(\pi /4 - \phi ))$, and then by (7)

$$\begin{aligned} A\left( 0, \frac{\pi }{4} +\phi \right) - A\left( 0, \frac{\pi }{4}- \phi \right) = s\left( \frac{200 \cdot 2\phi }{\pi }\right) . \end{aligned}$$

(8)

Because $200 \cdot 2\phi /\pi$ is the arc length in centesimal degrees we find that s is also the mean arc length between all latitudes symmetrically around the latitude $\pi /4$ or equivalently around 50 degrees (as well as around the more commonly used 45 degrees). This explains the importance of having the latitude $45^\circ$ (in common degrees) between the endpoints of the measured arc.

The transformation $200\phi /\pi$ gives the latitude in centesimal degrees. For simplicity, we continue to denote it by $\phi$ from now on. We also assume that all latitudes, if not otherwise stated, are in centesimal degrees as well as all trigonometric functions operate on centesimal degrees. The sequence of approximations

$$\begin{aligned} \frac{\frac{3}{8} e^2}{1 + \frac{3}{4} e^2} \approx \frac{3}{8} e^2 \approx \frac{3}{4} \rho \end{aligned}$$

yields by (7)

$$\begin{aligned} A(0,\phi ) \approx s\left[ \phi - \frac{3}{4} \cdot \frac{200}{\pi } \rho \sin 2\phi \right] . \end{aligned}$$

(9)

Laplace writes $200 \rho /\pi$ simply by $\rho$ saying that it is expressed in degrees.

The arc length between latitudes $\phi _1 < \phi _2$ can now be written by (9) as

$$\begin{aligned} A(\phi _1,\phi _2)= & {} s\left[ \phi _2 - \phi _1 - \frac{3}{4} \cdot \frac{200}{\pi } \rho (\sin (2\phi _2) - \sin (2\phi _1)) \right] \nonumber \\= & {} s\left[ \phi _2 - \phi _1 - \frac{3}{2} \cdot \frac{200}{\pi } \rho \sin (\phi _2 - \phi _1) \cos (\phi _1 + \phi _2)\right] . \end{aligned}$$

(10)

Next we find another approximation to the mean of the one degree arc length in terms of the parameters s and $\rho$ from (10). Let $\phi _2 - \phi _1$, be small. Then $\sin (\phi _2 - \phi _1) \approx \pi (\phi _2 - \phi _1)/200$, because the latitudes are now in centesimal degrees. Then the mean length of the one degree arc is by (10) as

$$\begin{aligned} \frac{A(\phi _1, \phi _2)}{\phi _2-\phi _1} \approx s\left( 1- \frac{3}{2} \rho \cos (\phi _1 + \phi _2) \right) . \end{aligned}$$

(11)

5 Laplace’s analysis of the meridian data

Table 1 The French meridian data. (Laplace 1799, p. 141)

In order to estimate $\rho$ from the French meridian data shown in Table 1, Laplace used the model (9). He added measurements errors³$\epsilon _i$, to the observed latitudes $\phi _i$, $i=1,\ldots ,5$, such that these together with the (unknown) arc lengths $A_1< \cdots < A_5$, from the equator to the five stations from Montjoui to Dunkerque of Table 1 satisfy the Eq. (9), i.e.

$$\begin{aligned} A_i = s\left( \phi _i + \epsilon _i - \frac{3}{4} \frac{200}{\pi }\rho \sin 2\phi _i\right) , \quad i = 1,\ldots ,5. \end{aligned}$$

Let the observed arc lengths or distances from Monjoui to other four locations of Table 1 be $a_2< \cdots < a_5$. Then Laplace set $a_i = A_i - A_1$, $i=2,3,4,5$, in other words, he assumed that all errors both in the observed latitudes and in the geodesic measurements are put into $\epsilon _i$, $i=1,\ldots ,5$ (Laplace 1799, p. 141). Moreover, the errors are silently ignored in the trigonometric functions. Finally, Laplace gives the four equations

$$\begin{aligned} \frac{a_i}{s} = \left( \phi _i -\phi _1 + \epsilon _i - \epsilon _1 - \frac{3}{4} \frac{200}{\pi }\rho (\sin 2\phi _i - \sin 2\phi _1)\right) , \quad i=2,3,4,5, \end{aligned}$$

(12)

where the arc lengths $a_i$ as well as the latitudes $\phi _i$ with the corresponding trigonometric expressions are given numerically (Laplace 1799, cf. the equations (B), p. 142).

Laplace had developed procedures for finding the solution for two unknowns $\rho$ and s such that the maximum absolute error, attains its minimum, i.e. procedures for solving minimax problems. With his first method, explained in (Laplace 1799, pp. 126–128), Laplace estimated

$$\begin{aligned} \rho = \frac{1}{150.6}\; \text {and}\; s=25649.8, \end{aligned}$$

(Laplace 1799, pp.  141, 142). The errors of the solution⁴ appeared to be

$$\begin{aligned} \epsilon _1=\epsilon _4=-\epsilon _3=-\epsilon _5 = 4''.43\; \text {and}\; \epsilon _2 = -3.''99, \end{aligned}$$

(Laplace 1799, pp. 142). But unfortunately the flattening 1/150.6 cannot stand (Bowditch 1832, p. 459)⁵:

“...the oblateness 1/150.6, which this combination of errors gives to the earth, does not agree, either with the phenomena of gravity, or with the observations of the precession and nutation; which do not allow us to suppose that the earth has a greater oblateness than in the case of homogeneity, namely 1/230.”

Then Laplace proceeded as follows. He inserted $\rho = 1/230$ into the Eq. (12) and estimated s with his second minimax method, where the error $\epsilon _1$ is assumed an unknown constant (Laplace 1799, pp. 128–136). He found $s = 25651.33$ modules. At this time Laplace found, for his disappointment, that the maximum absolute errors were $-\epsilon _1 = -\epsilon _5 = \epsilon _3 = -9'',98$, and he stated (Bowditch 1832, p. 461)⁶:

“An error of $9'',98$ is much greater than can be supposed to exist; therefore these measures will not allow us to suppose the oblateness to be 1/230, and still less will they agree with a smaller oblateness. It is therefore proved satisfactorily, that the earth varies very sensibly from an elliptical figure. But it is very remarkable, that the measures lately made in France, and in England, with great precision, in the direction of the meridian, and in the perpendicular to the meridian, both indicate an osculatory ellipsoid, in which the ellipticity is 1/150, and the mean length of a degree 25649,8 modules.”

Using the values $\rho =1/150$ and $s = 25649.8$, Laplace calculated the length 25837.6 modules for the one degree arc at the latitude $56^\circ .3144$ and compared this with the arc length of 25833.4 modules, measured in England at the same latitude (Laplace 1799, p. 143). Since the difference was only 4.2 modules (16.4 meters) he concluded (Bowditch 1832, pp. 462–3)⁷:

“From this near agreement it appears, that the great oblateness does not depend on the attractions of the Pyrenees, and the other mountains in the south of France; but that it arises from much more extensive attractions, the effect of which is sensible in the north of France and in England, as well as in Austria and in Italy. [...] The figure of the earth is therefore very complex, as is natural to suppose it would be, when we take into consideration the great inequalities of its surface, the different density of the parts which cover it, and the irregularities in the shores and in the bottom of the ocean.”

As we see, Laplace had encountered unexpected problems. The longest arc measured until then produced unacceptable results. The form of the earth seemed not to be what was expected. Nevertheless, something had to be done in order to convince the scientists convened to establish the new unit of length, the meter, (Bowditch 1832, p. 464)⁸:

“To determine the length of a quadrant of the terrestrial meridian, from the arc comprised between Dunkirk and Montjoui, we must adopt some hypothesis relative to the figure of the earth; and notwithstanding all the irregularities of its surface, the most simple and natural supposition is that of an ellipsoid of revolution. Making use of this hypothesis, a quadrant of the meridian will be nearly equal to one hundred times the arc included between Dunkirk and Montjoui, divided by the number of its degrees, if the middle of the arc correspond[s] to $50^\circ$ of latitude⁹: but it is a little to the north of it; therefore we must apply a small correction, depending upon the oblateness of the earth. We have selected the ellipticity which results from the comparison of the arc measured in France, with that at the equator. This last measure is preferred to any other, on account of its distance, and extent; as well as for the care which several excellent observers have taken in measuring it. The ellipticity derived from this comparison turned out to be 1/334.”

Choosing the ellipticity 1/334 Laplace ignores his previous finding that the French data does not allow to suppose the ellipticity 1/230 and even less any smaller values. However, Laplace does not tell us how he made the comparison with those two arc lengths. The next section gives the likely answer.

6 Finding the ellipticity

Table 2 The Equatorial and French meridian data

Laplace had the data set of seven arc measurements that contain the data of Table 2 (Laplace 1799, pp. 138,139). Equate now the ratios of the observed mean lengths of one degree arcs with their theoretical counterparts. By the Eq. (3) we set

$$\begin{aligned} \frac{25658.28}{25538.85} = \frac{1 + 3\rho \sin ^2(51^\circ .3327)}{1 + 3\rho \sin ^2(0^\circ )} = 1 + 3\rho \sin ^2(51^\circ .3327). \end{aligned}$$

(13)

Then $\sin ^2(51^\circ .33261) = 0.52093$ given in (Laplace 1799, p. 139) yields $\rho = 1/334$.

There is also another attempt in the modern literature to reconstruct Laplace’s solution (Hald 1998, pp. 116–118). Hald claims that the value 1/334 is found by means of the formula (11) (Hald 1998,formula (2), p. 117). Let us try. By (11) write

$$\begin{aligned} \frac{25658.28}{25538.85} = \frac{1 - \frac{3}{2} \rho \cos (2 \cdot 51^\circ .33261)}{1 - \frac{3}{2} \rho \cos (0^\circ )} = \frac{1 - \frac{3}{2} \rho \cos (2 \cdot 51^\circ .33261)}{1 - \frac{3}{2} \rho }. \end{aligned}$$

(14)

Its solution appears to be 1/335.7, which differs from 1/334 too much. But if we follow Bowditch’s derivation (Bowditch 1832, p. 464) and use the approximation

$$\begin{aligned} \frac{1}{1 - \frac{3}{2}\rho } \approx 1 + \frac{3}{2}\rho \end{aligned}$$

and then neglect the square $\rho ^2$, we are led to the equation

$$\begin{aligned} \frac{25658.28}{25538.85} = 1 + \frac{3}{2} \rho (1 - \cos (2 \cdot 51^\circ .3327)) \end{aligned}$$

(15)

given in (Bowditch 1832, the lines after [2033f] on p. 464). Due to the trigonometric identity $\cos (2\cdot 51^\circ .3327)= 1 - 2\sin ^2(51^\circ .3327)$, the Eq. (15) is exactly the same as the Eq. (13). Hald’s claim in his book (Hald 1998, p. 118) that the formula (11) can be used for deriving the ellipticity 1/334 is apparently based on Bowditch’s derivation, since he quotes the same passage (Bowditch 1832, p.464) that is also given here at the end of Sect. 5.

7 Determination of meter

The length of the meridian quarter can be found as follows. Let $A_2(\phi _1,\phi _2)$ be the approximation given by the first two terms of the series in (5), when $e^2 = \rho (2-\rho )$ with $\rho = 1/334$. The theoretical ratio

$$\begin{aligned} \frac{A_2(45^\circ .958281, 56^\circ .706944)}{A_2(0^\circ , 100^\circ )} \end{aligned}$$

depends only on $e^2$ and therefore is calculable numerically. Next, set it equal to the ratio of the measured French meridian arc of length 275792.36 between latitudes $45^\circ .958281$ and $56^\circ .706944$ and the yet unknown length of the meridian quarter S. Thus, we have an equation

$$\begin{aligned} \frac{A_2(45^\circ .958281, 56^\circ ,706944)}{A_2(0^\circ , 100^\circ )} = 0.1075059 = \frac{275792.36}{S}. \end{aligned}$$

The solution is $S = 275792.36/0.1075059 = 2565370$ modules (Laplace 1799, p. 145), given with six significant figures, as the meter ought to be defined. One module is 1728 lines, therefore the ten millionth part of the meridian quarter equals 443.296 lines. Bowditch has derived the same value $S = 2565370$ for the meridian quarter by a slightly different route of approximations (Bowditch 1832, p. 465).

Finally, the commission considered two additional corrections that are not mentioned in van Swinden’s report (Van Swinden 1799 but explained in (Delambre 1810, p. 138). The Parisian toise was equal to 864 lines, but the lengths of the rods, Toise du Nord and Toise du Pérou used in the measurements, were only 863.99 lines long. Therefore the obtained length 443.296 lines is too long and the corrected length is $443.296\cdot 863.99/864 = 443.291$ lines. But the meter was defined at the temperature $16^\circ .25$ C and the arc measurements were standardized at $17^\circ .6$ C. This means that the rod length 863.99 lines at $17^\circ .6$ is too long compared to the length at $16^\circ .25$. Therefore the corrected length above is too short. The heat expansion due to the difference $17^\circ .6 -16^\circ .25 = 1^\circ .35$ C gives the addition of 0.005 lines. Thus, the final length agrees with the original one derived by Laplace: $442.291 + 0.005 = 443.296$ lines according to Toise du Pérou.

In a grand ceremony held on 22 June 1799 the platinum bar of length 443.296 Parisian lines made by Lenoir was presented to the French legislative assemblies and deposited in the National Archives as the definite standard (Alder 2002, p. 266).

8 The members of the commission of weights and measures 1798–1799

The surnames and countries are based on (Van Swinden 1799, p. 23). The first names as well as the the life spans are provided by the present author.

Aeneae, Henricus (1743–1810), Batavian Republic,

Balbo, Prospero (1762-1837), Kingdom of Sardinia, (replaced by Vassalli)

Borda, Jean-Charles (1733–99), French Republic,

Brisson, Mathurin Jacques (1723–1806), French Republic,

Bugge, Thomas (1740–1815), Kingdom of Denmark,

Císcar, Gabriel (1760–1829), Kingdom of Spain,

Coulomb, Charles-Augustin (1736–1806), French Republic,

Darcet, Jean (1724–1801), French Republic,

Delambre, Jean-Baptist (1749-1822), French Republic,

Fabroni, Angelo (1732–1803), Tuscany,

Lagrange, Joseph-Louis (1736–1813), French Republic,

Laplace, Pierre-Simon (1749–1827), French Republic,

Lefévre-Gineau, Louis (1751–1829), French Republic,

Legendre, Adrian-Marie (1752–1833), French Republic,

Franchini, Pietro (1768–1827), Roman Republic,

Mascheroni, Lorenzo (1750–1800), Cisalpine Republic,

Méchain, Pierre-François-André (1744–1804), French Republic,

Multedo, Ambrogio, (1753–1840), Ligurian Republic,

Pederayes, Agustín (1744-1815), Kingdom of Spain,

Prony, Gaspard-Clair-François-Marie-Riche (1755-1839), French Republic,

Tralles, Johann Georg (1763–1822), Helvetian Republic,

Van-Swinden, Jan Hendrik (1746–1823), Batavian republic,

Vassalli-Eandi, Antonio (1761-1825), Provisional government of Piedmont.

9 Epilogue

• 1 In 1889 the 1st General Conference on Weights and Measures (Conférence Générale des Poids et Mesures, CGPM) replaced the old bar with a new standard of an alloy of platinum with 10% iridium and defined the meter as the distance between two lines on a new standard measured at the melting point of ice, (CGPM 1890, pp. 33-40).

• 2 In 1927 the $7\text {th}$ CGPM redefined the meter as the distance, at $0^\circ$ C ($273^\circ$ K), between the axes of the two central lines marked on the prototype bar of platinum-iridium, this bar being subject to one standard atmosphere of pressure and supported on two cylinders of at least 10 mm (1 cm) diameter, symmetrically placed in the same horizontal plane at a distance of 571 mm (57.1 cm) from each other, (CGPM 1927, p. 49).

• 3 In 1960 the $11{\text {th}}$ CGPM defined the meter as 1650763.73 wavelengths in a vacuum of the radiation corresponding to the transition between the 2p$^{10}$ and 5d$^5$ quantum levels of the krypton-86 atom, (CGPM 1960, p. 85).

• 4 In 1983 the $17{\text {th}}$ CGPM defined the meter as the length of the path travelled by light in a vacuum during a time interval of 1/299792458 of a second, (CGPM 1983, p. 98).

The circle has closed. In 1791 the French Academy of Science rejected the alternative of basing the new unit on the length of the simple pendulum, because it depended on the time unit second that was an arbitrary division of a day. However, the modern definition of second is defined as the duration of 9192631770 periods of the radiation corresponding to the transition between the hyperfine levels of the unperturbed ground state of the cesium-133 atom, (CGPM 1968, p. 103).

Since 2019 the magnitudes of all SI units (The International System of Units) have been defined by declaring that seven defining constants have certain exact numerical values when expressed in terms of their SI units (CGPM 2018, pp. 227, 472). Thus, the project started by the French revolution in 1791–99 has been completed.