1 Introduction

The success of any geophysical exploration project is determined by the quality of the available exploration data. These data have to be analyzed and interpreted as accurate as possible. During the realization of exploration projects, project managers are confronted with different kinds of data. The available data consist of density data sets from gravimetric surveys and/or data from magnetic surveys, but mainly from migration results from conducted seismic exploration.

In Freeden and Blick (2013), a novel mollifier technique for post-processing of exploration data as an improved interpretation technique based on the concept of a “geophysically relevant" wavelet construction was proposed. The concept for this technique goes back to an idea discussed in Freeden and Schreiner (2006) to obtain mollifier approximations of the deflections of the vertical in gravitational theory. Freeden and Blick (2013) was the point of departure for a series of mollifier approaches in gravimetry, magnetometry, and seismics in Freeden’s group. In the case of gravimetry, the mollifier method has been worked out and was realized by Freeden (2021), Freeden and Bauer (2020), Freeden and Nashed (2020), Freeden and Sansò (2020), Berg et al. (2020), Blick et al. (2018a), Freeden and Nashed (2018c), Freeden and Nashed (2018d), Blick et al. (2017), Möhringer (2014), and Freeden and Gerhards (2013) (see also the references therein). A similar technique applied to migration results via the Helmholtz equation is discussed in Blick et al. (2018b) and Augustin et al. (2014). For a summary of both methods, the reader is referred to Freeden et al. (2019), Freeden and Nutz (2015), and Freeden (2010). Further approaches were discussed in Blick (2015) for the acoustic wave equation and in Blick and Eberle (2019) for the static Cauchy–Navier equation. As a recent contribution, Freeden (2021) and Blick et al. (2021) also applied the mollifier approach to magnetometry, in addition to gravimetry. The presented paper gives a survey about perspectives in the field of seismics.

It should be noted that the elastic potential as discussed in this paper is not used for inversion purposes, instead, we apply the methodological framework only for post-processing of already existing geological models to establish a better interpretability. However, an inversion process can be applied as discussed e.g., in Freeden (2021), Freeden and Nashed (2020), Freeden and Nashed (2018d), Freeden and Nashed (2018e), as well as in the monograph (Freeden and Nashed 2018a) and more specifically, in the articles (Freeden and Nashed 2018b) and (Freeden and Nashed 2018c) contained therein.

Following some considerations in Blick and Eberle (2019) for density data modeling, we develop a method which enables us to specify also particular directional characteristics of a migration result. In order to establish such a decorrelation technique, we mathematically make the transition from the Helmholtz equation to the elasto-oscillatory Cauchy–Navier equation. In doing so, on the one hand, we leave the classically motivated Helmholtz approach, on the other hand, we are able to detect specific directional features by the elastic integral due to the tensorial nature of the fundamental solution.

2 Signature decorrelation based on the Helmholtz equation

In what follows, we summarize the results of the Helmholtz approach as given by Blick (2015) in order to present the idea of a physically relevant wavelet construction using Helmholtz wavelets. For the proofs of those results, the reader is referred to the cited literature.

The start of the wavelet development is the representation of the solution U of the Helmholtz equation

$$\begin{aligned} (\varDelta +k_0^2) U(x) = \alpha (x)F(x) \end{aligned}$$
(1)

in a regular region \({\mathcal {B}}\), i.e., an open, bounded, and connected set in \({\mathbb {R}}^3\) that contains the origin and whose closed, compact and locally \(c^{(2)}\)-smooth boundary \(\partial {\mathcal {B}}\) is free of double points and divides the space \({\mathbb {R}}^3\) into the inner space \({\mathcal {B}}\) and the outer space \({\mathcal {B}}^{ext}={\mathbb {R}}^3\backslash {\overline{{\mathcal {B}}}}\). Here, \(\alpha (x)\) denotes the solid angle in x subtended by the boundary \(\partial {\mathcal {B}}\). If \({\mathcal {B}}\) is a regular region, we have

$$\begin{aligned} \alpha (x)=\left\{ \begin{array}{ll} 1,&{}\quad x\in {\mathcal {B}}\\ \frac{1}{2},&{}\quad x\in \partial {\mathcal {B}}\\ 0,&{}\quad x\in {\mathcal {B}}^{ext} \end{array}\right. . \end{aligned}$$

Further, let \(F : {\overline{{\mathcal {B}}}}\rightarrow {\mathbb {R}}\) be a Hölder continuous function. For a fixed \(k_0\ge 0\), the Helmholtz integral equation

$$\begin{aligned} U(x) = \int _{{\mathcal {B}}}G(\varDelta +k_0^2;|x-y|)F(y)\, dy, \qquad x \in {\overline{{\mathcal {B}}}} \end{aligned}$$

relating a given contrast function F (i.e., acoustically given seismic data or a migration result) by convolution against the Helmholtz fundamental solution

$$\begin{aligned} G(\varDelta +k_0^2;r)=-\frac{\exp (ik_0r)}{4\pi r},\qquad 0<r, \end{aligned}$$
(2)

to the Helmholtz potential U is a solution of Eq. (1). By mollification of \(G(\varDelta +k_0^2;\cdot )\), we obtain a “mollifier potential scaling function” \(G_\tau (\varDelta +k_0^2;\cdot )\) with scale parameter \(\tau >0\). Helmholtz differentiation results in the Haar-like “mollifier source scaling function” \(\varPhi _\tau (k_0;\cdot )=(\varDelta +k_0^2) G_\tau (\varDelta +k_0^2;\cdot )\). Hence, even if our main focus lies on the application of the source scaling function, their theoretical construction always starts on the potential level.

Our considerations are summarized in the following theorem (cf. Müller 1969).

Theorem 1

If F is Hölder continuous in \({\overline{{\mathcal {B}}}}\), then the Helmholtz differential equation

$$\begin{aligned} (\varDelta +k_0^2) \int _{\mathcal {B}}G(\varDelta +k_0^2;|x-y|)F(y)\, dy = \alpha (x)F(x) \end{aligned}$$

holds true for all \( x \in {\overline{{\mathcal {B}}}}\). Here, \(\alpha (x)\) denotes the solid angle in x subtended by the boundary \(\partial {\mathcal {B}}\).

There exist several ways to mollify the fundamental solution. In this paper, we adopt the two mollifications based on taylorized approximations as announced in Freeden and Blick (2013) and numerically discussed in Blick (2015). First, we have a partial mollification (referred to in this paper by \(l=1\)), which is obtained by mollifying only the term \(-\frac{1}{r}\) in \(0\le r\le \tau \) while leaving the term \(\exp (ik_0r)\) as it is. The second mollification (\(l=2\)) is obtained by Taylor mollification of the whole fundamental solution. Following (Blick 2015), we obtain both mollifications of \(G(\varDelta +k_0^2;\cdot )\) via the continuously differentiable functions \(r \mapsto G_{\tau }^{l}(\varDelta +k_0^2;r),\) \(r \in [0,\infty )\), respectively, with

$$\begin{aligned} G_\tau ^1(\varDelta +k_0^2;r)=\left\{ \begin{array}{ll}-\frac{\exp (ik_0r)}{4\pi r},&{}\tau \le r\\ \\ -\frac{\exp (ik_0r)\left( 3\tau ^2-r^2\right) }{8\pi \tau ^3},&{}0\le r<\tau \end{array}\right. \end{aligned}$$
(3)

and

$$\begin{aligned} G_\tau ^2&(\varDelta +k_0^2;r)=\left\{ \begin{array}{ll}-\frac{\exp (ik_0r)}{4\pi r}, &{}\tau \le r\\ \\ -\frac{\exp (ik_0\tau )}{4\pi }\left( \frac{1}{\tau }+\frac{\tau -r}{\tau ^2}(1-k_0i\tau )\right) ,&{} 0\le r<\tau \end{array}\right. . \end{aligned}$$
(4)

By taking the Helmholtz derivative of \(G_\tau ^l(\varDelta +k_0^2;\cdot )\), \(l=1,2\), we find with \(r=|x|\)

$$\begin{aligned} \varPhi _\tau ^l(k_0;r)=(\varDelta _x+k_0^2) G_\tau ^l(\varDelta +k_0^2;r),\qquad l=1,2, \end{aligned}$$

where

$$\begin{aligned} \varPhi _\tau ^1(k_0;r)=\left\{ \begin{array}{ll}0,&{}\tau \le r\\ &{} \\ \frac{3\exp (k_0ir)\left( r+k_0i\left( r^2-\tau ^2\right) \right) }{4\pi r\tau ^{3}},&{} 0<r<\tau \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \varPhi _\tau ^2&(k_0;r)=\left\{ \begin{array}{ll}0 ,&{}\tau \le r\\ &{}\\ -\frac{\exp (ik_0\tau )}{4\pi \tau }\left[ k_0^2+\left( \frac{k_0^2(\tau -r)}{\tau }-\frac{2}{r\tau }\right) (1-k_0i\tau )\right] ,&{} 0<r<\tau \end{array}\right. . \end{aligned}$$

The kernels \(G_\tau ^l (\varDelta +k_0^2; \cdot )\) and \(\varPhi _\tau ^l (k_0; \cdot )\) are called “mollifier potential scaling functions” and “mollifier source scaling functions”, respectively. Note that \(r \mapsto G_\tau ^l(\varDelta +k_0^2;r),\ r \in [0,\infty ),\) is continuously differentiable. However in \((0,\infty )\), \(r \mapsto \varPhi _\tau ^l(k_0;r)\) is piecewise continuous. In addition, \(\varPhi _\tau ^l(k_0;r)\) is singular in \(r=0\) in the imaginary part for \(l=1\), and \(\varPhi _\tau ^l(k_0;r)\) is singular in both real and imaginary parts in \(r=0\) for \(l=2\). Analytically, this seems to be disadvantageous, but the scaling functions are integrable and hence can still be used for convolution purposes. From a numerical point of view, those integrals can be calculated efficiently by modified Euler summation techniques as discussed in Blick (2015).

For a graphical illustration of \(G_\tau ^l(\varDelta +k_0^2;\cdot )\) and its Helmholtz derivative \(\varPhi _\tau ^l(k_0;\cdot )\), see Fig. 1.

Fig. 1
figure 1

Sectional profile of the scaling functions \(G_\tau ^l(\varDelta +k_0^2;\cdot )\) and \(\varPhi _\tau ^l(k_0;\cdot )\), \(l=1,2\) for \(\tau =1.5\) and \(k_0=1\) (blue), \(k_0=3\) (green), and \(k_0=6\) (red)

Full size image

Summarizing our considerations, we are led to a result, which builds the theoretical basis for our approach of geological feature extraction in a post-processing process (cf. Blick 2015).

Theorem 2

The “\(\tau \)-mollifier Helmholtz potential functions”

$$\begin{aligned} U_\tau ^l (x)= \int _{\mathcal {B}}G_\tau ^l (\varDelta +k_0^2;|x-y|)F(y)\, dy \end{aligned}$$

and the “\(\tau \)-mollifier Helmholtz contrast functions”

$$\begin{aligned} F_\tau ^l (x)= \int _{\mathcal {B}}\varPhi _\tau ^l (k_0;|x-y|)F(y)\, dy \end{aligned}$$

satisfy the limit relations

$$\begin{aligned} \lim _{\tau \rightarrow 0+} \left| U (x) - U_\tau ^l (x)\right| = 0, \quad x \in {\overline{{\mathcal {B}}}},\quad l=1,2, \end{aligned}$$

and

$$\begin{aligned} \lim _{\tau \rightarrow 0+} \left| \alpha (x)F (x) -F_\tau ^l (x)\right| = 0, \quad x \in {\overline{{\mathcal {B}}}},\quad l=1,2, \end{aligned}$$

provided that F is Hölder continuous in \({\overline{{\mathcal {B}}}}\).

In fact, we have that both the real and imaginary part of \(U - U_\tau ^l\) converges with order \({\mathcal {O}}(\tau ^2)\) as \(\tau \) tends to zero.

A similar approach for the elasto-static Cauchy–Navier potential for the decorrelation of density data is discussed in Blick and Eberle (2019). For those cases, it could be shown that the source scaling functions are normalized, i.e., the respective integral in \({\mathbb {R}}^3\) is equal to one for all \(\tau >0\). Note that this is a helpful feature used in the theory of singular integrals, since the integral kernels are Dirac sequences (for more information, see e.g., Stein 1971; Hörmander 1998 and Wienholtz et al. 2009). This is not the case here. Nevertheless, we are led to the next theorem (cf. Blick 2015).

Theorem 3

The volume integral of \(\varPhi _\tau ^l(k_0;\cdot )\) amounts to

$$\begin{aligned} V_{\varPhi _\tau ^l(k_0;\cdot )}&=\int _{{\mathbb {R}}^3}\varPhi _\tau ^l(k_0;|x-y|)\, dy\nonumber \\&=\left\{ \begin{array}{lr} \frac{3(k_0\tau + 2i)(2 + k_0i\tau \exp (k_0i\tau ) - 2\exp (k_0i\tau ) + k_0i\tau )}{k_0^3\tau ^3},&{} \quad l=1\\ \\ -\exp (k_0\tau i)\left( - \frac{k_0^3\tau ^3i}{12} + \frac{5k_0^2\tau ^2}{12} + k_0\tau i - 1\right) ,&{} \quad l=2 \end{array}\right. \end{aligned}$$
(5)

with

$$\begin{aligned} \lim _{\tau \rightarrow 0+}V_{\varPhi _\tau ^l(k_0;\cdot )}=1,\quad l=1,2. \end{aligned}$$

The theorem is of special importance, since Eq. (5) is used to normalize the wavelets developed later on in this paper.

3 Signature decorrelation based on the elasto-oscillatory Cauchy–Navier equation

Our task now is to adopt the Helmholtz scheme for the elasto-oscillatory Cauchy–Navier equation. We again start with the potential equation, and more specifically, its solution via fundamental solutions. Introducing \({\varvec{C}}^{(n)}({\mathcal {B}})\) and \(c^{(n)}({\mathcal {B}})\) as the spaces of n-times continuously differentiable tensor and vector functions in \({\mathcal {B}}\), respectively, we adopt a scaled version of the setup introduced by Kupradze (1979) and present the classical theory of elasticity for homogeneous and isotropic media. A homogeneous and isotropic elastic medium is composed of a regular region \({\mathcal {B}}\) of the three-dimensional Euclidean space and a set of the constant quantities \(\rho _0\), \(\lambda _0\), and \(\mu _0\) satisfying the conditions

$$\begin{aligned} \rho _0>0, \qquad \mu _0>0, \qquad 3\lambda _0+2\mu _0>0, \end{aligned}$$

where \(\rho _0\) is the constant density of the medium and \(\lambda _0\), \(\mu _0\) are the constant Lamé parameters. Using scaled Lamé parameters

$$\begin{aligned} \lambda =\frac{\lambda _0}{\rho _0},\qquad \mu =\frac{\mu _0}{\rho _0} \end{aligned}$$

to enhance readability, we start with the following definition.

Definition 1

The oscillatory state of the medium \({\mathcal {B}}(\rho _0,\lambda _0,\mu _0)\) corresponding to the acceleration f is the pair \([u,\sigma ]\), which satisfies the conditions

$$\begin{aligned}&\text{ i) }&\sigma \in {\varvec{C}}^{(1)}({\mathcal {B}}),\qquad u\in c^{(2)}({\overline{{\mathcal {B}}}}),&\nonumber \\&\text{ ii) }&\sum _{j=1}^3\frac{\partial }{\partial x_j}\sigma _{ij}+\omega ^2u_i- f_i=0,&\end{aligned}$$
(6)
$$\begin{aligned}&\text{ iii) }&\sigma _{ij}=\lambda \delta _{ij}{\text{ div }}u+\mu \left( \frac{\partial }{\partial x_j} u_i+\frac{\partial }{\partial x_i}u_j\right)&\end{aligned}$$
(7)

with \(f\in {\mathbb {R}}^{3},\ u\in {\mathbb {C}}^3\), \(\sigma \in {\mathbb {C}}^{3\times 3}\) and the oscillation frequency \(\omega \in {\mathbb {R}}\).

Substituting (7) into (6), we obtain the (scaled) oscillation equation (of classical elasticity) or the (scaled) oscillatory Cauchy–Navier equation of the medium \({\mathcal {B}}(\rho _0,\lambda _0,\mu _0)\) corresponding to the acceleration f in terms of the displacement components

$$\begin{aligned} \mu \varDelta u+(\lambda +\mu )\nabla {\text{ div }}u+\omega ^2 u- f=0, \end{aligned}$$
(8)

where

$$\begin{aligned} \varDelta u=(\varDelta u_1,\varDelta u_2,\varDelta u_3)^T. \end{aligned}$$

By use of the matrix differential operator

$$\begin{aligned} {\varvec{A}}(\partial ,\omega )&=\{{\varvec{A}}_{ij}(\partial ,\omega )\}_{i,j=1,2,3} \end{aligned}$$

with

$$\begin{aligned} {\varvec{A}}_{ij}(\partial ,\omega )&=\delta _{ij} \mu \varDelta +(\lambda +\mu )\frac{\partial ^2}{\partial x_i\partial x_j}+\delta _{ij}\omega ^2, \end{aligned}$$

we can reformulate Eq. (8) as

$$\begin{aligned} {\varvec{A}}(\partial ,\omega )u- f&=0. \end{aligned}$$
(9)

We adopt the (tensor) fundamental solution \({\varvec{G}}({\varvec{A}}(\partial ,\omega ),x)\) of Eq. (9) from Kupradze 1979. \({\varvec{G}}({\varvec{A}}(\partial ,\omega ),x)\) is given by

$$\begin{aligned} {\varvec{G}}_{\!jl}({\varvec{A}}(\partial ,\omega );x-y)&=-\sum _{m=1}^2 \left( \delta _{jl}\alpha _m+\beta _m\frac{\partial ^2}{\partial x_j\partial x_l}\right) \frac{\exp (ik_m|x-y|)}{2|x-y|}, \end{aligned}$$
(10)

where

$$\begin{aligned} k_1^2&=\frac{\omega ^2}{\lambda +2\mu }, \qquad \qquad k_2^2 =\frac{\omega ^2}{\mu }, \end{aligned}$$
(11)
$$\begin{aligned} \alpha _m&=\frac{\delta _{2m}}{2\pi \mu }, \qquad \qquad ~~ \beta _m =\frac{(-1)^m}{2\pi \omega ^2}. \end{aligned}$$
(12)

It is easy to calculate that

$$\begin{aligned} {\varvec{A}}(\partial ,\omega ){\varvec{G}}({\varvec{A}}(\partial ,\omega ),x)&=0,\qquad x\ne 0. \end{aligned}$$

All in all, we are confronted with a potential

$$\begin{aligned} u(x)&=\int _{\mathcal {B}}{\varvec{G}}({\varvec{A}}(\partial ,\omega );x-y) f(y)\, dy \end{aligned}$$

that represents a solution of the Cauchy–Navier equation (9).

Remark 1

Since we only talk about the elasto-oscillatory Cauchy–Navier equation in this paper, we will just use the term Cauchy–Navier equation and drop the elasto-oscillatory part in order to keep the nomenclature short.

Remark 2

The Cauchy–Navier equation and the mollification of its fundamental solution can be applied in a number of other applications such as wave inversion (e.g., seismic imaging, Aki and Richards 2002) and specialized wave propagation (e.g., coupling of interior/exterior wave propagation problems, Eberle 2018, 2019, 2020).

Contrary to the construction of scaling functions for the scalar fundamental solutions discussed so far, we are faced with the problem, that we cannot simply obtain a mollification in a ball by application of the Taylor expansion as already presented in Blick and Eberle (2019). In order to mollify the fundamental solution, we rewrite Eq. (10) in terms of \(G(\varDelta +k_0^2;\cdot )\). Hence,

$$\begin{aligned}&{\varvec{G}}({\varvec{A}}(\partial ,\omega );x)=2\pi \alpha _2G(\varDelta +k_2^2;|x|){\varvec{I}}\nonumber \\&\quad -2\pi \beta _1G(\varDelta +k_1^2;|x|)\left( -4\pi G(\varDelta ;|x|)\right) ^4(|x|^2k_1^2+3|x|ik_1-3){\varvec{X}}\nonumber \\&\quad -2\pi \beta _1 G(\varDelta +k_1^2;|x|)\left( -4\pi G(\varDelta ;|x|)\right) ^2(1-|x|ik_1){\varvec{I}}\nonumber \\&\quad -2\pi \beta _2G(\varDelta +k_2^2;|x|)\left( -4\pi G(\varDelta ;|x|)\right) ^4(|x|^2k_2^2+3|x|ik_2-3){\varvec{X}}\nonumber \\&\quad -2\pi \beta _2G(\varDelta +k_2^2;|x|)\left( -4\pi G(\varDelta ;|x|)\right) ^2(1-|x|ik_2){\varvec{I}}, \end{aligned}$$
(13)

where \({\varvec{I}}\) is the \(3\times 3\) identity tensor, \({\varvec{X}}=xx^T\) for \(x=(x_1,x_2,x_3)^T\) and \(G(\varDelta ;\cdot )\) denotes the fundamental solution w.r.t. the Laplace operator and is formally included by setting \(k_0=0\) in \(G(\varDelta +k_0^2;\cdot )\).

Now, we are able to introduce the mollification \({\varvec{G}}_\tau ^l({\varvec{A}}(\partial ,\omega );\cdot )\), \(l=1,2\), by substituting \(G(\varDelta +k_m^2;|x|)\) by \(G_\tau ^l(\varDelta +k_m^2;|x|)\), \(l=1,2\), as well as \(G(\varDelta ;|x|)\) by \(G_\tau ^1(\varDelta ;|x|)\). Note that we exchange \(G_\tau (\varDelta ;|x|)\) only with the partial taylorization \(G_\tau ^1(\varDelta ;|x|)\) instead of \(G_\tau ^l(\varDelta ;|x|)\), \(l=1,2\). The reason is twofold. First, by only taking the case \(l=1\), we keep the number of terms small especially regarding that we have to take the fourth power of \(G_\tau ^l(\varDelta ;|x|)\). Secondly, \(G_\tau ^1(\varDelta ;|x|)\) is the mollified Laplace fundamental solution discussed in Blick (2015) and Blick and Eberle (2019) and hence should be applied to mollify \(G(\varDelta ;\cdot )\).

This enables us to define the mollification \({\varvec{G}}_\tau ^l({{\varvec{A}}}(\partial ,\omega );\cdot ):{\mathbb {R}}^3\rightarrow {\mathbb {C}}^{3\times 3}\) as

$$\begin{aligned} {\varvec{G}}_\tau ^1&({\varvec{A}}(\partial ,\omega );x)\\&=\left\{ \begin{array}{lcl}\sum \limits _{m=1}^2\left\{ \beta _m \frac{\exp (ik_m|x|)}{2|x|^5}\Bigl [{\varvec{X}}(|x|^2k_m^2+2|x|ik_m-3)\Bigr .\right. &{}&{}\\ \qquad \Bigl .+{\varvec{I}}(|x|^2-|x|^3ik_m)\Bigr ]-\left. {\varvec{I}}\alpha _m \frac{\exp (ik_m|x|)}{2|x|}\right\} , &{}\tau \le |x|\\ &{}\\ \sum \limits _{m=1}^2\left\{ \beta _m\frac{\exp (ik_m|x|)}{2} \left( \frac{\left( 3\tau ^2-|x|^2\right) }{2\tau ^3}\right) ^5{\varvec{X}}(|x|^2k_m^2 +3|x|ik_m-3)\right. &{}&{}\\ \qquad +\beta _m\frac{\exp (ik_m|x|)}{2}\left( \frac{\left( 3\tau ^2-|x|^2 \right) }{2\tau ^3}\right) ^3{\varvec{I}}(1-|x|ik_m)&{}&{}\\ \qquad -\left. {\varvec{I}}\alpha _m\frac{\exp (ik_m|x|)}{2}\left( \frac{\left( 3\tau ^2-|x|^2 \right) }{2\tau ^3}\right) \right\} , &{} 0\le |x|<\tau \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} {\varvec{G}}_\tau ^2&({\varvec{A}}(\partial ,\omega );x)\\&=\left\{ \begin{array}{lcl}\sum \limits _{m=1}^2 \left\{ \beta _m\frac{\exp (ik_m|x|)}{2|x|^5}\Bigl [{\varvec{X}}\left( |x|^2k_m^2+2|x|ik_m-3 \right) \Bigr .\right. &{}&{}\\ \qquad \Bigl .+{\varvec{I}}\left( |x|^2-|x|^3ik_m\right) \Bigr ]- \left. {\varvec{I}}\alpha _m\frac{\exp (ik_m|x|)}{2|x|}\right\} &{},&{} \tau \le |x|\\ &{}\\ \sum \limits _{m=1}^2\left\{ \frac{\exp (ik_m\tau )}{2\tau ^2} (2\tau - |x| - k_m\tau ^2i + k_m\tau |x|i)\right. &{}\\ \qquad \times \Bigl [\beta _m\frac{\left( |x|^2 - 3\tau ^2\right) ^4}{16\tau ^{12}}{\varvec{X}}\left( |x|^2k_m^2+3|x|ik_m-3\right) \Bigr .&{}&{}\\ \qquad +\beta _m\frac{\left( |x|^2 - 3\tau ^2\right) ^2 }{4\tau ^6}{\varvec{I}}(1-|x|ik_m)-\left. \Bigl .{\varvec{I}}\alpha _m\Bigr ]\right\} &{},&{} \quad 0\le |x|<\tau \end{array}\right. . \end{aligned}$$

We call \({\varvec{G}}_\tau ^l({{\varvec{A}}}(\partial ,\omega );\cdot )\) the Cauchy–Navier potential scaling function with scale parameter \(\tau \) and, in accordance with the construction of \({\varvec{G}}_\tau ^l({{\varvec{A}}}(\partial ,\omega );\cdot )\), the mollification is equal to \({\varvec{G}}({{\varvec{A}}}(\partial ,\omega );\cdot )\) for all \(|x|\ge \tau \).

Remark 3

Here, we lose the radial symmetric property of \(G(\varDelta +k_0^2;\cdot )\) due to the application of the Hessian matrix in the definition of \({\varvec{G}}({{\varvec{A}}}(\partial ,\omega );\cdot )\). However this is advantageous for decorrelation purposes, since we are now able to better highlight the spreading direction of the layers contained in the data.

Due to the continuous differentiability of \(G_\tau ^l(\varDelta +k_0^2;\cdot )\), we directly obtain the following lemma.

Lemma 1

The function \({\varvec{G}}_\tau ^l({{\varvec{A}}}(\partial ,\omega );\cdot )\) is continuously differentiable in \({\mathbb {R}}^3\backslash \{0\}\).

As in the Helmholtz case, the “\(\tau \)-mollifier Cauchy–Navier potential functions”

$$\begin{aligned} u_\tau ^l(x)=\int _{{\mathcal {B}}}{\varvec{G}}_\tau ^l({{\varvec{A}}}(\partial ,\omega );x-y) f(y)\, dy \end{aligned}$$

converge to the Cauchy–Navier potential u.

Theorem 4

Suppose that \({\mathcal {B}}\) is a regular region in \({\mathbb {R}}^3\). Further on, let \(x\in {\overline{{\mathcal {B}}}}\) be arbitrary and let \(f:{\overline{{\mathcal {B}}}}\rightarrow {\mathbb {R}}^3\) be continuous. Then,

$$\begin{aligned} \lim _{\tau \rightarrow 0+}\left| u(x)-u_\tau ^l(x)\right|&=0. \end{aligned}$$

Proof

We observe that

$$\begin{aligned} |{\varvec{G}}({\varvec{A}}(\partial ,\omega );x)-{\varvec{G}}_\tau ^l({\varvec{A}}(\partial ,\omega );x)|=0,\qquad x\in {\mathbb {R}}^3,\quad |x|\ge \tau . \end{aligned}$$

Hence, with

$$\begin{aligned} f_0(x)=\left\{ \begin{array}{cc} f(x),&{} \quad x\in {\overline{{\mathcal {B}}}}\\ &{}\\ 0,&{} \quad x\in {\mathcal {B}}^{ext}\end{array}\right. , \end{aligned}$$

and assuming \(0<\tau <1\), we cut out a small ball \({\mathbb {B}}_{\tau ^2}(x)\) of radius \(\tau ^2\) around the center x from the integral, so that we get

$$\begin{aligned}&\lim _{\tau \rightarrow 0+}\left| \int _{{\mathcal {B}}}({\varvec{G}}({\varvec{A}}(\partial ,\omega );x-y)-{\varvec{G}}_\tau ^l({\varvec{A}}(\partial ,\omega );x-y))f(y)\, dy\right| \nonumber \\&\quad =\lim _{\tau \rightarrow 0+}\left| \int _{{\mathbb {B}}_\tau (x)\backslash {\mathbb {B}}_{\tau ^2}(x)}({\varvec{G}}({\varvec{A}}(\partial ,\omega );x-y)-{\varvec{G}}_\tau ^l({\varvec{A}}(\partial ,\omega );x-y))f_0(y)\, dy\right| . \end{aligned}$$

Next, we split \(f_0\) into its positive and negative parts \(f_0^+\) and \(f_0^-\), respectively and split \(({\varvec{G}}({\varvec{A}}(\partial ,\omega );\cdot )-{\varvec{G}}_\tau ^l({\varvec{A}}(\partial ,\omega );\cdot )\) into its real \((\mathfrak {R})\) and imaginary part \((\mathfrak {I})\). Hence, we have

$$\begin{aligned}&\int _{{\mathbb {B}}_\tau (0)\backslash {\mathbb {B}}_{\tau ^2}(0)}\mathfrak {R}({\varvec{G}}({\varvec{A}}(\partial ,\omega );y)-{\varvec{G}}_\tau ^l({\varvec{A}}(\partial ,\omega );y))f_0^+(x-y)\, dy={\mathcal {O}}\left( \tau ^2\right) \end{aligned}$$

and

$$\begin{aligned}&\int _{{\mathbb {B}}_\tau (0)\backslash {\mathbb {B}}_{\tau ^2}(0)}\mathfrak {I}({\varvec{G}}({\varvec{A}}(\partial ,\omega );y)-{\varvec{G}}_\tau ^l({\varvec{A}}(\partial ,\omega );y))f_0^+(x-y)\, dy={\mathcal {O}}\left( \tau \right) \end{aligned}$$

as \(\tau \rightarrow 0+\). The same steps lead to equivalent results for \(f_0^-\), so that we obtain

$$\begin{aligned}&\lim _{\tau \rightarrow 0+}\left| u(x)-u_\tau ^l(x)\right| =0. \end{aligned}$$

\(\square \)

Now, we take a look at deriving the Cauchy–Navier source scaling function corresponding to the potential scaling function \(\left\{ {\varvec{G}}_\tau ^l({{\varvec{A}}}(\partial ,\omega );\cdot )\right\} _{\tau >0}\) by applying the operator \({{\varvec{A}}}(\partial ,\omega )\) to \({\varvec{G}}_\tau ^l({{\varvec{A}}}(\partial ,\omega );\cdot )\).

Theorem 5

For \(x,y\in {\mathbb {R}}^3\), we find

$$\begin{aligned} {{\varvec{A}}}(\partial _x,\omega ) {\varvec{G}}_\tau ^l({{\varvec{A}}}(\partial ,\omega );x-y)=\varvec{\varPhi }_\tau ^l(\omega ;x-y), \end{aligned}$$

where \(\varvec{\varPhi }_\tau ^l(\omega ;\cdot ):{\mathbb {R}}^3\backslash \{0\}\rightarrow {\mathbb {C}}^{3\times 3}\) is called the mollifier Cauchy–Navier source scaling function and is given by

$$\begin{aligned} \varvec{\varPhi }_\tau ^l(x)=\left\{ \begin{array}{lcl}{\varvec{O}}, &{} \tau \le r\\ &{}\\ \sum \limits _{m=1}^2\beta _m\left[ {\varvec{T}}^l_1(m)+{\varvec{T}}^l_2(m)\right] +\alpha _m\left[ {\varvec{T}}^l_3(m)+{\varvec{T}}^l_4(m)\right] ,&{} 0<r<\tau \end{array}\right. , \end{aligned}$$
(14)

with \({\varvec{T}}^l_1\), \({\varvec{T}}^l_2\), \({\varvec{T}}^l_3\) and \({\varvec{T}}^l_4\) as in (15) - (16), respectively, and \({\varvec{O}}\) denotes the zero tensor.

The terms \({\varvec{T}}^l_1\), \({\varvec{T}}^l_2\), \({\varvec{T}}^l_3\) and \({\varvec{T}}^l_4\) where computed by use of the MATLAB Symbolic Math Toolbox and are given by

$$\begin{aligned} {\varvec{T}}^1_1(m)=&-{\varvec{X}}\frac{\exp (r k_m i) (r^2 - 3 \tau ^2)}{64 r \tau ^{15}}\biggr \{r(2 \mu +\lambda ) \biggl [-r^{11} k_m^4\\&+ r^{10} k_m^3 26i + 12 r^9 k_m^4 \tau ^2 + 114 r^9 k_m^2 - r^8 k_m^3 \tau ^2 252i \biggr .\nonumber \\&+ r^8 k_m 420i - 54 r^7 k_m^4 \tau ^4 - 768 r^7 k_m^2 \tau ^2 - 420 r^7 + r^6 k_m^3 \tau ^4 864i \nonumber \\&- r^6 k_m \tau ^2 3060i + 108 r^5 k_m^4 \tau ^6 + 1476 r^5 k_m^2 \tau ^4 + 3060 r^5 \tau ^2 - r^4 k_m^3 \tau ^6 1184i\nonumber \\&+ r^4 k_m \tau ^4 7020i - 81 r^3 k_m^4 \tau ^8 - 384 r^3 k_m^2 \tau ^6 - 7020 r^3 \tau ^4 + r^2 k_m^3 \tau ^8 462i \nonumber \\&\biggl .- r^2 k_m \tau ^6 4956i - 630 r k_m^2 \tau ^8 + 4956 r \tau ^6 + k_m^3 \tau ^{10} 36i\biggr ] \biggr . \nonumber \\&+ \mu \biggl [r^{10} k_m^3 i + 9 r^9 k_m^2 - r^8 k_m^3 \tau ^2 12i + r^8 k_m 30i - 78 r^7 k_m^2 \tau ^2 - 30 r^7\biggr . \nonumber \\&+ r^6 k_m^3 \tau ^4 54i - r^6 k_m \tau ^2 270i + 216 r^5 k_m^2 \tau ^4 + 270 r^5 \tau ^2 - r^4 k_m^3 \tau ^6 112i \nonumber \\&+ r^4 k_m \tau ^4 810i - 210 r^3 k_m^2 \tau ^6 - 810 r^3 \tau ^4 + r^2 k_m^3 \tau ^8 105i - r^2 k_m \tau ^6 714i \nonumber \\&\biggl .+ 63 r k_m^2 \tau ^8 + 714 r \tau ^6 - k_m^3 \tau ^{10} 36i\biggr ] \nonumber \\&+\biggl . (r^2 - 3 \tau ^2)^4 \omega ^2 (r^2 k_m^2 + r k_m 3i - 3)\biggr \},\nonumber \\ {\varvec{T}}^1_2(m)=&-\biggl .{\varvec{I}}\frac{(r^2 - 3 \tau ^2) \exp (r k_m i)}{64 \tau ^{15}} \biggr \{ \lambda \biggl [13 r^{10} k_m^2 \nonumber \\&+ r^9 k_m 42i - 126 r^8 k_m^2 \tau ^2 - 42 r^8 - r^7 k_m \tau ^2 414i + 432 r^6 k_m^2 \tau ^4\biggr .\nonumber \\&+ 414 r^6 \tau ^2 - r^5 k_m^3 \tau ^6 108i + r^5 k_m \tau ^4 1458i - 590 r^4 k_m^2 \tau ^6 - 1458 r^4 \tau ^4 \nonumber \\&+ r^3 k_m^3 \tau ^8 8i - r^3 k_m \tau ^6 2130i + 219 r^2 k_m^2 \tau ^8 + 2130 r^2 \tau ^6 + r k_m \tau ^8 1044i \nonumber \\ \biggl .&+ 36 k_m^2 \tau ^{10} - 1044 \tau ^8\biggr ]\nonumber \\&+ \mu \biggl [15 r^{10} k_m^2 + r^9 k_m 48i - 150 r^8 k_m^2 \tau ^2 - 48 r^8 - r^7 k_m \tau ^2 486i + 540 r^6 k_m^2 \tau ^4\biggr .\nonumber \\&+ 486 r^6 \tau ^2 - r^5 k_m^3 \tau ^6 104i + r^5 k_m \tau ^4 1782i - 746 r^4 k_m^2 \tau ^6 - 1782 r^4 \tau ^4 \nonumber \\&+ r^3 k_m^3 \tau ^8 57i - r^3 k_m \tau ^6 2946i + 165 r^2 k_m^2 \tau ^8 + 2946 r^2 \tau ^6 + r k_m^3 \tau ^{10} 36i \nonumber \\&+ r k_m \tau ^8 1746i + 144 k_m^2 \tau ^{10} -\biggl . 1746 \tau ^8\biggr ] \nonumber \\&+(\lambda +\mu ) \biggl [r^7 k_m^3 (r^4 - 12 r^2 \tau ^2 + 54 \tau ^4) i\biggr ]\nonumber \\&- \biggl . \tau ^6 \omega ^2 (r^2 - 3 \tau ^2)^2 (r k_m + i) 4i\biggr \},\nonumber \\ {\varvec{T}}^1_3(m)=&{\varvec{X}}\frac{ k_2 \exp (r k_2 i) (\lambda + \mu ) (- k_2 r^3 + r^2 3i + 3 k_2 r \tau ^2 + \tau ^2 3i)}{4 r^3 \tau ^3},\nonumber \\ {\varvec{T}}^1_4(m)=&\biggl .{\varvec{I}}\frac{\exp (r k_2 i)}{4 r \tau ^3} \biggr \{r\left[ 2 \lambda + 8 \mu - r^2 k_2^2 \mu + r^2 \omega ^2 + r k_2 \lambda i + r k_2 \mu 7i\right] \nonumber \\&- 3\tau ^2 \left[ k_2 \mu 3i - r k_2^2 \mu + r \omega ^2 + k_2 \lambda i\right] \biggr \},\nonumber \\ {\varvec{T}}^2_1(m)=&\biggl .-{\varvec{X}}\frac{\exp (k_m \tau i)}{32 r^3 \tau ^{14}} \biggr \{ r^5 \tau ^5 \left[ 96 \lambda (k_m^3 \tau ^3 36i \right. \nonumber \\&+ 37 k_m^2 \tau ^2 + k_m \tau 163i - 108)\nonumber \\&\left. + 24 \mu (k_m^3 \tau ^3 306i + 310 k_m^2 \tau ^2 + k_m \tau 138i - 918)\right] \nonumber \\&- r^4 \tau ^6 \left[ 3 \lambda (- k_m^3 \tau ^3 567i + 2855 k_m^2 \tau ^2 + k_m \tau 2288i + 2288) \right. \nonumber \\&+ \left. 15 \mu (- k_m^3 \tau ^3 243i + 1219 k_m^2 \tau ^2 + k_m \tau 976i + 976)\right] \nonumber \\&- r^{10} (13 \lambda + 27 \mu ) (4 k_m^3 \tau ^3 + k_m^2 \tau ^2 5i - k_m \tau + i) 27i \nonumber \\&+ \tau ^{10} (36 \lambda + 36 \mu ) (k_m^2 \tau ^2 + k_m \tau i + 1) \nonumber \\&- r^{11} k_m (140 \lambda + 290 \mu ) (k_m^2 \tau ^2 i + k_m \tau + 3i) \nonumber \\&+ r^9 \tau (288 \lambda + 600 \mu ) (k_m^3 \tau ^3 4i + 4 k_m^2 \tau ^2 + k_m \tau 13i - 2) \nonumber \\&+ r^{12} k_m^2 (- 1 + k_m \tau i) (165 \lambda + 341 \mu ) \nonumber \\&- r^7 \tau ^3 (1080 \lambda + 2268 \mu ) (k_m^3 \tau ^3 3i + 3 k_m^2 \tau ^2 + k_m \tau i - 4) \nonumber \\&- r^8 \tau ^2 (1386 \lambda + 2898 \mu ) (- k_m^3 \tau ^3 3i + 5 k_m^2 \tau ^2 + k_m \tau 2i + 2) \nonumber \\&+ r^6 \tau ^4 (2430 \lambda + 5130 \mu ) (- k_m^3 \tau ^3 2i + 5 k_m^2 \tau ^2 + k_m \tau 3i + 3) \nonumber \\&+ r^2 \tau ^8 (1287 \lambda + 2745 \mu ) (k_m^2 \tau ^2 + k_m \tau i + 1) \nonumber \\&- 4 r^3 \lambda \tau ^7 (k_m^3 \tau ^3 243i + 291 k_m^2 \tau ^2 + k_m \tau 1757i - 1960)\nonumber \\&- \mu 2 r^3 \tau ^7 (k_m^3 \tau ^3 1053i + 1149 k_m^2 \tau ^2 + k_m \tau 7483i - 8456)\nonumber \\&- \omega ^2 r^3 (r^2 - 3 \tau ^2)^4 (r^2 k_m^2 + r k_m 3i - 3) (r - 2 \tau + k_m \tau ^2 i - r k_m \tau i)\biggl .\biggr \},\nonumber \\ {\varvec{T}}^2_2(m)=&-{\varvec{I}}\frac{\exp (k_m \tau i)}{32 r \tau ^{14}} \biggl \{\lambda (r^2 - 3 \tau ^2) \biggl [\nonumber \\&- r^8 (- k_m^3 \tau ^3 111i + 150 k_m^2 \tau ^2 + k_m \tau 39i + 39) \nonumber \\&- 6 r^7 \tau (k_m^3 \tau ^3 17i + 17 k_m^2 \tau ^2 + k_m \tau 57i - 12) + 4 r \tau ^7 (6 k_m^2 \tau ^2 + k_m \tau 91i - 170) \nonumber \\&- 15 r^{10} k_m^2 (- 1 + k_m \tau i) - 27 r^4 \tau ^4 (- k_m^3 \tau ^3 7i + 30 k_m^2 \tau ^2 + k_m \tau 23i + 23) \nonumber \\&+ 18 r^5 \tau ^3 (k_m^3 \tau ^3 13i + 13 k_m^2 \tau ^2 + k_m \tau 53i - 28) + 9 r^6 \tau ^2 (- k_m^3 \tau ^3 29i \nonumber \\&+ 60 k_m^2 \tau ^2 + k_m \tau 31i + 31) - 6 r^3 \tau ^5 (k_m^3 \tau ^3 27i + 31 k_m^2 \tau ^2 + k_m \tau 175i - 180)\biggr ]\nonumber \\&+ \mu \biggl [- r^{10} (- k_m^3 \tau ^3 180i + 225 k_m^2 \tau ^2 + k_m \tau 45i + 45) \nonumber \\&- 42 r^9 \tau (k_m^3 \tau ^3 4i + 4 k_m^2 \tau ^2 + k_m \tau 13i - 2) - 6 r \tau ^9 (48 k_m^2 \tau ^2 + k_m \tau 323i - 550) \nonumber \\&- 17 r^{12} k_m^2 (- 1 + k_m \tau i) + 234 r^8 \tau ^2 (- k_m^3 \tau ^3 3i + 5 k_m^2 \tau ^2 + k_m \tau 2i + 2) \nonumber \\&- 594 r^6 \tau ^4 (- k_m^3 \tau ^3 2i + 5 k_m^2 \tau ^2 + k_m \tau 3i + 3) \nonumber \\&+ 216 r^7 \tau ^3 (k_m^3 \tau ^3 3i + 3 k_m^2 \tau ^2 + k_m \tau 11i - 4) \nonumber \\&+ 24 r^3 \tau ^7 (k_m^3 \tau ^3 27i + 51 k_m^2 \tau ^2 + k_m \tau 217i - 224) \nonumber \\&- 12 r^5 \tau ^5 (k_m^3 \tau ^3 90i + 106 k_m^2 \tau ^2 + k_m \tau 421i - 270) \nonumber \\&+ r^4 \tau ^6 (- k_m^3 \tau ^3 729i + 3785 k_m^2 \tau ^2 + k_m \tau 3056i + 3056) \biggr ]\nonumber \\&+(\mu 108 \tau ^2-\lambda (r^2 - 3 \tau ^2) 12) \tau ^8 (k_m^2 \tau ^2 + k_m \tau i + 1)\nonumber \\&+(\lambda (r^2 - 3 \tau ^2) 14+\mu 16 r^2) r^9 k_m (k_m^2 \tau ^2 i + k_m \tau + 3i)\nonumber \\&+ (\lambda (r^2 - 3 \tau ^2) 425-\mu 2061 \tau ^2) r^2 \tau ^6 (k_m^2 \tau ^2 + k_m \tau i + 1)\nonumber \\&-4 r \tau ^6 \omega ^2 (r^2 - 3 \tau ^2)^2 (r k_m + i) (r i - \tau 2i - k_m \tau ^2 + r k_m \tau )\biggr \},\nonumber \\ {\varvec{T}}^2_3(m)=&{\varvec{X}}\frac{\exp (k_m \tau i) (\lambda + \mu ) (- 1 + k_m \tau i)}{2 r^3 \tau ^2}, \nonumber \end{aligned}$$
(15)
$$\begin{aligned} {\varvec{T}}^2_4(m)=&-{\varvec{I}}\frac{\exp (k_m \tau i)}{2 r \tau ^2} \biggl [(\lambda + 3 \mu ) (k_m \tau + i) i - (\omega ^2 r (r - 2 \tau + k_m \tau ^2 i - r k_m \tau i))\biggr ]. \end{aligned}$$
(16)

Similar to the Helmholtz source wavelets, \(\varvec{\varPhi }_\tau ^l(\omega ;\cdot )\) is singular in the imaginary part for \(l=1\), and \(\varvec{\varPhi }_\tau ^l(\omega ;\cdot )\) is singular in both real and imaginary parts for \(l=2\). Nonetheless, both scaling functions are integrable and the analytical disadvantage can be easily overcome by a numerical integration scheme as discussed in Blick (2015).

Figures 2 and 3 depict profiles of the scaling functions \({\varvec{G}}_\tau ^l({{\varvec{A}}}(\partial ,\omega );\cdot )\) and \(\varvec{\varPhi }_\tau ^l(\omega ;\cdot )\).

Remark 4

Taking a look at Fig. 1 and comparing it to the cuts depicted on the right side of Figs. 2 and 3, it is easy to observe the close relationship of the Cauchy–Navier and Helmholtz scaling functions.

Lemma 2

For all \(\tau >0\), the so-called volume integral of the mollifier scaling function \(\varvec{\varPhi }_\tau ^l(\omega ;\cdot )\) given by

$$\begin{aligned} {\varvec{V}}_{\varvec{\varPhi }_\tau ^l(\omega ;\cdot )}&=\int _{{\mathbb {R}}^3}\varvec{\varPhi }_\tau ^l(\omega ;y)\, dy \end{aligned}$$

satisfies

$$\begin{aligned} \lim _{\tau \rightarrow 0+}{\varvec{V}}_{\varvec{\varPhi }_\tau ^l(\omega ;\cdot )}={\varvec{I}}. \end{aligned}$$

Proof

By use of polar coordinates and by virtue of elementary calculation, we find

$$\begin{aligned} {\varvec{V}}_{\varvec{\varPhi }_\tau ^1(\omega ;\cdot )}=&\sum _{m=1}^2{\varvec{I}}\biggl \{-\beta _m \frac{2 \pi }{3 k_m^{15} \tau ^{15}} \biggl [ \omega ^2 784604620800i \\&- \omega ^2 \exp (k_m \tau i) 784604620800i + k_m^{17} \lambda \tau ^{15} \exp (k_m \tau i) \\&- k_m^{18} \lambda \tau ^{16} \exp (k_m \tau i) i + 2 k_m^{17} \mu \tau ^{15} \exp (k_m \tau i) - k_m^{18} \mu \tau ^{16} \exp (k_m \tau i) 2i \\&+ k_m^2 \tau ^2 \omega ^2 50295168000i + k_m^4 \tau ^4 \omega ^2 1714608000i + k_m^6 \tau ^6 \omega ^2 40975200i \\&+ k_m^8 \tau ^8 \omega ^2 748440i + k_m^{10} \tau ^{10} \omega ^2 10206i + k_m^{12} \tau ^{12} \omega ^2 81i \\&- 784604620800 k_m \tau \omega ^2 \exp (k_m \tau i) + k_m^2 \tau ^2 \omega ^2 \exp (k_m \tau i) 342007142400i \\&+ 80472268800 k_m^3 \tau ^3 \omega ^2 \exp (k_m \tau i) - k_m^4 \tau ^4 \omega ^2 \exp (k_m \tau i) 9258883200i \\&+ 129548160 k_m^5 \tau ^5 \omega ^2 \exp (k_m \tau i) - k_m^6 \tau ^6 \omega ^2 \exp (k_m \tau i) 189574560i \\&- 18658080 k_m^7 \tau ^7 \omega ^2 \exp (k_m \tau i) - k_m^8 \tau ^8 \omega ^2 \exp (k_m \tau i) 1307880i \\&- 390600 k_m^9 \tau ^9 \omega ^2 \exp (k_m \tau i) + k_m^{10} \tau ^{10} \omega ^2 \exp (k_m \tau i) 6930i \\&- 5670 k_m^{11} \tau ^{11} \omega ^2 \exp (k_m \tau i) + k_m^{12} \tau ^{12} \omega ^2 \exp (k_m \tau i) 444i \\&- 78 k_m^{13} \tau ^{13} \omega ^2 \exp (k_m \tau i) + k_m^{14} \tau ^{14} \omega ^2 \exp (k_m \tau i) 15i \\&- k_m^{15} \tau ^{15} \omega ^2 \exp (k_m \tau i) + k_m^{16} \tau ^{16} \omega ^2 \exp (k_m \tau i) i\biggr ]\\&+ \alpha _m \frac{2 \pi \exp ({k_m \tau i}{2})}{3 k_m^5 \tau ^3} \biggl [72 \omega ^2 \sin ({k_m \tau }{2})\\&+ k_m^5 \lambda \tau ^3 \exp ({k_m \tau i}{2}) - k_m^6 \lambda \tau ^4 \exp ({k_m \tau i}{2}) i \\&+ 4 k_m^5 \mu \tau ^3 \exp ({k_m \tau i}{2}) - k_m^6 \mu \tau ^4 \exp ({k_m \tau i}{2}) 4i - 36 k_m \tau \omega ^2 \exp ({k_m \tau i}{2}) \\&+ k_m^2 \tau ^2 \omega ^2 \cos ({k_m \tau }{2}) 18i - 3 k_m^3 \tau ^3 \omega ^2 \exp ({k_m \tau i}{2})\\&+ k_m^4 \tau ^4 \omega ^2 \exp ({k_m \tau i}{2}) 3i)\biggr ]\biggr \} \end{aligned}$$

and

$$\begin{aligned} {\varvec{V}}_{\varvec{\varPhi }_\tau ^2(\omega ;\cdot )}&=\sum _{m=1}^2{\varvec{I}}\biggl \{\beta _m\exp (k_m \tau i) \biggr [\\&\quad - \frac{2 \pi k_m^2 \lambda }{3} - \frac{4 \pi k_m^2 \mu }{3} + \frac{3753 \pi \omega ^2 }{10010} + \frac{\pi k_m^3 \mu \tau 4i}{3} + \frac{\pi k_m^3 \lambda \tau 2i}{3} \\&\quad + \frac{698483 \pi k_m^2 \tau ^2 \omega ^2 }{5765760} - \frac{\pi k_m^3 \tau ^3 \omega ^2 142643i}{5765760} - \frac{\pi k_m \tau \omega ^2 193i}{630}\biggr ]\\&\quad + \alpha _m \biggl [\frac{\pi \exp (k_m \tau i) (4 \lambda + 16 \mu - 5 \tau ^2 \omega ^2 - k_m \lambda \tau 4i - k_m \mu \tau 16i + k_m \tau ^3 \omega ^2 i)}{6}\biggr ] \biggr \}. \end{aligned}$$

Substituting \(\beta _m\), \(\alpha _m\) and \(k_m\) as given in Eqs. (11)–(12) and taking the limit \(\tau \rightarrow 0+\) via l’Hospital’s rule provides the desired result. \(\square \)

The scaling function \(\varvec{\varPhi }_\tau ^l(\omega ;\cdot )\) allows us to define the “\(\tau \)-mollifier Cauchy–Navier contrast functions” \(f_\tau ^l\) given by

$$\begin{aligned} f_\tau ^l(x)=\int _{\mathcal {B}}\varvec{\varPhi }_\tau ^l(\omega ;x-y) f(y)\, dy. \end{aligned}$$

This leads to the following theorem.

Fig. 2
figure 2

Profile of the real part of the scaling functions \({\varvec{G}}_\tau ^1({{\varvec{A}}}(\partial ,\omega );\cdot )\) (top left) and \(\varvec{\varPhi }_\tau ^1(\omega ;\cdot )\) (bottom left) in \(x_3=0\) and their respective cuts along the \(x_1/x_2\) direction (right) of the top left picture for \(\lambda =\mu =1\) and \(\omega =2\)

Full size image
Fig. 3
figure 3

Profile of the real part of the scaling functions \({\varvec{G}}_\tau ^2({{\varvec{A}}}(\partial ,\omega );\cdot )\) (top left) and \(\varvec{\varPhi }_\tau ^2(\omega ;\cdot )\) (bottom left) in \(x_3=0\) and their respective cuts along the \(x_1/x_2\) direction (right) of the top left picture for \(\lambda =\mu =1\) and \(\omega =2\)

Full size image

Theorem 6

The function \(\varvec{\varPhi }_\tau ^l(\omega ;\cdot )\) is piecewise continuously differentiable in \({\mathbb {R}}^3\backslash \{0\}\). In addition, assume that \({\mathcal {B}}\) is a regular region in \({\mathbb {R}}^3\) and that \(f:{\overline{{\mathcal {B}}}}\rightarrow {\mathbb {R}}^3\) is continuous for \(l=1\) and continuously differentiable for \(l=2\). Then,

$$\begin{aligned} \lim _{\tau \rightarrow 0+}| \alpha (x)f(x)-f_\tau ^l(x)|=0 \end{aligned}$$

holds true for all \(x\in {\overline{{\mathcal {B}}}}\), where \(\alpha \) denotes the solid angle in x subtended by the boundary \(\partial {\mathcal {B}}\).

Proof

We split \(\varvec{\varPhi }_\tau ^l(\omega ;\cdot )\) into its real and imaginary parts so that

$$\begin{aligned} \varvec{\varPhi }_\tau ^l(\omega ;x-y)=\mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y)+i\mathfrak {I}\varvec{\varPhi }_\tau ^l(\omega ;x-y). \end{aligned}$$

Since \(x\in {\overline{{\mathcal {B}}}}\) and \({\mathcal {B}}\) is open, there exists a \(\tau _0\) such that \({\overline{{\mathcal {B}}}}\cap {\mathbb {B}}_\tau (x)\) is simply connected for all \(0<\tau \le \tau _0\). With \(\mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;\cdot )=\left\{ \left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;\cdot ) \right) _{ij}\right\} _{i,j=1,2,3}\), we have

$$\begin{aligned} \int _{\mathcal {B}}\mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y)f(y)\ dy&= \int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y)f(y)\, dy\\&=\left\{ \sum _{j=1}^3\int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y) \right) _{ij}f_j(y)\, dy\right\} _{i=1,2,3}. \end{aligned}$$

We split \(\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;\cdot )\right) _{ij}\) into its positive and negative parts, so that

$$\begin{aligned}&\int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y)\right) _{ij}f_j(y)\, dy\\&\quad =\int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y)\right) ^+_{ij}f_j(y)\, dy\\&\qquad + \int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y)\right) ^-_{ij}f_j(y)\, dy, \end{aligned}$$

where \((\cdot )^+\) and \((\cdot )^-\) denote the positive and negative parts of the corresponding functions, respectively.

Since f is continuous and \(\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;\cdot )\right) ^+_{ij}\) as well as \(\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;\cdot )\right) ^-_{ij}\) are integrable and do not change the sign, the mean value theorem of integration guarantees the existence of \(\xi _1,\xi _2\in {\mathcal {B}}\cap {\mathbb {B}}_\tau (x)\), so that

$$\begin{aligned}&\int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y)\right) _{ij}f_j(y)\, dy\nonumber \\&\quad =f_j(\xi _1)\int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l (\omega ;x-y)\right) ^+_{ij}\, dy\nonumber \\&\qquad + f_j(\xi _2)\int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y)\right) ^-_{ij}\, dy. \end{aligned}$$
(17)

According to Lemma 2 and observing that \(\varvec{\varPhi }_\tau ^l(\omega ;\cdot )\) is point symmetric and that \(\partial {\mathcal {B}}\) as the boundary of a regular region is locally \(c^{(2)}\)-smooth, we have

$$\begin{aligned}&\lim _{\tau \rightarrow 0+}\left( \int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y) \right) ^+_{ij}\ \, dy + \int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y)\right) ^-_{ij}\, dy\right) \\&\quad =\alpha (x)\delta _{ij} \end{aligned}$$

and hence,

$$\begin{aligned}&\lim _{\tau \rightarrow 0+}\int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y) \right) ^-_{ij}\, dy \\&\quad =\alpha (x)\delta _{ij}-\lim _{\tau \rightarrow 0+}\int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)} \left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y)\right) ^+_{ij}\, dy. \end{aligned}$$

Substituting the last equation into Eq. (17), we get

$$\begin{aligned}&\lim _{\tau \rightarrow 0+}\int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y) \right) _{ij}f_j(y)\, dy \nonumber \\&\quad = \lim _{\tau \rightarrow 0+}\left( \alpha (x)f_j(\xi _2)\delta _{ij} +\left( f_j(\xi _1)-f_j(\xi _2)\right) \int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)} \left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y)\right) ^+_{ij}\, dy\right) . \end{aligned}$$
(18)

Now we need to estimate the integral on the right hand side. Exemplary taking a look at the case \(l=1\) (cf. Eq. (14)), we split the exponential function into cosinus and sinus and see that \(\left( \varvec{\varPhi }_\tau ^l(\omega ;x-y)\right) ^+_{ij}\) is composed of the following functions:

  1. 1.

    Terms of the form \(0\le \cos (rk_m)r^n\tau ^{m-15}\) for \(n+m\ge 12\) and \(0\le r\le \tau \le \frac{\pi }{2k_m}\) contribute to both the real and imaginary part. With polar coordinates, we get

    $$\begin{aligned} \int _0^\tau \cos (rk_m)r^{n+2}\tau ^{m-15}\, dr=\frac{\tau ^{m + n - 12}}{n + 3} {_1H_2}\left( \frac{n}{2} + \frac{3}{2}, \left[ \frac{1}{2}, \frac{n}{2} + \frac{5}{2}\right] , -\frac{k_m^2\tau ^2}{4}\right) , \end{aligned}$$
    (19)

    where \({_pH_q}(a,b,z)\) denotes the generalized hypergeometric function (Magnus et al. 1966; Luke 1969) of order p, q. Here, p denotes the length of the vector a and q the length of the vector b. We have

    $$\begin{aligned} {_pH_q}(a,b,z)=\sum _{j=0}^\infty \left( \frac{\left( a_1\right) _j\dots \left( a_j\right) _j\dots \left( a_p\right) _j}{\left( b_1\right) _j\dots \left( b_k\right) _j\dots \left( b_q\right) _j}\right) \left( \frac{z^j}{j!}\right) , \end{aligned}$$

    where

    $$\begin{aligned} (x)_j=\frac{\varGamma (x+j)}{\varGamma (x)} \end{aligned}$$

    with \(\varGamma \) as the Gamma function denotes the Pochhammer symbol. It should be noted that \({_pH_q}(a,b,z)\) is convergent for \(|z|<\infty \) if \(p\le q\). Hence for \(n+m\ge 13\), we have

    $$\begin{aligned} \lim _{\tau \rightarrow 0+}\int _0^\tau \cos (rk_m)r^{n+2}\tau ^{m-15}\, dr=0 \end{aligned}$$

    and for \(n+m=12\), the integral is bounded.

  2. 2.

    Observing that \(\beta _1=-\beta _2\) in Eq. (14) and \(k_2\ge k_1\), we find terms of the form \(0\le \left( \cos (rk_1)-\cos (rk_2)\right) r^n\tau ^{m-15}\) for \(n+m=10\) and \(0\le r\le \tau \) sufficiently small. Integration leads to

    $$\begin{aligned}&\lim _{\tau \rightarrow 0+}\int _0^\tau \left( \cos (rk_1)-\cos (rk_2) \right) r^{n+2}\tau ^{m-15}\, dr\\&\quad =\frac{\tau ^{m + n - 12}}{n + 1}\left( {_1H_2}\left( \frac{n}{2} + \frac{1}{2}, \left[ \frac{1}{2}, \frac{n}{2} + \frac{3}{2}\right] , -\frac{k_1^2\tau ^2}{4}\right) \right. \\&\qquad - \left. {_1H_2}\left( \frac{n}{2} + \frac{1}{2}, \left[ \frac{1}{2}, \frac{n}{2} + \frac{3}{2}\right] , -\frac{k_2^2\tau ^2}{4}\right) \right) \\&\quad =C, \end{aligned}$$

    where C is a constant. These terms contribute to the real part.

  3. 3.

    For the imaginary part, we have terms of the form \(0\le \sin (rk_m)r^n\tau ^{m-15}\) for \(n+m\ge 11\) and \(0\le r\le \tau \le \frac{\pi }{k_m}\). Integration yields

    $$\begin{aligned}&\int _0^\tau \sin (rk_m)r^{n+2}\tau ^{m-15}\, dr\nonumber \\&\quad =\frac{k_m\tau ^{m + n - 11}}{n + 4}{_1H_2}\left( \frac{n}{2} + 2, \left[ \frac{3}{2}, \frac{n}{2} + 3\right] , -\frac{k_m^2\tau ^2}{4}\right) \end{aligned}$$
    (20)

    which for \(\tau \rightarrow 0+\) converges to zero in the case of \(m+n\ge 12\) and is bounded for \(m+n=11\).

  4. 4.

    Terms of the form \(0\le C\left( k_m\cos (rk_m)r^{n}\tau ^{11-m}+\sin (rk_m)r^{n-1}\tau ^{11-m}\right) \) for \(\tau \le \pi /(2k_m)\) and C a positive constant contribute to the imaginary part. Observing (19) and (20), we have for \(n+m=11\)

    $$\begin{aligned} \lim _{\tau \rightarrow 0+}C\int _0^\tau \left( k_m\cos (rk_m)r^{n+2} \tau ^{11-m}+\sin (rk_m)r^{n+1}\tau ^{11-m}\right) \, dr=0. \end{aligned}$$

All in all using the triangle inequality, we can now state that for \(l=1\), both the real and imaginary part of the integral of \(\left( \varvec{\varPhi }_\tau ^l(\omega ;x-\cdot )\right) ^+_{ij}\) are bounded for \(\tau \rightarrow 0+\). Similar observations for the case \(l=2\) show that the real part of the integral of \(\left( \varvec{\varPhi }_\tau ^l(\omega ;x-\cdot )\right) ^+_{ij}\) is bounded and the integral of the imaginary part is of order \({\mathcal {O}}\left( \tau ^{-1}\right) \) as \(\tau \rightarrow 0+\). Hence, we have

$$\begin{aligned}&\lim _{\tau \rightarrow 0+}\int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y) \right) _{ij}f_j(y)\, dy \\&\quad = \lim _{\tau \rightarrow 0+}\Biggl (\alpha (x)\underbrace{f_j(\xi _2)}_{\rightarrow f_j(x)}\delta _{ij}\Biggr .+\Biggl .\underbrace{\left( f_j(\xi _1)-f_j(\xi _2)\right) \int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {R}\varvec{\varPhi }_\tau ^l(\omega ;x-y)\right) ^+_{ij}\, dy}_{\rightarrow 0}\Biggr )\\&\quad =\alpha (x) f_j(x), \end{aligned}$$

for \(l=1,2\), since f is continuous.

Following the same ideas, it is easy to show that for \(l=1\), we find

$$\begin{aligned}&\lim _{\tau \rightarrow 0+}\int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {I}\varvec{\varPhi }_\tau ^1(\omega ;x-y)\right) _{ij}f_j(y)\, dy =0, \end{aligned}$$

if f is continuous. Hence, it remains to prove the imaginary case for \(l=2\). However, if we want to realize that the imaginary part for \(l=2\) also converges to zero, we have to assume that \(f\in c^{(1)}({\mathcal {B}})\).

In order to continue the proof, we present estimates only used in the case \(l=2\). Here, we observe, that any function \(f\in c^{(1)}({\mathcal {B}})\) can be written as

$$\begin{aligned} f(y)=\left[ f(y)-(f(x) + \nabla f(x)(y-x))\right] +(f(x) + \nabla f(x)(y-x)). \end{aligned}$$

It is easy to explicitly calculate that the theorem holds true for all linear functions due to the point symmetry of the scaling functions. Hence, we can assume without loss of generality, that \(D^\alpha f(x)=0\) for \(|\alpha |\le 1\) and \(x\in {\overline{{\mathcal {B}}}}\) fixed. In that case, we apply Taylor’s theorem to approximate \(f_j(\xi _i)\) by expansion around x, so that

$$\begin{aligned} \left| f_j(\xi _1)-f_j(\xi _2)\right|&\le \left| \int _0^1\sum _{|\alpha |=1} \frac{(\xi _1-x)^\alpha }{\alpha !} D^\alpha f_j\left( x+t\left( \xi _1-x\right) \right) \, dt\right. \\&\quad \left. -\int _0^1\sum _{|\alpha |=1}\frac{(\xi _2-x)^\alpha }{\alpha !} D^\alpha f_j\left( x+t\left( \xi _2-x\right) \right) \, dt\right| \\&\le \int _0^1\sum _{|\alpha |=1}|\xi _1-x|^\alpha \left| D^\alpha f_j\left( x+t\left( \xi _1-x\right) \right) -D^\alpha f_j(x)\right| \, dt\\&\quad +\int _0^1\sum _{|\alpha |=1}|\xi _2-x|^\alpha \left| D^\alpha f_j\left( x+t\left( \xi _2-x\right) \right) -D^\alpha f_j(x)\right| \, dt\\&\le 2\tau \sum _{|\alpha |=1}\max _{y\in {\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}|D^\alpha f_j(y)-D^\alpha f_j(x)|, \end{aligned}$$

as \(\tau \) tends to zero. All in all, combining these estimates with the observation that

$$\begin{aligned} \int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {I}\varvec{\varPhi }_\tau ^2(\omega ;x-y)\right) ^+_{ij}\, dy={\mathcal {O}}\left( \tau ^{-1}\right) \end{aligned}$$

as \(\tau \rightarrow 0+\), we follow the previous considerations up to Eq. (18), so that

$$\begin{aligned}&\lim _{\tau \rightarrow 0+}\int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {I}\varvec{\varPhi }_\tau ^2 (\omega ;x-y)\right) _{ij}f_j(y)\, dy \\&\quad =\lim _{\tau \rightarrow 0+}\Biggl (\left( f_j(\xi _1)-f_j(\xi _2)\right) \int _{{\mathcal {B}}\cap {\mathbb {B}}_\tau (x)}\left( \mathfrak {I}\varvec{\varPhi }_\tau ^2(\omega ;x-y)\right) ^+_{ij}\, dy\Biggr )\\&\quad =0, \end{aligned}$$

which proves the theorem. \(\square \)

4 Wavelet representation of potential and contrast functions

Next, we deal with the mathematical mechanisms for interpretation and understanding of available seismic information inside a regular region \({\mathcal {B}}\). In order to do that, we again take a look at the Helmholtz case in order to make the reader more familiar with the idea of seismic decorrelation and introduce the associated notation. Our purpose is to demonstrate, how the multiscale procedure for the potential canonically transfers to seismic data by use of “Helmholtz derivatives” as shown in Blick (2015).

As already noted, the source wavelets in this paper do not have zero mean (neither in the real part, nor the entire function). Since the wavelets are constructed by taking the difference of scaling functions with different scales, this results in the following two cases which we want to avoid.

  1. (i)

    Since \(V_{\varPhi _\tau ^l(k_0;\cdot )}\) is not a constant but a function depending on \(\tau \), there exist \(\tau _1,\tau _2\), such that \(V_{\varPhi _{\tau _2}^l(k_0;\cdot )}\) compared to \(V_{\varPhi _{\tau _1}^l(k_0;\cdot )}\) is large. Calculating the difference, i.e., taking a look at the band-pass filtered signal, the result will be dominated by the low-pass filtered signal generated by filtering with \(\varPhi _{\tau _2}^l(k_0;\cdot )\) and hence, we do not get any new information from the decorrelation.

  2. (ii)

    The volume integral \(V_{\varPhi _\tau ^l(k_0;\cdot )}\) can be negative. Hence, suppose that \(V_{\varPhi _{\tau _1}^l(k_0;\cdot )}\) is negative and \(V_{\varPhi _{\tau _2}^l(k_0;\cdot )}\) positive, then the band-pass filtered version is in fact the summation instead of the subtraction of the information contained in the two low-pass filtered signals.

Hence, we normalize by the real part of the volume integral of the source scaling functions in order to construct wavelets that have zero mean in the real part. It would also be possible to construct the wavelets \(\varPsi _{\tau _j}^l(k_0;\cdot )\) in such a way that the entire wavelet has zero mean. However, this leads to a change in phase, which we want to avoid.

We start with the considerations regarding the scaling functions \(G_\tau ^l(\varDelta +k_0^2;\cdot )\). Suppose that \(\{\tau _j\}_{j \in {{\mathbb {N}}}_0}\) is a positive, monotonically decreasing sequence with \( \lim _{j \rightarrow \infty } \tau _j =0\) and with \(\mathfrak {R}V_{\varPhi _{\tau _j}^l(k_0;\cdot )}\ne 0\) for all \(j\in {{\mathbb {N}}}_0\). We consider the differences

$$\begin{aligned} {\mathcal {W}}_{\tau _j}^l(\varDelta +k_0^2;|x-y|)=G_{\tau _j}^l (\varDelta +k_0^2;|x-y|)-G_{\tau _{j-1}}^l (\varDelta +k_0^2;|x-y|) \end{aligned}$$

and

$$\begin{aligned} \varPsi _{\tau _j}^l (k_0;|x-y|)=\frac{\varPhi _{\tau _j}^l (k_0;|x-y|)}{\mathfrak {R}V_{\varPhi _{\tau _j}^l(k_0;\cdot )}}-\frac{\varPhi _{\tau _{j-1}}^l (k_0;|x-y|)}{\mathfrak {R}V_{\varPhi _{\tau _{j-1}}^l(k_0;\cdot )}}. \end{aligned}$$

\({\mathcal {W}}_{\tau _j}^l(\varDelta ;\cdot )\) and \(\varPsi _{\tau _j}^l(k_{0};\cdot )\) are called “mollifier Helmholtz potential wavelet function” and “mollifier Helmholtz source wavelet function”, respectively.

Seen from a numerical point of view, it is remarkable that both wavelet functions \(y \mapsto {\mathcal {W}}_{\tau _j}^l (\varDelta +k_0^2;|x-y|)\) and \(y \mapsto \varPsi _{\tau _j}^l (k_0;|x-y|)\) vanish outside a ball around the center x due to their construction. These functions are space-limited showing a ball as local support. Furthermore, the ball becomes smaller and smaller with increasing scale parameter j,  so that more and more high frequency phenomena can be highlighted without changing the features outside the ball.

The associated “\(\tau _j\)-mollifier potential wavelet functions” and the “\(\tau _j\)-mollifier contrast wavelet functions” are given by

$$\begin{aligned} (WU)_{\tau _j}^l (x)= \int _{{\mathbb {B}}_{\tau _j} (x)\cap {\mathcal {B}}}{\mathcal {W}}_{\tau _j}^l (\varDelta +k_0^2; |x-y |)F(y)\, dy \end{aligned}$$

and

$$\begin{aligned} (WF)_{\tau _j}^l (x)= \int _{{\mathbb {B}}_{\tau _j} (x)\cap {\mathcal {B}}}\varPsi _{\tau _j}^l (k_0;|x-y|)F(y)\, dy. \end{aligned}$$

The \(\tau _j\)-potential wavelet functions and the \(\tau _j\)-contrast wavelet functions, respectively, characterize the successive detail information contained in \(U_{\tau _j}^l-U_{\tau _{j-1}}^l \) and \(F_{\tau _j}^l -F_{\tau _{j-1}}^l, \ j \in {{\mathbb {N}}}_0\). In other words, we are able to recover the potential U and the contrast function, i.e., the “geological signatures” F, respectively, in form of “band structures”

$$\begin{aligned} (WU)_{\tau _j}^l =U_{\tau _j}^l -U_{\tau _{j-1}}^l \end{aligned}$$
(21)

and

$$\begin{aligned} (WF)_{\tau _j}^l =F_{\tau _j}^l -F_{\tau _{j-1}}^l. \end{aligned}$$
(22)

As a consequence, the essential problem to be solved in multiscale extraction of geological features is to identify those detail information, i.e., band structures, which specifically contain desired geological characteristics, for example, aquifers and salt domes.

Thus for \(x\in {\overline{{\mathcal {B}}}}\) and \(F\in C^{(0)}({\mathcal {B}})\), we finally end up with the following multiscale reconstruction

$$\begin{aligned} U(x)=\lim _{J\rightarrow \infty }U_{\tau _J}^l (x)=U_{\tau _0}^l (x)+\sum _{j=1}^\infty (WU)_{\tau _j}^l (x) \end{aligned}$$

and

$$\begin{aligned} \alpha (x)F(x)&=\lim _{J\rightarrow \infty }F_{\tau _J}^l (x)=\frac{F_{\tau _0}^l (x)}{\mathfrak {R}V_{\varPhi _{\tau _0}^l(k_0;\cdot )}}+\sum _{j=1}^\infty (WF)_{\tau _j}^l (x). \end{aligned}$$

In addition, if F is Hölder continuous, we have

$$\begin{aligned} \alpha (x)F(x) =\frac{(\varDelta +k_0^2)}{\mathfrak {R}V_{\varPhi _{\tau _0}^l(k_0;\cdot )}}U_{\tau _0}^l (x)+\sum _{j=1}^\infty (\varDelta +k_0^2)\left( \frac{U_{\tau _j}^l (x)}{\mathfrak {R}V_{\varPhi _{\tau _j}^l(k_0;\cdot )}} -\frac{U_{\tau _{j-1}}^l (x)}{\mathfrak {R}V_{\varPhi _{\tau _{j-1}}^l(k_0;\cdot )}} \right) . \end{aligned}$$

All in all, the potential U as well as the contrast function, i.e., the “geological signature” F can be expressed in an additive way as a low-pass filtered signal \(U_{\tau _0}^l\) and \(F_{\tau _0}^l\) and successive band-pass filtered signals \((WU)_{\tau _j}^l\) and \((WF)_{\tau _j}^l\), \(j=1,2,\ldots ,\) respectively.

It should be mentioned that this multiscale approach is constructed such that, within the spectrum of all wavebands (cf. Eqs. (21) and (22)), certain rock formations may be associated to a specific band within the multiscale reconstruction. Each scale parameter in the decorrelation is assigned to a data distribution which corresponds to the associated waveband and thus, leads to a low-pass approximation of the data at a particular resolution. The wavelet contributions are obtained as part of a multiscale approximation by calculating the difference between two consecutive scaling functions. In other words, the wavelet transformation (filtering) of a signal constitutes the difference of two low-pass filters, thus it may be regarded as a band-pass filter. Due to our construction, the wavelets show an increasing space localization as the scale increases. In this way, the characteristic signatures of a signal can be detected in certain frequency bands.

In the same way as for the Helmholtz equation, we obtain a multiscale procedure for the potential u as well as the contrast function \(f\in c^{(l-1)}\). Again suppose that \(\{\tau _j\}_{j \in {{\mathbb {N}}}_0}\) is a positive, monotonically decreasing sequence with \( \lim _{j \rightarrow \infty } \tau _j =0\) and with \(\mathfrak {R}{\varvec{V}}_{\varvec{\varPhi }_{\tau _j}^l(\omega ;\cdot )}\ne 0\) for all \(j\in {{\mathbb {N}}}_0\). We consider the differences

$$\begin{aligned} \varvec{{\mathcal {W}}}_{\tau _j}^l({{\varvec{A}}}(\partial ,\omega );x-y)={\varvec{G}}_{\tau _j}^l ({{\varvec{A}}}(\partial ,\omega );x-y)-{\varvec{G}}_{\tau _{j-1}}^l ({{\varvec{A}}}(\partial ,\omega );x-y) \end{aligned}$$

and

$$\begin{aligned} \varvec{\varPsi }_{\tau _j}^l (\omega ;x-y)=\frac{\varvec{\varPhi }_{\tau _j}^l (\omega ;x-y)}{\mathfrak {R}{\varvec{V}}_{\varvec{\varPhi }_{\tau _j}^l(\omega ;\cdot )}}-\frac{\varvec{\varPhi }_{\tau _{j-1}}^l (\omega ;x-y)}{\mathfrak {R}{\varvec{V}}_{\varvec{\varPhi }_{\tau _{j-1}}^l(\omega ;\cdot )}}. \end{aligned}$$

\(\varvec{{\mathcal {W}}}_{\tau _j}^l({{\varvec{A}}}(\partial ,\omega );\cdot )\) and \(\varvec{\varPsi }_{\tau _j}^l(\omega ;\cdot )\) are called “mollifier Cauchy–Navier potential wavelet function” and “mollifier Cauchy–Navier source wavelet function”.

The associated “\(\tau _j\)-mollifier Cauchy–Navier potential wavelet functions” and the “\(\tau _j\)-mollifier Cauchy–Navier contrast wavelet functions” are given by

$$\begin{aligned} ({\varvec{W}}u)_{\tau _j}^l (x)= \int _{\mathcal {B}}\varvec{{\mathcal {W}}}_{\tau _j}^l ({{\varvec{A}}}(\partial ,\omega ); x-y ) f(y)\, dy \end{aligned}$$

and

$$\begin{aligned} ({\varvec{W}}f)_{\tau _j}^l (x)= \int _{\mathcal {B}}\varvec{\varPsi }_{\tau _j}^l (\omega ;x-y) f(y)\, dy. \end{aligned}$$

As in the Helmholtz case, the \(\tau _j\)-Cauchy–Navier potential wavelet functions and the \(\tau _j\)-Cauchy–Navier contrast wavelet functions, respectively, characterize the successive detail information contained in \(u_{\tau _j}^l-u_{\tau _{j-1}}^l\) and \(f_{\tau _j}^l -f_{\tau _{j-1}}^l, \ j \in {{\mathbb {N}}}_0\). In other words, we are able to recover the potential u and the contrast function, i.e., the “signature” f, respectively, in form of “band structures”

$$\begin{aligned} ({\varvec{W}}u)_{\tau _j}^l =u_{\tau _j}^l -u_{\tau _{j-1}}^l, \end{aligned}$$

and

$$\begin{aligned} ({\varvec{W}}f)_{\tau _j}^l =f_{\tau _j}^l -f_{\tau _{j-1}}^l. \end{aligned}$$

Again, both wavelet functions \(y \mapsto \varvec{{\mathcal {W}}}_{\tau _j}^l ({{\varvec{A}}}(\partial ,\omega );x-y)\) and \(y \mapsto \varvec{\varPsi }_{\tau _j}^l (\omega ;x-y)\) vanish outside a ball around the center x due to their construction, which is of numerical advantage for the convolution. Furthermore, the ball becomes smaller and smaller with increasing scale parameter j,  so that more and more high frequency phenomena can be highlighted without changing the features outside the balls. Thus for \(x\in {\overline{{\mathcal {B}}}}\), we obtain the multiscale relations

$$\begin{aligned} u(x)=\lim _{J\rightarrow \infty }u_{\tau _J}^l (x)=u_{\tau _0}^l (x)+\sum _{j=1}^\infty ({\varvec{W}}u)_{\tau _j}^l (x) \end{aligned}$$

and

$$\begin{aligned} \alpha (x)f(x)&=\lim _{J\rightarrow \infty }f_{\tau _J}^l (x)=\frac{f_{\tau _0}^l (x)}{\mathfrak {R}{\varvec{V}}_{\varvec{\varPhi }_{\tau _0}^l(\omega ;\cdot )}}+\sum _{j=1}^\infty ({\varvec{W}}f)_{\tau _j}^l (x). \end{aligned}$$

In addition, if f is Hölder continuous in \({\overline{{\mathcal {B}}}}\), we have

$$\begin{aligned} \alpha (x)f(x) =\frac{{{\varvec{A}}}(\partial ,\omega )}{\mathfrak {R}{\varvec{V}}_{\varvec{\varPhi }_{\tau _0}^l(\omega ;\cdot )}} u_{\tau _0}^l (x)+\sum _{j=1}^\infty {{\varvec{A}}}(\partial ,\omega )\left( \frac{u_{\tau _j}^l (x)}{\mathfrak {R}{\varvec{V}}_{\varvec{\varPhi }_{\tau _j}^l(\omega ;\cdot )}} - \frac{u_{\tau _{j-1}}^l (x)}{\mathfrak {R}{\varvec{V}}_{\varvec{\varPhi }_{\tau _{j-1}}^l(\omega ;\cdot )}}\right) . \end{aligned}$$

Hence, the potential u as well as the contrast function f can be reconstructed as a low-pass filtered signal \(u_{\tau _0}^l\) and \(f_{\tau _0}^l \) and successive band-pass filtered signals \(({\varvec{W}}u)_{\tau _j}^l\) and \(({\varvec{W}}f)_{\tau _j}^l\), \(j=1,2,\ldots ,\) respectively.

5 Comparison of the Helmholtz and elasto-oscillatory Cauchy–Navier decorrelation based on the Marmousi migration result

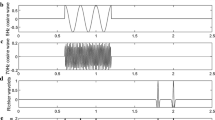
As point of departure, we construct a synthetic 3D migration result by continuing the model in the \(x_2\) direction by putting copies of a 2D migration result from Ilyasov (2011) (see also Martin et al. 2006; Irons 2015) behind each other in order to test the decorrelation ability of the wavelets. We specifically accept the downside of the model that it is constant in the \(x_2\) direction in favor of the fact that we have a complete interpretation of the model as depicted in Fig. 4.

Fig. 4
figure 4

The Marmousi model (top, Ilyasov 2011) and its interpretation (bottom, Martin et al. 2006)

Full size image

The essential ingredients of the decorrelation applied to the Helmholtz equation are illustrated for 2D cuts of a 3D version of the Marmousi migration result by the scheme depicted in Fig. 5. The figure shows that the Helmholtz potential does not yield usable information about the geology because of its smoothness (Fig. 5, top left), since the differences may be understood as a discrete version of Eq. (1). However, if we go over to the multiscale decorrelation in terms of band-pass filtered data \(U_{\tau _j}-U_{\tau _{j-1}}\) of the potential U at scale j, structural information of the Marmousi model become visible (Fig. 5, bottom left). The key idea of the method is that the potential wavelets generating the potential decorrelation (Fig. 5, left) can be correlated via the application of the Helmholtz operator to Haar-type wavelets in the migration level (right). In fact, the decorrelation of the migration result in band signals (Fig. 5, bottom right) clearly shows that information about the geological interfaces becomes available.

Fig. 5
figure 5

Schematic visualization of the multiscale decorrelation mechanism as depicted in Blick et al. (2018b)

Full size image

The aforementioned wavelet construction is particularly powerful because of its “geophysical relevance”, i.e., it forms a compromise reflecting the underlying physics (in accordance with the underlying differential equation) while still delivering an adequate multiscale decorrelation of geological signatures. Transitions of geological strata can be detected, but of course not the specific geological formations themselves. Nevertheless, the structure of the geological configuration and even the faults become visible by mollifier decorrelation. The wavelets employed for establishing the Helmholtz scheme constitute radial basis functions, so that they are only dependent on the mutual distance of two points of the area under investigation. This means that no specific directionally-reflected information can be verified by the model described above.

5.1 Decorrelation using Helmholtz wavelets

We are more interested in the decorrelation of the source data, even if our mathematical setup allows us to also decorrelate the potential. We borrow the results of the Helmholtz case from (Blick 2015) and present them here as a reference for the comparison to the Cauchy–Navier decorrelation scheme.

We concentrate on the real part of the decorrelation of the 3D synthetic Marmousi migration result for \(k_0=0.036\,\frac{{\text{ rad }}}{\text {m}}\) based on a conducted parameter study in Blick (2015). The range of \(k_0\) for the study is given by \(\left[ 0.0018\,\frac{{\text{ rad }}}{\text {m}}, 0.1\,\frac{{\text{ rad }}}{\text {m}}\right] \) and results from the choice of an excitation frequency between 10 and \(150\,\frac{{\text{ rad }}}{\text {s}}\) for occuring rock velocities between 1500 and \(5500\,\frac{{\text {m}}}{{\text {s}}}\). For a comparison to the decorrelation for other values of \(k_0\), the reader is also referred to (Blick 2015). The sequence \(\tau _j\) is adopted from (Blick 2015) as well. The sequence is constructed in such a way that for scales \(j=1,\ldots ,5\), the real part of \(V_{{\varPhi }_\tau ^{2}(k_0;\cdot )}\) is close to one. Since a smaller spacing of \(\tau _j\) is also required for large scale parameters j, a dyadic sequence for scales \(j=6,\ldots ,9\) is taken.

Remark 5

The depicted figures in this section denote 2D cuts of the complete 3D convolution result of the 3D Marmousi migration result as used in Blick (2015).

A decorrelation of the 3D Marmousi migration result F via the partially and fully taylorized normalized Helmholtz source scaling functions and wavelets is illustrated in Figs. 6, 7, 8 and 9 for \(k_0=0.036\,\frac{{\text{ rad }}}{\text {m}}\).

We observe that the convolution with the partially taylorized normalized Helmholtz source scaling function and wavelet tends to oscillate heavily and hence is blurred due to ghost images for low scales. This phenomenon gets worse if \(k_0\) is increased. Comparing with Fig. 4b, we notice that the salt dome in the lower left part of the migration result and some coarser structures are clearly represented in the band-pass filtered signal at scales \(j=3\).

Fig. 6
figure 6

Real part of the multiscale approximation of the Marmousi migration result F by convolution with the normalized and partially taylorized (\(l=1\)) Helmholtz source scaling function and wavelet for \(k_0=0.036\,\frac{{\text{ rad }}}{\text {m}}\)

Full size image
Fig. 7
figure 7

Real part of the multiscale approximation of the Marmousi migration result F by convolution with the normalized and partially taylorized (\(l=1\)) Helmholtz source scaling function and wavelet for \(k_0=0.036\,\frac{{\text{ rad }}}{\text {m}}\)

Full size image
Fig. 8
figure 8

Real part of the multiscale approximation of the Marmousi migration result F by convolution with the normalized and fully taylorized (\(l=2\)) Helmholtz source scaling function and wavelet for \(k_0=0.036\,\frac{{\text{ rad }}}{\text {m}}\)

Full size image
Fig. 9
figure 9

Real part of the multiscale approximation of the Marmousi migration result F by convolution with the normalized and fully taylorized (\(l=2\)) Helmholtz source scaling function and wavelet for \(k_0=0.036\,\frac{{\text{ rad }}}{\text {m}}\)

Full size image

In comparison, the decorrelation via the fully taylorized normalized Helmholtz source scaling function and wavelet does not oscillate as heavily. As such, the characteristics of the salt dome can be seen at scales \(j=4\) in the band-pass filtered data. The structure changes for increasing scales j for both types of scaling functions. The dominating layer at scale \(j=6\) is the shale layer directly above the salt dome. Moreover, we find finer layers in the band-pass filtered signal such as sand layers for higher scales.

Another useful property is that the noise in the upper left corner can be filtered out with both methods. Here, the band-pass filtered signal of the partially taylorized source scaling function does not contain the noisy data for all depicted scales, whereas the band-pass filtered signal of the fully taylorized source scaling function is noiseless starting with scales \(j=4\).

5.2 Decorrelation using Cauchy–Navier wavelets

For the Cauchy–Navier wavelet decorrelation, we have to prepare the data set beforehand. The reason is, that the wavelets are based on the Cauchy–Navier equation, which models a homogeneous medium with constant Lamé parameters \(\lambda _0\) and \(\mu _0\), as well as a constant density \(\rho _0\). Hence, we choose a reference medium, in this case sandstone, with the parameters \(\rho _0=2066.38\,\frac{\text {kg}}{\text {m}^3}\), \(\lambda _0=1.9\cdot 10^9 \text { Pa}\) and \(\mu _0=6.3\cdot 10^9 \text { Pa}\) (Gopalakrishnan 2016) to decorrelate the migration result. Hence, we have \(\lambda =9.1948\times 10^5\frac{\text {m}^2}{\text {s}^2}\) and \(\mu =3.0488\times 10^6 \,\frac{\text {m}^2}{\text {s}^2}\). We use the frequency \(\omega =95.3\,\frac{{\text{ rad }}}{\text {s}}\) so that \(k_1\) equates to \(k_0=0.036\,\frac{{\text{ rad }}}{\text {m}}\) used in the Helmholtz case. Further, we need vectorial input data f. Taking \(f=Fe_i\), \(i=1,2,3\), where \(\{e_1,e_2,e_3\}\) denotes the canonical orthonormal system in \({\mathbb {R}}^3\), the decorrelation will be concentrated along the \(x_i\) direction in the \(i-th\) component of the resulting vector. Moreover the remaining two components of the solution vector contain the decorrelation in the diagonal direction of \(x_i\) and \(x_j\), \(j\ne i\). Hence, for a complete decorrelation, we choose

$$\begin{aligned} f=(1,1,1)^TF=(e_1 + e_2+e_3)F \end{aligned}$$

(cf. Fig. 10) and present the resulting decorrelation in the form of convolutions \(*\) by

$$\begin{aligned} \left( \varvec{\varPhi }_{\tau _j}*( e_1F) + \varvec{\varPhi }_{\tau _j}*( e_2F) + \varvec{\varPhi }_{\tau _j}*( e_3F)\right) =\varvec{\varPhi }_{\tau _j}*f. \end{aligned}$$
Fig. 10
figure 10

Cut of the input data for the decorrelation via the Cauchy–Navier source scaling functions and wavelets

Full size image

We are now prepared to take a look at the decorrelation depicted in Figs. 11, 12, 13 and 14 using Cauchy–Navier wavelets and concentrate on its real part. We only present selected scales of low-pass and band-pass data since a full decorrelation would be to extensive for the scope of this paper. The Cauchy–Navier wavelets and scaling functions are able to highlight the same structural information as the corresponding decorrelation via Helmholtz wavelets. More specifically, both, the partially and the fully taylorized Cauchy–Navier wavelets and scaling functions can filter out the noise in the upper left corner of the dataset as can be seen by taking a look at the low-pass filtered data in Fig. 11 for the partially and Fig. 13 for the fully taylorized case.

Both methods present noiseless band-pass filtered data starting at scale \(j=4\) (cf. Figs. 12 and 14) which also contain the structural information of the salt dome on the lower left side in the pictures on the diagonal. The shale layers discussed in the Helmholtz case can also be found in Figs. 12 and 14.

As pointed out numerous times throughout this paper, we developed the decorrelation based on the Cauchy–Navier equation in order to highlight directional characteristics of migration results.

It turns out, that the partially taylorized Cauchy–Navier source wavelets and scaling functions oscillate heavily inside its support especially for large \(\omega \). As such, they behave similarly to the partially taylorized Helmholtz source wavelets and scaling functions. In both the Helmholtz and the Cauchy–Navier case, this may result in ghost images in the decorrelation for small scales j.

Further, directional characteristics in the data can clearly be highlighted via the Cauchy–Navier wavelets and source scaling functions. For example, Figs. 11 and 13 show structures extending along the directions of \(x_1=x_2\) and \(x_1=-x_2\) in the off-diagonal entries in both the low-pass and band-pass filtered signal. This behavior continues along all depicted scales, but is more pronounced for lower scales due to the size of the support of the wavelets and scaling functions.

It is clear that the mixed directions involving the direction \(x_3\) are close to zero with an amplitude of \(10^{-12}\) and contain only numeric noise. This is due to the symmetry of \(\varvec{\varPhi }_{\tau _j}^l(\omega ;\cdot )\) and that f is constant in the \(x_3\) direction. The major improvement compared to the decorrelation using Helmholtz wavelets is, that we can further decorrelate the model so that we can precisely highlight structures stretching in the \(x_i\) direction, as well as diagonally in the data set. Therefore, an interpretation of a given migration result using Cauchy–Navier wavelets will be more precise then by applying Helmholtz wavelets.

Fig. 11
figure 11

Real part of the multiscale approximation of the data f (cf. Fig. 10) by convolution with the normalized and partially taylorized \((l=1)\) Cauchy–Navier source scaling function (top) and wavelet (bottom) for \(\omega =95.3\,\text {Hz}\), \(\tau _j=9200\cdot 2^{-j} \,\text {m}\), and \(j=2\)

Full size image
Fig. 12
figure 12

Real part of the multiscale approximation of the data f (cf. Fig. 10) by convolution with the normalized and partially taylorized \((l=1)\) Cauchy–Navier source scaling function (top) and wavelet (bottom) for \(\omega =95.3\,\text {Hz}\), \(\tau _j=9200\cdot 2^{-j}\,\text {m}\), and \(j=4\)

Full size image
Fig. 13
figure 13

Real part of the multiscale approximation of the data f (cf. Fig. 10) by convolution with the normalized and fully taylorized \((l=2)\) Cauchy–Navier source scaling function (top) and wavelet (bottom) for \(\omega =95.3\,\text {Hz}\), \(\tau _j=9200\cdot 2^{-j} \,\text {m}\), and \(j=2\)

Full size image
Fig. 14
figure 14

Real part of the multiscale approximation of the data f (cf. Fig. 10) by convolution with the normalized and fully taylorized \((l=2)\) Cauchy–Navier source scaling function (top) and wavelet (bottom) for \(\omega =95.3\,\text {Hz}\), \(\tau _j=9200\cdot 2^{-j}\,\text {m}\), and \(j=4\)

Full size image

6 Conclusion

We discussed the scalar wavelet decorrelation using mollifier Helmholtz wavelets and presented an approach for the directional interpretability by tensorial mollifier Cauchy–Navier wavelet and scaling functions. Decorrelation results were presented and compared for both types of wavelets. The mollifier Helmholtz wavelets lead to a good decorrelation of the data, which aids the interpretation effort in exploration. The mollifier Cauchy–Navier wavelets however, allow a more precise decorrelation since the data set is even further disassembled so that structures stretching in either of the three Cartesian directions as well as all diagonal directions can be highlighted. In fact, the decorrelation via the mollifier Cauchy–Navier source wavelet yields further information on the migration result by highlighting signatures spreading in the three Cartesian coordinate directions on the diagonal and the mixed directions on the off-diagonal of the decorrelation.