The effects of grain size and different multi-stage shearing techniques on shear strength along rock discontinuities

Abstract

The effects of grain size and different multi-stage shearing techniques on shear strength along discontinuities were analyzed in this study. Laboratory direct shear tests were carried out on plaster mortar with maximum grain sizes of 0.5 mm and 1.0 mm. All specimen surfaces were essentially similar, copied from the same natural, Hungarian coarse-grained sandstone joint with a low joint roughness coefficient (JRC = 8). Tests within two different normal stress ranges (σ_n = 0.25–0.5 and 0.5–1.5 MPa) were performed simultaneously. Specimens tested using the technique involving modified shearing with repositioning were sheared three times while being subjected to the same degree of normal stress (shearing sequence n = 1, 2, 3) and those with multi-stage technique without repositioning were subjected to shearing once at three different degrees of normal stress. The changing values of the peak friction angle calculated from the resulting peak shear strength-normal stress data pairs (τ_p − σ_n) were examined. Failure curves were estimated using linear regression, according to the Mohr–Coulomb failure criterion. The differences between the various peak friction angles obtained from experiments in which different multi-stage shearing techniques were used tend to increase in significance with the increasing number of shearing sequences. Peak friction angle values vary according to grain size of the material, though further investigations using more grain sizes are required to establish the extent of the effect on shear strength along discontinuities.

1 Introduction

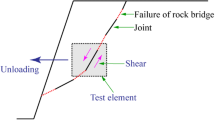
The failure of a rock slope or the rock environment of an engineering structure is usually not caused by the low quality of intact rock, but rather by fractures in the rock mass. Problems like the loss of rock slope or rock wall stability are generated by the exhaustion of shear strength along discontinuities. In addition, water flow or fluid flow in general may change along joints, cleavages or fractures (Köppel et al. 2019); or fluid flow may generate even new cracks (Mentes 2019). A number parameters of any rock joint can affect shear resistance to a great degree: water content, the filler material between the sides of a joint, exposure to weather (Barton 1973, 1976; Miščević and Vlastelica 2009), length of joint (Barton and Bandis 1982), surface roughness (Barton 1973; Haberfield and Seidel 1999; Grasselli and Egger 2003; Lee et al. 2014), the morphology of surface asperities (Patton 1966; Yang et al. 2016; Niktabar et al. 2017), the dilation angle (Barton 1973; Kumar and Verma 2016), the contact surface area (Zhao 1997; Grasselli and Egger 2003; Pirzada et al. 2020), inclination of the joint (Buocz et al. 2017), and the compressive strength of the joint (Barton 1973; Barton and Choubey 1977; Lee et al. 2014).

One of the most common ways to measure the shear strength of discontinuities, and analyze the influence of the parameters mentioned above, is the direct shear test, which can be performed in situ or in laboratory conditions. In situ tests can be carried out during the construction of structures such as a dam (Sanei et al. 2015), tunnel or waste repository, but in engineering practice shear strength is usually predicted in laboratory conditions, using shearing specimens with surfaces much smaller than the original discontinuities. Tests can be performed under constant normal load (CNL), which represents the failure mode of a slope, or constant normal stiffness (CNS), following the failure mode of a tunnel wall. Peak shear strength (τ_p), which is the highest recorded shear stress and after which shear load decreases, and residual shear strength (τ_rez), which is constant with increasing shear displacement, are obtained from a shear stress versus shear displacement diagram based on the results of the test (Fig. 1).

Fig. 1

Peak and residual shear strength on shear stress τ versus shear displacement Δs diagram

The final purpose of direct shear testing is to gain a failure curve based on shear strength-normal stress data pairs (τ − σ), which could then be used in the design of rock stability, as it shows the shear resistance of a rock joint in a given set of rock environmental stresses. To obtain the exact failure curve, as many τ − σ data pairs as possible need to be determined. A single sample is normally sheared once in one direction, but when it is not possible to obtain a sufficient number of specimens from the joint, it is possible to shear the same specimen repeatedly at different normal load stages with or without its replacement in its initial position between the stages (Muralha et al. 2015). With the help of this technique more points can be obtained on the τ − σ diagram.

Due to the inhomogeneity of a single joint, and because it is difficult to obtain a sufficient number of samples with similar qualities, the use of artificial rock specimens (plaster, cement mortar) with similar qualities to the original rock joints is common in research practice (Patton 1966; Grasselli and Egger 2003; Lee et al. 2014; Kumar and Verma 2016; Niktabar et al. 2017). In this way, tests are repeatable and it is possible to analyze the effect of a single property on shear strength by keeping the other effective parameters constant.

Measuring the uniaxial compressive strength of the intact rock (σ_c) from rock mass surrounding the joint is highly recommended, since the condition of the rock environment can be estimated from its value, especially in the case of unweathered or slightly weathered rock mass, and it is very easy to measure compared to shear strength.

One of the basic failure criteria which can describe an empirical relationship between the shear strength and the examined parameter is the Mohr–Coulomb (M–C) form:

$$ \tau = \sigma_{n} *\tan \varphi + c $$

(1)

where τ is shear strength, σ_n is normal stress, φ is friction angle and c is cohesion, respectively. Over the last few decades, however, it has been observed that a non-linear failure curve may well represent a better fit to experimental results than the linear M–C envelope. Many advanced non-linear failure criteria have been developed, modifying the M–C form, as the effect of the parameters mentioned above on shear strength along discontinuities have been examined (Table 1). Patton (1966) created a bilinear model (2) which, though still linear, was not as simple as the basic form while examining the effect of the number and angle of asperities on specimens made of plaster of Paris under different constant normal load conditions. Barton (1973) developed one of the formulae most commonly used in practice (3) by examining surface morphological parameters over a wide range of loading conditions and on several types of unweathered natural rock joints; later, together with Choubey (Barton and Choubey 1977), this was then done on weathered natural rock joints (4). It was Barton, who created the concept of the joint roughness coefficient (JRC), which is capable of describing the magnitude of surface roughness with a maximum value of 20. Zhao (1997) adopted and modified the formula derived by Barton and Choubey (4) in the course of establishing the effects of matching area on granite rock joints under a maximum of 2.0 MPa constant normal stress and thence derived an original Eq. (5) more suitable to use with empirical data. The criterion used by Grasselli and Egger (2003), in their study of surface morphology and matching area, resulted from shear tests at different values of constant normal stresses (σ_n = 0.2–5.0 MPa) on various natural soft and hard rock types with a wide range of compressive strength (σ_c = 5–184 MPa). In addition, artificial plaster material was also used (σ_c = 46 MPa). Their formula (7) is based on a highly comprehensive study, and represents a good fit to experimental data, but due to its complexity it is difficult to use in research practice. Yang et al. (2016) also performed several direct shear tests on granite and sandstone samples with high compressive strength (σ_c = 65–161 MPa) over a representative range of constant normal stresses (σ_n = 0.325–8.0 MPa). Their study focused on surface morphology, as seen in their non-linear Eq. (9). The failure criterion employed Lee et al. (2014) (8) is closer to Barton’s (3) and focuses on the joint wall compressive strength measured on cement mortar replicas with high compressive strength (σ_c = 54.19–83.91 MPa). Kumar and Verma (2016) formed a criterion (10) by analyzing the way in which anisotropic shear behavior is influenced by surface morphology; the tests were conducted on cement mortar joint replicas (σ_c = 40.83 MPa) at σ_n = 0.25–1.5 MPa.

Table 1 Failure criteria based on the Mohr–Coulomb failure criterion

Although many researchers have shown that a non-linear failure envelope is capable of reflecting real shearing behavior, in some cases linear forms do represent a valid approach. Haberfield and Seidel (1999) (Table 1) developed their failure criterion (6) on the basis of Patton’s model as they studied the complex sliding behavior on artificial siltstone samples of low compressive strength (σ_c = 3.5 MPa) with regular and irregular asperities. Buocz et al. (2017) also adopted a bilinear criterion for the study of the effect of discontinuity inclination on Opalinus Claystone samples. Pirzada et al. (2020) applied an M–C failure criterion based on the results of different natural rock types with different normal strengths (σ_c = 6.3–143.2 MPa) and artificial rock samples (σ_c = 27.0 MPa). Tests were performed at σ_n = 0.5–3.0 MPa. They found that, even in saturated conditions, the failure envelope can give a good fit to the experimental results by taking into account contact surface area of the joints.

In geotechnical engineering, the grain size of soil or other granular materials like sand has a great effect on shearing behavior. According to a study by Zelasko et al. (1975), in which three types of sand were investigated, increases in mean particle diameter can cause a decrease in the friction angle parameter. Some researchers, however, have observed the opposite phenomenon in the course of their investigations. Nakao and Fityus (2008), who studied coarse samples, have found that a higher friction angle resulted from samples with a higher grain diameter. The same tendency was observed by Wang et al. (2013), who investigated particle size distribution and the median value of grain diameter. The direct shear test results obtained by Islam et al. (2011) shows that both in cases of uniform particles (samples consisting of sand of uniform grain size) and in cases of graded particles (samples consisting of sand of different grain sizes) higher grain size causes a higher friction angle. Alias et al. (2014) reached the conclusion that peak and residual friction angles increase with increases in the grain size of granular materials. The shear resistance of a rock surface consists of the shear strength of the intact material and the frictional shear strength of the joint surface (Patton 1966). Although the mechanical shear behavior of soil or other granular materials in the geotechnical field more closely resembles the shear behavior of the intact rock, grain size may also have an effect on the shear resistance of a joint of compacted granular materials, such as sandstone.

Aim of this study is to investigate the effect of grain size on shear strength resulting from different multi-stage shearing techniques under constant normal stress. Direct shear tests were carried out under laboratory conditions under constant normal stress σ_n = 0.25–1.5 MPa to simulate the weight of a rock slope above a joint at shallow depth beneath the surface. In order to make the tests repeatable and eliminate the effects of different surface morphologies, specimens were made of plaster mortar with surfaces copied from the same natural sandstone joint with irregular asperities and low roughness (JRC = 8). Sand aggregates with a maximum grain diameter of 0.5 and 1.0 mm were chosen, as both are small enough to follow the original surface asperities adequately. As mentioned above, multi-stage direct shearing is allowable in the case of a small number of samples, but shearing with and without repositioning can result a somewhat different values for shear strength. In this study, multi-stage shearing tests without repositioning and modified multi-stage shearing tests with repositioning were carried out simultaneously. Since linear regression lines displayed a good fit to resulting peak shear strength-normal stress data pairs, the linear Mohr–Coulomb failure criterion was used in this study. The object of the examination was the changing of the peak friction angle derived from M–C failure envelopes based on laboratory tests with different techniques at different constant normal stresses on specimens with different maximum grain sizes. The uniaxial compressive strengths of plaster types were measured simultaneously since this is one of the most important mechanical properties of the intact rock mass.

2 Materials and methods

2.1 Materials and sample preparation

In the interests of making laboratory tests repeatable, both sides of a natural Hungarian (Hárshegyi) sandstone joint were copied to surfaces of shearing specimens made of plaster mortar. There was no filler material between the two sides of the original rock joint, and the value of the joint roughness coefficient (JRC) of the section as measured by a Barton comb was 8. Sand aggregates with a maximum diameter of 0.5 mm and 1.0 mm was used in the preparation of the specimens. One portion of plaster mortar mixture consisted of 40% sand aggregate, 40% high strength dental plaster powder and 20% water, and from this one shearing specimen with a rectangular surface size of 6540 mm² and three cubes with size of 30 × 30 × 30 mm³ for uniaxial compressive tests were made. Before starting the shearing process, the upper and lower parts of shearing specimen were embedded separately in concrete in order to keep them fixed in the shear box during the test. The samples were kept and tested in air dry laboratory conditions after 28 days.

2.2 Methods

2.2.1 Direct shear test

In this study, in order to imitate the failure mode of a rock slope, direct shear tests under constant normal load (CNL) were performed using a manually operated CONTROLS D0548 direct shear machine in laboratory conditions. During the shearing process, the separate upper and lower parts of the specimen are put into the shearing equipment and pressed together at a constant value of normal load, and this is applied in the shear plane. The lower part of the shear box with the lower part of the specimen inside is fixed in all directions while the upper part of the box with the upper part of the specimen inside can move continuously parallel to the shear plane (Fig. 2).

Fig. 2

Model of direct shearing

Shear load, applied normal load, shear displacement and time are measured continuously (10 data/s) while the test is being conducted. Graphs of shear load and applied normal load via shear displacement are plotted. On the basis of suggestions made by the International Society of Rock Mechanics and Rock Engineering (ISRM), the test should be finished after the residual shear load is reached (curve becomes horizontal on shear load vs shear displacement diagram) or when shear displacement is about 10% of the specimen length (Muralha et al. 2015).

Usually a specimen is sheared only once under an applied normal load, but in cases when the number of specimens is inadequate, two types of multi-stage shearing procedures are used. In the first type of test, the same specimen is sheared repeatedly under increasingly higher normal loads, with the repositioning the specimen (joint) to its initial position before each shearing stage. In the other type of test, the specimen is sheared under increasingly higher normal loads, but it is not returned to its initial position between the shearing stages. Three, but preferably five stages are recommended in all types of test, and one stage is considered finished after residual shear load is reached. According to the ISRM suggestions low normal stresses should be used in the case of multi-stage shearing to minimize damage to surface asperities.

The purpose of this test is to obtain a value for peak shear strength (τ_p) and residual shear strength (τ_r) as a function of applied normal stress (σ_n) parameters which are calculated using peak shear load (T_p), residual shear load (T_r) and applied normal load (N), respectively, divided by specimen surface area (A). On the basis of the Mohr–Coulomb failure criterion, the arctangent of the ratio of peak shear strength and the corresponding normal stress gives the peak friction angle, which is calculated from the envelope of linear regression; in this study, however, the term ‘peak friction angle’ (ϕ_p) is used to designate the inclination of a single τ_p − σ_n point, as seen in Fig. 3a, while for the peak friction angle of the failure curve, ϕ_pf is used (Fig. 3b).

Fig. 3

Peak friction angle ϕ_p on shear stress τ versus normal stress σ_n diagrams: ϕ_p as the arctangent of the ratio of peak shear strength τ_p and applied normal stress σ_n (a); ϕ_pf as the slope of the curve of the Mohr–Coulomb failure criterion (b)

In this study, changes in the peak friction angle based on shear test results of specimens with two different maximum grain sizes was examined. In cases where no peak shear strength appeared on the shear stress-normal stress graph, the maximum value of shear stress was in the place of peak shear strength (Fig. 4a, b). The shear displacement rate was about 0.5 mm/min.

Fig. 4

Peak shear strength on shear stress τ versus shear displacement Δs diagrams: as ‘τ_peak’, after which shear stress decreases immediately (a); as ‘τ_max’, after which shear stress does not decrease immediately (b)

Multi-stage direct shear tests were carried out using two different techniques: (i) a multi-stage test without the repositioning of the samples between stages, (ii) a modified multi-stage test with the repositioning of the samples.

• (i) In the first case, a single sample was sheared under low normal stresses (3 different stages: 0.25, 0.375 and 0.5 MPa), and another sample under higher applied normal stresses (3 different stages: 0.5, 1.0 and 1.5 MPa). Shear displacement was maximized at 5 mm in every normal stress stage, so the test was performed until 15 mm total displacement (18% of the specimen length) had been achieved. A total of four specimens with two different maximum grain sizes was examined (Table 2). Peak friction angles based on failure curves (ϕ_pf) from the 3 peak shear strength-normal stress data pairs resulting from tests were determined and compared in the cases of the two different maximum grain sizes.

  Table 2 Specimen number, shearing sequence and diagram legend of specimens with different maximum grain sizes D_max sheared using the two shearing techniques in different normal stress ranges σ_n

• (ii) In the second case, modified multi-stage tests with samples being repositioned between shearing stages, were performed. Each sample was sheared three times under the same applied normal stress, which means a shearing sequence of n = 1, 2, 3. (In this case, ‘modified’ refers to the repeating of multi-stage shearing with repositioning, although shearing tests were performed three times at one stage per sample.) The aim of the modification is to analyze, to what extent the friction angle changes over the course of repeated shearing tests, and not necessarily under increasingly higher normal stresses, but even at the same level of normal stress. Tests were carried out at five different normal stresses (0.25; 0.375; 0.5; 1.0; 1.5 MPa) in accordance with the first type of shearing test mentioned above, and on 12 samples with two different maximum grain sizes (Table 2).

The object of the investigation was changes in the peak friction angle (ϕ_p) as the number of shearing sequences increases as a function of different normal loads and different maximum grain sizes. Furthermore, as was also the case in the first type of shearing, failure curves based on 3 peak shear strength-normal stress data pairs resulting from tests in low ranges of applied normal stress (0.25; 0.375; 0.5 MPa), and in higher ranges of applied normal stress (0.5; 1.0; 1.5 MPa) were determined in every shearing sequence. Changes in the peak friction angle on these curves (ϕ_pf) by increasing the number of shearing sequences as a function of different normal stress ranges and different maximum grain sizes was also of interest. Finally, peak friction angles (ϕ_pf) belonging to these curves and to curves based on data pairs from tests without repositioning were compared, taking into consideration the different normal stress ranges and different maximum grain sizes.

2.2.2 Uniaxial compressive test

Parallel to this shearing, uniaxial compressive tests were performed on three plaster cubes pertaining to each shearing specimen. In the course of the test, a cube is placed between two parallel platens, of which the upper is fixed, while the lower elevates the specimen right up to the point of failure due to the compression. The speed of compression and vertical (axial) load are measured continuously. Uniaxial compressive strength (UCS) is equal to the ratio of the collapsing compressive force (F_c) and compressed area (A). In this study, the speed of compression was 0.9 kN/s. The average UCS values of the three cubes pertaining to each shearing specimen are in Table 3.

Table 3 Uniaxial compressive strength (UCS) of specimens with different maximum grain sizes D_max sheared using the two shearing techniques in different normal stress ranges σ_n

3 Results and discussion

• (1) Peak shear strength (τ_p)-applied normal stress (σ_n) data pairs based on multi-stage shear tests without repositioning, peak friction angle (ϕ_pf) and apparent cohesion (c) as the parameters of Mohr–Coulomb failure curves calculated from these data pairs are represented in Table 4, presenting in terms of normal stress range and maximum grain size (D_max). The failure curves calculated from these τ_p − σ_n data pairs using linear regression, the equations of the linear regression as a failure criterion, the regression coefficient r² values and calculated peak friction angle in the normal stress range of 0.25–0.375–0.5 MPa are shown in Fig. 5a, and the results in the normal stress range of 0.5–1.0–1.5 MPa in Fig. 5b.

  The minimum value of r² is 0.875, except in one of the four groups (D_max = 0.5 mm; σ_n = 0.5–1.5 MPa), and * indicates significance levels of p ≤ 0.1. As in the experiments of Nakao and Fityus (2008), Islam et al. (2011) and Alias et al. (2014) in lower (Fig. 5a) and also higher ranges of normal stress (Fig. 5b), peak friction angle values associated with D_max = 1.0 are higher than those associated with D_max = 0.5 mm (at the values of 4.6% and 20.3%, respectively). As in the experiments of Buocz et al. (2017), the M–C linear failure criterion displays a good fit to these experimental data pairs, the peak friction angle values based on tests with D_max = 0.5 and also those based on tests with D_max = 1.0 mm (Table 4) are, however, lower in the higher normal stress range than corresponding values in the lower normal stress range (24.9% and 8.7%, respectively).

  Table 4 Mohr–Coulomb failure criterion parameters peak friction angle ϕ_pf and apparent cohesion c based on peak shear strength τ_p—applied normal stress σ_n data pairs resulting from direct shearing without repositioning. Shear tests were carried out in different normal stress ranges on specimens with different maximum grain sizes D_max

  Fig. 5

  

  Curves of the Mohr–Coulomb failure criterion on peak shear strength τ_p versus normal stress σ_n diagrams resulting from direct shearing without repositioning (Pm_ms) in a lower normal stress range σ_n (a) and in a higher normal stress range σ_n (b) with the formulae of failure criterion, values of correlation coefficient r² and peak friction angle ϕ_pf beneath the diagrams. In both normal stress ranges shear tests were carried out on plaster mortar specimens with different maximum grain sizes: D_max = 0.5 mm [0.5] and 1.0 mm [1.0]

• (2) Peak shear strength (τ_p)-applied normal stress (σ_n) data pairs yielded by modified multi-stage shear tests with repositioning and the corresponding peak friction angle (ϕ_p) in each three shearing sequence; peak friction angle values in each shearing sequence (n = 1, 2, 3) compared to the friction angle of the first test (ϕ_pn/ϕ_p1); and the maximal value of the friction angle differences ((Δϕ_p)_max) calculated from ϕ_pn minus ϕ_p1 are presented in Table 5. When the friction angle resulting from repeated shearing (ϕ_pn) is higher than friction angle of the first shearing (Δϕ_p)_max, the parameter is positive; otherwise it is negative. All results are grouped according to the five different applied normal stresses (σ_n = 0.25–1.5 MPa) and two different maximum grain sizes (D_max = 0.5 mm; 1.0 mm).

  Table 5 Peak shear strength τ_p—applied normal stress σ_n data pairs resulting from modified shearing with repositioning (shearing sequence n = 1, 2, 3); peak friction angle ϕ_p as the arctangent of ratio of the data pairs; ratio of repeated shearing tests ϕ_pn and the first tests ϕ_p1, and the maximum values of this ratio (Δϕ_p)_max at different normal stresses σ_n. Tests were carried out on specimens with different maximum grain sizes D_max

  The values of the ϕ_pn: ϕ_p1 ratio in the first tests never fall between the corresponding values of the second and the third tests, so results based on repeated shearing may be either higher or lower than the first results. It has to be noted, however, that only in three of the 12 cases, did the ratio increase continuously (D_max = 0.5 mm, σ_n = 0.5 and 1.0 MPa; D_max = 1.0 mm, σ_n = 1.5 MPa) and only in one case does it decrease continuously (D_max = 1.0 mm, σ_n = 1.0 MPa) with the increasing number of shearing sequences. The values of (Δϕ_p)_max are positive in half of the six cases (σ_n = 0.25, 0.5, 1.5 MPa), with D_max = 0.5 mm, as are those with a value for D_max = 1.0 mm in four from the six cases (σ_n = 0.25, 0.5, 0.5(2), 1.5 MPa). Furthermore, the maximum value of any decrease is 9–13% (D_max = 0.5 mm) and 7–12% (D_max = 1.0 mm), while the maximum increases are 20–46% and 8–83%, respectively. Though it has to be noted that if a positive difference of 83% is regarded as an exception, the maximum increase is only in the range of 8–19%.

• (3) Peak friction angle (ϕ_pf) and apparent cohesion (c) as the parameters of Mohr–Coulomb failure curves based on the results of modified multi-stage shear tests with repositioning are shown in Table 6. Curves of the shearing sequences are calculated from peak shear strength (τ_p)—applied normal stress (σ_n) data pairs in the same sequences. Furthermore, the table shows the peak friction angle values in each shearing sequence (n = 1,2,3) compared to the friction angle of the first sequence (ϕ_p1), and the value of friction angle differences (Δϕ_pf) calculated from ϕ_pfn minus ϕ_p1. When the friction angle resulting from repeated shearing tests (ϕ_pfn) is higher than the friction angle obtained in the first shearing tests, the parameter Δϕ_pf is positive; otherwise it is negative. All results are grouped according to the two different applied normal ranges (σ_n = 0.25–0.5 MPa; 0.5–1.5 MPa) and two different maximum grain sizes (D_max = 0.5 mm; 1.0 mm).

  Table 6 Mohr–Coulomb linear failure criterion parameters peak friction angle ϕ_pf and apparent cohesion c, based on peak shear strength-applied normal stress data pairs resulting from modified shear tests with repositioning (shearing sequence n = 1, 2, 3); ratio of peak friction angle of repeated shearing tests ϕ_pfn to that of the first test ϕ_pf1; and the change in this ratio Δϕ_pf. Tests were carried out in different applied normal stress ranges, on specimens with different maximum grain sizes D_max

  Figure 6a presents in graphic form failure curves from Table 6 in each shearing sequence based at tests performed at σ_n = 0.25–0.5 MPa with D_max = 0.5 mm, together with the failure curves from tests without repositioning under the same range of normal stress, and with the same maximum grain size. The equations of linear regression, the regression coefficient r² values, and calculated peak friction angles are also shown in the figure. The same parameters of tests carried out at σ_n = 0.25–0.5 MPa with D_max = 0.5 mm; at σ_n = 0.25–0.5 MPa with D_max = 1.0 mm; at σ_n = 0.5–1.5 MPa with D_max = 0.5 mm and at σ_n = 0.5–1.5 MPa with D_max = 1.0 mm, are shown in Fig. 6b–d, respectively.

  Fig. 6

  

  Curves of the Mohr–Coulomb failure criterion on peak shear stress τ_p versus normal stress σ_n diagrams resulting from direct shearing without repositioning (Pm_ms) and from modified direct shearing with repositioning (Pm_ms_1,2,3) in a lower normal stress range σ_n (a, b) and higher normal stress range σ_n (c, d). Formulae of the failure criterion, the values of correlation coefficient r² and peak friction angle ϕ_pf are beneath the diagrams. In both normal stress ranges shear tests were carried out on plaster mortar specimens with different maximum grain sizes: D_max = 0.5 mm [0.5] (a, c) and 1.0 mm [1.0] (b, d)

  Peak friction angle (ϕ_pf) and apparent cohesion (c) as the parameters of Mohr–Coulomb failure curves based on the results of modified multi-stage shear tests with repositioning are presented in Table 7. The curves of the shearing sequences are calculated from peak shear strength (τ_p)-applied normal stress (σ_n) data pairs in the same sequences. Parameters yielded by multi-stage shearing tests without repositioning are also to be found in Table 7. All results are grouped according to the two different applied normal stress ranges (σ_n = 0.25–0.5 MPa; 0.5–1.5 MPa) and two different maximum grain sizes (D_max = 0.5 mm: 1.0 mm). Furthermore, the table also shows peak friction angle values in each shearing sequence (n = 1,2,3) compared to the friction angle resulting from tests without repositioning (ϕ_pfI), and the value of friction angle differences (Δϕ_pf) calculated from ϕ_pfn minus ϕ_pfI.

  Table 7 Mohr-Coulomb linear failure criterion parameters peak friction angle ϕ_pf and apparent cohesion c based on the results of shear tests without repositioning and modified shear tests with repositioning (shearing sequences n = 1, 2, 3); the ratio of peak friction angle of repeated shearings of modified shear tests ϕ_pfn and of the tests without repositioning ϕ_pfI; and changing of this ratio Δϕ_pf. Tests were carried out in different applied normal stress ranges, on specimens with different maximum grain sizes D_max

  Focusing on the differences between the results of tests with repositioning, the values of ϕ_pf increase with an increasing number of shearing sequences, with the exception of one of the four groups (D_max = 1.0 mm: σ_n = 0.5–1.5 MPa) (Table 6). The values of the second sequences are 22–28% higher than those of the first tests while in the exceptional group, ϕ_pf is 11% lower. The values of third sequences are the highest in all groups, with differences of 33–43%, while in the exceptional group, this is 7%. The values of apparent cohesion decrease as the corresponding friction angles increase. The value of r² is at least 0.835, except in one case (D_max = 0.5 mm: σ_n = 0.25–0.5 MPa, 1. shearing sequence) as can be seen in Fig. 6a–d, in which * and ** indicate significance levels of p ≤ 0.1 and 0.05, respectively. The differences between corresponding values of friction angle and cohesion are not significant in the low normal stress range by increasing number of shearing sequences, for either of the grain sizes (Table 6). In the higher normal stress range, however, trends in the change of friction angle and cohesion with an increasing number of shearing sequences are not similar in the cases of different grain sizes. In the case of D_max = 0.5 mm, the values of the friction angle in a lower normal stress range are similar to the corresponding values in the higher stress range, though the differences between the corresponding cohesion values are significant within the different ranges. In case of D_max = 1.0 mm, a similar trend cannot be observed. In contrast to the experiments of Nakao and Fityus (2008), Islam et al. (2011) and Alias et al. (2014), a higher maximum grain size of aggregate did not give rise to higher peak friction angle values, although no opposite trend in results can be observed.

  Comparing the results of tests conducted using the two shearing techniques, in Table 7, the value of ϕ_pf of the first sequence of tests with repositioning and those without repositioning are quite close to each other: Δϕ_pf has a maximum of 12%, and a minimum of -12%. The values of Δϕ_pf in the case of comparing second shearing tests and tests without repositioning are also quite low (-8 to 12%), with the exception of one of the four groups (D_max = 0.5 mm, σ_n = 0.5–1.5 MPa), in which the difference is higher, 44%. The results of the third sequences show more significant differences (18–52%) from the results of the other shearing technique, with the exception of one group (D_max = 1.0 mm: σ_n = 0.5–1.5 MPa), in which that value remains 12%. It has to be noted that, except in three cases, peak shear strength (τ_p)-applied normal stress (σ_n) data pairs based on modified shearing tests with repositioning are above the regression line of data pairs from tests without repositioning. Exceptions are the 3rd data pair of the first sequence in group of D_max = 0.5 mm: σ_n = 0.25–0.5 MPa (Fig. 6a), the 1st and the 3rd data pairs of the first sequence in group of D_max = 1.0 mm: σ_n = 0.5–1.5 MPa (Fig. 6d).

4 Conclusion

In this study, plaster mortar samples with two different maximum grain sizes of sand aggregate (D_max = 0.5; 1.0 mm) were examined by performing laboratory direct shear tests along discontinuities using two different multi-stage techniques (without repositioning and modified with repositioning); these were conducted in two different ranges of constant normal stresses (σ_n = 0.25–0.5 MPa and 0.5–1.5 MPa). The surfaces of the samples were essentially similar, imitating a natural sandstone joint with low surface roughness (JRC = 8). Furthermore, the various values of uniaxial compressive strength were quite similar: σ_c = 16.04–26.84 MPa (D_max = 0.5 mm) and σ_c = 18.84–24.15 MPa (D_max = 1.0 mm). Mohr–Coulomb (M–C) failure curves were calculated from the resulting peak shear strength-applied normal stress data pairs (τ_p − σ_c) using linear regression. Changes in the peak friction angle as a ratio of peak shear strength–applied normal stress (ϕ_p), and as an M–C parameter (ϕ_pf) were studied.

• (1) Although the Mohr–Coulomb linear failure criterion displays a good fit to experimental data pairs based on shear tests without repositioning both in the lower normal stress range (σ_n = 0.25–0.5 MPa) and in a higher normal stress range (σ_n = 0.5–1.5 MPa) for both grain sizes, the differences between the M–C parameter ϕ_pf in the different normal stress ranges are significant. Further studies are therefore needed in higher normal stress range σ_n = 1.5–2.5 MPa in order to analyse the possible changing trend of the ϕ_pf values. Moreover, since these values are quite similar for both grain sizes in the lower normal stress range, while in the higher normal stress range the ϕ_pf associated with higher grain size had a higher value, further investigations on specimens with sand aggregate with maximum diameters of 2.0 mm and 4.0 mm are required in order to explore the differences between any possible changing trends in the value of ϕ_pf.

• (2) Since the first sequence of the modified multi-stage shearing technique is equivalent to the employment of the single shearing technique, quite low differences between ϕ_pf of the first sequences of modified multi-stage shearing with repositioning and those of the multi-stage shearing without repositioning fell within the range of expectations both in different normal stress ranges and for different grain sizes. A shearing distance of 5 mm under different normal stresses during multi-stage tests without repositioning was found to be suitable for specimens 8.5 cm in length.

However, with an increasing number of shearing sequences, differences between the values of ϕ_pf on the basis of different techniques become higher, due to the fact that the value of ϕ_pf resulting from shear tests with repositioning changes significantly with the increasing number of shearing sequences and with a decreasing value of c. Although, as was the case of the results of shearing tests without repositioning, linear regression displays a good fit to τ_p − σ_c data pairs based on tests with repositioning, nonetheless, differences between M–C parameters resulting from the two different techniques do not show a clear increasing or decreasing trend, even when grain sizes or normal stress ranges are changed. Finally, a significant difference between the results of the third shearing and the results of shearing without repositioning is always found.

In this study, laboratory direct shear tests were performed in a range of σ_c/σ_n = 11 to 107 on plaster mortar replicas with relatively low joint roughness coefficient JRC = 8. Under these conditions, different peak friction angles were obtained from repeated direct shear tests, and this remained true even in the same normal stress ranges. Further investigations with different conditions (e.g. materials with higher compressive strength σ_c) are required to analyse the question of under which conditions the repeated shear tests might yield the same result, and even the ISRM has suggested multi-stage direct shear tests with repositioning could be employed.