Coupling of multiscale and multi-continuum approaches

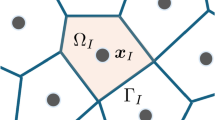
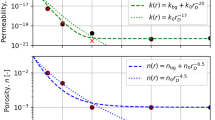
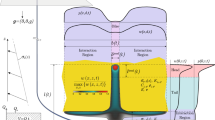
Abstract

Simulating complex processes in fractured media requires some type of model reduction. Well-known approaches include multi-continuum techniques, which have been commonly used in approximating subgrid effects for flow and transport in fractured media. Our goal in this paper is to (1) show a relation between multi-continuum approaches and Generalized Multiscale Finite Element Method (GMsFEM) and (2) to discuss coupling these approaches for solving problems in complex multiscale fractured media. The GMsFEM, a systematic approach, constructs multiscale basis functions via local spectral decomposition in pre-computed snapshot spaces. We show that GMsFEM can automatically identify separate fracture networks via local spectral problems. We discuss the relation between these basis functions and continuums in multi-continuum methods. The GMsFEM can automatically detect each continuum and represent the interaction between the continuum and its surrounding (matrix). For problems with simplified fracture networks, we propose a simplified basis construction with the GMsFEM. This simplified approach is effective when the fracture networks are known and have simplified geometries. We show that this approach can achieve a similar result compared to the results using the GMsFEM with spectral basis functions. Further, we discuss the coupling between the GMsFEM and multi-continuum approaches. In this case, many fractures are resolved while for unresolved fractures, we use a multi-continuum approach with local Representative Volume Element information. As a result, the method deals with a system of equations on a coarse grid, where each equation represents one of the continua on the fine grid. We present various basis construction mechanisms and numerical results. The GMsFEM framework, in addition, can provide adaptive and online basis functions to improve the accuracy of coarse-grid simulations. These are discussed in the paper. In addition, we present an example of the application of our approach to shale gas transport in fractured media.

Appendix: Convergence analysis

In this appendix, we present the convergence analysis of our schemes. We will consider both the un-coupled multiscale basis functions and the coupled multiscale basis functions as well as an abstract formulation to be defined in the following. Note that the abstract formulation can be applied to the practical cases presented in this paper. We consider the N-continuum problem: find $u=(u_{1},u_{2},\ldots u_{N})$ such that $u_i(t,\cdot ) \in H^1(\Omega )$, $i=1,\ldots , N$, and

$$\begin{aligned} \sum _{i}c_i \left( \frac{\partial u_i}{\partial t},v_i \right)&=-\sum _{i}a_{i}(u_{i},v_{i})+q(u,v)+(f,v), \quad t\in (0,T) \end{aligned}$$

(12)

for all test functions $v=(v_1,v_2,\ldots , v_N)$ with $v_i(t,\cdot )\in H^1_0(\Omega )$, where

$$\begin{aligned} c_i(u,v)= & {} \int _{D_m}c_i \,u \, v \, {dx} + \sum _j \int _{D_{f,j}}c_{j,i} \, u \, v \, {dx}, \\ q(u,v)= & {} \sum _{j}\sum _{i\ne j}Q_{i}\int _{D} (u_{i}-u_{j})v_{j} \, {dx}, \\ a_{i}(u,v)= & {} \int _{D_m}\kappa _{i}\nabla u\cdot \nabla v \, {dx}+\sum _j \int _{D_{f,j}}\kappa _{j,i}\nabla _{f}u\cdot \nabla _{f}v \, {dx}. \end{aligned}$$

Note that all the summations are summing over all continua, that is, they are summing over $i,j=1,2,\ldots , N$. Next we define two global bilinear operators $c(\cdot ,\cdot )$ and $a(\cdot ,\cdot )$ by

$$\begin{aligned} c(u,v)=\sum _i c_i(u_i,v_i), \quad a(u,v) = \sum _i a_i(u_i,v_i). \end{aligned}$$

Clearly, we have $q(u,v)=q(v,u)$ and $q(u,u)\le 0$ for all $u(t,\cdot ),v(t,\cdot ) \in [H^{1}(\Omega )]^{N}$. Equation (12) defines our multi-continuum problem.

We next define the operator $a_{i}^{(j)}(\cdot ,\cdot )$ by

$$\begin{aligned} a_{i}^{(j)}(u,v)=\left( \int _{\omega _{j}}\kappa _{i}\nabla u\cdot \nabla v \, {dx}+\sum _l \int _{D_{f,l}\cap \omega _j}\kappa _{l,i}\nabla _{f}u\cdot \nabla _{f}v \, {dx} \right) \end{aligned}$$

for all $u(t,\cdot ),v(t,\cdot ) \in H_{0}^{1}(\omega _{j})$. This operator corresponds to the contribution of $a_i(u,v)$ in the coarse region $\omega _j$. We also define the corresponding global operator

$$\begin{aligned} a^{(j)}(u,v)=\sum _{i}a_{i}^{(j)}(u_{i},v_{i}){.} \end{aligned}$$

Finally, we define two bilinear operators $a_{Q}^{(j)}(\cdot ,\cdot )$ and $a_{Q}(\cdot ,\cdot )$ by

$$\begin{aligned} a_{Q}^{(j)}(u,v)=a^{(j)}(u,v)-q(u,v), \quad a_{Q}(u,v)=a(u,v)-q(u,v) \end{aligned}$$

for all $u(t,\cdot ),v(t,\cdot ) \in H_{0}^{1}(\omega _{j})$.

In the following, we will present the definitions of the un-coupled multiscale basis functions and the coupled multiscale basis functions. For each case, we follow the general procedure to first construct a local snapshot space for each coarse region $\omega _j$, and then construct an offline space (consisting of multiscale basis functions) using a suitable spectral problem defined on the snapshot space. Note that the snapshot functions and the basis functions are independent of time.

1.1 Coupled GMsFEM (snapshot space)

For each coarse region $\omega _{j}$, we obtain the k-th snapshot function by solving the following local problem: find $\psi _{k}^{(j),\text {snap}}\in [V_{h}(\omega _{j})]^{N}$ such that

$$\begin{aligned} a^{(j)}\left( \psi _{k}^{(j),\text {snap}},v\right) -q\left( \psi _{k}^{(j),\text {snap}},v\right)&=0,\quad \forall v\in \left[ V_{h,0}(\omega _{j})\right] ^{N}, \\ \text {with the boundary condition}\quad \psi _{k}^{(j),\text {snap}}&=\delta _{k}, \quad \text {on } \partial \omega _j, \end{aligned}$$

where $V_{h}(\omega _{j})$ is a fine-scale space and $V_{h,0}(\omega _{j})$ is the subspace of $V_{h}(\omega _{j})$ containing functions with zero trace on the boundary of $\omega _j$. In the above definition, the discrete delta function $\delta _{k}$ is defined as $\delta _{k} = (\delta _{k,1}, \delta _{k,2},\ldots , \delta _{k,N})$ and each $\delta _{k,i}$ is the discrete delta function such that $\delta _{k,i} = 1$ at the fine-grid node $x_k\in \partial \omega _j$ and $\delta _{k,i} = 0$ at all other fine-grid nodes on $\partial \omega _j$. Using the above snapshot functions, we can define the local snapshot space by

$$\begin{aligned} V_{\text {snap}}(\omega _{j})=\text {span}\left\{ \psi _{k}^{(j),\text {snap}} \; : \; \forall k\right\} . \end{aligned}$$

1.2 Coupled GMsFEM (offline space)

We will construct the offline space in this section. The offline space is spanned by all multiscale basis functions. To find the multiscale basis functions, we use a local spectral problem defined in the snapshot space. More precisely, for each coarse region $\omega _{j}$, we consider the following local eigenvalue problem: find the k-th eigenfunction $\phi _{k}^{(j)}\in V_{\text {snap}}(\omega _{j})$ and the k-th eigenvalue $\lambda ^{(j)}_k$ such that

$$\begin{aligned} a_Q^{(j)}\left( \phi _{k}^{(j)},v\right)&=\lambda _{i}^{(j)} \, s^{(j)}\left( \phi _{k}^{(j)},v\right) , \quad \;\forall v\in V_{\text {snap}}(\omega _{j}), \end{aligned}$$

where the bilinear form $s^{(j)}$ is defined as

$$\begin{aligned} s^{(j)}(u,v)=\sum _{i}\left( \int _{\omega _{j}}\kappa _{i}|\nabla \chi _{j}|^{2}u \, v \, {dx}+\sum _l \int _{D_{f,l}}\kappa _{l,i}|\nabla _{f}\chi _{j}|^{2} u \, v \, {dx} \right) \end{aligned}$$

and the eigenvalues are arranged in ascending order. Using the eigenfunction $\phi _{k}^{(j)}$, we can define the k-th multiscale basis function by ${\hat{\phi }}_{k}^{(j)}=\chi _{j} \phi _{k}^{(j)}$, where $\{ \chi _j\}$ is a set of partition of unity functions for the coarse-grid partition of the domain $\Omega$. Finally, the local offline space is defined by $V_{H}(\omega _{j})=\text {span}\{{\hat{\phi }}_{i}^{(j)}|\; i\le L_j\}$, which is formed by using the first $L_j$ eigenfunctions. In addition, the global offline space, $V_{H}$, is defined by $V_{H}=\sum _j V_{H}(\omega _{j})$.

1.3 Un-coupled GMsFEM (snapshot space)

Now, we will present the construction of the basis for the un-coupled case. We first consider the construction of the snapshot space. For each coarse region $\omega _{j}$ and for each continuum i, we obtain the k-th snapshot function by solving the problem: find $\psi _{k,i}^{(j),\text {snap}}\in V_{h}(\omega _{j})$ such that

$$\begin{aligned} a_{i}^{(j)}(\psi _{k,i}^{(j),\text {snap}},v)&=0, \quad \;\forall v\in V_{h,0}(\omega _{j}),\\ \text {with the boundary condition}\quad \psi _{k,i}^{(j),\text {snap}}&=\delta _{k,i}, \quad \text {on } \partial \omega _j. \end{aligned}$$

Then, the local snapshot space for the coarse region $\omega _j$ and for the i-th continuum is defined by

$$\begin{aligned} V_{\text {snap}}^{(i)}(\omega _{j})=\text {span}\{\psi _{k,i}^{(j),\text {snap}} \; : \; \forall k \}, \quad i=1,2,\ldots , N. \end{aligned}$$

1.4 Un-Coupled GMsFEM (offline space)

We will construct multiscale basis functions for each coarse region $\omega _j$ and for each continuum i. To do so, we consider the following local eigenvalue problem: find the k-th eigenfunction $\phi _{k,i}^{(j)}\in V_{\text {snap}}^{(i)}(\omega _{j})$ and the k-th eigenvalue $\lambda _{k,i}^{(j)}$ such that

$$\begin{aligned} a_{i}^{(j)}(\phi _{k,i}^{(j)},v)&=\lambda _{k,i}^{(j)}\, s_{i}^{(j)}(\phi _{k,i}^{(j)},v), \quad \;\forall v\in V_{\text {snap}}^{(i)}(\omega _{j}), \end{aligned}$$

where

$$\begin{aligned} s_{i}^{(j)}(u,v)=\int _{\omega _{j}}\kappa _{i}|\nabla \chi _{j}|^{2}u \, v \, {dx} +\sum _l \int _{D_{f,l}}\kappa _{l,i}|\nabla _{f}\chi _{j}|^{2}u \, v \, {dx}. \end{aligned}$$

We assume that the eigenvalues are arranged in ascending order. Using the above eigenfunctions, we can define the k-th multiscale basis function by ${\hat{\phi }}_{k,i}^{(j)}=\chi _{j}\phi _{k,i}^{(j)}$. To define the offline space for the i-th continuum and for the coarse region $\omega _j$, we take the first $L_j$ eigenfunctions and define $V_{H}^{(i)}(\omega _{j})=\text {span}\{{\hat{\phi }}_{k,i}^{(j)}|\; k\le L_j\}$. Note that $L_j$ can depend on i, but we omit this index to simplify the notation. Then the global offline space for the i-th continuum is given by $V_{H}^{(i)}=\sum _j V_{H}^{(i)}(\omega _{j})$. Finally, the offline space, $V_{H}$, is defined by $V_{H}=V_{H}^{1}\times V_{H}^{2}\times \cdots \times V_{H}^{N}$.

1.5 Analysis

Now we are ready to present the analysis. We will first prove the following best approximation estimates (see Lemmas 1 and 2). We will compare the difference between the reference solution u, defined by (12), and the multiscale solution $u_{ms}\in V_H$ defined by

$$\begin{aligned} \sum _{i}c_i \left( \frac{\partial u_{ms,i}}{\partial t},v_i \right)&=-\sum _{i}a_{i}(u_{ms,i},v_{i})+q(u_{ms},v)\nonumber \\&\qquad +(f,v), \;\forall v\in V_H, \, t\in (0,T). \end{aligned}$$

(13)

We also define the following norms

$$\begin{aligned} \Vert u\Vert _c^2 = c(u,u), \quad \Vert u\Vert _a^2 = a(u,u), \quad \Vert u\Vert _{a_Q}^2 = a_Q(u,u). \end{aligned}$$

Lemma 1

Let u be the reference solution defined in (12) and $u_{ms}$ be the multiscale numerical solution defined in (13). We have

$$\begin{aligned}&\Vert u(t,\cdot )-u_{ms}(t,\cdot )\Vert _{c}^2+\int _{0}^{T}\Vert u-u_{ms}\Vert _{a_{Q}}^{2} {dt} \nonumber \\&\quad \le C\inf _{w\in V_{H}}\left( \int _{0}^{T}\left\| \frac{\partial (w-u)}{\partial t}\right\| _{c}^2 {dt} + \int _{0}^{T}\Vert w-u\Vert _{a_{Q}}^{2} {dt} +\Vert w(0,\cdot )-u(0,\cdot )\Vert _{c}^2 \right) . \end{aligned}$$

(14)

Proof

We write $u_{ms} = (u_{ms,1},\ldots , u_{ms,N})$, where $u_{ms,i}$ is the component for the i-th continuum. Using (12) and (13), we have

$$\begin{aligned}&c \left( \frac{\partial (u-u_{ms})}{\partial t}, v \right) +\sum _{i}a_{i}(u_{i}-u_{ms,i},v)-q(u-u_{ms},v) =0,\\&\quad \forall v\in V_{H}, \, t\in (0,T). \end{aligned}$$

Let $w\in V_H$ and $v=w-u_{ms}$ in the above equation, we obtain

$$\begin{aligned}&c \left( \frac{\partial (w-u_{ms})}{\partial t},w-u_{ms} \right) {+}\sum _{i}a_{i}(w_{i}-u_{ms,i},w_{i}-u_{ms,i})-q(w-u_{ms},w{-}u_{ms})\\&\quad = c \left( \frac{\partial (w-u)}{\partial t},w-u_{ms} \right) +\sum _{i}a_{i}(w-u_{i},w-u_{ms,i})-q(w-u,w-u_{ms})\\&\quad \le \left\| \frac{\partial (w-u)}{\partial t}\right\| _{c}\Vert w-u_{ms}\Vert _{c}+\Vert w-u\Vert _{a_{Q}}\Vert w-u_{ms,}\Vert _{a_{Q}}. \end{aligned}$$

Therefore, integrating the above in time, we obtain (14). $\square$

In the next lemma, we prove a similar result as (14) by assuming an additional condition on q, namely,

$$\begin{aligned} -q(v,v)\le D\Vert v\Vert _{a}^{2}, \quad \forall \quad v\in [H^{1}(\Omega )]^{N}. \end{aligned}$$

(15)

Lemma 2

Assume that $-q(v,v)\le D\Vert v\Vert _{a}^{2}, \forall v\in [H^{1}(\Omega )]^{N}$. For the same u and $u_{ms}$ as in Lemma 1, we have

$$\begin{aligned}&\Vert u(t,\cdot )-u_{ms}(t,\cdot )\Vert _{c}^{2}+\int _{0}^{T}\Vert u-u_{ms}\Vert _{a}^{2} \, {dt} \\&\quad \le C\inf _{w\in V_{H}} \left( \int _{0}^{T}\left\| \frac{\partial (w-u)}{\partial t}\right\| _{c}^{2} \, {dt}\right. \\&\quad \quad \left. + (D+1)\int _{0}^{T}\Vert w-u\Vert _{a}^{2} \, {dt} +\Vert w(0,\cdot )-u(0,\cdot )\Vert _{c}^{2}\right) . \end{aligned}$$

Proof

Since $\int _{0}^{T}\Vert u-u_{ms}\Vert _{a}^{2} \, {dt} \le \int _{0}^{T}\Vert u-u_{ms}\Vert _{a_{Q}}^{2} \, {dt}$ and $-q(v,v)\le D\Vert v\Vert _{a}^{2}$, we have

$$\begin{aligned}&\Vert u(t,\cdot )-u_{ms}(t,\cdot )\Vert _{c}^{2} +\int _{0}^{T}\Vert u-u_{ms}\Vert _{a}^{2} \, {dt} \\&\quad \le \Vert u(t,\cdot )-u_{ms}(t,\cdot )\Vert _{c}^{2} +\int _{0}^{T}\Vert u-u_{ms}\Vert _{a_{Q}}^{2} \, {dt}\\&\quad \le C\inf _{w\in V_{H}}\left( \int _{0}^{T}\left\| \frac{\partial (w-u)}{\partial t}\right\| _{c}^{2} \, {dt} +\int _{0}^{T}\Vert w-u\Vert _{a}^{2}\right. \\&\qquad \left. -q(w-u,w-u) \, {dt} +\Vert w(0,\cdot )-u(0,\cdot )\Vert _{c}^{2}\right) \\&\quad \le C\inf _{w\in V_{H}}\left( \int _{0}^{T}\left\| \frac{\partial (w-u)}{\partial t}\right\| _{c}^{2} \, {dt}\right. \\&\qquad \left. +(D+1)\int _{0}^{T}\Vert w-u\Vert _{a}^{2} \, {dt} +\Vert w(0,\cdot )-u(0,\cdot )\Vert _{c}^{2}\right) . \end{aligned}$$

This completes the proof. $\square$

We will use the above two lemmas to prove the convergence of our scheme. In particular, we need to find a suitable function $w\in V_H$ and estimate the difference $w-u$ in various norms. The following is our strategy. We define the snapshot projection $u_{snap} \in V_{snap}$ by

$$\begin{aligned} u_{snap} = \sum _j \chi _j u^{(j)}_{snap},\quad \text { {with} } \; u^{(j)}_{snap}|_{\partial \omega _j} = u|_{\partial \omega _j} , \end{aligned}$$

(16)

where $V_{snap}$ is the snapshot space obtained by collecting all snapshot functions. We note that, since the snapshot functions for each coarse region $\omega _j$ take all possible values on $\partial \omega _j$, the problem in (16) is well-defined. Since $w-u = w-u_{snap} + u_{snap}-u$, it suffices to estimates the two terms $w-u_{snap}$ and $u_{snap}-u$. Note that the term $u_{snap}-u$ corresponds to an irreducible error of our scheme, since this error cannot be improved by using our scheme. We assume that this irreducible error is small by using a large set of snapshot functions. Based on this argument, it suffices to estimate $w-u_{snap}$ by choosing an appropriate function $w\in V_H$.

Note that $u_{snap}$ is in the snapshot space, which means that we can represent u as a linear combination of all multiscale basis functions. To define $w\in V_H$, we will take w as the projection of $u_{snap}$ in the offline space. More precisely, we use the following construction. First, for the case of un-coupled basis functions, we can represent

$$\begin{aligned} u_{snap} = (u_{snap,1},u_{snap,2},\ldots ,u_{snap,N}), \quad u_{snap,i} = \sum _{j}\sum _{k}c_{k,i}^{(j)}(t)\chi _{j}(x)\phi _{k,i}^{(j)}(x).\nonumber \\ \end{aligned}$$

(17)

Then the projection w of u in the offline space is defined as

$$\begin{aligned} w = (w_1,w_2,\ldots ,w_N), \quad w_i = \sum _{j}\sum _{k \le L_j}c_{k,i}^{(j)}(t)\chi _{j}(x)\phi _{k,i}^{(j)}(x). \end{aligned}$$

(18)

Second, for the case of coupled basis functions, we can represent

$$\begin{aligned} u_{snap}= \sum _{j}\sum _{k}c_{k}^{(j)}(t)\chi _{j}(x)\phi _{k}^{(j)}(x). \end{aligned}$$

(19)

Then the projection w of $u_{snap}$ in the offline space is defined as

$$\begin{aligned} w = \sum _{j}\sum _{k \le L_j}c_{k}^{(j)}(t)\chi _{j}(x)\phi _{k}^{(j)}(x). \end{aligned}$$

(20)

Next, we will state and prove the main results (Theorems 1 and 2) of this appendix. As we will see, Theorems 1 and 2 follow from Lemmas 3, 5, and 6.

Theorem 1

For the un-coupled GMsFEM, let u and $u_{snap}$ be the reference solution and snapshot projection in (12) and (13) and let $w\in V_{H}$ be the projection of $u_{snap}$ defined in (18). We assume (15). Then we have

$$\begin{aligned} \begin{aligned}&\int _{0}^{T}\left\| \frac{\partial (w-u_{snap})}{\partial t}\right\| _{c}^{2} \, {dt} +\int _{0}^{T}\Vert w-u_{snap}\Vert _{a}^{2} \, {dt} +\Vert w(0,\cdot )-u_{snap}(0,\cdot )\Vert _{c}^{2} \\&\quad \le \frac{C}{\Lambda _1}\left( \int _{0}^{T}\left\| \frac{\partial u}{\partial t}\right\| _{a}^{2} \, {dt} +\int _{0}^{T}\Vert u\Vert _{a}^{2} \, {dt} +\Vert u(0,\cdot )\Vert _{a}^{2}\right) , \end{aligned} \end{aligned}$$

where $\Lambda _1=\min _{j,i}\{\lambda _{L_j+1,i}^{(j)}\}$.

Theorem 2

For the coupled GMsFEM, let u and $u_{snap}$ be the reference solution and snapshot projection in (12) and (13) and let $w\in V_{H}$ be the projection of $u_{snap}$ defined in (20). Then we have

$$\begin{aligned} \begin{aligned}&\int _{0}^{T}\left\| \frac{\partial (w-u_{snap})}{\partial t}\right\| _{c}^{2} \, {dt} +\int _{0}^{T}\Vert w-u_{snap}\Vert _{a_{Q}}^{2} \, {dt} +\Vert w(0,\cdot )-u_{snap}(0,\cdot )\Vert _{c}^{2} \\&\quad \le \frac{C^2}{\Lambda _2}\left( \int _{0}^{T}\left\| \frac{\partial u}{\partial t}\right\| _{a_{Q}}^{2} \, {dt} +\int _{0}^{T}\Vert u\Vert _{a_{Q}}^{2} \, {dt} +\Vert u(0,\cdot )\Vert _{a_{Q}}^{2}\right) , \end{aligned} \end{aligned}$$

where $\Lambda _2=\min _{j}\{\lambda _{L_j+1}^{(j)}\}$.

We will proof the above two theorems by estimating $\int _{0}^{T} \Big \Vert \frac{\partial (w-u_{snap})}{\partial t} \Big \Vert _{c}^{2} \, {dt}$, $\int _{0}^{T}\Vert w-u_{snap}\Vert _{a}^{2}$, $\int _{0}^{T}\Vert w-u_{snap}\Vert _{a_{Q}}^{2} \, {dt}$, and $\Vert w(0,\cdot )-u_{snap}(0,\cdot )\Vert _{c}^{2}$ separately in the following lemmas. Unless otherwise specified, the constant C is independent of any scales and continuum.

Lemma 3

Let u, $u_{snap}$, and w be defined as in Theorems 1 and 2. For the un-coupled basis functions, we have

$$\begin{aligned} \int _{0}^{T}\left\| \frac{\partial (w-u_{snap})}{\partial t}\right\| _{c}^{2} \, {dt} \le \frac{CE}{\Lambda _1}\, \left\| \frac{\partial u}{\partial t}\right\| _{a}^{2} \, {dt}. \end{aligned}$$

For the coupled basis functions, we have

$$\begin{aligned} \int _{0}^{T}\left\| \frac{\partial (w-u_{snap})}{\partial t}\right\| _{c}^{2} \le \frac{CE}{\Lambda _2}\, \left\| \frac{\partial u}{\partial t}\right\| _{a_{Q}}^{2}, \end{aligned}$$

where $E=\max _{i,j,l}\left\{ \frac{c_{i}\chi _{j}^{2}}{\kappa _{i}|\nabla \chi _{j}|^{2}},\, \frac{c_{l,i}\chi ^{2}_{j}}{\kappa _{l,i}|\nabla _{f}\chi _{j}|^2}\right\}$.

Proof

We will present the proof for the case of un-coupled basis functions. First, note that

$$\begin{aligned}&\Vert (u_{snap})_{t}-w_{t}\Vert _{c}^{2} \\&\quad \le \sum _{i}\left\| \sum _{j}\left( \chi _{j}\frac{\partial u^{(j)}_{snap,i}}{\partial t} -\sum _{k\le L_j}\frac{\partial c_{k,i}^{(j)}}{\partial t}\chi _{j} \phi _{k,i}^{(j)} \right) \right\| _{c}^{2}\\&\quad \le D\sum _{i}\sum _{j}\int _{\omega _{j}}\frac{c_i\chi _{j}^{2}}{\kappa _{i}|\nabla \chi _{j}|^{2}}\kappa _{i}|\nabla \chi _{j}|^{2}\left( \frac{\partial u^{(j)}_{snap,i}}{\partial t}-\sum _{k\le L_j}\frac{\partial c_{k,i}^{(j)}}{\partial t} \, \phi _{k,i}^{(j)}\right) ^{2} \, {dx}\\&\qquad +\sum _{i,j,l}\int _{D_{f,l}\cap \omega _j} c_{l,i}\frac{\chi ^{2}_{j}}{\kappa _{l,i}|\nabla _{f}\chi _{j}|^2}\kappa _{l,i}|\nabla _{f}\chi _{j}|^2 \left( \frac{\partial u^{(j)}_{snap,i}}{\partial t}-\sum _{k\le L_j}\frac{\partial c_{k,i}^{(j)}}{\partial t} \, \phi _{k,i}^{(j)}\right) ^{2} \, {dx} \\&\quad \le DE\sum _i \sum _{j}s_i^{(j)} \left( \sum _{k>L_j}\frac{\partial c_{k,i}^{(j)}(t)}{\partial t}\phi _{k,i}^{(j)},\sum _{k>L_j}\frac{\partial c_{k,i}^{(j)}(t)}{\partial t}\phi _{k,i}^{(j)} \right) \end{aligned}$$

with $D=\max _{K\in {\mathcal {T}}^H} \{D_K\}$ where $D_K$ is the number of coarse neighborhoods intersecting with K. By using the orthogonality of eigenfunctions, we have

$$\begin{aligned}&s_i^{(j)} \left( \sum _{k>L_j}\frac{\partial c_{k,i}^{(j)}(t)}{\partial t}\phi _{k,i}^{(j)},\sum _{k>L_j}\frac{\partial c_{k,i}^{(j)}(t)}{\partial t}\phi _{k,i}^{(j)} \right) \\&\quad \le \sum _{k>L_j} \frac{1}{\lambda _{k,i}^{(j)}} \left( \frac{\partial c_{k,i}^{(j)}(t)}{\partial t}\right) ^{2} a_i^{(j)}\left( \phi _{k,i}^{(j)},\phi _{k,i}^{(j)}\right) \\&\quad \le \frac{1}{\lambda _{L_j+1,i}^{(j)}}\sum _{k}\left( \frac{\partial c_{k,i}^{(j)}(t)}{\partial t}\right) ^{2} a_i^{(j)}\left( \phi _{k,i}^{(j)},\phi _{k,i}^{(j)}\right) \\&\quad =\frac{1}{\lambda _{L_j+1,i}^{(j)}} a_i^{(j)} \left( \frac{\partial u^{(j)}_{snap,i}}{\partial t},\frac{\partial u^{(j)}_{snap,i}}{\partial t} \right) . \end{aligned}$$

Since $u^{(j)}_{snap,i}$ is the $a^{(j)}_i$-harmonic expansion of $u_i$ in $\omega _j$, we have

$$\begin{aligned} a^{(j)}_i(u^{(j)}_{snap},u^{(j)}_{snap}) \le a^{(j)}_i(u_i,u_i) \end{aligned}$$

and similarly

$$\begin{aligned} a^{(j)}_i \left( \frac{\partial u^{(j)}_{snap,i}}{\partial t},\frac{\partial u^{(j)}_{snap,i}}{\partial t} \right) \le a^{(j)}_i \left( \frac{\partial u_{i}}{\partial t},\frac{\partial u_{i}}{\partial t} \right) . \end{aligned}$$

Therefore, by summing over all i, j, we obtain

$$\begin{aligned}&\sum _{i,j}s_i^{(j)} \left( \sum _{k>L_j}\frac{\partial c_{k,i}^{(j)}(t)}{\partial t}\phi _{k,i}^{(j)},\sum _{k>L_j}\frac{\partial c_{k,i}^{(j)}(t)}{\partial t}\phi _{k,i}^{(j)} \right) \\&\quad \le \sum _{i,j}\frac{1}{\lambda _{L_j+1,i}^{(j)}} a_i^{(j)} \left( \frac{\partial u_i}{\partial t},\frac{\partial u_i}{\partial t} \right) \\&\quad \le \frac{1}{\min _{i,j}\{\lambda _{L_j+1,i}^{(j)}\}}\sum _{i,j} a_i^{(j)} \left( \frac{\partial u_i}{\partial t},\frac{\partial u_i}{\partial t} \right) \\&\quad \le \frac{D}{\min _{i,j}\{\lambda _{L_j+1,i}^{(j)}\}}a \left( \frac{\partial u}{\partial t},\frac{\partial u}{\partial t} \right) . \end{aligned}$$

For the case of coupled basis functions, we have $s^{(j)}(\cdot ,\cdot )=\sum _i s^{(j)}_i(\cdot ,\cdot )$. By using the same arguments, we have

$$\begin{aligned} \Vert (u_{snap})_{t}-w_{t}\Vert _{c}^{2} \le DE \sum _{j}s^{(j)} \left( \sum _{k>L_j}\frac{\partial c_{k}^{(j)}(t)}{\partial t}\phi _{k}^{(j)},\sum _{k>L_j}\frac{\partial c_{k}^{(j)}(t)}{\partial t}\phi _{k}^{(j)} \right) \end{aligned}$$

and

$$\begin{aligned} s^{(j)} \left( \sum _{k>L_j}\frac{\partial c_{k}^{(j)}(t)}{\partial t}\phi _{k}^{(j)},\sum _{k>L_j}\frac{\partial c_{k}^{(j)}(t)}{\partial t}\phi _{k}^{(j)} \right) \le \frac{1}{\lambda _{L_j+1}^{(j)}} a^{(j)}_{Q} \left( \frac{\partial u^{(j)}_{snap}}{\partial t},\frac{\partial u^{(j)}_{snap}}{\partial t} \right) . \end{aligned}$$

Since $u^{(j)}_{snap}$ is the $a^{(j)}_{Q}$-harmonic expansion of $u_i$ in $\omega _j$, we have

$$\begin{aligned} a^{(j)}_{Q}(u^{(j)}_{snap},u^{(j)}_{snap}) \le a^{(j)}_{Q}(u,u) \end{aligned}$$

and

$$\begin{aligned} a^{(j)}_{Q} \left( \frac{\partial u^{(j)}_{snap}}{\partial t},\frac{\partial u^{(j)}_{snap}}{\partial t} \right) \le a^{(j)}_{Q} \left( \frac{\partial u}{\partial t},\frac{\partial u}{\partial t} \right) . \end{aligned}$$

Therefore the proof is complete. $\square$

Before we estimate the terms $\int _{0}^{T}\Vert w-u_{snap}\Vert _{a}^{2} \, {dt}$ and $\int _{0}^{T}\Vert w-u_{snap}\Vert _{a_{Q}}^{2} \, {dt}$, we first prove the following lemma.

Lemma 4

For the case of coupled basis functions, if u satisfies

$$\begin{aligned}&\sum _{i}\int _{\omega _{j}}\kappa _{i}\nabla u_{i}\cdot \nabla v_{i} \, {dx} +\sum _l \int _{D_{f,l}\cap \omega _j}\kappa _{l,i}\nabla _{f}u_{i}\cdot \nabla _{f}v_{i} \, {dx} -q(u,v)\\&\quad =\int _{\omega _{j}}f v \, {dx}, \quad \forall v\in [H_{0}^{1}(\omega _{j})]^{N}, \end{aligned}$$

then we have

$$\begin{aligned}&\sum _{i}\int _{\omega _{j}}\kappa _{i}\chi _{j}^{2}|\nabla u_{i}|^{2} \, {dx} +\sum _l \int _{D_{f,l}\cap \omega _j}\kappa _{l,i}\chi _{j}^{2}|\nabla _{f_{j}}u|^{2}-q(\chi _{j}u,\chi _{j}v) \, {dx} \\&\quad \le C\sum _{i}\left( \int _{\omega }\frac{\chi _{j}^{4}}{\kappa _{i}|\nabla \chi _{j}|^{2}}f_{i}^{2} \, {dx} +\int _{\omega _{j}}\kappa _{i}|\nabla \chi _{j}|^{2}u^{2} \, {dx} ]\right. \\&\qquad \left. +\sum _l \int _{D_{f,l}\cap \omega _j}\kappa _{l,i}|\nabla _{f}\chi _{j}|^{2}u^{2} \, {dx} \right) . \end{aligned}$$

For the case of un-coupled basis functions, if u satisfies

$$\begin{aligned} \int _{\omega _{j}}\kappa _{i}\nabla u\cdot \nabla v \, {dx} +\sum _l \int _{D_{f,l}\cap \omega _j}\kappa _{l,i}\nabla _{f}u\cdot \nabla _{f}v \, {dx} =\int _{\omega _{j}}f v \, {dx}, \quad \forall v\in H_{0}^{1}(\omega _{j}) , \end{aligned}$$

then we have

$$\begin{aligned}&\sum _{i}\int _{\omega _{j}}\kappa _{i}\chi _{j}^{2}|\nabla u_{i}|^{2} \, {dx} +\sum _l \int _{D_{f,l}\cap \omega _j}\kappa _{l,i}\chi _{j}^{2}|\nabla _{f}u|^{2} \, {dx} \\&\quad \le C\sum _{i}\left( \int \frac{\chi _{j}^{4}}{\kappa _{i}|\nabla \chi _{j}|^{2}}f_{i}^{2} \, {dx} +\int _{\omega _{j}}\kappa _{i}|\nabla \chi _{j}|^{2}u^{2} \, {dx} \right. \\&\qquad \left. +\sum _l \int _{D_{f,l}\cap \omega _j}\kappa _{l,i}|\nabla _{f}\chi _{j}|^{2}u^{2} \, {dx}\right) . \end{aligned}$$

Proof

For the case of coupled basis functions, we take $v=\chi _{j}^{2}u$ and obtain

$$\begin{aligned}&\sum _{i}\int _{\omega _{j}}\kappa _{i}\nabla u_{i}\cdot \nabla (\chi _{j}^{2}u_{i}) \, {dx} +\sum _l \int _{D_{f,l}\cap \omega _j}\kappa _{l,i}\nabla _{f}u_{i}\cdot \nabla _{f}(\chi _{j}^{2}u_{i}) \, {dx} -q(\chi _{j}u,\chi _{j}u) \\&\quad =\int _{\omega _{j}}\chi _{j}^{2}fu \, {dx}. \end{aligned}$$

This implies

$$\begin{aligned}&\sum _{i}\left( \int _{\omega _{j}}\kappa _{i}\chi _{j}^{2}|\nabla u_{i}|^{2} \, {dx} +\sum _l \int _{D_{l,i}\cap \omega _j}\kappa _{l,i}\chi _{j}^{2}|\nabla _{f}u_{i}|^{2} \, {dx} -q(\chi _{j}u,\chi _{j}u)\right) \\&\quad = \int _{\omega _{j}}\chi _{j}^{2}fu \, {dx} -2\sum _{i}\left( \int _{\omega _{j}}\kappa _{i}\chi _{j}u_{i}\nabla u_{i}\cdot \nabla \chi _{j} \, {dx}\right. \\&\qquad +\left. \sum _l\int _{D_{f,l}\cap \omega _j}\kappa _{l,i}\chi _{j}u_{i}\nabla _{f} u_{i}\cdot \nabla _{f}\chi _{j} \, {dx} \right) \\&\quad \le C\sum _{i}\left( \int \frac{\chi _{j}^{4}}{\kappa _{i}|\nabla \chi _{j}|^{2}}f_{i}^{2} \, {dx} +\int _{\omega _{j}}\kappa _{i}|\nabla \chi _{j}|^{2}u_{k}^{2} \, {dx}\right. \\&\qquad \left. +\sum _l \int _{D_{f,l}\cap \omega _j}\kappa _{l,i}|\nabla \chi _{j}|^{2}u_{i}^{2} \, {dx}\right) . \end{aligned}$$

This completes the proof for the case of coupled basis functions. For the case of un-coupled basis functions, the proof is similar and is therefore omitted. $\square$

Lemma 5

Let u, $u_{snap}$ and w be defined as in Theorems 1 and 2. For the case of un-coupled basis functions, we have

$$\begin{aligned} \int _{0}^{T}\Vert w-u_{snap}\Vert _{a}^{2} \, {dt} \le \frac{C}{\Lambda _{1}}\Vert u\Vert _{a}^{2}. \end{aligned}$$

For the case of coupled basis functions, we have

$$\begin{aligned} \int _{0}^{T}\Vert w-u_{snap}\Vert _{a_{Q}}^{2} \, {dt} \le \frac{C}{\Lambda _{2}}\Vert u\Vert _{a_{Q}}^{2}, \end{aligned}$$

where $\Lambda _1$ and $\Lambda _2$ are defined in Theorems 1 and 2.

Proof

We first define $e^{(j)}_{i}$ by

$$\begin{aligned} e^{(j)}_{i} = {\left\{ \begin{array}{ll} \sum _{k>L_j}\frac{\partial c_{k,i}^{(j)}(t)}{\partial t}\phi _{k,i}^{(j)}, &{}\quad \text {for un-coupled basis {functions}}, \\ {} \\ \sum _{k>L_j}\frac{\partial c_{k}^{(j)}(t)}{\partial t}\phi _{k}^{(j)}, &{}\quad \text {for coupled basis {functions}}. \end{array}\right. } \end{aligned}$$

Note that

$$\begin{aligned}&\Vert w-u_{snap}\Vert _{a}^{2} \\&\quad =\sum _{i}\left( \int _{\omega _{j}}\kappa _{i}\nabla \sum _{j}\chi _{j}e_{i}^{(j)}\cdot \nabla \sum _{j}\chi _{j}e_{i}^{(j)} \, {dx}\right. \\&\qquad \left. +\sum _l \int _{D_{f,l}\cap \omega _j} \kappa _{l,i}\nabla _{f}\sum _{j}\chi _{j}e_{i}^{(j)}\cdot \nabla _{f}\sum _{j}\chi _{j}e_{i}^{(j)} \, {dx} \right) \\&\quad \le D\sum _{i}\sum _{j}\left( \int _{\omega _{j}}\kappa _{i}|\nabla \chi _{j}e_{i}^{(j)}|^{2} \, {dx} +\sum _l \int _{D_{f,l}\cap \omega _j} \kappa _{l,i} |\nabla _{f}\chi _{j}e_{i}^{(j)}|^{2} \, {dx} \right) \\&\quad \le CD\sum _{i,j}\left( \int _{\omega _{j}}\kappa _{i}\chi _{j}^{2}|\nabla e_{i}^{(j)}|^{2} \, {dx}\right. \\&\qquad \left. +\sum _l \int _{D_{f,l}\cap \omega _j}\kappa _{l,i}\chi _{j}^{2}|\nabla _{f}e_{i}^{(j)}|^{2} \, {dx} +s^{(j)}_i(e^{(j)}_i,e^{(j)}_i)\right) . \end{aligned}$$

In addition, we have

$$\begin{aligned} -q \left( \sum _{j}\chi _{j}e^{(j)},\sum _{j}\chi _{j}e^{(j)} \right) \le -D\sum _j \left( q(\chi _{j}e^{(j)},\chi _{j}e^{(j)})\right) , \end{aligned}$$

where D is defined in the proof of Lemma 3.

For the case of coupled basis functions, using Lemma 4, we obtain

$$\begin{aligned}&\sum _{i}\int _{\omega _{j}}\kappa _{i}|\nabla \chi _{j}e_{i}^{(j)}|^{2} \, {dx} + \sum _l \int _{D_{f,l} \cap \omega _j} \kappa _{l,i}|\nabla _{f}\chi _{j}e_{i}^{(j)}|^{2} \, {dx} -q(\chi _{j}e^{(j)},\chi _{j}e^{(j)})\\&\quad \le C\, s^{(j)}(e^{(j)},e^{(j)}). \end{aligned}$$

Therefore, we have

$$\begin{aligned} \Vert w-u_{snap}\Vert ^2_{a_Q}&\le \Vert w-u_{snap}\Vert ^2_a - D\sum _j \left( q(\chi _{j}e^{(j)},\chi _{j}e^{(j)})\right) \\&\le C\,s^{(j)}(e^{(j)},e^{(j)}). \end{aligned}$$

For the case of un-coupled basis functions, using Lemma 4 again, we obtain

$$\begin{aligned} \sum _{k}\int _{\omega _{j}}\kappa _{i}|\nabla \chi _{j}e_{k}^{(j)}|^{2} \, {dx} + \sum _l \int _{D_{f,l}\cap \omega _j} \kappa _{l,k}|\nabla _{f}\chi _{j}e_{k}^{(j)}|^{2} \, {dx} \le C\,s^{(j)}(e^{(j)},e^{(j)}). \end{aligned}$$

Therefore, we have

$$\begin{aligned} \Vert w-u_{snap}\Vert ^2_{a}&\le C\sum _i\,s^{(j)}_i(e^{(j)}_i,e^{(j)}_i). \end{aligned}$$

Finally, by the definition of the eigen-projection, for the case of coupled basis functions, we have

$$\begin{aligned} s^{(j)}(e^{(j)},e^{(j)})&\le \frac{1}{\lambda _{L_j+1}^{(j)}} \, a^{(j)}_{Q}\left( e^{(j)},e^{(j)}\right) \le \frac{1}{\lambda _{L_j+1}^{(j)}} \, a^{(j)}_{Q}(u_{snap},u_{snap})\\&\le \frac{1}{\lambda _{L_j+1}^{(j)}} \, a^{(j)}_{Q}(u,u) \end{aligned}$$

and, for the case of un-coupled basis functions, we have

$$\begin{aligned} s^{(j)}_{i}\left( e^{(j)}_i,e^{(j)}_i\right)&\le \frac{1}{\lambda _{L_j+1,i}^{(j)}} \, a^{(j)}_i\left( e^{(j)}_i,e^{(j)}_i\right) \le \frac{1}{\lambda _{L_j+1,i}^{(j)}} \, a^{(j)}_i(u_{snap,i},u_{snap,i})\\&\le \frac{1}{\lambda _{L_j+1,i}^{(j)}} \, a^{(j)}_i(u,u). \end{aligned}$$

This completes the proof. $\square$

Finally, by using arguments similar as in the proof of Lemma 3, we can prove the following lemma.

Lemma 6

Let u, $u_{snap}$, and w be defined as in Theorem 1 and 2. For the case of un-coupled basis functions, we have

$$\begin{aligned} \Vert w(0,\cdot )-u_{snap}(0,\cdot )\Vert _{c}^{2}\le \frac{CE}{\Lambda _{1}}\Vert u(0,x)\Vert _{a}^{2}. \end{aligned}$$

For the case of coupled basis functions, we have

$$\begin{aligned} \Vert w(0,\cdot )-u_{snap}(0,\cdot )\Vert _{c}^{2}\le \frac{CE}{\Lambda _{2}}\Vert u(0,x)\Vert _{a_{Q}}^{2}. \end{aligned}$$