A Novel Fuzzy Model for Knowledge-Driven Process Optimization in Renewable Energy Projects

Abstract

This study is aimed at identifying key indicators to increase knowledge-based process optimization for renewable energy projects. Within this context, a novel fuzzy decision-making model is introduced that has two different stages. The first stage is related to the weighting of the knowledge-based determinants of process optimization in investment decisions by using quantum picture fuzzy rough sets (QPFR)-based multi-step wise weight assessment ratio analysis (M-SWARA). On the other side, the second stage consists of ranking the investment alternatives for process optimization in renewable energy projects via the QPFR-based technique for order preference by similarity (TOPSIS) methodology. The main contribution of this study is that a priority analysis is conducted for information-based factors affecting the performance of renewable energy projects. This situation provides an opportunity for the investments to implement appropriate strategies to increase the optimization of these investments. It is concluded that quality is the most essential indicator with respect to the process optimization of these projects. It can be possible to increase the efficiency of these projects by using better quality products. Innovation has an important role in ensuring the use of quality products in environmental sustainability. Owing to new technologies, it is easier to use more effective and innovative products. This condition also contributes to increasing the efficiency of the energy production process. Furthermore, the findings also denote that the most appropriate energy innovation alternative is the variety of clean energy sources. By focusing on different clean energy alternatives, the risk of interruptions in energy generation can be minimized. In other words, the negative impact of climatic conditions on energy production can be lowered significantly with the help of this situation.

Introduction

Making correct investment decisions in renewable energy projects is vital. The main purpose of these projects is to produce energy without harming the environment. In this context, owing to the success of these investments, the fight against climate change can be much easier. On the other hand, investments in these projects also contribute to increasing energy supply security. In other words, with the help of these projects, countries are not dependent on others for energy (Dong et al., 2023a). Furthermore, the right investments in renewable energy projects support economic development. Owing to these investments, new employment opportunities emerge in the country (Dzwigol et al., 2023). With the right investment decision in these types of energy, the costs can be reduced to more reasonable levels. This situation can help these investments to be sustainable. Moreover, the correct investments in these projects encourage the development of innovative technologies that allows the industry to develop (Shang et al., 2023). In summary, making the right investment decisions in renewable energy projects provides a wide range of benefits, both socially and economically.

Knowledge-based process optimization is essential for performance improvements of renewable energy projects. This situation allows the processes of energy projects to be analyzed comprehensively. In this way, deficiencies in the processes of the projects can be detected (Abbas et al., 2023). This issue allows to increase the efficiency of the projects by taking specific actions. Knowledge-based process optimization also helps to reduce the risks of projects (Peng et al., 2023). Owing to a detailed analysis, it is possible to make the processes in the projects safer. On the other hand, analyzing processes in this context encourages the emergence of new ideas and innovative solutions. Thus, it can be easier to discover new technologies for these projects and to develop new business models (Jiang et al., 2023). Moreover, the analysis of processes in this way requires the use of information based on real data. In this way, it is possible to make objective decisions (Pan et al., 2023). Additionally, opportunities for improvement can be identified by analyzing processes in an information-based manner. This ensures that projects evolve continuously over time. Consequently, knowledge-based process optimization is essential to increase the effectiveness of renewable energy projects.

There are various knowledge-based determinants of process optimization in renewable energy investment decisions. In this scope, providing efficiency is a key issue for this condition. The quality of energy generation equipment also contributes significantly to increasing the performance of these projects (Martínez et al., 2023). Owing to the preference of high-quality materials, less resources will be used in the process of obtaining energy. This contributes significantly to the achievement of the environmental sustainability targets of the projects. Flexible services contribute to the successful fight against this problem by providing quick responses to the energy system. Flexible service delivery also enables more efficient use of energy resources. In this way, energy demand management will be carried out more successfully (Li & Umair, 2023). Meeting customer expectations correctly is another issue that plays an important role in this process. Since customers may prefer companies that can meet their expectations more, businesses need to take action to ensure customer satisfaction demands (Sirr et al., 2023).

It is necessary to improve the knowledge-based factors to increase the performance of renewable energy projects. This will contribute to achieving process optimization in these projects. Otherwise, renewable energy projects will not be able to compete with other types of energy investment, and as a result, the sustainability of these projects will become increasingly difficult. However, there are many knowledge-based variables that can affect the development of these projects (Razzaq et al., 2023). Moreover, improvements to these factors also create new costs. As it can be understood from here, making too many improvements in the first place causes the costs of the enterprises to increase very much. Since this situation will make the projects financially difficult, it is more reasonable for businesses to start the process with limited improvements. Therefore, it is necessary to conduct a priority analysis for information-based factors affecting the performance of renewable energy projects (Wan et al., 2023).

The objective of this study is to identify key indicators to increase knowledge-based process optimization for renewable energy projects. Hence, the main research question of this study is to understand which determinants play the most critical role to provide optimization in these projects. For this purpose, a novel fuzzy decision-making model is introduced by the integration of the quantum picture fuzzy rough sets (QPFR), multi-step wise weight assessment ratio analysis (M-SWARA), and technique for order preference by similarity (TOPSIS). In Stage 1, the knowledge-based determinants of process optimization in investment decisions are identified through a thorough analysis using M-SWARA based on QPFRs. In Stage 2, investment alternatives for process optimization in renewable energy projects are identified and evaluated using linguistic evaluations from decision-makers with QPFR-TOPSIS. The main motivation for making this study is the need for a new decision-making model to examine the optimization of renewable energy projects. Most of the existing models in the literature cannot consider the causal directions of the determinants. However, the indicators of renewable energy optimization may have an influence on each other. Hence, to make a more appropriate evaluation, an impact relation map should be taken into consideration. To satisfy this situation, the M-SWARA methodology is used in this proposed model to weight the indicators.

The main contributions of the study are denoted below.

• (i) Conducting a priority analysis for information-based factors affecting the performance of renewable energy projects is the main contribution of the study. Knowledge-based factors should be improved to increase the performance of renewable energy projects (Peng et al., 2023). With the help of this issue, project optimization can be achieved more effectively. In this process, there are a lot of knowledge-based variables that can affect the development of these projects. However, the main problem is that improvements to these factors also create new costs. Therefore, because of the budget limitation, it is quite difficult to make improvement for many of these variables. Thus, this priority evaluation helps to increase the performance of renewable energy projects. Additionally, the best investment alternatives for process optimization can be provided to the investors. Hence, more specific strategies can be presented for investors so that effectiveness of the investments can be achieved more easily (Abbas et al., 2023).

• (ii) Another contribution of this study is considering a new decision-making technique with the name of M-SWARA. In spite of many advantages of classical SWARA, the causal directions cannot be identified (Yüksel & Dinçer, 2023). This situation is accepted as the main drawback of this technique. To minimize this problem, Xu et al. (2023) implemented some improvements to the classical SWARA approach, and a new methodology (M-SWARA) is generated so that causal directions can be evaluated. Knowledge-based determinants of process optimization in renewable energy investment decisions may have an influence on each other (Wan et al., 2023). Hence, the causality relationship between these items should be considered to make more effective evaluation.

• (iii) Considering picture fuzzy rough sets in the analysis process provides significant advantages. In this context, the concepts of picture fuzzy sets and rough sets are combined. Hence, uncertainty in the analysis process can be handled more effectively. Using picture fuzzy sets helps to represent membership degrees as intervals. With the help of this issue, vague information can be modeled in a more effective manner. However, in the traditional fuzzy sets, a single membership degree is taken into consideration. Therefore, it can be understood that PFRs help to achieve more accurate findings.

The second section includes the evaluation of literature. The third section focuses on methodology. The fourth section gives information about analysis results. The final parts make discussion and conclusion.

Literature Review

It is of great importance that the projects be efficient to achieve process optimization in renewable energy projects. Ensuring efficiency in these projects means less loss in energy production. Vásquez-Ordóñez et al. (2023) stated that the efficient use of materials taken into consideration in energy production allows these projects to be more economical and sustainable. On the other hand, Sharif et al. (2023) identified that an efficient energy investment project contributes to cost savings (Li & Shao, 2023). Efficiency is possible by using less amount of resources in energy production. This situation also enables less labor requirement. In this way, it is possible to reduce the costs of energy investment projects (Ainou et al., 2023; Iqbal et al., 2023). The competitiveness of the projects with less cost also increases significantly. Moreover, Adebayo et al. (2023) determined that the efficiency of the project also helps to increase performance. In this way, it is possible for renewable energy projects to generate more income. Alharbi et al. (2023) concluded that the efficiency of projects is also directly related to environmental sustainability. By ensuring efficiency, renewable energy projects can be increased and thus both natural resources and the environment can be successfully protected.

Customer expectations must be met correctly to achieve process optimization in renewable energy projects. Customers have different expectations from renewable energy projects such as safety and low cost. Meeting these expectations increases customers’ satisfaction with the project (Kolte et al., 2023). On the other hand, Dong et al. (2023b) claimed that meeting customer expectations also ensures the acceptance of the project by the community. Increasing competitiveness is one of the important benefits of customer satisfaction. The energy sector is a highly competitive field. In this context, Ramzan et al. (2023) identified that businesses need to meet the expectations of their customers correctly to increase their competitiveness. Since customers may prefer companies that can meet their expectations more, businesses need to take actions to ensure customer satisfaction (Zhu et al., 2023; Abid et al., 2024). Furthermore, Wang et al. (2023) stated that meeting customer expectations positively affects the image and reputation of the project. This allows businesses to have an environmentally friendly image. Moreover, according to Hille and Oelker (2023), taking into consideration customer feedback and requests is a factor that increases customer loyalty. This increases the sustainability and long-term success of the projects.

Flexible service is required to ensure process optimization in renewable energy projects. In this way, energy supply and demand balance can be achieved. Yang and Song (2023) defined that since renewable energy types are affected by weather conditions, differences in production capacity may occur. To minimize this problem, flexible services are needed (Chien et al., 2023; You et al., 2023). This variability in renewable energies can cause fluctuations in energy production. Lee et al. (2023) mentioned that flexible services contribute to the successful fight against this problem by providing quick responses to the energy system. On the other hand, Prokopenko et al. (2023) identified that flexible service provision also enables more efficient use of energy resources. In this way, energy demand management will be carried out more successfully. Moreover, Temesgen Hordofa et al. (2023) defined that flexible service delivery is important to meet customer. At different times, there may be variability in the demands of customers for energy. This increases customer satisfaction and enables more effective management of energy demand.

Quality products play a critical role to ensure process optimization in renewable energy projects. In this context, it is possible to increase the efficiency of the project thanks to the quality of energy production equipment (Zhong et al., 2024; Zhang et al., 2023a). Additionally, Taghizadeh-Hesary et al. (2023) concluded that since this will also mean that more energy can be produced, the performance of the project will also be increased. In addition to this issue, Ai et al. (2023) claimed that quality products also increase the reliability of the project. Preferring higher quality power generation equipment reduces the possibility of failure in projects. In this way, it is much more possible to ensure the sustainability of the projects (Karimi Alavijeh et al., 2024; Gao et al., 2023). Moreover, Norouzi et al. (2023) determined that cost savings can be achieved by using quality products in the energy production process. Also, Liu et al. (2023) identified that quality products are also important in terms of using advanced technology in the energy sector. In other words, quality products also encourage businesses to use innovative products. Another benefit of choosing quality products is that the negative effects on the environment can be reduced. According to Hou et al. (2023), owing to the preference of high-quality materials, less resources will be used in the process of obtaining energy. This contributes significantly to the achievement of the environmental sustainability targets of the projects.

As a result of the literature evaluation, the following points can be reached. Renewable energy projects have some significant contributions to both social and economic improvements of the companies. However, there are some barriers for the developments of these projects. In this process, high initial investment costs make the investors worried about these projects. Hence, necessary actions should be taken to solve this problem. Within this framework, optimization plays a critical role to increase the performance of these investments. However, it is quite important to identify which factors play the critical role in this optimization process. Therefore, a comprehensive decision-making model should be generated to make this evaluation effectively.

Methodology

The details of the approaches used in the proposed model are given in this section.

Modeling Uncertainty with QPFRs with Golden Cuts

Managing uncertainty in decision-making processes is of great importance. Otherwise, this uncertainty prevents the analysis results from being accurately predicted. Therefore, there is a risk that the results will be wrong. QPFRs with golden cuts is introduced in this study for decreasing the subjective and uncertain evaluations of decision-making process (Al-Binali et al., 2023). In this process, the lower and upper limits as well as a rough boundary interval in the concept of quantum mechanics and golden ratio are taken into consideration. Various probabilities are considered in Quantum theory (Dinçer et al., 2023). These sets are adapted to the PFRs. Equations 1, 2, and 3 indicate these issues (Carayannis et al., 2023).

$$Q\left(\left|u>\right.\right)=\varphi e^{j\theta}$$

(1)

$$\left|C>\right.=\left\{\left|{u}_{1}>\right.,\left|{u}_{2}>\right.,\dots ,\left|{u}_{n}>\right.\right\}$$

(2)

$${\textstyle\sum_{\left|u>\subseteq\right|C>}}\left|Q(\left|u>)\right.\right|=1$$

(3)

In this scope, C demonstrates the collection of events, ${\varphi}^{2}$ is the amplitude results, u demonstrates the event and ${\theta}^{2}$ refers to the phase angle. Picture fuzzy numbers (A) are an evolution of traditional numbers (He & Wang, 2023). Owing to these numbers, it is aimed to minimize the uncertainties in the decision-making processes. In these numbers, each element is represented by a degree (Kaya, 2023). This also contributes to increasing the flexibility in the analysis process. Equation (4) indicates classical sets in which $\mu_A$ shows the membership degree (Zhao et al., 2023).

$$A=\left\{\left.\left\langle x,\mu_A\left(x\right)\right\rangle\right|x\in X\right\}$$

(4)

Intuitionistic fuzzy sets are explained in Eq. 5 where non-membership function is identified as ${v}_{A}$.

$$A=\left\{\left\langle x,\;\mu_A\left(x\right),\;v_A\left(x\right)\right\rangle\left|x\right.\in X\right\}$$

(5)

PFRs are explained in Eq. (6) in which $n_A$ and $h_A$ denote neutral and refusal degrees. The details of the condition are given as $\mu_A\left(x\right)+n_A\left(x\right)+v_A+h_A\left(x\right)=1$.

$$A=\left\{\left.\left\langle x,\;\mu_A\left(x\right),\;n_A\left(x\right),\;v_A\left(x\right),\;h_A\left(x\right)\right\rangle\right|x\in X\right\}$$

(6)

Equations 7, 8, 9, 10, and 11 identify the details of the operations.

$$A\subseteq B\;\mathrm{if}\;\mu_A(x)\leq\mu_B(x)\;\mathrm{and}\;n_A(x)\leq n_B(x)\;\mathrm{and}\;v_A(x)\geq v_B(x),\forall x\in X$$

(7)

$$A=B\;\mathrm{if}\;A\subseteq B\;\mathrm{and}\;B\subseteq A$$

(8)

$$A\cup B=\left\{\left(x,max\left(\mu_A\left(x\right),\mu_B\left(x\right)\right),min\left(n_A\left(x\right),n_B\left(x\right)\right),min\left(v_A\left(x\right),v_B\left(x\right)\right)\right)\left|x\right.\in X\right\}$$

(9)

$$A\cap B=\left\{\left(x,min\left(\mu_A\left(x\right),\mu_B\left(x\right)\right),min\left(n_A\left(x\right),n_B\left(x\right)\right),max\left(v_A\left(x\right),v_B\left(x\right)\right)\right)\left|x\right.\in X\right\}$$

(10)

$$coA=\stackrel{-}{A}=\left\{\left(x,{v}_{A}\left(x\right),{n}_{A}\left(x\right),{\mu }_{A}\left(x\right)\right)\left|x\right.\in X\right\}$$

(11)

Lower $\left(\underline{Apr}\left(C_i\right)\right)$, upper $\left(\overline{Apr}\left({C}_{i}\right)\right)$ approximation, and boundary region $\left(Bnd\left({C}_{i}\right)\right)$ are identified in Eqs. 12, 13, and 14.

$$\underline{Apr}\left(C_i\right)=\cup\left\{Y\in X/R\left(Y\right)\leq C_i\right\}$$

(12)

$$\overline{Apr}\left({C}_{i}\right)=\cup \left\{Y\in X/R\left(Y\right)\ge {C}_{i}\right\}$$

(13)

$$Bnd\left({C}_{i}\right)=\cup \left\{Y\in X/R\left(Y\right)\ne {C}_{i}\right\}$$

(14)

Equations 15, 16, and 17 refer to the lower $\left(\underline{Lim}\left({C}_{i}\right)\right)$, upper $\left(\overline{Lim}\left({C}_{i}\right)\right)$ limits, and the rough number $\left(RN\left({C}_{i}\right)\right)$.

$$\underline{Lim}\left(C_i\right)=\sqrt[N_L]{\prod\nolimits_{i=1}^{N_L}Y\in}\underline{Apr}\left(C_i\right)$$

(15)

$$\overline{Lim}\left({C}_{i}\right)=\sqrt[{N}_{U}]{{\prod }_{i=1}^{{N}_{U}}Y\in }\overline{Apr}\left({C}_{i}\right)$$

(16)

$$RN\left(C_i\right)=\lceil\underline{Lim}\left(C_i\right),\overline{Lim}\left(C_i\right)\rfloor$$

(17)

QPFRSs are given in Eq. 18. In this context, ${C}_{i{\mu }_{A}}$, ${C}_{i{n}_{A}}$, ${C}_{i{v}_{A}}$, and ${C}_{i{h}_{A}}$ indicate membership, neutral, non-membership, and refusal degrees (Qahtan et al., 2023).

$$\left|C_A>\right.=\begin{Bmatrix}\langle u,(\lceil\underline{Lim}\left(C_{i\mu_A}\right),\overline{Lim}\left(C_{i\mu_A}\right)\rfloor\left(u\right),\lceil\underline{Lim}\left(C_{in_A}\right),\overline{Lim}\left(C_{in_A}\right)\rfloor\left(u\right),\\\lceil\underline{Lim}\left(C_{iv_A}\right),\overline{Lim}\left(C_{iv_A}\right)\rfloor\left.\left(u\right),\lceil\underline{Lim}\left(C_{ih_A}\right),\overline{Lim}\left(C_{ih_A}\right)\rfloor\left(u\right)\right|u\in2^{\left|C_A>\right.}\end{Bmatrix}$$

(18)

The definitions of these issues are denoted in Eqs. 19, 20, 21, 22, 23, 24, 25, and 26 (Dinçer et al., 2022a).

$$\underline{Lim}\left(C_{i\mu_A}\right)=\frac1{N_{L\mu_A}}\sum_{i=1}^{N_{L\mu_A}}Y\in\underline{Apr}\left(C_{i\mu_A}\right)$$

(19)

$$\underline{Lim}\left({C}_{i{n}_{A}}\right)=\frac{1}{{N}_{L{n}_{A}}}\sum _{i=1}^{{N}_{L{n}_{A}}}Y\in \underline{Apr}\left({C}_{i{n}_{A}}\right)$$

(20)

$$\underline{Lim}\left(C_{iv_A}\right)=\frac1{N_{Lv_A}}\sum_{i=1}^{N_{Lv_A}}Y\in\underline{Apr}\left(C_{iv_A}\right)$$

(21)

$$\underline{Lim}\left({C}_{i{h}_{A}}\right)=\frac{1}{{N}_{L{\pi }_{A}}}\sum _{i=1}^{{N}_{L{\pi }_{A}}}Y\in \underline{Apr}\left({C}_{i{h}_{A}}\right)$$

(22)

$$\overline{Lim}\left(C_{i\mu_A}\right)=\frac1{N_{U\mu_A}}{\textstyle\sum_{i=1}^{N_{U\mu_A}}}Y\in\overline{Apr}\left(C_{i\mu_A}\right)$$

(23)

$$\overline{Lim}\left(C_{in_A}\right)=\frac1{N_{Un_A}}{\textstyle\sum_{i=1}^{N_{Un_A}}}Y\in\overline{Apr}\left(C_{in_A}\right)$$

(24)

$$\overline{Lim}\left(C_{iv_A}\right)=\frac1{N_{Uv_A}}{\textstyle\sum_{i=1}^{N_{Uv_A}}}Y\in\overline{Apr}\left(C_{iv_A}\right)$$

(25)

$$\overline{Lim}\left(C_{ih_A}\right)=\frac1{N_{U\pi_A}}{\textstyle\sum_{i=1}^{N_{U\pi_A}}}Y\in\overline{Apr}\left(C_{ih_A}\right)$$

(26)

${N}_{L{\mu }_{A}}$, ${N}_{L{n}_{A}}$, ${N}_{L{v}_{A}}$, and ${N}_{L{h}_{A}}$ are the number of elements in $\underline{Apr}\left({C}_{i{\mu }_{A}}\right)$, $\underline{Apr}\left(C_{in_A}\right)$, $\underline{Apr}\left({C}_{i{v}_{A}}\right)$, and $\underline{Apr}\left({C}_{i{h}_{A}}\right)$, respectively, while ${N}_{U{\mu }_{A}}$, ${N}_{U{n}_{A}}$, ${N}_{U{v}_{A}}$, and ${N}_{U{h}_{A}}$ are defined for $\overline{Apr}\left({C}_{i{\mu }_{A}}\right)$, $\overline{Apr}\left({C}_{i{n}_{A}}\right)$, $\overline{Apr}\left({C}_{i{v}_{A}}\right)$, and $\overline{Apr}\left({C}_{i{h}_{A}}\right)$ as in Eqs. 27, 28, 29, 30, 31, 32, 33, and 34.

$$\underline{Apr}\left({C}_{i{\mu }_{A}}\right)=\cup \left\{Y\in X/\stackrel{\sim}{R}\left(Y\right)\le {C}_{i{\mu }_{A}}\right\}$$

(27)

$$\underline{Apr}\left({C}_{i{n}_{A}}\right)=\cup \left\{Y\in X/\stackrel{\sim}{R}\left(Y\right)\le {C}_{i{n}_{A}}\right\}$$

(28)

$$\underline{Apr}\left({C}_{i{v}_{A}}\right)=\cup \left\{Y\in X/\stackrel{\sim}{R}\left(Y\right)\le {C}_{i{v}_{A}}\right\}$$

(29)

$$\underline{Apr}\left(C_{ih_A}\right)=\cup\left\{Y\in X/\widetilde R\left(Y\right)\leq C_{ih_A}\right\}$$

(30)

$$\overline{Apr}\left({C}_{i{\mu }_{A}}\right)=\cup \left\{Y\in X/\stackrel{\sim}{R}\left(Y\right)\le {C}_{i{\mu }_{A}}\right\}$$

(31)

$$\overline{Apr}\left({C}_{i{n}_{A}}\right)=\cup \left\{Y\in X/\stackrel{\sim}{R}\left(Y\right)\le {C}_{i{n}_{A}}\right\}$$

(32)

$$\overline{Apr}\left({C}_{i{v}_{A}}\right)=\cup \left\{Y\in X/\stackrel{\sim}{R}\left(Y\right)\le {C}_{i{v}_{A}}\right\}$$

(33)

$$\overline{Apr}\left({C}_{i{h}_{A}}\right)=\cup \left\{Y\in X/\stackrel{\sim}{R}\left(Y\right)\le {C}_{i{h}_{A}}\right\}$$

(34)

The formulation of QPFSs with the amplitude and the angle results are demonstrated in Eqs. 35 and 36.

$$C=\left[{C}_{\mu }.{e}^{j2\pi .\alpha },{C}_{n}.{e}^{j2\pi .\gamma },{C}_{v}.{e}^{j2\pi .\beta },{C}_{h}.{e}^{j2\pi .T}\right]$$

(35)

$${\varphi }^{2}=\left|{C}_{\mu }\left(\left|{u}_{i}>\right.\right)\right|$$

(36)

Golden ratio (G) is used in the proposed model to compute degrees more appropriately (Kou et al., 2023b). Equations 37, 38, 39, 40, and 41 give information about these details in which b and a show high and low values (Moiseev et al., 2023).

$${C}_{n}=\frac{{C}_{\mu }}{G}$$

(37)

$${C}_{h}=\frac{{C}_{v}}{G}$$

(38)

$$\alpha =\left|{C}_{\mu }\left(\left|{u}_{i}>\right.\right)\right|$$

(39)

$$\gamma =\frac{\alpha }{G}$$

(40)

$$T=\frac{\beta }{G}$$

(41)

${X}_{1}$ and ${X}_{2}$ are two universes, and ${\stackrel{\sim}{A}}_{c}$ and ${\stackrel{\sim}{B}}_{c}$, respectively, represented by

$$\begin{pmatrix}\lceil\underline{Lim}\left(C_{\mu_{\widetilde{A}}}\right),\overline{Lim}\left(C_{\mu_{\widetilde{A}}}\right)\rfloor e^{j2\pi.\lceil\left(\frac{{\underline{\alpha}}_{\widetilde{A}}}{2\pi}\right),\left(\frac{{\overline{\alpha}}_{\widetilde{A}}}{2\pi}\right)\rfloor},\lceil\underline{Lim}\left(C_{n_{\widetilde{A}}}\right),\overline{Lim}\left(C_{n_{\widetilde{A}}}\right)\rfloor e^{j2\pi.\lceil\left(\frac{{\underline{\gamma}}_{\widetilde{A}}}{2\pi}\right),\left(\frac{{\overline{\gamma}}_{\widetilde{A}}}{2\pi}\right)\rfloor},\\\lceil\underline{Lim}\left(C_{v_{\widetilde{A}}}\right),\overline{Lim}\left(C_{v_{\widetilde{A}}}\right)\rfloor e^{j2\pi.\lceil\left(\frac{{\underline{\beta}}_{\widetilde{A}}}{2\pi}\right),\left(\frac{{\overline{\beta}}_{\widetilde{A}}}{2\pi}\right)\rfloor},\lceil\underline{Lim}\left(C_{h_{\widetilde{A}}}\right),\overline{Lim}\left(C_{h_{\widetilde{A}}}\right)\rfloor e^{j2\pi.\lceil\left(\frac{{\underline{T}}_{\widetilde{A}}}{2\pi}\right),\left(\frac{{\overline{T}}_{\widetilde{A}}}{2\pi}\right)\rfloor}\end{pmatrix}$$

$$\begin{pmatrix}\lceil\underline{Lim}\left(C_{\mu_{\widetilde B}}\right),\overline{Lim}\left(C_{\mu_{\widetilde B}}\right)\rfloor e^{j2\pi.\lceil\left(\frac{{\underline\alpha}_{\widetilde B}}{2\pi}\right),\left(\frac{{\overline\alpha}_{\widetilde B}}{2\pi}\right)\rfloor},\lceil\underline{Lim}\left(C_{n_{\widetilde B}}\right),\overline{Lim}\left(C_{n_{\widetilde B}}\right)\rfloor e^{j2\pi.\lceil\left(\frac{{\underline\gamma}_{\widetilde B}}{2\pi}\right),\left(\frac{{\overline\gamma}_{\widetilde B}}{2\pi}\right)\rfloor},\\\lceil\underline{Lim}\left(C_{v_{\widetilde B}}\right),\overline{Lim}\left(C_{v_{\widetilde B}}\right)\rfloor e^{j2\pi.\lceil\left(\frac{{\underline\beta}_{\widetilde B}}{2\pi}\right),\left(\frac{{\overline\beta}_{\widetilde B}}{2\pi}\right)\rfloor},\lceil\underline{Lim}\left(C_{h_{\widetilde B}}\right),\overline{Lim}\left(C_{h_{\widetilde B}}\right)\rfloor e^{j2\pi.\lceil\left(\frac{{\underline T}_{\widetilde B}}{2\pi}\right),\left(\frac{{\overline T}_{\widetilde B}}{2\pi}\right)\rfloor}\end{pmatrix}$$

and they are two QPFRs derived from the universes of discourse ${X}_{1}$ and ${X}_{2}$. The operations are denoted by Eqs. 42, 43, 44, and 45.

$$\begin{array}{c}\lambda\ast{\widetilde A}_c=\begin{Bmatrix}\lceil\underline{Lim}\left(C_{\mu_{\widetilde A}}\right)\lambda,\overline{Lim}\left(C_{\mu_{\widetilde A}}\right)\lambda\rfloor e^{j2\pi.\lceil\left(\frac{{\underline\alpha}_{\widetilde A}}{2\pi}\right)\lambda,\left(\frac{{\overline\alpha}_{\widetilde A}}{2\pi}\right)\lambda\rfloor},\lceil\underline{Lim}\left(C_{n_{\widetilde A}}\right)\lambda,\overline{Lim}\left(C_{n_{\widetilde A}}\right)\lambda\rfloor e^{j2\pi.\lceil\left(\frac{{\underline\gamma}_{\widetilde A}}{2\pi}\right)\lambda,\left(\frac{{\overline\gamma}_{\widetilde A}}{2\pi}\right)\lambda\rfloor},\\\lceil\underline{Lim}\left(C_{v_{\widetilde A}}\right)\lambda,\overline{Lim}\left(C_{v_{\widetilde A}}\right)\lambda\rfloor e^{j2\pi.\lceil\left(\frac{{\underline\beta}_{\widetilde A}}{2\pi}\right)\lambda,\left(\frac{{\overline\beta}_{\widetilde A}}{2\pi}\right)\lambda\rfloor},\lceil\underline{Lim}\left(C_{h_{\widetilde A}}\right)\lambda,\overline{Lim}\left(C_{h_{\widetilde A}}\right)\lambda\rfloor e^{j2\pi.\lceil\left(\frac{{\underline T}_{\widetilde A}}{2\pi}\right)\lambda,\left(\frac{{\overline T}_{\widetilde A}}{2\pi}\right)\lambda\rfloor}\end{Bmatrix},\\\lambda>0\end{array}$$

(42)

$$\begin{array}{c}\widetilde A_c^\lambda=\begin{Bmatrix}\lceil{\underline{Lim}\left(C_{\mu_{\widetilde A}}\right)}^\lambda,{\overline{Lim}\left(C_{\mu_{\widetilde A}}\right)}^\lambda\rfloor e^{j2\pi.\lceil\left(\frac{{\underline\alpha}_{\widetilde A}}{2\pi}\right)^\lambda,\left(\frac{{\overline\alpha}_{\widetilde A}}{2\pi}\right)^\lambda\rfloor},\lceil{\underline{Lim}\left(C_{n_{\widetilde A}}\right)}^\lambda,{\overline{Lim}\left(C_{n_{\widetilde A}}\right)}^\lambda\rfloor e^{j2\pi.\lceil\left(\frac{{\underline\gamma}_{\widetilde A}}{2\pi}\right)^\lambda,\left(\frac{{\overline\gamma}_{\widetilde A}}{2\pi}\right)^\lambda\rfloor},\\\lceil{\underline{Lim}\left(C_{v_{\widetilde A}}\right)}^\lambda,{\overline{Lim}\left(C_{v_{\widetilde A}}\right)}^\lambda\rfloor e^{j2\pi.\lceil\left(\frac{{\underline\beta}_{\widetilde A}}{2\pi}\right)^\lambda,\left(\frac{{\overline\beta}_{\widetilde A}}{2\pi}\right)^\lambda\rfloor},\lceil{\underline{Lim}\left(C_{h_{\widetilde A}}\right)}^\lambda,{\overline{Lim}\left(C_{h_{\widetilde A}}\right)}^\lambda\rfloor e^{j2\pi.\lceil\left(\frac{{\underline T}_{\widetilde A}}{2\pi}\right)^\lambda,\left(\frac{{\overline T}_{\widetilde A}}{2\pi}\right)^\lambda\rfloor},\end{Bmatrix},\\\lambda>0\end{array}$$

(43)

$${\widetilde A}_c\cup{\widetilde B}_c=\begin{Bmatrix}\begin{array}{c}\lceil min\left(\underline{Lim}\left(C_{\mu_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\underline\alpha}_{\widetilde A}}{2\pi}\right)},\underline{Lim}\left(C_{\mu_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\underline\alpha}_{\widetilde B}}{2\pi}\right)}\right),max\left(\overline{Lim}\left(C_{\mu_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\overline\alpha}_{\widetilde A}}{2\pi}\right)},\overline{Lim}\left(C_{\mu_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\overline\alpha}_{\widetilde B}}{2\pi}\right)}\right)\rfloor,\\\lceil\min\left(\underline{Lim}\left(C_{n_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\underline\gamma}_{\widetilde A}}{2\pi}\right)},\underline{Lim}\left(C_{n_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\underline\gamma}_{\widetilde B}}{2\pi}\right)}\right),\max\left(\overline{Lim}\left(C_{n_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\overline\gamma}_{\widetilde A}}{2\pi}\right)},\overline{Lim}\left(C_{n_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\overline\gamma}_{\widetilde B}}{2\pi}\right)}\right)\rfloor,\\\lceil min\left(\underline{Lim}\left(C_{v_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\underline\beta}_{\widetilde A}}{2\pi}\right)},\underline{Lim}\left(C_{v_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\underline\beta}_{\widetilde B}}{2\pi}\right)}\right),max\left(\overline{Lim}\left(C_{v_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\overline\beta}_{\widetilde A}}{2\pi}\right)},\overline{Lim}\left(C_{v_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\overline\beta}_{\widetilde B}}{2\pi}\right)}\right)\rfloor,\end{array}\\\lceil min\left(\underline{Lim}\left(C_{h_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\underline T}_{\widetilde A}}{2\pi}\right)},\underline{Lim}\left(C_{h_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\underline T}_{\widetilde B}}{2\pi}\right)}\right),max\left(\overline{Lim}\left(C_{h_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\overline T}_{\widetilde A}}{2\pi}\right)},\overline{Lim}\left(C_{h_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\overline T}_{\widetilde B}}{2\pi}\right)}\right)\rfloor\end{Bmatrix}$$

(44)

$${\widetilde A}_c\cap{\widetilde B}_c=\begin{Bmatrix}\begin{array}{c}\lceil\max\left(\underline{Lim}\left(C_{\mu_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\underline\alpha}_{\widetilde A}}{2\pi}\right)},\underline{Lim}\left(C_{\mu_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\underline\alpha}_{\widetilde B}}{2\pi}\right)}\right),\min\left(\overline{Lim}\left(C_{\mu_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\overline\alpha}_{\widetilde A}}{2\pi}\right)},\overline{Lim}\left(C_{\mu_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\overline\alpha}_{\widetilde B}}{2\pi}\right)}\right)\rfloor,\\\lceil\max\left(\underline{Lim}\left(C_{n_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\underline\gamma}_{\widetilde A}}{2\pi}\right)},\underline{Lim}\left(C_{n_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\underline\gamma}_{\widetilde B}}{2\pi}\right)}\right),\min\left(\overline{Lim}\left(C_{n_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\overline\gamma}_{\widetilde A}}{2\pi}\right)},\overline{Lim}\left(C_{n_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\overline\gamma}_{\widetilde B}}{2\pi}\right)}\right)\rfloor,\\\lceil\max\left(\underline{Lim}\left(C_{v_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\underline\beta}_{\widetilde A}}{2\pi}\right)},\underline{Lim}\left(C_{v_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\underline\beta}_{\widetilde B}}{2\pi}\right)}\right),\min\left(\overline{Lim}\left(C_{v_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\overline\beta}_{\widetilde A}}{2\pi}\right)},\overline{Lim}\left(C_{v_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\overline\beta}_{\widetilde B}}{2\pi}\right)}\right)\rfloor,\end{array}\\\lceil\max\left(\underline{Lim}\left(C_{h_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\underline T}_{\widetilde A}}{2\pi}\right)},\underline{Lim}\left(C_{h_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\underline T}_{\widetilde B}}{2\pi}\right)}\right),\min\left(\overline{Lim}\left(C_{h_{\widetilde A}}\right)e^{j2\pi.\left(\frac{{\overline T}_{\widetilde A}}{2\pi}\right)},\overline{Lim}\left(C_{h_{\widetilde B}}\right)e^{j2\pi.\left(\frac{{\overline T}_{\widetilde B}}{2\pi}\right)}\right)\rfloor\end{Bmatrix}$$

(45)

M-SWARA with QPFRs

SWARA is used to define the weights of different factors. This technique has some significant advantages. First, weights can be easily calculated with the SWARA method. In addition, the SWARA method can perform consistency analysis of comparisons (Kou et al., 2023a). In this way, it can be checked whether the data received from users is consistent. However, causality analysis of the criteria cannot be determined with this technique. Some improvements have been made in the classical SWARA method in this study. A new technique called multi-SWARA (M-SWARA) has been developed (Xu et al., 2023). The decision matrix is formed from the expert opinions obtained as in Eq. 46.

$$C_k=\begin{bmatrix}0&C_{12}&\cdots&&\cdots&C_{1n}\\C_{21}&0&\cdots&&\cdots&C_{2n}\\\vdots&\vdots&\ddots&&\cdots&\cdots\\\vdots&\vdots&\vdots&&\ddots&\vdots\\C_{n1}&C_{n2}&\cdots&&\cdots&0\end{bmatrix}$$

(46)

Aggregated values are explained in Eq. 47.

$$\textit{C}=\begin{pmatrix}\lceil min_{i=1}^k\left(\underline{Lim}\left(C_{\mu_{ij}}\right)\right),max_{i=1}^k\left(\overline{Lim}\left(C_{\mu_{ij}}\right)\right)\rfloor e^{j2\pi.\lceil min_{i=1}^k\left(\frac{{\underline\alpha}_{ij}}{2\pi}\right),max_{i=1}^k\left(\frac{{\overline\alpha}_{ij}}{2\pi}\right)\rfloor},\\\lceil min_{i=1}^k\left(\underline{Lim}\left(C_{n_{ij}}\right)\right),max_{i=1}^k\left(\overline{Lim}\left(C_{n_{ij}}\right)\right)\rfloor e^{j2\pi.\lceil min_{i=1}^k\left(\frac{{\underline\gamma}_{ij}}{2\pi}\right),max_{i=1}^k\left(\frac{{\overline\gamma}_{ij}}{2\pi}\right)\rfloor},\\\lceil min_{i=1}^k\left(\underline{Lim}\left(C_{v_{ij}}\right)\right),max_{i=1}^k\left(\overline{Lim}\left(C_{v_{ij}}\right)\right)\rfloor e^{j2\pi.\lceil min_{i=1}^k\left(\frac{{\underline\beta}_{ij}}{2\pi}\right),max_{i=1}^k\left(\frac{{\overline\beta}_{ij}}{2\pi}\right)\rfloor},\\\lceil min_{i=1}^k\left(\underline{Lim}\left(C_{h_{ij}}\right)\right),max_{i=1}^k\left(\overline{Lim}\left(C_{h_{ij}}\right)\right)\rfloor e^{j2\pi.\lceil min_{i=1}^k\left(\frac{{\underline T}_{ij}}{2\pi}\right),max_{i=1}^k\left(\frac{{\overline T}_{ij}}{2\pi}\right)\rfloor}\end{pmatrix}$$

(47)

Equation 48 is taken into consideration to compute defuzzified items.

$${Defc}_i=\frac{\begin{pmatrix}\underline{Lim}\left(C_{\mu_i}\right)-\underline{Lim}\left(C_{n_i}\right)+\underline{Lim}\left(C_{\mu_i}\right).\left(\underline{Lim}\left(C_{v_i}\right)-\underline{Lim}\left(C_{h_i}\right)\right)+\left(\frac{{\underline\alpha}_{ij}}{2\pi}\right)-\left(\frac{{\underline\gamma}_{ij}}{2\pi}\right)+\left(\frac{{\underline\alpha}_{ij}}{2\pi}\right).\left(\left(\frac{{\underline\beta}_{ij}}{2\pi}\right)-\left(\frac{{\underline T}_{ij}}{2\pi}\right)\right)+\\\overline{Lim}\left(C_{\mu_i}\right)-\overline{Lim}\left(C_{n_i}\right)+\overline{Lim}\left(C_{\mu_i}\right).\left(\overline{Lim}\left(C_{v_i}\right)-\overline{Lim}\left(C_{h_i}\right)\right)+\left(\frac{{\overline\alpha}_{ij}}{2\pi}\right)-\left(\frac{{\overline\gamma}_{ij}}{2\pi}\right)+\left(\frac{{\overline\alpha}_{ij}}{2\pi}\right).\left(\left(\frac{{\overline\beta}_{ij}}{2\pi}\right)-\left(\frac{{\overline T}_{ij}}{2\pi}\right)\right)\end{pmatrix}}2$$

(48)

Next, ${s}_{j}$ (importance rate), ${k}_{j}$ (coefficient), ${q}_{j}$ (recomputed weight), and ${w}_{j}$ (weight) are identified as in Eqs. 49, 50, 51 (Niu et al., 2023).

$$k_j=\left\{\begin{array}{cc}1&j=1\\s_j+1&j>1\end{array}\right.$$

(49)

$$q_j=\left\{\begin{array}{cc}1&j=1\\\frac{q_{j-1}}{k_j}&j>1\end{array}\right.$$

(50)

If $s_{j-1}=s_j,q_{j-1}=q_j$; If $s_j=0,k_{j-1}=k_j$   

$${w}_{j}=\frac{{q}_{j}}{\sum _{k=1}^{n}{q}_{k}}$$

(51)

After that, the values are transposed and limited to the power of 2t + 1 to define the weights. Moreover, with the help of the threshold values, impact-relation degrees can be identified (Mikhaylov et al., 2023).

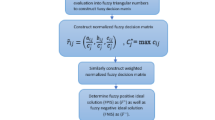
TOPSIS with QPFRs

TOPSIS technique is taken into consideration to rank various alternatives. In this process, the distances to the optimal solutions are used (Pour et al., 2023). This proposed model includes the extension of the classical TOPSIS with QPFRNs. Hence, more effective evaluations can be conducted (Bhatia & Diaz-Elsayed, 2023). The evaluations are obtained from the experts and decision matrix is generated as in Eq. 52.

$$X_k=\begin{bmatrix}0&X_{12}&\cdots&&\cdots&X_{1m}\\X_{21}&0&\cdots&&\cdots&X_{2m}\\\vdots&\vdots&\ddots&&\cdots&\cdots\\\vdots&\vdots&\vdots&&\ddots&\vdots\\X_{n1}&X_{n2}&\cdots&&\cdots&0\end{bmatrix}$$

(52)

The values are defuzzified and normalized with Eq. 53.

$${r}_{ij}= \frac{{X}_{ij}}{\sqrt{\sum _{i=1}^{m}{X}_{ij}^{2}}}.$$

(53)

Equation 54 is used to define weighted values (Aydoğdu et al., 2023).

$$v_ij=w_ij\times r_ij$$

(54)

The positive and negative ideal solutions, ${A}^{+}$ and ${A}^{-}$, can be identified as in Eqs. 55 and 56.

$$A^+=\left\{v_1j,v_2j,\dots,v_mj\right\}=\left\{\max\;v_1j\;for\mathit\;\forall\;j\in n\right\},$$

(55)

$$A^-=\left\{v_1j,v_2j,\dots,v_mj\right\}=\left\{\min\;v_1j\;\mathrm{for}\mathit\;\forall\;j\in n\right\}.$$

(56)

Next, by Eqs. 57 and 58, the distances to the best and worst alternatives, ${D}_{i}^{+}$ and ${D}_{i}^{-}$, are computed.

$$D_i^+=\sqrt{{\textstyle\sum_{j=1}^n}\left(v_{ij}-A_j^+\right)^2},$$

(57)

$$D_i^-=\sqrt{\textstyle\sum_{j=1}^n\left(v_{ij}-A_j^-\right)^2}.$$

(58)

The relative closeness to the ideal solutions, ${RC}_{i}$ is used to rank the alternatives as in Eq. (59) (Pour et al., 2023).

$${RC}_i=\frac{D_i^-}{D_i^++D_i^-}.$$

(59)

Model Construction

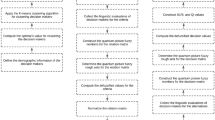
Existing models in the literature are criticized due to some conditions. For instance, in some of the models, analytical hierarchy process was taken into consideration to weigh the determinants (Moslem, 2024; Yorulmaz & Eti, 2024). Similarly, some scholars also used analytical network process methodology to compute the weights of the items (Nalbant, 2024; Quaiser & Srivastava, 2024). However, these studies could not consider the causality relationship between these indicators. On the other side, decision-making techniques were integrated with the fuzzy sets in some of the previously generated models. In this process, the main reason is to minimize the uncertainties in this process. For this purpose, some studies considered triangular fuzzy sets (Dinçer et al., 2022b; Dong et al., 2021; Wang, 2020), whereas some other scholars used trapezoidal fuzzy numbers (Kou et al., 2021; Zhao et al., 2021; Dombi & Jónás, 2020). However, these sets are also criticized because a single membership degree is taken into consideration. These results indicate that there is a strong need for a new decision-making model to evaluate the optimization of renewable energy investments. While integrating previously explained techniques, a new model is defined. In this process, the M-SWARA methodology is used to weigh the indicators so that the causality relationship between these factors can be considered. Similar to this issue, for the purpose of handling uncertainties more effectively, picture fuzzy rough sets are used in the analysis process that was introduced by Cuong and Kreinovich (2013). With the help of this situation, the concepts of picture fuzzy sets and rough sets can be combined. Owing to using picture fuzzy sets, membership degrees can be represented as intervals. Moreover, rough sets can help understand patterns in the data set and sort them into specific categories. The details of the proposed model are shown in Fig. 1.

Fig. 1

The algorithm of hybrid model

In the first stage, the knowledge-based determinants of process optimization in investment decisions are identified. For this purpose, an analysis is performed by using DEMATEL based on QPFRs. In this process, a decision matrix is generated, the values are defuzzified and normalized, and stable matrix is constructed. In the next stage, investment alternatives for process optimization in renewable energy projects are defined. In this context, QPFR-TOPSIS is taken into consideration. Within this framework, the values are defuzzified, normalized, and weighted. Finally, the most significant alternatives can be defined. In the second stage, the weights computed in the first stage are taken into consideration. Hence, there is a progressive relationship between these two stages.

Analysis Results

The proposed model has two different parts. In this section, the results are given for each part separately.

Weighting the Knowledge-Based Determinants of Process Optimization

First, the knowledge-based determinants of process optimization in renewable energy investment decisions are selected. They are detailed in Table 1.

Table 1 Determinants of process optimization in renewable energy investment decisions

Ensuring efficiency in renewable energy projects means less loss in energy production. On the other hand, an efficient energy investment project contributes to cost savings. In this way, it is possible to reduce the costs of energy investment projects. Customers have different expectations from renewable energy projects such as safety and low cost. Meeting these expectations increases customers’ satisfaction with the project. Flexible service delivery is another essential element for process optimization in renewable energy projects. In this way, energy supply and demand balance can be achieved. On the other hand, flexible service provision also enables more efficient use of energy resources. In this way, energy demand management will be carried out more successfully. Owing to the quality of energy production equipment, it will be easier to increase the efficiency of the project. Preferring higher quality power generation equipment reduces the possibility of failure in projects. In this way, it is much more possible to ensure the sustainability of the projects.

After that, evaluations are obtained from the expert team that consists of three different people. The first expert is the general manager in an energy production company. He has 25 years working experience with a master’s degree. The second expert is an academician that has lots of publications related to the energy transition. He has more than 20 years of working experience. The final expert works as a chief finance officer in a renewable energy company who has 23 years of working experience. While they evaluate the questions related to the criteria, the values in Table 2 are considered.

Table 2 Linguistic scales and QPFRs for evaluation

The evaluations are denoted in Table 3.

Table 3 Evaluations for indicators

QPFRs for the relation matrix are computed as in Table 4.

Table 4 QPFRs for the relation matrix

Moreover, the QPFRs for the relation matrix are provided in Table 5.

Table 5 QPFRs for the direct relation matrix

Defuzzified values are calculated as in Table 6.

Table 6 The defuzzified values of QPFRSs

Normalized relation matrix is constructed as in Table 7.

Table 7 The normalized relation matrix

Critical values for the relationship degrees of each criterion are computed as in Table 8.

Table 8 Sj, kj, qj, and wj values

Relation matrix can be created as in Table 9. In this table, impact directions are also presented.

Table 9 Relation matrix and the impact directions

Table 9 demonstrates that flexibility is the most influencing factor because it affects both efficiency and quality. Furthermore, quality is the most influenced indicator since it is influenced by both customer needs and flexibility. The stable matrix is created in the following step as in Table 10.

Table 10 Stable matrix

The weights of the indicators are also demonstrated in Fig. 2.

Fig. 2

Weights

Quality is the most important factor for project optimization in renewable energy investments. In addition, customer expectations are another prominent variable in this process. Efficiency and flexibility, on the other hand, have a lower weight of importance compared to the others. As it can be understood from here, it is important that the materials used in renewable energy investments are of high quality. This will contribute to minimizing the disruptions in the energy production process. Thus, it will be possible to produce uninterrupted energy. Furthermore, investors should also pay attention to issues that increase customer satisfaction. In this respect, meeting these expectations increases the satisfaction and trust of the customers in the project. This allows the products to be preferred more by customers.

Ranking the Investment Alternatives for Process Optimization of Renewable Energy Projects

This part of the analysis is related to the alternative ranking. In this context, first, investment alternatives are selected regarding the process optimization of renewable energy projects. They are explained in Table 11.

Table 11 Investment alternatives for process optimization of renewable energy projects

Environmental regulations and incentives play an important role in increasing the optimization of renewable energy investment projects. These practices can reduce the costs of projects or shorten their turnaround times. This reduces the risks of investors and ensures that projects are competitive. On the other hand, environmental regulations and incentives encourage innovation in renewable energy technologies. This process also contributes significantly to increasing energy efficiency. Diversification of renewable energy projects plays an important role in increasing the optimization of renewable energy investment projects. This type of diversification will allow for the distribution of risks. Similarly, diversifying renewable energy projects helps secure energy supply. The development of technological infrastructure has a key importance in increasing the optimization of renewable energy investment projects. Technological advances can improve the efficiency and performance of renewable energy technologies. More efficient technologies also allow for higher productivity. On the other hand, to increase the optimization of renewable energy investment projects, effective financing resources are required. Appropriate and sufficient financing ensures the realization of the projects and initiates the optimization process. Similarly, effective sources of finance play an important role in reducing the financial risks of renewable energy projects. A successful supply chain also plays an important role in increasing the optimization of renewable energy investment projects. Timely and accurate sourcing of materials and equipment required for renewable energy projects is critical. This, in turn, contributes significantly to increasing the efficiency of the processes of the projects. Table 12 identifies the evaluations for these alternatives.

Table 12 Linguistic evaluations of decision makers for the alternatives

QPFRs for the decision matrix are constructed and the details are presented in Table 13.

Table 13 QPFRs for the decision matrix

Next, QPFRs for the decision matrix are demonstrated in Table 14.

Table 14 QPFRs for the decision matrix

Defuzzified decision values are given in Table 15.

Table 15 The defuzzified decision values

Normalized decision values are created as in Table 16.

Table 16 The normalized decision values

Weighted decision values are identified in Table 17.

Table 17 The weighted decision values

Investment alternatives for process optimization of renewable energy projects are ranked in the following step. These results are indicated in Table 18.

Table 18 The ranking results of the alternatives

They are also illustrated in Fig. 3.

Fig. 3

Ranking results

Variety of the renewable energy sources is the most critical alternative to improve the optimization of this source. Additionally, technological infrastructure is the second most important alternative for this condition. Financial and environmental regulations are in the last ranks. Diversification of renewable energy projects is very important in terms of distributing risks. In this way, dependency on a single energy source or technology can be reduced. Diversification of renewable energy projects also ensures that the energy supply is secured. The development of technological infrastructure has an important role in increasing the optimization of renewable energy investment projects. Technological advances can improve the efficiency and performance of renewable energy technologies. More efficient technologies allow investment projects to achieve higher energy production and therefore higher efficiency.

Discussions

Quality is found as the most critical determinant for project optimization in renewable energy investments. Quality products increase the performance and efficiency of renewable energy projects. In this context, power generation equipment should be designed to provide high performance. On the other hand, quality products increase the reliability and durability of the project. High-quality power generation equipment reduces the probability of failure. This contributes significantly to uninterrupted electricity generation. Thus, energy security and continuity of the project are possible. Furthermore, quality products provide long-term cost savings. In this way, the products will need less maintenance and repair. This allows the project to save costs in the long run. On the other hand, high-quality equipment helps to use less resources during power generation. Thus, less waste and lower emissions can occur.

Some strategies should be implemented to use quality products in renewable energy projects. Choosing the right supplier is vital in this process. For the products used to be of high quality, it is necessary to do business with reliable suppliers. According to Alonso-Travesset et al. (2023), this condition helps to ensure a continuous quality in the products used. In this context, compliance with standards is also necessary for the use of quality products. Ottonelli et al. (2023) identified that it may be easier for the products that comply with certain standards to have high quality and performance. In this context, the conformity of the products to the standards should be checked periodically. Karakislak et al. (2023) mentioned that to achieve this goal, it is very important to have an effective control mechanism. On the other hand, Naqvi et al. (2023) discussed that technological developments in the renewable energy sector are advancing rapidly. Therefore, it is very important to follow these current developments in the sector effectively for the quality of the products used in the projects.

According to the results obtained, the diversification of renewable energy projects plays an important role in increasing the optimization of renewable energy investment projects. In this context, projects based on different technologies and energy sources need to create a portfolio. Van Song et al. (2023) claimed that this condition reduces the dependency on a single energy source. Additionally, Zhang et al. (2023b) concluded that the diversification of renewable energy projects ensures that the energy supply is secured. In this framework, projects should depend on different energy sources. This situation supports a more balanced energy production in different climatic and weather conditions. Moreover, Yi et al. (2023) denoted that the diversification of renewable energy projects supports innovation and technological development. In other words, by focusing on different technologies, it is possible to develop more innovative products.

Conclusion

In this study, it is aimed to determine the most critical knowledge-based determinants and the most suitable investment alternatives of process optimization in renewable energy investment decisions. For this purpose, this study introduces a novel integration of the QPFR-M-SWARA and QPFR-TOPSIS frameworks to optimize investment decisions in the renewable energy sector. In Stage 1, the knowledge-based determinants of process optimization in investment decisions are identified through a thorough analysis using DEMATEL based on QPFRs. In Stage 2, investment alternatives for process optimization in renewable energy projects are identified and evaluated using linguistic evaluations from decision-makers with QPFR-TOPSIS. Quality is defined as the most important factor for project optimization in renewable energy investments. Moreover, customer expectations also play a critical role in this process. However, efficiency and flexibility have a lower weight of importance compared to the others. With respect to the alternative ranking results, it is found that a variety of renewable energy sources is the most convenient alternative to improve the optimization of this source. Furthermore, technological infrastructure is the second most important alternative for this condition.

The main contribution of the study is that a priority analysis is conducted for information-based factors affecting the performance of renewable energy projects. Knowledge-based factors should be improved to increase the performance of renewable energy projects. However, the main problem is that improvements to these factors also create new costs. Therefore, because of the budget limitation, it is quite difficult to make improvements for many of these variables. Thus, this priority evaluation helps to increase the performance of renewable energy projects. Another critical contribution of this study is that a new decision-making technique is proposed with the name of M-SWARA. In classical SWARA, an impact relation map of the factors cannot be created. To solve this problem, the SWARA technique is enhanced in this study with some improvements. As a result, the M-SWARA methodology is created so that the causal directions of the criteria can be identified. In addition, considering picture fuzzy rough sets helps to achieve more accurate findings because they represent membership degrees as intervals.

In this study, different types of renewable energy investments are not analyzed separately. Instead, a general analysis of renewable energy projects was carried out. This situation can be addressed in more detail in future studies. In other words, a more specific analysis of the process optimization of solar projects can be performed. Similarly, a comparative analysis can be performed to identify important knowledge-based variables in different types of renewable energy. In this way, it will be possible to develop different strategy proposals for each type of clean energy. On the other hand, a new model suitable for the subject of the study is proposed. A new decision-making model can be developed in future studies. It will also be possible to determine the direction of the relations between the variables with a new model to be created using sine trigonometric numbers. CRITIC technique can also be taken into consideration to consider the correlation between the items. Similarly, the innovation theories and concepts of triple helix, quadruple helix, and quintuple helix can be considered for future studies (Carayannis & Campbell, 2010; Carayannis et al., 2022).