Skip to main content
SpringerLink
Log in

Feature selection using neighborhood uncertainty measures and Fisher score for gene expression data classification

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

Abstract

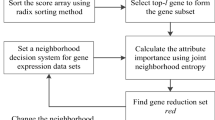
The classification of gene expression data provides a basis for the study of pathogenesis and treatment. However, this type of data is characterized by high dimensionality and small samples, which seriously affect the classification results. Consequently, it is necessary to use a gene selection algorithm to select key genes from gene expression data to improve the classification results, but the existing gene selection algorithm has the problems of low classification precision and high time complexity. Therefore, this paper proposes a gene selection algorithm using neighborhood uncertainty measures and Fisher score. First, to make full use of the information provided by the neighborhood decision system, the neighborhood fusion coverage and neighborhood fusion credibility are defined based on the neighborhood coverage and neighborhood credibility, and they are used to characterize neighborhood uncertainty measures. Second, the neighborhood uncertainty measures are extended by combining the algebraic and information theory views, and a heuristic nonmonotonic gene selection algorithm is designed based on the neighborhood uncertainty measures. The algorithm makes full use of the information in the neighborhood decision system to evaluate the importance of genes from the algebraic and information theory views, thereby selecting an optimal gene subset and improving classification precision. Third, Fisher score method is introduced into the proposed algorithm to preliminarily eliminate redundant genes to reduce the time cost of calculation and improve the performance of the algorithm. Finally, by comparing the experimental results of our algorithm with those of existing gene selection algorithms on ten gene datasets, it is proved that our algorithm can effectively improve the classification results for gene data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Liu KY, Yang XB, Yu HL, Fujita H, Chen XJ, Liu D (2020) Supervised information granulation strategy for attribute reduction. Int J Mach Learn Cybern 11(9):2149–2163. https://doi.org/10.1007/s13042-020-01107-5

    Article  Google Scholar 

  2. Xu JC, Qu KL, Meng XR, Sun YH, Hou QC (2022) Feature selection based on multiview entropy measures in multiperspective rough set. Int J Intell Syst 37(10):7200–7234. https://doi.org/10.1002/int.22878

    Article  Google Scholar 

  3. Sang BB, Chen HM, Yang L, Li TR, Xu WH (2022) Incremental feature selection using a conditional entropy based on fuzzy dominance neighborhood rough sets. IEEE Trans Fuzzy Syst 30(6):1683–1697. https://doi.org/10.1109/TFUZZ.2021.3064686

    Article  Google Scholar 

  4. Qian WB, Dong P, Wang YL, Dai SM, Huang JT (2022) Local rough set-based feature selection for label distribution learning with incomplete labels. Int J Mach Learn Cybern 13(8):2345–2364. https://doi.org/10.1007/s13042-022-01528-4

    Article  Google Scholar 

  5. Yang YY, Chen DG, Zhang X, Ji ZY, Zhang YJ (2022) Incremental feature selection by sample selection and feature-based accelerator. Appl Soft Comput. https://doi.org/10.1016/j.asoc.2022.108800

    Article  Google Scholar 

  6. Chen Y, Liu KY, Song JJ, Fujita H, Yang XB, Qian YH (2020) Attribute group for attribute reduction. Inf Sci 535:64–80. https://doi.org/10.1016/j.ins.2020.05.010

    Article  MATH  Google Scholar 

  7. Xu WH, Yuan KH, Li WT (2022) Dynamic updating approximations of local generalized multigranulation neighborhood rough set. Appl Intell 52(8):9148–9173. https://doi.org/10.1007/s10489-021-02861-x

    Article  Google Scholar 

  8. Pawlak Z, Skowron A (2007) Rough sets: Some extensions. Inf Sci 177(1):28–40. https://doi.org/10.1016/j.ins.2006.06.006

    Article  MathSciNet  MATH  Google Scholar 

  9. Parthalain NM, Shen Q (2009) Exploring the boundary region of tolerance rough sets for feature selection. Pattern Recogn 42(5):655–667. https://doi.org/10.1016/j.patcog.2008.08.029

    Article  MATH  Google Scholar 

  10. Sun L, Wang LY, Ding WP, Qian YH, Xu JC (2020) Neighborhood multi-granulation rough sets-based attribute reduction using Lebesgue and entropy measures in incomplete neighborhood decision systems. Knowl-Based Syst. https://doi.org/10.1016/j.knosys.2019.105373

    Article  Google Scholar 

  11. Wang CZ, Huang Y, Shao MW, Hu QH, Chen DG (2020) Feature selection based on neighborhood self-information. IEEE Transactions on Cybernetics 50(9):4031–4042. https://doi.org/10.1109/TCYB.2019.2923430

    Article  Google Scholar 

  12. Hu QH, Yu DR, Liu JF, Wu CX (2008) Neighborhood rough set based heterogeneous feature subset selection. Inf Sci 178(18):3577–3594. https://doi.org/10.1016/j.ins.2008.05.024

    Article  MathSciNet  MATH  Google Scholar 

  13. Sun L, Xu JC, Tian Y (2012) Feature selection using rough entropy-based uncertainty measures in incomplete decision systems. Knowl-Based Syst 36:206–216. https://doi.org/10.1016/j.knosys.2012.06.010

    Article  Google Scholar 

  14. Sun L, Wang LY, Ding WP, Qian YH, Xu JC (2021) Feature selection using fuzzy neighborhood entropy-based uncertainty measures for fuzzy neighborhood multigranulation rough sets. IEEE Trans Fuzzy Syst 29(1):19–33. https://doi.org/10.1109/TFUZZ.2020.2989098

    Article  Google Scholar 

  15. Wang CZ, Huang Y, Ding WP, Cao ZH (2021) Attribute reduction with fuzzy rough self-information measures. Inf Sci 549:68–86. https://doi.org/10.1016/j.ins.2020.11.021

    Article  MathSciNet  MATH  Google Scholar 

  16. Tsumoto S (2002) Accuracy and coverage in rough set rule induction. Int Conf Rough Sets CurrTrends Comput. https://doi.org/10.1007/3-540-45813-1_49

    Article  MATH  Google Scholar 

  17. Sun L, Zhang XY, Qian YH, Xu JC, Zhang SG (2019) Feature selection using neighborhood entropy-based uncertainty measures for gene expression data classification. Inf Sci 502:18–41. https://doi.org/10.1016/j.ins.2019.05.072

    Article  MathSciNet  MATH  Google Scholar 

  18. Wong SKM, Ziarko W (1985) On optimal decision rules in decision tables. Bull Polish Acad Sci Math 33(11):693–696

    MathSciNet  MATH  Google Scholar 

  19. Hu QH, Zhang L, Zhang D, Pan W, An S, Pedrycz W (2011) Measuring relevance between discrete and continuous features based on neighborhood mutual information. Expert Syst Appl 38(9):10737–10750. https://doi.org/10.1016/j.eswa.2011.01.023

    Article  Google Scholar 

  20. Sun L, Zhang XY, Qian YH, Xu JC, Zhang SG, Tian Y (2019) Joint neighborhood entropy-based gene selection method with fisher score for tumor classification. Appl Intell 49(4):1245–1259. https://doi.org/10.1007/s10489-018-1320-1

    Article  Google Scholar 

  21. Xu JC, Wang Y, Mu HY, Huang FZ (2019) Feature genes selection based on fuzzy neighborhood conditional entropy. J Intell Fuzzy Syst 36(1):117–126. https://doi.org/10.3233/JIFS-18100

    Article  Google Scholar 

  22. Jiang ZH, Yang XB, Yu HL, Liu D, Wang PX, Qian YH (2019) Accelerator for multi-granularity attribute reduction. Knowl-Based Syst 177:145–158. https://doi.org/10.1016/j.knosys.2019.04.014

    Article  Google Scholar 

  23. Fan J, Jiang YL, Liu Y (2017) Quick attribute reduction with generalized indiscernibility models. Inf Sci 397:15–36. https://doi.org/10.1016/j.ins.2017.02.032

    Article  Google Scholar 

  24. Sun L, Zhang XY, Xu JC, Wang W, Liu RN (2018) A gene selection approach based on the fisher linear discriminant and the neighborhood rough set. Bioengineered 9(1):144–151. https://doi.org/10.1080/21655979.2017.1403678

    Article  Google Scholar 

  25. Li WT, Xu WH, Zhang XY, Zhang J (2021) Updating approximations with dynamic objects based on local multigranulation rough sets in ordered information systems. Artif Intell Rev. https://doi.org/10.1007/s10462-021-10053-9

    Article  Google Scholar 

  26. Miao DQ, Hu GR (1999) A heuristic algorithm for knowledge reduction. J Comput Res Dev 36(6):681–684

    Google Scholar 

  27. Wang GY, Yu H, Yang DC (2002) Decision table reduction based on conditional information entropy. Chin J Comput 25(7):759–766. https://doi.org/10.3321/j.issn:0254-4164.2002.07.013

    Article  MathSciNet  Google Scholar 

  28. Wu D, Guo SZ (2019) An improved Fisher Score feature selection method and its application. J Liaoning Tech Univ 38(5):472–479

    Google Scholar 

  29. Sun L, Zhang XY, Xu JC, Zhang SG (2019) An attribute reduction method using neighborhood entropy measures in neighborhood rough sets. Entropy. https://doi.org/10.3390/e21020155

    Article  MathSciNet  Google Scholar 

  30. Xu JC, Qu KL, Yang Y (2021) Feature selection combining information theory view and algebraic view in the neighborhood decision system. Entropy 23(6):704. https://doi.org/10.3390/e23060704

    Article  MathSciNet  Google Scholar 

  31. Chen XW, Xu WH (2022) Double-quantitative multigranulation rough fuzzy set based on logical operations in multi-source decision systems. Int J Mach Learn Cybern 13(4):1021–1048. https://doi.org/10.1007/s13042-021-01433-2

    Article  Google Scholar 

  32. Shukla AK, Singh P, Vardhan M (2018) A hybrid gene selection method for microarray recognition. Biocybern Biomed Eng 38(4):975–991. https://doi.org/10.1016/j.bbe.2018.08.004

    Article  Google Scholar 

  33. Ye CC, Pan JL, Jin Q (2019) An improved SSO algorithm for cyber-enabled tumor risk analysis based on gene selection. Future Gener Comput Syst 92:407–418. https://doi.org/10.1016/j.future.2018.10.008

    Article  Google Scholar 

  34. Dong HB, Li T, Ding R, Sun J (2018) A novel hybrid genetic algorithm with granular information for feature selection and optimization. Appl Soft Comput 65:33–46. https://doi.org/10.1016/j.asoc.2017.12.048

    Article  Google Scholar 

  35. Huang XJ, Zhang L, Wang BJ, Li FZ, Zhang Z (2018) Feature clustering based support vector machine recursive feature elimination for gene selection. Appl Intell 48(3):594–607. https://doi.org/10.1007/s10489-017-0992-2

    Article  Google Scholar 

  36. Sun SQ, Peng QK, Zhang XK (2016) Global feature selection from microarray data using Lagrange multipliers. Knowl-Based Syst 110:267–274. https://doi.org/10.1016/j.knosys.2016.07.035

    Article  Google Scholar 

  37. Sun L, Liu RN, Xu JC, Zhang SG, Tian Y (2018) An affinity propagation clustering method using hybrid kernel function with LLE. IEEE Access 6:68892–68909. https://doi.org/10.1109/ACCESS.2018.2880271

    Article  Google Scholar 

  38. Xu FF, Miao DQ, Wei L (2009) Fuzzy-rough attribute reduction via mutual information with an application to cancer classification. Comput Math Appl 57(6):1010–1017. https://doi.org/10.1016/j.camwa.2008.10.027

    Article  MATH  Google Scholar 

  39. Chen YM, Zhang ZJ, Zheng JZ, Ma Y, Xue Y (2017) Gene selection for tumor classification using neighborhood rough sets and entropy measures. J Biomed Inform 67:59–68. https://doi.org/10.1016/j.jbi.2017.02.007

    Article  Google Scholar 

  40. Yang J, Liu YL, Feng CS, Zhu GQ (2016) Applying the Fisher score to identify Alzheimer’s disease-related genes. Genet Mol Res. https://doi.org/10.4238/gmr.15028798

    Article  Google Scholar 

  41. Xu JC, Qu KL, Sun YH, Yang J (2022) Feature selection using self-information uncertainty measures in neighborhood information systems. Appl Intell. https://doi.org/10.1007/s10489-022-03760-5

    Article  Google Scholar 

  42. Fan XD, Zhao WD, Wang CZ, Huang Y (2018) Attribute reduction based on max-decision neighborhood rough set model. Knowl-Based Syst 151:16–23. https://doi.org/10.1016/j.knosys.2018.03.015

    Article  Google Scholar 

  43. Sun L, Xu JC, Wang W, Yin Y (2016) Locally linear embedding and neighborhood rough set-based gene selection for gene expression data classification. Genet Mol Res. https://doi.org/10.4238/gmr.15038990

    Article  Google Scholar 

  44. Zhang W, Chen JJ (2018) Relief feature selection and parameter optimization for support vector machine based on mixed kernel function. J Mater Eng Perform 14(2):280–289. https://doi.org/10.23940/ijpe.18.02.p9.280289

    Article  Google Scholar 

  45. Aziz R, Verma CK, Srivastava N (2016) A fuzzy based feature selection from independent component subspace for machine learning classification of microarray data. Genomics Data 8:4–15. https://doi.org/10.1016/j.gdata.2016.02.012

    Article  Google Scholar 

  46. Apolloni J, Leguizamon G, Alba E (2016) Two hybrid wrapper-filter feature selection algorithms applied to high-dimensional microarray experiments. Appl Soft Comput 38:922–932. https://doi.org/10.1016/j.asoc.2015.10.037

    Article  Google Scholar 

  47. Lu HJ, Chen JY, Yan K, Jin Q, Xue Y, Gao ZG (2017) A hybrid feature selection algorithm for gene expression data classification. Neurocomputing 256:56–62. https://doi.org/10.1016/j.neucom.2016.07.080

    Article  Google Scholar 

  48. Li JT, Dong WP, Meng DY (2018) Grouped gene selection of cancer via adaptive sparse group lasso based on conditional mutual information. IEEE-ACM Trans Comput Biol Bioinform 15(6):2028–2038. https://doi.org/10.1109/TCBB.2017.2761871

    Article  Google Scholar 

  49. Dunn QJ (1961) Multiple comparisons among means. J Am Stat Assoc 56(293):52–64. https://doi.org/10.1080/01621459.1961.10482090

    Article  MathSciNet  MATH  Google Scholar 

  50. Friedman M (1940) A comparison of alternative tests of significance for the problem of mrankings. Ann Math Stat 11(1):86–92. https://doi.org/10.1214/aoms/1177731944

    Article  MATH  Google Scholar 

  51. Su ZG, Hu QH, Denoeux T (2021) A distributed rough evidential K-NN classifier: Integrating feature reduction and classification. IEEE Trans Fuzzy Syst 29(8):2322–2335. https://doi.org/10.1109/TFUZZ.2020.2998502

    Article  Google Scholar 

  52. Xu WH, Yuan KH, Li WT, Ding WP (2022) An emerging fuzzy feature selection method using composite entropy-based uncertainty measure and data distribution. IEEE Trans Emerg Top Comput Intell. https://doi.org/10.1109/TETCI.2022.3171784

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China under Grant (61976082, 62002103).

Author information

Authors and Affiliations

  1. College of Computer and Information Engineering, Henan Normal University, Xinxiang, 453007, China

    Jiucheng Xu, Kanglin Qu, Qincheng Hou & Xiangru Meng

  2. Engineering Lab of Intelligence Business & Internet of Things, Xinxiang, Henan Province, China

    Jiucheng Xu, Kanglin Qu, Qincheng Hou & Xiangru Meng

  3. College of Computer Engineering, Nanjing Institute of Technology, Nanjing, 210000, China

    Kangjian Qu

Authors
  1. Jiucheng Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kanglin Qu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kangjian Qu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Qincheng Hou
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xiangru Meng
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

JX: Conceptualization, Writing review and editing, Visualization, Project administration. KQ: Methodology, Software, Writing-original draft preparaton. QH: Formal analysis, Writing review and editing, Visualization. KQ: Writing review and editing, Visualization. XM: Formal analysis, Writing review and editing, Visualization. All authors have read and agreed to the published version of the manuscipt.

Corresponding authors

Correspondence to Kanglin Qu or Xiangru Meng.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

Proof of Proposition 1

From Eq. (2) and Eq. (8), we can get \(\left| {n_b^\delta \left( {{u_i}} \right) } \right| \ge \left| {n_c^\delta \left( {{u_i}} \right) } \right|\) and \({P_b}\left( D \right) \le {P_c}\left( D \right)\). According to Definition 4, \(N{H_\delta }\left( c \right) \ge N{H_\delta }\left( b \right)\) holds.

Proof of Property 1

$$\begin{aligned}{} & {} N{H_\delta }\left( {D|c} \right) + N{H_\delta }\left( c \right) \\{} & {} \quad = - \frac{{{P_c}\left( D \right) }}{{\left| U \right| }}\mathop \sum \limits _{i = 1}^{\left| U \right| } \log \left( {\frac{{{{\left| {n_c^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }^2}}}{{\left| {n_c^\delta \left( {{u_i}} \right) } \right| \left| {{n_{\left( {c,D} \right) }}\left( {{u_i}} \right) } \right| }}} \right) \\{} & {} \quad - \frac{{{P_c}\left( D \right) }}{{\left| U \right| }}\mathop \sum \limits _{i = 1}^{\left| U \right| } \log \left( {\frac{{\left| {n_c^\delta \left( {{u_i}} \right) } \right| }}{{\left| U \right| }}} \right) \\{} & {} \quad = - \frac{{{P_c}\left( D \right) }}{{\left| U \right| }}\mathop \sum \limits _{i = 1}^{\left| U \right| } \log \left( {\frac{{{{\left| {n_c^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }^2}}}{{\left| {n_c^\delta \left( {{u_i}} \right) } \right| \left| {{n_{\left( {c,D} \right) }}\left( {{u_i}} \right) } \right| }}*\frac{{\left| {n_c^\delta \left( {{u_i}} \right) } \right| }}{{\left| U \right| }}} \right) \\{} & {} \quad = - \frac{{{P_c}\left( D \right) }}{{\left| U \right| }}\mathop \sum \limits _{i = 1}^{\left| U \right| } \mathrm{{log}}\left( {\frac{{{{\left| {n_c^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }^2}}}{{\left| U \right| \left| {{n_{\left( {c,D} \right) }}\left( {{u_i}} \right) } \right| }}} \right) \end{aligned}$$

According to Definition 6, \(N{H_\delta }\left( {D,c} \right) = N{H_\delta }\left( {D|c} \right) + N{H_\delta }\left( c \right)\) holds.

Proof of Proposition 2

$$\begin{aligned} N{H_\delta }\left( {D,c} \right)= & {} - \frac{{{P_c}\left( D \right) }}{{\left| U \right| }}\mathop \sum \limits _{i = 1}^{\left| U \right| } \mathrm{{log}}\left( {\frac{{{{\left| {n_c^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }^2}}}{{\left| U \right| \left| {{n_{\left( {c,D} \right) }}\left( {{u_i}} \right) } \right| }}} \right) \\= & {} - \frac{{{P_c}\left( D \right) }}{{\left| U \right| }}\mathop \sum \limits _{i = 1}^{\left| U \right| } \mathrm{{log}}\left( {\frac{{\left| {n_c^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| \left| {n_c^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }}{{\left| U \right| \left| {{n_{\left( {c,D} \right) }}\left( {{u_i}} \right) } \right| }}} \right) \\= & {} - \frac{{{P_c}\left( D \right) }}{{\left| U \right| }}\mathop \sum \limits _{i = 1}^{\left| U \right| } \mathrm{{log}}\left( {\frac{{\left| {n_c^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }}{{\left| U \right| }}\frac{{\left| {n_c^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }}{{\left| {{n_{\left( {c,D} \right) }}\left( {{u_i}} \right) } \right| }}} \right) \\= & {} - \frac{{{P_c}\left( D \right) }}{{\left| U \right| }}\mathop \sum \limits _{i = 1}^{\left| U \right| } \mathrm{{log}}\left( {{\kappa _i}*\,{\alpha _i}} \right) \end{aligned}$$

Proof of Proposition 3

From Eq. (2), we know that \(n_b^\delta \left( {{u_i}} \right) \supseteq n_c^\delta \left( {{u_i}} \right)\), so \(n_b^\delta \left( {{u_i}} \right) \cap {\left[ {{u_i}} \right] _D} \supseteq n_c^\delta \left( {{u_i}} \right) \cap {\left[ {{u_i}} \right] _D}\), \(n_b^\delta \left( {{u_i}} \right) \cup {\left[ {{u_i}} \right] _D} \supseteq n_c^\delta \left( {{u_i}} \right) \cup {\left[ {{u_i}} \right] _D}\) and \({n_{\left( {b,D} \right) }}\left( {{u_i}} \right) \supseteq {n_{\left( {c,D} \right) }}\left( {{u_i}} \right)\). Thus, the numerical relationship between \(\frac{{{{\left| {n_b^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }^2}}}{{\left| {{n_{\left( {b,D} \right) }}\left( {{u_i}} \right) } \right| }}\) and \(\frac{{{{\left| {n_c^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }^2}}}{{\left| {{n_{\left( {c,D} \right) }}\left( {{u_i}} \right) } \right| }}\) is unknown, so the numerical relationship between \(- \frac{1}{{\left| U \right| }}\mathop \sum \limits _{i = 1}^{\left| U \right| } \mathrm{{log}}\left( {\frac{{{{\left| {n_b^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }^2}}}{{\left| U \right| \left| {{n_{\left( {b,D} \right) }}\left( {{u_i}} \right) } \right| }}} \right)\) and \(- \frac{1}{{\left| U \right| }}\mathop \sum \limits _{i = 1}^{\left| U \right| } \mathrm{{log}}\left( {\frac{{{{\left| {n_c^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }^2}}}{{\left| U \right| \left| {{n_{\left( {c,D} \right) }}\left( {{u_i}} \right) } \right| }}} \right)\) is not clear. From Eq. (8), \({P_b}\left( D \right) \le {P_c}\left( D \right)\) can be known. Therefore, the relation between \(- \frac{{{P_b}\left( D \right) }}{{\left| U \right| }}\mathop \sum \limits _{i = 1}^{\left| U \right| } \mathrm{{log}}\left( {\frac{{{{\left| {n_b^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }^2}}}{{\left| U \right| \left| {{n_{\left( {b,D} \right) }}\left( {{u_i}} \right) } \right| }}} \right)\) and \(- \frac{{{P_c}\left( D \right) }}{{\left| U \right| }}\mathop \sum \limits _{i = 1}^{\left| U \right| } \mathrm{{log}}\left( {\frac{{{{\left| {n_c^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }^2}}}{{\left| U \right| \left| {{n_{\left( {c,D} \right) }}\left( {{u_i}} \right) } \right| }}} \right)\) is not clear. According to Eq. (20), Proposition 3 holds.

Example

A Neighborhood decision system \(NS = \left( {U,C,D,\,\delta } \right)\) is shown below, where the universe \(U = \left\{ {{u_1},{u_2},{u_3},{u_4}} \right\}\); the conditional attribute set \(C = \left\{ {{c_1},{c_2},{c_3}} \right\}\); the decision attribute \(D = d\); the neighborhood radius \(\delta = 0.3\). Let initial gene subset \(c = \emptyset\), the base of log is 10, and \(P = 2\) in Eq. (1).

U

\({c_1}\)

\({c_2}\)

\({c_3}\)

d

\({u_1}\)

0.12

0.41

0.61

Y

\({u_2}\)

0.21

0.15

0.14

Y

\({u_3}\)

0.31

0.11

0.26

N

\({u_4}\)

0.61

0.13

0.23

N

From Eq. (3), \({\left[ {{u_1}} \right] _D} = {\left[ {{u_2}} \right] _D} = \left\{ {{u_1},{u_2}} \right\}\), \({\left[ {{u_3}} \right] _D} = {\left[ {{u_4}} \right] _D} = \left\{ {{u_3},{u_4}} \right\}\).

From Eq. (1), when \(c = \left\{ {{c_1}} \right\}\), we know that \(D{F_{\left\{ {{c_1}} \right\} }}\left( {{u_1},\,{u_1}} \right) = 0 \le \delta\), \(D{F_{\left\{ {{c_1}} \right\} }}\left( {{u_1},\,{u_2}} \right) = 0.09 \le \delta\), \(D{F_{\left\{ {{c_1}} \right\} }}\left( {{u_1},\,{u_3}} \right) = 0.19 \le \delta\), \(D{F_{\left\{ {{c_1}} \right\} }}\left( {{u_1},\,{u_4}} \right) = 0.49 > \delta\), \(D{F_{\left\{ {{c_1}} \right\} }}\left( {{u_2},\,{u_2}} \right) = 0 \le \delta\), \(D{F_{\left\{ {{c_1}} \right\} }}\left( {{u_2},\,{u_3}} \right) = 0.1 \le \delta\),      \(D{F_{\left\{ {{c_1}} \right\} }}\left( {{u_2},\,{u_4}} \right) = 0.4 > \delta\), \(D{F_{\left\{ {{c_1}} \right\} }}\left( {{u_3},\,{u_3}} \right) = 0 \le \delta\), \(D{F_{\left\{ {{c_1}} \right\} }}\left( {{u_3},\,{u_4}} \right) = 0.3 \le \delta\), \(D{F_{\left\{ {{c_1}} \right\} }}\left( {{u_4},\,{u_4}} \right) = 0 \le \delta\).

From Eq. (2), \(n_{\left\{ {{c_1}} \right\} }^\delta \left( {{u_1}} \right) = \left\{ {{u_1},{u_2},{u_3}} \right\}\), \(n_{\left\{ {{c_1}} \right\} }^\delta \left( {{u_2}} \right) = \left\{ {{u_1},{u_2},{u_3}} \right\}\), \(n_{\left\{ {{c_1}} \right\} }^\delta \left( {{u_3}} \right) = \left\{ {{u_1},{u_2},{u_3},{u_4}} \right\}\), \(n_{\left\{ {{c_1}} \right\} }^\delta \left( {{u_4}} \right) = \left\{ {{u_3},{u_4}} \right\}\).

From Eq. (14), \({n_{\left( {\left\{ {{c_1}} \right\} ,D} \right) }}\left( {{u_1}} \right) = n_{\left\{ {{c_1}} \right\} }^\delta \left( {{u_1}} \right) \cup {\left[ {{u_1}} \right] _D} = \left\{ {{u_1},{u_2},{u_3}} \right\}\), \({n_{\left( {\left\{ {{c_1}} \right\} ,D} \right) }}\left( {{u_2}} \right) = n_{\left\{ {{c_1}} \right\} }^\delta \left( {{u_2}} \right) \cup {\left[ {{u_2}} \right] _D} = \left\{ {{u_1},{u_2},{u_3}} \right\}\), \({n_{\left( {\left\{ {{c_1}} \right\} ,D} \right) }}\left( {{u_3}} \right) = n_{\left\{ {{c_1}} \right\} }^\delta \left( {{u_3}} \right) \cup {\left[ {{u_3}} \right] _D} = \left\{ {{u_1},{u_2},{u_3},{u_4}} \right\}\), \({n_{\left( {\left\{ {{c_1}} \right\} ,D} \right) }}\left( {{u_4}} \right) = n_{\left\{ {{c_1}} \right\} }^\delta \left( {{u_4}} \right) \cup {\left[ {{u_4}} \right] _D} = \left\{ {{u_3},{u_4}} \right\}\).

From Eq. (6), Eq. (7), and Eq. (8), \(\underline{{N_{\left\{ {{c_1}} \right\} }}} \left( D \right) = \,\left\{ {{u_4}} \right\}\), \(\overline{{N_{\left\{ {{c_1}} \right\} }}} \left( D \right) = \left\{ {{u_1},{u_2},{u_3},{u_4}} \right\}\), \({P_{\left\{ {{c_1}} \right\} }}\left( D \right) = \,\frac{{\left| {\underline{{N_{\left\{ {{c_1}} \right\} }}} \left( D \right) } \right| }}{{\left| {\overline{{N_{\left\{ {{c_1}} \right\} }}} \left( D \right) } \right| }} = \frac{1}{4}\).

From Eq. (20), \(N{H_\delta }\left( {D,\left\{ {{c_1}} \right\} } \right) = - \frac{{{P_{\left\{ {{c_1}} \right\} }}\left( D \right) }}{{\left| U \right| }}\mathop \sum \limits _{i = 1}^{\left| U \right| } \log \left( {\frac{{{{\left| {n_{\left\{ {{c_1}} \right\} }^\delta \left( {{u_i}} \right) \cap {{\left[ {{u_i}} \right] }_D}} \right| }^2}}}{{\left| U \right| \left| {{n_{\left( {\left\{ {{c_1}} \right\} ,D} \right) }}\left( {{u_i}} \right) } \right| }}} \right)\)

\(= - \frac{1/4}{4}\left( {\log \left( {\frac{{{2^2}}}{{4 \times 3}}} \right) + \log \left( {\frac{{{2^2}}}{{4 \times 3}}} \right) + \log \left( {\frac{{{2^2}}}{{4 \times 4}}} \right) + \log \left( {\frac{{{2^2}}}{{4 \times 2}}} \right) } \right) = 0.116\)

Similarly, \(N{H_\delta }\left( {D,\left\{ {{c_2}} \right\} } \right) = 0\), \(N{H_\delta }\left( {D,\left\{ {{c_3}} \right\} } \right) = 0.191\), \(N{H_\delta }\left( {D,\left\{ {{c_1},{c_2}} \right\} } \right) = 0.345\), \(N{H_\delta }\left( {D,\left\{ {{c_1},{c_3}} \right\} } \right) = 0.496\), \(N{H_\delta }\left( {D,\left\{ {{c_2},{c_3}} \right\} } \right) = 0.191\),          \(N{H_\delta }\left( {D,\left\{ {{c_1},{c_2},{c_3}} \right\} } \right) = 0.496\).

From Eq. (21), when \(c = \emptyset\), \(Sig\left( {{c_2},\emptyset ,D} \right) = 0< Sig\left( {{c_1},\emptyset ,D} \right) = 0.116 < Sig\left( {{c_3},\emptyset ,D} \right) = 0.191\), so \({c_3}\) is added into c. Because \(Sig\left( {{c_2},\left\{ {{c_3}} \right\} ,D} \right) = 0 < Sig\left( {{c_1},\left\{ {{c_3}} \right\} ,D} \right) = 0.305\), \({c_1}\) is added into c. Because \(Sig\left( {{c_2},\left\{ {{c_1},{c_3}} \right\} ,D} \right) = 0\) satisfies the termination condition, \(c = \left\{ {{c_1},{c_3}} \right\}\) is an optimal gene subset.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, J., Qu, K., Qu, K. et al. Feature selection using neighborhood uncertainty measures and Fisher score for gene expression data classification. Int. J. Mach. Learn. & Cyber. 14, 4011–4028 (2023). https://doi.org/10.1007/s13042-023-01878-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-023-01878-7

Keywords

Search

Navigation