Introduction

The synergy between vacuum-based analysis and electrochemistry has a long history [1,2,3,4,5,6,7]. However, particularly for low mass and highly mobile species such as hydrogen, the direct quantification of coverages by in situ electrochemical techniques, which by now are highly developed [8,9,10,11,12,13], has still proven elusive. In addition, the quantification of electrochemical signals to determine such adlayer coverages is often fraught with uncertainties due to the presence of parasitic side processes which can introduce their own pseudocapacitance. However, the determination of accurate thermodynamic and kinetic parameters relevant in electrocatalysis, including those pertaining to the long studied hydrogen evolution reaction (HER) and hydrogen oxidation reaction (HOR), actually depends on these coverages being determined with a reasonable precision [14,15,16,17]. Therefore, in this work, we relate the desorption kinetics obtained in vacuum with the electrocatalysis of the HER/HOR, and we analyse the electrochemical behaviour in view of the surface coverage according to cyclic voltammetry data (with and without H2 in the solution).

Single crystalline surfaces play an important role in the understanding of the link between structure and reactivity in electrocatalysis [18,19,20,21,22,23,24,25,26,27,28,29]. The research strives to elucidate reactions relevant to proton exchange membrane (PEM) fuel cells [30,31,32]. Technically, those rely on particles of electrocatalysts, but research makes frequent use of planar single crystalline systems as model surfaces. Among other advantages, those allow more specific insights on the role of adsorbed species for key reactions such as hydrogen evolution/oxidation (HER/HOR) [33,34,35], CO oxidation [21, 22, 36, 37], and oxygen reduction (ORR) [3, 27, 38, 39]. From a fundamental research point of view, planar model surfaces come with the advantage that they closely resemble the slabs that are used in density functional theory (DFT) calculations [40,41,42]. This facilitates the link between theory and experiment and enables easier cross-validation between the two.

Most of these catalysts are based on Pt, by far the most active monometallic catalysts for HER/HOR as well as ORR. A well-explored strategy is to allow Pt with another metal, thereby reducing the Pt content. In the case of Pt x Ru1 − x [30, 43,44,45] and many other alloy systems [46,47,48,49], the alloying component is known to suppress CO poisoning during the oxidation of hydrogen feedstocks obtained from reformate methane or methanol. It is well known that electronic and geometrical modification from the alloying component can also influence (positively or negatively) the reaction with hydrogen itself [33,34,35, 38, 45, 46, 50, 51]. There are challenges associated with the preparation of high quality Ru(0001) surfaces, which have a high bonding enthalpy for a range of different adsorbates [52, 53]. Ultra-high vacuum (UHV)-based preparation and analysis techniques therefore provide an opportunity to gain increased insight into this system. It is also known that up to four atomic layers of Pt can be grown pseudomorphically on Ru(0001) [40, 52, 54], which allows the catalytic properties to be tuned in a controlled manner and further assist the comparison with models. In a recent review paper concerned primarily with quantitative imaging of UHV prepared Ru(0001) and Pt/Ru(0001) model surfaces, we flagged precisely how sensitive the adsorption of H, O, and CO is to slight local variations in the structure of the surface [7], which is a factor often neglected in overlayer systems such as Pt/Ru(0001).

In terms of model surfaces, this work will restrict itself to two examples and look deeper into their chemical and electrochemical interaction with hydrogen at the solid/gas and the solid/liquid interfaces. We will discuss UHV-prepared Ru(0001), with and without a 1.1-ML pseudomorphic film of Pt [35], which are structurally similar (which is down to the same lateral spacing in the surface layer) but very different in their interaction with hydrogen. In combination with existing trends and data known for Pt(111), this permits a comparison of surfaces that bind hydrogen strongly (Ru(0001), close to optimally (2 ML Pt/Ru(0001)) and weakly (1 ML Pt/Ru(0001)). Moreover, the low electrocatalytic activity of bare Ru(0001) yields well-defined cyclo-voltammetric features not only in plain but also in H2-saturated electrolyte. This provides textbook-like insights not only into the HER/HOR kinetics (steady-state Butler-Volmer type profile) but also in the potential dependent sequence of adlayers formed on Ru(0001), with and without H2 in the solution. We highlight that, under conditions where H2 is in the electrolyte or accumulated there during HER, the driving force to adsorb hydrogen underpotential/overpotential deposition (UPD/OPD) may be stronger for non-electrochemical adsorption rather than proton discharge.

From understanding gained from temperature programmed desorption (TPD) of D2 molecules, we highlight that it is important to account for the actual adsorbate coverage under real electrochemical conditions [55, 56], rather than simply assuming that the results obtained from DFT calculations at an adsorbate coverage of 0.25 ML [57], as commonly used for other noble metals, or 1 ML [15], as used in the models of Nørskov et al. on Ru(0001), are representative of real reaction conditions. Due to the scaling of the computational cost of density functional theory (DFT) models with the system size, such models are often constrained to examine only periodic, fixed stoichiometric adlayer coverages, such as 0.25, 0.5, or 1 ML, neglecting the fact that the relevant adlayers under reaction conditions may be disordered and/or non-stoichiometric.

The understanding of hydrogen adsorption and reaction thus gained may be of relevance for systems beyond Ru(0001), particularly ones in which the potential regions for H and O adsorption overlaps. A recent work by Quaino et al. [16] highlighted that all of the metals that, on the traditional volcano plot [58], bind H too strongly in reality are covered by an oxide layer, which makes the interaction of H with their surfaces in metallic state irrelevant from a model perspective. Once the oxide covered metals are disregarded, there is actually no convincing evidence of a volcano on that half of the plot. However, Ru(0001), which undergoes a place exchange of OHad with Had in the potential region where H evolution occurs [2, 59, 60], provides an important data point on the high H-binding energy side of the volcano, provided that the true adsorbate coverage taken into account in the analysis.

However, after taking proper account of these phenomena, and collating together the data from other works, we show that it is possible to display a volcano plot that adequately correlates the variation in H-binding energy with the number of Pt layers on Ru(0001), as well as on bare Ru(0001) itself, with the measured exchange current density of the HER/HOR. This has implications for the best approaches for the examination and interpretation of other surface-sensitive reaction systems, particularly the ones on the high H/O-binding energy side of the volcano.

Ru(0001): Cyclic Voltammetry in Perchloric Acid

The electrochemistry of Ru(0001) in perchloric acid electrolyte is central to the results reviewed in this paper and will thus be briefly summarized in the following. Figure 1a shows the cyclic base voltammetry for two different cathodic limits and gives an evaluation/interpretation of the resulting key features along the lines thoroughly discussed in refs. [2, 59, 61, 62]. Note that the potential scale for this figure and all subsequent cyclic voltammograms is with respect to the reversible hydrogen electrode (RHE). The assignment of the different potential regions to a domination of Had, OHad, and Oad (bottom line) relies on CO displacement data (see explanation below) [2, 59], charge integration in cyclic voltammograms, and ex-situ studies of the potential-dependent adlayers by electron diffraction [1].

Fig. 1
figure 1

a Detailed H2-free voltammograms of the Ru(0001) surface (0.1 M HClO4, 50 mV s−1). The vertical lines mark adlayer structures according to ex-situ low-energy electron diffraction (LEED) [1] and the transferred charges in multiples of electrons per surface atom (the solid black line indicates the potential 0.1 V, where the dominating adlayer switches between OHad and Had) [2, 59, 60, 62]. Reproduced with permission from ref. [62]. b Close-up of peak B/B′, which reflects the reversible hydrogenation of 0.5 ML Oad and shows a textbook-like Nernstian peak shape. c Textbook figure reproduced with permission from ref. [64]

Full size image

The voltammograms are best understood by starting from the most positive potential limit and considering a cathodic potential sweep. Peaks C/C′ exhibit a pronounced hysteresis, indicating that they reflect more complex, less reversible surface processes that possibly involve place exchange between Ru and O atoms. This is supported by ex-situ STM studies which showed clear evidence of morphology changes after potential scans beyond 0.9 V [63]. For the discussions in this paper, however, those two peaks play only a spectator role.

Although peaks B/B′ (Fig. 1b) have been observed by many groups, it is surprising that one aspect was not yet discussed: they present a textbook-like “Nernstian” shape (Fig. 1c), i.e., the profile that one would expect for Langmuir adsorption without adsorbate-adsorbate attraction or repulsion or for the behaviour of an adsorbed electroactive species [64]. The characteristic bell shapes of those peaks reflect the configurational entropy of a random distribution of adsorbates and vacancies or of oxidized and reduced species in the adlayer [65]. Since there is no in situ structural information available about the adlayers that form peaks B/B′, an interpretation based on the CO displacement charge, the voltammetric charge, and some ex-situ electron diffraction patterns [1] was performed in refs. [61, 62]. It suggests the reversible protonation of 0.5 ML Oad (which would form a 2 × 1 pattern on Ru(0001)) towards 0.5 ML OHad as a likely scenario behind peak B/B′ (see Fig. 1b). This process is therefore a form of UPD-Had, but not forming on the bare metal but on an Oad layer. In another view, Oad/OHad could be interpreted as an adsorbed redox couple [64], possibly as part of a few-layer hydrogen-bonded H2O adlayer.

The Ru(0001) base CV in the range 0.1 V < E < 1.1 V bears many similarities with the one of polycrystalline platinum, which is why peaks B/B′ were initially assigned to UPD-Had and C/C′ to OHad reduction/formation, both peak couples separated by a double-layer regime. This interpretation did not stand up to scrutiny in deeper analyses: in ref. [59], current transients were recorded whilst CO was admitted into the electrochemical cell with the Ru(0001) electrode at constant potential. If peak B′ was passed in a cathodic scan and the potential halted at around 0.1 V, a negative current transient was observed, indicating that the non-electrochemical CO adsorption displaces a species that needs to be electrochemically reduced to remove it from the surface. This could be OHad or Oad. Only a positive current transient would indicate Had as a dominating surface species, which would release an electron upon “desorption” into dissolved H+. Such a positive transient was only observed if the cathodic peak A′ was passed prior to CO admission. This indicates that Had adsorption only occurs when the negative potential limit is extended in the window shown by the red dotted line in Fig. 1a. The same results were found for Ru(0001) modified by Pt islands [2]. The integrated charge of peak A′ and of the mentioned CO displacement transients indicates that the peak reflects the replacement of ~0.5 ML OHad by ~0.5 ML Had. In contrast to Pt(111), there is no actual “double-layer” region where Ru(0001) is free of adsorbates. This fact has recently been shown by DFT calculations performed by Sakong and Groß (Fig. 1b of ref. [66]).

Peaks A/A′ are the most important ones for the discussions in the following section. As discussed in detail in refs. [61, 62], those two peaks most likely involve an EC mechanism, i.e., electrochemically formed precursors that feed into subsequent chemical surface reactions. Specifically, peak A′ reflects the formation of Had, which is initially consumed by a subsequent chemical surface reaction with the incumbent OHad. Only after all OHad is removed, the Had layer, which is thermodynamically more favourable below 0.1 V (vertical dotted line in Fig. 1a), dominates the Ru(0001) surface [2, 59, 60, 62]. In the positive going scan, Had is stable against H+ formation up to rather high potentials [2] but the even more favourable OHad will tend to displace it at E > 0.1 V. Again, that process is sluggish, which can be interpreted as resulting from a two-step reaction: dissociative H2O adsorption, forming OHad and Had, with Had getting oxidized at rather low rates and thus leaving the surface crowded and hindering ongoing H2O adsorption. It should be highlighted that the hysteresis between peaks A and A′ is drastically reduced in the presence of even small amounts of Pt at the surface, which can act as a channel for much faster Had formation and oxidation [2, 60, 62]. This implies that the hysteresis between A and A′ on unmodified Ru(0001) is a kinetic, rather than thermodynamic, effect. The strong interaction of Ru(0001) with Had and the related sluggishness of any H2 or H+ involving surface reactions on Ru(0001) are recurring themes in the following discussions.

Kinetic Analysis of Electrochemical Flow Cell Data for Ru(0001) and Pt/Ru(0001)

The dotted line in Fig. 2a depicts a CV of a clean, UHV-prepared Ru(0001) surface in 0.1 M HClO4 solution. This voltammogram was measured with the same potential limits as the one shown by the red dotted line in Fig. 1a, albeit at a different sweep rate. The red solid line in Fig. 2a shows the effect of saturating the electrolyte with H2 on the voltammograms. These results were obtained in a flow cell under conditions of enhanced mass transport; further details of how these experiments were performed are available elsewhere [27, 39, 62]. The flow rate in these experiments was on the order of 1 mL s−1, which allowed diffusion limited current densities of about 2 mA cm−2 to be reached (on sufficiently active surfaces, such as Pt/Ru(0001) as shown in Fig. 2b), enabling accurate kinetic measurements.

Fig. 2
figure 2

a Cyclic voltammograms of Ru(0001) in flowing H2-saturated (solid curve) and H2-free (dotted curve) electrolyte (0.1 M HClO4, 10 mV s−1). The dashed curve shows j(E) according to the Butler-Volmer equation (see text). The point where the number value of the HER current density surpasses that of the exchange current density, j 0, is marked on the plot. For the numbers 1, 2, and 3 and the related vertical lines, see the discussion of Fig. 3. The blue dotted curve is similar to the dotted line shown in Fig. 1a (mind the different scan rates). Inset: STM image [2] of UHV prepared Ru(0001), 150 × 150 nm2, with an overlaid atomic resolution image (2.6 × 2.6 nm2). b Voltammogram of a UHV prepared 1.1 ML/Ru(0001) surface in a flow of H2-saturated 0.1 M HClO4 electrolyte; scan rate 10 mV s−1. The curve for Ru(0001) is plotted for comparison but nearly vanishes on this scale. c STM image of UHV prepared 1.1 ML/Ru(0001), 200 × 200 nm2. The variation in sample height along the line profile is visualized. d Film thickness histogram obtained from image c. e Cyclic base voltammograms (0.1 M HClO4, 50 mV s−1) of 1.1 ML Pt/Ru(0001) (blue solid line), Pt(111) (grey dashed line), and sigmoidal fit to the Pt(111) voltammogram (orange dotted line), shifted negatively to account for the binding energy difference of H on 1.1 ML Pt/Ru(0001) with respect to Pt(111). Reprinted with permission from ref. [35]

Full size image

In a flow of H2-saturated electrolyte, the CV only changes in the region −0.1 V < E < 0.4 V, whereas peaks E, C, and C′ remain largely unaffected. This is because the surface is covered by 0.5 ML (or more) of Oad at E > 0.4 V, as shown in the detailed voltammograms of the H2-free Ru(0001) surface (Fig. 2a) and explained in the preceding section. Looking at the negative going potential sweep, hydrogen oxidation only begins to occur during peak B′. In H2-saturated electrolyte (Fig. 2a, solid line), the transition between a CV that is essentially identical to the H2-free voltammogram and a textbook-like Butler-Volmer profile (dashed line) is rapid in either scan direction. It is safe to assume that in the “Butler-Volmer” regime the surface is dominated by Had. In H2-saturated solution, the replacement of OHad by Had already occurs at 0.2 V; the onset potential of peak A′, associated with the same place exchange in plain electrolyte, is at or below 0.1 V [2, 59, 60, 62] (likewise for the opposite process). Hence, the potential window where a Had-dominated surface is more stable than the OHad-dominated one is twice as large in H2-saturated electrolyte.

This observation has not been interpreted in detail before, although it is quite significant for an understanding of the interfacial chemistry at conditions where HOR/HER takes place. For Pt surfaces, the formation of UPD or OPD-Had is typically discussed in the context of H+ discharge [14, 17, 67,68,69,70]. This is the right approach in plain electrolyte, but in H2-containing solution, the driving force to form Had out of H2 may be higher than the one for H+ discharge under certain circumstances, i.e., it may be closer to a gas-phase adsorption situation than to electrochemical Had formation.

The interplay of non-electrochemical adsorption with potential-dependent adlayer formation is easier to disentangle if the non-electrochemical species is not an H2O fragment. For instance, Ru(0001) shows well-defined stationary CVs in CO-saturated electrolyte, which are totally different from the ones in plain electrolyte due to the competition between electrochemical and chemical adsorbates for the same sites (CO oxidation currents are rather small on Ru(0001)) [61]. “Chemically formed” adsorbates do not involve charge transfer and thus do not generate their own peaks in CVs, but they can change the position, shape, and amplitude of the other peaks.

In H2-saturated acidic electrolyte, Had can form by H+ discharge or by H2 dissociation. An important Gedanken experiment is that if the H2 activity (or partial pressure in the gas phase above the electrolyte) was high enough, H2 dissociation would always dominate. For a given potential, that can result in a higher Had coverage than would be obtainable from a purely electrochemical process. On Ru(0001), Had competes with OHad for adsorption sites. Above 0.1 V, OHad is more stable and cannot be displaced by Had from H+ discharge. If the surface was kept at, say, 0.2 V, however, a sufficiently high H2 concentration would raise the chemical potential high enough that the gain in free energy through an adsorption process would be sufficient to thermodynamically displace OHad (in the same way that CO can do this, as discussed above [2, 59]).

In the following, we will show that dissolved H2 with a partial pressure around atmospheric pressure (equivalent to a reversible hydrogen reference electrode) will necessarily dominate the Had layers over the electrochemically (OPD/UPD) formed ones. Figure 3 schematically plots the free energy difference between the Had or OHad covered and the plain Ru(0001) surface, as a function of the electrode potential, in analogy to the approach used for Pt, Au, Ni, and Ag previously [71, 72]. The exact vertical positions of these curves do not matter for the following discussions, which is why the y-axis is left somewhat unspecific. The slopes of the lines reflecting 0.5 ML of Had and OHad are +0.5 and −0.5 eV/V (both involve the transfer of 0.5 electrons per Ru surface atom), respectively. Other phases and coverages exist at other potentials, but here shall simplify the scenario for the sake of simplicity. We let the two curves cross at 0.1 V, where the dominating adsorbate is experimentally observed to swap (vertical dotted lines in Figs. 1a and 2a [2, 60]). Since the CO displacement results indicate that there is no “double-layer region” [2, 60], the vertical position of the crossing point in Fig. 3 was chosen such that its free energy value is negative, and therefore, there is no potential region where either Had or OHad adsorption is thermodynamically unfavourable.

Fig. 3
figure 3

Semi-quantitative phase diagram to explain the stability of Had and OHad on Ru(0001). Depicting the free energy of the adlayer covered minus the one of the plain surface, the solid red and blue lines correspond to electrochemical Had and OHad adsorption, respectively, at 0.5 ML coverage. The dashed line reflects Had formation out of H2 in H2-saturated electrolyte. The bars above the plot indicate the resulting stability regimes of Had- and OHad-dominated surfaces. The double arrows under points 2 and 3 reflect the transition points between Had- and OHad-dominated surface in plain and H2-covered electrolyte, respectively

Full size image

Had formation, by dissociating H2 dissolved in the electrolyte (dashed line), does not involve an electron transfer; hence, the free energy does not change with potential. This is why the dashed line is horizontal. This line is of relevance only in H2-saturated electrolyte, whereas the other two are valid in plain and H2-saturated solution. At 0 V (under the conditions of H2/H+ equilibrium), “plain” electrolyte would be at equilibrium with H2 gas at a partial pressure of 1 atm, very close to the partial pressure of H2 gas in H2-saturated solution. Hence, the free energy of 0.5 ML Had should be the same with and without externally added H2 at this point, meaning that the dashed and the solid lines must cross here. Electrochemically formed Had will thus be more relevant for E < 0 V, whereas chemically formed Had will dominate at E > 0 V. The latter fact can also be rationalized via a Born-Haber cycle: via the Nernst equation, the potentials in the range E > 0 V could be calculated into effective H2 partial pressures which will necessarily be lower than the one in a RHE and thus imply a smaller driving force towards adsorption. Note that the actual Had coverage at 0 V will of course be higher than 0.5 ML (see below), but this is not relevant for the point discussed here.

Due to the symmetry of the “gable” construction in Fig. 3, the dashed line crosses the OHad curve at 0.2 V. The resulting potential dependent adlayer regimes in plain and H2-saturated electrolyte are illustrated in the two bars at the top of Fig. 3. This simple prediction agrees well with the experimental observation that no voltammetric features other than the Butler-Volmer profile are visible below 0.2 V in H2-saturated electrolyte, which excludes the presence of electrochemically formed/reduced OHad. This makes the potential regime with Had as dominating surface species about twice as large as for the plain electrolyte.

In Fig. 2a, the current profiles for E < 0 V are similar in plain and H2-saturated electrolyte, apart from a small vertical shift. This results from the higher positive oxidation current contributions in the H2-saturated electrolyte as compared to the anodic currents in the system where near-surface-dissolved H2 is slowly building up during the negative going scan. In contrast to electrochemical UPD-Had formation, the CV in H2-saturated electrolyte does not give any direct evidence of the Had coverage or its potential dependent variation. Indirect evidence could in principle be derived from changes in the HOR/HER kinetics, but since it was possible to fit the entire region of E < 0.2 V with a single exchange current density and transfer coefficient (see discussion more below), there do not seem to be any obvious features of this kind.

The switching between “base CV” and HER-/HOR-dominated region occurs at higher potentials in the positive than in the negative going scan. This is similar to the hysteresis of the peak couple A′/A, and may have the same origin: OHad formation occurs from dissociative H2O adsorption in both cases, followed by electrochemical Had oxidation, whereas OHad reduction occurs via chemical reaction with Had. The two different pathways result from the slow kinetics of the processes and the crowding of the adlayer, which must be displaced before the next process can proceed. In both directions, further (dissociative) adsorption on a crowded surface initiates the adlayer replacement, which come with time delays and thus shifts in the related CV features.

We shall now discuss the HER/HOR kinetics in more detail. The Butler-Volmer profile in the region close to the RHE potential (E = 0), where the overall reaction

$$ {\mathrm{H}}_2 + {2\ \mathrm{H}}_2\mathrm{O}\rightleftharpoons {2\mathrm{H}}_3{\mathrm{O}}^{+}+2\mathrm{e} $$
(1)

is (by definition) in equilibrium, clearly splits into a positive and a negative branch which reflect HOR and HER, respectively. Figure 4 depicts the HER/HOR CV in a semi-log plot. The straight lines for |E| > 0.75 V confirm the exponential profile of the curves. From the slope of the anodic branch, we deduce a transfer coefficient α = 0.377, which is equivalent to a Tafel slope of 165 mV/decade [73]. The intersection of the straight line with the j-axis yields an exchange current density of j 0 = 4.6 μA cm−2. The accuracy of these parameters can be verified by the dashed curve in Fig. 2a which is a plot of the result of the Butler-Volmer equation

$$ j(E)={j}_0\times \left[ \exp \left(\alpha {\left( kT/ e\right)}^{-1} E\right)- \exp \left(\left(\alpha -1\right)\cdot {\left( kT/ e\right)}^{-1} E\right)\right], $$
(2)
Fig. 4
figure 4

Semi-log plot of the data in Fig. 2a as used to determine transfer coefficient α and exchange current density j 0

Full size image

using j 0 = 4.6 μA cm−2, α = 0.377, kT/e = 0.0256 V (at T = 297 K), E = potential vs. RHE. The value of j 0 will be discussed in more detail below.

Figure 2b shows the same experiment for a UHV prepared Pt thin film on Ru(0001) (black curve). For comparison, the corresponding curve for bare Ru(0001) (i.e., the CV from Fig. 2a) is plotted as a red line into the same graph. Due to the much higher currents attained at the Pt film, however, the Ru(0001) related curve is hardly distinguishable from the j = 0 line. The Pt film is the 1.1 ML Pt/Ru(0001) surface depicted in Fig. 2c which was found to have very weak adsorption related features in its base CV (Fig. 2e). It is dominated by areas with 1 ML Pt, with a few holes of exposed Ru, and a few islands with locally 2 ML Pt. The structure of this surface is most clearly shown by the STM image (Fig. 2c) and histogram of the populations of Pt islands of each height (Fig. 2d).

For the Pt film, an evaluation of the exchange current density via a half-logarithmic plot does not appear feasible. Instead, we follow the procedure used by Markovic et al. in ref. [74], in which the slope dj/dE is evaluated in an interval of −0.01 V < E < 0.01 V, i.e., just close to the equilibrium potential E = 0 V. We find a slope of 100 mA cm−2 V−1. Assuming j 0 = (kT/e) (dj/dE) = 8.617 × 10−5 V K−1, 297 K, and 100 mA cm−2 yields j 0 = 2.6 mA cm−2. This is more than five times higher than the value reported for Pt(111) at 303 K (j 0 = 0.45 mA cm−2) [74]. It should be pointed out, however, that the evaluation of the micropolarisation region to determine the exchange current density is potentially problematic, since the shape of the curve obviously does not resemble Butler-Volmer characteristics in the same way that the one for Ru(0001) does. In general, the exchange current density of highly active metals such as platinum will be underestimated by this method since transport effects can dominate over electrochemical kinetics even in the micropolarisation region [75, 76].

The orders of magnitude that distinguish the HER/HOR exchange current densities at Ru(0001) with and without the Pt layer are a necessary consequence of the Sabatier principle [77]. Ru(0001) has a high affinity to all kinds of adsorbates. Here, it will readily dissociate H2 and form Had, with a high stability that makes H+ formation comparably unfavourable, thus introducing a high barrier for this process and also the reverse one of forming H2 out of 2 Had (Tafel reaction). For HER/HOR at atomically smooth surfaces, Greeley, Kitchin, and coworkers suggested a simple kinetic model, which, in combination with adsorption energy values for H2, was already shown to have a good predictive capability [34, 57]. Apart from inputting DFT calculated adsorption energies, the model only requires a single fitting parameter, which is a pre-exponential factor derived from the known behaviour of some pure metal surfaces.

One important question that arises is the reason that the transfer coefficients α and (1 −α) in the Butler-Volmer curve of Ru(0001) on either side of the E = 0 V line are the same, even though the Had coverage in the region −0.1 V < E < 0 V may deviate somewhat from the 0.5 ML assumed here, due to the possibility of a superposition of the electrochemical and chemical routes to forming the adlayer. One possibility is that the coverage varies only slightly in this potential region. It also further possible that the HER/HOR activity is dominated by the presence of a few step edges on Ru(0001), and is therefore not strongly sensitive to the adsorbate coverage. However, in the subsequent section, we compare data from temperature programmed desorption experiments to provide a more accurate value for the coverage under the relevant reaction conditions, and relate this to a volcano plot for the HER/HOR.

Re-examination of the Volcano Plot for HER/HOR on Pt/Ru(0001)

Figure 5 shows a volcano-curve calculated according to the principles described in refs. [34, 57]. Rationalizing the results discussed here requires the adsorption energies of Had on Ru(0001), 1 ML Pt/Ru(0001) and 2 ML Pt/Ru(0001). Those energies are listed in Table 1 and are shown in Fig. 6. The table also includes the Gibbs free energies of hydrogen adsorption and the resulting predicted exchange current densities for HER/HOR (calculated according to the procedures in ref. [57]).

Fig. 5
figure 5

Volcano plot showing the DFT predicted and measured exchange current densities for HER/HOR on various model surfaces (see text). On the left-hand side, the strongly adsorbing Ru(0001) will have a higher coverage than the 0.25 ML commonly used for the DFT-based adsorption energy. On the right-hand side, the coexistence of areas with different local properties has to be taken into account. Reprinted with permission from ref. [35]

Full size image
Table 1 Enthalpies of adsorption ΔHads for ½H2 → Had, free energies of adsorption ΔGH*on selected model surfaces, and HER/HOR exchange current density j 0 according to theory and experiment (see text); ΔHads values according to DFT calculations in ref. [40] for Had coverage of 0.25 ML (for the value at ~1.1 ML Had on Ru(0001): see text); and ΔGH* = ΔHads (H2) + 0.24 eV [57]
Full size table
Fig. 6
figure 6

Binding energies of atomic hydrogen calculated from DFT. The points are plotted as a function of the number of pseudomorphic overlayers of Pt on Ru(0001). The left-hand energy scale is the absolute binding energy; the right-hand scale ΔE bind is the energy with respect to the binding energy of Had on the hcp site of Pt(111), which is represented as a dashed line. Reprinted with permission from ref. [40]

Full size image

The calculated points in Table 1 are represented by open circles along the line of the volcano plot itself (Fig. 5). For Ru(0001), a very reactive surface, one has to expect a Had coverage higher than 0.25 ML under conditions of H2 in the solution. A reasonable upper limit would be 1 ML Had, which according to ref. [78] will make the adsorption energy less negative by roughly 0.1 eV as compared to 0.25 ML Had. This is in agreement with trends found in thermal desorption experiments (also known as temperature programmed desorption, TPD) of deuterium on Ru(0001) in UHV [79,80,81], as well as the discussion in the previous section, in which a constant coverage of 0.5 ML was assumed for the potential region E < 0.2 V in H2-saturated electrolyte and E < 0.1 V in H2-free electrolyte. D2 is commonly used in place of H2 in TPD experiments, because its background signal from the residual gas in the vacuum chamber of the mass spectrometer is much lower. Figure 7a shows a set of thermal desorption spectra of D2 from Ru(0001) recorded after increasing gas dosages [80, 81]. The leading edges of the spectra indicates the temperature region where desorption sets in at relevant rates. The initial coverage of each desorption profile is reflected in the integrated area under the curve. The saturation coverage is θ(Dad) = 1 ML, corresponding to the curve with the highest peaks in Fig. 7a. Integration of this spectrum allows a normalisation factor to be determined that can be used to compute the initial coverages of all of the other curves. For reference, the spectrum starting with θ(Dad) = 0.83 ML is drawn as a dotted line. The dataset underlines that measurable desorption rates at 300 K require a coverage way beyond θ(Dad) = 0.25 ML.

Fig. 7
figure 7

Temperature programmed desorption spectra of D2 from a Ru(0001) and b 1.15 ML Pt/Ru(0001) [81]; initial Dad coverage decreases from left to right; maximum coverage: θ(Dad) = 1 ML; dotted line in a: θ(Dad) = 0.83 ML; crosshairs: see text; inset: coverage dependent desorption energy E Des [80]. Reproduced with permission from refs. [80, 81]

Full size image

For comparison of the TPD spectra with the HER/HOR exchange current density at the solid/liquid interface, we suggest the following Gedanken experiment: let us assume that the HER follows a Volmer-Tafel mechanism, i.e., 2 H+ + 2e− → 2 Had followed by 2 Had → H2, with the latter step being rate determining. A current density of j 0 = 4.6 μA/cm−2 (i.e., the number value of the exchange current density, see also Fig. 2a) would then have to be matched by a desorption rate of 0.018 ML s−1 under steady-state conditions. The crosshair in Fig. 7a marks the point where this desorption rate is reached at 300 K. By integrating the dotted TPD spectrum onwards from the marked point, it can be determined that the Dad coverage corresponding to this desorption rate would be about θ(Dad) = 0.7 ML. Any initial coverage under 0.5 ML would lead to one of the spectra with a single peak centred on point β2, which all have negligible desorption rates at 300 K. This comparison highlights that the desorption rates involved in the HER can only be achieved at Had coverages that would be required to allow for the corresponding desorption rates at the solid/vacuum interface. We caution that desorption rates obtained at the solid/vacuum interface may differ somewhat from those at the solid/electrolyte interface due to solvation effects and the presence of the electrical double layer. However, previous DFT calculations on Pt(111) reveal that the difference in the Had-binding energy with or without the presence of the water layer is negligible for a Had coverage <1 ML (Fig. 1a of ref. [65]). Thus, a quantitative comparison between the two desorption rates can be made. Furthermore, the high coverage destabilizes the adsorbed state via adsorbate-adsorbate repulsion, reducing the binding energy of the adsorbate. With Ru(0001) binding Had too strongly when the adsorbate coverage tends to zero, the adsorbate-adsorbate repulsion and the resulting destabilisation of Had will increase the HER/HOR exchange current density (Sabatier principle). This brings it closer to the peak of the volcano as shown in Fig. 5.

For the 1.1 ML Pt/Ru(0001) surface, on the other hand, the set of TPD spectra in Fig. 7b confirms that this surface should be essentially free of hydrogen at 300 K (a vertical line is added to guide the eye). This is also consistent with the rather featureless cyclic voltammograms recorded for this type of surface, as shown in Fig. 2e.

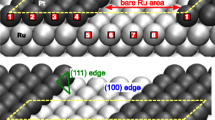
To give an idea about the possible lateral distribution of Had (or Dad) with increasing coverage at the solid/gas interface, Fig. 8 gives an overview of a UHV-STM study imaging four different Had layers on Ru(0001) at 50 K [82]. Given that these structures are essentially determined by adsorbate-adsorbate repulsions in combination with the underlying lattice, it is not unlikely that the structures at the solid/liquid interface under reaction conditions are similar. In that picture, a coverage of θ(Had) = 0.7 ML would be realized by a coexistence of the structures in Fig. 8h and Fig. 8i.

Fig. 8
figure 8

Ru(0001) in UHV, with increasing coverages of Had. a–e STM images at 50 K, where Had atoms appear dark (depressions) and vacancies light (protrusions). f–j Structure models for the various Had coverages; black points = Had, grey circles in i = vacancies. Reproduced with permission from ref. [82]

Full size image

The value of j 0 measured for Ru(0001) lies between the predictions for high and low Had coverage. This is indicated by the two full circles connected by a horizontal line on the left side of Fig. 5. The horizontal line reflects the experimentally observed value for j 0, whereas the two terminating circles stand for two different DFT-based predictions for the adsorption energies, which coincide with the two possible extreme cases of the Had coverage under reaction conditions (0.25 and 1 ML). According to a prediction that can be inferred from a combination of the data presented in refs. [40], 2 ML Pt on Ru(0001) should have adsorption properties close to the optimum that one can achieve at planar model surfaces—very close to the prediction for a Pd monolayer on a PtRu alloy [34]. One monolayer Pt on Ru(0001), however, should still be slightly less active than Pt(111) because it binds H too weakly.

For a quantitative comparison of the experimentally prepared 1.1 ML Pt surface with the DFT-based predictions, one must thus consider that the STM data in Fig. 2c reveals the coexistence of areas with local layer thicknesses of 0, 1, and 2 ML Pt. According to Table 1, the areas with locally 2 ML Pt should be expected to be much more active than those with 1 ML Pt, specifically, by a factor of more than 200. Hence, the 10% of the surface that has a local Pt thickness of 2 ML will dominate the overall activity and should yield an exchange current density of 2.1 mA cm−2 averaged over the surface, in good agreement with the experimental value of 2.6 mA cm−2. In Fig. 5, the 1.1 ML Pt surface is represented by a short horizontal line that is terminated by two circles representing 1 and 2 ML Pt. The lines terminated by the open and closed circles represent the predicted and measured exchange current densities, respectively. It should be noted that the results for the Pt covered surface may be partially influenced by parasitic surface alloy formation, as shown elsewhere [7, 44, 83, 84]. Since the adsorption energies on mixed PtRu sites will be similar to those on the Pt bilayer [40, 60], however, those two influences cannot be properly disentangled. The concept of breaking down an overall catalytic activity as an additive superposition of local contributions was also successfully applied for the oxygen reduction reaction on Pt mono- and multilayers and also on surface alloys on Ru(0001) [27].

Conclusions

We have reviewed the (electro)chemical and the electrocatalytic interactions of H2 and Had with Ru(0001) and 1.1 ML Pt/Ru(0001) at the solid/liquid and the solid/gas interfaces and related them to kinetic predictions based on DFT calculations. We can summarize the most salient points from the work as follows:

  1. 1.

    Ru(0001) is shown to serve as a prototype system for any smooth metal surface where the Sabatier principle predicts sluggish HOR/HER kinetics due to too strong Had adsorption. Clear voltammetric profiles suggest that, unlike many other metals with potentially strong Had adsorption, Ru(0001) is not covered by an oxide layer under reaction conditions.

  2. 2.

    A correct correlation with theoretical predictions must consider that Ru(0001) spontaneously accumulates appreciable Had coverages under HOR/HER conditions. Via adsorbate-adsorbate repulsion, this destabilizes Had and thus increases the HOR/HER rates by an order of magnitude as compared to lower Had coverages (0.25 ML). This crowding effect must be considered in any DFT-based kinetic prediction for strongly adsorbing electrodes. Likewise, an assumption of 1 ML Had overcompensates for this effect, overestimating the HER/HOR activity by approximately an order of magnitude.

  3. 3.

    D2 thermal desorption rates of Ru(0001) in UHV at 300 K approximately match the exchange current density for HOR/HER. Again, this is only true if similar adsorbate coverages are compared in both the electrochemical and UHV systems.

  4. 4.

    In the case of Had adsorption on Ru(0001), it can be argued that thermal desorption in vacuum provides a more meaningful value of the Had coverage under electrochemical conditions than an analysis of the voltammograms themselves, firstly because the in situ quantification of hydrogen coverages even in the absence of background electrochemical processes is challenging, secondly those processes themselves introduce extra uncertainty, and thirdly chemical processes, such as those involved in adlayer exchange, are not directly visible. For Pt1.1 ML/Ru(0001), on the other hand, thermal desorption confirms that the coverage of Had at E 0 is insignificant and unlikely itself to influence the reaction kinetics.

  5. 5.

    For the 1.1 ML Pt/Ru(0001) model system, the coexistence of areas with locally variable Pt film thicknesses must be taken into account for quantitative relations between prediction and experiment. This observation is likely to be true for any system that comprises a Pt overlayer pseudomorphically grown on a substrate that, when unmodified, binds Had strongly. Due to the fact that j 0 varies by several orders of magnitude with a change in thickness of only 1 ML, then taking the average thickness of the layer is not likely to be representative of the average activity of the film. If the film thickness locally varies, quantitative surface imaging is required for a comparison between theory and experiment. Areas of the film with a film thickness coinciding with the peak of the volcano would dominate the observed HER/HOR current.

  6. 6.

    Finally, we have discussed the role of dissolved H2 as a reference reservoir that is in equilibrium with Had as an adsorbed reaction intermediate. Higher H2 concentrations in the electrolyte increase the potential window where Had is more favourable than other adsorbates on the electrode, and within this window, the majority of adsorbates may result from chemical rather than electrochemical adsorption. For Ru(0001), this was inferred from the electrochemical and LEED data and rationalized in a simple thermodynamic model. For electrodes with higher electrocatalytic activity, one can assume similar trends, but they are less visible due to the absence of unambiguous adlayer-related voltammetric features on top of the electrocatalytic reaction currents.