1 Introduction

For generation companies operating in deregulated electricity markets, a core activity is the process of selling the generated power in the various markets that are available. This activity is challenging because of the sequential and stochastic nature of the power auctions [1, 2] and also because the marginal cost of generation is hard to specify precisely, since for many technologies, marginal costs depend on unknown future unit commitment patterns [3, 4]. In fact, since electricity generation planning involves mixed integer programming, there are no standard ways to calculate marginal costs [5].

In European-style electricity markets, market participants have to internalize nonconvexities in their market offers. In many cases, there is a main physical spot market, as well as various adjustment, balancing and ancillary services markets. Thus a possible approach is to consider how to bid in the main market, and, when this market has cleared, to consider how to participate in the remaining markets.

One strand of literature views this as a problem of deciding how much of the generation capacity to allocate between the different markets [6]. Others emphasize the sequential, and (by design) partly independent nature of these markets, allowing optimization of bidding strategies to benefit from backwards induction, viewing bidding as a sequential decision making problem [7, 8].

In a sequential approach, generation companies can choose to simplify the bidding problem by ignoring the effect future (adjustment or balancing) market opportunities may have on the optimal bids to the main market. Such sequential bidding is considered in [9, 10] and can be justified by the small volumes in these markets, and that they trade different products. Furthermore, the relevant information motivating trading in these products is not available until the main (spot) market has cleared. Boomsma et al. [11] call this sequential bidding. The alternative is coordinated bidding, where bidding is planned across markets in a joint optimization model [12,13,14,15,16]. An important question for the generation companies is then how much there is to gain by using a coordinated approach over a sequential approach. We shed light on this issue by developing a benchmark framework that allows for extensive backtesting over historical days.

A vital supporting activity in the process of selling the generation through the physical auctions is forecasting of market outcomes such as prices in different time intervals [17], geographic locations [18] and across market types, as well as other clearing outcomes such as power flows, load and generation, also distributed across future time intervals, geographically and across markets. A challenge in the forecasting process is to capture the complex dependencies that exist across these dimensions in modern power systems that increasingly are being penetrated by intermittent renewable generation. There is a large literature on both forecasting and power market bidding, see [19, 20] for reviews. For a generation company, it is necessary to do well in both these activities. This leads to a question of how to measure and benchmark the performance across alternative approaches for bidding and forecasting.

Many authors suggest simulation [2, 21] using real or artificial data. In this paper we opt for a backtesting approach, i.e. a simulation on real data where a counterfactual experiment is carried out over a sufficiently long historical period. We assume that the generation company has a database of historical forecasts and other relevant time series such as resource states and generator commitments. We use hydropower production as the base technology because we are considering data for the Nordic power market where hydropower accounts for 50% of annual production.

Our contributions include:

  • The main contribution of this paper is a backtesting framework that can measure the gain of a coordinated bidding process, both the forming of bids given forecasts, and the forecasting activity itself, both of which are vital to the business process. A novelty is that the framework identifies the relative performance of bidding versus forecasting over time.

  • We present a three-stage stochastic programming model that optimizes bid curves for both the spot and balancing market. Our modelling is thus an extension of [10] who determine bid curves in the spot market but only a single bid volume in the balancing market.

  • Using real data from a Norwegian hydropower producer, we compare the sequential and coordinated approach for different prediction models for the balancing market, where we use a naive forecasting method predicting zero imbalance (in expectation) to give a lower bound and a forecast with perfect information to give an upper bound. Between these two extremes we also develop an artificial neural network (ANN) forecast to give a more realistic estimate.

The rest of this paper is organized as follows: The formulation of a mathematical optimization model for coordinated bidding is presented in Sect. 2. Section 3 describes the backtesting procedure. Section 4 presents the prediction models for the balancing market. Results from a case study are given in Sect. 5, before conclusions are drawn in Sect. 6.

2 Coordinated bidding of hydropower generation

In this work, we consider the market rules of European-style day-ahead and balancing market, as shown in Fig. 1. Similar market structures may be found in other regions. In Europe, the day-ahead market is the main arena for trading power. Orders or bids have to be placed within 12:00 CET the day before delivery. The market prices for the delivery day are determined from the market equilibrium, and are typically announced to the market at 12:42 CET or later, as shown in Fig. 1. To calculate the commitments, the market organizer makes a linear interpolation between the individual producer’s bid curve and the market price.

Fig. 1
figure 1

Time-line for clearing of the Nordic day-ahead market and balancing market

Full size image

In addition to the day-ahead market, we consider a balancing market, which for the case of Norway is a real-time market for replacement reserves with an activation time of up to 15 min. These reserves are manually activated by the TSO and replace the more flexible automatically activated reserves. Preliminary orders in the balancing market must be placed within 21:30 CET the day before delivery, as shown in Fig. 1, but may be changed up to 45 min prior to the delivery hour. The prices in the balancing market are based on activating the bids in merit order. In contrast to the piecewise linear bid curves submitted to the day-ahead market, bids for the balancing market are piecewise constant.

The problem of determining optimal bids in the day-ahead and balancing market can be formulated as a three-stage stochastic mixed-integer programming model. We use a deterministic equivalent formulation of the stochastic program. The first-stage decisions are the hourly bid curves for the day-ahead market. The uncertain day-ahead market prices are revealed in the second stage and determines the day-ahead commitments. The second-stage decisions are the hourly bid curves for the balancing market. In our model, the bids for the balancing market are determined for all hours at the same time, and not for individual hours as they close. This assumption enables the use of a three-stage and not multi-stage model. Entering the third stage, the uncertain balancing market prices and demand are revealed and the commitments in the balancing market are determined. The third-stage decisions determine an optimal production schedule for the river system that cover the market commitments.

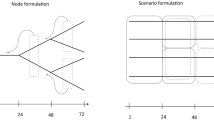
The planning horizon for the hydropower producer has hourly steps, denoted by \({\mathcal {T}} = \{1,\ldots , T \}\), coinciding with the current granularity of the markets. The subset \({\mathcal {T}\,}^P = \{1, \ldots , 24\} \subset {\mathcal {T}}\) represents the day of bidding (Fig. 1), which is deterministic with a predetermined production schedule from the day before. The hours of operation make up the second day of the planning horizon, and are thus denoted by the subset \({\mathcal {T}\,}^O = \{25,\ldots ,48\} \subset {\mathcal {T}}\) . Bids are only placed for the day of operation, but a longer planning horizon has to be included for coupling to longer term hydropower scheduling models. After hour 48, bidding is relaxed and the producer schedules production according to the spot market prices, without going through the process of bidding. This period is denoted by the subset \({\mathcal {T}\,}^H = \{49,\ldots , T\} \subset {\mathcal {T}}\).

The prices in hour t for the day-ahead market and the balancing market are described by the stochastic processes \(\rho ^D_t\) and \(\rho ^B_t\), respectively. The balancing market price is defined as the sum of the day-ahead market price and a balancing market premium, \(\mu ^B_t\), such that \(\rho ^B_t = \rho ^D_t + \mu ^B_t\). The premium can be positive or negative, leading to a balancing market price above or below the day-ahead market price. The demand in the balancing market is described by \(\upsilon ^B_t\). We model the demand in the balancing market as stochastic because there is limited market depth depending on the uncertain future demand for ramping. The continuous stochastic process for the market prices and demand is approximated by a scenario tree as shown in Fig. 2. The set of possible outcomes for the day-ahead market is denoted \({\mathcal {S}}\), while the set of possible outcomes for the balancing market is denoted \({\mathcal {C}}\). A subset \({\mathcal {C}}_s \subset {\mathcal {C}}\) is introduced, which represents the possible outcomes for the balancing market given an outcome s in the day-ahead market. A scenario is defined as a combination of the two markets; given an outcome \(s \in {\mathcal {S}}\) and \(c \in {\mathcal {C}}_s\). The market parameters are thus denoted by \(\rho ^D_{ts}, \rho ^B_{tsc}, \upsilon ^B_{tsc}\). The probability for an outcome s in the day-ahead market is given by \(\pi ^D_s\), while the probability for an outcome c in the balancing market is given by \(\pi ^B_{sc}\). The probability for a scenario is thus defined \(\pi ^D_s \pi ^B_{sc}\).

Fig. 2
figure 2

Scenario tree for the coordinated bidding problem

Full size image
Fig. 3
figure 3

Example of an hourly bid curve for the day-ahead market where \({\mathcal {I}} = \{1,2,3 \}\)

Full size image

For the day-ahead market, bids are given as price-volume pairs, which make up a set of bid points \({\mathcal {I}} = \{1,\ldots , I\}\), as shown in Fig. 3. The number of bid points, I, is freely chosen by the producer, but an upper limit is given by \(I = 64\) according to the market rules. The process of placing bids gives a nonlinear problem when determining both the bid price and the bid volume [22]. Solving this nonlinear problem would have a too large computational burden for real cases, and thus we want to use a linear formulation. Therefore, to preserve the linearity of the model, the bid prices for the day-ahead market, \(P^D_i\), are modeled as fixed parameters, while the bid volumes are modeled as decision variables [23]. The bid volumes are denoted \(u^D_{ti}\). Accumulated volumes are used, and not the marginal increase for each bid point. The decision variables representing commitments, \(w^D_{ts}\) are determined by linear interpolation between adjacent price-volume pairs \((u^D_{ti-1}, P^D_{i-1})\) and \((u^D_{ti}, P^D_{i})\), as expressed by (1):

$$\begin{aligned}&w^D_{ts} = u^D_{ti-1} + (u^D_{ti} - u^D_{ti-1}) \frac{\rho ^D_{ts} - P^D_{i-1}}{P^d_{i} -P^d_{i-1} }, \quad \text{if} \ P^D_{i-1} \le \rho ^D_{ts} < P^D_{i}, \\&\quad t \in {\mathcal {T}\,}^O,\ s \in {\mathcal {S}},\ i \in {\mathcal {I}} {\setminus } \{1\}. \end{aligned}$$
(1)

The market rules also require that the bid curves are monotonically non-decreasing. This requirement is enforced by (2):

$$\begin{aligned} u^D_{ti} \ge u^D_{ti-1},\quad t \in {\mathcal {T}\,}^O, \ i \in {\mathcal {I}} {\setminus } \{1\}. \end{aligned}$$
(2)

The accumulated bid volume for hour t in the day-ahead market cannot exceed the available production capacity of the set of \({\mathcal {G}} = \{1,\ldots ,G\}\) production units in the system. The hourly available production capacity, \(\overline{Q_{gt}}\), is defined in (3). \(A_{gt}\) represents the hourly percentage of availability for the generator, while \(\overline{Q_g}\) denotes the upper production limit of the generator. The highest bid cannot exceed the total available production capacity, as expressed by (4):

$$\begin{aligned} \overline{Q_{gt}} = A_{gt} \overline{Q_g},\quad g \in {\mathcal {G}},\ t \in {\mathcal {T}} \end{aligned}$$
(3)
$$\begin{aligned} u^D_{t|I|}\le & {} \sum _{g \in {\mathcal {G}}} \overline{Q_{gt}}\quad t \in {\mathcal {T}\,}^O. \end{aligned}$$
(4)

The producer can both sell to and buy from the balancing market but cannot be activated for both in the same period. One supply curve and one demand curve are thus submitted for each hour of operation. If the demand in the system exceeds the available supply, the TSO activates sell orders (up ramping). If the demand in the system is smaller than available supply, the TSO activates buy orders (down ramping). The stochastic demand parameter, \(\upsilon ^b_{tsc}\), defines the direction and quantity demanded in hour t, and therefore also determines the market state \({\mathcal {M}}\), defined by (5)

$$\begin{aligned} {\mathcal {M}} = \left\{ \begin{array}{ll} 1,&{}\quad \text{upward balancing market}\\ 2,&{}\quad \text{downward balancing market}. \end{array}\right. \end{aligned}$$
(5)
Fig. 4
figure 4

Bid curves in the upward (left) and downward (right) balancing market

Full size image

As for the day-ahead market, bids for the balancing market are given as price-volume pairs with bid prices, \(P^B_{im}\), as parameters, and bid volumes, \(u^B_{tsim}\) as decision variables, but the bid curves are now piecewise constant, as shown in Fig. 4. The bid prices for upward ramping are increasing, whereas they are decreasing for downward ramping. The commitments in the upward and downward balancing market are determined by (6) and (7), respectively:

$$\begin{aligned} w^B_{tsc1}= & {} \left\{ \begin{array}{ll} u^B_{tsi-11} &{}\quad \text{if } P^B_{i-11} \le \rho ^B_{tsc} < P^B_{i1} \text{ and } \upsilon ^B_{tsc} > 0 \\ 0, &{}\quad \text{if } \upsilon ^B_{tsc} \le 0 \end{array}\right. \end{aligned}$$
(6)
$$\begin{aligned} w^B_{tsc2}= & {} \left\{ \begin{array}{ll} u^B_{tsi-12} &{}\quad \text{if } P^B_{i-12} \ge \rho ^B_{tsc} > P^B_{i1} \text{ and } \upsilon ^B_{tsc} < 0 \\ 0, &{}\quad \text{if } \upsilon ^B_{tsc} \ge 0. \end{array}\right. \end{aligned}$$
(7)

The market rules require a minimum bid volume for the balancing market, denoted \(N^B\). As it is assumed that the replacement reserves are needed the entire hour, \(\upsilon ^B_{tsc}\) is either zero, or in the intervals \([-\infty , -N^B]\) or \([N^B, + \infty ]\).

Bid curves are required to be monotonically nondecreasing for upward ramping, and monotonically nonincreasing for downward ramping. The bid volumes are defined to be positive, so the requirement for both states is enforced by (8):

$$\begin{aligned} u^B_{tsim} \ge u^B_{tsi-1m},\quad t \in {\mathcal {T}\,}^O, \ s \in {\mathcal {S}}, \ i \in {\mathcal {I}} {\setminus } \{1\}, m \in {\mathcal {M}}. \end{aligned}$$
(8)

As the balancing market clears after the day-ahead market, the available capacity for adjustments is dependent on the day-ahead market commitments. For upward ramping, the quantity available for adjustment is defined as the total available production capacity in hour t, less the committed volume in the day-ahead market (9). The quantity available for downward ramping is equal to the commitment in the day-ahead market (10) because the producer can ramp down to zero:

$$\begin{aligned} u^B_{ts|I|1}\le & {} \sum _{g \in G} \overline{Q_{gt}} - w^D_{ts},\quad t \in {\mathcal {T}\,}^O,\ s \in {\mathcal {S}} \end{aligned}$$
(9)
$$\begin{aligned} u^B_{ts|I|2}\le & {} w^D_{ts}, \quad t \in {\mathcal {T}\,}^O,\ s \in {\mathcal {S}}. \end{aligned}$$
(10)

The commitments in the balancing market are also limited by the demand, \(\upsilon ^B_{tsc}\). The demand in the balancing market is very low compared to the demand in the day-ahead market, and often so low that a single market participant is able to supply the entire volume. As the balancing market price is set from the last activated bid, a producer can in theory set the market price in cases when there are no other producers placing lower bids. However, low liquidity in the balancing market is in itself not an argument for market power [17]. The price taker assumption can thus still be considered valid.

The commitments are defined as positive for both balancing market states, while the demand is negative when the system is in the downward balancing market state. A market indicator, \(U_m\), which equals \(+1\) for \(m = 1\) and \(-1\) for \(m = 2\), is therefore introduced. Multiplying the market indicator with the demand gives a positive upper limit for both balancing states. The upper and lower limits for the commitments in the balancing market are expressed by (11). The binary variable, \(\delta ^B_{tscm}\), forces the commitments to be between the upper and lower bounds, if different from zero:

$$\begin{aligned} N^B \delta ^B_{tscm} \le w^B_{tscm} \le \upsilon ^B_{tsc} U_m \delta ^B_{tscm}\quad t \in {\mathcal {T}\,}^O,\ s \in {\mathcal {S}},\ c \in {\mathcal {C}}_s,\ m \in {\mathcal {M}}. \end{aligned}$$
(11)

The sum of the commitments in the markets must be covered by production from the hydropower system. The total production in the system is the sum of production for each generator, \(x_{gtsc}\), as expressed in (12). The market indicator is multiplied with the balancing market commitments, as downward ramping is a repurchase of production:

$$\begin{aligned} w^D_{ts} + \sum _{m \in {\mathcal {M}}} U_m w^B_{tscm} = \sum _{g \in {\mathcal {G}}} x_{gtsc},\quad t \in {\mathcal {T}\,}^O,\ s \in {\mathcal {S}},\ c \in {\mathcal {C}}_s. \end{aligned}$$
(12)

The produced volume must be found based on a feasible production schedule for the hydropower river system. We introduce a set of reservoirs \({\mathcal {R}} = \{1,\ldots , R\}\), and a subset \({\mathcal {G}}_r \in {\mathcal {G}}\), which define the generators connected to reservoir r. The reservoir volume, \(v_{trsc}\), at the end of hour t is given by the reservoir balance in (13). Initial reservoir volumes must be given for the first time step. The reservoir volume increases due to inflow, \(I_{tr}\), and decreases with discharge, \(d_{gtsc}\), spill, \(s_{trsc}\), and bypass, \(b_{trsc}\). Inflow is modeled as a deterministic parameter due to its low impact for a short time horizon. The term \(o_{trsc}\), is defined as the sum of the discharge, spill, and bypass coming from connected reservoirs at a higher level (14). Reservoirs are connected using indicator matrices, which defines if water can be sent from reservoir \(r'\) to reservoir r. The different matrices are the discharge matrix, \(J^D_{r'r}\), the spill matrix, \(J^S_{r'r}\), and the bypass matrix, \(J^B_{r'r}\):

$$\begin{aligned} v_{trsc}&= v_{t-1rsc} + I_{tr} - \sum _{g \in {\mathcal {G}}} d_{gtsc} - s_{trsc} - b_{trsc} + o_{trsc}, \\&\quad t \in {\mathcal {T}} {\setminus } {1},\ r \in {\mathcal {R}},\ s \in {\mathcal {S}}, c \in {\mathcal {C}}_s \end{aligned}$$
(13)
$$\begin{aligned} o_{trsc}&= \sum _{r' \in {\mathcal {R}}} ( J^D_{r'r} \sum _{g \in {\mathcal {G}}_{r'}} d_{gtsc} + J^S_{r'r} s_{tr'sc} + J^B_{r'r} b_{tr'sc} ), \\&\quad t \in {\mathcal {T}},\ r \in {\mathcal {R}},\ s \in {\mathcal {S}},\ c \in {\mathcal {C}}_s. \end{aligned}$$
(14)

The reservoir volume and bypass have upper and lower limits as expressed by (15) and (16), respectively:

$$\begin{aligned} \underline{V_r}\le & {} v_{trsc} \le \overline{V_r},\quad t \in {\mathcal {T}},\ r \in {\mathcal {R}},\ s \in {\mathcal {S}},\ c \in {\mathcal {C}}_s \end{aligned}$$
(15)
$$\begin{aligned} \underline{B_r}\le & {} b_{trsc} \le \overline{B_r},\quad t \in {\mathcal {T}},\ r \in {\mathcal {R}},\ s \in {\mathcal {S}},\ c \in {\mathcal {C}}_s. \end{aligned}$$
(16)

A linear relationship between the power output, \(x_{gtsc}\), and the discharge rate, \(d_{gtsc}\), is assumed. The production-discharge curve is thus approximated as a concave piecewise linear function in (17), where a set of discharge segments, \({\mathcal {E}} = \{1,\ldots ,E\}\) with coefficients \(R_{ge}\) as well as a minimum production level (\(\underline{Q_g}\)) is introduced. The discharge for each segment is denoted \(d^E_{gtesc}\) and is restricted by an upper limit, \(\overline{D_{ge}}\) as expressed by (18). The total generator discharge, \(d_{gtsc}\), equals the sum of the minimum discharge and the all segment discharges, as expressed by (19). An example of a production-discharge curve with five discharge segments is illustrated in Fig. 5:

Fig. 5
figure 5

Example of a power-discharge curve with five discharge segments

Full size image
$$\begin{aligned} x_{gtsc}&= \underline{Q_g} \delta ^G_{gtsc} + \sum _{e \in {\mathcal {E}}} R_{ge} d^E_{gtesc}, \quad g \in {\mathcal {G}},\ t \in {\mathcal {T}},\ s \in {\mathcal {S}},\ c \in {\mathcal {C}}_s \end{aligned}$$
(17)
$$\begin{aligned} d^E_{gtesc}\le D_{ge},\quad g \in {\mathcal {G}},\ t \in {\mathcal {T}},\ e \in {\mathcal {E}},\ s \in {\mathcal {S}},\ c \in {\mathcal {C}}_s \end{aligned}$$
(18)
$$\begin{aligned} d_{gtsc}= D_g \delta ^G_{gtsc} + \sum _{e \in {\mathcal {E}}} d^E_{gtesc},\quad g \in {\mathcal {G}},\ t \in {\mathcal {T}},\ s \in {\mathcal {S}},\ c \in {\mathcal {C}}_s. \end{aligned}$$
(19)

In (17), \(\delta ^G_{gtsc}\) is a binary variable indicating if the generator is on or off. This variable is also used in (20) to force the production, \(x_{gtsc}\), to be within the maximum and minimum capacity if the unit is running:

$$\begin{aligned} \underline{Q_g} \delta ^G_{gtsc} \le x_{gtsc} \le \overline{Q_{gt}} \delta ^G_{gtsc},\quad g \in {\mathcal {G}},\ t \in {\mathcal {T}},\ s \in {\mathcal {S}},\ c \in {\mathcal {C}}_s. \end{aligned}$$
(20)

A start-up cost, \(C^S_g\), is induced each time a generator starts after not running the hour before. In (21), multiplying the unit start-up cost with the binary on/off variables gives the total start-up cost, \(y_{gtsc}\):

$$\begin{aligned} C^S_g (\delta ^G_{gtsc} - \delta ^G_{g(t-1)sc}) \le y_{gtsc},\quad g \in {\mathcal {G}},\ t \in {\mathcal {T}} {\setminus } {1},\ s \in {\mathcal {S}},\ c \in {\mathcal {C}}_s. \end{aligned}$$
(21)

As explained in regard to Fig. 1, the schedule for the first deterministic day (\(T^P\)) are known from the market clearing and planning process the day before. This is imposed by (22), where \(P_{gt}\) is the known schedule:

$$\begin{aligned} x_{gtsc} = P_{gt},\quad g \in {\mathcal {G}},\ t \in {\mathcal {T}\,}^P , \ s \in {\mathcal {S}},\ c \in {\mathcal {C}}_s. \end{aligned}$$
(22)

The objective of the bidding problem is to maximize the expected profits from participating in the day-ahead and balancing market. Given the stochastic nature of prices and volumes for the various products, it might also be relevant for generating companies to consider other objective functions that include some sort of risk management, like CVaR. This could be incorporated into our modelling framework if needed but would require strategic input in the form of trade-offs parameters between mean profit and risk. In lack of this input, we have chosen to maximize the expected profits in the analyses presented in this paper.

The revenue from each market during the hours of operation is calculated as the market price multiplied with the commitment in the market. A longer planning horizon (\({\mathcal {T}\,}^H\)) has to be included in addition to the hours of operation (\({\mathcal {T}\,}^O\)), in order to prevent the model from only seeing opportunities the following day. For the hours after operation, \(t \in {\mathcal {T}\,}^H \subset {\mathcal {T}}\), bidding is relaxed, and it is assumed that the producer sells all its output to the day-ahead market. The revenue from this period is thus included in the objective function by multiplying the day-ahead market price by production \(x_{gtsc}\), and not commitments. Including these future profits is not enough to keep the model from producing at full capacity during the short-term horizon, as it would be beneficial to produce as long as there is water in the reservoirs. Thus, the value of water remaining in the reservoirs after the end of the horizon must be considered. This is described by the water value \(W_r\) which is assumed to be a known input calculated from longer term hydropower scheduling models. The water value is multiplied with the reservoir volume in the final hour, \(v_{|T|rsc}\), less the initial volume, \(V^0_r\). An energy equivalent, \(E_r\), indicating how much energy that can be extracted for each \(m^3\) of water, is included in the expression to obtain the correct units. Start-up costs, \(y_{gtsc}\), are included for all time intervals, except the first deterministic day. The market indicator, \(U^m\), is included in the calculation of revenues for the balancing market. A penalty, Z, for spill is included to make sure that spill is undesired in the system, even in cases where spill ends up in a lower reservoir and increase the power output downstream. The objective of the three stage stochastic mixed integer program is presented in (23):

$$\begin{aligned}&\sum _{s \in {\mathcal {S}}} \pi _s \left( \sum _{t \in T^O} \rho ^D_{ts} w^D_{ts} + \sum _{c \in {\mathcal {C}}_s} \pi _{sc} \left( \sum _{t \in {\mathcal {T}\,}^O} \sum _{m \in {\mathcal {M}}} \rho ^B_{tsc} w^B_{tscm} U_m \right. \right. \\&\quad + \sum _{g \in {\mathcal {G}}} \left( \sum _{t \in {\mathcal {T}\,}^H} \rho ^D_{ts}x_{tgsc} - \sum _{t \in {\mathcal {T}} {\setminus } \{{\mathcal {T}\,}^P\}} y_{gtsc} \right) \\&\quad \left. \left. + \sum _{r \in {\mathcal {R}}} \left( W_r E_r (v_{|T|rsc}- \underline{V^0_r}) - \sum _{t \in {\mathcal {T}}} s_{trsc} Z \right) \right) \right) . \end{aligned}$$
(23)

3 Backtesting framework

When evaluating the performance of the bid optimization model presented in Sect. 2, the decisions should be compared with current practice. In today’s hydropower industry, the bidding process often rests on the skills of the operating engineers. Most producers consider each market separately in the order of market clearing. Even if coordinated bidding models can be formulated, implementing more complex models in operations has a cost. Therefore it is essential to determine the gain from coordinated bidding. Experimenting with alternative bidding strategies in real operations can lead to loss in profits, so a backtesting framework using historical data is a safe alternative.

Fig. 6
figure 6

Framework for backtesting the coordinated and sequential bidding strategy

Full size image

To test the practical performance of the coordinated bidding method, the model is executed in three parts, as shown in Fig. 6. For the coordinated strategy, model 1 is the model as described by (1)–(23) in Sect. 2, for which all market prices and balancing market volumes are uncertain. To mimic the sequential clearing of the markets, the day-ahead market decisions are the first to be submitted. The day-ahead bid curves are thus saved as output of the first model. To calculate the commitments in the day-ahead market, these bid curves are used as input in model 2, along with the realized day-ahead market prices. Using this information, the day-ahead market commitment \(w_{ts}^D\) is calculated based on (1) and used as input to model 2. Model 2 re-optimizes the balancing market bids based on the now known commitments from the day-ahead market (i.e. \(w_{ts}^D\) fixed) as a solution to an optimization model consisting of (3)–(23). The bid curves for the balancing market are saved as output of model 2. The bids are then used together with the realized balancing market price to determine the balancing market commitments, \(w_{tscm}^B\). In model 3, both the commitments from the day-ahead market and the balancing market are fixed, and the optimization calculates an optimal production schedule according to (3)–(5), (12)–(23).

A similar approach is also implemented for a sequential bidding strategy. In this case, model 1 optimizes the bid curves for the day-ahead market without considering the opportunities in the balancing market, that is, using (1)–(4), (12)–(23). Model 2 and 3 are the same as for the coordinated bidding strategy. The difference between the coordinated and sequential approach is that the coordinated approach may optimize the day-ahead bid curves while seeing opportunities in the balancing market, whereas the sequential approach may not.

For each day in the sample period, the optimization models are run in three parts as described above. The results are saved, and the procedure is repeated for the next day. The production plan for the bidding day as well as reservoir levels from model 3 are used as input for the next day. Water values are obtained as historical data from an industrial partner and updated weekly in the period. The input with a dashed perimeter is updated every day, this includes forecasts/scenarios for market prices and demand as well as historical realized values for the same parameters and inflow.

Forecasts for the day-ahead market prices have been obtained from an industrial partner, whereas forecasts for the balancing market have however been specifically developed for the backtesting procedure, see Sect. 4. Scenarios are generated using the method described in [24], where historical forecast errors are combined with point forecasts to generate scenarios. For the day-ahead market, historical forecast errors have been obtained by considering the differences between the industrial partners historical forecasts and realized prices. For the balancing market, historical forecast errors have been obtained by using the prediction model presented in Sect. 4 to predict daily forecasts and comparing this to realized prices and demand in the balancing market.

The backtesting procedure is carried out for 200 consecutive days in the period from July 1, 2017 to January 16, 2018, for a hydropower system located in south-west Norway. The river system consists of four reservoirs in cascade. There is only one power station, which is located downstream of the lowest reservoir. The power station contains one generator with a minimum and maximum capacity of 16 and 80 MW.

The number of day-ahead outcomes S used is 40, and for each day-ahead market scenario, 10 balancing market outcomes are used. To evaluate the stability of the solution, we ran calculations using 10 to 140 day-ahead market outcomes for selected days, and the solution stabilized around 40 scenarios. So this number of scenarios was chosen for the benchmark procedure. Similarly, tests using 40 day-ahead outcomes and varying number of balancing market outcomes on selected days indicated that the solution became stable at around 10 balancing market outcomes, so this was selected.

The number of bid points I highly affect the run time of the models and is therefore set to a relatively low number of 10 points for both the day-ahead and balancing markets. This is the same number of points used by [11]. Our own calculations using a higher number of points on selected days did not lead to any significantly different results than what is presented. The price points are found by dividing the historical data into eight quantiles. In addition, minimum and maximum points are set at \(-500\) and 3000 EUR according to the market rules. As the market prices varies throughout the year, the quantiles are recalculated monthly based on the historical data.

The optimization models are implemented in Xpress-IVE 64 bit using Xpress-Mosel, and solved with Xpress-Optimizer. The backtesting procedure is implemented using Python 2.7, and run on computers with an Intel Core i7-7700 3.60 GHz CPU and 32.0 GB installed RAM.

4 Forecasting the balancing market

Prediction models for the day-ahead market have been an important tool in the power industry since deregulation [19]. Due to expectations of increasing volumes in the other short-term markets, methods for predicting these markets has become more relevant.

The balancing market is designed to handle unforeseen events, and the prices and volumes should thus be random. If the balancing market is an efficient market, [17] points out that any predictable event that can cause an imbalance in the system the day of operation, should be incorporated in the day-ahead market settlements. However, in order to do coordinated bidding, market agents need to have information or predictions about the balancing market outcome before the day-ahead market clears.

For stochastic models, the evaluation of a decision made under uncertainty is dependent on the stochastic process. An optimal solution of the bidding problem is only optimal for the discrete stochastic process given by the scenario tree. The scenario tree is based on forecasts and it may therefore be difficult to separate the performance of the forecast from the performance of the optimization model. We therefore compare the sequential and coordinated approach for different prediction models, where we use a naive forecast method predicting zero imbalance in expectation to give a lower bound and a forecast with perfect information to give an upper bound. Between these two extremes we develop an artificial neural network (ANN) forecast to give a more realistic estimate. ANNs are able to model nonlinear relationships between variables and have been successfully used for forecasting electricity prices in earlier work [25, 26]. We develop a simple ANN that is used as an example of a viable forecasting method for the balancing market but admit that fine-tuning of a forecasting method has been left for further work. For all prediction models we do use (perfect information, zero imbalance and the ANN), we follow [17] and model the balancing market premium rather than prices, as well as the available balancing volume.

To develop the ANN forecasting method, we considered relevant market and climate data. Forecasts for day-ahead market prices and weather forecasts are provided by an industrial partner. Forecasts for consumption and production were retrieved from Nord Pool’s database, and historical climate data were downloaded from the Norwegian Meteorological Institute’s database eKlima. The data is mainly based on the NO2 price area, but also include data for connecting areas such as DK1. All data is available from 1 January 2013 to 16 January 2018. However, we use the data from July 1, 2017 to January 16, 2018 for the backtesting procedure, and the rest of the available data is randomly divided into training (80%) and testing data (20%) for the ANNs.

To identify possible input data for the ANNs, we calculated the correlation coefficients between historical observations of the different data series. We also tested the relationship between different exploratory variables and the balancing market through multiple linear regression, both for raw data, their lagged values and processed versions. For instance, we developed indicator series using logical statements based on the data that considered changes from day to day and calendar effects as well as daily, hourly and seasonal effects. This gave some information on input variable selection for the ANNs, and we further validated the selection by sensitivity tests. The sensitivity tests were done by varying one variable in the neural network at a time, while holding the remaining variables constant. The input variables which proved to give the best accuracy of the ANNs are presented in Table 1.

The ANNs are designed as multi-layer perceptron models (MLP), which is a class of feedforward neural networks. The models are created as three-layer networks with one hidden layer, though several hidden layers were tested. Supervised learning is used to train the networks, using a backpropagation network learning algorithm to adjust the weights and biases. The root mean squared error (RMSE) is used to measure the error between the output value and the target value.

In the backtesting procedure, the ANNs generate daily forecasts that are used together with the scenario generation method in [24] to generate scenarios for the optimization models. The naive method of predicting zero imbalance gives no new information about the future, but provides a scenario tree with the historical distribution of the volumes’ and premiums’ deviations from zero. With the perfect information model, there is no need for scenarios in the optimization model and the balancing market prices and demand are deterministic and equal to the historical realized values.

Table 1 Exogenous variables included in the ANNs for the balancing market premium and volume
Full size table

5 Results

5.1 Coordinated versus sequential bidding

We evaluate the gain of coordination by considering the total value for the coordinated and sequential approach in Table 2. The total value is the sum of market revenues for each day in the testing period, less start-up costs plus the value of water stored in the reservoirs at the end of the testing period. An insignificant gain of 0.07% in total value is obtained by using the coordinated model with the ANN forecast. We observe that the coordinated model utilizes the balancing market more, as expected. It obtains higher revenues from upward ramping, but also higher costs from downward ramping. The sequential model obtains higher revenues in the day-ahead market, which is not surprising as it allocates the optimal amount of capacity for the day-ahead market first. However, the amount offered in the day-ahead market restricts the idle capacity that can be used in the balancing market. The results show that the sequential model obtains lower start-up costs than the coordinated model, which is somewhat unexpected for a coordinated strategy which takes both markets into account during the bidding process. However, the total difference in revenue is small.

In order to compare the production patterns of the two approaches, we calculate the distribution of the production volumes, i.e. the number of hours the generators is run on various levels. The results are shown in Fig. 7. It is evident that for zero, minimum production (16 MW) and maximum production (80 MW) are the most used production levels for both methods. However, the coordinated model utilizes more of the volume levels in the range between minimum and maximum capacity in order to be able to ramp up to maximum capacity, or ramp down to either minimum capacity or zero.

Fig. 7
figure 7

The production levels for the coordinated (top) and sequential approach (bottom)

Full size image

We also consider the average revenue per MWh for the two approaches. The average revenue per MWh is calculated by dividing the sum of market revenues by the total production in the period. While the total value illustrates the ability of the model to utilize the water in the best possible way, the average revenue is a measure of how well the bidding strategy adjusts the production allocation according to the market prices. Producing at high prices in the day-ahead market, and utilizing high premiums in the balancing market, increases the average revenue.

Table 2 Total value, accumulated revenues/costs, and water value for coordinated and sequential bidding
Full size table

The coordinated model has an average revenue of 30.63 [EUR/MWh], while the sequential method has an average revenue of 30.57 [EUR/MWh]. This difference indicates that the coordinated model is slightly (0.17%) better at adjusting the power production according to the market prices which maximizes the total revenues. Our results of limited gains are in line with previous results (e.g. [27]) but are moderate compared to [28], which find gains up to 2%. However, they do not model uncertain demand in the balancing market as we do and thus their estimates are more optimistic. If demand in the balancing market increase due to more intermittent production, the gain from coordination may increase.

5.2 Quality of the balancing market forecast

We also want to quantify the effects of the quality of the forecasting method. We therefore run the backtesting procedure for the coordinated model when predicting zero imbalance in expectation and having perfect information.

Predicting zero imbalance is a naive method, however, it is still reasonable because the system should be in balance in expectation. The value of coordination using the zero imbalance forecast is estimated to be 0.0%. This gives a lower bound on coordination that is in line with theory: the coordinated approach will do equally well or better than the sequential approach.

The other case considered is having perfect information of the balancing market. With perfect information, the performance of the model increases substantially. The perfect information case obtains a gain of coordination of 3.80% higher total value and a 5.60% higher average revenue. These values are the upper limit of the coordination gain that can be achieved with a very accurate prediction model for the balancing market. It is also evident from these results that the ANN prediction model developed in this paper has room for improvement—a gain of 0.07% may not be significantly different than the lower bound at zero.

6 Conclusions

The coordinated bidding problem for a hydropower producer considering the Nordic day-ahead and balancing market is formulated as a three-stage stochastic mixed integer program. The optimization model and different prediction models are evaluated in an extensive backtesting procedure simulating real operations. The results are analysed in two dimensions; first, we consider the gain of using a coordinated over a sequential approach for solving the bidding problem, second, we consider the value of improved prediction models for the balancing market. For this we tested the bidding model using a forecast predicting zero imbalance in expectation and a forecast having perfect information as well as developing a three-layer perceptron artificial neural network with one hidden layer for forecasting prices, direction (up or down) and volume.

By comparing the results of the coordinated approach to the sequential approach using the ANN forecast, only modest improvements (0.07%) in total value are found. This may not be significantly different than the lower bound at 0% that is estimated using the zero imbalance forecast. By using perfect information forecasts, an upper limit of the gain for coordination is estimated to be 3.8%, which indicate that a substantial gain in profits can be obtained by coordinated bidding if accurate forecasts could be developed. Our recommendation is that further research and industrial efforts should be focused on developing high quality prediction models for the balancing market. This could be done by using machine learning methods that utilize a larger set of input data than what is used in our work.

In addition, another strand of future research could be devoted to the modelling of the bidding problem itself. Modest calculation times are needed for our test case that uses a limited number of scenarios, but the scalability of formulations based on deterministic equivalents of stochastic programs is limited. Formulations that better enable representations of the distribution of future prices, ramping direction, volume and inflows to a cascaded set of reservoirs, will improve the applicability of the bidding model. This can for example be done by using decomposition, dynamic programming methods or robust optimization.