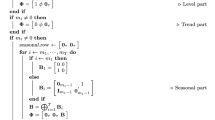1 Introduction

One strategic objective that companies operating in energy markets is to obtain accurate forecasts which, by reducing uncertainty in predicting the effects of management, can lead to substantial improvements in operating efficiency, reduction of maintaining costs and increased reliability of the power supply. A descriptive statistics analysis of the performances of energy companies is given in [26]. Over the last few decades, there have been many references with regard to the efforts being made to improve the accuracy of short term load forecasting.

The main goal of the paper is to develop a Regression-plus-SARMA (Reg-SARMA) approach for short term forecasting of hourly electricity demand in the Italian electricity market.

Usually, the classical linear regression is a popular tool for investigating the relationship between a set of regressors and load, so as to forecast the load on the basis of the values of the predictors. Model parameters are estimated by applying the ordinary least squares method, which involves the minimization of the sum of squared deviations (residuals) between observed and expected values given the fitted model. Applications of the regression model, for example, to Italian electricity consumption can be found in [3, 5, 15, 38].

There are many reasons why classical linear regression (CLR) might fail, ranging from the inability to represent non-linear relationships to the often unrealistic requirement of a constant error variance. Also, special care should be taken regarding the possible existence of outliers and/or multi-collinearity in the regressor matrix because either may alter the perception of the importance of the predictors and lead to inaccurate forecasts. Furthermore, residuals may be auto-correlated. Therefore, the question arises of whether we can improve our forecasts by incorporating information on residuals.

In this paper, to deal with the correlation problem we introduce a combination of statistical methods, classical linear regression plus a SARMA model for the residuals.

The intent is to provide a more comprehensive, flexible and effective methodology for short term predictions particularly for the case of the high-frequency time series of the energy market. The novel approach will enable reliable forecast of data that exhibit high volatility, strong mean reversion, and leptokurtosis. In the first stage, estimated loads are derived from a classical linear regression model with non-stochastic predictors. In stage two, the residuals of stage one are examined by means of Box–Jenkins processes to ascertain whether they are random, or whether they exhibit patterns that can be used to improve fitting and enhance forecast accuracy. Finally, the computation of marginal prediction intervals (PIs) is used to evaluate the uncertainty associated with forecasts of hourly electricity load. The combination of the three-model building phases constitutes the specific contribution of this paper. We will demonstrate that the Reg-SARMA approach is not only effective in eliminating the harmful presence of serial dependence between regression residuals, but also it is easy to implement and satisfactory with respect of the predicted loads. The proposed methodology shows that intelligent integration of linear regression, time series and computational resources into a unique approach may provide accurate predictions for short-term electric loads.

The paper proceeds as follows. Section 2 outlines the construction of the classical linear regression model, which will be based on a standard set of hypotheses so that the only problem will be the selection of the explanatory variables. We use principal component analysis and backward stepwise elimination to choose the predictors (essentially, polynomials in time and calendar dummy variables) to be inserted in the regression model. Section 3 discusses the choice of the SARMA process that best describes the behavior of the estimated regression residuals. We consider a very broad class of processes. The stationary and invertible process associated with the smaller Akaike information criterion and the smaller Ljung–Box statistics are selected. Then, the residuals in the original regression model are replaced by the fitted values of a SARMA process. Finally, regression and SARMA parameters are re-estimated simultaneously by using the ordinary least squares and taking advantage of the fact that the new regressors eliminate the serial correlation between the original residuals. Applications of the proposed methodology to Italian data (thanks to the ample availability of complete time series) show that Reg-SARMA models are very useful for point and interval forecasting of hourly electric demand. Section 4 includes concluding remarks and future research.

2 Related work

The importance of energy demand management has been more vital in recent decades as the resources are getting less, emission is getting more and developments in applying renewable and clean energies has not been globally applied. Demand forecasting plays a vital role in energy supply-demand management for both governments and private companies. Therefore, using models to accurately forecast the future energy consumption trends is an important issue for the power production and distribution systems. Several techniques have been developed over the last few decades to accurately predict the future in energy consumption. Over the years, several methods have been developed to model the electricity load. See [21, 49] for a review. There has been a recent increase in literature, also under the impulse of [22]. In general terms, the various methods of load forecasting that can be applied at the macro level give rise to two main classes of procedures: first, statistical techniques such as seasonal autoregressive moving average, linear regression, non-parametric e semi-parametric regression, periodic stochastic time series, general exponential smoothing, state space model and Kalman filter analysis (e.g., [38, 42, 51]); second, artificial intelligence based techniques such as support vector machines fuzzy logic, artificial neural networks and expert based systems (e.g. [23, 29, 47, 48]). In the present paper, we describe and test a methodology based on linear statistical methods for short term load forecasting (STLF). An overview on this theme is provided in [1, 10]. Results of simple regression time series are often promising, and lead to developing univariate and multivariate models. [4] believe that some of the developed time series models such as ARIMA models and state space models are among the most useful short-term forecasting models (see also [13, 37]). A time series approach was also applied by [46] to forecast very short-term electricity demand in south Australia. The used approach slices the seasonal univariate time series into a time series of curves, and applies functional principal component analysis prior to using the regression techniques and univariate time series forecasting method. The authors believed that their approach is able to improve the accuracy for both point and interval forecasts.

Various techniques have been investigated to solve the problem of short term forecasting, with varying degrees of success and there are widespread studies making efforts for improving the accuracy of prediction. The reason of applying various methods to predict the energy consumption is that when the accuracy and computing time of several methods are the same, simpler methods are preferred to more complex methods. Therefore, developing simple methods with acceptable accuracy is an attractive area of future studies.

3 Building the CLR model

The predictor selection is the most important phase in the construction of a classical linear regression model. Due to the lack of an established theoretical base for convincing derivation of the explanatory variables to be employed in the analysis of the hourly electricity load, we are compelled to consider many potential factors. After analyzing a number of potential predictors, we settled on two sets of explanatory variables.

The first set comprises calendar variables that capture various features and special conditions concerning consumer habits. Calendar events that affect electricity demand are the hours of the day: 23 dummy variables excluding the 24-th hour (note that at least one category of each group of dummy variables must be omitted to prevent complete collinearity between predictors); the days of the week: 6 dummy variables excluding Wednesday; months of the year: 11 dummy variables for the months excluding February. The choice of the omitted dummies arises from auto-correlation analysis and experience with the utility companies. Another predictor considered is the daylight saving time. In Italy, daylight saving time begins in the last Sunday of March at 2:00 a.m. At that time all clock times are set ahead one hour. Loads corresponding to the non-observation at 2:00 a.m. are imputed using the average of the loads at 1:00 a.m. and 3:00 a.m. In the last Sunday of October, at 3:00 a.m., returns the standard time and clock times are moved back one hour. Loads corresponding at 2:00 a.m. are imputed using the average of the loads at 2:00 a.m. and 3:00 a.m. Other predictors taken into account are public holidays (official and religious), days before and days after holidays (including week-end days). In short, a set of \(m=4+23+6+11+4=48\) variables is allowed.

The second set of explanatory variables derives from the trend always noted in load time series. Therefore, a standard procedure would be to include orthogonal polynomials in the regression up to the order needed to characterize the most complicated trend. In the time series studied in our paper, orthogonal polynomials were fitted adaptively up to the order four. The use of orthogonal polynomials results in uncorrelated regressors so that multi-collinearity cannot occur.

Predictors such as sociological and demographic factors, temperature, relative humidity, solar radiation, wind speed, cloud cover, etc. were ignored because they are unusable in aggregation at large regional scale. Additionally, prediction of changes in social and climate factors raises the question of whether these variables are predictable and, if they are, whether predictability can be achieved for changes at an hourly time step (see, for example, [6, 9]). Furthermore, if one or more predictors must, themselves, be forecast, then the formula for forecast variances has to be modified to incorporate the uncertainty in forecasting those predictors that are not known perfectly, ex ante. This will vastly complicate the computation, particularly when taking into account relationships between errors in the predictor generating process and errors in the load generating process. Many authors view this problem as simply intractable. See [16, p. 127–128].

In any event, indicators for the climate could be introduced at the cost of setting load forecasting within a more general framework of a system of time series regression equations (some based on atmospheric physics) which are beyond the scope of this paper. The undeniable influences of climatic variations are captured implicitly by the joint action of a polynomial trend and calendar dummies. In summary, the proposed model has the following form

$$\begin{aligned} L_t=\beta _0+\sum _{j=1}^m\beta _jX_{t,j}+e_t, \end{aligned}$$
(1)

where \(L_t\) is the hourly electric load expressed in MWh and \(X_{t,i}, i=1,2,\ldots ,m\) are the regressors or predictors. Each \(\beta _j\) is a parameter that measures how \(L_t\) is related to the j-th predictor: \(\partial L_t/\partial X_{t,j}=\beta _j\). Thus, coefficients measure the marginal effects of the predictor variables. One way to interpret \(\beta _0\) is that it coincides with the expected load (in MWh) when all dummy variables are in their respective reference category. Each combination of 0/1 gets its own regression surface, still parallel to each other. The addend \(e_t\) is an unobserved residual that accounts for disturbing factors other than the variation in the \(L_t\) that predictors do not explain.

Within the framework of the classical linear regression model, the term \(e_t\) requires making explicit assumptions. We follow [50, ch.10]

  1. 1.

    The conditional expectation of the residual at time t, given the predictors for all time periods, is zero \(E(e_t|{\mathbf {X}})=0\) for each t.

  2. 2.

    The conditional variance \(E(e^2_t| {\mathbf {X}})=\sigma ^2_e, t=1,\ldots ,n\) is finite and constant for each t.

  3. 3.

    Conditional on the matrix of predictors \({\mathbf {X}}\), the residuals in two different periods are uncorrelated with each other \(E(e_te_r|{\mathbf {X}})=0\) for each \(t\ne r\).

  4. 4.

    The \(e_t\)s are independent of \({\mathbf {X}}.\)

  5. 5.

    The \(e_t\)s are independently and identically distributed as Gaussian random variables with zero mean and variance \(\sigma ^2_e\).

Under the above conditions the method of least squares yields the best linear unbiased estimators of the unknown coefficient \({\boldsymbol{\beta }}\), conditional on \({\mathbf {X}}\). A consequence of assumption 5 is that the least squares estimators have a Gaussian distribution, conditional on \({\mathbf {X}}\), providing in this way, an inferential framework for the regression model. In this case, the parameter estimates obtained by least squares are equivalent to maximum likelihood estimates.

3.1 Discarding some of the predictors

Due to the high number of predictors, it is advisable to perform some sort of screening procedure before building a regression model with sequential strategies such as stepwise selection. To this end we carry out a preliminary, albeit schematic, selection based on principal component analysis. The set of predictors is then further refined by applying stepwise backward elimination. Before we start, it is important to emphasize that in most cases the testing based screening procedures tend to include fewer regressors than desirable for forecasting purposes. In this sense, the variable selection will not involve the regressors in the trend component because it is better to use them to predict hourly electricity demand, even when they are not highly significant.

Let \(P_1,\ldots ,P_{\nu }\) be the first \(\nu\) principal components (PC) of the correlation matrix of the potential regressors, ordered according to the percentage of explained variance from most to least. We consider useful components the PCs associated with an eigenvalue greater than or equal to 0.70 and which have three or more substantial loadings. We presume that if a data set were more parsimoniously represented by only \(\nu\) PCs, then it will often be true that the data set can be replaced by a subset of \(\nu\) “principal variables” with a relatively small loss of information.

We have selected the principal variables using the technique B4 described in [25, Sec. 6.3]. Principal variable analysis helps reduce the complexity of model (1) by identifying those variables that contain the most information. Specifically, method B4 first considers the predictor, which has the highest correlation coefficient (in absolute term) with the first principal component. This predictor is retained and is followed by another predictor that has the highest absolute correlation coefficient with the second principal component. Naturally, selections subsequent to the first are limited only to the principal variables that have not been retained in the preceding selections. The procedure is continued until \(\nu\) potential regressors have been identified. Nonetheless, \(\nu\) predictors can be still too large.

A refinement is carried by means of the backward elimination procedure, which cancels sequentially the predictors “most useless” from the current set of predictors, one at a time until no more predictors can be removed. At each stage, the predictors are identified whose p-value of the corresponding t-statistic is higher than a prefixed threshold \({\bar{\pi }}\). The constant \({\bar{\pi }}\) is the minimum level of significance to reject the hypothesis \(H_0: \beta _i=0\), that is, \(p_i>{\bar{\pi }}\) implies that the predictor \(X_i\) is a candidate to be removed. The p-values should not be taken too literally because we are in a multiple testing situation where we cannot assume independence between trials. Moreover, the removal of less significant regressors alters the significance of the remaining ones. Thus, one often overstates the importance of the remaining predictors. Accordingly, we have established \({\bar{\pi }}=0.0000001\). The choice of such a small value is motivated by the desire to limit the adverse effect of huge samples (which are typical in the load forecasting domain) on stepwise regression. See [36].

If, at a given stage, there are more than one predictors verifying the condition \(p_i>{\bar{\pi }}\), then the predictor which has the largest VIF (variance inflation factor) is canceled from the set. Removals continue until the candidate to exit has a p-value lower than the minimum level \({\bar{\pi }}\).

3.2 Adequacy of fitting

The adequacy of the fitting models is studied by using the values of the adjusted \(R^2\) and the bias-corrected Akaike information criterion

$$\begin{aligned} {\bar{R}}^2=1-\left( 1-R^2\right) \left[ \dfrac{n-1}{n-m-1}\right] ; \quad AICc=n\left[ \log \left( {\widehat{\sigma }}^2_e\right) +\dfrac{n+m}{n-m-2}\right] \end{aligned}$$
(2)

where \(R^2\) is the coefficient of multiple determination of the regression equation, m is the number of unknown parameters of the model and \({\widehat{\sigma }}^2_e\) is the estimated variance for the fitted regression.

3.3 Serial correlation of estimated residuals

The CLR model presupposes the absence of serial correlation between residuals. If this is not true, then this fact can be detected through the auto-correlations of the estimated residuals. In this regard, a commonly used statistic is that suggested in [35]

$$\begin{aligned} LB=n\left( n+2\right) \sum _{t=1}^{k_1}\dfrac{r^2_j}{n-t} \end{aligned}$$
(3)

where \(r_t\) is the auto-correlation of lag t for the estimated residuals \({\widehat{e}}_t\)s. Given the hourly seasonality of the loads, we set \(k_1=2\cdot 24=48\). Large values of LB lead to the rejection of the hypothesis of no auto-correlation between the residuals.

4 Point and simultaneous interval forecasts

Let \({\widehat{L}}_{n+h}\) be the conditional expectation of the load demanded at day \(n+h\), \({L}_{n+h}\), given the past loads \(\left\{ L_n,\ldots ,L_1\right\}\)

$$\begin{aligned} {\widehat{L}}_{n+h}=E\left( {L}_{n+h}|L_n, L_{n-1},\ldots ,L_1\right) , \quad h=1,2,\ldots ,H \end{aligned}$$
(4)

where H is the prediction horizon of interest. We denote the conditional forecast error corresponding to \({\widehat{L}}_{n+h}\) by \(e_{n+h}=(L_{n+h} -{\widehat{L}}_{n+h})\). It can easily be shown that (4) is the forecast for which the mean squared error of prediction, defined as \(E(e_{n+h})^2\), is as small as possible. The execution of (4) leads to

$$\begin{aligned} {\widehat{L}}_{t+h}={\widehat{\beta }}_0+\sum _{i=1}^m{\widehat{\beta }}_iX_{t+h,i}. \end{aligned}$$
(5)

Expression (5) does not create any major problem because forecasts include either values of the orthogonal polynomials, which have already been used as regressors or future values of calendar effects, which are predetermined on the basis of international conventions.

Now we turn to the question of how to facilitate the comparison of the forecasting performance of regression models. For the purpose of this study, we have not used the entire time series, but kept the very last time points (validation period) untouched because to serve as a benchmark against which the quality of the forecasts is to be judged. In detail, we evaluate the predictive accuracy by the relative absolute error of forecast (RAEF).

$$\begin{aligned} RAEF=100\left[ 1-H^{-1}\sum _{h=1}^H\dfrac{|L_{n+h}-{\widehat{L}}_{n+h} |}{|L_{n+h}|+|{\widehat{L}}_{n+h}|+\epsilon }\right] \end{aligned}$$
(6)

where H is the time horizon and \(\epsilon\) is a small positive number (e.g. \(\epsilon =0.00001\)) which acts as a safeguard against division by zero. The integer h runs on the hours of the validation period. Coefficient (6) is independent on the scale of the data and, due to the triangle inequality, ranges from zero to 100. The maximum is achieved in the ideal case of perfect forecasts: \(L_{n+h}={\widehat{L}}_{n+h}\) for each h. The lower the RAEF is, the less accurate the model is. The minimum stands for situations of inadequate forecasting such as \({\widehat{L}}_{n+h}=0\) or \({\widehat{L}}_{n+h}=-L_{n+h}, h=1,2,\ldots ,H\).

4.1 Simultaneous forecast intervals

Load forecasting is necessary, but it is at least as important to provide an assessment of the uncertainty associated with forecasts. The usual method of evaluating the uncertainty associated with forecasts requires the computation of marginal prediction intervals (PIs) at each individual horizon. However, Marginal intervals are overly optimistic, and may, therefore, be misleading since H marginal \(100(1-\alpha )\%\) predictions give a probability lower than the nominal level \((1-\alpha )\%\) for the joint H intervals.

Managers of electric power and light systems are frequently confronted with decision problems that require assessment of the set of possible upper/lower bounds that demand of electricity will follow over time and there are several methods for computing simultaneous forecast intervals. See [40, 114–116]. In this regard, [34] derived an exact probabilistic representation of the future loads corresponding to the settings \(X^*_{t,i}, t=(n+1),\ldots ,H\ i=1,\ldots , m\). Whether a particular pattern of loads \(L_{n+1},\ldots , L_H\) falls within the region is easily ascertained by substituting these values into the multi-dimensional ellipsoid equation representing the prediction region. Path forecast evaluation falls within this context. See [27].

The exact approach is impractical if one is not interested in potential trajectories, but rather in a system of intervals, each covering a future observation. Given the availability of H future values, a more simple strategy is to determine two bands such that, under the condition of independent Gaussian distributed random errors, the probability of consecutive future loads \(L_{n+h}, h=1,2,\ldots ,H\) that lie simultaneously within their respective range is at least is \((1-\alpha )\). In this regard, Lieberman proposes the hyper-cuboid region

$$\begin{aligned} \left[ {\widehat{L}}_{n+h} \pm {\widehat{\sigma }}_h\ t\left( \dfrac{\alpha }{2H},n-m-1\right) \right] ,\quad h=1,2,\ldots ,H, \end{aligned}$$
(7)

where \(t(\alpha /2H,n-\nu )\) is the \(\alpha /2H\) percentage point of the t distribution, which has \((n-\nu )\) degrees of freedom. We remark that there are other formulations for the prediction intervals in a regression model (e.g. [17]), but (7) is simple to compute and it is equivalent to the other statistics for large samples as those used in this paper. Furthermore, \({\widehat{L}}_{n+h}=\widehat{{\boldsymbol{\beta }}}^t{\mathbf {X}}_{n+h}^*\). The estimate of \(\sigma _h\) is

$$\begin{aligned} {\widehat{\sigma }}_h= {\widehat{\sigma }}_e\sqrt{n^{-1}(n+1)+\sum _{i=1}^m\sum _{j=1}^m a^{i,j}\left( X_{h,i}-\bar{X_i}\right) \left( X_{h,i}-\bar{X_i}\right) }. \end{aligned}$$
(8)

Here \({\widehat{\sigma }}_e\) is the estimated mean square error of the regression and \(\bar{X_i}\) is the mean of the i-th predictor. The quantity \(a^{i,j}\) is the (i,j) element of the inverse matrix of the unscaled variance-covariance matrix of the predictors

$$\begin{aligned} a_{i,j}=\sum _{t=1}^nX_{t,i}X_{t,j}-n\bar{X_i}\bar{X_j},\quad i,j=1,2,\ldots ,m. \end{aligned}$$
(9)

The intervals (7) give the box-shaped region in H-dimensional space that circumscribes the exact confidence ellipsoid of minimum volume. However, if n is large, the approximate method is expected to give good results since the regression plan is essentially known. Finally, it is important to note that the predictors of the model (1) can be established ex-ante without uncertainties by the researcher.

The most important characteristic of PIs is their actual coverage rate (ACR), which is usually measured by the proportion of true loads observed in the validation period that are enclosed within the bounds

$$\begin{aligned} ACR_{\alpha }=100H^{-1}\sum _{h=1}^Hd_{h,\alpha }\quad \text{where}\ d_{h,\alpha }= \left\{ \begin{array}{ll} 1&{}\quad \text{if} \ L_{n+k}\in \left[ L_{1,h,\alpha }, L_{2,h,\alpha }\right] \\ 0&{}\quad \text{otherwise}. \end{array} \right. \end{aligned}$$
(10)

If \(ACR_{\alpha }\ge \left( 1-\alpha \right)\) then future loads tend to be covered by the bands, but it may also imply that the estimated variances of forecast errors are positively biased. A level of \(ACR_{\alpha }\) less than \(\left( 1-\alpha \right)\) indicates under-dispersed forecast errors with overly narrow prediction intervals and unsatisfactory coverage behavior.

All other things being equal, narrow PIs are desirable as they reduce the uncertainty associated with forecast-based decision-making. However, higher accuracy level can be easily obtained by widening PIs. A complementary measure that quantifies the sharpness of PIs might be useful in this context. Here, we use the score function.

$$\begin{aligned} g_{h,\alpha }=\dfrac{\left( L_{2,h,\alpha }-L_{1,h,\alpha }\right) }{2L_{n+h}}, \quad h=1,2,\ldots , H. \end{aligned}$$
(11)

Expression (11) reflects a penalty proportional to the narrowness of the intervals that encompass the true values at the nominal rate. Of course, the lower \(R_{h,\alpha }\) is, the more accurate PIs will be. The average value of the score width across time points

$$\begin{aligned} ASW_{\alpha }=\dfrac{1}{H}\sum _{h=1}^L g_{h,\alpha } \end{aligned}$$
(12)

provides general indications of PI performance for what concerns their width.

4.2 Application to Italian data

We have implemented the procedure outlined in the preceding paragraphs to hourly time series of electricity loads from 1 a.m. on Friday, January 1, 2016 to 12 p.m. on Monday April 9, 2018, one for each zone of the Italian electricity market. See [14]. All the time series are \(n=19{,}704\) h long. The last nine days (216 hourly loads) act as validation period for assessing the accuracy of forecasting. Original data have been subjected to the filtering procedure of outliers described in [2].

OLS provide the results in Table 1 (note that only the significant predictors are shown). A quick glance is sufficient to note many interesting features. First of all, the presence of a quartic trend is evidenced by the significance of the regression parameters. It should be noticed that the response variable is not standardized so that the scale of the predictors can be compared within the same zone, but only the sign of the coefficients can be fairly compared between different zones. The hourly pattern of electric demand is made clear by the preponderance of significant coefficients associated with the dummies of the hours. The sign is negative for hours before 8 a.m. and generally positive for business hours from 9 a.m. onwards.

Table 1 Estimation of the parameters with ordinary least squares
Full size table

Overall, the dummies are not important for the central days of the week, but significant for Monday, Saturday and Sunday. The sign of the coefficients is, as expected, negative for Saturday and Sunday confirming that consumption of electricity is lower at weekends (note that the coefficient is lower on Saturdays than on Sundays). Apparently, this effect extends to Mondays because, contrary to expectations, the sign of the Monday dummy is negative in each zone.

Regarding the dummies of the months, we observe that the coefficients are always negative in the four months from September to December whereas, in the other months, the sign is not constant. A negative sign is systematically found both for the dummy of holidays and the dummies concerning the days before and the days after holidays. We consider this a result of a small hourly electricity consumption when the productive activities slow down. The principal reason for introducing daylight saving time (DST) is projected energy savings, particularly for electric lighting (e.g. [33]). Our study suggests that the policy seems to have scarce effect because the dummy associated with DST is slightly significant (and negative) only for the two largest zones: North and South.

In general, the results are unsatisfactory because, even though most of the coefficients associated to the dummies are highly significant (p-values lower than \(10^{-3}\)), the adjusted \(R^2\) values are relatively small (not greater than 0.90) and insufficient for forecasting purposes. This is in contradiction with the high RAEF indices, which all remain above \(93\%\). The probability coverage rate (row headed “ARC”) always exceeds the nominal level of \(90\%\). On the other hand, the widths shown in the row headed “ASW” indicate over liberal forecast intervals because the width of the bands is typically about one half of the average hourly load.

The major drawback of the OLS method is clearly found in the Ljung–Box statistics (row “LB”) in Table 1. The values reported are extremely high (with p-values virtually zero), so indicating that estimated residuals are serially correlated in all regression models. The combination of small R-squared, high t-Student and strong serial correlation are clear symptoms that either some important regressors have been omitted and/or that auto-correlation has to be taken seriously into account.

5 Regression models with SARMA residuals

Serially correlated residuals have several effects on regression analysis. Least squares estimators remain unbiased but are not efficient in the sense that they no longer have minimum variance. The estimated standard errors of the coefficients may be seriously understated or overstated, depending on the underlying process by which they interact with the explanatory variables of the model. The forecast intervals and the various tests of significance commonly employed in CLR would no longer be strictly valid, even asymptotically.

The presence of serial correlation reveals that there is additional information in the data that has not been exploited in the CLR model. This is a fact of which we are fully aware since we have omitted to account for short-run effects on electricity demand. Many studies, in effect, state that consumers remember the past and this implies that the electricity load demanded in previous periods will matter in demanding decision today (the “recency effect”).

5.1 The Reg-SARMA method

To correct for auto-correlation, we assume that the unobservable residuals follow a multiplicative SARMA process

$$\begin{aligned} e_t=\left[ \phi ^*\left( B\right) \right] ^{-1}\theta ^*\left( B\right) a_t \end{aligned}$$
(13)

where B is the usual backward shift operator \(B^jz_t=z_{t-j}\) and

$$\begin{aligned} \phi ^*\left( B\right) =1-\phi ^*_1B-\phi ^*_2B^2-\cdots -\phi ^*_{p^*}B^{p^*}; \quad \theta ^*\left( B\right) =1-\theta ^*_1B-\theta ^*_2B^2-\cdots -\theta ^*_{q^*}B^{q^*} \end{aligned}$$
(14)

are polynomials in B. The polynomials are constrained so that the roots of \(\phi ^*\left( B\right) =0\) and \(\theta ^*\left( B\right) =0\) have magnitudes strictly greater than one, with no single root common to both polynomials, that is, only processes which are stationary and invertible are considered. Due to the massive presence of binary variables in the regressors, the process in (13) does not include difference operators. The “burden of non-stationarity” is placed entirely on the orthogonal polynomials used as regressors in Sect. 3.

Expression (13) may be considered as special case of the standard ARMA by taking \(p^*=p+sP\), \(q^*=q+sQ\). The integer s is the seasonal period (\(s=24\) for hourly time series). Some of the \(\phi ^*\)s and \(\theta ^*\)s could be set equal to zero. The errors \(a_t\) are independent and identically distributed random variables with zero mean and finite variance \(\sigma ^2_a\). The substitution of \(e_t\) of (1) into the model in (13) yields

$$\begin{aligned} L_t=\beta _0+\sum _{i=1}^m\beta _iX_{t,i}+\sum _{j=1}^{p^*}\phi ^*e_{t-j}+\sum _{j=1}^{q^*}\theta ^*a_{t-j}+a_t. \end{aligned}$$
(15)

The above relationship (15) requires much more parameters than classical regression model. To reduce the number of unknowns, we set the values of the newly added regressors \(e_t,\ t=0,-1,\ldots ,-(p^*-1)\) and \(a_t, t=0,-1,\ldots ,-(q^*-1)\) to zero because zero is their expected value. Residuals and errors at the other time points remain unknown. For sufficiently large n however the effect of the chosen initialization procedure will be negligible.

A number of approaches to improving OLS estimates in the presence of serial correlation (e.g. [7, 12, 30, 31, 41]) have approximated the residuals by using

$$\begin{aligned} {\widehat{e}}_t=\left( L_t-{\widehat{L}}_t\right) =\sum _{j=1}^{p^*}\phi ^*_j{\widehat{e}}_{t-j}-\sum _{j=1}^{q^*}\theta ^*_ja_{t-j}+a_t,\quad t=1,2,\ldots ,n. \end{aligned}$$
(16)

where \({\widehat{L}}_t, t=1,2,\ldots ,n\) are the estimated responses.

Let us suppose for the moment that \(p^*\) and \(q^*\) are known or given. The estimation of the SARMA parameters can be carried out by optimizing the log-likelihood function of (16) provided that the errors \(a_t\) are Gaussian random variables. Now, let \({\widetilde{e}}_t,\ t=1,2,\ldots ,n\) be the estimate residuals produced by the ARMA \((p^*,q^*)\) process

$$\begin{aligned} {\widetilde{e}}_t=\sum _{j=1}^{p^*}{\widehat{\phi }}^*_j{\widehat{e}}_{t-j}-\sum _{j=1}^{q^*}{\widehat{\theta }}^*_ja_{t-j}+a_t,\quad t=1,2,\ldots ,n. \end{aligned}$$
(17)

The \({\widetilde{e}}_t\)s are substituted into (15) yielding

$$\begin{aligned} {\widetilde{e}}_t=\sum _{j=1}^{p^*}{\widehat{\phi }}^*_j{\widetilde{e}}_{t-j}-\sum _{j=1}^{q^*}{\widehat{\theta }}^*_j{\widetilde{a}}_{t-j},\quad t=1,2,\ldots ,n, \end{aligned}$$
(18)

where

$$\begin{aligned} {\widetilde{a}}_t=\left\{ \begin{array}{ll} 0 &{}\quad \text{for}\ t=p^*, p^*-1,\ldots , \\ {\widetilde{e}}_t-\sum _{j=1}^{p^*}{\widehat{\phi }}^*_j{\widetilde{e}}_{t-j}-\sum _{j=1}^{q^*}{\widehat{\theta }}^*_j{\widetilde{a}}_{t-j} &{}\quad \text{for}\ t=p^*+1, p^*+2,\ldots . \end{array}\right. \end{aligned}$$
(19)

In practice, the one-step-ahead forecast \({\widetilde{e}}_{t+1}\) is used as an estimate of the unknown residual \(e_{t+1}\) and the unknown error \(a_{t+1}\) is set to its expected value of zero. In doing so, we can avoid the long auto-regression approximation of the MA component as is required in various GLS-type estimation methods such as [8, 18, 30, 44].

Thanks to the equations (17)–(19), the regressors of the extended relationship (15) are fully specified

$$\begin{aligned} L_t=\beta _0+\sum _{i=1}^m\beta _iX_{t,i}+\sum _{j=1}^{p^*}\phi _j^*{\widehat{e}}_{t-j}+\sum _{j=1}^{q^*}\theta _j^*{\widetilde{a}}_{t-j}+ a_t. \end{aligned}$$
(20)

The \({\widetilde{a}}_t\)s in the last sum are pairwise uncorrelated and do not contribute to the multi-collinearity of the new regression model. Even the third addend does not appear to pose problems of multi-collinearity. The Reg-SARMA approach consists of the OLS method applied to the estimation of (20)

$$\begin{aligned} {\widehat{L}}_t=\widehat{\beta _0}+\sum _{i=1}^m{\widehat{\beta }}_iX_{t,i}+\sum _{j=1}^{p^*}{\widehat{\phi }}_j^*{\widehat{e}}_{t-j}+\sum _{j=1}^{q^*}{\widehat{\theta }}_j^*{\widetilde{a}}_{t-j}\ . \end{aligned}$$
(21)

5.2 Orders of the SARMA components

One problem is still open. Since we ignore the orders of autoregressive-moving average components, the modelling procedure outlined in the preceding section should be repeated for each reasonable value of \(p^*\) and \(q^*\). In order to reduce the computational effort required to maximize the Gaussian likelihood function, several estimation procedures have been suggested. See [32]. For example, a number of authors: [18, 19, 39, 45], among others, propose to identify the orders \((p^*, q^*)\) by using a sequence of linear regressions of \(L_t\) on lagged variables \(L_{t-1}, L_{t-2}, \ldots , L_{t-p^*}, {\widehat{e}}_{t-1}, {\widehat{e}}_{t-2}, \ldots , {\widehat{e}}_{t-q^*}\) where the \({\widehat{e}}_t\) are obtained by fitting a long auto-regressive process to the time series of the residuals. Being a linear problem, the repetition for different values of \(p^*\) is computationally much cheaper than the maximum likelihood estimation of an ARMA process. Unfortunately, there is very little empirical evidence of the effectiveness and efficiency of these techniques in seasonal ARMA processes.

Let us assume that there is a true SARMA for the time series: \((p^0,0,q^0)\times (P^0,0,Q^0)_s\) and fix the constraints \(0\le p\le {\overline{p}}, 0\le q\le {\overline{q}}, 0\le P\le {\overline{P}}, 0\le Q\le {\overline{Q}},\) where \({\overline{p}}, {\overline{q}}, {\overline{P}}, {\overline{P}}\) are chosen beforehand trying to make sure the intervals include true orders, that is \(p^0 \le {\overline{p}},\quad q^0 \le {\overline{q}},\ P^0 \le {\overline{P}},\ Q^0 \le {\overline{Q}}\). One method used to locate a good solution is a trawling search through the \({\overline{p}}\times {\overline{q}}\times {\overline{P}}\times {\overline{Q}}\) possible processes. In our experiments, the processes are estimated by using the function arima() in the R package stats. In general, brute-force methods are unmanageable for extremely long time series because of the computational complexity. If \({\overline{p}}=4, {\overline{q}}=4, {\overline{P}}=3, {\overline{Q}}=3\) then considering all possible processes involves estimating 400 different processes. Actually, the obstacle is more apparent than real. Improvements in computers and reductions in hardware costs allow us to consider the trawling search solution attractive for many more research and real-world applications than in the past.

Another objection against trawling search concerns the fact that there are no guarantees that the family of considered processes will include the “true” process. Even if it does, minimization over all combinations of polynomial orders necessarily leads to the estimation of over-parametrized and, thus, unidentified models, that is, integers p, q, P, Q larger that the true orders. Note, in this sense, that many different processes may perform reasonably similarly and difference between their diagnostic statistics are often only marginal. [24] observe, however, that these issues are not so important in forecasting, where the focus of model selection is usually on the predictive ability of the chosen model, rather than on the correctness of the selection. In this light, we use the trawling search to detect the most suitable process aiming at maximizing predictive ability of the model.

It remains to be established how to choose between two different SARMA processes. It seems logical to start from the AICc and LB statistics obtained from the CLR model shown in Table 1. A process would be considered admissible for forecasting purposes only if it fulfills the conditions on the polynomials (14) and improves both AICc and LB for the estimated residuals of (16). The admissible process associated with the smaller AICc and LB is preferred.

Reg-SARMA equation (21) is a revised CLR model that should yield better statistics than the original CLR model (1). See [11, 20, 43]. Through extensive experimentation, [28, 31] showed that GLS-type schemes allow the analyst to perform a generalized least squares estimation without the cumbersome computational difficulties associated with the inversion of large size variance-covariance matrices.

5.3 Forecasts in Reg-SARMA models

The expanded relationship (21) can produce predictions of the new loads \(\widehat{{\mathbf {L}}}_{n,H}=({\widehat{L}}_{n+1},\) \({\widehat{L}}_{n+2}, \ldots , {\widehat{L}}_{n+H})\)

$$\begin{aligned} \widehat{{\mathbf {L}}}_{n,H}={\mathbf {Z}}_H\hat{\varvec{\gamma }}\quad \text{with}\ {\mathbf {Z}}_H=\left[ {\mathbf {X}}_H|{\mathbf {E}}_H|{\mathbf {A}}_H\right] ,\qquad {\widehat{\gamma }}^{\ t}=\left[ \widehat{{\boldsymbol{\beta }}}|\widehat{\varvec{\phi }}|\widehat{\varvec{\theta }}\right] \end{aligned}$$
(22)

where H is the time horizon and \({\mathbf {X}}_H\) is a \([H\times (m+1)]\) matrix of the H predetermined values of the original regressors for \(t=n, (n+1), \ldots ,H\). \({\mathbf {E}}_H\) is a \((H\times p^*)\) matrix constructed by using the predicted values of the OLS residuals estimated by the selected SARMA process. Each column of \({\mathbf {E}}_H\) is an instance of \({\widetilde{e}}_t\) at lags \(1,2,\ldots ,p^*\) and \(t=n, (n+1), \ldots ,H\). Analogously, \({\mathbf {A}}_H\) is a \((H\times q^*)\) matrix constructed by using the estimated errors of the process. Each column of \({\mathbf {A}}_H\) is an instance of \({\widetilde{a}}_t\) at lags \(1,2,\ldots ,q^*\) and \(t=n, (n+1), \ldots ,H\). The values of (22) serve to compute the diagnostic statistics for the expanded regression model. In particular, the AICc statistic (2) and the forecast intervals (7). The new results are summarized in Table 2, together with the results achieved with CLR (row “Ols1”). The R scripts for computing the Reg-SARMA estimates are available from the authors on request.

As can be seen, Reg-SARMA offers a substantial improvement over OLS estimation. The precision of the fitting procedure is increased as one can see from the columns in Table 2, which are dedicated to the AICc and \({\bar{R}}^2\) statistics. In both cases the improvement is quite substantial. Furthermore, the stability of the RAEF index across the estimation methods, is a demonstration that the predictive accuracy does not deteriorate when generalized least squares are used.

Table 2 Comparison of Ols and Reg-sarma estimates
Full size table

The new method has resulted in a general upgrading of the quality of forecasts. As can be readily appreciated, the width of the simultaneous forecast intervals (ASW) is reduced of about one half compared with OLS. The cost of this enhancement is a lower coverage rate (ACR), which, however, ensures a confidence level greater than the nominal level of \(90\%\). The most striking finding is the extraordinary decrease in the LB statistic whose p-value passes from a probability virtually zero with OLS to a probability virtually one with the Reg-SARMA method in all the six time series.

The preceding discussion assumes that the future values \({\mathbf {Z}}_H\) are known without errors or can be forecast perfectly or almost perfectly, ex ante. If, on the contrary, \({\mathbf {Z}}_H\) or part of it must themself be forecast then formula (7) has to be modified to incorporate the uncertainty in forecasting \({\mathbf {Z}}_H\). [16, Section 4.6.4] points out that firm analytical results for the correct forecast variance for this case remain to be derived except for simple special cases. For example, formula (8) may lead to a serious underestimate of the forecast standard error, if, as is not uncommon in practice, the uncertainty about the future value of regressors is of the same order of magnitude as the uncertainty about the residuals.

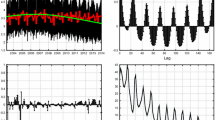
In the case of the expanded model (21), the regressors in \({\mathbf {X}}_H\) are purely deterministic and hence appropriate to interval forecasts by the Lieberman method. Figure 1 shows the forecasts of electricity demand and the lower and upper bands of the PIs .

Fig. 1
figure 1

Prediction intervals (PIs)

Full size image

The same is not true for \({\mathbf {E}}_H\) and \({\mathbf {A}}_H\) because these “pseudo” regressors are almost completely random in their behavior. It follows that, the application of the prediction intervals in (7) is based upon the strong and unrealistic assumption of making correct inference as if the serial correlation structure of regression residuals follow exactly the selected SARMA process. This partially explains why the coverage range of Reg-SARMA models is more conservative than that of CLR models.

6 Conclusions and future work

Classical linear regression (CLR) relies on strong assumptions that are rarely satisfied. The major contribution of this paper is to develop a new dynamic regression method (linear regression model with seasonal autoregressive-moving average residuals or Reg-SARMA model) for predicting the expected magnitude and direction of change of electricity demand. To build the Reg-SARMA model, we follow a two-step procedure. First, ordinary least squares (OLS) are applied to estimate a CLR model based on purely deterministic regressors. In the case wherein the regression residuals are not a white noise series, a SARMA process is identified and estimated on the basis of a multiple criteria optimization problem, which evaluates all possible processes encompassed within a \((4,0,4)\times (3,0,3)_{24}\) model involving 400 different processes. The stationary and invertible process associated with the smaller AICc and LB statistics, is selected. Secondly, two sets of pseudo regressors derived from the estimated residuals and from estimated SARMA errors are added to the CLR model. The extended model is estimated by using the ordinary least squares method and taking advantage of the fact that the new regressors eliminate serial correlation.

The proposed approach has been applied to obtain point and interval forecasts for the nine-day ahead hourly electric loads in six Italian macro-regions. Two facts emerge clearly from the results. The most significant variables that influence electricity demand belong to a small set of calendar dummy variables. The fitting performance is very satisfactory as evidenced by the adjusted \(R^2\), by the bias-corrected Akaike information criterion and by the predictive accuracy coefficient RAEF. Additionally, from a computational point of view, the method is not very demanding for currently available computers.

In summary, the technique outlined in this paper is appreciable because errors involved with modeling and parameter estimation are at a tolerable level, so that it can be effectively applied for short-term load forecasting, thus ensuring important improvement with respect to the conventional regression models.

A obvious limitation of the our work is the absence of regressors that influence customer behavior with particular reference to explanatory variables representative of socio-demographic factors and climatic changes characterizing the various zones. The modification of the simultaneous forecast intervals to take into account the increased variability is the next logical step of the study.