1 Introduction

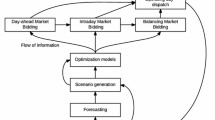
Modern, deregulated power markets often consist of a series of markets where power is traded. Electricity may thus be traded several times before actual consumption or production takes place. The fact that there are several markets for the same product gives rise to a complex decision situation for market agents. In addition, the various markets represent different degrees of flexibility. In the day-ahead market, power may be traded well ahead of the operating hour, which may be necessary for inflexible technologies with long warm-up times or start-up costs. In the intraday and balancing market, power may be traded closer to real-time, which may be necessary for technologies that are more difficult to schedule in advance, such as wind power. For flexible technologies such as hydropower, participating in the intraday or balancing market may bring increased profits.

Coordinating trades in sequential power markets is a complex challenge that combines market aspects with details of the physical production system. This paper presents how coordination of trades across multiple markets may be formulated within the framework of the optimization models used by the Nordic hydropower industry [1]. We also show how a set of time series models that describes the nature of prices and turnovers in the Nordic power markets are used for scenario generation to create input to the optimization model. Using the optimization model and the scenarios, we analyze the value of participating in and coordinating trades across multiple markets. By letting the market agent have limited or perfect information about the balancing market, we develop lower and upper bounds on the value of coordination. The main contribution of this paper is to show how these bounds are calculated for a case study representing a realistic hydropower system.

In [2] the multi-market bidding problem is defined as the problem faced by a producer that participates in several markets. A producer may take two approaches to the multi-market bidding problem: sequential or coordinated bidding. Sequential bidding is when the producer participates in both the day-ahead and an additional market, but consider the two markets sequentially and determines the volumes in the day-ahead market without considering the other market(s). In the coordinated case, the producer decides its trades in the day-ahead market while accounting for potential trades in the other market(s). In this way, the trading strategy is optimized across markets as a joint problem.

A joint optimization problem requires more computational resources than sequential optimization. It is therefore of interest to determine the value of coordination. If the value of coordination is large, it is well worth the effort to model this more complex problem. However, if the value is small, producers might be better off using the sequential approach and rather improve other parts of their operations or modelling. In fact, very few Nordic hydropower companies use formal optimization methods to determine the trades in markets beyond the day-ahead market. The day-ahead market is the main market place for power and therefore receives the most attention in the planning process. Trades in the other markets may be done more on an ad-hoc basis. The value of both the sequential and coordinated approach may therefore be compared to participating in the day-ahead market only, in order to find the value of participating in the other markets. Bounds on the potential added value for market agents that participate in the Nordic day-ahead and balancing market are calculated in [2]. They find a gain of participating in the balancing market that varies from 9.60 to 30.79% over the months of the year. The gain of coordinated versus sequential bidding was found to vary between 8.03 and 24.79% over months of the year. Additional tests show that the gain of coordinated bidding do not necessarily increase with an increase in balancing prices (as this increases the value of up regulation but decreases the value of down regulation) but rather with an increase in the difference between balancing and day-ahead prices.

A complicating factor when comparing literature on multi-market bidding, is that market arrangements and terminology vary around the world. Most power markets consist of a series of sequential markets where power and related products are traded. The markets differ in respect to the product traded (energy, capacity or ancillary services), the time to delivery, the auction or market clearing format, and demand side competition. In Europe and most North American regions, the wholesale power market consists of a day-ahead market, where expected production and consumption for the next day is traded, followed by an intraday market that may have continuous trade and a real-time balancing market for handling instantaneous imbalances in the power system.

The day-ahead market works pretty much in the same manner around the world. However, possibilities for adjustments in intraday markets and procurement of reserves for the transmission system operator (TSO) may take many forms depending on institutions, energy mix and traditions in each area. In this paper we use the rules and framework of the current Nordic market operated by NordPool, but the methods presented may be applicable to other market arrangements with some modifications. Specifically, the Nordic market consists of a day-ahead market, an intraday market with continuous trade and a real-time balancing market where the TSO procures reserves. We consider joint optimization of trades in the Nordic day-ahead and balancing market in this work, as this was previously analyzed by [2].

In existing literature, a common approach for the multi-market bidding problem is stochastic programming [3], which has been applied by [2, 4,5,6,7,8]. Stochastic programming is also used in this work. Formulations based on stochastic programming require that the stochastic parameters. i.e., the prices and turnovers in the markets, are described by scenario trees. Several methods have been suggested for generating scenario trees [9, 10], each using different methods and requiring different types of information about the stochastic parameters. Sometimes the best available information about an uncertain future is a single forecast. A single forecast does not provide enough information to construct a scenario tree, but may be combined with historical data on forecast errors to produce a scenario tree using the method in [9]. In the current work, time-series models for the prices in the Nordic day-ahead and balancing market are applied to generate forecasts that are used together with the forecast-based scenario generation method to generate scenarios trees.

The rest of this paper is organized as follows. In Sect. 2, we formulate the multi-market bidding problem for hydropower as a stochastic problem. In Sect. 3, we describe how two existing time-series models, namely the models developed by [13, 14], have been fitted to data for prices and turnovers in the day-ahead and balancing market. The resulting forecasts are used together with the forecast-based scenario-generation method [9] to generate scenarios trees as described in Sect. 4. Sect. 5 contains results from a case study where the optimization model is applied to an example hydropower system. Section 6 gives some conclusions.

2 The multi-market bidding problem

This section presents the basic mathematical modeling of a stochastic optimization model that coordinates multi-market trades for a power producer. Each market is described, in every time-step t and scenario s, by a price (or a premium) and a limit on the maximum volume that may be traded at that price. The volume limit is used to describe markets where there is a limited turnover, such as the Nordic intraday or balancing market. The volume limit, \(V^m_{ts}\) is a time series and may be a stochastic input to the model. In every time step and scenario, the volume \(y_{ts}^m\) sold in any market m must be less than the demand in the market, i.e.

$$\begin{aligned} y^m_{ts} \le V^m_{ts}. \end{aligned}$$
(1)

Prices, \(P_{ts}^{m}\), may naturally also be stochastic. The objective function is to maximize profits from sales in all markets, as in

$$\begin{aligned} max \sum _t \sum _s \sum _m \pi _s \Big ( P_{ts}^{m} y_{ts}^{m} \Big ), \end{aligned}$$
(2)

where the summation is over all time-steps, all scenarios and all markets. \(\pi _s\) is the probability of each scenario and \(y_{ts}^m\) is the volume offered in each market. \(y_{ts}^m\) must be subtracted if the producer buys energy from the market (e.g. for pumping or for substituting own production if cheaper energy is available) and when the producer offers downward balancing, otherwise the sales in each market are added. The sum of the position made in each market must be equal to the produced volume (perhaps with some small deviations \(z_{ts}^{+/-}\)), according to

$$\begin{aligned} \sum _m y_{ts}^{m} = \sum _g x_{tsg} + z_{ts}^+ - z_{ts}^- \end{aligned}$$
(3)

where \(x_{tsg}\) is the produced volume from each generator g in time step t and scenario s. The deviations \(z_{ts}^{+/-}\) are penalized in the objective function in order to reflect the cost of trading these unblances in yet another (imaginary or real) adjustment market. The above model assumes that any volume \(x_{tsg}\) may be produced. Actual production systems are much more complex. Details of hydropower production are however omitted from the presentation here. In fact, the above model may be used by any producer that participates in multiple markets as long as it is combined with a representation of the specific production system. In our case, the multi-market model is implemented within the framework of optimization models that is used for short-term production scheduling by most large hydropower producers in the Nordic region [1]. The volume to be produced from the generating units, \(x_{tsg}\), is thus determined by this more complex model that includes all technical, hydrological and environmental constraints relevant for hydropower production, e.g., minimum production levels, forbidden operating zones, start/stop, discharge dependent losses in tunnels and penstocks, minimum and maximum reservoir levels, minimum and maximum river or tunnel flows and more. This also includes more terms in the objective function, for instance start or stop costs that are modelled by integer variables. A value of water left in the reservoir at the end of the optimization period is also included. This may be interpreted as the marginal cost of production and is referred to as the water value in hydropower scheduling. A description of the production scheduling model can be found in [11].

The simple model formulation above is however not complete without modelling the information structure in the multi-market setting. Scenario trees should represent how information is revealed to the market agent over time. In the case of a market agent that coordinates its trades across sequential markets, the prices in the different markets will be revealed in sequence over time. The day-ahead prices are revealed once every day when the market clears, while the balancing market prices are revealed in real-time. The decisions for each market must also be taken in sequence. In the current set-up of the Nordic power market, the trades (or bids) for the day-ahead market must be submitted at noon the day before operations. Trades in the balancing market may be submitted up to 45 min before the delivery hour. This market structure must be reflected decision problem. Particularly, decisions in all markets must be made prior to the prices for that market are revealed. In terms of a stochastic programming problem, the trade decisions cannot depend on any particular scenario being realized. The question is then to maximize profits across all markets given the information that is available to market agents at any stage in the decisions process. The need for coordination across markets arises because the final commitment, i.e. the actual volume to be produced in a specific hour, is the summation over the position made in each market. For every hour, agents must make sure that their trades summarize to a feasible output level.

Consider the left part of Fig. 1 for a closer look at the scenario tree structure for the multi-market problem. The day-ahead prices are revealed once every day when the market clears. This means that the scenario tree for day-ahead prices must have a new stage every 24 h. For a 72-h horizon where the scenario tree branches into two new scenarios at each branching step, daily branching would yield \(2^2 = 4\) scenarios. In the balancing market, however, prices and volumes are revealed in real-time, which would lead to a scenario tree with hourly or even finer branching. This would quickly lead to a very large problem, especially considering that more than two new scenarios at each branching point is necessary to represent the full uncertainty of prices. To avoid this curse of dimensionality, we choose to have daily branching also for the balancing market, i.e., that both the day-ahead prices and the balancing market prices and volumes are revealed together when the day-ahead market clears. This assumption means that the models sees no uncertainty in the balancing market during each day.

Fig. 1
figure 1

(Left) Node representation of a scenario tree with daily branching. The dotted grey boxes illustrate that the traded volumes must be determined before prices are revealed. (Right) Scenario representation of a scenario tree with daily branching. The fully drawn grey boxes illustrate the normal non-anticipativity constraints, while the dotted grey boxes represent the market non-anticipativity constraints

Full size image

In the stochastic program, we use a scenario representation rather than a node formulation, see the right part of Fig. 1. This means that we must explicitly include non-anticipativity constraints stating that if two scenarios s and \(s'\) are indistinguishable at time t on the basis of information available at time t, then the decisions made in scenario s must be equal to the decisions made in scenario \(s'\). In our case, this means that the traded volume must be equal between all scenarios belonging to the same node,

$$\begin{aligned} y_{ts}^m = y_{ts'}^m. \end{aligned}$$
(4)

The non-anticipativity constraints are illustrated by the fully drawn grey boxes in Fig. 1. The optimization model also needs to know that day-ahead trades must be done prior to market clearing and that day-ahead trades must be made prior to balancing market trades. This means that the day-ahead trades cannot depend on any particular realization of prices for the next day. We call this the market non-anticipativity constraints and formulate them as

$$\begin{aligned} y_{ts}^{DAM} =y_{ts'}^{DAM} \end{aligned}$$
(5)

where the superscript DAM denotes the day-ahead market. The market non-anticipativity constraints are illustrated by the dotted grey boxes in Fig. 2. Similar constraints may be applied to any market trade volume variable, \(y_{ts}^{m}\), depending on whether the trades in the particular market are to be decided in real-time or not. If the constraint is imposed on the balancing trades and the current scenario tree structure is kept, it means that the balancing market trades must be determined prior to clearing of the day-ahead market, i.e. at the same time at determining the day-ahead market trades. If the constraints are not imposed, the balancing trades may be determined after clearing of the day-ahead market. Since there is no uncertainty within each day regarding the balancing market, this means that the producer has knowledge of the realized balancing market prices and volumes. This is of course not possible in reality, but we include it in our case study to measure the value of having perfect information in the balancing market. The results in the case study in Sect. 4 may thus be interpreted as bounds on the value of participating in the balancing market. If the producer has to decide the balancing market trades before clearing of the day-ahead market, this will underestimate the true value. If the producer can decide the balancing trades in real-time, i.e. with perfect information, this overestimates the true value. As stated earlier, daily branching of the scenario tree is used in this work for computational reasons. If we had used hourly branching or blocks of hours being revealed during each day for the balancing market, we would have gotten better estimates of the value of participating in the balancing market.

3 Modelling the markets

In this work, we consider the Nordic day-ahead and balancing market. The day-ahead market is operated by NordPool and cover the Nordic and Baltic countries. The day-ahead market is the main market place for power in the Nordics with 394 TWh traded in 2017 [12]. The balancing market is the Norwegian market for tertiary reserve, also called the regulating power market or manual frequency restoration reserves (FRR-M) market. For both the day-ahead market and the balancing market, we use data for the Norwegian price zone NO2.

For each market, we fit time-series models that describe the main properties of the market, i.e. the price or premium and the turnover. The time-series models are used to forecast or simulate future values to be used for scenario generation. Most effort is devoted to developing a good model for the balancing market. To the author’s knowledge, hydropower producers often have their own forecasting models for the day-ahead market, either in-house or supplied by external forecasting companies. The aim of this work is not to compete with such models. For the balancing market, however, good forecasts are harder to come by. Reasons for this is discussed in [13], which also formulate the balancing market model used in this work. The model for the day-ahead market is based on [14].

3.1 The day-ahead market

Due to the daily clearing of the day-ahead market, the hourly day-ahead market prices cannot really be represented as a pure time-series process. In normal time series, the information set is assumed to be updated when moving from one time step to the next. This is not the case for day-ahead prices, because the information set is updated on a daily rather than an hourly basis. The prices for all 24 h of the next day are set simultaneously in the market clearing. Thus, it is more correct to model the day-ahead prices as a time series of 24-h panel data rather than a single time series. Our method is based on [14], but we also account for seasonal variations. The model in [15] is a more advanced model in that it includes exogenous variables such as reservoir filling, temperature and wind power production forecasts, but we aim to keep the modelling more simplistic. Following [14], the day-ahead price \(P_{td}^{DAM}\) in hour t on day d is the sum of two independent components: a deterministic component \(f_{td}\) and a stochastic component \(x_{td}\),

$$\begin{aligned} P_{td}^{DAM}= f_{td}+ x_{td}. \end{aligned}$$
(6)

The deterministic component accounts for predictable regularities, such as the mean price level and daily and seasonal variations,

$$\begin{aligned} f_{td}= \mu _t + \sum _d \beta _t^d I_t^d + \sum _s \beta _t^s I_t^s. \end{aligned}$$
(7)

The mean price level is denoted \(\mu _t\) and may vary between hours. Daily variations are modelled by dummy variables \( I^d_t\) that equals 1 if the delivery day d is a specific weekday, d = 1 is Saturday, d=2 is Sunday ...and d =7 is Friday. The coefficient \(\beta ^d_t\) is the daily and hourly difference from the mean level, and \(\beta ^{Fri}_t\) is taken to be 0 to avoid collinearity. We also include dummy variables \(I^s_t\) for the season of the year. We choose to work with seasons instead of months or weeks to keep the model small. We define Winter to be weeks 48–8, Spring to be weeks 9–21, Summer to be weeks 22–34 and Fall to be weeks 35–47. Again, \(\beta ^{Fall}_t\) is taken to be 0 to avoid collinearity.

The stochastic component accounts for the variation in price around the deterministic component. In this work, the stochastic component is an AR(1)-model, i.e. it accounts for the dependency between the prices in 1 h of today, \( p_{td}^{DAM}\), and the same hour the day before, \(p_{td-1}^{DAM}\). Notice that the AR(1)-process is not between consecutive hours on the same day (as in a normal time-series), but between similar hours on consecutive days. This is due to the daily clearing of the day-ahead market. The stochastic component thus becomes

$$\begin{aligned} x_{td}= \alpha _h x_{td-1}+ \epsilon _{td} \end{aligned}$$
(8)

where the errors \(\epsilon _{td}\) will be \(IID \sim (0, \varSigma )\).

To estimate the model, i.e. to determine the parameters \(\mu _t\), \(\alpha _t\), \(\beta ^d_t\), \(\beta _t^s\) and \(\varSigma \), we use the method of seemingly unrelated regressors (SUR). SUR is appropriate for linear regression models that consists of several regression equations, each having its own dependent variable and potentially different sets of explanatory variables. In the case of day-ahead prices, we have one regression equation for each hour in the panel, that is, the system of equations is 24 copies of Eq. (6). The equation for each hour is a valid linear regression on its own and can be estimated separately. However, the error term may be correlated across equations, and it is likely that it is, since the bids for each hour underlying the market clearing prices are all quoted based on the same information set the day before [14, 15]. The correlation between error terms will be described by the covariance matrix \(\varSigma \). The panel data model is estimated using SUR-techniques in the R package systemfit [16]. The fitted values can be found in Tables 1 and 2. Another important output from the SUR-estimation is the covariance matrix that describes the covariance between the error-terms in the stochastic component, \(\varSigma \). The covariance matris for our fitted model is given in Table 3. Almost all hours have significant correlations with the other hours. This is different from [14] where mainly the peak-hours had significant correlations.

In the formulation of the optimization model in Sect. 2, each market must be modelled by a volume limit as well as a price. However, we do not model a time-series for the day-ahead market volume. The volume in the day-ahead market is never binding because the market turnover is much larger than the production capacity of an individual market agent. The volume limit in the day-ahead market is therefore taken to be a large, non-stochastic parameter.

Table 1 Estimated coefficients for the model for day-ahead prices. Hours 1–12
Full size table
Table 2 Estimated coefficients for the model for day-ahead prices.Hours 12–24
Full size table
Table 3 Cross-sectional correlation matrix of the error terms in the stochastic part of the model for the day-ahead market
Full size table

3.2 The balancing market

For the balancing market, we consider premiums rather than prices. In an optimization model for multi-market trade, it is the difference between the prices that are important for the trading strategy, i.e. if there is a premium over the day-ahead prices to be gained by participating in the balancing market. By analyzing the data for prices, it was found that the correlation between the day-ahead price and the premiums in the balancing markets is much weaker than the correlation between prices in these markets. The weak correlation between day-ahead prices and balancing premiums enables us to model day-ahead prices and the premiums by independent models.

Several methods for forecasting the balancing market are tested in [13]. The balancing market is event-driven, where hours with regulation in either direction are followed by hours of no regulation in an irregular pattern. This behavior cannot properly be modelled by a regular time-series model, since the timing between nonzero-observations is unevenly spaced. The balancing market only really exist in the time steps where there is demand in the market, i.e. when there is an unbalance. The size of demand is the amount of power that is needed to bring the system back in balance. The amount needed to bring the system back in balance may be less than the production capacity of individual agents, so there is a limitation on the amount that can be sold in the balancing market.

Due to this limited volume in balancing market, we model the trade limit in this market as well as the premiums. That is, for each time step, the maximum volume that may be traded in the market is limited by an upper bound. This upper bound is a stochastic parameter in the multi-market optimization problem, see Sect. 2. The balancing markets is thus described by two time series, one for premiums and one for the volume or trade limit. We model these together using one of the methods proven to have good performance in [13], namely the method of unevenly spaced time-series based on the work of [17].

The key for unevenly spaced time-series is to distinguish between the probability of the arrival of demand and the size of the demand. We define demand for balancing to exist whenever there is a need for either up or down regulation. In the training period, there is demand for balancing in 71% of the hours. The average time between demand is 1.23 h. We use the approach of [18] and model the time between arrival of demand as a moving average process where \(\pi _t\) is the (moving) average time between arrivals and \(q_t\) is the number of time steps since the last event. If we denote the balancing volume in hour t as \(V_t^{BM}\), then

$$\begin{aligned} \pi _t= {\left\{ \begin{array}{ll} \pi _{t-1} &{} \text {if} \ \ V_t^{BM} = 0\\ \pi _{t-1} + \alpha (q_{t-1} - \pi _{t-1}) &{} \text {if} \ \ V_t^{BM} \ne 0.\\ \end{array}\right. } \end{aligned}$$
(9)

The probability of balancing for each hour is then \(1/ \pi _t\). The parameter \(\alpha \) needs to be estimated, and this is done by minimizing the sum of square of residuals from the empirical arrival rate from historical data and the estimated arrival rate. The optimal value was found to be close to 0.01. The model for the arrival rate is not complete without information of the balancing volume, \( V_t^{BM}\), as this volume is needed in each hour to update the moving average process for probability of demand. The balancing volume is modelled as a stationary unevenly spaced time series of order 1, using the methods in [19]. That is, if \(\varDelta \) is the irregular time between non-zero values, the balancing volume in hour \(t+\varDelta \) is

$$\begin{aligned} V_{t+\varDelta }^{BM}= \theta ^{\varDelta } V_t^{BM}+ \sigma _{\varDelta } + \epsilon _{t+\varDelta } \end{aligned}$$
(10)

where \(\epsilon _{t+\varDelta } \sim N(0,1)\) and \(Cov(\epsilon _t,\epsilon _s) = 0\) for every \( t \ne s\) and \(\sigma _{\varDelta }^2 = \sigma ^2 \frac{(1- \theta ^{2\varDelta })}{(1-\theta ^2 )} \) for some \(\sigma > 0\). The parameters \(\theta \) and \(\sigma \) must be estimated, again using the method in [19]. For our data set, we obtain values for \(\hat{\theta } = 0.83\) and \(\hat{\sigma } = 70.54\). Our combined model for state determination and volume is thus an unevenly spaced time series, where the arrival rate is specified by a moving average process.

Notice that with this method, the moving average process will determine, in each time step, if there is demand for regulation or not. However, this does not give us any information about whether the demand is for up or down regulation. The direction of regulation is thus determined by the sign of the balancing volume, which may take both positive and negative values. The above model neither say anything about premiums. However, the balancing market premium is only relevant when there is a demand for balancing power. Thus, the premium for up regulation is only needed in the hours where there is a volume for up regulation, and vice versa for down regulation. In the modelling, we therefore use the same moving average process that determines the arrival of demand for regulation to determine the “demand” for regulation premiums. In this manner, only the hours with up or down regulation will have a corresponding premium. The AR process that determines the size of the premium is however fitted separately. That is, we determine the coefficients \(\hat{\theta }\) and \(\hat{\sigma }\) of the equivalent of Eq. (10) for the balancing premiums. We estimate the parameters using the same methods as for the balancing volume. The obtained values are \(\hat{\theta } = 0.76\), and \(\hat{\sigma }= 38.58\).

The historical data used to fit the time-series for the balancing market describes the total volume of activated power in the NO2 area. We must make assumptions on how much of the total volume that can be supplied by an individual agent or hydropower system. One approach is to assume that the individual producer may take a percentage of the total market volume, e.g., 10%, in every hour where there is demand. This means that a small volume is available to the producer in most hours. Another approach is to assume that in each hour, the total market volume may be activated from a single producer with a given probability, e.g., one in ten times. The probability may be related to the number of agents in the power market. The latter approach is taken in this work.

4 Scenario generation

With the specified models, we proceed to forecasting future values and scenario generation. The method used for scenario generation is described in [9], and is based on combining point forecasts with historical forecast errors, i.e., the difference between historical forecasted values and historical realized values. For this reason, we divide our data into 3 sets: a training set for the time series models, a training set for the scenario-based forecast method (where we find the forecasting errors), and a final set where we test the scenario generation method, see Fig. 2. All data is taken from Nord Pool’s ftp server and include day-ahead prices, balancing market prices and turnovers. In addition, we also make use of historical exchange rates between Euros and NOK. The training set for the time-series models are the years 2014–2016. The next period is the training period for the forecast-based scenario generation method, which is taken to be data for 2017. This period may also be seen as the test period for the forecasting models. For each day in this period, we use the time-series models to forecast prices and volumes in the markets. We then compare the forecasted values with realized values to find historical forecast errors. The historical forecast errors are used as input for generating scenarios for the final data set. In this period, we generate scenarios by computing daily point forecasts and combining this with the historical forecast errors. The test period for scenario generation is the first 33 weeks of 2018.

Fig. 2
figure 2

An illustration of how the data is divided into test and training sets for the different steps of the modelling process

Full size image

In this work, we use a 72-h forecast horizon. This corresponds to the time-horizon of the optimization model. Usually, short-term hydropower scheduling have a horizon of about one week ahead. This is to avoid end-of-horizon effects and for consistent linking to longer-term models. The 72-h horizon is used here for computational reasons.

As stated earlier, we use daily branching. Specifically, this means that the scenario trees have branching points at the end of Hour 24 and 48. The tree structure is illustrated in Fig. 1 when the tree branches into 2 new scenarios at each branching step. In this section, we make individual scenario trees for each market, see Fig. 3. For the balancing market, positive values represent up regulation while negative values represents down regulation (Fig. 4).

Fig. 3
figure 3

Examples of the generated scenario values for day-ahead prices (a), the balancing market premium (b) and the balancing market volumes (c). The black line is the point forecast

Full size image

In stochastic programming models, the variation or distribution of the uncertain parameters is important. It is the variation of prices we want to describe in the scenario tree. Therefore, we would like to test the probabilistic quality of the generated scenarios. For this we use a percentile-based test similar to the approach used in [9]. That is, for forecast length \(\varDelta t\) on each day d in the test period for scenario generation, we compute the percentile of the observed value within the generated scenarios:

$$\begin{aligned} p_{d \varDelta t} =| \{ s \in 1 \dots S_{\varDelta t} : x_t^s \le x_{\varDelta t} \}| / |S_{t\varDelta t} | \end{aligned}$$
(11)

where \(x_{\varDelta t}^s\) are the scenarios values and \(x_{\varDelta t} \) are the actual observed values. This means that \(p_{d \varDelta t }\) is zero/one if the value is lower/higher than in the scenarios. If the scenarios represented the uncertainty perfectly, we should see \(p_{d \varDelta t} \le q\) in 100q percent of the cases, for each \(\varDelta t\). To test this, we compute the frequencies of the quantiles,

$$\begin{aligned} F_{\varDelta t}=| \{ d \in D : p_{d \varDelta t} \le q\}| / |D|, \end{aligned}$$
(12)

for each q and plot this against q in a probability plot, see Fig. 2. In the plots, the horizontal axis is q, the vertical axis is \(F_{\varDelta t}\), and each line is \(F_{\varDelta t}\) for individual forecast lengths \(\varDelta t\). If the percentiles of the scenarios perfectly match the observed values, the lines should be close to the optimal line between (0, 0) and (1,1).

Fig. 4
figure 4

Probability plots showing actual vs. expected percentiles of the generated scenarios when the tree has 2*2=4 scenarios. Each line represents one forecast length t

Full size image

For day-ahead prices, the percentiles of the scenario values deviate quite a bit from the optimal line. Note that, since the scenario generation method adds noise to an externally provided point forecast, the quality of the scenarios depends on the quality of the time-series model as well as the scenario generation method. The QQ-plot for the day-ahead prices indicates that the model for day-ahead prices is not very good because we are constantly underpredicting the true percentiles of the distribution. The reason for this is that the day-ahead prices were higher than normal in 2018, see Fig. 5 that shows the realized prices and the first-day forecast for the day-ahead prices in the first 33 weeks of 2018. From the plot, it is clear that the model underpredicts the realized values. Even though the day-ahead model shows poor performance, we use it to generate input for the tests presented in Sect. 5. The objective here is not to make an advanced forecasting model for the day-ahead market, but rather to test the multi-market bidding model. The tests are valid as long as all the tests use the same (poor) model for the day-ahead market.

Fig. 5
figure 5

The realized prices (pink) and first-day forecast (black) for the day-ahead prices in 2018

Full size image

Next, observe that there are several intervals of constant values on the curves in Fig 2. These occur because the scenarios trees used here only have 4 scenarios in total. In fact, for the shortest time horizons (within the second day), the scenarios only take on two possible values. This corresponds to the blue and green lines in Fig. 2. Since the scenarios are equiprobable, the values of \(p_{d \varDelta t}\) must be multiples of 0.5 here. For the third day, there are 4 possible scenario values and the red and pink lines have steps that are multiples of 0.25.

The stepwise curves in Fig. 2 illustrates that 4 scenarios (i.e. branching into 2 new scenarios at each branching step) only provides a rough approximation to the true uncertainty of prices and volumes in the markets. Using more scenarios would allow the approximation to become closer to the optimal diagonal line as the steps would be smaller, see Fig. 6 where the scenario trees have 9 scenarios in total . However, for large watercourses consisting of several reservoirs and power plants, the size and complexity of the optimization model is large, even in the deterministic case. Including multiple products and their stochastic price and volume adds new layers of complexity. In addition, in the above presentation, we have generated separate scenario trees for the day-ahead price and the balancing market price and volume. Before being used in the optimization model, these separate scenarios trees are combined all-against-all to generate a total tree. If the scenario tree for the day-ahead prices has 4 scenarios and the scenario tree for the balancing market has 4 scenarios, the total tree will have 16 scenarios. If each of the markets have 3 scenarios, the total tree will have 81 scenarios. The size of the scenario tree will be a trade-off between accurate representation of the markets and computational time.

Fig. 6
figure 6

Probability plots showing actual vs. expected percentiles of the generated scenarios when the tree has 3*3=9 scenarios. Each line represents one forecast length t

Full size image

5 Case study

We illustrate use of the multi-market model by analyzing the value of participating in the balancing market and the value of coordination across markets. We run several cases to evaluate these gains:

  1. 1.

    Day-ahead only: Optimize the trades in the day-ahead market in an optimization model that only sees the day-ahead market.

  2. 2.

    Sequential bidding: Optimize trades in the day-ahead market as if this was the only market (same as in case 1). Lock the decisions for the day-ahead market and then determine the balancing market trades in an optimization that sees both the day-ahead and balancing market.

  3. 3.

    Coordinated bidding: Jointly optimize trades in the day-ahead and balancing markets in an optimization model that sees both markets.

The above three cases are first run with the market non-anticipativity constraints in Eq. (5) applied to both the day-ahead market trades and the balancing market trades. This means that the balancing volumes must be determined at the same time as the day-ahead trades, i.e. with limited information. Notice that this does not necessarily mean trades are coordinated across markets. In the sequential approach, the day-ahead market trades are locked to the values obtained when optimizing without seeing the balancing market. The balancing market volumes may then be optimized against uncertain prices and volumes. The effect of including Eq. (5) for the balancing trades is namely that the balancing market trades must be determined before knowing the balancing market prices and volumes. The cases including Eq. (5) will give a lower bound on the value of participating in the balancing market, because the balancing market trades have to be determined the day before instead of 45 min before delivery.

If, however, the constraints in Eq. (5) are applied only to the day-ahead trades, the trades in the balancing market may be determined in real-time, i.e. with perfect information about the prices and volumes in the balancing market. Again, this does not necessarily mean that the trades are coordinated. In the sequential approach, the day-ahead trades cannot be changed to accommodate favorable opportunities in the balancing market, even if the balancing trades can be optimized against known prices and volumes. The cases not including Eq. (5) for the balancing trades will thus give an upper bound on the value of participating in the balancing market because the balancing market trades may be determined with perfect information.

In total, 6 different runs of the model are executed each test day; the 3 cases in the list above for limited and perfect information about the balancing market. Tests are performed for 46 instances corresponding to market input for different indivudial days in the first 33 weeks of 2018.

The analysis is done for an example hydropower system, where a plant with two generating units is located downstream of a single reservoir. The storage capacity of the reservoir is 50 Mm\(^3\). The maximum discharge is 150 m\(^3\)/s, which means that the reservoir may be emptied in about 90 h. This is a very flexible production system, since there is large reservoir capacity and no complicated waterways or other operating constraints. The generators have a minimum production level of 30 and a maximum level of 50 MW.

On each test day, separate scenario trees for the day-ahead market prices and the balancing premiums and volumes are generated using the time-series models and the forecast-based scenario generation method. As a base case, we use 3 scenarios at each branching point (e.g. at the end of Hour 24 and Hour 48), resulting in 9 scenarios for each market. Combining these into a total tree, the optimization model sees 81 scenarios. Each run of the model take about 15 seconds on an Intel 3.00 GHz lab top computer with 64-bit RAM.

The value of storing water in the reservoir is set to the average of the day-ahead prices in the scenario tree for the current day. This means that the optimization problem finds the balance of selling and producing within the optimization period versus storing the water for use in the future. Traditionally, the value of water is determined from longer-term optimization models that consider management of the reservoir over months or years. In hydropower scheduling, the long-term effect of the trading strategy is important because of the inventory problem of storing water over time. Use of the multi-market model should therefore be tested over longer time horizons, and ideally over several years to cover seasonal variations and dry/wet years. However, such aspects are postponed for future work and we use the more simple way of calculating the value of water as the average day-ahead price each day. Also, the initial reservoir level is re-set at 50% filling each day and the tests consider separate days as individual problem instances.

5.1 Limited information

The results for the limited information case is shown in Fig. 7. The figure shows bar plots of the objective function value for each day. The objective function value is made up of the end value (EV) which is the value of water stored in the reservoir at the end of the optimization horizon, income from the day-ahead market (DAM), income from the balancing market (BM) and start-up costs (Start). In the first case when the producer only participates in the day-ahead market, there is no income from the balancing market. The optimization finds a balance between producing within the optimization period and saving water in the reservoir. This balance is determined by the water values (shown as black dots) and the prices in the market. For the two cases involving the balancing market, we see that both the sequential and coordinated approach gives added profits over participating in the day-ahead market only.

Fig. 7
figure 7

Bar plots showing the objective function value for each test day. The left y-axis shows the objective function value in NOK. The right y-axis and the black dots gives the water value for each day

Full size image

To better discern the differences between the 3 cases, consider Fig. 8 which shows the results for 6 selected days. For the cases involving the balancing market, the total objective function is slightly larger and the contribution from each element (EV, DAM, BM and Start) is also different. The effects are small, but in general, when the balancing market is included, more of the objective function value comes from trades. This can be seen from the fact that the balance of producing vs storing water (e.g the size of BM+DAM vs the size of EV) is shifted more towards producing when the balancing market is included. This effect is more pronounced in the coordinated case than in the sequential case. Figure 9 gives boxplots of the percentage gain in objective function value when participating in the balancing market using the sequential and coordinated approach. The rightmost plot shows the added gain of coordination. The average gain of using the sequential approach is 0.8%, while the average gain of the coordinated approach is 1.4%. The extra gain of the coordinated approach over the sequential is on average 1.7%.

Fig. 8
figure 8

Comparison between the 3 strategies on 6 selected days. Limited information

Full size image
Fig. 9
figure 9

Box plots of the gains from using different strategies. Limited information

Full size image

5.2 Perfect information

Moving to the perfect information case, Fig. 10 shows the equivalent of Fig. 8. Again, in general, more of the value comes from trades when the balancing market is included. This effect is largest when using the coordinated approach. This is natural because the producer has more freedom in the joint optimization, and, in addition, the balancing market prices and volumes are known because of the assumption of pefect information. Figure 11 shows boxplots of the gains of using different approaches when having perfect information about the balancing market. The average gain of using the sequential approach is 2.6%, while the average gain of the coordinated approach is 2.9%. The extra gain of the coordinated approach over the sequential is on average 1.1%.

Fig. 10
figure 10

Comparison between the 3 strategies on 6 selected days. Perfect information

Full size image
Fig. 11
figure 11

Box plots of the gains from using different strategies. Perfect information

Full size image

Summarizing the results for the limited and perfect information case, the value of participating in the balancing market using the sequential approach is between 0.8 and 2.6%. Using the coordinated approach, the producer may gain between 1.4 and 2.9%. So participating in the balancing market using either method provides increased revenues compared to only participating the day-ahead market. The value of coordination, i.e. the value of using the coordinated over the sequential approach, is found to be higher in the limited information case (1.7%) than in the perfect information case (1.1%). This indicates that, the more uncertainty, the higher is the value of coordination.

Even though we calculate lower and upper bounds on the value of participating in the balancing market, the results obtained are only valid for the example hydropower system being tested. This system is very flexible and the gain might thus be higher than for other river chains with more constrained production systems. Results will be case-specific, but repeating the analysis outlined above will give lower and upper bounds in each case.

Another interesting result is that the balance of producing versus saving water is shifted towards producing in the cases where the balancing market is included. When participating in the balancing market, the producer is able to get a higher price for the water produced. When this is compared to the value of water (which in this case is determined based on the day-ahead prices only) a higher price means that more water should be produced within the optimization period instead of saved for later production. Multiple short-term markets mean that producers may trade their way to the higher prices for their production. The results here indicates that opportunities in multiple markets should be reflected in longer-term models that calculate the value of water.

5.3 Stability of the solution

As a final note, the stability of the bounds on the gain of participating in the balancing market is tested with respect to the number of scenarios used. To test for stability, we generate trees of different sizes each representing the same day. The cases described above are repeated for each test day using 2 new scenarios at each branching point and using 4 new scenarios at each branching point. This means that the separate trees for each market will have \(2*2 = 4\) or \(4*4 = 16\) scenarios, resulting in 16 or 256 scenarios in the total tree. The cases with 16 scenarios takes only seconds to solve, but using 256 scenarios takes over 1 h for each run of the model. Larger instances are therefore not tested.

The results are summarized in Tables 4 and 5 and shows that the calculated bounds vary for different tree sizes. The general results are however the same: there is a gain from participating in the balancing market using either the sequential or the coordinated approach, and the gain of coordination is smaller when the producer has perfect information.

Table 4 Stability of calculated lower bounds
Full size table
Table 5 Stability of calculated upper bounds
Full size table

6 Conclusions

In this paper, we formulate the multi-market bidding problem for power producers as a stochastic program. The formulation is implemented within the framework of optimization models that is used by the Nordic hydropower industry. We also present how input to the stochastic program may be generated by using a forecast-based scenario generation method combined with time-series models that predicts future prices and turnovers in the markets. The model is applied in a case study to investigate the value of participating in the Nordic day-ahead and balancing market. A producer may participate in the balancing market either by considering trades in the markets sequentially or coordinated.

Using cases with limited and perfect information about the balancing market to calculate lower and upper bounds, we find that the value of participating in the balancing market using the sequential approach is between 0.8 and 2.6%. Using the coordinated approach, the producer may gain between 1.4 and 2.9%. These results show that participating in the balancing market using either method provides increased revenues compared to only participating in the day-ahead market. The value of coordination, i.e. the value of using the coordinated over the sequential approach, is found to be higher in the limited information case (1.7%) than in the perfect information case (1.1%). This indicates that, the more uncertainty, the higher is the value of coordination. The results obtained are case-specific and only valid for the example hydropower system being tested. The method of using limited and perfect information to calculate bounds may however be applied to other systems.

Further work on the topic of coordinated bidding should include efforts to improve the modelling of prices and volumes in the various markets, as well as dependencies and correlations between them. To test the long-term effect of using different trading strategies or forecasting methods, simulation or backtesting frameworks could be developed to evaluate and compare the performance of different modelling choices and assumptions. In addition, investigation could be made into also including the stochastic nature of activation of reserves or balancing power in the formulation of the optimization model.