Introduction

Drought is a natural hazard that is becoming very frequent across the globe (Nones et al. 2024). It could be described as a temporal deficit in water supply over an extended period (Mishra and Singh 2010), and broadly classified into four main categories: hydrological, meteorological, socioeconomic and agricultural drought (Wilhite and Glantz 1985; Zargar et al. 2011).

While meteorological drought is the result of a lack of precipitation, hydrological drought is due to water scarcity in stream flow, groundwater, or total water storage. The severity, duration and intensity of meteorological drought are of great importance, and generally depend on the location, as precipitation varies in space depending on the local atmospheric conditions. The severity and frequency of hydrological drought are usually determined at the river basin scale and happens when the actual flow is below a certain threshold for a selected period (Mishra and Singh 2010).

Hydrological drought refers to water scarcity in the hydrological system, producing itself in fluvial streamflow and water levels in lakes, reservoirs, and groundwater below the normal (Van Loon 2015). In terms of time, Whipple (1966) defined a year as a drought year if the actual flow results less than a certain threshold for a selected period.

Agricultural drought is defined by Heathcote (1988) as “a lack of water damaging human agricultural activities. It results from a combination of agricultural activities (i.e., demand) and natural phenomena (i.e., supply) and leads to insufficient water volumes or quality for plant and/or animal needs.” This leads to socioeconomic drought, which is characterized by poor water supply with respect to the demand for water for concomitant uses (Wilhite 2005; Van Loon 2015). Soil moisture deficit is generally the main cause of agricultural drought (Sheffield et al. 2004; Mishra et al. 2018).

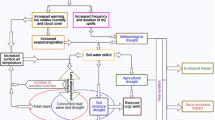
Groundwater, a major source of freshwater, is crucial for the sustainability of a region's agriculture, industry, and socioeconomic conditions. It can also be an alternative source of water to control drought, providing drought resistance at the initial stage (Hughes et al. 2012; Mussá et al. 2015). Groundwater drought is a different type of hydrological drought dealing with different groundwater resource characteristics and can be measured by looking at groundwater discharge, recharge, volume and levels. Calow et al. (1999) defined a groundwater drought as “a situation in which groundwater resources are inadequate as a direct consequence of drought”. However, groundwater drought has also been described considering recharge and storage (Chang and Teoh 1995; Eltahir and Yeh 1999; Goodarzi et al. 2016; Peters et al. 2001). Decreases in the groundwater and reservoir levels in downstream parts of the basin can lead to severe impacts on hydroelectric power production, water supplies, recreation, agriculture, transportation, and other sectors.

During dry seasons, the river flow mainly feeds from groundwater baseflow (Hayashi and Rosenberry 2002) eventually having a significant impact on the groundwater-dependent ecosystems (GWECs), causing groundwater depletion, decreasing surface water and agricultural supply, as well as reduction of base flow discharge (Bekesi et al. 2009; Martens et al. 2015). Van Loon et al. (2017) stated that groundwater drought can increase beyond the natural state due to human activities (i.e. water abstraction, irrigation, dam construction and land use, etc.), while Mishra and Singh (2010) noted that some groundwater data can be used to characterize and compute the groundwater drought in connection with groundwater recharge (Marsh et al. 1994) and discharge (Peters et al. 2001). To assess groundwater drought, several indices have been proposed in the literature (Lee et al. 2018; Guo et al. 2021; Dhawale et al. 2022), including the Standardized Groundwater Level Index—SGI (Mendicino et al. 2008; Bloomfield and Marchant 2013; Guo et al. 2021).

In many countries, groundwater still serves as the primary source of irrigation and drinking water (Mishra et al. 2018). However, knowing the availability of groundwater remains a major challenge, in particular in developing countries, mainly because of the lack of in-situ measurement. To overcome this limitation, Li and Rodell (2015) suggested that the monitoring of groundwater drought using hydrological models could be a valuable alternative. At the same time, several researchers investigated groundwater drought using satellite-retrieved information such as the Gravity Recovery and Climate Experiment (GRACE) data (Thomas et al., 2014; Van Loon et al. 2017; Li et al. 2019). For example, Thomas et al. (2017) pioneered using the GRACE satellite observations to evaluate groundwater drought in the Central Valley of California. Seo and Lee (2019) used the GRACE satellite data and remote sensing methods to analyze the groundwater drought in South Korea using an artificial neural network model. The GRACE Groundwater Drought Index (GGDI) was used as an indicator to assess groundwater drought in the North China Plain by Wang et al. (2020). Based on the time series of measured groundwater levels, information about the behaviour of groundwater flow can be derived by dividing between upward, downward and stable trends (Le Brocque et al. 2018). This can provide very useful information on drought drivers (Famiglietti and Rodell 2013). For example, Castle et al. (2014) stated that a significantly downward trend in groundwater level can lead to frequent and severe droughts. Mimicking this approach, other researchers have conducted groundwater-level studies to assess groundwater trends (Panda et al. 2012; Patle et al. 2015). In a study covering Iran, Tabari et al. (2012) determined dominant positive trends in the summer and spring seasons based on annual, seasonal and monthly groundwater trends. The effect of climate change on the groundwater level for the future was also investigated based on different scenarios (Ghazi et al. 2021, 2022; Wunsch et al. 2022).

It is worth noticing that results obtained using only one drought index might sometimes be only site-specific and hard to transfer to other regions. In fact, climate variability from one region to another plays a major role in determining drought conditions, and consequently in the selection of the most appropriate drought indices. For instance, the standardized precipitation evapotranspiration index (SPEI) and Palmer Drought Severity Index (PDSI) are largely used in the USA (Palmer 1965), while the SPI is gaining more popularity worldwide, as it does not depend strictly on climatic conditions. Several indices are applied by national meteorological organizations: Modified China-Z Index (MCZI) and China-Z Index (CZI) by the National Meteorological Center of China (Wu et al. 2001), Decile Index (DI) by the National Meteorological Center of Australia (Gibbs 1967), Reconnaissance Drought Index (RDI) in some meteorological organizations of European countries (Tsakiris et al. 2007). Besides them, other indexes like the Percent of Normal Index (PNI), Z Index (ZI) and Rainfall Anomaly Index (RAI) are also used to monitor drought events, showing a very scattered situation in monitoring drought dynamics.

Many researchers looked at different indexes and their combinations to adequately describe the local drought conditions and trends (Berhail 2022; Berhail and Katipoğlu 2023; Darabi et al. 2023; Ghazi et al. 2023). For example, Morid et al. (2006) used seven drought indices for Iran, including EDI, PDN, SPI, DI, Chinese Z-index, Z-index and modified CZI, and recommended the application of SPI and EDI for drought monitoring. Focusing on the same country, Jamshidi et al. (2011) compared the performance of the RDI and SPI, finding that the number of extreme drought periods in RDI is much higher than in SPI. Okpara and Tarhule (2015) studied the performance of three indices in the Upper Niger Basin in West Africa and found that SPI is more appropriate than the others. Vicente-Serrano et al. (2012a, b) analyzed the performance of SPI, SPEI and PDSI on a global scale and proposed that SPEI identifies drought events properly. Barua et al. (2011) calculated five drought indices for the Yarra River Basin of Australia, namely PDN, SPI, DI, Aggregated Drought Index (ADI) and Surface Water Supply Index (SWSI), concluding that the ADI performance capability is better for monitoring historical drought events based on transparency, robustness, traceability, complexity, and extensibility. The SPI and SPEI were compared by Bachmair et al. (2014), Dikshit et al. (2021) and Liu et al. (2021). The SDI index has been applied to determine regional stream drought characteristics (Tabari et al. 2013; Tigkas et al. 2015; Ozkaya and Zerberg 2019). Past studies demonstrated that these indices give good statistical performance for meteorological, hydrological, or hydrogeological. Indeed, such indexes were used to analyze the correlation between climatological and groundwater drought (e.g., Leelaruban et al. 2017; Krogulec 2018; Lee et al. 2018; Bloomfield et al. 2019; Haas and Birk 2019; Kubicz and Bąk 2019; Pathak and Dodamani 2019; Huang et al. 2021; Minea et al. 2022), as well as the relationship between meteorological drought and streamflow (Haslinger et al. 2014).

When it comes to reviewing the literature on drought phenomena in Türkiye, several studies have been performed on precipitation, temperature, and variability of extremes (Gumus et al. 2022; Topçu et al. 2022; Gümüş et al. 2023; Simsek et al. 2023). For example, Dikici (2022) assessed the drought for the Seyhan Basin based on vegetation indices and meteorological drought indices. The author concluded that there was an upward trend in the frequency of drought based on the VCI and NDVI indices. Keskin et al. (2015) analyzed annual and monthly water level data for Lake Egirdir, showing that the annual water level reduction was determined as approximately 0.026 m by using Mann–Kendall and Sen's slope tests. For temperature variabilities, Türkeş and Erlat (2018) have investigated variability and trends of maximum and minimum temperature across Türkiye and stated that minimum temperature showed a downward trend since the mid-1980s, whereas maximum temperature showed an upward trend from 2000. Ay (2020) studied homogeneity and trends in temperature and precipitation time series over the western Black Sea region, reporting the monthly total precipitation trends were very different across the region. Danandeh Mehr and Vaheddoost (2020) focused on the Ankara area to detect SPI and SPEI trend, drought and severity, showing that, unlike SPI, SPEI exhibited a significant decrease. Fırat et al. (2018) studied the Van Lake Basin and compared different drought indices to quantify drought events over the basin. Dikici (2020) conducted a drought analysis for the Asi basin based on different drought indices (DI, SPI, SPEI, and SRI) and compared these drought indices to assess the drought. It was determined that there was a good relationship between the calculated drought indices. Dogan et al. (2012) investigated the meteorological drought in the semi-arid Konya Closed Basin using DI, PNI, RDDI, SPI, Z-score, CZI and EDI indices. EDI was found the best to describe drought conditions over the investigated time scales, suggesting that this index could be preferable and suitable to monitor drought events in arid and semi-arid regions. They analyzed the drought in the Konya Closed Basin based on the meteorological drought. SPI, CZI, MCZI, ZSI and SDI are listed by the World Meteorological Organization as key metrics to investigate drought (Svoboda et al. 2012). Four drought indices were selected for this study based on a similar study conducted by Dogan et al. (2012). Recently there are several studies about these drought indices in Türkiye (Nuri Balov and Altunkaynak 2020; Bayer Altin and Altin 2021; Yuce and Esit 2021; Dikici 2022; Koycegiz and Buyukyildiz 2022; Turhan et al. 2022; Esit et al. 2023; Şimşek et al. 2023; Tsesmelis et al. 2023).

It is important to understand the relationships and feedback between meteorological, hydrological and groundwater drought from both a practical and a theoretical point of view. Indeed, knowing such links is paramount for adequately managing water resources in water-scarce environments and under the threat of climate change, especially in regions not adequately monitored.

In literature, usually, meteorological drought and hydrological drought are separately investigated, eventually including groundwater drought. This is particularly true in Türkiye, where limited drought studies were conducted by considering hydrological, meteorological and groundwater drought together. This implies a lack of information in the literature about the relationship between hydrological, meteorological, and groundwater droughts. The Konya Closed Basin is known as Türkiye's grain storage because it has an agricultural area of approximately 3.5 million hectares. The semi-arid climate is dominant in a large part of the basin, and the average annual rainfall is around 300–350 mm. This is insufficient to provide the necessary conditions for the river flow. This situation is even more critical due to the decreasing amount of annual precipitation (10–25 mm) due to dry periods that have been dominant since the early 1980s, and thus the basin is shifting from semi-arid to arid climate characteristics (Dogdu et al. 2007; Şen and Başaran 2007). Therefore, it is essential to examine the drought of the Konya Closed Basin in detail, combining meteorological, hydrological and groundwater drought indexes.

To the best of our knowledge, studies on the assessment of the correlation among meteorological, hydrological and groundwater droughts have not been carried out in Türkiye in general and in the Konya Closed Basin in particular. To fill this knowledge gap, in this paper, a detailed regional analysis of the link between meteorological, hydrological and groundwater drought indices for the Konya Closed Basin in Türkiye is performed to identify dry and wet periods. The link between streamflow, groundwater and meteorological drought indices was analyzed using the Mann–Kendall Test and Sen’s slope for nineteen stations uniformly distributed over the basin. Multiple indexes were analyzed at the monthly, seasonal, and yearly time scale, aiming to evaluate (i) hydrological drought based on SDI and SWSI; (ii) meteorological drought using SPI, CZI, MCZI and ZSI; and (iii) groundwater drought using SGI.

Materials and methods

Study area

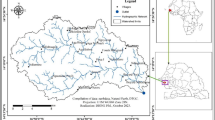
The Konya Closed Basin is located between latitudes 36°51' N and 39°29' N and longitudes 31°36' and 34°52' E, in the Central Anatolia Region of Türkiye (Fig. 1). The main provinces of the basin are Konya, Nigde, Ankara, Aksaray, Nevsehir and Karaman. The total area of the river basin is 49.786 km2, covering approximately 6.4% of Türkiye's surface area (Ministry of Agriculture and Forestry 2018). One of the most important rivers is the Çarsamba Stream in the southwest of the Konya Closed Basin, in the Konya province, which flows into the Beysehir Lake by merging with Beysehir Canal near Pinarcik in the east. The Melendiz Stream, originating from the Melendiz Mountains of Aksaray, is another important stream of the Konya Closed Basin that, after merging with the Belisirma and Ilisu streams, flows into the Tuz Lake. The Mamasin Dam Lake, which is the most important water source of Aksaray and meets the drinking water and irrigation water needs of the province, was built on the Melendiz Stream in 1962. Besides this lake, other two main lakes are part of the Konya Closed Basin, namely the Salt Lake and the Beysehir Lake.

Fig. 1
figure 1

Study area and gauging stations

Full size image

The Konya Closed Basin is paramount in grain production thanks to its natural resources such as soil, climate and topography. In fact, 57% of the basin land is agricultural land, and 92% of this agricultural land is reserved for grain, while 5% for fruits and 3% for vegetables.

The climate characteristics of the basin are the Mediterranean climate in the south, arid climate towards the center and north, and desert climate in Karapınar and its surroundings in the southeast of the basin. Precipitation in the basin was generally observed in winter and spring (Durduran 2010). The average annual precipitation in most parts of the basin, which has a semi-arid climate, is around 300–350 mm (Şen and Başaran 2007). The soil in the region generally has alluvial and salty characteristics.

This study is based on multi-source data time series covering the period 1978–2020 and collected from a total of 19 stations (10 meteorological, 4 hydrological and 5 groundwater stations) distributed across the Konya Closed Basin (Fig. 1). Streamflow and groundwater data were supplied by the General Directorate of State Water Works (DSI), while meteorological data was obtained from the General Directorate of Meteorology (MGM). Groundwater stations are located at different depths, spanning from 81 to 250 m. Additional station details are summarized in Table 1. To account for data irregularities in hydro-meteorological studies (loss of recordings due to measurement problems or data incompleteness, etc.), a data reconstruction method is usually applied to fill or regain the loss of information in the provided data. In this study, data losses are filled using homogeneity and linear interpolation methods.

Table 1 Characteristics of the monitoring stations
Full size table

Methodology

Meteorological drought indices

There are several indices in the literature to evaluate meteorological drought, such as the Effective Drought Index-EDI (Byun and Wilhite 1999), the Palmer Drought Severity Index-PDSI (Palmer 1965), the Standardized Precipitation Evapotranspiration Index-SPEI (Vicente-Serrano et al. 2010) and the Reconnaissance Drought Index-RDI (Tsakiris and Vangelis 2005). Among them, particular relevance has the CZI, SPI, ZSI and SPI, as they are recommended by the World Meteorological Organization (Svoboda et al. 2012; WMO 2023) and can be easily applied. Indeed, the SPI and CZI are listed by the World Meteorological Organization as key metrics to investigate drought (Svoboda et al. 2012). Following the approach proposed by Dogan et al. (2012), four drought indices were selected for this study: the Standardized Precipitation Index (SPI), the China Z Index (CZI), the Modified China Z Index (MCZI) and the Z Score Index (ZSI).

Standardized precipitation index—SPI

The Standardized Precipitation Index was introduced by McKee et al. (1993) and has been widely applied to assess the intensity of rainfall droughts (Du et al. 2013; Liu et al. 2016; Modaresi Rad et al. 2016; Huang et al. 2017; Lorenzo-Lacruz et al. 2017; Karamuz et al. 2021). It is also listed by the World Meteorological Organization (Svoboda et al. 2012) as the most appropriate index for describing meteorological droughts.

SPI is based only on long-term precipitation data that can be cumulated over different time scales, and can be computed as:

$$g\left(x\right)=\frac{{P}^{\alpha -1}{e}^{\frac{-P}{\beta }}}{{\beta }^{\alpha }T\left(\alpha \right)}$$
(1)
$$T\left(\alpha \right)={\int }_{0}^{\infty }{y}^{\left(\alpha -1\right)}{e}^{-y}dy$$
(2)
$$\alpha =\frac{1}{4}\left(1+\sqrt{1+\frac{4A}{3}}\right)$$
(3)
$$\beta =\frac{\overline{x}}{\alpha }$$
(4)
$$A={\text{ln}}\left(\overline{x }\right)-\frac{\sum {\text{ln}}\left(\overline{x }\right)}{n}$$
(5)
$$H\left(x\right)=q+\left(1-q\right)G(x)$$
(6)

where α is the shape parameter, β is the scale parameter, P is the rainfall, \(\overline{x }\) is the arithmetic mean T is the Gamma function with respect to integration and n is the number of observations. q is the probability of zero and G(x) is the cumulative distribution for the desired month and time scale. The cumulative distribution H(x) is then transformed into the standard normal random variable Z representing the SPI value (Tsakiris et al. 2007).

Once the SPI value is computed, it can be categorized according to its range to identify different drought event intensities, following the classification proposed by McKee et al. (1993), where a drought event is considered to have occurred when the SPI value is below – 1 (Table 2).

Table 2 Drought classification of CZI, MCZI, SPI and ZSI (adapted from Morid et al. 2006; Barua et al. 2011)
Full size table

China Z index—CZI

The China International Climate Centre initially employed the CZI for drought monitoring in China (Dogan et al. 2012; Jain et al. 2015; Wu et al. 2001). CZI presumes that rainfall values tend to follow a Pearson Type III distribution ( Wu et al. 2001; García-León et al. 2019; Payab and Türker 2019), and is related to the Wilson–Hilferty cube-root transformation (Wilson and Hilferty 1931) from the chi-square variable to the Z-scale (Kendall and Stuart 1977). CZI is computed as below:

$$CZ{I}_{j}=\frac{6}{{C}_{st}}{\left(\frac{{C}_{st}}{2}{\varphi }_{j}+1\right)}^\frac{1}{3}-\frac{6}{{C}_{s}}+\frac{{C}_{st}}{6}$$
(7)
$${C}_{st}={\sum }_{j=1}^{N}\frac{{\left({X}_{j}-\overline{X }\right)}^{3}}{N\times {\sigma }^{3}}$$
(8)
$${\varphi }_{j}=\frac{{X}_{j}- \overline{X}}{\sigma }$$
(9)

where t is the time, which can be equal to 1, 2, 3, …9, 12, 24 months, etc., Cst denotes a coefficient of skewness for the time step t, φj shows a standard deviation (also called Z-Score, which is the statistical Z score computed for the same time step (t), N is the total number of observation years, \(\overline{X }\) and σ are the average and standard deviation, respectively, while precipitation is denoted by Xj.

Sometimes, the median rainfall is employed to assess the Modified China-Z Index (MCZI), as opposed to the mean rainfall used in the calculation of the CZI. This empirical method was developed by Wu et al. (2001) to minimize the difference between MCZI and SPI.

Z-score—ZSI

An equation developed by Triola (1995) can be employed to compute the Z-Score, without the need to adjust the index by fitting the data to Gamma or Pearson Type III distributions. For this reason, the Z-Score may not be as representative of shorter time scales as the SPI (Edwards and McKee 1997). It is worth noticing that the drought classification of CZI, SPI and ZSI are similar (Morid et al. 2006; Wu et al. 2001).

Following Morid et al. (2006) and Barua et al. (2011), the above-reported indices can be used to classify drought conditions (Table 2).

Hydrological drought indices

Streamflow drought index—SDI

This index was first introduced by Nalbantis and Tsakiris (2009) and is useful to characterize the hydrological drought status of a study area. The SDI has the advantage of controlling hydrological drought or water availability in the short, medium and long term as it is based on monthly observed streamflow volumes over various time scales. The SDI is based on cumulative streamflow volumes for each of the k reference periods of the first hydrological year (Nalbantis and Tsakiris 2009; Tareke and Awoke 2022). Cumulative monthly stream flow volume (Qij) k is estimated from consecutive time series, and can be obtained as:

$${V}_{i,k}=\sum_{i}^{3k}{Q}_{ij}i=\mathrm{1,2},3, \dots ,12; \quad k=\mathrm{1,2},\mathrm{3,4}$$
(10)

in which the cumulative streamflow volume for the i−th hydrological year and the k−th reference period is symbolized as \({V}_{i,k}\),

$$SDI=\frac{{V}_{i, k}-{V}_{km}}{{S}_{k}}$$
(11)

where i represents the hydrological year and k = 1 for October–December, k = 2 for October–March, k = 3 for October–June, and k = 4 for October–September.

Since these are calculated over a long period, \({V}_{km}\) and \({S}_{k}\) are the mean and standard deviation of the cumulative streamflow volumes of the reference period k, respectively. The SDI criteria for identifying the worst and most intense drought occurrences are shown in Table 3.

Table 3 Classification of hydrological drought, adapted from Tareke and Awoke (2022) and Barua et al. (2011)
Full size table

Surface water supply index—SWSI

The SWSI, generally used for basin-level drought analyses, was introduced by Doesken et al. (1991) to complete the Palmer Drought Severity Index (PDSI), considering streamflow, reservoir storage and snowpack (Muli Wambua 2018).

The main inputs for SWSI are streamflow, rainfall, reservoir storage (or lake levels) and (optionally) groundwater level, and allow for computing this index following the approach proposed by Tareke and Awoke (2022):

$$SWSI=\frac{a{PN}_{stream}+bP{N}_{rain}+cP{N}_{lakelevel}-50}{12}$$
(12)

where PNstream, PNrain, and PNlakelevel are percentages of non-exceedance of monthly streamflow, rainfall, and lake level respectively, while a, b and c are weights for each hydrologic component, if their sum equals 1. The non-exceedance probabilities are taken from probability distributions fitted to each hydrologic component.

Groundwater drought indices

Standardized groundwater level index – SGI

McKee et al. (1993) proposed that SPI could be extended to other drought-related variables, so Bloomfield and Marchant (2013) introduced groundwater data into a calculation process similar to that of SPI, developing the Standardized Groundwater Level Index method, which can study the intensity and variations of groundwater drought (Table 4). The original SGI theory is based on monthly data and there is no need to accumulate at different time scales.

Table 4 Drought classification of groundwater drought, following Bloomfield and Marchant (2013)
Full size table

The calculation of SGI is (Hsin-Fu Yeh and Chang 2019):

$$SG{I}_{q}=\frac{{X}_{q}-\overline{{X }_{q}}}{{S}_{q}}$$
(13)

where \(SG{I}_{q}\) represents the SGI value at time scale I, \({X}_{q}\) is the cumulative groundwater level, \(\overline{{X }_{q}}\) is the mean long-term groundwater data, and \({S}_{q}\) represents the standard deviation of long-term groundwater level data.

Mann–Kendall test

To identify the trend in time series data, the Mann–Kendall (MK) test has been commonly applied in hydrology studies (Wu et al. 2008; Patle et al. 2015). The MK test was proposed by Mann (1945) as a nonparametric test for trend detection and was introduced by Kendall (1975) as a test statistic, which is applied to statistically identify whether the variable of interest has an upward or downward trend. It can be computed as below (Mersin et al. 2022): Recently, there have been several studies to detect trends in hydrological and meteorological parameters with the Mann–Kendall test and other tests (Acar et al. 2022; Demir 2022; Koycegiz and Buyukyildiz 2022; Darabi et al. 2023; Ozocak et al. 2023; Acar 2024).

$$S=\sum_{k=1}^{n-1}\sum_{j=k+1}^{n}sgn({x}_{j}-{x}_{k})$$
(14)
$$sgn\left({x}_{j}-{x}_{k}\right)=f\left(x\right)=\left\{\begin{array}{c}1, if ({x}_{j}-{x}_{k})>0\\ 0 if \left({x}_{j}-{x}_{k}\right)=0\\ -1, if \left({x}_{j}-{x}_{k}\right)<0\end{array}\right.$$
(15)

where xi and xj are the data magnitudes at time i and j, respectively, while n is the data length. An upward trend has S > 0, while a downward trend has S < 0 (Rahman et al. 2017).

$$Var\left(S\right)=\frac{n\left(n-1\right)\left(2n+5\right)-\sum_{i=1}^{p}{t}_{i}({t}_{i}-1)(2{t}_{i}+5)}{18}$$
(16)

where p = number of groups, ti = data number at p-th group.

The Z value can be computed as suggested by Rahman et al. (2017):

$$Z=\left\{\begin{array}{c}\frac{S-1}{\sqrt{Var\left(S\right)}}, \quad if\, S>0\\ 0 \quad if\, S=0\\ \frac{S+1}{\sqrt{Var\left(S\right)}},\quad if\, S<0\end{array}\right.$$
(17)

The Z statistics of the MK test identify whether the data has an upward trend (Z > 0), downward trend (Z < 0) or no trend (Z = 0). To analyze the significance of the trend test, the null hypothesis H0 (trend) is tested against the alternative hypothesis H1 (no trend). H0 is rejected if |Z|> Za/2, which shows that there is a trend. The MK trend test was carried out for all the stations at the 95% confidence level for rainfall and average temperature, and the trend magnitude was assessed by the Sen’s slope method.

Sen’s slope

This non-parametric test was first proposed by Sen (1968) and then applied by many researchers such as Adnan et al. (2018) and Mersin et al. (2022).

Sen’s slope method is generally applied to detect the trend slope of a time series, calculating the change per unit of time, following.

$$F\left(x\right)=ax+b$$
(18)

in which F(x) is the linear trend function and a and b are the slope and intercept of the fitting, respectively. The trend magnitude β can be computed as:

$$\beta =median\left(\frac{{x}_{i}-{x}_{j}}{{t}_{i}-{t}_{j}}\right)$$
(19)

where xi and xj are the data values at time ti and tj respectively (i > j).

Results

Analysing the data for the period 1978–2020, this study provides a detailed drought analysis of the Konya Closed Basin at different time scales comparing multiple meteorological (SPI, ZSI, CZI, MCZI), hydrological (SDI, SWSI) and groundwater (SGI) indices.

Drought effects occur over a long period and can be felt months, years, decades, or centuries later (WMO 2023). So, drought is investigated at different scales (1, 3, 12, 24, 36, 48 months). To assess the hydrological and meteorological droughts, monthly scale is commonly used (Yuce and Esit 2021; Gulmez et al. 2023), while seasonal and yearly scales are more important in assessing agricultural drought (Vicente-Serrano et al. 2012a, b; Tigkas et al. 2022). Longer periods (12, 24, 36, 48 months) commonly assess the socio-economic drought since the effect of drought can be formed in the long term.

Meteorological drought

As reported above, the CZI, SPI, ZSI and SPI indices were used to evaluate meteorological drought since they are recommended by the World Meteorological Organization and can be easily applied (Svoboda et al. 2012; WMO 2023).

In this investigation, the SPI, ZSI, CZI and MCZI indices at 1, 3, 12, 24, 36 and 48 months were calculated and used to depict meteorological drought over the study area.

The number of extremely (ED), severely (SD), and moderately (MD) dry months between 1978 and 2020 for the Konya Closed basin is shown in Fig. 2. Extremely dry occur 2, 6, 4, 4, 7, 6, 2, 2 and 4 times based on CZI-1 for Aksehir, Beysehir, Cihanbeyli, Eregli, Karaman, Karapinar, Konya, Nevsehir and Nigde, respectively. According to the SPI index, the most extreme dry conditions occurred 13 times in Karaman, Konya, Karaman, Cihanbeyli and Nevşehir. The higher frequency of extremely dry events was 7 in Karaman, according to CZI, while MCZI pointed out 5 times for Beysehir and Nigde ZSI shown 2 times for both Nevsehir and Karaman. The highest number of extremely dry events was obtained for SPI in all stations based on the indices calculated for meteorological drought across the basin.

Fig. 2
figure 2

Meteorological drought events for a 1-month duration are subdivided depending on the severity: a extremely, b severely, c moderately dry. d Percentage of drought

Full size image

The monthly scale is commonly used to compare drought indexes (Bayer Altin and Altin 2021; Yuce and Esit 2021; Tsesmelis et al. 2023). The total percentage of extreme droughts (ED) by SPI (1.9–2.5%) was higher than that of all indices at the monthly scale for all stations as seen in Fig. 2d. ZSI was used to investigate extreme and severe drought, but it failed to estimate moderate drought, showing an underestimation of all indices (Fig. 2d). It was determined that the percentage of SPI and CZI has greater total drought (ED + SD + MD) (10.7–13.4% for CZI, 10.7–14.2% for SPI) than those of ZSI and MCZI. Moreover, the percentage of MCZI has fewer total droughts (ED + SD + MD) (6.2–10%).

The severity of drought during dry and wet periods MCZI-12 in Aksaray can be observed in Fig. 3. The larger drought severity (DS) for dry periods (3.76) based on MCZI-12 in Aksaray was obtained after 2002, while the larger DS for wet periods (5.72) is evident after 2008. The severity of drought of dry and wet periods for ZSI-12 in Aksaray is provided in Fig. 3. The larger DS for dry periods (7.56) based on ZSI-12 in Aksaray was obtained after 1997, while the larger DS for wet periods (5.47) was obtained after 2008.

Fig. 3
figure 3figure 3

Drought severity in Aksaray station: a dry and wet periods for MCZI-12 b dry and wet periods for ZSI-12

Full size image

The seasonal variation of meteorological drought is shown in Fig. 4. Dry and wet periods were obtained for SPI-3, CZI-3, ZSI-3 and MCZI-3 between 1978 and 2020. The findings show that there are extreme, severe and moderate drought and wet periods for SPI-3, ZSI-3, MCZI-3 and CZI-3. At the same time, no extremely dry periods occurred in all stations outside of Konya and Nevsehir for MCZI-3.

Fig. 4
figure 4

Seasonal variations of meteorological drought at the Konya station

Full size image

It was determined that drought occurred in the Konya Closed Basin in almost every season, but extreme droughts usually occurred during the Autumn.

The variation of meteorological drought for 1, 24, 36 and 48 months were reported in Fig. 5. The values above the + 2 line represent an extremely wet situation while the values below the -2 line represent an extremely dry situation.

Fig. 5
figure 5

Variations of meteorological drought at 1-, 24-, 36- and 48-month scale for the Konya station

Full size image

As seen in Fig. 5, extremely dry events occurred for the Konya station based on CZI, SPI, ZSI and MCZI at 1-, 24-, 36- and 48-month scale. In just one station (Nevsehir), the driest period is the same based on all indices computed at the monthly scale. No extremely dry periods occurred at the Konya, Beysehir and Cihanbeyli stations based on ZSI-1. Looking at the Karaman station, the wettest value is obtained for SPI-48 (5.95), while the driest value (-4.40) is computed via MCZI-24 (Table 5).

Table 5 Driest times for all stations
Full size table

As seen in Table 5, the results of SPI and ZSI indexes are more consistent than those of MCZI and CZI in the assessment of meteorological drought.

It is possible to notice that severe and moderate dry occurred more frequently than extremely dry events. Although there were differences in the results of indices, similar results were obtained for ZSI and SPI values at 1, 24, 36, and 48 months.

The variation of meteorological drought indices at the yearly scale is given in Fig. 6. As mentioned above, the values below the -2 line represent an extremely dry situation, while the values above the + 2 line represent an extremely wet situation. As seen in Fig. 6, no extremely dry events occurred for Aksaray, Karaman and Nevsehir based on CZI-12, SPI-12, ZSI-12 and MCZI-12. However, extremely dry events occurred at the Beysehir, Cihanbeyli, Eregli, Konya and Nigde stations. Extremely dry occurred in Konya in 1998 for all indices. It occurred in 1983, 1985, and 1993 for ZSI-12 and SPI-12 at the Beysehir station. Extremely dry formed in 1993 for Cihanbeyli for SPI-12. For Eregli, it happened in 1989 based on all indices but in 2004 it formed based on SPI-12. As a result, severe and moderate dry are more frequent than extremely dry events. Although there are differences in the results, the results of ZSI-12 and SPI-12 are more compatible than those of CZI and MCZI.

Fig. 6
figure 6

Variations of meteorological drought at the yearly scale

Full size image

Hydrological drought

There are several indices to assess the hydrological drought in the literature, such as the Streamflow Drought Index—SDI (Nalbantis and Tsakiris 2009) and the Surface Water Supply Index -SWSI (Garen 1993). SDI and SWSI indices were used to assess drought in this study. The SDI and SWSI theories are different due to considered parameters. The variation of SWSI-1, SWSI-3 and SWSI-12 values for different stations is shown in Fig. 7. Here the values below the -4 line represent an extremely dry situation, while the values above the + 4 line represent an extremely wet situation for SWSI. No extremely dry events occurred for the D16A140 station based on SWSI-1 and SWSI-3, while extremely dry events occurred for stations D16A003, D16A100 and D16A117 based on SWSI-12. For D16A003, wet periods were observed in Spring and Winter. Similarly, dry periods were observed in Summer and Fall. For D16A117 and D16A100, Summer faced drought in 1978–2022. For D16A140, Winter and Fall faced drought, while Spring was wet in the period 1978–2020. Wet periods were seen in longer periods compared to dry periods for station D16A117. As a result, although extremely dry occurs, severe and moderate dry periods are more common. Extremely wet periods were also observed in all stations excluding the D16A003 station. Based on SWSI-1, the driest period is observed in February 2014 (– 3.80) for D16A140, in September 2002 (– 4.15) for D16A100, in October 1989 (– 4.14) for D16A003 and in July 1997 (– 3.59) for D16A117.

Fig. 7
figure 7

The variation of hydrological drought for D16A003 station: a SWSI-1, b SWSI-3, c SWSI-12

Full size image

The variation of SDI-1, SDI-3, SDI-6, and SDI-12 values for different stations is shown in Fig. 8. The drought classification of SDI is different from SWSI and similar to SPI, CZI and ZSI. Here values below -2 represent an extremely dry situation, while values above 2 represent an extremely wet situation for SDI. No extremely dry and wet events occurred in all stations based on SDI at a 3, 6, 8 and 12-month scale. However, extremely dry occurred in all stations. The driest period is observed in April 2001 (-2.59) for D16A140, in October 2002 (-4.16) for D16A100, in February 2009 (-3.50) for D16A003 and in April 2015 (-2.23) for D16A117 based on SDI-1.

Fig. 8
figure 8

Variation of hydrological drought for the D16A003 station: a SDI-3, SDI-6, and SDI-12, b SDI-1

Full size image

The number of extremely, severely, and moderate dry periods between 1978 and 2020 for the Konya Closed basin is shown in Fig. 9. SWSI and SDI are classified differently: for SDI < -2.00, extremely dry drought occurs, while severely dry occurs for SWSI < -4.00. As summarized in Fig. 9, extremely dry occurred 15 and 35 times for D16A003, 9 and 10 times for D16A100, 2 and 0 times for D16A117 and 15 and 0 times for D16A140 based on SDI-1 and SWSI-1, respectively.

Fig. 9
figure 9

Hydrological drought events for 1-month duration, subdivided depending on the severity

Full size image

According to the SDI index, the most extremely dry conditions were obtained for D16A003 and D16A140 with 15 times each. According to CZI, the highest number of times (3) was obtained in Cihanbeyli. The maximum number of times for SWSI was obtained for D16A003 with 35 times. The highest number of extremely dry events was obtained for SPI in all stations excluding the D16A003 station based on the SDI-1 and SWSI-1. However, the number of severe and extreme dry events for SWSI-1 is larger than that of SDI-1 for all stations. No extremely dry event occurred in the D16A140 and D16A117 stations based on SWSI-1.

The severity of drought of dry and wet periods for SWSI-12i in D16A003 is provided in Fig. 10. One can notice that the larger DS for dry periods (11.96) based on SWSI-12 in Aksaray was obtained before 2012, while the larger DS for wet periods (17.13) was obtained after 2011.

Fig. 10
figure 10

Severity of drought (SWSI-12) at D16A003 station: a dry, b wet periods

Full size image

Groundwater drought

The SGI index was used to evaluate groundwater drought. Based on the results of SGI, a significant number of groundwater droughts are observed and the variation of SGI-1 for different wells is depicted in Fig. 11. The values of SGI above 2 indicate wet months, and the values below – 2 show dry months. One can observe that groundwater drought occurred after 2008 in all stations. In summary, the Konya Closed Basin generally has faced groundwater drought since 2008. Extremely dry occurred in all wells. It was determined that the driest period was observed in July 2020 (– 3.37) for station 181, in April 1998 (– 3.2) for station 1167, in August 2020 (– 2.74) for station 9431, in August 2019 (– 2.76) for station 17,171 and in August 2020 (– 2.54) for station 52,258.

Fig. 11
figure 11

Variations of SGI-1 values for different stations: a 181, b 9431, c 1167, d 17,171, e 52,258

Full size image

The dry events for groundwater drought are given in Fig. 12. Extremely dry events occurred 25, 26,19,1 and 28 times for 181, 52,258, 9431, 1167and 17,171 stations, respectively. 181 and 1167 stations are located in Cumra, 1167 is in Kazımkarabekir, Karaman, 17,171 is in the Centre of Karaman, and 52,258 is in the Karapinar.

Fig. 12
figure 12

The dry drought event for groundwater drought

Full size image

Different dry events were obtained for different wells (Fig. 12), and are likely connected to the local meteorological, hydrological and groundwater conditions.

The comparison of SGI-1 values in the same regions is shown in Fig. 13. As seen in Fig. 13, the SGI-1 values of Cumra (R2 = 0.924) are more compatible than those of Karaman (R2 = 0.45), as the Karaman well is in a different region.

Fig. 13
figure 13

Comparison of SGI-1 values for a) Cumra and b) Karaman stations

Full size image

Comparison between hydrological, meteorological and groundwater drought

While SPI, CZI, MCZI, SGI, ZSI and SDI are determined by the same drought classification, SWSI is subject to a different drought class. To address this, the dry events were used to compare these indices. The number of dry events between 1978 and 2020 for the Konya Closed Basin is given in Fig. 14. These indices were compared for the stations located in the same region, and it is possible to notice that extremely dry occurred in groundwater stations more frequently than in meteorological stations for Karapinar (26) and Cumra (25 and 19).

Fig. 14
figure 14

The comparison of groundwater, hydrological and meteorological drought events for the stations of a Cumra, b Karapinar, c Eregli, d Konya, e Karaman

Full size image

Extremely dry events occurred 2 times for SDI, 0 times for SWSI, 7 times for CZI, 13 times for SPI and 28, and 1 time for SGI. The maximum number of moderate dry events (194) was obtained for SWSI, whereas the maximum number of extreme dry events (28) was obtained for groundwater drought. As shown in Fig. 14, extremely dry events occurred 9 times for SDI, 10 times for SWSI, 4 times for CZI and 10 times for SPI for Eregli. The maximum number of extreme dry events (10) was obtained for meteorological drought for Eregli. Extremely dry events occurred 9 times for SDI, 0 times for SWSI, 2 times for CZI and 13 times for SPI for Konya. The maximum number of extreme dry events (13) was obtained for meteorological drought at Konya.

As a result, the different dry events were obtained for meteorological, hydrological and groundwater droughts.

Mann–Kendall and Sen’s slope

This study analyzed Konya Closed Basin’s precipitation, streamflow, groundwater level and average temperature between 1978 and 2020 applying Mann–Kendall (MK) and Sen's slope. The MK trend test was carried out for all the stations at the 95% confidence level.

The test could be interpreted by looking at H0 (no trend in the series) and Ha (a trend is present in the series). As the computed p-value is lower than the significance level α = 0.05, one should reject the null hypothesis H0, and accept the alternative hypothesis, Ha.

As summarized in Table 6, a decreasing trend was detected in precipitation data for Aksehir, Nevsehir and Cumra. Similarly, a downward trend was detected in streamflow data for all stations excluding the D16A100 station. However, an upward trend was detected in groundwater level for all stations excluding the 1167 station based on Mann Kendall and Sen slope. An upward trend in average temperature was detected for all stations.

Table 6 Mann–Kendall and Sen’s slope results, along with descriptive statistics of data
Full size table

Discussion

This study investigated the meteorological, hydrological and groundwater droughts in the Konya Closed Basin, based on different indices, and considering the period 1978–2020 (43 years, equal to 516 months). To infer connections between the different types of droughts, specific indices were compared and statistically assessed.

In the present study, no extreme droughts (ED) occurred in the stations of Cihanbeyli, Konya and Beysehir based on ZSI– 1. The highest rate of extreme drought (ED) was detected by SPI– 1 (1.9–2.5), while the lowest was detected by ZSI-1 (0–0.4). As the monthly scale is commonly used to compare drought indexes (Yuce and Esit 2021; Dikici 2022; Şimşek et al. 2023; Tsesmelis et al. 2023), the analysis reported here mostly uses this time horizon. Considering all stations at the monthly scale, the total percentage of ED by SPI (1.9–2.5%) was higher than the one computed using the other indices. The SPI overestimates extreme and severe droughts on a monthly scale, while the ZSI overestimates moderate drought conditions. However, SPI and ZSI generally yielded similar results since SPI and ZSI indices are both based on measured precipitations. These findings are in line with the ones reported in the study by Katipoglu et al. (2020). It was determined that the percentage of SPI and CZI had greater total drought (ED + SD + MD) (10.7–13.4% for CZI; 10.7–14.2% for SPI) than those of ZSI and MCZI. Moreover, the percentage of MCZI has fewer total droughts (ED + SD + MD) (6.2–10%).

This study places in a relatively large literature on drought research in Türkiye. For example, Katipoglu et al. (2020) studied meteorological drought to assess the impact of drought across the Euphrates Basin in Türkiye. It was reported that the precipitation-based SPI and ZSI yield similar results, and the SPEI and RDI, which are based on precipitation and temperature, are also similar indices. The authors also found that the RDI was more reliable than the other indices in identifying periods of extremely dry or wet over the study area. Gumus and Algin (2017) studied hydrological and meteorological drought affecting the Seyhan − Ceyhan River Basin in Türkiye by employing SPI and SDI methods. They pointed out that there is a specific lag time between hydrological and meteorological droughts, such as meteorological drought occurs at year t while hydrological drought characterizes the following year t + 1. Ozkaya and Zerberg (2019) studied the hydrological drought of the Upper Tigris Basin in Türkiye using SDI. They reported that almost all stations experienced at least one severe drought during the study period and the study area has become drier since the early 1990s. They also noted that time-domain regions at lower latitudes tend to experience drought earlier than those located at higher latitudes. Dogan et al. (2012) studied the meteorological drought of the Konya Closed basin between 1972 and 2009, using the Effective Drought Index—EDI, Percent of Normal—PN, ZSI, CZI, DI, SPI, and Rainfall Decile based Drought Index – RDDI over 38 years (416 months). They determined that no extreme drought and very low severe drought rates were detected based on ZSI-1, while SPI-6 detected the highest rate of extreme drought. CZI underestimated extreme droughts compared to EDI at all time scales. In Dogan et al. (2012), the EDI was higher than that of ZSI for all the considered time steps. Moderate drought events were similar in EDI and ZSI The ZSI underestimated extreme and severe droughts based on EDI at all time scales. They reported that drought indices at a monthly scale had low weak correlations in arid/semi-arid regions since there is generally short-term/seasonal water scarcity. ZSI calculation procedure is compatible with SPI and CZI.

Comparing the present investigation with the work of Dogan et al. (2012), a few differences are evident: (i) Dogan et al. (2012) focused on the period 1972–2009 (38 years), while here the study was conducted covering a longer temporal horizon (43 years, between 1978 and 2020); (ii) hydrological, meteorological and groundwater droughts where here considered, while Dogan et al. (2012) studied only meteorological droughts; (iii) SPI and CZI had the greater total droughts (ED + SD + MD) and MCZI had the fewer total droughts in the present study, while EDI had greater total droughts and ZSI had the fewer percentage of ED in Dogan et al. (2012). On the other part, some similarities are also present between the two studies: i) SPI, CZI and ZSI indices were used in both cases to assess the meteorological drought; ii) in both studies, ZSI provided the smallest percentage of ED.

At the international level only a few studies combine drought types. Zhang et al. (2021) studied meteorological, agricultural and groundwater droughts in humid and arid/semi-arid basins in China. They reported that the link between groundwater drought and meteorological/agricultural drought is weak. Indeed, the groundwater droughts experienced in the Yangtze River may be due to the high groundwater consumption and low reservoir storage volume during this period. Moreover, the decreasing but still relatively high groundwater consumption for agriculture and the increasing groundwater consumption in other sectors (industrial, domestic, public and eco-environmental) have kept the total groundwater consumption at a stable and high level, resulting in significant pressure on groundwater. Thus, it is likely to be the major factor in worsening groundwater drought.

This short review pointed out that considering different drought types is paramount to developing an integrated drought warning and prevention system (Zhang et al. 2021). In fact, focusing on a long period and investigating multiple drought indices, the present study provides additional insights into the behaviour of the Konya Closed Basin and the connections between meteorological, hydrological and groundwater droughts, eventually helping in developing warning systems and climate-resilient management strategies.

Conclusions

This study assessed the meteorological, hydrological and groundwater droughts in the Konya Closed Basin based on different indices for 43 years (516 months). The Mann–Kendall and Sen’s slope were applied to determine the trend of rainfall, groundwater level and streamflow data. The results show that extreme drought (ED) by SPI-1 (1.9–2.5%) was higher than that of all indices for all stations, while this index underestimated extreme and severe droughts. At the same time, ZSI underestimated all indices for moderate drought at the monthly scale. It was determined that the percentage of SPI and CZI had greater total drought (ED + SD + MD) (10.7–13.4% for CZI; 10.7–14.2% for SPI) than those of ZSI and MCZI. Moreover, the percentage of MCZI has fewer total droughts (ED + SD + MD) (6.2–10%).

In summary, in the study basin, extremely dry events occurred in the groundwater drought more than meteorological and hydrological droughts. A larger number of dry events is visible starting from 2008, indicating a possible influence of climate change. However, to confirm the present results, future studies should focus on a larger number of gauging stations covering multiple basins, considering longer records that could eventually point out a clearer impact of climate-driven variations.

The present study can be used by local authorities or central government to further shed light on drought conditions in Türkiye, and on the usefulness of combining multiple indices to investigate correlations and feedback between meteorological, hydrological and groundwater droughts. At the same time, the data presented here could be used for numerical modelling, which might provide additional insights into drought dynamics over the Konya Close Basin, eventually suggesting science-based management strategies.