Introduction

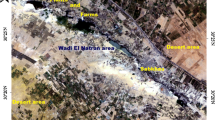
The Nile Delta, renowned for being one of the oldest and largest river delta systems, encompasses an expansive onshore area of 22,000 square kilometers and stretches along a coastline measuring 225 km (Stanley 2005). As it extends northward, the delta progressively widens, ultimately giving rise to a remarkable off-shore deep-sea fan that holds significant deposits of sedimentary clastic material in the eastern Mediterranean Sea (Ducassou et al. 2009). Our focus lies within the Qelabshowah–Belqas region, situated in the northern Nile Delta (as depicted in Fig. 1), which spans from latitudes 31° 24′ 17.5″ N to 31° 24′ 22.5″ N and longitudes 31° 23′ 00″ E to 31° 23′ 07.5″ E. This area is delimited by small canals on its northern and western sides, primarily consisting of agricultural land that relies on irrigation for cultivation.

Fig. 1
figure 1

a Map of Egypt, courtesy of Google, is included for reference purposes. b Location map highlighting the study area, situated in the northern Nile Delta region, is presented. It showcases a total of seven sites from which surface water samples were collected. In addition, a DC resistivity survey was carried out using the Schlumberger array technique at 15 vertical electrical sounding (VES) sites along three primary profiles that extend in a northwest–southeast direction. Moreover, an ERT survey using the dipole–dipole array was conducted along the same northwest–southeast direction

Full size image

The contamination of irrigated surface water poses a significant risk due to anthropogenic factors, such as agricultural practices, urban development, industrial effluent discharge, sewage release, and the use of fertilizers and pesticides (Datel et al. 2009). In addition, natural factors, including water–rock interaction, evaporation, salt solubility, and changes in water quality due to recharge, can contribute to water pollution (Hosseinifard and Mirzaei Aminian 2015; Gamal et al. 2023).

The geoelectrical resistivity method is widely employed for investigating salinity distribution, subsurface resistivity materials, and hydrogeological and environmental concerns. The DC resistivity method has been extensively employed, utilizing the Schlumberger and dipole–dipole configurations, to conduct in-depth assessments of the area in question. In addition, a comprehensive collection of seven surface water samples was taken and subsequently subjected to meticulous hydrochemical analysis. Researchers have increasingly utilized vertical electrical sounding (VES) survey of Schlumberger array and electrical resistivity tomography (ERT) survey of dipole–dipole array to analyze these issues, as seen in the works of Kaya et al. (2007, 2015), Ulugergerli (2017), Genedi et al. (2021b), Mahmud et al. (2022), Mohamed et al. (2023), and Ezeh and Maike (2023). Both 1D and 2D inversions of DC resistivity data, utilizing the Schlumberger array, have been extensively discussed by experts, including Tripp et al. (1984), Genedi et al. (2021a), and Genedi and Youssef (2023). Furthermore, researchers such as Arif et al. (2023) and Bamerni and Mohammad (2023) have explored and analyzed the 2D inversion of the ERT data obtained through the dipole–dipole array. There has been a growing emphasis on integrating geophysical and hydrochemical analyses, specifically through the analysis of DC electrical resistivity data, by researchers (Mokoena et al. 2021; Capa-Camacho et al. 2022; Daud et al. 2022; Bayowa et al. 2023; Gouasmia et al. 2023). These studies aim to achieve a comprehensive understanding of the factors influencing water quality in irrigated agricultural areas and improve the capability to monitor and address potential issues effectively.

When dealing with relatively horizontal and laterally homogeneous subsurface layers, a one-dimensional approximation often yields highly reliable outcomes. Nonetheless, it is important to acknowledge that data interpretation may be subject to a degree of ambiguity due to the non-uniqueness of the inverted data. In order to mitigate this, geostatistics are employed to analyze both the geoelectrical and hydrochemical data, enabling the mapping of two-dimensional (2D) spatial distribution trends. This approach is crucial in providing an accurate and trustworthy representation of the subsurface features. Geostatistics is a statistical method that specializes in analyzing the spatial or temporal variability of different data sets. Its primary goal is to assess the spatial correlation between apparent resistivity and hydrochemical data sets and improve geological interpretations, particularly in data-limited areas (Joelle et al. 2011). Using geostatistics, narrower intervals can be estimated for model parameters, leading to reduced uncertainties in quantitative interpretations (Kumar et al. 2007). One of the key techniques used in geostatistics is kriging interpolation, which predicts values for non-data points based on the spatial correlation obtained from the variogram model's parameters (Abdulkadir and Fisseha 2022). The concept behind kriging interpolation is that spatially close observations tend to be more similar to each other than those that are further apart (Abdulkadir and Fisseha 2022). Therefore, in situations where data are scarce and cover large areas, interpolation becomes crucial for estimating values in the absence of actual data points. The applications of geostatistics are widespread across various environmental and geoscientific disciplines, including geochemistry, geophysics, and environmental analysis (Prades 2018; Bourges et al. 2012; Danilov et al. 2018). Numerous researchers have employed geostatistical analysis for electrical resistivity data, such as Oh (2013), Mostafaei and Ramazi (2018), Swileam and Shahin (2019), Abdulkadir and Fisseha (2022), Khan et al. (2023), and Sandeep et al. (2023).

The main objective of this study is to effectively integrate 1D and 2D inversion results from geoelectrical data with geochemical analysis of collected surface water samples, enabling a comprehensive assessment of both salinity distribution and properties of shallow subsurface layers. The second goal is to reach a clear understanding of the relationship between water quality and geological characteristics, determine their suitability for agricultural irrigation, and evaluate any potential impacts on agricultural production. The geoelectrical and hydrochemical data sets are analyzed geostatistically to gain better visualization and obtain a complete and reliable picture of the subsurface geology. Two-dimensional maps were generated from these analyzes to illustrate the 2D spatial distribution trends of some specific parameters identified from the results of one-dimensional inversion of VES data and hydrochemical analysis.

Geologic setting

The lithostratigraphic sequence of the Nile Delta comprises the Mit Ghamr and Bilqas formations, which have been previously identified in studies conducted by Schlumberger (1984) and Kamel et al. (1998). The Mit Ghamr Formation is primarily composed of sand and gravels, with clay interbeds. The sand is predominantly composed of quartz, while the gravels consist of flint and dolomites (Nashaat 1992). The Bilqas Formation is largely composed of very coarse sand, interspersed with clay-rich molluscan fragments. The observed faunal association suggests that the presence of a lagoon or brackish swamps environment occasionally mixed with beach sand (Barakat 1982). The surface geological map of the Nile Delta (Fig. 2), provided by the Egyptian geological survey in 1994, depicts the Quaternary Nile deposits. Geomorphologically, the region is characterized by the presence of aged sand dunes. The Nile Delta basin is divided by a hinging faulted flexure zone that extends from east to west across the Mid Delta area, resulting in two distinct structural sub-basins: the North Nile Delta basin and the South Nile Delta block (Said 1981). This flexure zone acts as the boundary between the carbonate platform of the Mesozoic era and the considerably thick tertiary clastic basin situated to the north (Kamel et al. 1998). The North Delta Basin is distinguished by the presence of two primary structural patterns: a deep pre-Tortonian fault pattern predominantly consisting of east–west fault blocks, and a shallow post-Messinian fault pattern found in recent sediments within the unstable Delta area (Kamel et al. 1998).

Fig. 2
figure 2

Surface geological map of the Nile Delta region, as conducted by the Egyptian Geological Survey in the year 1994 (Egyptian Geological Survey 1994)

Full size image

Methodology

Geoelectrical method

The DC resistivity method is used in this study to measure and map the resistivity of the subsurface. The VES survey was carried out using the Schlumberger array at 15 different locations along three VES profiles, as depicted in Fig. 1. Each profile consisted of five VES points. The Schlumberger configuration was utilized with varying separations of current electrodes (AB/2) ranging from 1.5 to 100 m. For the ERT resistivity imaging survey, the dipole–dipole array was exclusively employed along ERT profile. A fixed inter-electrode spacing of 2 m was maintained, while the inter-dipole separation factor (n) was adjusted between 1 and 6. The DC resistivity data have been interpreted at different steps. The 1D and 2D inversion of VES data have been applied using IPI2WIN (Bobachhev et al. 2001) and Uchida algorithms (Uchida and Murakami 1990), respectively, where the Marquardt’s method is used to solve the inversion problem. The 2D inversion models of VES data not accounted for the topographical effect, because the study area is approximately flat. All VES data at the five sites along the same profile are inverted simultaneously by one conductivity model and the forward calculation is performed at each VES data point by applying the same initial model of 30 Ω m homogeneous earth. The 2D inversion of ERT data has been applied using Zond software, where the regularized least-squares method is used to solve the inverse problem. Regularization results in a more stable solution and allows you to obtain a smoother distribution of the resistivity in the medium (Constable et al. 1987). From the above different inversions, the starting models were adjusted to obtain a best fit between the observed and synthetic data.

Hydrochemical method

Geochemical analysis was applied to surface water samples to determine the ionic concentration and hydrochemical properties of these samples using pie chart, ion balance, and Stiff, Piper, and Durov plots integrated into the Aq.QA software using cation and anion concentrations. Surface water samples were collected from seven locations within the study area (Fig. 1) and subjected to a comprehensive geochemical analysis of major anions (HCO3−, NO3−, Cl, SO42−) and major cations (Ca2+, Mg2+, K+, Na+). This thorough analysis was conducted at the Atomic Absorption Laboratory of the Faculty of Science, Mansoura University. The purpose of this analysis was to determine the levels of total dissolved solids (TDS) and total hardness (TH) present in the water samples, as higher concentrations of minerals such as calcium (Ca) and magnesium (Mg) contribute to water hardness. The surface water samples were further analyzed to assess their impact on soil permeability, evaluate their suitability for agricultural irrigation, and determine potential effects on agricultural yield and quality. These analyses involved various parameters, including the sodium adsorption ratio (SAR), sodium content (SC), residual sodium (RSC), permeability index (PI), corrosivity ratio (CR), and chloro-alkaline indices (CAI). The equation, classification and range of these hydrochemical parameters have been discussed by many authors, such as Richards (1954), Wilcox (1955), Donen (1964), Schuller (1977), Lloyd and Heathcote (1985), Balasubramanian (1986), Aravindan (2004), Todd and Mayes (2005), Shankar et al. (2011), Fetter (2014), Sen (2014, 2015), Das et al. (2015) and Rawat et al. (2018).

The SAR serves as a measure of the alkaline/sodium hazard that affects crops. It estimates the potential movement of sodium in water, which can accumulate in the soil, predominantly at the expense of calcium, magnesium, and potassium due to regular use of sodic water (Rawat et al. 2018). The SC plays a significant role in crop productivity, as the presence of sodium fills the void spaces in the soil, leading to increased soil hardness and reduced permeability (Şen 2014). The RSC indicates the risk of soil alkalinity and represents the concentration of sodium carbonate and sodium bicarbonate in the irrigation water. If the concentration of carbonate and bicarbonate ions surpasses that of calcium and magnesium ions, it can lead to alkalinity in the soil (Raghunath 1987). The PI is utilized to assess the water's capacity for vertical movement through soil, measuring its suitability for irrigation purposes from any water source. The CR indicates the proportion of alkaline earths to saline salts in surface water. This offers valuable insights into the corrosive nature of the water and its potential to cause pipe corrosion. It helps to determine whether the use of metallic pipes for water transportation is safe or not. The CAI provides valuable information regarding the chemical composition changes that occur during the movement of water, specifically the ion exchange between surface water and its surrounding environment (Sastri 1994). To analyze the chemical composition of water samples, the Stiff (1951), Durov (1948), and Piper (1944) diagrams are employed for this purpose. These graphical analysis methods utilize cation and anion concentrations. The Piper plot, specifically, is utilized to evaluate the similarities and differences between water samples by considering the dominant cation and anion.

Geostatistical method

The geostatistical analysis has been applied on the geoelectrical and hydrochemical data sets to interpolate and grid some selected parameters at sparse points in unsampled regions using variogram model and ordinary kriging interpolation method. These parameters include the real subsurface resistivity layers from 1D inversion results of VES data, and the sodium content (SC) and permeability index (PI) data from hydrochemical analysis. The resulting grids are contoured and presented as a series of 2D prediction maps using ArcGIS software (ESRI 2016) that highlight the spatial distribution of these parameters within the study area.

The variogram plays a crucial role in measuring the spatial correlation in geostatistics and quantifying the variability in geographically or spatially distributed data (Abdulkadir and Fisseha 2022). It is particularly useful in correlating and quantifying spatial relationships found in discretely sampled data (Farid et al. 2017). During the gridding and modeling stage of data interpolation and visualization, the variogram is commonly employed (Farid et al. 2017). The experimental variogram serves as a means to quantify the dissimilarities between unsampled values and their neighboring data counterparts. This metric involves evaluating the autocorrelation at different distances, referred to as lags (h). The experimental semi-variogram, denoted as γ and represented by Eq. (1), quantifies half of the average squared difference between values at Z(xi) and Z(xi + h). The calculation of this semi-variogram heavily relies on the number of data pairs within a specific distance and direction category, known as N(h) (Abdulkadir and Fisseha 2022). A low value of γ signifies a substantial degree of autocorrelation between values separated by a given lag (h). On the other hand, a higher value of γ indicates a greater dissimilarity between these values:

$$\gamma \left(h\right)=\frac{1}{2N\left(h\right)}\sum_{i=1}^{N\left(h\right)}{\left(Z\left({x}_{i}\right)-Z\left({x}_{i}+h\right)\right)}^{2}$$
(1)

Multiple theoretical variogram models are available, which include linear, Gaussian, and exponential models, as described by Goovaerts in 1999. To properly fit the experimental variogram with these established theoretical models, the method of iterative reweighted least squares estimation is employed. The determination of weights is accomplished using the formula (Nj/h2j), where Nj represents the number of point pairs at a specific lag and hj denotes the distance or lag, as outlined by Abdulkadir and Fisseha in 2022. The validity of these models is typically assessed through cross-validation metrics, such as mean standardized error (MSE) and root mean square standardized error (RMSSE), with the optimal model being the one that minimizes the error values (Abdulkadir and Fisseha 2022). Root mean square error (RMSE) is a measure of how closely a model predicts actual values, representing the average difference between predicted and observed values. RMSSE, on the other hand, evaluates the validity of prediction standard errors by measuring the standard deviation of the residual values. It is desirable for the RMSSE to approach a value of one (Abdulkadir and Fisseha 2022). Four theoretical variogram models such as circular, spherical, exponential, Gaussian models have been tested and compared, where the RMSSE of spherical model is the minimum and near to one as compared to other models. To closely align with the experimental data sets, the spherical model, as defined in Eq. (2) (Abdulkadir and Fisseha 2022), was chosen for utilization in this study:

$$\gamma \left( h \right) = \left\{ {\begin{array}{*{20}c} {C_{0} + \left\{ {\frac{3h}{{2r}} - \frac{1}{2}\left( \frac{h}{r} \right)^{3} } \right\}} & {{\text{for}}\,\,0 < h \le r} \\ {C_{0} + C} & {{\text{for}}\,\,h > r} \\ 0 & {{\text{for}}\,\,h = 0} \\ \end{array} } \right.$$
(2)

To refine the experimental variogram, variograms are computed at different lags and variogram parameters, such as sill, range, and the nugget are determined (Abdulkadir and Fisseha 2022). The nugget value reflects short-range variability, while the sill value represents overall variability within the variables. The semi-variogram reach its sill at a finite distance called the range which represents the distance limit beyond which the data are no longer correlated.

A geostatistical approach known as ordinary kriging was utilized to predict values in locations, where no samples were taken. In kriging, the estimation of unknown values at a specific location is achieved using a weighted average of neighboring samples. These weights are determined based on variogram models (Abdulkadir and Fisseha 2022). The kriging method incorporates the spatial continuity of variables in the resistivity and hydrochemical data, taking into account both the spatial correlation and the dependence in the prediction of a known variable (Seyed mohammadi et al. 2016). The process involves utilizing the fitted model from the variogram, the spatial data configuration, and the values obtained from measured sample points surrounding the prediction location.

To accurately reflect the geometry and continuity of the sampled data, an analytical model must be inputted when using any variogram-aided kriging and interpolation technique. The resulting output provides insights into the spatial trends present in the data, facilitating the interpretation process (Farid et al. 2017). Kriging and semivariogram interpretation are then employed to analyze spatial correlation based on the Nugget/sill ratio (%) of the model variogram. A valid variogram should have a nugget-to-sill ratio ranging from 0 to 1. A ratio below 0.25 indicates a strong spatial dependence, while a ratio between 0.25 and 0.75 suggests moderate spatial dependence. On the other hand, a ratio exceeding 0.75 indicates weak spatial dependence (Ghazi et al. 2014; Xiao et al. 2016).

Results and discussion

1D Inversion of VES data

The resistivity data along the primary profiles (refer to Fig. 3a–c) provided conventional 1D inversion models comprising four geoelectric layers. These layers exhibited a wide range of resistivity values, ranging from 0.14 Ω m to 3787 Ω m, indicating a diverse lithological composition, including surface clastic deposits, sand, clay, gravel, and massive salt rocks of the Pleistocene deposits. The first geoelectric layer showcased distinct resistivity values varying from 21.16 Ω m to 3787 Ω m. This layer exhibited a thickness ranging from 0.23 m to 0.86 m, indicating the presence of unconsolidated surface deposits. The second layer, characterized by higher conductivity to low resistivity values that range between 0.14 Ω m and 18.16 Ω m, displayed a thickness ranging from 0.36 m to 12.43 m and at depths ranging from 0.23 m to 0.86 m. This layer probably corresponds to a clays sand deposits infiltrated by rain. The third layer exhibited higher conductivity values ranging from 0.29 Ω m to 3.83 Ω m, with a thickness varying between 3.95 m and 29.40 m. This layer appeared to be more conductive due to the presence of salt precipitates within the saturated sand deposits. The increase in conductivity can be attributed to the intrusion of salty irrigation surface water from the surrounding canals. The depth of this layer was found to range from 1.02 m to 12.83 m. The fourth layer, characterized by higher resistivity values ranging from 4.9 Ω m to 1882 Ω m, presented a top depth ranging from 6.25 m to 35.05 m. This layer likely represented ancient soils containing salted-rich layers deposited in marsh or swamp environments.

Fig. 3
figure 3

Conventional 1D-inversion models of the VES data are employed along the primary three profiles, namely profile one (a), profile two (b), and profile three (c)

Full size image

2D Inversion of VES data

The area of study is characterized by three to four distinct geo-electrical layers from 2D inversion results of VES data utilizing the Schlumberger configuration along the three VES profiles (Fig. 4). The upper layer, with resistivity values up to 30 Ω m, exhibits low resistivity. However, there is lateral variation within this layer, transitioning from a low resistive part (1–30 Ω m) to a highly conductive part (0.1–1 Ω m) observed below VES-06 along profile two, and below VES-13 and VES-14 along profile three. This transition is believed to be caused by the infiltration of salty surface water inside clayey sand deposits. The second layer, found at depths ranging from 10 to 15 m along the main profiles, is characterized by low to intermediate resistivity values (30–300 Ω m) which reflect saturated sand deposits from rainfall infiltration. The third layer, with resistivity values starting at 1000 Ω m, is observed at depths between 25 and 35 m along all three profiles. Within this layer, there are areas of extremely high resistivity values (up to 40,000 Ω m), particularly at the center of profile one, the northwestern portion of profile two, and the southeastern portion of profile three. These high resistivity values suggest the presence of significant salt rock occurrences in these areas. The final layer, which shows higher conductivity values below 1 Ω m, is exclusively found along profile one (Fig. 4a). This indicates the presence of an exceptionally conductive material within wet sand deposits and suggests the possibility of infiltration from the overlaying layers, potentially involving the dissolution of salt minerals (Fig. 4a).

Fig. 4
figure 4

Obtained cross sections through the 2D inversion analysis of DC resistivity data using the approach outlined by Uchida algorithm (Uchida and Murakami 1990) are presented for three primary profiles within the study area, namely profile one (a), profile two (b), and profile three (c)

Full size image

2D inversion of ERT data

Figure 5 shows the results of the 2D inversion of ERT data utilizing the dipole–dipole configuration along the ERT profile. The dipole–dipole cross section effectively visualizes three geoelectrical layers within the study area, with a maximum achievable depth of 16 m and a resistivity range spanning from 2 to 3900 Ω m. The topmost layer corresponds to unconsolidated deposits exhibiting varying resistivity values from 2 to 3900 Ω m. The intermediate layer consists of saturated sand deposits with conductive to moderate resistivity values ranging from 2 to 200 Ω m, resulting from the downward infiltration of rainwater, particularly beginning from the 18-m mark from the initial electrode. The bottom layer comprises compacted dry sand and gravel, characterized by high resistivity values ranging from 500 to 1500 Ω m. Moreover, notable lateral resistivity contrasts are observed at the electrode points between the distances of 7 and 14 m, as well as between 18 and 23 m from the initial electrode in the northwestern section. These contrasts highlight the presence of geological entities with resistivity values exceeding 3500–3900 Ω m in the northwestern and central portions of the section. These anomalies can be interpreted as indications of an empty cave located approximately 2 m deep within the second layer from the northwestern part of the section, and the burial of small water channels on the ground surface that stem from the central part of the section. These anomalies are filled with a cluster of fragmented red bricks. Therefore, the ERT cross-sectional data using dipole–dipole array obtained show significant improvements in lateral geometry accuracy and offers a comparable representation of the subsurface geological conditions when compared to the VES data using Schlumberger configuration.

Fig. 5
figure 5

Obtained inversion results for resistivity measurement using a dipole–dipole configuration in a two-dimensional (2D) model

Full size image

Hydrochemical analysis and water quality

In the area, the most prevalent cation is sodium (Na), followed by magnesium (Mg), calcium (Ca), and potassium (K). Among the anions, chloride (Cl) is the most abundant, followed by bicarbonates (HCO3), sulfate (SO4), and carbonate (CO3). Specifically, sodium (Na) concentrations range from 2832 ppm at WS-3 to 8618 ppm at WS-6. Magnesium (Mg) levels range from 245 ppm (WS-4) to 883 ppm (WS-6). Calcium (Ca) concentrations vary from 88 ppm at WS-7 to 426 ppm at WS-5. Potassium (K) concentrations range between 46 ppm (WS-1&WS-7) and 249 ppm (WS-6). Furthermore, chloride (Cl) content varies from 4422 ppm at WS-3 to 13,939 ppm at WS-6. Bicarbonate (HCO3) concentration values in surface water range from 584 ppm (WS-1) to 1278 ppm (WS-2 & WS-4). Sulfate (SO4) content ranges from 573 ppm at WS-2 to 2622 ppm at WS-6. Carbonate (CO3) concentration values fall between 880 ppm (WS-1) and 1574 ppm (WS-2, WS-4, and WS-6). The elevated levels of sodium (Na) and chloride (Cl) in the surface water are likely attributed to natural factors, such as the dissolution of mineral salts caused by evaporation in the area.

The circular diagram (pie chart), as illustrated in Fig. 6, visually represents the proportional distribution of the overall ionic concentration. Each segment within the chart corresponds to the fraction of distinct ions expressed in milliequivalents per liter (meq/L). Upon analysis, it was observed that the cations in the surface water samples followed the order of Na > Mg > Ca > K consistently across all samples. Similarly, the prevailing order of anions was found to be Cl > HCO3 > SO4 > CO3 in most samples, with the exception of sample number five and six. In these particular samples, the concentration of SO4 was observed to be either equal to or greater than that of HCO3.

Fig. 6
figure 6

Pie charts represent the distribution and composition of surface water samples collected from seven distinct locations within the study area

Full size image

Figure 7, which displays the ionic balance diagram, presents the degree of imbalance between positively charged cations and negatively charged anions. The summation of major cations and anions with opposite charges demonstrates near equality, with only a slight variance within the range of milliequivalents (meq/L). Moreover, it is noteworthy that Cl and Na emerged as the primary anion and cation, respectively, exhibiting notably high concentrations in samples WS-5 and WS-6.

Fig. 7
figure 7

Ionic balance diagram displays the analysis of surface water samples collected from seven sites within the study area

Full size image

The surface water in the study area displays a significant variation in total dissolved solids (TDS) values, as depicted in Fig. 8a, b. The lowest recorded TDS value is 10,494 ppm (352.2 meq/L) at WS-1, while the highest value is 29,275 ppm (985.3 meq/L) at WS-6. The average TDS value across all samples is 15,198.7 ppm (506.9 meq/L), indicating a general increase towards WS-5 and WS-6. This classification aligns with Fetter (2014) categorization which determines the surface water as saline water based on ppm levels. These elevated TDS values can be attributed to factors, such as saline intrusion and anthropogenic influences. The salinity of the surface water is observed to increase due to significant evaporation, leading to the loss of freshwater to the atmosphere and subsequently elevated salinity levels. Figure 8c illustrates the total hardness (TH) values, which range from 1472.9 ppm at WS-1 to 4270.3 ppm at WS-6. The average TH value is determined to be 2255.3 ppm. Notably, the hardness of the water increases towards WS-5 and WS-6, with peak values ranging from 3664.4 to 4270.3 ppm. According to Sen (2015) classification, all water samples are categorized as very hard water.

Fig. 8
figure 8

Spatial distribution maps were generated to depict the Total Dissolved Solids (TDS) content in surface water (a and b). In addition, maps were created for the Total Hardness (TH) concentration (c), Sodium Adsorption Ratio (SAR) level (d), sodium content (SC) value (e), Residual Sodium Carbonate (RSC) index (f), permeability index (PI) (g), Corrosive ratio (CR) analysis (h), and the chloro-alkaline index (CAI) (i) of the surface water at seven designated sample sites within the study area

Full size image

The SAR values, ranging from 31 (WS-3) to 57.3 (WS-6) with an average of 37.7, exhibit a concerning increase at WS-5 (SAR = 42) and WS-6. These elevated SAR values have detrimental effects on water infiltration and soil permeability, ultimately compromising soil structure and negatively impacting crop yield (Sen 2014). Based on the research by Todd and Mays (2005) and Sen (2015), it can be concluded that none of the water samples are suitable for irrigation due to the associated risks and unsatisfactory outcomes for all types of crops. The SC values, ranging from 77.9% (WS-5) to 81.7% (WS-1) with an average of 80.5%, raise doubts about the suitability of samples collected from WS-3 (SC = 79.9%) and WS-5 (SC = 77.9%) for irrigation. On the other hand, samples with SC values exceeding 80% are considered unsuitable for irrigation. The RSC values fall between -24.3 (WS-5) and 41.5 (WS-4). A negative RSC value at WS-5 and WS-6 indicates an increase in calcium (Ca) and magnesium (Mg) concentration in the soil. Conversely, positive values in other samples suggest the presence of sodium in the soil and the precipitation of Ca and Mg, which adversely affect soil structure (Sen 2014; Rawat et al. 2018). According to Richards (1954), Lloyd and Heathcote (1985), and Rawat et al. (2018), water in samples WS-5 and WS-6 is suitable for irrigation (RSC < − 14.6). However, WS-1 (RSC = 9.4) is only marginally appropriate as an irrigation source, while all other samples in the study area are unsuitable for irrigation (RSC > 28). The analysis conducted by the SAR, SC, and RSC indicated a notable increase in sodium levels present in surface irrigation water. This elevation in sodium content can result in plumbing corrosion issues and adversely impact agricultural crops, such as beans, potatoes, and fruits. Plants experience hindered water absorption due to the presence of sodium, ultimately leading to reduced crop yield and diminished economic returns. Furthermore, the inhibition of plant absorption of calcium can contribute to excessive leaching of calcium and magnesium.

Moreover, the high concentration of sodium bicarbonate ions in irrigation water has the potential to cause toxicity. The samples examined displayed a range of PI percentages, from 78.8% at WS-5 to 83.5% at WS-1, with an average of 82.3% across all samples (Fig. 8g). According to the classification system developed by Doneen (1964), the soil's permeability falls under class (I), indicating its suitability for irrigation purposes.

However, it is crucial to consider the long-term impact of utilizing irrigation water with a high salt concentration, as it can affect the water movement capability within the soil, as noted by Rawat et al. (2018). This becomes a significant concern in areas where the presence of sodium ions is prevalent.

Evaluation of all water samples (Fig. 8h) revealed CR values ranging between 5.5 (WS-2) and 17.6 (WS-5), with an average value of 9.9. The highest levels of corrosion were observed at WS-5 and WS-6 (CR = 17.2). According to Rawat et al. (2018), an increase in calcium (CI) can elevate the rate of corrosion in water, resulting in the leakage of lead and copper from pipes into drinking water and potential plumbing leaks. Consequently, all water samples fall into the unsafe category, as the CR value exceeds one with an increasing chlorine concentration.

The CAI values range from − 0.009 (WS-2) to 0.084 (WS-5), with an average value of 0.025. A majority of the water samples (WS-1, WS-4, WS-5, WS-6, and WS-7), 71.4% in total, exhibit positive CAI ratios, indicating a direct base exchange reaction. Conversely, 28.6% of the samples have negative ratios, suggesting an indirect base exchange reaction. The map (Fig. 8i) predominantly shows positive CAI values, indicating a direct base exchange reaction between the waters' Na and K ions and the rocks' Mg and Ca ions, or vice versa. However, the upper northeastern part of the map (Fig. 8i) displays negative CAI values, indicating an indirect base exchange reaction between the waters' Mg and Ca ions and the rocks' Na and K ions, or vice versa.

The concentration of sodium (Na+), potassium (K+), and chloride (Cl−) is significantly higher compared to other cations and anions in all seven water samples (Fig. 9). On the other hand, calcium (Ca2+) displays a lower concentration among cations across all samples. In addition, sulphates (SO42−) generally exhibit lower concentrations in all samples, except for sample numbers five and six, where carbonates (CO32−) and bicarbonates (HCO3−) show lower concentrations compared to sulphates.

Fig. 9
figure 9

Stiff plots of surface water samples at seven specific locations within the study area

Full size image

The concentrations of cations demonstrate minimal variation, whereas anions exhibit significant variation across all the water samples. According to the Durov diagram illustrated in Fig. 10a, the majority of the samples exhibit a total dissolved solids (TDS) level of approximately 1000 mg/L, with chloride being the primary anion and sodium as the predominant cation. However, two specific samples, WS-5 and WS-6, exhibit higher TDS content of over 2000 mg/L, accompanied by elevated concentrations of chloride and sodium. All the water samples can be classified as brackish water, with TDS ranging from 1000 to 3000 mg/L. All the samples fall within the field (3), located in the lower-left corner of the square grid at the base of each triangle. The prevalence of chloride and sodium is commonly observed, unless there is pollution present. The surface water is primarily categorized as the Cl–Na type, which may be attributed to mixing with salted water.

Fig. 10
figure 10

Durov (a) and Piper (b) diagrams were employed to conduct an assessment of the attributes exhibited by seven water samples gathered within the specified region

Full size image

The piper plot representation of the water samples, depicted in Fig. 10b, further supports this classification, as the samples fall within the sodium and potassium (Na + K) type zone and the chloride (Cl) type zone within the cationic and anionic triangular fields of the piper diagram, respectively. Therefore, based on the hydro-chemical classification of the surface water, it can be concluded that all the samples can be classified as Na–Cl water type.

Geostatistical analysis

The geostatistical method was employed to interpolate and grid the subsurface resistivity data, incorporating the 1D inversion results of VES data, along with the SC and PI data derived from hydrochemical analysis of surface water samples. The resulting grids were then contoured and visually presented as a series of 2D spatial distribution maps.

The spherical model was selected as the model that best fit the experimental variogram, based on cross-validation results. The obtained spherical models were created for six selected parameters, as shown in Fig. 11. These parameters include the true resistivity of the four subsurface layers (Res.1, Res.2, Res.3, Res.4) and hydrochemical parameters (SC and PI). These models show that there is an expected increase in variability γ(h) as the distance (h) increases. The cross-validation parameters demonstrated a satisfactory performance for all six variogram models, with MSE values nearing zero (-0.04 and 0.04) and RMSSE values approaching one (ranging from 0.98 to 1.17). The semivariogram model parameters, such as nugget, sill, and range values, are outlined in Table 1. From the spherical variogram models of the true resistivity parameters, the range values fall between 99.6 and 219.4 m. It is found between 702.5 and 2042.9 m from spherical models of SC and PI parameters.

Fig. 11
figure 11

Semi-variogram spherical models are utilized to characterize the true resistivity values of the subsurface geo-electrical layers (a–d) and the sodium content (e) as well as the permeability index (f) values obtained through hydrochemical analysis

Full size image
Table 1 Semi-variogram parameters associated with the true resistivity spherical model, as well as the SC and PI values, depict the spatial correlation present in the data
Full size table

The subsurface geological formations indicate continuous characteristics, with resistivity values gradually changing from one point to another rather than abruptly. Therefore, the nugget effect has a minimal impact on the variogram analysis of resistivity data. Depending on the nugget to sill ratio (%), the analysis of subsurface spatial variability revealed that Res.1, Res.2, and Res.3 exhibit weak spatial dependency at 100%, 77%, and 94%, respectively, while Res.4 shows a moderate spatial dependency at 47%. The spatial dependence varies between the four geoelectric layers due to lithological changes with depth. In contrast, both SC and PI demonstrate strong spatial dependencies at 22% and 3%, respectively.

Figure 12 shows the 2D spatial distribution maps of the true resistivity of subsurface layers (Res.1, Res.2, Res.3, Res.4) and the hydrochemical parameters (SC and PI). These maps effectively highlighting the spatial distribution of resistivity, SC, and PI trends within the study area. The first geoelectrical layer, representing the surface, exhibits varying resistivity values ranging from 21.15 to 3787 Ω m (Fig. 12a). This variation can be attributed to changes in lithology, consisting of alternating layers of sand, clay, and gravel from the Pleistocene deposits. The second layer (Fig. 12b) displays relatively higher conductivity to low resistivity sediments, ranging from 0.13 to 18.15 Ω m, within the interval zone of 0.23–0.86 m depth with a gradual increase in resistivity from the northeast towards the southwest. The third layer (Fig. 12c) exhibits resistivity values ranging from 0.29 to 3.83 Ω m. It signifies the presence of highly conductive sediments within the interval zone of 1.02–12.83 m depth. Most of this map denotes constant resistivity values (1.33–1.74 Ω m), except for some small patches where the values decrease in the southeast, west, and eastern parts (below VES-11), and only increase below VES-15. The last layer (Fig. 12d) represents a more resistive zone, with resistivity values ranging from 4.28 to 1882 Ω.m. It is located at a depth interval between 6.25 and 35.02 m. The resistivity values gradually increase from the northeast towards the southwest of the map. The resistivity values exhibit a progressive decrease from the first to the third layer, suggesting the presence of a variable resistive soil layer at a deeper level. This may indicate the existence of clay or moisture from rainfall infiltration in the second layer of clayey sand deposits. Furthermore, the decrease in resistivity in the third layer may indicate the precipitation of salt within saturated sand deposits due to the infiltration of irrigation water in the northern portion. Subsequently, there is a subsequent increase in resistivity values from the third layer downwards, albeit to varying degrees. This increase is believed to indicate the presence of extensive ancient salt layers within this specific region.

Fig. 12
figure 12

Spatial distribution of resistivity maps for the four subsurface geo-electrical layers (designated as a–d for layer number one, two, three, and four, respectively) as well as the sodium content (e) and permeability index (f) values obtained from the hydrochemical analysis are illustrated

Full size image

The sodium content (SC) map (Fig. 12e) shows values ranging from 77.86% (WS-5) to 81.73% (WS-1). These values tend to decrease in the northern, western, and southern parts surrounding the study area, which are characterized by high SC concentration (> 80.7%). As a result, the suitability of irrigation using water in this particular area is questionable. The permeability index (PI) map (Fig. 12f) illustrates values ranging from 78.78% (WS-5) to 83.52% (WS-1). The values tend to increase in the northern, northeastern, and northwestern sections surrounding the study area, while they decrease in the southern direction. This region coincides with the high SC and PI concentration areas indicated in the resistivity maps for the second and third layers derived from the 1D-inversion. Therefore, the soil permeability is suitable for irrigation in this specific area, with all samples falling into class (I).

The elevated levels of sodium in surface water can be attributed to both anthropogenic factors, such as the use of fertilizers, as well as natural sources like salt deposits. The increasing salinity of surface waters can mainly be attributed to the substantial evaporation and natural salt deposits. In addition, the long-term use of salty irrigation water negatively affects the movement of water in the soil due to the presence of sodium ions, which affects the permeability of the soil.

The excessive concentration of sodium in irrigation water impedes the ability of plants to absorb water and calcium, resulting in the leaching of excessive amounts of calcium and magnesium. This detrimental effect on agricultural crops leads to reduced yields for produce, such as beans, potatoes, and fruits. As a consequence, farmers involved in these crops experience significant impairments in their economic returns.

The illustrated maps (Fig. 12a–f) provided can be instrumental in enhancing the management of agricultural irrigation systems and their pivotal role in land reclamation efforts within this region. These maps can help identify suitable plant species and fruits that are not adversely affected by the rising sodium levels in irrigation water. By strategically selecting crops resilient to sodium, farmers can optimize their agricultural practices and mitigate the negative impact on crop productivity.

Conclusion

The study aimed to evaluate the shallow surface layers and salt distribution using VES and ERT resistivity data, combined with geochemical analysis of surface water samples. Geostatistical analysis was utilized to reduce uncertainty from multiple interpretations of geoelectrical data inversion and to clarify 2D spatial distribution patterns of some selected parameters, such as subsurface resistivity, sodium content and permeability index in the region. This analysis facilitated the interpretation of maps in which the resolution subsurface image was presented.

The DC resistivity survey identified four geoelectric layers in the study area with lithologies varying between sand, clay, gravel and salt-rich sediments from the Pleistocene region. The 1D inversion of VES data indicated four layers, with the first layer containing unconsolidated deposits with variable resistivity range. The second layer comprised saturated clayey sand with low resistivity due to rainfall irrigation, while the third layer exhibited high conductivity from salt precipitates in wet sand deposits. The deepest layer had higher resistivity due to a salt enrichment layer deposited in ancient times from water invasion and evaporation, forming in marsh or swamp environments. The 2D inversion of VES data using Schlumberger array revealed three to four layers with a maximum depth of 45 m. The upper layer shows lateral variation in resistivity from conductive to highly conductive zone due to salty irrigation water seepage. The second layer reflect wet sand deposits and had low to medium resistivity. The third layer had extremely high resistivity from ancient soils. There was a highly conductive layer along profile one caused by salt minerals infiltrating from the overlying layers. The 2D inversion of ERT data using dipole–dipole array showed three distinct layers with a maximum depth of 16 m. The first layer consisted of surface deposits with varying resistivity, the second layer was saturated sand from rainwater infiltration, and the final layer was compacted dry sand and gravel. From the above different inversion results, the first three layers have low to medium resistivity values, likely influenced by factors, such as irrigation, saline water and fertilizers. In contrast, the last layer consisted of highly resistive salt-rich layer formed from ancient water intrusion and evaporation. The inversion results from both VES and ERT data provided valuable insights into the subsurface features, including the presence of different layers with varying resistivity due to geological and anthropogenic factors. The ERT profile demonstrated precise lateral geometric accuracy compared to the Schlumberger array, revealing geological features like an empty cave and buried water canal filled with red bricks.

Surface water samples were analyzed and found to be mainly composed of sodium and chloride ions. Depending on stiff, piper and durov diagrams, the water samples were classified as Na–Cl type with high salinity and sodium levels, possibly mixed with salt water. The samples were also determined to be very hard and fall into the brackish to saline water category due to saline water intrusion and evaporation. The water was determined to be unsafe for transportation through metal pipes due to its corrosive nature from high sodium levels. Five water samples exhibited a direct base exchange reaction between sodium and potassium ions in the water and magnesium and calcium ions in the soil, while the rest showed an indirect base exchange reaction. The soil has suitable permeability but the most water samples were not suitable for irrigation due to high levels of sodium adsorption ratio, sodium content, and residual sodium carbonate, potentially harming crop productivity.

Geostatistical analysis was conducted for VES data and hydrochemical analysis using the best-fitted spherical semivariogram model and ordinary kriging interpolation method. Depending on the geostatistical analysis (nugget/sill ratio), the subsurface resistivity layers have indicated a weak to moderate spatial resistivity variability due to the lithological variation in both vertical and lateral directions. The SC and PI had strong spatial dependencies. Site conditions may negatively affect agricultural crop productivity. To maximize regional utilization and land reclamation, it is recommended to include 2D spatial distribution maps of resistivity and hydrochemical parameters in the reclamation process of similar areas. Choosing crops less affected by excess sodium can help mitigate the harmful effects on agricultural productivity in the area with high salinity and sodium levels present in the water samples.