Introduction

One of the essential prerequisites for statistical analysis in hydrology is to have a complete time series data (Hamzah et al. 2022). For instance, methods such as autocorrelation function, spectrum analysis and extreme value analysis based on the generalized extreme value distribution of annual blocks or principal component analysis all can be applied only to datasets without missing values (Kim and Pachepsky 2010; Tencaliec et al. 2015). Typically, data are usually collected in observation stations over a given period of time (hence time series data) and stored in databases that can subsequently be accessed for research purposes.

However, numerous hydrological and research databases contain missing values (Elshorbagy et al. 2002; Yilmaz and Onoz 2019; Mesta et al. 2021; Luna et al. 2020) and are therefore only of limited use to researchers seeking to apply state-of-the-art statistical methods. The reasons behind missing data are multiple and often idiosyncratic. They include failure of observation station, incomparable measurements, manual data entry procedures that are prone to errors, lack of financial resources, and also equipment errors (Gyauboakye and Schultz 1994; Adeloye 1996; Teegavarapu et al. 2009; Johnston 1999; Khampuengson and Wang 2023). To address this issue, an important data preprocessing operation—the so-called missing value imputation—should be performed (Adeloye 1996; Adeloye et al. 2011; Mwale et al. 2012; Taie Semiromi and Koch 2019).

A time series comprising gap/missing data was formerly either removed or its missing values were simply substituted with mean or zero numbers. As a consequence, a lot of information can be lost, thus necessitating to impute missing values meticulously (Gill et al. 2007; Oyerinde et al. 2021), although it is an unenviable task (Gill et al. 2007). Therefore, it is of paramount importance to impute missing data cautiously and properly, because an impoverished imputation of missing data, especially for streamflow time series, would result in a poor watershed simulation and therefore, an ineffective water resources management (Bardossy and Pegram 2014; Benzvi and Kesler 1986).

In dealing with incomplete data, researchers have to find a solution to missing data problems as all of the approaches listed above can be applied properly only using complete data where less information is missing (Dembélé et al. 2019; Luna et al. 2020). In this endeavour, researchers often resort to imputation methods where missing values are replaced with a numerical value that is obtained from a more or less sophisticated statistical method and seeks to approximate missing values by some predictions.

Over the last decades, imputation methods which attempt to ‘fix’ datasets characterized by missing data by replacing them with inserting numerical values have improved dramatically (Peugh and Enders 2004). The rise of more sophisticated imputation methods led many researchers to prefer replacing missing values with imputed values over excluding them from the analysis entirely (Saunders et al. 2006; Arriagada et al. 2021).

In hydrological settings, the choice of an appropriate imputation method needs to take into account the most important features of hydrological data (Haile et al. 2023). Hydrological data are time series data that is often characterized by stable trends over time and a high autocorrelation of the observations. Moreover, hydrological time series often display random deviations from these trends and these deviations are not constant over time (Guzman et al. 2013). Given these features of the data generating process underlying hydrological data, imputation of missing values should be based on statistical time series methods that take into account the time series nature of hydrological data.

While thus far several studies have been conducted to assess variegated approaches including advanced statistical algorithms for imputation of missing values, in particular for streamflow data (Elshorbagy et al. 2002; Yilmaz and Onoz 2019; Mesta et al. 2021; de Souza et al. 2020; Tencaliec et al. 2015; Khampuengson and Wang 2023; Weilisi and Kojima 2022; Oyerinde et al. 2021; Chapon et al. 2023), impacts of seasonality and periodicity of streamflow discharge on the efficacy of the imputation methods have been poorly documented.

Imputation of missing values in streamflow data is essential for various reasons, especially when dealing with data of different periodicities (e.g., daily, monthly, annual). The importance of imputation lies in ensuring the accuracy and reliability of hydrological analyses, water resources management, and environmental decision-making (Arriagada et al. 2021; Haile et al. 2023). Overall, the imputation of missing values in streamflow data is crucial for maintaining data integrity, supporting hydrological analyses, and aiding informed decision-making in various water-related sectors. It enables us to gain a better understanding of water resources, adapt to changing hydrological conditions, and mitigate the impacts of water-related hazards (Chapon et al. 2023; Baddoo et al. 2021).

Thus, in the present study, we assess the efficacy of simple and advanced statistical approaches in the imputation of streamflow time series imparted by artificially variegated variances and seasonalities. To that end, we employ imputation techniques that are widespread and easy to use, but ignore the time series nature of the data in comparison with imputation techniques exploiting the time series nature of hydrological data. In particular, we are interested in the performance of advanced statistical techniques such as Autoregressive Moving Average/Autoregressive Integrated Moving Average (ARMA/ARIMA) and Autoregressive Conditional Heteroscedasticity (ARCH). Although the former has been widely used in hydrological studies (e.g., Zhang et al. 2011), the application of the latter in hydrological studies and in particular for imputation of streamflow/groundwater missing values has not been reported as of yet. Indeed, ARCH has originated from finance and econometrics and thus its suitability in hydrological studies should be appraised.

The remainder of the paper proceeds as follows: first, we describe Materials and methods including Study area, second, in the Results and Discussion section, we evaluate how different imputation techniques perform under different conditions and discuss our findings. The paper concludes with a summary of the key findings and a short presentation of the most important implications of this study.

Materials and methods

Study area

The spatial scope of this study is the federal state of Brandenburg located in Northeast Germany (Fig. 1). Brandenburg is located within the Northeast German lowlands between the rivers Elbe and Oder draining to the Northern Sea and Baltic Sea, respectively. According to climate projections, it is located in the transition zone between increasing streamflow in northern Europe and decreasing streamflow in southern Europe.

Fig. 1
figure 1

a The geographical location of the Brandenburg State on the Germany map; b the position of the Karthane catchment, its gauging station (Bad Wilsnack), and the observation well (GW23) for which the imputation of streamflow and groundwater missing data was conducted, respectively

Full size image

Time series of observed precipitation, evapotranspiration, temperature spanning from November 2001 to October 2006 from the Karthane catchment at the gauging station in Bad Wilsnack region were chosen (Fig. 1). The whole area, excluding Berlin in its center, is 29,479 km2 and has a population of 2.5 million.

In this region, forest area constitutes 35% of the landuse. Agricultural land is another main landuse type with 34% cropland and 9% pasture. With a mean annual precipitation of 557 mm and a mean annual temperature of 8.7 °C (period: 1960–1990; German Weather Service 2012), it is one of the areas with the lowest climatic water balance in Germany. Due to high climatic water demand, the evapotranspiration here is approximately 510 mm per year, only leaving 100 mm per year as runoff (Lischeid and Nathkin 2011).

The runoff exhibits substantial spatial variability, depending on local meteorological conditions. Groundwater flow and groundwater discharge into rivers and channels are the dominating hydrological components of the regional water cycle. About 80% of total annual streamflow discharge occurs as baseflow, whereas surface runoff contributes only a minor fraction, accounting for less than 20% of the total streamflow discharge (Merz and Pekdeger 2011).

The whole region is part of a postglacial landscape, formed since the last Pleistocene glaciations. Low gradients across the land surface accompanied by large number of closed postglacial depressions, i.e., kettle holes (Kalettka and Rudat 2006) and periglacial channels that expose locally raised relative relief. These hummocky terrains form a hydrogeologically complex interplay between groundwater and water bodies, including streams and kettle holes (Vyse et al. 2020).

Moreover, the region exhibits a wide array of anthropogenic impacts on the fresh systems. These include weirs, dams, and flood protection, resulting in extensive use and alteration of regional freshwater quantity and quality. Due to these specific characteristics, observed discharge time series are disturbed by anthropogenic influences.

Thus, to assess different imputation methods relying on more representative reference data and more importantly to appraise the impacts of artificial seasonalities and variances imparted to the streamflow data on the performance of imputation methods, we construct discharge time series using a hydrological model. This allows us to simulate discharge as the reference data that is more likely to reflect common characteristics as hydrological time series. For a more detailed description and overview on hydrological changes within this landscape, we refer to Merz and Pekdeger (2011) and Germer et al. (2011).

Methodology

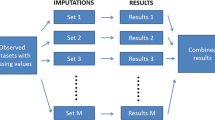
Researchers can replace missing values by applying imputation methods that yield approximations for the missing values derived from the observed data points. There is a multitude of imputation methods available for this purpose and it is not always clear which of the different methods will deliver more satisfactory results in specific applications. We propose a simple research design that allows us to evaluate the performance of different imputation techniques in hydrological settings.

The basic idea of our research design is to use discharge time series data that can be found typically in hydrological applications as reference data. To evaluate different imputation methods, we randomly replace a certain fraction of the observations of the reference data with missing values. These missing values will then be replaced by approximations obtained from different imputation methods. Comparing the reference time series data with the imputed time series will allow us to draw conclusions regarding the performance of different imputation methods.

Despite this clear structure, it is hard to directly implement this research design for one simple reason: for most of our study regions complete discharge time series for variables of interest hardly exists. The available data often are either characterized by some missing values or with specific values that keep repeating for consecutive days or even weeks, which are used as substitute for missing values. Therefore, we adjust the basic idea of our research methodology slightly.

To obtain reference data that does not suffer from missing values itself, we resort to using output discharge data obtained from a hydrological model. This simulated discharge data is likely to reflect common characteristics of hydrological data found in typical applications. In the following, we detail the single steps of our research design, which is also summarized in Fig. 2.

Fig. 2
figure 2

The methodological steps designed for assessment of 5 algorithms for imputation of missing values

Full size image

Data

To simulate discharge data, we rely on time series of evapotranspiration, observed precipitation, temperature, collected from the gaging stations in Bad Wilsnack region (Fig. 1) for 5 years (from November 2001 to October 2006). The dataset was provided by the Leibniz Centre for Agricultural Landscape Research (ZALF).

Moreover, to learn more about the performance of various imputation methods, we vary the characteristics of the input data to simulate reference data with different features. In particular, we vary the variance of the original precipitation data (P_seasonal) and generate three different precipitation time series: (1) one with low variance (P_low); (2) one with high variance (P_high); and (3) one time series whose variance is preserved, but white noise is added (P_noise). Similarly, we remove seasonality from the original precipitation time series (P_seasonal) and obtain precipitation time series without clear seasonality (P_nonseasonal). Therefore, we force the hydrological model with five sets of inputs, which have been subject to artificial nuances.

We use the Byråns Vattenbalansavdelning (HBV) model to simulate a time series of daily discharge \({Q}_{s}^{t}\), which serves as a reference data for the evaluation of different imputation methods. The HBV model requires daily precipitation, temperature, and evapotranspiration as input data. The datasets have been obtained for the study region described above for a period of 5 years (November 2001 to October 2006).

Figure 3 presents the time series of the evapotranspiration and observed temperature over the observational time period. As illustrated, both time series are characterized by typical seasonality patterns with low temperatures and low evaporation during winter months.

Fig. 3
figure 3

Time series of temperature and evapotranspiration input. Note that the left vertical axis contains the temperature scale in degree Celsius, whereas the right vertical axis contains the scale for evapotranspiration in mm/day

Full size image

Figure 4 presents the time series of the observed precipitation between November 2001 and October 2006. It should be noted that Fig. 4 contains two time series. First, P_seasonal is the original time series of precipitation. Second, we de-trended P_seasonal by removing seasonal effects on a monthly basis, yielding P_nonseasonal. We de-trend the time series to simulate discharge time series with different structural characteristics using the HBV model. This allows us to gain insights into performance differences of the imputation methods, depending on structural characteristics of the time series to be imputed.

Fig. 4
figure 4

Precipitation input data with/without seasonality

Full size image

Since, in this study, we use data from only one catchment, i.e., the Karthane catchment, we further manipulate the original precipitation data with regard to its volatility to gain further insights how the different imputation methods perform under different conditions.

Figure 5 indicates additional manipulations of the original precipitation data which differ according to the variance. The first manipulation consists of replacing all values of the original time series that are higher than 10 mm by zero to generate a novel time series with low variance (P_low). Second, and departing from the derived P_low, we increase its variance (and mean) by multiplying P_low with a constant multiplier and obtain an additional time series P_high. Finally, we preserve P_high’s variance but add white noise.

Fig. 5
figure 5

Generated precipitation input data with variegated variances

Full size image

White noise here refers to an error term or shock which is drawn from a normal distribution with zero mean and finite variance. Adding independent draws from such a normal distribution to each daily observation yields an additional time series P_noise having the same mean as P_high, but higher variance due to the addition of the random component. Note that Fig. 5 displays P_low, P_high and P_noise over the full 5-years period (upper half), but also contains a presentation over only 3 months (January 2002 to March 2002) (lower half). The latter makes typical precipitation patterns and the differences between the three time series visible in a clearer way. Using these different time series as input data for the HBV model described below allows us to simulate discharge data that reflects different characteristics despite the fact that we work with data from only one catchment (the Karthane catchment). To further evaluate the effectiveness of the imputation method, we employ groundwater time series, which observed in the vicinity of Lake Bötzsee (Fig. 1). The region is about 20 km northeast of Berlin, also in Brandenburg in Northeast Germany in the time period from January 2012 to May 2014.

Simulation of the streamflow discharge

We use the observed temperature, evapotranspiration and the five different patterns of the precipitation time series described above to simulate discharge data using the HBV hydrological model (Fig. 6). The use of the different precipitation time series allows us to generate reference data exhibiting different patterns of variance and seasonality. These differences help us to identify under which conditions imputation methods might perform differently.

Fig. 6
figure 6

The Architecture of the HBV model

Full size image

The HBV hydrological model has a long history and the model has found applications in more than 30 countries. Its first application dates back to the early 1970s (Bergström and Forsman 1973). Originally, the HBV model was developed at the Swedish Meteorological and Hydrological Institute (SMHI) for runoff simulation and hydrological forecasting, but the scope of applications has increased steadily (Bergström and Singh 1995; Li et al. 2014; Killingtveit and Sand 1990; Renner and Braun 1990; Osuch et al. 2019).

The model simulates daily discharge using daily precipitation, temperature and potential evaporation as input. Precipitation is simulated to be either snow or rain depending on whether the temperature is above or below a threshold temperature, TT (°C). All precipitation simulated to be snow, i.e., falling when the temperature is bellow TT (°C), is multiplied by a snowfall correction factor, SFCF. Snowmelt is calculated with the degree-day method according to Eq. 1:

$$\mathrm{melt}=\mathrm{CFMAX}\left(\text{T}\left(t\right)-\text{TT}\right).$$
(1)

Melt water and rainfall are retained within the snowpack until it exceeds a certain fraction, CWH, of the water equivalent of the snow. Liquid water within the snowpack refreezes according to Eq. 2:

$$\mathrm{refreezing}=\mathrm{CFR}\cdot \mathrm{CFMAX}\left(\text{TT}-\text{T}\left(t\right)\right).$$
(2)

Rainfall and snowmelt (P) are divided into water filling the soil box and groundwater recharge depending on the relation between water content of the soil box (SM (mm)) and its largest value (FC (mm)) following Eq. 3:

$$\frac{\mathrm{recharge}}{P\left(t\right)}={\left(\frac{\mathrm{SM}\left(t\right)}{\mathrm{FC}}\right)}^{\mathrm{BEAT}}.$$
(3)

Actual evaporation from the soil box equals the potential evaporation if SM/FC is above LP, while a linear reduction is used when SM/FC is below LP (Eq. 4):

$${E}_{\mathrm{act}}{=E}_{\mathrm{pot}}\cdot \mathrm{min}\left(\frac{\mathrm{SM}\left(T\right)}{\mathrm{FC}\cdot \mathrm{LP}},1\right).$$
(4)

Groundwater recharge is added to the upper groundwater box and to the water percolates from upper to the lower groundwater box. Runoff from the groundwater boxes is computed as the sum of two linear outflows by linear reservoir function (Eq. 5):

$${Q}_{{GW}_{(t)}}={Q}_{1}+{Q}_{2}={K}_{1}\cdot U{Z}^{1+\alpha }+{K}_{2}\cdot LZ.$$
(5)

The recession components threshold of upper groundwater box is defined by a linear drainage equation. The runoff is finally transformed by a triangular weighting function to give the simulated runoff according to Eq. 6:

$${Q}_{\mathrm{sim}\left(t\right)}=\sum_{i=1}^{\mathrm{MAXBAS}}\left({\int }_{i-1}^{i}\frac{2}{\mathrm{MAXBAS}}-\left|u-\frac{\mathrm{MAXBAS}}{2}\right|\frac{4}{{\mathrm{MAXBAS}}^{2}}\mathrm{du}\right)\cdot {Q}_{{\mathrm{GW}}_{(t-i+1)},}$$
(6)

where P(t), T(t), SM(t), QGW(t) and Qsim(t) are precipitation, temperature, soil moisture, groundwater discharge and simulated discharge at time t. CFMAX, CFR, FC, LP, K1, K2, \(\alpha\) and MAXBAS are model parameters.

For both snow and soil routine, calculations are performed for each different elevation zone, but the response routine is a lumped representation of the catchment. The list of the model parameters are given in Table 1.

Table 1 The hydrological model parameters and their feasible range
Full size table

Application of imputation methods

We randomly delete a given fraction of the simulated discharge time series obtained from the HBV model. In particular, in different steps we delete 5%, 10%, 20%, 30% and 40% of the data. Subsequently, we impute the missing values applying five different imputation techniques to fill the missing values with approximations. We apply imputation techniques commonly used in hydrology, including arithmetic mean, ordinary least squares (OLS) and preceding value (PV), but also more advanced imputation techniques, including autoregressive integrated moving average (ARIMA) and autoregressive conditional heteroscedasticity (ARCH) models. It should be noted that we used R and STATA to apply the imputation methods that we had considered in this study.

Overview of the applied imputation methods

Before applying different imputation methods to the simulated discharge time series \({Q}_{s}^{t}\) obtained from applying the HBV model to the observed data, we briefly discuss different imputation methods. As described above, we apply these methods to impute different shares of missing values (5%, 10%, 20%, 30%, and 40%) to obtain a time series \({Q}_{i}^{t}\) including imputed values. For the following notation, we denote with \({Q}_{m}^{t}\) the time series of including missing values, which is treated as the basis for our imputation exercises. After the discussion of the different imputation methods used, we assess their performance using the Mean Squared Error (MSE) and the Nash–Sutcliffe Efficiency (NSE) criteria, which we also introduce below.

Arithmetic mean imputation

A commonly used and simple imputation method for the approximation of missing values is the so-called arithmetic mean imputation. It replaces missing values in a variable with the arithmetic mean of the observed values of the same variable (Roth 1994). In our context, the missing values are replaced with the arithmetic mean of the non-missing observed values, which is \({Q}_{i}^{t}=\frac{1}{T}{\sum }_{i=1}^{T}{Q}_{m}^{t}\) with T being the number of non-missing observations here.

Preceding value

An alternative approach to replace missing values is using the last observed preceding value as best predictor for a missing values. Missing values in that case sequentially replaced according to \({Q}_{i}^{t}={Q}_{m}^{t-k}\) where k is the difference in the number of periods between a missing value and the last observed value of Q. If, for instance, two missing values occur subsequently, the second missing value is replaced with \({Q}_{i}^{t}={Q}_{m}^{t-2}\) as \({Q}_{m}^{t-2}\) is the last previously observed value.

Ordinary least squares (OLS) regression imputation

Regression-based imputation replaces missing data with predicted values from a regression estimation (Greenland and Finkle 1995). The basic idea behind this method is using information from all observations with complete values in the variables of interest to fill in the incomplete values, which is intuitively appealingly (Frane 1976). While different regression models can be applied to impute missing values, we start with the most basic regression model—the linear regression.

The first step of the imputation process is to estimate regression equations that relates the variable that contains missing data (the dependent variable of the regression) to a set of variables which have complete information across all observations in the dataset (independent variables of the regression). In our context, we estimate how the non-missing values \({Q}_{m}^{t}\) are related to the observed precipitation data on the same day \({P}_{o}^{t}\). The regression function we are estimating is then given by \({Q}_{m}^{t}={\beta }_{0}+{\beta }_{1}{P}_{m}^{t}+{\varepsilon }_{t}\), where \({\varepsilon }_{0}\) accounts for measurement errors and other unobserved influences on discharge. The regression parameter \({\beta }_{0}\) and \({\beta }_{1}\) are estimated only for the subset of the data that contains all observations that have complete information both for the dependent variable and the independent variables using the ordinary least square estimator yielding the estimates \(\widehat{{\beta }_{0}}\) and \(\widehat{{\beta }_{1}}\).

The second step uses the regression results from the first step and missing values for the observations that could not have been included in the regression are replaced by predictions obtained from combining the observed values precipitation and the estimates from the first step of how it is related to the discharge. These predicted values fill in the missing values and produce a complete dataset in which the missing values are replaced according to \({Q}_{i}^{t}=\widehat{{\beta }_{0}}+\widehat{{\beta }_{1}}{P}_{o}^{t}\) for all t with missing data.

While regression-based imputations most frequently rely on simple linear regressions, it is worth noting that more flexible regression approaches can equally be used and might even be more advantageous depending on the application. We discuss more advanced time series regression approaches below.

Auto regressive integrated moving average model

Similar to the linear regression framework introduced above, time series regressions can equally be employed for imputations purposes. Imputed values are then derived from a prediction based on time series regression instead of a linear regression.

A time series—such as hydrological data—can be interpreted as a stochastic process where yt and yt–j are correlated over time, i.e., autocorrelation between different measures of y exists. One possible specification is an autoregressive process AR (p) of pth order with

$${y}_{t}={a}_{1}+{a}_{1}{y}_{t-1}+{a}_{2}{y}_{t-2}+\dots +{a}_{p}{y}_{t-p}+{\varepsilon }_{t}.$$
(7)

In Eq. 7 epsilon is a random error term that follows a standard normal distribution and is independent over time with E(\({\varepsilon }_{t}\),\({ \varepsilon }_{t-i}\)) = 0 for all i ≠ t.

p here denotes the number of lagged values of \({y}_{t}\) that enter the process. \({\varepsilon }_{t}\) is an identically distributed (iid) error term with zero mean and constant variance. An alternative specification of a stochastic process that generates autocorrelation in a time series is moving average (MA) processes in which the contemporary value of \({\mathrm{y}}_{t}\) is a function of its mean µ and a sequence of random shocks with

$${y}_{t}=\upmu +{\varepsilon }_{t}+{\theta }_{1}{\varepsilon }_{t-1}+{\theta }_{2}{\varepsilon }_{t-2}+{\theta }_{p}{\varepsilon }_{t-q}.$$
(8)

The commonly used ARMA model fits an observed autoregressive (AR) time series by combining it with a moving-average (MA) component consisting of a sum of weighted lags of the error term εt (Box et al. 2015). The resulting ARMA model is written as

$${y}_{t}={\alpha }_{0}+{\alpha }_{1}{y}_{t-1}+{\alpha }_{2}{y}_{t-2}+\dots +{\alpha }_{p}{y}_{t-p}+{\upvarepsilon }_{t}-{\theta }_{1}{\upvarepsilon }_{t-1}-\dots {\theta }_{p}{\varepsilon }_{t-q}.$$
(9)

Equation 9 is often referred to as an ARMA (p, q) model as it contains a pth order autoregressive component in the observable time series, \({\mathrm{y}}_{t}\), and a qth order moving average component of the unobservable random shocks \({\upvarepsilon }_{t}\). It is generally assumed that εt follows a so-called white-noise process with zero mean E(\({\upvarepsilon }_{t}\)) and constant variance E(\({\upvarepsilon }_{t}^{2}\)) = σ2.

It is important to highlight that ARMA models can be fitted to data only if the underlying time series \({\mathrm{y}}_{t}\) is weakly stationary (Gao et al. 2018). In case a time series \({\mathrm{y}}_{t}\) is not stationary, stationarity can often be achieved by differencing the time series one or more times (Box and Jenkins 1976). If differencing is required, the ARMA (p, q) model (Autoregressive Moving Average) becomes an ARIMA (p, d, q) model (Autoregressive Integrated Moving Average) where d denotes the order of differencing, i.e., the number of time \({\mathrm{y}}_{t}\) is differenced to achieve stationarity.

In our application, we fit an ARIMA (p, d, q) model to the data and use the estimates obtained as the basis for predictions used to impute missing values as described for the linear OLS regression above.

Autoregressive conditional heteroscedasticity model

ARMA and ARIMA models are based on the assumption of constant variance of the error terms E(\({\varepsilon }_{t}^{2}\)) = σ2 over time. This assumption often is too restrictive. In hydrology, the local climate might be characterized by a period of stable conditions followed by change in weather that drastically alters relevant outcomes (Hughes et al. 2011). The assumption of constant autocorrelation is then too narrow. More realistic would be an assumption of changing variance and hence changing autocorrelation of the observed outcomes over time (heteroscedasticity).

Auto Regressive Conditional Heteroscedasticity (ARCH) models originating from finance and econometrics are regression models that in addition to past values of \({y}_{t}\) also captures time varying volatility within the structure of standard time series models described above. ARCH models hold the unconditional variance of \({\upvarepsilon }_{t}\) constant with E(\({\upvarepsilon }_{t}^{2}\)) = σ2, but allow its conditional variance to follow an AR process of its own with

$${\varepsilon }^{2}= \zeta +{\alpha }_{1}{\varepsilon }_{t-1}^{2}+\dots +{\alpha }_{m}{\varepsilon }_{t-m}^{2}+{\upsilon }_{t},$$
(10)

where \({\upsilon }_{t}\) is a new white noise process.

Based on this specification, the ARCH model extends the standard ARMA/ARIMA model to incorporate time varying volatility. The estimation of ARCH is again possible relying on standard statistical software packages and predictions can be used to impute missing values in a time series. In our case, we fit an ARCH model that extends ARIMA (p, d, q) model by a first-order autoregressive process for the variance of the error term \({\upvarepsilon }_{t}^{2}\).

Evaluation of imputation performance

We evaluate the performance of the two different imputation methods by comparing the imputed time series with the reference time series obtained from the HBV model described above. In particular, we use the Mean Squared Error (MSE) and the Nash–Sutcliffe efficiency (NSE) measure for this purpose. The description of the two evaluation metrics is given below.

Mean Squared Error (MSE)

The Mean Squared Error is a commonly used measure in statistics to assess the quality of an estimator or—as in the case of imputation—a predictor (Harville and Jeske 1992). The MSE measures the average of the squares of the errors or deviations, i.e., the difference between the predictions and the observed values (Schunn and Wallach 2005). Note that the MSE can be compared across different models to assess which one performs better.

Formally, let \({Q}_{s}^{t}\) be the simulated discharge time series (our reference data) and \({Q}_{i}^{t}\) be the time series of discharge including imputed values from one of the imputation methods for the periods \(t=1, \ldots , T\). The MSE is then defined as

$$MSE = \frac{1}{T}\sum_{i=1}^{T}{({Q}_{i}^{t}-{Q}_{s}^{t})}^{2}.$$
(11)

A MSE of zero would indicate error-free prediction (imputation) of missing values, but is in reality not to achieve.

Nash–Sutcliffe efficiency (NSE)

Nash and Sutcliffe (1970) proposed an efficiency measure for hydrological models. The Nash–Sutcliffe efficiency is defined as one minus the sum of the squared differences between the predicted \({Q}_{i}^{t}\) and observed values \({Q}_{s}^{t}\), normalized by the variance of the observed values during the period under investigation with:

$$\mathrm{NSE}=1-\frac{{\sum }_{t=1}^{T}{\left({Q}_{s}^{t}-{Q}_{i}^{t}\right)}^{2}}{{\sum }_{t=1}^{T}{\left({Q}_{s}^{t}-\overline{{Q}_{s}}\right)}^{2}}.$$
(12)

The range of the NSE lies between 1.0 (perfect fit) and − ∞. An efficiency of lower than zero indicates that the mean value of the observed time series would have been a better predictor than the model. In this case, the imputation method performs worse than a simple imputation based on the mean of the observed data.

Note that the NSE is related to the MSE. It can be interpreted as dividing MSE by the variance of the observations and subtracting that ratio from 1 with

$$\mathrm{NSE}=1-\frac{{\sum }_{t=1}^{T}{\left({Q}_{s}^{t}-{Q}_{i}^{t}\right)}^{2}}{{\sum }_{t=1}^{T}{\left({Q}_{s}^{t}-\overline{{Q}_{s}}\right)}^{2}}=1- \frac{\text{MSE}}{{\sigma }_{{Q}_{s}}^{2}}.$$
(13)

Results and discussion

Streamflow simulation obtained from the HBV model

In the context of hydrological settings, selecting an appropriate imputation method requires careful consideration of the key characteristics of hydrological data (Haile et al. 2023). Hydrological data consist of time series that typically exhibit stable trends over time and high autocorrelation of observations. Additionally, these time series often manifest random fluctuations around the trends, and these fluctuations are not constant over time (Guzman et al. 2013). Given these underlying data features in hydrology, imputing missing values should rely on statistical time series methods that account for the temporal nature of hydrological data.

Several studies have been conducted to evaluate different approaches, including advanced statistical algorithms, for imputing missing values, particularly in streamflow data (Yilmaz and Onoz 2019; Mesta et al. 2021; de Souza et al. 2020; Tencaliec et al. 2015; Khampuengson and Wang 2023; Weilisi and Kojima 2022; Oyerinde et al. 2021; Chapon et al. 2023). However, the impact of seasonality and periodicity of streamflow discharge on the effectiveness of these imputation methods has not been well-documented.

Below, we briefly summarize the simulated time series \({Q}_{s}^{t}\) we obtained from applying the HBV model to the original input data obtained from Brandenburg and the derived precipitation time series. In total, we simulated five different discharge time series. Figure 7 presents \({Q}_{\mathrm{seasonal}}^{t}\) as well as \({Q}_{\mathrm{non}-\mathrm{seasonal}}^{t}\) based on the original as well as the de-trended precipitation data. Note, that \({Q}_{\mathrm{non}-\mathrm{seasonal}}^{t}\) unsurprisingly displays much less pronounced seasonality patterns than \({Q}_{\mathrm{seasonal}}^{t}\). Remaining seasonality effects are due to seasonality in the other input variables, temperature and evapotranspiration.

Fig. 7
figure 7

Simulated discharge output data with/without seasonality

Full size image

Figure 8 presents the time series of the simulated discharge data which are based on precipitation inputs with manipulated variance, i.e., \({Q}_{\mathrm{low}}^{t}\), \({Q}_{\mathrm{high}}^{t}\) and \({Q}_{\mathrm{noise}}^{t}\). Note, that \({Q}_{\mathrm{low}}^{t}\) displays much less variance than \({Q}_{\mathrm{high}}^{t}\) and \({Q}_{\mathrm{noise}}^{t}\). Since white noise is added to the input data P_high for creating P_noisy, \({Q}_{\mathrm{noise}}^{t}\) is characterized by higher fluctuations than \({Q}_{\mathrm{high}}^{t}\) but preserves its mean.

Fig. 8
figure 8

Simulated discharge output data with different variances

Full size image

Mean Squared Error

In a first step, we evaluate how the different imputation mechanisms perform by applying the MSE criterion discussed above before moving on to the NSE results. All results are presented both graphically (see Figs. 9 and 10) and in tables (see Table 2).

Fig. 9
figure 9

Mean Squared Error of the imputation methods for seasonality

Full size image
Fig. 10
figure 10

Mean Squared Error of the imputation methods for different scenarios

Full size image
Table 2 Results of Mean Squared Error for the different imputation methods
Full size table

Independently of which of the five reference time series \({Q}_{s}^{t}\) we focus, clear patterns from the imputation simulations emerge. First, the MSE monotonously increase in the share of data points that are missing from a data set, irrespectively of the imputation technique applied. This is unsurprising, as by definition, a smaller share of missing values implies a higher share of identical values in both the reference time series \({Q}_{s}^{t}\) and the imputed time series \({Q}_{i}^{t}\) and hence a smaller MSE. Moreover, most imputation methods perform better in cases where only few observations are missing as the approximations for the missing values will be based on a relatively larger number of complete observations.

Second, we observe clear performance differences in the different types of imputation techniques used. Most importantly, imputation techniques that ignore the time series character of the data to be imputed perform significantly worse than imputation methods that explicitly take the time series nature of the data into account. In particular, both the results from arithmetic mean imputations as well as the results from OLS-based imputations are characterized by similarly high MSEs relative to the other methods.

Imputations techniques that account for the time series nature of the data (preceding value, ARIMA and ARCH) perform significantly better in terms of MSE. In fact, their MSEs are by a factor of 20–40 times smaller than the MSEs observed for mean imputation and OLS-based imputation (see Table 2). Within the approaches that exploit the time series structure of the data, the flexible ARCH model performs best with its MSEs being clearly smaller than those of the ARIMA model. While the preceding value imputation clearly is superior mean value or OLS-based imputations, it is outperformed by the more sophisticated time series models. Moreover, the outperformance of ARIMA/ARCH models over the preceding value technique is more pronounced in situations where a large fraction of observations is characterized by missing values (see Fig. 10).

It is worth noting that the performance differences across the different imputation methods are independent of the particular characteristics of the reference time series. As discussed above, we evaluated the performance of the different imputation techniques using five reference time series which differ regarding the existence of seasonal trends and their variance. The ranking and the relative difference between the five tested imputation methods are similar across all five reference time series.

Not surprisingly, however, comparisons of the results within the different imputation methods reveal that their performance depends significantly on the characteristics of the reference time series. The higher the variance of the reference time series is, the more challenging imputation becomes and MSEs within a given imputation technique increase for reference time series with higher volatility. We also observe that MSEs are higher if seasonal trends are present compared to the MSEs obtained for the reference time series where we removed seasonality. Moreover, one cannot notice a clear difference between MSEs obtained from the imputation methods in response to varying missing data percentage (i.e., 5–40%) (Table 2). For instance, MSEs of OLS obtained under no seasonality differ from 0.0003 to 0.004. It should be, however, noted that the MSEs obtained from ARIMA and ARCH are much smaller; for example they change from 0.000006 to 0.0001 as resulted from ARCH under no seasonality. Shi et al. (2017) found that even with a high missing ratio (90%), the calculated Root Mean Squared Error (RMSE) remains small, corroborating our findings.

Nash–Sutcliffe efficiency

In addition to using the MSE criterion, we also evaluate the performance of the different imputation methods by applying the NSE criterion. Note that given the NSE is a function of the MSE (with \(NSE=1- \frac{\text{MSE}}{{\sigma }_{{Q}_{s}}^{2}}\)), the patterns discussed above hold also when the NSE criterion is applied.

Indeed, and most importantly, imputation methods that acknowledge the time series nature of the reference data (preceding value, ARIMA and ARCH) perform significantly better than the other methods (mean imputation and OLS) with the flexible ARCH model achieving NSEs that are closest to the maximum possible (see Figs. 11, 12 and Table 3). Supporting our findings, Tencaliec et al. (2015) found that their dynamic regression model, which is a combination of ARIMA and regression models, demonstrated its capability to provide reliable estimates for missing data in eight daily streamflow datasets of the Durance river watershed. The effect of an increasing variance/seasonality on the performance is different when the NSE criterion is applied in comparison with the MSE criterion because the NSE criterion uses the reference time series’ volatility as normalizing denominator in its definition. As a result, the observed NSE values across different volatility scenarios are less sensitive to changes in the volatility of the underlying reference data than the MSE.

Fig. 11
figure 11

Nash-Sutcliffe efficiency of the imputation methods for seasonality

Full size image
Fig. 12
figure 12

Nash-Sutcliffe efficiency of the imputation methods for different scenarios

Full size image
Table 3 Results of Nash–Sutcliffe efficiency for the different imputation methods
Full size table

Application of ARIMA and ARCH models for groundwater time series

We found that ARIMA and ARCH models perform significantly better in imputing missing hydrological data than alternative and widely used methods that do not consider the characteristic of time series data. In this section, we additionally apply ARIMA and ARCH models to groundwater time series which observed in the vicinity of Lake Bötzsee (Fig. 1).

The region is about 20 km northeast of Berlin, also in Brandenburg in Northeast Germany in the time period from January 2012 to May 2014. We do so to validate the performance advantage of time series models in an additional context beyond the streamflow discharge used in this study. In this endeavor, we not only model the observed groundwater time series (GWBR1) to impute missing values following the identical approach described above, we also model artificially smoothed versions of the observed groundwater time series to analyze how different degrees of volatility in a time series affect the relative performance of ARIMA and ARCH models.

We have three additional time series that have been smoothed by Moving Average (MA) processes by three different levels (MA101, MA501, MA1001). Figure 13 shows the four different groundwater time series. The results from this exercise are relatively clear and can be summarized as follows: ARCH models consistently outperform ARIMA models in their imputation performance also in this setting. Additionally, the performance differences between ARIMA and ARCH models seem to be relatively unaffected by the applied smoothing.

Fig. 13
figure 13

Observed groundwater time series from a piezometer in the vicinity of Lake Bötzsee and three smoothed time series

Full size image

The detailed results for comparisons according to the MSE can be found in Table 4, whereas comparisons according to the NSE criterion can be found in Table 5.

Table 4 Mean Squared Error of imputation application for groundwater time series
Full size table
Table 5 Nash–Sutcliffe Efficiency of imputation application for groundwater time series
Full size table

Figure 14 clearly demonstrates that ARCH models are characterized by lower MSEs than ARIMA models. While the relative advantage of using ARCH models for imputation in the context of groundwater data is relatively small for low shares of missing data. Figure 14 shows that with increasing share of missing data, ARCH models outperform ARIMA models more significantly. This reflects the findings that we presented with respect to the simulated discharge data. The pattern of a bigger relative advantage of ARCH models can also be found in the smoothed time series (MA101, MA501 and MA1001).

Fig. 14
figure 14

Graphical results of Mean Squared Error of ARIMA/ARCH

Full size image

As before, higher shares of missing values are accompanied by a bigger relative advantage of ARCH models (see Fig. 14 and Table 4).

Regarding the NSE, we report similar results (see Table 5). For low shares of missing values the imputation performance of both ARCH and ARIMA is very similar. For increasing shares of missing data, however, ARCH models achieve significantly higher NSEs than comparable ARIMA models. Again, this pattern does not affect the degree of smoothing applied to the time series as can easily be seen in Fig. 15.

Fig. 15
figure 15

Graphical results of Nash-Sutcliffe Efficiency of ARIMA/ARCH

Full size image

Not surprisingly, the performance of both ARIMA and ARCH models increases with higher levels of autocorrelation in the time-series data to be modeled. This is intuitive as an increase in autocorrelation makes the behavior of the time series more “predictable”: the value of y if period t has a stronger link to past values and can therefore be approximated with higher precision. In Table 6 and Fig. 16 we report detailed findings comparing the performance of not only ARIMA and ARCH models but also relatively simple methods in the case of 40% of the observations are missing for different levels of autocorrelation.

Table 6 Mean Squared Error of imputation application when data have 40% missing
Full size table
Fig. 16
figure 16

MSE of imputation application when data have 40% missing

Full size image

Note that the original time series GWBR1 is characterized by modest levels of autocorrelation, while the smoothed time series MA101, MA501 and MA1001 are characterized by increasing levels of autocorrelation. It can be clearly seen that the performance of these methods increases with increasing levels of autocorrelation and is highest for MA1001—which is the time series with the highest levels of autocorrelation.

Taie Semiromi et al. (2019) used Singular Spectrum Analysis (SSA) and Multichannel Singular Spectrum Analysis (MSSA) to fill gaps in groundwater level data from 25 piezometric stations in Ardabil Plain, Iran. Both methods effectively imputed missing groundwater levels. MSSA performed better for piezometers showing strong spatial correlation with groundwater level data from other stations, as it takes advantage of this correlation. On can draw a conclusion that as both ARIMA and ARCH are not dependent on the spatial correlation, they can be used effectively to impute the missing values of groundwater level in remote areas, where a sparse network of piezometers/observation wells is established.

Assessment of the imputation methods considering the nature of time series

ARMA and ARCH as two methods take into account characteristics of time series when being used for imputation of missing values of time series. Results show that ARCH and ARIMA with the average of MSEs 0.0000704 and 0.0000828, respectively yielded the best performance in filling the gap data of  the streamflow under without seasonality condition. Similarly, in comparison with ARIMA, ARCH could demonstrate its capability in imputation of the streamflow missing data with the average of MSEs 0.0003487, 0.0000663, 0.0015667, and 0.0028448 under seasonality, low and high variance, and high variance (white noise) conditions, respectively.

Regarding the other evaluation metric, i.e. NSE, ARCH outperformed ARIMA with the average of NSEs 0.9957710, 0.9947722, 0.9982036, 0.9965222, 0.9966348, which were obtained under without seasonality, seasonality, low and high variance, and high variance (white noise) conditions, respectively. Nonetheless, it should be noted that the difference between ARCH and ARIMA in terms of performance is subtle, with the biggest difference noticed under high variance condition with the average of NSEs 0.9965222 and 0.9936020 for ARCH and ARIMA, respectively. The outperformance of ARCH could be associated with capturing and incorporating the volatility of the streamflow time series, leading to improved accuracy in imputing missing data (Modarres and Ouarda 2013).

In the same vain, ARCH and ARIMA exceled their capability to impute the missing values of the other hydrological time series, i.e., the groundwater level data. Results showed that ARCH could produce the best performance with the average of MSEs 0.000635040, 0.000001120, 0.000000052, and 0.000000021, which were resulted under GWBR1, MA101, MA501, and MA1001 conditions, respectively.

The same holds true according to the average of NSEs resulted from applying ARCH for the imputation of the groundwater missing data. To that respect, the average of NSEs tend to 1 and are 0.9971351, 0.9999932, 0.9999996, and 0.9999998 under GWBR1, MA101, MA501, and MA1001 conditions, respectively.

According to our best knowledge, there is only one study, conducted by Wang et al. (2005), in which both ARIMA and ARCH have been tested in modelling the streamflow processes. They showed that the primary cause of the ARCH effect is the seasonal variability in the residual series’ variance. However, this seasonal variance can fully explain the ARCH effect in monthly streamflow data but only partially explains it for daily flow data. Moreover, while the Periodic Autoregressive Moving Average (PARMA) model suffices for modelling monthly flows, none of the conventional time series models are suitable for capturing daily streamflow processes due to their failure to consider both the seasonal variation in variance and the ARCH effect in the residuals.

To address these limitations and accurately capture the complexities of daily streamflow data, they proposed a new approach, called the ARMA–GARCH (Generalized Auto Regressive Conditional Heteroscedasticity) error model. This model aims to account for the presence of the ARCH effect in daily streamflow series while preserving the seasonal variation in variance in the residuals. The ARMA–GARCH error model combines an ARMA model to handle the mean behavior and a GARCH model to address the variance behavior of the residuals derived from the ARMA model. By incorporating both elements, the ARMA–GARCH model presents a more comprehensive solution for effectively analyzing and modelling daily streamflow data.

Summary and conclusion

Complete time series data are a necessary precondition for most statistical and hydrological modelling in hydrology, including model calibration/validation, determination of the flow duration curve, autocorrelation function, spectrum analysis, hydroclimate extreme value analysis based on the generalized extreme value distribution of annual blocks, principal component analysis, etc. In these cases, researchers need to resort to imputation methods to replace missing values with approximations as these statistical approaches require gap-free dataset.

In this paper, we evaluated the performance of five different imputation methods. To that end, we created five time series of discharge data that exhibit different patterns of volatility using the HBV model. From these reference time series, we randomly deleted a given share of observations to be imputed by the different approaches whose performance has been evaluated by the MSE and the NSE criteria. Our findings reveal that imputation methods that neglect the time series nature of the underlying reference data perform significantly worse than imputation methods that exploit this feature of the data. Moreover, advanced time series methods such as ARCH significantly outperform relatively simple time series method such as the preceding value imputation.

ARMA and ARCH are two methods that consider the characteristics of time series when used to impute missing values. The results indicate that when filling the gap data of streamflow without seasonality, ARCH and ARIMA achieved the best performance with average MSEs of 0.0000704 and 0.0000828, respectively.

In scenarios with seasonality, low and high variance, and high variance (white noise), ARCH showed its capability in imputing the streamflow missing data, outperforming ARIMA. The average MSEs for ARCH were 0.0003487, 0.0000663, 0.0015667, and 0.0028448 under these respective conditions.

Regarding another evaluation metric, NSE, ARCH consistently outperformed the other imputation methods. The average NSEs for ARCH were 0.9957710, 0.9947722, 0.9982036, and 0.9966348 for scenarios without seasonality, with seasonality, low and high variance, and high variance (white noise), respectively.

It is worth noting that the performance difference between ARCH and ARIMA is generally subtle, with the most noticeable disparity observed under the high variance condition, where ARCH achieved an average NSE of 0.9965222, compared to 0.9936020 for ARIMA.

Similarly, in the case of imputing missing values in the groundwater level data, both ARCH and ARIMA demonstrated their proficiency. However, ARCH exhibited superior performance with average MSEs of 0.000635040, 0.000001120, 0.000000052, and 0.000000021 under GWBR1, MA101, MA501, and MA1001 conditions, respectively.

Moreover, when considering NSE as the evaluation metric, ARCH consistently outperformed other imputation methods for the groundwater data. The average NSEs approached 1, with values of 0.9971351, 0.9999932, 0.9999996, and 0.9999998 recorded under GWBR1, MA101, MA501, and MA1001 conditions, respectively. These high NSE values indicate the effectiveness of ARCH in accurately imputing the missing groundwater level data.

These findings are important for number of reasons: first, hydrological data are by their definition time series data that are typically characterized by typical feature such as autocorrelation and seasonality. In the presence of these features, the results obtained from commonly used imputation methods such as the wide-spread mean-value imputation can be improved significantly. As our study clearly reveals, even a relatively simple imputation algorithm that exploits the time series nature of the data—the preceding value approach—performs significantly better.

Second, we were also able to demonstrate that advanced regression-based time series imputation method such as ARIMA and ARCH models yield better results than the relatively simple preceding value imputation. While the latter is easy to implement and still performs much better than mean-value or OLS imputation techniques, imputation results can be optimized by relying on advanced econometric techniques. This is true in particular in situations where a large fraction of observations is characterized by missing values. The larger the share of missing values the higher the performance advantage of advanced time series methods. The performance advantage of econometric time series methods is noteworthy as—as of now—their application in hydrological settings still is.

As hydrological data often exhibit autocorrelation, stable trends, and varying variances over time, the ARCH model is designed to account for time-dependent changes in variance, making it well-suited for capturing the volatility and fluctuations present in hydrological time series data. Normally, streamflow and other variables may display different levels of volatility and exhibit heteroscedasticity, which means that the variance of observations is not constant over time, especially in response to changing weather patterns and seasonal effects. Thus, the ARCH model can help in capturing such volatility, enabling more accurate imputations and making it more appropriate for handling data with varying levels of uncertainty. Overall, the ARCH model's ability to capture time series characteristics and handle varying variances makes it a valuable tool for imputing missing values in hydrological studies, enhancing the reliability of data analysis and decision-making in this field.

Despite the overall encouraging findings there are, however, some caveats to be mentioned. On the conceptual level, our results have been obtained using data from only one application area (Brandenburg) and the results might differ for data obtained from other catchments. To ameliorate concerns regarding the broader applicability of our results, we varied the original data to obtain four additional time series that exhibit different volatility/seasonality characteristics. The results obtained are robust towards these variations. On the practical level, the implementation of the advanced econometric models (ARIMA and ARCH) requires statistical software packages such as R or STATA as these model typically are not implemented in standard hydrological software packages.

In addition, despite the fact that ARCH assumes that the data exhibit conditional heteroscedasticity, meaning that the variance of the data is related to past values, streamflow data may not always exhibit such volatility patterns, leading to potential inaccuracies in imputations. Estimating the parameters of the ARCH model can be computationally demanding, especially for large and complex datasets. This complexity may make the model less practical for routine imputation tasks.

As ARIMA assumes that the data are stationary, streamflow data often exhibit trends and seasonality, violating the stationarity assumption. In such cases, the ARIMA model may not provide accurate imputations. ARIMA can handle simple seasonal patterns, thus struggling with complex seasonal variations and irregularities that are common in streamflow data. This can lead to suboptimal imputations in cases of highly seasonal streamflow patterns. Choosing the appropriate orders (p, d, q) of the ARIMA model requires expertise and careful analysis of the data. An incorrect choice of parameters can result in poor imputations and misleading conclusions.