Derivation of heterogeneous material distributions and their sensitivity to HM-coupled two-phase flow models exemplified with the LASGIT experiment

Abstract

Advective gas transport in bentonite, a possible buffer material in repositories for radioactive materials, is difficult to simulate in numerical continuum models, partly due to the complicated microstructure of bentonite. To generate reliable models of repositories nevertheless, spatially distributed heterogeneous material properties can be used to allow localization of gas flow. In this study, a pore-size-dependent stochastic approach of the gas entry pressure is derived from Mercury Intrusion Porosimetry, which is used to replicate measurements from the LASGIT experiment. In addition, three benchmark tests are simulated to investigate the dependence of heterogeneous distributions of material properties on the mesh discretization, the temporal dependence, and the coupling between the processes influenced by the heterogeneous parameters. The numerical modeling results of the LASGIT experiment show that the onset of gas flow into the system and the subsequent increase in pressure and stress can be well reproduced using heterogeneous distributions. Compared to a model with homogeneous material properties, heterogeneous distributions may allow the generation of dilatancy-controlled microfractures—an important feature with regard to the advective gas flow in bentonites. However, it can be observed that the heterogeneous distributions in LASGIT are less significant, as technical gaps or differences in material types could have a greater impact.

Introduction

Predicting gas flow in low-permeable, saturated materials is a challenging but important task in the risk assessment of a deep geological repository (DGR), the widely accepted approach to deal with high-level radioactive waste (Guo and Fall 2021). The long-term safety in a DGR is ensured through a multi-barrier system provided by engineered barrier and natural barrier systems (Wikramaratna 1993). In most multi-barrier system concepts in crystalline and clay rock, argillaceous materials (clay rock or bentonite) are envisaged to use for barrier elements. Argillaceous material is suitable for isolating the waste container from the surroundings due to its swelling capacity, low permeability, and high absorption capacity (Brú and Pastor 2006; Seiphoori 2015). Therefore, it is important to maintain the barrier integrity throughout the life of a repository. However, in the post-closure phase of a DGR, gas can be generated due to several processes, i.e., water radiolysis, microbial reaction, and metal corrosion (Weetjens and Sillen 2006). Since gas migration is very limited in the barrier system, the emerging gas may accumulate in the vicinity of the DGR and the gas pressure may rise to a critical level where micro- or even macro-fractures form (Bai et al. 1999). These fracture processes are associated with dilatation of the material, which is why they are often referred to as dilatancy-controlled. Gas-induced fractures may impair the barrier integrity by establishing flow paths for the surrounding groundwater. Therefore, the study of dilatancy-controlled gas flow is important for the safety analysis of a DGR.

Dilatancy-controlled gas flow in bentonite is characterized by different hydro-mechanical (HM) processes, which are unique in comparison to conventional two-phase flow. Gas flow is restricted to the so-called preferential pathways, where intrinsic permeability is greatly increased compared to the undisturbed pore space (Cuss et al. 2014). Experimental results show that these preferential pathways are created by gas pressure in a series of microfractures called fingering. The aperture of the pathways is hereby a function of the effective stress in the solid matrix, which controls its opening and closing (Harrington et al. 2017). Dilatant flow paths occur almost immediately when the gas pressure is near or above the minimum principal stress. In experiments where volume dilation is constrained, the threshold for the occurrence of gas microfractures is the sum of the confining pressure and the water pressure (Gerard et al. 2014). Gas breakthrough has become a common term for the first measured gas leakage in tests where the gas outflow is monitored. Gas breakthrough is usually accompanied by a sharp increase in pore pressure and total stress (Harrington et al. 2017). The dilatancy-controlled gas flow that occurs in bentonite dominates the flow behavior, but its HM coupling is very complicated and difficult to simulate due to the scaling of the process.

Numerical studies of dilatancy-controlled gas flow apply various constitutive models to simulate the HM coupling between unsaturated fluid flow, solid matrix deformation, and fracture aperture. There is a great variety in numerical approaches to model preferential pathways implicitly or explicitly (Cardoso et al. 2020; Damians et al. 2020; Guo & Fall 2019). Numerical methods for explicit fracture evolution are of great importance for detailed fracture processes, but are expensive to compute and rarely appropriate to large-scale application processes (Guo and Fall 2021). Conceptual models based on equivalent porous media which couple solely intrinsic permeability with gas pressure, effective stress, porosity, or strain are capable of reproducing some measurements of laboratory experiments and large-scale observations, but are rarely capable of simulating localized gas flow.

To simulate localized gas flow, stochastic methods are used in some models. Damians et al. (2020) used spatial distributions for intrinsic permeability, fracture width, and water retention curve parameters combined with an embedded fracture model. Guo and Fall (2019) employed spatial distributions for mechanical properties, i.e., Young’s modulus and critical tensile stress, and hydraulic properties, i.e., intrinsic permeability and gas entry pressure in combination with the phase field method. In Radeisen et al. (2022), the authors used spatial distributions of Young’s modulus and gas entry pressure applied with a deformation-dependent permeability model. All approaches yielded reasonable results when compared to experimental measurements. Most parameters describing the spatial distributions were selected based on literature data and assumptions. Although some sensitivity analyses were performed for all approaches, a comprehensive analysis of the effects of each spatial distribution was not performed.

Sensitivity studies are an important means of confirming and calibrating the methods used. With regard to localized gas flow in otherwise low-permeability material, the discretization of the domain might be very important. Therefore, the analysis of stochastic methods should pay particular attention to a suitable discretization. Due to the strong coupling of the processes involved in gas pressure-induced fluid transport, the verification of stochastic methods used must be carried out in various configurations. Comparisons of individual processes with analytical solutions show the relative deviation from the solution in the homogeneous case. The comparison of calculations with several heterogeneous distributions of material properties also reflects the coupling of the processes involved with each other and the magnitude effects. These sensitivity tests are a good tool for assessing the validity of the approaches used.

This paper presents a comprehensive sensitivity analysis of heterogeneous distributions of the gas entry pressure and Young’s modulus. First, in the general part, laboratory and in-situ measurements are used to make predictions about possible heterogeneous distributions of material properties. In the sections “Benchmark 1: Terzaghi consolidation test” and “Benchmark 2: Mc Whorter and Sunada test case”, two benchmark tests are used to perform sensitivity analyses of heterogeneous distributions of the hydraulic and mechanical processes, respectively. In the section “Benchmark 3: coupling between HM processes with heterogeneous distributions”, the effects of the heterogeneous material distributions and the processes involved are compared with regard to their effects on the gas flow. The section “Large-scale application” presents the Large-Scale Gas Injection Test (LASGIT) experiment and the approach for the numerical model using pore-size-related heterogeneity. LASGIT is a full-scale gas transport test performed at the Äspö Hard Rock Laboratory in Sweden based on the Swedish KBS-3 V repository concept (SKB 2016). The section “Results” shows the results for different simulations regarding the LASGIT experiment. The section “Discussion and conclusion” addresses potential problems with the application of the approach to a large-scale model and concludes the findings of the work. All numerical simulations were performed with the numerical code OpenGeoSys (OGS).

Modeling approach

Material heterogeneity

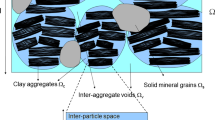
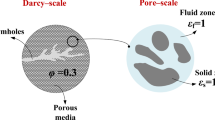
Various laboratory and in-situ studies have demonstrated the influence of heterogeneity and micromechanics in low-permeability materials: In a large-scale experiment with a compacted and saturated bentonite, it was found that significant water content and dry density differences were present throughout the barrier after 18 years of operation (Fraser Harris et al. 2016; Villar et al. 2020). The authors concluded that the bentonite barriers must be irreversibly inhomogeneous. Similar observations were made by Brú and Pastor (2006) for repacked bentonite and by Darde et al. (2022) for saturated pellet-based bentonite. This work focuses on the HM-related processes response of low-permeable materials based on spatial distributions of the Young’s modulus E and gas entry pressure p_entry. Mechanical and capillary processes can both effect the gas breakthrough and migration process in low-permeability materials. Using mechanical and hydraulic material parameters, individual aspects of the involved processes and their coupling can be investigated separately. The heterogeneous distributions are important to enable the formation of preferential pathways in combination with constitutive equations. In the following, the probability curves of the material parameters are derived from experimental values, more precisely from the pore size density (PSD). The pore size density is used to identify the dominant pore modes and also to analyze the porosity and void ratio in the structure (Seiphoori 2015).

Mercury Intrusion Porosimetry (MIP) can be used to investigate the PSD of a material. Seiphoori (2015) did this, for example, for MX-80 bentonite (Fig. 1). Figure 1 shows three different PSDs for states of saturation of MX-80 bentonite: compacted but dry (A), compacted and with a saturation of S_w = 0.60 (B) and compacted and fully saturated (C). These PSDs are the basis for deriving the gas entry pressure and Young’s modulus in the following.

Fig. 1

Pore size density in relation to different pore size diameters for three states: compacted but dry (A) with equal amounts of micropores and macropores, compacted and partially saturated (B) with twice as many of micropores than macropores, and compacted and fully saturated state (C) with mainly micropores (edited after Seiphoori 2015)

Water retention curve

In unsaturated porous mediums, the relation between water pressure, gas pressure, and saturation can be described using water retention curves. The effects described by water retention curves increase with a decrease of the pore spaces, due to a stronger capillarity. The main parameter describing the water retention curve is the capillary pressure (p_c) or suction. Capillary pressure is defined as the pressure difference between the non-wetting phase and the wetting phase in a two-phase porous medium. This relation can be expressed as follows:

$${p}_{\mathrm{c}}={p}_{\mathrm{g}}-{p}_{\mathrm{w}},$$

(1)

where p_g is the pressure of the gaseous phase (non-wetting phase) and p_w is the pressure of the liquid phase (wetting phase). The relation between capillary pressure and effective degree of water saturation is characterized by the water retention curve and a material parameter called gas entry pressure (p_entry). The gas entry pressure represents the pressure of the non-wetting phase at which it is starting to enter a porous medium. There are several models for a water retention curve (Zhu et al. 2022); here, the van Genuchten’s equation (van Genuchten 1980) is applied, which is expressed for the capillary pressure as follows:

$${p}_{\mathrm{c}}=\left\{\begin{aligned}&{}{p}_{\mathrm{entry}}{\left({S}_{\mathrm{e}}^{\frac{-1}{m}}-1\right)}^\frac{1}{n}, &{}0<{S}_{\mathrm{e}}<1\\ &{}0, &{}{S}_{\mathrm{e}}=1\end{aligned},\right.$$

(2)

where m and n are both empirical van Genuchten material parameters, related as m = 1–1/n. Values of m = 0.5 and n = 2 can be assumed for an MX-80 bentonite (Villar 2005). S_e is the effective degree of saturation and can be expressed as follows:

$${S}_{\mathrm{e}}=\frac{{S}_{\mathrm{w}}-{S}_{\mathrm{r}}}{{S}_{\mathrm{w},\mathrm{max}}-{S}_{\mathrm{r}}},$$

(3)

where S_w is the saturation of the wetting fluid and S_r is the residual saturation. At the microscopic level, the capillary pressure can be described according to the Young–Laplace equation (Laplace 1806; Young 1805) as a function of the pore throat width/radius as follows:

$${p}_{\mathrm{c}}=\frac{{2T}_{\mathrm{s}}\mathrm{cos}\left(\theta \right)}{a},$$

(4)

where T_s = 0.072 N/m is the surface tension of the wetting fluid, θ is the angle between the wetting fluid and the solid phase, and a is the radius of the pore throat. To derive the gas entry pressure from the Young–Laplace equation, the constant state of quasi-full saturation (θ = 0°) is assumed. Since the gas entry pressure corresponds to the gas pressure that must be applied for the gas phase to enter the pore space, the gas entry pressure can be derived using Eqs. (1) and (4) as follows:

$${p}_{\mathrm{entry}}=\frac{2{T}_{\mathrm{s}}}{a}+{p}_{\mathrm{w}}.$$

(5)

Equation (5) shows that the gas entry pressure depends on the radius of the pore throat and the water pressure. The derivation for the gas entry pressure at quasi-full saturation and constant water pressure is calculated here. For the process of gas percolation through a fully saturated compacted bentonite, most parameters can be determined directly. Using the PSD of the compacted and fully saturated state (Fig. 1), relative proportions of pore sizes can be estimated. The relative proportions of the pore sizes can be applied in Eq. (5), which allows a pore size-related stochastic distribution to be calculated for the gas entry pressure. Several derived distributions are examined in the following benchmarks. When carrying out this approach, it is important to set the maximum saturation to S_{w, max} = 1, since the non-linear behavior of the retention curve leads to a very steep curvature near full saturation.

Young’s modulus variability

Young’s modulus represents the compressive or tensile stiffness in the elastic mechanical region. It is influenced by several factors such as the density, porosity, and microstructure of the material. For an isotropic elastic material, two elastic properties can be used to fully describe the mechanical regime with the following equation:

$$E=2G\left(1+\nu \right)=3K\left(1-2\nu \right),$$

(6)

where G is the shear modulus, ν is the Poisson’s ratio, and K is the bulk modulus. The here applied numerical code OGS requires the input of both the Poisson’s ratio and the Young’s modulus to describe elastic deformation. To determine the distribution curves of Young's modulus, the variability of the dry density is selected as the determining parameter. The dry density is related to the Young's modulus (at higher dry densities, the Young's modulus is higher) and can be measured directly or determined indirectly from the swelling pressure. To analyze the dry density of a compacted bentonite, Saba et al. (2014) conducted a laboratory experiment in which the swelling pressure was measured in different locations during 350 days. During the experiment, the swelling of the bentonite is first in all directions restricted. At a later stage, one axial piston is released and swelling is allowed in this direction. After 58 days, a dry density variability of ρ_d = 1650–1750 g/m³ is measured. At the end of the experimental observation, the authors report that the sample was not homogeneous even after 350 days.

It is reported that the relation between dry density and Young’s modulus might have an exponential form (Zhang 2021). However, there is no clear correlation between these two values for bentonite. There has also been little research on this topic, although a clear relation between the mechanical properties and hydraulic properties in bentonite has been established in many studies (Cardoso et al. 2020; Harrington et al. 2018; Senger et al. 2018). To derive a distribution from pore size measurements, a variant of the Gibson–Ashby model (Gibson et al. 1982) is used to predict Young’s modulus based on Fig. 1

$$E=\overline{E }{\left(\frac{\overline{d}}{d }\right)}^{3}.$$

(7)

Balance equations

Basic balance equations of a porous domain for HM processes are employed for all numerical simulations. The coupled processes satisfy the following equations at all times. The momentum balance equation derived from the effective stress law can be expressed as follows (Wang et al. 2010):

$$\nabla \cdot \left[{{\varvec{\upsigma}}}^{\mathrm{^{\prime}}}-\alpha \left({p}_{\mathrm{g}}-{S}_{\mathrm{w}}{p}_{\mathrm{c}}\right)\mathbf{I}\right]+\rho \mathbf{g}=0,$$

(8)

where $\nabla$ is the Nabla operator, σ′ is the effective stress, α is the Biot coefficient, I is the identity tensor, ρ is the bulk density, and g is the gravitational acceleration. Assuming an isothermal two-phase flow process, in which the wetting phase behaves as an immiscible Newtonian fluid, the balance equation for the wetting phase can be expressed as follows:

$$\phi {\rho }_{\mathrm{w}}\frac{\partial {S}_{\mathrm{w}}}{\partial {p}_{c}}{\dot{p}}_{\mathrm{c}}+\alpha {\rho }_{\mathrm{w}}{S}_{\mathrm{w}}\nabla \cdot \dot{\mathbf{u}}+\nabla \cdot \left[{\rho }_{\mathrm{w}}\frac{{\mathbf{k}}^{\mathrm{int}}{k}_{\mathrm{w}}^{\mathrm{r}}}{{\mu }_{\mathrm{w}}}\left(-\nabla {p}_{\mathrm{g}}+\nabla {p}_{\mathrm{c}}+{\rho }_{\mathrm{w}}\mathbf{g}\right)\right]={Q}_{\mathrm{w}},$$

(9)

where ϕ is the porosity, ρ_w is the density of the wetting fluid, ${\dot{p}}_{\mathrm{c}}={\mathrm{d}p}_{c}/\mathrm{d}t$ is the temporal derivative of the capillary pressure, and $\dot{\mathbf{u}}=\mathrm{d}\mathbf{u}/\mathrm{d}t$ is the temporal derivative of the displacement vector. k^int is the intrinsic permeability, k^r_w is the relative permeability of the wetting fluid, μ_w is the viscosity of the wetting fluid, and Q_w represents the source and sink term of the wetting fluid. Similarly, the mass balance equation of the gas phase can be expressed as follows:

$$-\phi {\rho }_{\mathrm{g}}\frac{\partial {S}_{\mathrm{w}}}{\partial {p}_{\mathrm{c}}}{\dot{p}}_{\mathrm{c}}+\alpha {\rho }_{\mathrm{g}}{(1-S}_{\mathrm{w}})\nabla \cdot \dot{\mathbf{u}}+\phi (1-{S}_{\mathrm{w}})\left(\frac{\partial {\rho }_{\mathrm{g}}}{\partial {p}_{\mathrm{g}}}{\dot{p}}_{\mathrm{g}}+\frac{\partial {\rho }_{\mathrm{g}}}{\partial {p}_{\mathrm{c}}}{\dot{p}}_{\mathrm{c}}\right)+\nabla \cdot \left[{\rho }_{\mathrm{g}}\frac{{\mathbf{k}}^{\mathrm{int}}{k}_{\mathrm{g}}^{\mathrm{r}}}{{\mu }_{\mathrm{g}}}\left(-\nabla {p}_{\mathrm{g}}+{\rho }_{\mathrm{g}}\mathbf{g}\right)\right]={Q}_{\mathrm{g}},$$

(10)

where ρ_g is the density of the non-wetting fluid, ${\dot{p}}_{\mathrm{g}}=\mathrm{d}{p}_{g}/\mathrm{d}t$ is the temporal derivative of the gas pressure, k^r_g is the relative permeability of the non-wetting fluid, μ_g is the viscosity of the non-wetting fluid, and Q_g represents the source and sink term of the non-wetting fluid. Note that all balance equations are formulated with the primary variables u, p_g and p_c. Detailed derivations of the balance equations can be found in (Kolditz et al. 2012).

Constitutive equations

Let $\Omega \in {\mathbb{R}}^{n}, 1\le n\le 3$ be the reference domain of an elastic isotropic domain. According to Biot’s theory (Biot 1941), the consolidation process must satisfy the following system of equations for all time t Є (0, T):

Hooke’s law for an isotropic material:

$${\varvec{\upsigma}}=2\mu \varepsilon +\lambda \mathrm{tr}\left(\varepsilon \right)\mathbf{I}\, \mathrm{in} \,\Omega .$$

(11)

Compatibility condition:

$$\varepsilon \left(\mathbf{u}\right)=\frac{1}{2}\left(\nabla \mathbf{u}+\nabla {\mathbf{u}}^{^{\prime}}\right) \mathrm{in} \, \Omega .$$

(12)

Generalized Darcy’s law:

$${\mathbf{q}}_{\xi }=-{\rho }_{\xi }\frac{{\mathbf{k}}^{\mathrm{int}}{k}_{\xi }^{\mathrm{r}}}{{\mu }_{\xi }}\left(\nabla {p}_{\xi }-{\rho }_{\xi }\mathbf{g}\right),$$

(13)

where q_ξ is the fluid flux, p_ξ is the pressure, and k^r_ξ is the relative permeability of the corresponding phase (w = water, g = gas). The parameter $\lambda =\frac{\nu }{1-2\nu }\frac{1}{1+\nu }E$ and $\mu =\frac{1}{2}\frac{1}{1+\nu }E$ are the first and second Lamé constants, respectively.

Sensitivity analysis

In the following, three benchmarks for mechanical and hydraulic processes are presented on which sensitivity analyses regarding the heterogeneous material properties are carried out. The calculation results are compared with analytical calculations to determine deviations. An evaluation is made with stochastic means such as the standard deviation and the coefficient of determination.

When calculating the standard deviation, the deviations of the values of the material properties in each element from the mean value are determined, summed, and normalized. The following equation is used to determine the standard deviation:

$$s=\sqrt{\frac{1}{n}{\sum }_{i=0}^{n}{\left({x}_{\mathrm{i}}-\overline{x }\right)}^{2},}$$

(14)

where x_i and x̅ are the value of the material property in each element and the mean value of the domain, respectively. The accuracy of the calculations with heterogeneous distributions of the material properties is quantified in the following with the coefficient of determination R²:

$${R}^{2}=1-\frac{\sum_{i}{\left({x}_{i}-\widehat{{x}_{i}}\right)}^{2}}{\sum_{i}\left({x}_{i}-\overline{x }\right)},$$

(15)

where $\widehat{x}$  is the corresponding value of the linear or non-linear regression.

Benchmark 1: Terzaghi consolidation test

A simple one-dimensional consolidation problem, also known as Terzaghi consolidation, is presented here (Terzaghi 1943). The presented test, which is often used for verification of HM-coupled processes (Kolditz et al. 2012), is used here to analyze and compare the pore size-related spatial distributions of Young’s modulus for three saturation states in bentonite. The differences between the distributions and the analytical solution are analyzed in the process. For this purpose, a 2D mesh with 20,000 equally sized square elements is created. The benchmark is defined by the following characteristics:

• Fully saturated porous medium.

• Both sides and the bottom are rigid and impermeable (Fig. 2).

• The top is free to drain and prescribed with a mechanical stress load σ₀.

• The mesh generation is performed by a Galerkin finite-element spatial discretization.

• The time discretization is performed by a first-order finite difference scheme.

• No time dependence.

• Coupled linear equations for pressure p and solid displacement u.

• It is solved monolithically.

Fig. 2

Model domain with boundary conditions and the length in y-direction with the maximum length H

The Terzaghi test describes a simple hydro-mechanically coupled process, in which fluid pressure is generated by mechanical compression. On the other hand, pressure storage and dissipation influence the mechanical state via the effective stress. In this full saturated test, the relative permeability of the water phase is ${k}_{\mathrm{w}}^{\mathrm{r}}=1$. The analytical solution for this test of the effective axial stress can be found in Murad and Loula (1992) as

$${\sigma \mathrm{^{\prime}}}_{yy}=-1+\sum_{n=0}^{\infty }\frac{2}{M}\mathrm{sin}\left(M{y}_{D}\right){e}^{-{M}^{2}{t}_{D}},$$

(16)

where

$${y}_{D}=\frac{y}{H},\quad{ t}_{D}=\frac{\left(\lambda +2\mu \right){\mathbf{k}}^{\mathrm{int}}T}{{\eta }_{\mathrm{w}}{H}^{2}}, \quad M=\frac{1}{2}\pi \left(2n+1\right)$$

(17)

are non-dimensional quantities, and

$${\sigma \mathrm{^{\prime}}}_{yy}=\frac{\sigma }{{\sigma }_{0}}$$

(18)

is the non-dimensional effective stress.

Table 1 shows the model parameters for the Terzaghi test. These can be freely chosen, but correspond to comparable studies (Kolditz et al. 2012). By applying Eq. (7) to the pore size density functions of Fig. 1, different distributions can be generated for the respective saturation state (Fig. 3A–C). The values for the Young’s modulus in theses distributions range from 7 to 60 kPa.

Table 1 Model parameters for the Terzaghi consolidation simulation

Fig. 3

Three different modes of Young's modulus distribution are shown in the left column. The calculated effective stress along the depth of the domain is shown in the middle column. A contour plot of the effective axial stress for each mode is shown in the right column. The modes represent three saturation levels: a compacted but dry bentonite with double porosity (A), a partially saturated bentonite with mainly micropores (B), and a fully saturated bentonite with almost only micropores (C)

The left column of Fig. 3 shows the calculated distributions, with four distributions calculated for each mode. The results of the calculation regarding the effective axial stress were plotted along the depth (y-axis) and are shown in the middle column of Fig. 3. For each simulation per stochastic distribution, 40 lineplots are created. These are averaged and a confidence level of 95% is calculated. The averaged results are shown in the respective colors of the distributions, with the confidence interval marked as an area. The analytical solution is visualized as a black dotted line. The right column shows the effective axial stress in a contour plot of one calculation. The results show that all three stages can approximate the analytical solution. However, the stage representing the fully saturated bentonite has the best agreement with the analytical solution.

Benchmark 2: McWhorter and Sunada test case

A one-dimensional benchmark for the investigation of hydraulic properties is the McWhorter and Sunada test (McWhorter and Sunada 1990). This benchmark analyzes capillary effects of the countercurrent displacement of two incompressible, immiscible fluids. The derivation of the quasi-analytical solution can be found in McWhorter and Sunada (1990). The domain of the benchmark test is initially fully saturated by a non-wetting fluid (Fig. 4). A wetting fluid can enter the domain through an open boundary on the left side. Efflux of the non-wetting fluid occurs at the same boundary and equal in magnitude. All other boundaries are no flow boundaries. Both fluids have the same flow properties (Table 2). The controlling force is the capillary pressure. Gravity is neglected and there are no sources or sinks. In the unsaturated case, capillary pressure, effective saturation, and relative permeability are applied to quantify the relation between the two fluid phases. The capillary pressure and relative permeabilities are parameterized by the Brooks–Corey (Fig. 5) functions, which can be expressed as follows:

$${p}_{c}={p}_{entry}{S}_{e}^{-\frac{1}{{m}_{BC}}}$$

(19)

$${k}_{\mathrm{r}}^{\mathrm{w}}={S}_{\mathrm{e}}^{3+\frac{2}{{m}_{BC}}}$$

(20)

$${k}_{\mathrm{r}}^{\mathrm{g}}={\left(1-{S}_{\mathrm{e}}\right)}^{3+\frac{2}{{m}_{BC}}},$$

(21)

where m_BC is the pore size distribution coefficient. In this case, we assume a pore size distribution coefficient of m_BC = 2.

Fig. 4

Domain of the McWhorter and Sunada test with the initial and boundary conditions ${\left(x, y\right)}^{T}\in {\mathbb{R}}^{2}:\left[0, 2.6\right] \cdot \left[0, 0.5\right]$  

Table 2 Model parameters for the McWhorter and Sunada test

Fig. 5

Relative permeabilities with the Brooks–Corey function

The two-phase flow is controlled by a pressure-pressure regime, i.e., the primary variables in OGS are the gas pressure and the capillary pressure. To simulate the open boundary with full saturation, a capillary pressure of p_c = 0 Pa is applied on the left side of the domain. An initial capillary pressure of p_c,ini = 5 $\cdot$ 10⁴ Pa is applied for the entire domain to account for a full saturation in the initial state. The domain is 2.6 m long and 0.5 m wide. The heterogeneous distributions of the gas entry pressure are generated using Eq. (5) and the PSDs of Fig. 1. Since Eq. (5) is derived for the fully saturated case, only case C from Fig. 1 is calculated in this benchmark (Fig. 6a). The distributions are normalized to a mean gas entry pressure of p_entry = 5 $\cdot$ 10³ Pa. For this benchmark, a mesh with 20,080 square, equally sized elements is created. The properties of the domain can be found in Table 2.

Fig. 6

a Histogram of four distributions for the gas entry pressure, representing the fully saturated state. b Calculated saturation of the wetting phase of the McWhorter and Sunada test. Mean values per simulation are plotted with dark lines; confidence intervals are mapped with light areas. Overlapping confidence intervals have a darker color. c Contour plot of the water saturation of a realization at t = 10,000 s. d Standard deviations of the saturation of the wetting phase to mean standard deviations of the gas entry pressure

To capture the distribution of the entire domain, the values are calculated at a distance of dy = 0.0125 m plotted along the x-axis and then normalized. The mean values (dark line) of each simulation and the confidence interval (light area), with a confidence level of 95%, are presented in Fig. 6b. The contour plot of one simulation is shown in Fig. 6c. Although large differences in water saturation are visible in the contour plot at points with the same x-value, the statistical evaluation in Fig. 6d and the probability areas in Fig. 6b show that, on average, there is good agreement with the analytical values.

Benchmark 3: coupling between HM processes with heterogeneous distributions

Another sensitivity analysis compares the coupling effects of the processes involved when two heterogeneously distributed material properties are used simultaneously. For this purpose, ten stochastic distributions (labeled with an index i from 0 to 9) were created for the gas entry pressure and the Young’s modulus. The random generation of the stochastic distributions was chosen in such a way that the mean values are approximately constant, but the variance increases linearly. One hundred calculations were carried out in which both stochastic distributions varied. The simulations were performed with a rectangular experimental setup (Fig. 7) with a total number of 396 square elements and element sizes of 0.25 m². The experimental setup consisted of two materials:

• Filter material on both sides with high permeability and no displacement, and

• Test material with a low-permeability, elasto-plastic deformation, and a strain-dependent permeability.

Fig. 7

Test geometry for sensitivity analysis

The two-sided interval material consists of a total of 72 square elements, while 324 square elements are used for the test material in between. The properties of the test material roughly correspond to the values of an MX-80 bentonite, which is also used in the LASGIT experiment (Table 3). All sides have no displacement boundary in normal direction. The gas inflow is applied by a gas flow rate of $1\cdot {10}^{-7} \frac{\mathrm{kg}}{\mathrm{s}}$ on the left boundary. A Dirichlet boundary of 0.1 MPa gas pressure is applied on the right side of the domain to ensure the gas outflow. Initial pressures of p_c = 0.1 MPa and p_g = 0.1 MPa are applied in the domain. Full hydro-mechanical coupling is employed, in which quadratic elements were used for the displacement field and linear elements for the pressure field. The total duration of the simulation is $2\cdot {10}^{6}$ s, with a fixed time-stepping scheme of $\Delta t=1000\mathrm{ s}$. This benchmark aims not to represent a realistic behavior or material, but rather analyze the coupling between the two heterogeneous distributions.

Table 3 Model parameters for the benchmark 3 test

In this test setup, it is assumed that displacement in the test material will create microfractures leading to an increased permeability. The applied constitutive model for this process is a strain-dependent permeability function (Xu et al. 2013) which is expressed as follows:

$${\mathbf{k}}^{\mathrm{int}}\left({\varepsilon }_{\mathrm{vol}},{\overline{\varepsilon }}_{\mathrm{p}}\right)={10}^{{b}_{1}{\varepsilon }_{\mathrm{vol}}}{e}^{{b}_{2}{\overline{\varepsilon }}_{\mathrm{p}}}{\mathbf{k}}_{0}^{\mathrm{int}},$$

(22)

where ε_vol is the volumetric strain, ${\overline{\varepsilon }}_{\mathrm{p}}$ is the equivalent plastic strain, and b₁ = 30 and b₂ = 2000 are non-dimensional empirical quantities. The empirical function enables the generation of high permeabilities dependent on the value of the volumetric or equivalent plastic strain. When this model is applied, the mechanical deformation affects the hydraulics and thus the total gas outflow. It reflects the process of dilatancy-controlled flow and the coupling between mechanical and hydraulic parameters.

Since the strain-dependent permeability function is also dependent on the equivalent plastic strain, plasticity is added to the model. The yield-condition used here is the so-called Drucker–Prager criterion (Drucker and Prager 1952). The Drucker–Prager yield criterion is a pressure sensitive plasticity model and can be enhanced by a tension cut-off model. It has a smooth yield surface and was established as a generalization of the van Mises yield criterion. As indicated by Vermeer and De Borst (1984), the Drucker–Prager yield criterion is suitable for stiff clayey material with low friction angles. It can be expressed based on the stress invariants as follows:

$${\Phi }_{\mathrm{pl}}\left({\varvec{\sigma}}\right)=\sqrt{{J}_{2}}+l{I}_{1}-\lambda ,$$

(23)

where

$${J}_{2}=\frac{1}{2}\mathrm{tr}\left({{\varvec{\sigma}}}_{d}^{2}\right)$$

(24)

$${I}_{1}=\mathrm{tr}({\varvec{\upsigma}})$$

(25)

$${{\varvec{\upsigma}}}_{\mathrm{d}}= {\varvec{\upsigma}}-\frac{1}{3}\mathrm{tr}\left({\varvec{\upsigma}}\right)\mathbf{I},$$

(26)

where $l$ and λ are material constants, ${J}_{2}$ is the second invariant of the stress deviator tensor, ${{\varvec{\upsigma}}}_{\mathrm{d}}$ is the deviatoric stress, and ${I}_{1}$ is the first invariant of the Cauchy stress tensor. The material constants $l$ and λ are derived from friction angle $(\varphi$) and cohesion (c) as follows:

$$l=\frac{2\mathrm{sin}\varphi }{\sqrt{3}(3-\mathrm{sin}\varphi )}$$

(27)

$$\lambda =\frac{6c\mathrm{cos}\varphi }{\sqrt{3}(3-\mathrm{sin}\varphi )}.$$

(28)

A tensile cut-off is applied to the yield criterion for the test material. The values for Young’s modulus and gas entry pressure were randomly assigned based on a uniform distribution for all 324 low-permeable elements. While the mean value for both parameter is nearly constant ($\overline{E }=1\cdot {10}^{9}\pm 0.01\cdot {10}^{9};{\overline{p} }_{\mathrm{entry}}=2\times {10}^{5}\pm 0.04\cdot {10}^{5})$, the variance is increased stepwise. As a result, the influence of the variance of both parameters can be compared, based on the calculated total gas outflow volume

$${E}_{i}^{\mathrm{min}}={E}_{0}-\left(5\cdot {10}^{7}i\right),{E}_{i}^{\mathrm{max}}={E}_{0}+\left(5\cdot {10}^{7}i\right)$$

(29)

$${p}_{\mathrm{entry},i}^{\mathrm{min}}={p}_{\mathrm{entry}, 0}-\left({10}^{4}i\right),{p}_{\mathrm{entry},i}^{\mathrm{max}}={p}_{\mathrm{entry}, 0}+\left({10}^{4}i\right).$$

(30)

Figure 8 shows the calculated gas outflow for each distribution pair with one pixel. The highest gas outflow is shown in yellow and lowest outflow in purple. A relative uniformity with respect to the gas outflow can be observed for each stochastic distribution of the gas entry pressure (Fig. 8). In this comparison, the heterogeneous gas entry pressure is clearly the determining factor with regard to the gas outflow. A trend of increasing gas outflow with higher variance of the gas entry pressure is evident. Despite a clear general trend, some simulations show different results. A good example is the model with the stochastic distributions of p_entry,5 and E₈. The calculated gas outflow at this combination of spatial distributions exceeds the calculated values in the column by a factor of 1000 and in the row at least by 100. This shows that very specific combinations can have very strong effects. The reasons for this behavior can be manifold. There can be increased coupling between the different distributions. This coupling ensures that different influences are potentiated and, as in this example, increase the gas flow. Furthermore, a direct path between the two filter ends could be given by good conditions of both material distributions. The material distributions would not have low values on the same elements, but would complement each other in a certain path. An example of this behavior is the distribution pair E₉ and p_{entry, 7} (Fig. 9).

Fig. 8

Calculated total gas outflow for all stochastic distribution pairs

Fig. 9

Spatial distributions E₉ and p_{entry, 7}

The results of an exemplary simulation are shown in Fig. 10. The figure shows the plastic and volumetric deformation, as well as the gas velocity and water saturation. One can clearly see how the area with increased gas velocity starts where there is also a low water saturation, i.e., the gas entry pressure is low. The lower values probably set the condition for the gas to enter and volumetric and later plastic deformation takes place.

Fig. 10

Test simulation with the spatial distributions E₉ and p_{entry, 7}

Large-scale application

Concept

The application of spatial material distributions in a complex system is carried out with the measurements from the Large-Scale Gas Injection Test (LASGIT), an in-situ experiment performed by SKB in the Äspö Hard Rock Laboratory in Sweden. The LASGIT experiment examines the response of a pre-compacted bentonite buffer to the injection of gas in a deposition hole with a length of 8.5 m and a diameter of around 1.75 m (Cuss et al. 2010). This highly instrumented experiment was performing four different gas injection tests over a period of 15 years. The here presented gas injection test is the “LASGIT gas injection test 4”, that starts at approximately 2950 days after the start of the experiment. The processing of this work is carried out within the framework of the DECOVALEX-2023 project, an international research project in which numerical codes are compared and validated (Birkholzer and Bond 2022). The gas injection test 4 of the LASGIT experiment had a duration of approximately 350 days. For more information on the LASGIT experiment, see Cuss et al. (2010).

MX-80 bentonite was used as buffer material for this experiment. The pre-compacted bentonite blocks were placed in the hole between the copper canister wall and the rock wall, which is mainly Äspö diorite. The bentonite blocks had a thickness of about 0.5 m and a difference of outer radius and inner radius of 0.29 m (Fig. 11). There were two technical voids in the structure, one on both sides of the bentonite. The one between the bentonite and the diorite was filled with bentonite pellets. The other one between the copper canister wall and the bentonite was left open. The swelling of the bentonite should close all remaining spaces during hydration.

Fig. 11

Cross-section sketch of the LASGIT experiment (Cuss et al. 2010)

The gas injection test 4 consists of four pressure ramps between which the pressure was kept constant (Fig. 12). The gas pressure was increased with the inflow of water into the injector system (FL903). The gas pressure in the injector reached a maximum value of around 6.2 MPa after 3205 days, after that, a drop in gas pressure was measured in the injection filter due to a gas efflux. A few days after the gas flow event had been detected, the inflow of water into the injector system was reduced in three steps. Using the gas volume in the injector and the gas pressure profile, a Neumann boundary condition was applied to the injection filter in the numerical model.

Fig. 12

Temporal gas pressure evolution in the injection filter of gas injection test 4

A 3D domain with a structured mesh was generated for the spatial discretization. A quarter of the entire LASGIT experiment is recreated. The mesh consist of 21,088 nodes and 19,660 hexahedral elements (Fig. 13a). Six materials are used to recreate the structure of LASGIT experiment (Fig. 13b).

• Three layers (R1—R3) of pre-compacted MX-80 bentonite. The values of the HM parameters correspond to the values measured for LASGIT.

• In the upper third, approximately at the level of bentonite layer R3, a filter material is modeled (FL903).

• A material group describes the swollen bentonite. The selected areas have been filled with bentonite pellets or have been left open before the hydration. For this group of materials, similar values were chosen as for the pre-compacted bentonite, but with some changes due to the reduction of the dry density as a result of the swelling (Table 4):

  • Young’s modulus is reduced by 10%; cohesion and tensile strength are lower than in the bentonite blocks.

  • Permeability is doubled.

  • A pore-size-related distribution of the gas entry pressure is applied for this material group in some models according to Table 7.

• An interface between the bentonite blocks with the same properties as the bentonite blocks, but zero tensile strength.

• The material group representing the Äspö diorite has a permeability of 1·10^–19 m², which was measured by Cuss et al. (2010). There are three areas with a higher permeability in the xy-plane, representing fractures in the rock. These artificial fractures are in z = 0.25 m, z = 0.75 m, and z = 1.25 m.

• The material group representing the copper canister has a very low permeability (k = 1·10^–25 m²) and high mechanical strength.

Fig. 13

Model domain representing part of the LASGIT experiment: ${\left(x, y, z\right)}^{T}\in {\mathbb{R}}^{3}:\left[0, 1.5\right]\cdot \left[0, 1.5\right]\cdot \left[0, 1.5\right]$  

Table 4 Material parameter for LASGIT experiment

Figure 13c shows the locations of the sensors simulated in the model. All sensors are located at the boundary between the swollen bentonite and the granite. Three pore pressure sensors (UR 904, UR905, and UR 909) and three stress sensors (PR 905, PR 908, and PR 909) are located in the quarter section of LASGIT modeled in this work. However, the recorded data show that the localized gas flow enters between the bentonite pre-compacted blocks on the opposite side of the filter. Therefore, not only the measured values in the modeled domain are taken for comparison, but all measured values of the sensors that are located in the bentonite rings R1–R3.

The boundary conditions are presented in Table 5.

Table 5 Boundary conditions of the LASGIT numerical model according to the boundaries in Fig. 13d

The study period begins on day 2950 and ends on day 3300. Due to seasonal variations, stress and pore pressure change continuously during the study period (Fig. 14). These fluctuations are not taken into account in the numerical model, as the effects are negligible for short-term observations. The measured stresses in the study area and study period range from approx. 4.7 MPa (PR907) to 6.3 MPa (PR904). For the pore pressure, values of approx. 1.7 MPa (UR910) to 2.8 MPa (UR904) were measured. To simplify the comparison with the numerical results, the measured values and the numerically calculated values are normalized to their respective values at the beginning of the study period (t = 2950).

Fig. 14

Stress on the rock wall and pore pressure of the selected sensors in the LASGIT experiment

Model variations and parameters

Three models were run to simulate the stress and pressure developments of the LASGIT experiment. The base case is an isotropic and homogeneous poroelasticity model without considering the swelling deformation of bentonite blocks and pellets. The initial conditions of the domain $\Omega \in {\mathbb{R}}^{3}$ can be described as follows:

$${p}_{c,0}=0.4\,\mathrm{ MPa}\to {S}_{\mathrm{w},0}=0.998\,\mathrm{ in }\,\Omega$$

$${p}_{g,0}=1.85\,\mathrm{ MPa in }\,\Omega$$

$${\sigma }_{xx,0}={\sigma }_{yy,0}=-4.23\,\mathrm{ MPa in }\,\Omega$$

$${\sigma }_{zz,0}=-4.73\,\mathrm{ MPa in }\,\Omega .$$

In the second model, swelling pressure, a plasticity model, and a deformation-dependent permeability model were added to the base test. To account for swelling pressure in the bentonite, a linear swelling model proposed by Rutqvist et al. (2011) is employed in the model that can be expressed as follows:

$$\Delta {{\varvec{\upsigma}}}_{\mathrm{sw}}={{\varvec{\upsigma}}}_{\mathrm{sw},\mathrm{max}}\Delta {S}_{\mathrm{w}}\mathbf{I}, \forall {S}_{\mathrm{w}}\in \left[{S}_{\mathrm{res}},{ S}_{\mathrm{max}}\right].$$

(31)

The maximum swelling pressure, due to hydration under confined conditions, increases in an non-linear form with the increase of the dry density. An empirical relation for MX-80 bentonite was established by Seiphoori (2015) as follows:

$${{\varvec{\sigma}}}_{\mathrm{sw},\mathrm{max}}=0.01{e}^{3.85{\rho }_{\mathrm{d}}}.$$

(32)

The measured dry density of the bentonite blocks before they were deployed can be found in Cuss et al. (2010). Applying the dry density of the bentonite blocks R₁, R₂, and R₃, maximum swelling pressures of ${\sigma }_{\mathrm{sw},\mathrm{R}1}=6.1 \mathrm{MPa}$, ${\sigma }_{\mathrm{sw},\mathrm{R}2}=6.3 \mathrm{MPa}$, and ${\sigma }_{\mathrm{sw},\mathrm{R}3}=6.4 \mathrm{MPa}$ are calculated.

To create the best possible match with the in-situ conditions before the gas injection test, the hydration of the bentonite blocks is simulated. This is achieved using a pre-phase calculation with an initial capillary pressure of 3 MPa. During a period of 810 days, the hydration is simulated with boundary conditions on each side reducing capillary pressure continuously from 3 MPa to 0.4 MPa. The plasticity model is the Drucker–Prager model (Eq. 23), the coupling between mechanics and permeability is achieved by the strain-dependent permeability model (Eq. 22), both of which are used in the benchmark test. Other HM coupling processes are the effective stress law and the swelling model.

The third model uses the same constitutive laws as second model, with the addition of heterogeneous distributions of gas entry pressure and Young's modulus. Since the data for distributions of elastic parameters in bentonites are relatively poor, as shown in the section “Young’s modulus variability”, only the gas entry pressure is directly linked to measured data. Since it can be assumed that both the gas entry pressure and the Young’s modulus increase with increasing dry density, the Young’s modulus is directly coupled to the distribution of the gas entry pressure. As shown in the comparative sensitivity analysis (“Benchmark 3: Coupling between HM processes with heterogeneous distributions”), the Young's modulus also has a smaller influence on the gas flow and has only an auxiliary character compared to the gas entry pressure.

The pore size distribution of MX-80 bentonite from the LASGIT experiment can be estimated using the measurements of Seiphoori (2015). For this purpose, the pore size distribution of the compacted and subsequently fully saturated bentonite is used from Fig. 1. Applying Eq. (5) on the pore size distribution, a spatial distribution for the gas entry pressure can be generated (Fig. 15). Since the mean Young's modulus of MX-80 bentonite is about 29 times the mean gas entry pressure (Seiphoori 2015; Tamayo-Mas et al. 2021), all heterogeneous values of the gas entry pressure are increased by a factor of 29 to obtain a linear correlated, stochastic distribution of the Young's modulus. Both distributions are applied to the bentonite materials in the domain.

Fig. 15

Gas entry pressure distribution

Results

Comparison between model configurations

The comparison between the applied model configurations can ideally be conducted using the gas pressure in the injection filter. The gas inflow rate is identical in all model configurations and the gas pressure shows how much gas from the filter actually enters the bentonite buffer, if compared to the calculated gas pressure without outflow (Fig. 16). The three numerically calculated gas pressures in the injection filter are shown for the configurations described in Table 6.

Fig. 16

Evolution of the gas pressure in the injection filter and the gas flow rate out of the filter and into the alumina of different model configurations, with zoom of the breakthrough event

Table 6 Model variations and constitutive equations

The comparison between the three model configurations shows that only the model with spatially heterogeneously distributed material properties is able to simulate a breakthrough event at the time it is measured in LASGIT. A sudden gas entry into the system is simulated, indicated by the drop of gas pressure at 3205 days, representing a generation of micro-channels in the buffer system. In comparison, a breakthrough event in the homogeneous model occurs only at much higher gas pressures in the injector system. No gas leakage is predicted in the base test.

The fact that the domain geometry is only a quarter of the actual LASGIT experiment has computational advantages. The processes involved are the same in a quarter of the domain as in a round domain. However, if the same gas flow rate is applied to the injection filter, the volume of gas entering only one-quarter of the LASGIT is most likely smaller than in the experiment. This effect can be seen in Fig. 16. The gas pressure in the heterogeneous simulation increases to 7 MPa after the initial breakthrough. In the LASGIT experiment, however, the gas pressure in the filter decreases after its peak of about 6.1 MPa. The differences in the slope to the calculated gas pressure without outflow show that there is still a gas outflow, but it is smaller than in the experimental measurements. In the homogeneous case, the pressure peak in the filter is 7.5 MPa and a larger breakthrough takes place at this pressure.

Fully coupled H²M model with heterogeneity

The relevant changes in measured stress and pore pressure occur in the period t = 3200–3210 d, during the main efflux event. In the following, the focus of the comparison is on this period.

A comparison between the recorded stresses and pore pressures in the LASGIT test and the results of the calculation, recorded at the same locations, are shown in Fig. 17. The gas pressure peak in the filter leads to stress and pore pressure changes in the system, but not uniformly. While the two measured pressures in UR904 and UR909 show no significant changes, the pressure in UR905 shows a similar trend to the modeled one, indicating a strong channeling effect in the system that could not be simulated with a conventional continuum model.

Fig. 17

Comparison between stress and pore pressure measurements of LASGIT and numerical results of the heterogeneous model during the breakthrough event (3200–3210 days). The locations of the points corresponds to those of the sensors of LASGIT

Due to the choice to run the simulation in one-quarter of the actual LASGIT test and the observations by Cuss et al. (2010) that the flow paths have expanded near the copper cylinder, the effective magnitude of the results has been reduced to one-quarter. The comparison illustrates the spatial variability of measured stresses and pressures, which are presumably caused by localized preferential gas paths. The moment of the stress or pressure change can be well reproduced by the simulation. However, the changes in stress are on average overestimated in the numerical calculation. The same applies to the pore pressure, although the difference does not appear to be so pronounced. One reason for these differences could be the approach of the continuum model, which cannot represent the localized gas flow process of the dilatancy-controlled gas flow in all aspects.

Since, as demonstrated in Cuss et al. (2014), the strongest effect of the gas flow is on the opposite side of LASGIT, a comparison with all sensors in the bentonite blocks R1, R2, and R3 is shown in the following (Fig. 18). In the presented comparison, the curves are normalized to their values at t = 2950 d. In the period of the breakthrough (3200–3210 d), an increase in stress similar to the numerical calculation can be observed in the sensor PR 906. The pore pressure of the sensor UR908 shows a similar increase in pressure during the breakthrough as calculated in the numerical simulation. This suggests that the overall magnitude of the numerical simulation might be representing the effects of the breakthrough event observed in the LASGIT experiment. Figure 19 shows how the gas phase flows in the plane between the bentonite blocks, which was also suspected by Cuss et al. (2014). The heterogeneously distributed material properties have only a subordinate role after the first gas entry into the buffer.

Fig. 18

Comparison between measured stress/pore pressure and numerical calculated results (H²M). Values are normalized to their value at t = 2950 d to increase the comparability of the breakthrough effects

Fig. 19

Gas velocity magnitude at t = 3205 d. The model is bisected in the middle along the z-axis

Stress path in the meridional stress space $\sqrt{{J}_{2}}$ and I₁ (mechanical invariants)

Four points are selected for an analysis of the stress paths during the simulation (Fig. 20). The points lie on a plane with the same height (z = 1.016 m). The plane is located between two pre-compacted bentonite blocks (R2 and R3). The stress paths are shown in the meridional plane and follow three phases:

• (1) The initial condition of the domain is defined with zero stress. Thereafter, the hydration of the model begins and the swelling pressure increases the compressive stress.

• (2) In the fully saturated state, the points are under maximum compressive stress.

• (3) The increase of the pore pressure reduces the first invariant of stress. The stress paths cross the yield surface at the tension cut-off line. As a result, a Mode I (tensile) failure occurs and the plasticity increases.

Fig. 20

Stress paths in the meridional stress space of four points located between two pre-compacted bentonite blocks (z = 1.017 m)

Discussion and conclusion

The application of the pore size-related heterogeneity for the gas entry pressure and the Young’s modulus in a model of the LASGIT experiment shows that, compared to the model with homogeneous material properties, a high level of agreement with the measured data can be achieved with regard to the gas breakthrough. However, this agreement cannot be maintained after the initial gas breakthrough and large differences occur between numerically calculated and measured gas pressure in the injection filter FL903. This may be due to the stochastic distribution of the gas entry pressure, which is only a possible approximation for modeling the microstructure in the bentonite due to the following limitations:

Young–Laplace equation: The Young–Laplace equation [Eq. (4)] characterizes an idealized pore structure shaped as a bundle of not-connected capillary tubes that does not reproduce the complex structure of a bentonite.

Imprecise pore spaces: The MIP is limited to the accessible porosity. Enclosed, constricted, and non-detected porosity is not included in the pore space distribution.

Besides the limitations of the approach, there are also uncertainties regarding the comparison between numerical results and measured values due to typical properties of an in-situ experiment. As already described in the evaluation of the measurements by Cuss et al. (2014), the flow is significantly influenced by the structure of LASGIT. The technical voids and engineered boundaries provide areas in which preferential pathways can form more easily than in the pre-compacted bentonite. The very specific properties of LASGIT are difficult to transfer into the numerical model; therefore, the pore-related heterogeneity is in this example of lower significance.

The sensitivity tests show that pore-size-related heterogeneity can be used for mechanical deformation simulation and gas transport in bentonite. When comparing the effects of several heterogeneous distributions on coupled processes, strong differences between the effects of the variance of the individual material properties can be seen. For example, the effect of the gas entry pressure on the gas flow rate is larger than that of Young's modulus (in combination with a strain-dependent permeability method).

In summary, our results show that the application of heterogeneous material properties can be used for the simulation of gas flow in low-permeable materials, characterized by strongly localized gas flow through preferential pathways. The following characteristics should be emphasized:

• Pore-size-related distributions can be used for coupled HM models and agree well with analytical solutions.

• At low mesh densities, there is a high variance when using heterogeneous distributions. This variance decreases with increasing mesh density. With a higher variance of the input value, the mesh density should also increase.

• Following the analysis of coupled processes, it is assumed that the heterogeneous distribution of the gas entry pressure has a greater influence on the flow process than the Young's modulus.

• The microscale heterogeneity and micromechanics in bentonite have a significant effect on local gas flow. However, in in-situ experiments such as LASGIT, artificially created gaps and boundaries can have a stronger effect on localized gas flow than a macroscopically homogeneous bentonite.

Appendix

See Table 7.

Table 7 Location of sensors in bentonite blocks R1, R2, and R3