Introduction

Creep is the time-dependent strain due to a sustained constant load. Creep behavior in geomaterials can affect the long-term stability of foundation, excavation, and slope. Karimpour and Lade (2013) studied the creep behavior of sand and suggested that the phenomenon is a time-dependent static fatigue caused by particle breakage and reorientation. On the other hand, creep in rock might be caused by its formation and the propagation of fractures, which could contribute to the damage and strength degradation of the rock leading to a creep failure. Creep behavior is similar to the fatigue behavior by cyclic loading (Chen et al. 2011). Under a constant load, the creep behavior can be characterized by three stages. In the primary stage, the strain increases with a decelerating rate. In the secondary stage, the strain increases with a constant rate, also known as the steady-state creep strain rate. In the tertiary stage, the strain increases with an accelerating rate, which ultimately leads to the failure of the material. Many models have been proposed to describe the creep behavior and its failure time. Typically, assumptions are made with regard to the creep failure stress threshold or creep failure strain threshold, which are related to the residual strength or the strain corresponding to the peak strength (Bi et al. 2019).

Cyclic and fatigue behaviors of geomaterials have been evaluated and considered in engineering applications. Geomaterials could creep when subjected to multiple freeze–thaw cycles; for example, Güllü and Khudir (2014) found that the unconfined compressive strength and the resilient modulus of a low-plasticity fine-grained soil decreased with increasing number of freeze–thaw cycles at a constant water content. The damage propagation of surrounding rock from a cold-region tunnel induced by the freeze–thaw cycle conditions was studied by Zhang et al. (2004), and they found that damage was accelerated with crack growth due to the water migration during freeze–thaw cycles. The freeze–thaw cycles might result in the variation of the mean stress. Underground storage facilities for crude oil, gas, and other liquids can experience fatigue failure when subjected to successive emptying and filling loading cycles during their operations (Roberts et al. 2015; Wang et al. 2015). To study slope movement due to fluctuations of reservoir water level, Chen et al. (2018) conducted triaxial tests with cyclic changes in pore water pressure and constant deviator stress. Under such stress path, an accumulation of creep strain in silty clay was observed.

Factors that influence the creep behavior of a material include compositions of the material, time, stress state, and temperature. When subjected to the same elapsed time, the higher the shear stress or deviator stress, the greater are the creep strain and steady-state creep strain rate (Zhang et al. 2016a; Zhao et al. 2017; Jia et al. 2018a; Berest et al. 2019; Herrmann et al. 2020). The effects of mean stress on the creep strain and steady-state creep strain rate are, however, less conclusive (Zhang et al. 2016a; Liu et al. 2018; Herrmann et al. 2020). Some researchers defined a stress ratio to examine the cyclic creep behavior of carbon fiber reinforced polymer and steel (Petermann and Schulte 2002; Kim et al. 2017). Zhang et al. (2016b) studied the discontinuities in rock and found that the long-term direct shear strength is approximately 60–70% of its peak strength. Park et al. (2019) suggested that the contractive or dilative behavior of a silty sand during creep is related to the initial porosity and mean effective stress.

Evaluation of creep in geomaterials typically involves uniaxial compression test, triaxial test, or direct shear test to determine time-dependent strain subjected to constant deviator stress or shear stress (Nedjar and Le Roy 2013; Aydan et al. 2014; Rybacki et al. 2017). The time needed to reach creep failure is long, and multiple years may be needed to show meaningful results; for example, a creep test that lasted 20 years for tuff under uniaxial compression has been reported by Hashiba and Fukui (2020). In recent years, some creep tests were performed by increasing the deviator stress or shear stress stepwise over time (Zhang et al. 2011; Yang et al. 2014; Zhang et al. 2016b; Jia et al. 2018b; Yu et al. 2019). Creep tests by means of cyclic loadings have also been investigated (Mehrara and Khodaii 2011; Tang et al. 2011; Xiao et al. 2018). A common theme in these recent creep tests is that the applied load is not constant. The main advantage of these cyclic creep tests is that the testing time is greatly reduced.

Sawicki et al. (2014) performed triaxial tests with constant deviator stress and applied cyclic pore water pressure; test results indicated an increase in deviator strain in response to the cyclic changes of effective mean stress. Based on the findings of Sawicki et al., cyclic stress-induced creep test (hereafter termed “cyclic creep test”) was adopted in this study in addition to the constant load creep test (hereafter termed “conventional creep test”). Note that the elapsed time required to reveal creep behavior of a soft rock is relatively short as compared to a hard rock. Due to the shorter testing time, most creep tests found in the literature were performed on soft rocks (Fabre and Pellet 2006; Nedjar and Le Roy 2013; Wu et al. 2016). To evaluate the effects of stress state on the creep behavior, a cemented sand, resembling a typical soft rock, was artificially fabricated in the present study to achieve consistent test specimens and to avoid variability often encountered in natural rock specimens.

In the present study, the specimen of the conventional creep test was subjected to constant mean stress and deviator stress. In the cyclic creep test, after reaching an assigned stress state, cyclic confining pressure was applied. When the deviator stress is kept constant, cyclic changes of confining pressure represent cyclic changes of mean stress. The stress state in this study was characterized by a mean stress and a stress ratio at the beginning of the creep test. Both the cyclic creep and conventional creep tests were first performed to compare the creep behavior of the cemented sand. Second, in some creep tests, additional triaxial compression was applied after reaching some creep strain to obtain the post-creep strength so as to study the effect of creep strain on the strength. Also, in some of the cyclic creep tests, an equal number of cyclic loads was applied to study the effect of stress state on the creep axial strain and the steady-state creep strain rate. In addition, the effect of stress state on the time to reach creep failure was evaluated. Through a systematic evaluation, mean stress and stress ratio were identified as key factors that influence the creep behavior.

Materials and methods

Specimen preparation and test equipment

To achieve consistent specimens for testing, the cemented sand was produced with reference to Indraratna (1990) for preparing synthetic soft sedimentary rocks. The constituents of the cemented sand specimen are silica sand, gypsum cement, and water. The procedure enables the production of a homogeneous and isotropic specimen with reduced variability between batches. A mold was used to form the cylindrical specimen with a diameter of 50 mm and a height of 100 mm. The cemented sand was prepared by mixing the silica sand, gypsum cement, and water by weight in proportions of 73, 10, and 17 percent, respectively. The ASTM C778 20–30 standard sand (a poorly graded sand) was used, which is predominately a silica sand characterized by 97 percent of particles with diameters between 0.6 and 0.85 mm. The chemical composition of gypsum cement is calcium sulfate hemihydrate (i.e., CaSO4·\(\frac{1}{2}\) H2O). The specimens were cured for 14 days at a constant temperature of 25 °C and a relative humidity of 65 percent. At the end of curing period, the uniaxial compressive strength of the cemented sand was approximately 1.2 MPa. The cemented sand is classified as a soft rock according to the International Society for Rock Mechanics (ISRM) Classification, which requires a uniaxial compressive strength ranging from 0.25 to 25 MPa. The physical properties of the cemented sand are summarized in Table 1.

Table 1 Properties of cemented sand
Full size table

The tests were performed using the GDS Triaxial Automated System, which consists of a load frame, triaxial cell, two pressure/volume controllers, load cell, axial displacement transducer, 8-channel serial pad, and the GDSLAB software (GDS Instrument 2017). The test equipment is capable of providing cyclic changes of mean stress while maintaining a constant deviator stress for a prolonged period of time. For baseline, the cemented sand was subjected to triaxial compression at different confining pressures (\({\sigma }_{3}\)) of 100, 200, 300, and 500 kPa, and the resulting peak deviator stresses were 1557, 1701, 1812, and 2078 kPa, respectively. Unlike the conventional triaxial test, cemented sand specimens were not saturated and had negligible water content. The pore water valve connected to the specimen was closed to prevent transmission of water from the pressure/volume controller during the test. The baseline compression tests were performed with a constant strain rate of 0.15 mm/min, and the cemented sand exhibited strain softening behaviors.

Test program

Stress path of a triaxial test can be represented by the mean stress, \(p=({\sigma }_{1}+2{\sigma }_{3})/3\), and the deviator stress, \(q=({\sigma }_{1}-{\sigma }_{3})\), where \({\sigma }_{1}\) and \({\sigma }_{3}\) are major and minor principal stresses, respectively. For the cyclic creep test, the specimen, after isotropic compression, was first subjected to the prescribed mean stress and deviator stress without failing the specimen. Subsequently, the deviator stress was held constant while the cyclic confining pressure was applied. As a result, the mean stress changed cyclically due to cyclic changes in confining pressure, and the mean stress increment is equal to the confining pressure increment. Figure 1 shows the application of sinusoidal cyclic mean stress with an amplitude of 100 kPa and a period of 10 min. The creep of the cemented sand was induced by the application of cyclic mean stress. In some tests, the completion of the cyclic creep test was followed by a post-creep triaxial compression, where the deviator stress was increased until failure to obtain the post-creep shear strength parameters (Fig. 2). Note that triaxial compression was conducted under strain control, whereas cyclic creep and conventional creep were conducted under stress control.

Fig. 1
figure 1

Sinusoidal cyclic mean stress \(p\) and constant (or controlled) deviator stress \(q\) applied to a cyclic creep test

Full size image
Fig. 2
figure 2

Triaxial compression test following the termination of creep test

Full size image

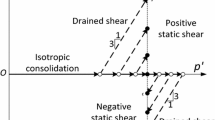
The cemented sand has a measurable cohesion (i.e., peak cohesion \({C}_{p}\) = 473 kPa). As shown in Fig. 3, the peak strength envelope has an intercept on the abscissa, \({T}_{p}\), which for the cemented sand, was found to be 1110 kPa in the \(q-p\) stress space. The stress state can be described by the mean stress and the stress ratio. In this study, the stress ratio is defined as \(q/{p}^{*}\), where \({p}^{*}={T}_{p}+p\). The higher the stress ratio, the closer is the stress state to the peak strength envelope. The specific stress paths evaluated in this study are presented in Fig. 4. The five main stress ratios selected for this study were 0.1, 0.31, 0.46, 0.64, and 0.82, which are represented by the inclined dashed lines in Fig. 4. Note that the tests along the same inclined dashed line have a constant stress ratio but with different mean stresses. In addition, the tests can be categorized by the mean stress \(p\) as depicted by the vertical dotted lines in Fig. 4; the three main mean stresses selected were 348, 554, and 687 kPa. Along a vertical dashed line, the mean stress is constant while the stress ratio varies. The two sets of curves (i.e., inclined and vertical dashed lines) devised in the test program enabled a systematic evaluation of creep as functions of the mean stress and stress ratio.

Fig. 3
figure 3

Definition of stress state and stress path for cyclic creep test with \({\sigma }_{3}\) being isotropic confining pressure (Readers may refer to Bardet (1997) for the equation of the peak strength envelope)

Full size image
Fig. 4
figure 4

Stress ratio (\(q/{p}^{*}\)) and mean stress (\(p\)) assigned in cyclic creep tests

Full size image

Results and discussion

Experimental results

Table 2 summarizes the test program of cyclic creep test, in which the deviator stress was kept constant while the mean stress was varied cyclically. Table 3 summarizes the test program of conventional creep test, where both the deviator stress and mean stress were kept constant until creep failure occurred or when a prescribed creep strain was reached. The discussion of the experimental results is divided into four different parts. The comparison between the cyclic creep test and the conventional creep tests was first made to verify the applicability of cyclic creep test. The second part was to evaluate the effect of creep strain on the strength of the cemented sand. The third part pertained cyclic creep tests only, where the influence of mean stress and stress ratio on the creep behavior was evaluated; cyclic creep tests were subjected to the same number of loading cycles. The fourth part also pertained cyclic creep tests only, where the influence of mean stress and stress ratio on the number of cycles to reach creep failure was evaluated. Discussions of the four parts are presented in the following sections.

Table 2 Test program of cyclic creep test
Full size table
Table 3 Test program of conventional creep test
Full size table

Comparison between cyclic creep tests and conventional creep tests

For this comparison, the same stress ratio \(q/{p}^{*}\) = 0.82 with mean stresses of 554, 687, and 830 kPa was applied to both the cyclic creep tests (tests CIC1 to CIC3) and conventional creep tests (CC1 to CC3). The three stress states corresponded to the confining pressures of 100, 200, and 300 kPa. All tests were loaded to failure, in which the specimen could not sustain the prescribed load, and the apparatus ceased automatically. Figure 5 compares the axial creep strain with time for these tests. Under the same mean stress and stress ratio, the cyclic creep tests yielded less creep strain and less elapsed time until failure than the conventional creep tests.

Fig. 5
figure 5

Variation of axial strain with time for cyclic creep (CIC1 to CIC3) and conventional creep (CC1 to CC3) tests with the stress ratio \(q/{p}^{*}\) of 0.82 (The tests were terminated at failure)

Full size image

The variations of strain rate with time from the creep curves of CIC1 and CC1 (i.e., with mean stress of 554 kPa) are shown in Fig. 6. The variations of strain rate help delineate the three stages of creep response: in the primary stage, axial strain rate decreases with time; in the secondary stage, the strain rate is constant for some elapsed time; and in the tertiary stage, strain rate increases with time until creep failure. It can be seen that during the secondary stage, the strain rate in the cyclic creep test is higher than that in the conventional creep test. However, the conventional creep test shows an increasing strain rate more pronouncedly in the tertiary stage than the cyclic creep test.

Fig. 6
figure 6

Axial strain rate of cyclic creep test CIC1 and conventional creep test CC1 with stress ratio \(q/{p}^{*}\) = 0.82 and mean stress \(p\) = 554 kPa (I, II, and III represent the three stages of creep behavior)

Full size image

The time required to reach creep failure for the cyclic (CIC1 to CIC3) and conventional (CC1 to CC3) creep tests is compared in Fig. 7a. Given the same mean stress and stress ratio, the time required to reach creep failure in cyclic creep tests is less than the conventional creep tests. The axial strain for the two sets of tests is compared in Fig. 7b, which indicates that the failure strains from the cyclic creep tests are also lower than those of the conventional creep tests. Furthermore, the observed trends are consistent with the notion that, for the same geomaterial, a higher mean stress would result in a larger strain at failure. In the cyclic creep test, the specimen experienced momentary loss and gain in mean stress from the initial value; as a result, the specimen fatigued progressively and failed more rapidly at a smaller axial strain than the conventional creep test. Regardless, both tests show similar trends in creep responses.

Fig. 7
figure 7

Comparison between cyclic creep (CIC1 to CIC3) and conventional creep (CC1 to CC3) tests at the same stress ratio \(q/{p}^{*}\) of 0.82 a time to reach creep failure and b axial strain during creep

Full size image

Stress–strain curves of CIC1 and CC1 tests are plotted in Fig. 8 along with the companion triaxial compression test. The volumetric strain was estimated by measuring the volume change of water in the pressure/volume controller connected to the triaxial cell chamber. Under the applied load levels, water is considered as incompressible, and the reduction of water volume in the pressure/volume controller is equivalent to the increase of water volume in the triaxial cell chamber due to the contraction of the specimen. In the triaxial compression test, the cemented sand, which has a noticeable cohesion showed initial contraction followed by a dilation after reaching the peak strength. The dilative behavior, however, was not observed in both the cyclic creep and the conventional creep tests. Both the cyclic creep and conventional creep tests had an initial confining pressure of 100 kPa followed by an increase in deviator stress to 1360 kPa. Both tests showed additional contraction in the creep tests in comparison to the triaxial compression test. The volumetric strain at creep failure is similar between the two creep tests, but the failure plane from the cyclic creep test was more well-defined at a high stress ratio. Other cyclic creep tests with lower stress ratio also show additional contraction during the application of cyclic mean stress. Similar contractive behavior during creep tests has also been reported by Fu et al. (2018).

Fig. 8
figure 8

Stress–strain curves from triaxial compression, conventional creep (CC1), and cyclic creep (CIC1) tests with confining pressure \({\sigma }_{3}\) = 100 kPa (Positive volumetric strain denotes contraction)

Full size image

Influence of creep strain on strength

Figure 9a and b shows results of cyclic creep tests with stress ratios of 0.82 and 0.31, respectively. These tests had a confining pressure of 100 kPa. After reaching the prescribed stress state, different numbers of loading cycles were applied to each test (e.g., 50, 100, 150, and 300 cycles). The sinusoidal cyclic load had an amplitude of 100 kPa and a period of 10 min. The cyclic creep tests were terminated after the assigned numbers of loading cycles. Triaxial compression was then applied after the termination of cyclic creep test, and the specimen was loaded until failure to obtain the post-creep strength. Cyclic creep tests CIC5 to CIC7 are illustrated in Fig. 9a, while tests CIC8 to CIC11 are illustrated in Fig. 9b.

Fig. 9
figure 9

Post creep strengths from cyclic creep tests subjected to the same confining pressure \({\sigma }_{3}\) of 100 kPa with a stress ratio \(q/{p}^{*}\) = 0.82 (CIC5 to CIC7) and b stress ratio \(q/{p}^{*}\) = 0.31 (CIC8 to CIC11). (Arrows indicate completion of prescribed number of loading cycles; note curves of 100 and 150 cycles with \(q/{p}^{*}\) = 0.31 are similar)

Full size image

For comparison, the triaxial compression test with confining pressure of 100 kPa is also included in Fig. 9. As indicated in the figure, with 50 cycles of loading (CIC5 and CIC8), the post-creep strength is higher than the peak strength of the triaxial compression test. It was also observed that the post-creep strength decreases with increasing number of loading cycles.

Figure 10a and b shows the test results of conventional creep tests with stress ratios of 0.82 and 0.31, respectively. These tests have the same confining pressure and the same prescribed stress state as those in Fig. 9. However, to be comparable, the conventional creep test in Fig. 10 was terminated when its axial strain reached the termination strain observed in the companion cyclic induced creep test in Fig. 9; the termination strains are summarized in Table 3. Triaxial compression was then applied after the termination of the conventional creep test, and the specimen was loaded to failure to obtain the post-creep strength. Conventional creep tests CC4 to CC6 are illustrated in Fig. 10a, while tests CC7 to CC9 are illustrated in Fig. 10b. Note that in Fig. 10a, the test CC6 with a stress ratio of 0.82 and a termination strain of 0.01 was unable to reach a peak strength, which suggested that failure had already occurred in the specimen prior to the post-creep triaxial compression.

Fig. 10
figure 10

Post creep strengths from conventional creep tests subjected to the same confining pressure \({\sigma }_{3}\) = 100 kPa with a stress ratio \(q/{p}^{*}\) = 0.82 (CC4 to CC6) and b stress ratio \(q/{p}^{*}\) = 0.31 (CC7 to CC9). (Arrows indicate termination strains found in corresponding cyclic creep tests)

Full size image

Both the cyclic creep test and the conventional creep test show similar trends. When the creep strain is small, upon the subsequent post-creep triaxial compression, the post-creep strength is, in general, higher than the peak strength of the triaxial compression test, yet it decreases with increasing creep strain.

Influence of mean stress and stress ratio on creep behavior

After reaching the specified mean stresses and stress ratios, cyclic creep tests CIC1, CIC2, and CIC11 to CIC27 were subjected to 300 cycles of loading while maintaining the controlled deviator stress. The sinusoidal cyclic loading consisted of an amplitude of 100 kPa and a period of 10 min, which resulted in a duration of 50 h. Results of tests with 300 cycles of loading, along with their initial conditions, are summarized in Table 4. Figure 11 depicts results with stress ratios of 0.10, 0.31, 0.46, 0.51, 0.64, and 0.82. The results indicated that the creep axial strain increases with increasing mean stress; this trend is especially pronounced in tests having a stress ratio of 0.82 (Fig. 11a). The secondary creep stage was distinguished in all of these tests. The steady-state creep strain rate of each test is also reported in Table 4 and illustrated in Fig. 11b. It can be seen that the steady-state creep strain rate also increases with increasing mean stress. Large creep axial strain and high steady-state creep strain rate are associated with high mean stress, and these positive relationships might be attributed to the pore collapse within the cemented sand, which has a high porosity of 36.2 percent.

Table 4 Summary of mean stress and stress ratio for cyclic creep test with 300 loading cycles
Full size table
Fig. 11
figure 11

Variations of a axial strain and b steady-state axial strain rate with mean stress \(p\) for cyclic creep tests with 300 cycles of loading

Full size image

The creep axial strain and the steady-state creep strain rate versus stress ratio are shown graphically in Fig. 12a and b, respectively. Test results with mean stresses of 348, 554, and 687 kPa were selected for comparison. Under the same mean stress, the creep axial strain and the steady-state creep strain rate increase with increasing stress ratio.

Fig. 12
figure 12

Variations of a axial strain and b steady-state axial strain rate with stress ratio \(q/{p}^{*}\) for cyclic creep tests with 300 cycles of loading

Full size image

Influence of mean stress and stress ratio on the number of cycles to reach creep failure

The number of cycles required to reach creep failure in the cyclic creep test was evaluated for the cemented sand. Tests CIC1, CIC2, CIC3, and CIC4 have the same stress ratio of 0.82, and the respective mean stresses are 554, 687, 830, and 1103 kPa. Numbers of cycles to reach creep failure for the four tests are 156, 190, 415, and 845 cycles, which correspond to 26, 31.6, 69.1, and 140.8 h, respectively. The results indicated that the number of cycles causing creep failure increases with increasing mean stress, which is consistent with the notion that a geomaterial with higher mean stress can sustain larger strain at failure; hence, more cycles are needed to reach failure. Conversely, tests CIC1, CIC28, CIC29, and CIC30 have the same mean stress of 554 kPa but different stress ratios; the respective stress ratios are 0.82, 0.64, 0.59, and 0.46. Numbers of cycles to reach creep failure for tests CIC1, CIC28, CIC29, and CIC30 are 156, 196, 677, and 1254 cycles, which correspond to 26, 32.6, 112.8, and 209 h, respectively; this suggests that the number of cycles to reach creep failure decreases with increasing stress ratio. This is because a higher stress ratio represents a stress state that is closer to the failure envelope. The interrelationship regarding the number of cycles to reach creep failure is depicted in Fig. 13.

Fig. 13
figure 13

Effects of mean stress \(p\) and stress ratio \(q/{p}^{*}\) on the number of cycles needed to reach creep failure

Full size image

Discussion

Some of the experimental results can be compared with the data presented in the literature. In both the cyclic creep and conventional creep tests, the volume of the specimen would contract; contractions from creep tests are higher than those of the triaxial compression tests. When the creep strain is small, contraction causes an increase in stiffness and strength. As such, when the triaxial compression was applied after the termination of creep test, its post-creep strength would be higher than the peak strength of the triaxial compression test. This observation is in agreement with Mitchell and Soga (2005), where they also indicate that the compression after creep would increase a soil’s stiffness, and the strength could be higher, equal, or lower than the strength from the triaxial compression tests. Herrmann et al. (2020) studied creep behavior of shale and indicated that creep is due to deformation of weak minerals and the pore space reduction, and the microcrack growth occurs mostly during the secondary creep stage. In this study, the cemented sand has a high porosity of 36.2 percent and clearly underwent contraction during creep. When the creep strain is large, microcrack within the cemented sand is likely to have developed, which resulted in a lower post-creep strength than the peak strength from the triaxial compression test. It is perceived that the larger the strain, the more likely is the microcrack growth, and hence the lower the post-creep strength. Almost all of the tests in Fig. 14 showed a lower post-creep strength after 300 cycles of loading than the peak strength from the triaxial compression test. The two exceptions are tests CIC12 and CIC13, which had the same stress ratio of 0.82 and mean stresses of 830 kPa and 1103 kPa, respectively; these two tests were subjected to high stress ratio and mean stress. Nevertheless, it is believed that after numerous cycles of loading or at larger creep strain, lower post-creep strength than peak strength from the triaxial compression test will exhibit or even failure will occur.

Fig. 14
figure 14

Comparison between peak strength from triaxial compression test (without creep) and post-creep strength from cyclic creep test with 300 cycles of loading

Full size image

In this study, the stress state was represented by the mean stress \(p\) and stress ratio \(q/{p}^{*}=q/({T}_{p}+p)\), which is not the stress ratio \(q/p\) typically defined in soil mechanics (e.g., Wood 1990). For a material with significant cohesion, the stress ratio \(q/p\) is not appropriate to describe the approaching level of a stress state to failure; this is especially true when the mean stress \(p\) is small. As indicated by the cyclic creep test results, under the same mean stress, creep is more pronounced when the stress ratio \(q/{p}^{*}\) is high (Fig. 12). The trend was also observed in the literature (Zhang et al. 2016a; Zhao et al. 2017; Jia et al. 2018a; Berest et al. 2019; Herrmann et al. 2020), where shear stress or deviator stress is analogous to the stress ratio. In terms of the stress path, a higher stress ratio means that the stress state is closer to the failure envelope, and due to its close proximity to the failure envelope, creep behavior and creep failure are more likely to occur. In addition, under the same stress ratio \(q/{p}^{*}\), the higher the mean stress, the larger is the creep strain (Fig. 11). These observed behaviors could be attributed to the high porosity of the cemented sand; higher mean stress would result in greater pore space reduction, which in turn causes the increase in creep strain and the creep strain rate. On the other hand, a higher mean stress would result in a larger strain at failure, which in turn would increase the number of cycles to reach creep failure (Fig. 13). Liu et al. (2018) studied a claystone with porosity between 14 and 20 percent and obtained a similar trend that having the same deviator stress, the higher the confining pressure, the higher are the creep strain rate and creep strain. Studies conducted by Zhang et al. (2016a) and Herrmann et al. (2020), however, showed results that are somewhat contrary to the results presented herein. The materials used by Zhang et al. and Herrmann et al. were a cataclastic rock with porosity in the range of 13–20% and a shale with porosity in the range of 1–12%, respectively. The inconsistency with the present study might be due to the low porosities of the two rock materials, where the pore space reduction is not significant. Another reason for the inconsistency might be that when the deviator stress is the same, a higher mean stress would result in a lower stress ratio, which in turn makes the creep behavior less conspicuous.

The mean stress evaluated in the test program is considered as a total mean stress, which is also equivalent to an effective mean stress, since the pore water pressure within the test specimens is zero. The stress paths and stress states evaluated in this study are similar to those of an underground geomaterial that is subjected to cyclic fluctuations of groundwater table or pore water pressure (Chang and Huang 2015; Harley et al. 2016; Chen et al. 2018; Santos et al. 2020). Ground subsidence has been being a serious problem in southwestern Taiwan. Even though pumping of groundwater has been prohibited by the government for years, ground subsidence persists, and the exact mechanism remains unknown. The groundwater fluctuates seasonally in the area, and the difference in groundwater level can exceed 10 m. Fluctuations of the groundwater may impose cyclic variation of effective mean stress with a constant deviator stress on the geomaterial under the groundwater table. Experimental results from the present study show that without changes in the deviator stress, cyclic effective mean stress alone can induce contraction of the cemented sand. Inferring from the experimental results, the cyclic fluctuation of the groundwater table could contribute to one of the reasons causing ground subsidence of a soft porous geomaterial.

Conclusion

A cemented sand resembling soft rocks was produced artificially for the purpose of creating laboratory specimens with consistent material properties. Test programs were developed to evaluate creep behavior of the cemented sand when subjected to different stress states, which was characterized by the mean stress and the stress ratio in this study. Experiments conducted include the cyclic stress-induced creep test (or simply the cyclic creep test) and the conventional creep test. In the cyclic creep test, after reaching the prescribed mean stress and stress ratio, the deviator stress was kept constant while cyclic mean stress was applied. The advantage of the cyclic creep test over the conventional creep test is that the time required to reach creep failure is greatly reduced. The saving in time from cyclic creep test in turn allowed a more elaborated evaluation of the creep behavior subjected to various stress states. In addition, since the pore water pressure within the test specimens is considered zero, the total mean stress is equal to the effective mean stress. The cyclic creep tests conducted in this study reflect an effective stress path of an underground geomaterial subjected to cyclic fluctuations of groundwater table. The experimental results imply that for a soft porous geomaterial, cyclic fluctuations of groundwater table may induce ground subsidence or lead to a slope failure if the stress ratio is high. Conclusions drawn from this study are listed as follows:

  1. 1.

    In comparison to the conventional creep test, the cyclic creep test exhibits smaller creep strain at failure and is associated with a well-defined failure surface at a high stress ratio.

  2. 2.

    The triaxial compression applied after cyclic creep and conventional creep shows that the post-creep strength depends on the creep strain. As the creep strain becomes large enough, the larger the creep strain accumulates, the lower is the post-creep strength.

  3. 3.

    When subjected to the same number of cyclic loading (i.e., 300 cycles), under the same stress ratio, it was observed that both the creep axial strain and the steady-state creep strain rate increase with increasing mean stress due to pore space reduction of the high porosity cemented sand.

  4. 4.

    When subjected to the same number of cyclic loading (i.e., 300 cycles), under the same mean stress, it was observed that both the creep axial strain and the steady-state creep strain rate increase with increasing stress ratio due to the proximity of the stress state to the failure envelope.

  5. 5.

    Under the same stress ratio, the higher the mean stress, the more loading cycles are needed to reach creep failure. This reflects that the cemented sand with higher mean stress can sustain larger strain at failure. Conversely, under the same mean stress, the higher the stress ratio, the less loading cycles are needed to reach creep failure. A higher stress ratio represents a stress state that is closer to the failure envelope.